离散系统的状态空间描述状态方程

格式：ppt
大小：777.50 KB
文档页数：2

下载文档原格式

线性离散系统状态方程的解

Z变换法(2/7)
在Z反变换中对标量函数存在下述公式和性质:
Z 1 1 /(1 az 1 ) a k Z {W1 ( z )W2 ( z )} w1 (k i ) w2 (i )
1 i 0 k
Βιβλιοθήκη 其中W1(z)和W2(z)分别为w1(k)和w2(k)的Z变换。将上述公式推广到向量函数和矩阵函数,则可得
离散卷积
Z变换法(3/7)—例3-14
因此,离散系统的状态方程的解为:
x(k ) G k x(0) G k j 1Hu( j )
j 0
k 1
该表达式与前面递推法求解结果一致。例已知某系统的状态方程和初始状态分别为 1 0 1 1 x(k 1) x( k ) u ( k ) x(0) 0.16 1 1 1
( k 1 , k0 ) G ( k ) ( k , k 0 ) ( k0 , k0 ) I
其解为
(k , k0 ) G(k 1)G(k 2)...G(k0 ) , k k0
线性时变离散系统状态方程的解(3/6)
与线性定常离散系统类似,线性时变离散系统的状态求解公式可用迭代法证明。对线性时变离散系统的状态方程，依次令k= k0, k0+1, k0+2, …,从而有
2. 引入状态转移矩阵概念和表示之后,线性连续系统和线性离散系统的状态方程的求解公式在形式上一致,都由零输入响应和零状态响应叠加组成, 只是相应的零状态响应在形式上略有不同,一为求积分(卷积),一为求和(离散卷积),但本质是一致的。 3. 在由输入所引起的状态响应中,第k个时刻的状态只取决于此采样时刻以前的输入采样值,而与该时刻的输入采样值u(k)无关。

自动控制原理状态空间法

自动控制原理状态空间法
目录
• 引言 • 状态空间法基础 • 线性系统的状态空间表示 • 状态反馈与极点配置 • 最优控制理论 • 离散系Biblioteka 的状态空间表示01引言
状态空间法的定义
状态空间法是一种基于状态变量描述线性时不变系统的方法，通过建立系统的状态方程和输出方程来描述系统的动态行为。
状态变量是能够完全描述系统内部状态的变量，可以是系统的物理量或抽象的数学变量。
最优控制问题
在满足一定约束条件下，寻找一个控制输入，使得被控系统的某个性能指标达到最优。
性能指标
通常为系统状态或输出函数的积分，如时间加权或能量加权等。
约束条件
包括系统动态方程、初始状态、控制输入和终端状态等。
线性二次调节器问题
线性二次调节器问题是最优控制问题的一个特例，其性能指标为系统状态向量的二次范数。
THANKS
状态方程描述了系统内部状态变量之间的动态关系，而输出方程则描述了系统输出与状态变量之间的关系。
状态空间法的重要性
1
状态空间法提供了系统分析和设计的统一框架，可以用于线性时不变系统的各种分析和设计问题。
2
通过状态空间法，可以方便地实现系统的状态反馈控制、最优控制、鲁棒控制等控制策略。
3
状态空间法具有直观性和易于实现的特点，能够直接反映系统的动态行为，便于理解和分析。
02
状态空间法基础
状态与状态变量
状态
系统在某一时刻的状态是由系统的所有内部变量共同决定的。
状态变量
描述系统状态的变量，通常选择系统的输入、输出和内部变量作为状态变量。
状态方程的建立
根据系统的物理或数学模型，通过适当的方法建立状态方程。

离散系统的状态空间表达式

1.7 离散系统的状态空间表达式
（1）连续系统：用微分方程来表示，采用拉普拉斯变换传递函数进行分析。
离散系统：用差分方程来描述，用Z变换脉冲传递函数进行分析。
因此，离散系统的状态空间表达式可通过差分方程或脉冲传递函数。
（2）离散系统的信号采用数字形式，输入和输出都是脉冲序列或数字序列。计算机控制系统属离散系统。
试写出其状态方程和输出方程。
解：
x1 (k 1) 0
1
0 x1(k) 0
x2
(k
1)
0
0
1
x
2
(k
)
0
u(k)
x3 (k 1) 6 5 2x3 (k) 1
x1(k)
y(k) x(k) 1
0
0x2 (k)
x3 (k )
例1.10 已知 y(k+3)+2y(k+2)+5y(k+1) +6y(k)=3u(k+2)+2u(k+1)+6u(k)
脉冲传递函数：
G(z)
Y (z) u(z)
bmzm bm1zm1 b1z b0 zn an1zn1 a1z a0
二、状态方程的建立
1、由差分方程
设T=1 输入仅有(kT)项，b0=1 整个方程可以写为： y(k+n)+an-1y（k+n-1)+……+a0y（k）=u（k）设x1(k)=y(k) x2(k)=y(k+1)=x1(k+1) x3(k)=y(k+2)=x2(k+1) ……
xn(k)=y(k+n-1)=xn-1(k+1) xn(k+1)=y(k+n)=-a0 x1(k)-a1 x2(k)-

现代控制原理2-3离散系统

−T −T −T
−T −T
−T
)
−T
z 2 − (1 + e −T ) z + e −T
)
0 x( k + 1) = −T -e
0 x ( k ) + u( k ) −T 1+ e 1 1
y( k ) = 1 − e −T − Te − T
T − 1 + e −T x( k )
x(k+1) = [I +TA]x(k) + TBu(k) G = I +TA H =TB
17
0 1 0 & 的近似离散化方程。例2-13 求 x = x + 1 u 的近似离散化方程。 0 −2
解： G = I + TA = 1 0 + 0 − T = 1 − T 0 1 0 − 2T 0 1 − 2T
x( k + 1) = G ( k ) x( k ) + H ( k )u( k ) y( k ) = C ( k ) x ( k ) + D( k )u( k )
2
2.结构图 2.结构图
3
3.差分方程和脉冲传递函数与离散状态空间表 3.差分方程和脉冲传递函数与离散状态空间表达式之间的转换在单变量离散系统中，在单变量离散系统中，数学模型分为差分方程和脉冲传递函数两类，和脉冲传递函数两类，它们与离散状态空间表达式之间的变换，和连续系统分析相类似。之间的变换，和连续系统分析相类似。离散差分方程连续 D.E
x1 ( k ) y ( k ) = [1 −4 ] + u( k ) x2 ( k )

离散系统的状态空间描述

x1(k)
y(k) 1
0
0
x2
(k
)
x3 (k )
4 离散状态方程求解
1. 迭代法
离散状态方程的通式 x(k 1) Fx(k) Gu(k)
已知k=0时系统状态x(0)以及 k 0 k 之间各个时刻的输入量 u(0),u(1), ,u(k)
得到现时刻k的状态
k 1
x(k) F k x(0) F ki1Gu(i) i0
x1(k x2 (k
1) 1)
h1u (k ) h2u(k )
xn (k) xn1(k 1) hn1u(k)
则可得到离散系统状态方程，且有：
式中
h0 b0 h1 b1 a1h0
hh32
b2 b3
a1h1 a1h2
a2h0 a2h1
a3h0
hn bn a1hn1 a2hn2
I
AT
I
AT 2
I
AT 3
I
AT L 1
I
AT L
计算项数L可由精度要求确定。
输入矩阵
G(T ) T eAt Bdt (eAT I ) A1B T AiT i B
0
i0 (i 1)!
T
I
AT 2
I
AT 3IAT L 1 NhomakorabeaI
AT L
B
2. 状态转移阵的求解——(2)拉普拉斯变换
可得方程（有不同方法）
x3(k 1) 0.9x3(k) e(k)
u(k) 0.01x3(k) 0.9e(k)
（2）广义被控对象部分：
被控对象连续状态方程
x1 x2
0 0
1 1
x1 x2

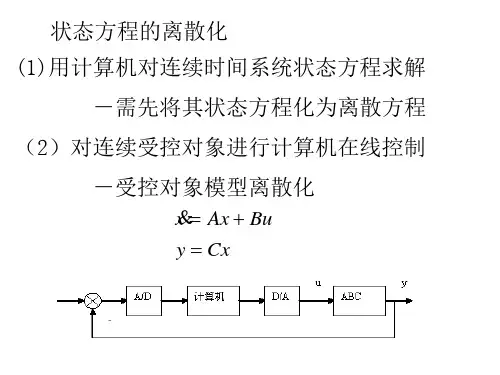
离散化的状态方程

=
T ∫0
I ⋅ B ⋅ dt = BT
结论：上式为近似计算方法例2.6 已知时变系统
0 5(1 − e −5t ) 5 5e −5t u ɺ x= x + −5t −5t 0 5(e − 1) 0 5(1 − e )
试将它离散化，并求出输入和初始条件分别为
0, x(0) = 0时，方程在采样时刻的近似解 u (t ) = 0 1
1 (3)H(T) = ∫ 0 0
T T 1/ 2(1−e )0 1 dt= ∫0 −2t e 1 0 −2t −2t
x 1 [( k + 1)T] x 1 (kT ) (4) = [G (T)] x (kT ) + [H (kT) U (kT)] x 2 [( k + 1)T] 2
归纳：将连续状态方程离散化步骤
1、求Φ(t )＝e = L [ SI − A] 2、G(T ) = Φ(T ) = Φ(t ) t = T T At 3、求H (T ) = ∫0 e Bdt 4、求x[(k + 1)T ] = G(T ) x(kT ) + H (T )u (kT )
At
−1
−1
例2.5已知控制对象满足 1 x + 0u，求其离散化方程 ɺ = 0 x 0 1 −2
系统离散状态方程（T＝0.1）可见T较小时， x1[(k + 1)T ] 0.9 0.1 x1(kT ) 0 = + r (kT ) 两种方法得 x2[(k + 1)T ] − 0.1 0.9 x2 (kT ) 0.1 状态空间表 x1(kT ) 达式近似相输出y(kT ) = [1 0] 等。 x2 (kT ) 离散方程求解可按2.3递推法或Z变换求解

状态空间表达式

（28）状态空间方程实现非唯一，书p28, 图1.16b求得其对应的传递函数为：（29）
为求得令式（29）与式（26）相等，通过对多项式系数的比较得：故得：（30）
也可将式(30)写成式(31)的形式，以便记忆。（31）
将上图a的每个积分器输出选作状念变最，如图所示，得这种结构下的状态空间表达式：
解：
→
→
u
y
－
＋
例：解：比例积分环节： → → u y ＋
例：
解：
综合惯性环节、积分环节模拟结构图得：
u
y
－
＋
u
y
解：选积分器的输出为状态变量得：
u
y
状态方程：
输出方程：
状态空间表达式
1.3.2 从系统的机理出发建立状态空间表达式
一般常见的控制系统，按其能量属性，可分为电气、机械、机电、气动液压、热力等系统。根据其物理规律，如基尔霍夫定律、牛顿定律、能量守恒定律等，即可建立系统的状态方程。当指定系统的输出时，很容易写出系统的输出方程。
同一系统，经非奇异变换后，得：
其特征方程为：
（44）
1.5.2 系统特征值的不变性及系统的不变量
1.系统特征值
式(43)与式(44)形式虽然不同，但实际是相等的，即系统的非奇异变换，其特征值是不变的。可以证明如下：
将特征方程写成多项式形式由于特征值全由特征多项式的系数唯一确定，而特征值经非奇异变换是不变的，那么这些系统也是不变的量。所以称特征多项式的系数为系统的不变量。
(3)有共轭复根时，以四阶系统其中有一对共轭复根为例，即此时
1.6 从状态空间表达式求传递函数阵
1.6.1 传递函数(阵)

现代控制理论知识点汇总

１．状态空间表达式n 阶DuCx y Bu Ax x+=+= 1:⨯r u 1:⨯m y n n A ⨯:r n B ⨯:n m C ⨯:rm D ⨯:A 称为系统矩阵，描述系统内部状态之间的联系；Ｂ为输入（或控制）矩阵，表示输入对每个状态变量的作用情况；C 输出矩阵，表示输出与每个状态变量间的组成关系，Ｄ直接传递矩阵，表示输入对输出的直接传递关系。

２．状态空间描述的特点①考虑了“输入－状态－输出”这一过程，它揭示了问题的本质，即输入引起了状态的变化，而状态决定了输出。

②状态方程和输出方程都是运动方程。

③状态变量个数等于系统包含的独立贮能元件的个数，n 阶系统有n 个状态变量可以选择。

④状态变量的选择不唯一。

⑤从便于控制系统的构成来说，把状态变量选为可测量或可观察的量更为合适。

⑥建立状态空间描述的步骤：a 选择状态变量；b 列写微分方程并化为状态变量的一阶微分方程组；c 将一阶微分方程组化为向量矩阵形式，即为状态空间描述。

⑦状态空间分析法是时域内的一种矩阵运算方法，特别适合于用计算机计算。

３．模拟结构图（积分器加法器比例器）已知状态空间描述，绘制模拟结构图的步骤：积分器的数目应等于状态变量数，将他们画在适当的位置，每个积分器的输出表示相应的某个状态变量，然后根据状态空间表达式画出相应的加法器和比例器，最后用箭头将这些元件连接起来。

４．状态空间表达式的建立1由系统框图建立状态空间表达式：a 将各个环节（放大、积分、惯性等）变成相应的模拟结构图；b 每个积分器的输出选作i x ，输入则为i x；c 由模拟图写出状态方程和输出方程。

2由系统的机理出发建立状态空间表达式：如电路系统。

通常选电容上的电压和电感上的电流作为状态变量。

利用KVL 和KCL 列微分方程，整理。

③由描述系统的输入输出动态方程式（微分方程）或传递函数，建立系统的状态空间表达式，即实现问题。

实现是非唯一的。

方法：微分方程→系统函数→模拟结构图→状态空间表达式。

离散系统的基本概念

06
CATALOGUE
离散系统的发展趋势与展望
离散系统的新理论与方法
离散系统的新理论
随着科技的不断发展，离散系统的新理论也在不断涌现。例如，离散概率论、离散控制论、离散信息论等，这些新理论为离散系统的发展提供了重要的理论支持。
离散系统的新方法
在实践中，人们不断探索新的方法来处理离散系统的问题。例如，离散数学、离散优化算法、离散模拟技术等，这些新方法为离散系统的研究提供了更有效的工具。
状态转移图的绘制方法
根据状态方程，通过计算或模拟得到状态变量的时间序列解，并绘制成图形。
状态转移图的应用
通过观察状态转移图，可以直观地了解系统动态行为和变化趋势。
04
CATALOGUE
离散系统的稳定性分析
线性离散系统的稳定性分析
定义
线性离散系统是指系统的数学模型可以表示为离散时间的线性方程组，如差分方程或离散时间状态方程。
状态方程
1
状态方程是描述离散时间动态系统状态变化的基本方程，通常表示为离散时间序列的递推关系。
2
状态方程通常由当前状态和输入量来预测下一个状态，是离散系统分析的重要基础。
3
状态方程的解法包括递归法和矩阵法等，其中递归法较为直观，而矩阵法适用于大规模系统。
转移矩阵
转移矩阵是描述离散系统状态转移关系的矩阵，其元素表示状态之间的转移概率。
社会科学领域
在社会学、经济学、管理学等领域中，离散系统也有着广泛的应用。例如，在经济学中，离散模型被用于描述经济活动中的离散事件；在社会学中，离散模型被用于描述社会结构和社会动态。
离散系统未来的研究方向
要点一
复杂离散系统的研究
随着科技的不断发展，复杂离散系统的研究已经成为一个重要的研究方向。例如，复杂网络、离散事件动态系统等，都是复杂离散系统的研究重点。

现代控制理论基础-第2章-控制系统的状态空间描述精选全文完整版

(2-18)
解之,得向量-矩阵形式的状态方程
(2-19)
输出方程为
(2-20)
(5) 列写状态空间表达式
将式(2-19)和式(2-20)合起来即为状态空间表达式,若令
则可得状态空间表达式的一般式,即
(2-21)
例2.2 系统如图
取状态变量:
得：
系统输出方程为：
写成矩阵形式的状态空间表达式为：
1.非线性系统
用状态空间表达式描述非线性系统的动态特性，其状态方程是一组一阶非线性微分方程，输出方程是一组非线性代数方程，即
(2-7)
2. 线性系统的状态空间描述
若向量方程中和的所有组成元都是变量和的线性函数，则称相应的系统为线性系统。而线性系统的状态空间描述可表示为如下形式：（2－8）式中，各个系数矩阵分别为（2－9）
4．线性定常系统的状态空间描述
式中的各个系数矩阵为常数矩阵
当系统的输出与输入无直接关系（即）时，称为惯性系统；相反，系统的输出与输入有直接关系（即）时，称为非惯性系统。大多数控制系统为惯性系统，所以，它们的动态方程为
（2－11）
1.系统的基本概念 2. 动态系统的两类数学描述 3. 状态的基本概念
2.2 状态空间模型
2.2.1状态空间的基本概念
1.系统的基本概念
■系统:是由相互制约的各个部分有机结合，且具有一定功能的整体。 ■静态系统:对于任意时刻t，系统的输出惟一地取决于同一时刻的输入，这类系统称为静态系统。静态系统亦称为无记忆系统。静态系统的输入、输出关系为代数方程。 ■动态系统:对任意时刻，系统的输出不仅与t时刻的输入有关，而且与t时刻以前的累积有关(这种累积在t0(t0<t)时刻以初值体现出来)，这类系统称为动态系统。由于t0时刻的初值含有过去运动的累积，故动态系统亦称为有记忆系统。动态系统的输入、输出关系为微分方程。

状态、状态变量、状态空间、状态方程和动态方程

系统输入U(t)以及时间t的关系的方程就称作系统的输出方程,
如式(2-2)所示。
其中,G=(g1,g2,…,gm ),G 是一个函数矢量。
第2章状态空间分析法
在现代控制理论中,用系统的状态方程和输出方程来描
述系统的动态行为,状态方程和输出方程合起来称作系统的
状态空间表达式或动态方程。
根据函数向量F 和G 的不同情况,一般控制系统可以分
取每个积分器的输出端信号为状态变量x1 和x2,积分器的输
入端即ሶ 1 和ሶ 2,从图可得系统状态方程:
第2章状态空间分析法
第2章状态空间分析法
例2-6 求如图2-10(a)所示系统的动态方程。
图2-10 方块图
第2章状态空间分析法
第2章状态空间分析法
第2章状态空间分析法
2.4 由系统的微分方程或传递函数求其动态方程
第2章状态空间分析法
第2章状态空间分析法
第2章状态空间分析法
例2-2-电路如图2-6所示。以ei 作为系统的控制输入u(t),
eo 作为系统输出y(t)。建立系统的动态方程。
图2-6 RLC 电路
第2章状态空间分析法
解该RLC 电路有两个独立的储能元件L 和C,我们可以
取电容C 两端电压和流过电感L 的电流作为系统的两个状态
性,因此会产生一定程度上的结构差异,这也会导致动态方程
差异的产生;从系统微分方程或传递函数出发的系统实现问
题,更是会导致迥然不同的系统内部结构的产生,因而也产生
了不同的动态方程。所以说系统动态方程是不唯一的。
第2章状态空间分析法
例如图2-11所示的传递函数的直接法实现,按照图上所
示各状态变量的取法,我们有式(2-24)所示动态方程。如果将

计算机控制系统---第三章

的z变换。
解：
另一种由F(s) 求取F(z) 的方法是留数计算方法。本书对此不予讨论
利用MATLAB软件中的符号语言工具箱进行F(s)部分分式展开
已知
，通过部分分式展开法求F(z) 。
MATLAB程序：
F=sym(′(s+2)/(s*(s+1)^2*(s+3))′)； %传递函数F(s)进行符号定义
即得到
3.4.4 干扰作用时闭环系统的输出
根据线性系统叠加定理，可分别计算指令信号和干扰信号作用下的输出响应。
G(z)
Z
1
esT s
G1(s)G2 (s)
R(s)单独作用时的系统输出[N(s)=0]
干扰单独作用时的系统输出[R(s)=0]
共同作用时的系统输出
图3-13 有干扰时的计算机控制系统
图3-10采样控制系统典型结构
一般系统输出z变换可按以下公式直接给出：
C(z)
前向通道所有独立环节z变换的乘积 1闭环回路中所有独立环节z变换的乘积
3.4.3 计算机控制系统的闭环脉冲传递函数
1. 数字部分的脉冲传递函数
控制算法，通常有以下两种形式：
差分方程
脉冲传递函数D(z)
(z变换法)
连续传递函数
2. 由脉冲传递函数求差分方程
z反变换
z反变换
3.4.1 环节串联连接的等效变换
1. 采样系统中连续部分的结构形式
并不是所有结构都能写出环节的脉冲传递函数
3.4.1 环节串联连接的等效变换
2. 串联环节的脉冲传递函数
3.4.1 环节串联连接的等效变换
3. 并联环节的脉冲传递函数
根据叠加定理有：

《自动控制原理》线性定常离散系统状态方程的建立及求解

向量－矩阵形式为
x1 (k + 1) 0 1 0 0 x1 (k) 0
x2 (k
+ 1)
0
0
1
0
x2 (k)
0
= 0 0 0 0 + u(k)
xn−1
(k
+
1)
0
0
0
1
x
n−1
(k
)
0
xn (k + 1) − a0 − a1 − a2 − an−1 xn (k) 1
量和输入量：ai ,bi (i = 0,1,2,, n且an = 1) 为表征系统特性的常系
数。考虑初始条件为零时的z变换关系有
[ y(k)] = Y (z), [ y(k + i)] = ziY (z)
对式(9—87)两端取z变换并加以整理可得
G(z)
=
Y (z) U (z)
=
bn z n + bn−1 z n−1 + + b1 z + b0 z n + an−1 z n−1 + + a1 z + a0
（9－95）
三、线性定常离散动态方程的解
求解离散动态方程的方法友递推法和z变换法，这里只介绍常
用的递推法，对z变换法感兴趣的读者可参阅有关书籍。下面以解
离散化状态方程为例来说明如何使用递推法求解。令式（9－93）
中的k = 0,1,, k −1可得到 T,2T,, kT 时刻的状态，即
k = 0 : x(1) = (T )x(0) + G(T )u(0)
=
bn
+
z n−1 n−1
+

第八章(3) 离散系统状态方程的求解

在用状态分析系统时, 在用状态分析系统时,求状态转移矩阵(k) 是关键步骤. 是关键步骤. 例 8.4-1 已知矩阵求其矩阵函数A 求其矩阵函数 k.
0 1 A= 2 1
矩阵A的特征方程为解矩阵的特征方程为
λ 1 = λ2 λ 2 = 0 q( λ ) = det( λI A) = det 2 1 λ 方程有两个相异的特征根
其全解 x(k) = xx (k) + x f (k)
(3)求系统的输出
y(k) = Cx(k) + Df (k) = C(k)x(0) + C(k 1)B* f (k) + Df (k)
代入, 将 (k)代入,得零输入响应
1 k 1k ( 2) 1 0 ( 2) yx (k) = C(k)x(0) = = 1 , k ≥ 0 1 1 1 ( )k + ( 1)k ( )k 4 4 2
零输入解的象函数零状态解的象函数
1
1
x(k) = (k)x(0) +(k 1)B* f (k)
于是, 于是,得状态转移矩阵 (k) = Ak = Z1{[zI A]1 z} 为了方便, 为了方便,定义
将它们代入, 将它们代入,得状态转移矩阵
1 1 k 1 0 1 k 1 k 2 1 k k (k) = A = ( ) + 2( ) + 4( 2) 4( 4) 1 4 0 1 2 4 1k 0 ( 2) = 1k 1k 1 k ( ) ( ) ( ) 4 4 2 0 1 4
i =0
k1
x(k) = (k)x(0) +(k 1)B* f (k)
x(k) = (k)x(0) + ∑(k 1 i )Bf (i)

simulink 离散状态空间方程

simulink 离散状态空间方程离散状态空间方程是描述离散时间系统的一种数学模型。

它利用状态变量和输入输出的关系来描述系统的行为。

离散状态空间方程的一般形式可以表示为：x(k + 1) = A · x(k) + B · u(k)y(k) = C · x(k) + D · u(k)其中，x(k)为系统的状态向量，表示系统在第k个时间步的状态；u(k)为系统的输入向量，表示系统在第k个时间步的输入；y(k)为系统的输出向量，表示系统在第k个时间步的输出；A、B、C、D为系统的参数矩阵。

对于离散状态空间方程，有以下几个重要的概念和特点：1.系统的状态：离散状态空间方程中的状态变量x(k)表示系统在某个时间步的内部状态。

它由系统的历史输入和状态转移方程决定。

2.系统的输入：离散状态空间方程中的输入向量u(k)表示系统在每个时间步的外部输入。

它是由外界对系统的作用而产生的，例如控制器的输出信号。

3.系统的输出：离散状态空间方程中的输出向量y(k)表示系统在每个时间步的输出信号。

它是系统的状态和输入的函数。

4.系统的参数：离散状态空间方程中的参数矩阵A、B、C、D决定了系统的特性。

参数矩阵A描述了状态转移的关系，参数矩阵B描述了输入对状态的影响，参数矩阵C描述了状态对输出的影响，参数矩阵D描述了输入对输出的影响。

离散状态空间方程的求解可以利用状态转移矩阵进行。

状态转移矩阵是用来表示系统状态在连续时间和离散时间之间的关系。

在连续时间系统中，状态转移矩阵由指数函数e^(A·t)来表示，在离散时间系统中，状态转移矩阵由矩阵幂A^k来表示。

求解离散状态空间方程的过程包括以下几个步骤：1.根据系统的参数矩阵A、B、C、D，构造系统的状态转移方程。

利用状态转移方程可以求解系统在每个时间步的状态。

2.根据系统的状态和输入，可以计算系统在每个时间步的输出。

利用参数矩阵C和D，可以得到系统的输出向量y(k)。

K3.05-离散系统状态方程和输出方程

c12 c22
cq2
c1n
c2n
cqn

x1(k) x2(k) xn(k)
d11 d21 dq1
d12 d22
d1p
d2
p
f1 f2
dq2
dqp
fp
Y(k)
C
X(k)
D
f (k)
Y (k) CX (k) Df (k)
5
f
p
X (k 1)
A
X (k)
B
f (k)
矩阵形式： X (k 1) AX (k) Bf (k)
离散系统状态方程和输出方程
(5)输出方程：描述系统输出、输入、状态之间关系的代数方程组。
一般形式：n阶系统，n个状态，p个输入，q个输出。
y1(k) c11
y2
(k)
c21
yq(k) cq1
离散系统状态方程和输出方程
知识点K3.05
离散系统状态方程和输出方程
主要内容：
1.状态变量 2.状态方程 3.输出方程
基本要求：
掌握离散系统状态方程和输出方程的基本概念
1
离散系统状态方程和输出方程
K3.05 离散系统状态方程和输出方程 (1)初始状态：定义：离散系统在k0时刻的状态是最少数目的一组数，知道了这组数和区间[k0,k]上的输入，就可以完全确定系统在k时刻的输出，该组数即为初始状态，表示为：
状态变量：x1(k), x2 (k)......, xn (k)
(3) 状态矢量、状态空间：
状态矢量：由状态变量构成的列矢量X(k) 。
x1(k)
X
(k
)
x2
(k
)

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

对于：x(k 1) Gx (k) Hu(k) ，其模拟结构图如下： y(k) Cx(k) Du(k)
u(k) H
D
z x(k 1)
x(k)
1

C
y(k)

G
2019/12/15
单位如同连续系统中积分器和1/s的关系
迟延
5
3、Z传递函数（矩阵）和特征方程
1）离散系统的Z传递函数为：零初始条件下，脉冲输出序列的z变换与输入脉冲序列的z 变换之比，称为系统的脉冲传递函数或Z传递函数。
整理上式得： Y (z) [C(zI G)1 H D]U(z) G(z)U(z)
所以Z传递矩阵为：G(z)＝C(zI G)1 H D
3）离散系统的特征方程为： zI G 0
而此特征方程的根就是线性离散系统的极点，也是系统矩阵G的特征值。
2019/12/15
7
4、将差分方程化为状态空间描述：或转换为Z传递函数，再求
c2

cn

x2
(kT
)

Du(kT
)

xn
(
kT
)
（T为采样周期，经常省去不写）
写成矩阵形式，得离散系统的状态空间描述：
x(k 1) Gx (k) Hu(k)
y(k) Cx(k) Du(k)
2019/12/15
4
2、线性定常离散系统状态空间描述的模拟结构图
2）系统中信号既有离散量，也有连续量。描述方式：离散量部分用一阶差分方程描述连续量部分用一阶微分方程描述，需要离散化。
2019/12/15
2
一、Z变换及相关理论知识
拉氏变换是分析、设计线性连续系统的主要数学工具。Z变换是分析、设计线性离散控制系统的主要数学工具。
连续输入信号
线性系统
离散
2019/12/15
拉氏变换 S域代数方程
微分方程
直接求解
时域解
差分方程
Z变换
Z域代数方程
S域解拉
氏反变换
Z 反变换
Z域解
3
二、离散系统的状态空间描述
1、线性定常离散系统的状态空间描述为：
x1(k 1)T g11 g12 g1n x1(kT ) h1
输出方程：
选择状态变量：x1(k) y(k)

x2 x3
( (
k k
) )

y(k y(k
1) 2)

xn(k) y(k n 1)
2019/12/15
8
化为一阶差分方程组：
x1(k 1) y(k 1) x2(k)

x2
(
k
1)

y(k
2019/12/15
10
2）差分方程的输入函数中包含高于一阶的差分项 y(k n) an1 y(k n 1) a0 y(k) bnu(k n) b0u(k)
x1(k) y(k) h0u(k)
选择状态变量：

x2 x3
( (
k k
G(z) Y(z) U(z)
用方框图表示为： U(z) G(z) Y (z)
2）MIMO离散系统的Z传递矩阵：
当初始状态 x(0) 0 时，对以下状态空间描述做Z变换：
x(k 1) Gx (k) Hu(k)
y(k) Cx(k) Du(k)
2019/12/15
6
得：
zX (z) GX(z) HU(z) Y(z) CX(z) DU(z)
) )

x1 ( k x2 ( k
1) 1)

h1u( k ) h2u( k )

xn(k) xn1(k 1) hn1u(k)
上式中：
h0 bn

h1 h2

bn1 bn2

an1h0 an1h1

an2h0
离散系统差分方程描述形式：
y(k n) an1 y(k n 1) a1 y(k 1) a0 y(k)
bnu(k n) bn1u(k n 1) b0u(k)
(k 0,1,2)
1）差分方程的输入函数中不包含高于一阶的差分项 y(k n) an1 y(k n 1) a1 y(k 1) a0 y(k) b0u(k)

2)

x3 ( k )

xn1(k 1) y(k n 1) xn(k)

xn
(
k
1)

y(k

n)

a0 y(k) a1 y(k 1) an1 y(k n 1) b0u(k)

a0 x1(k) a1x2(k) an1xn(k) b0u(k)
x2 ( k

1)T

g21
g22

g2n

x2
(
kT
)

h2

u(
kT
)

xn
(
k

1)T

gn1
gn2

gnn

xn
(
kT
)
hn

x1(kT )
状态方程：y(kT ) c1
y(k) x1(k)
2019/12/15
9
写成矩阵形式，得到离散系统的状态空间表达式：
x1(k 1) 0

x2(k 1)

0
10 01
0 x1(k) 0

x2 ( k )

0

0 u(k)

xn1
(
k

1)

0
0 01 来自 xn1(k
)

0

xn(k 1) a0 a1 an2 an1 xn(k) b0
x1(k)
y 1
0

0

x2
(
k
)

xn
(
k
)
第一节线性离散时间系统的状态空间描述
1. Z变换及相关理论知识 2. 离散时间系统的状态方程 3. 连续时间系统的离散化
2019/12/15
1
离散系统基本知识：
定义：在系统中，只要有一处信号不是时间t的连续函数，这种系统就称为离散系统。
分类： 1）系统中所有信号均是离散量。描述方式：一阶差分方程描述