当前位置：文档之家 › 根轨迹的讲解

根轨迹的讲解

  • 格式：ppt
  • 大小：1.06 MB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

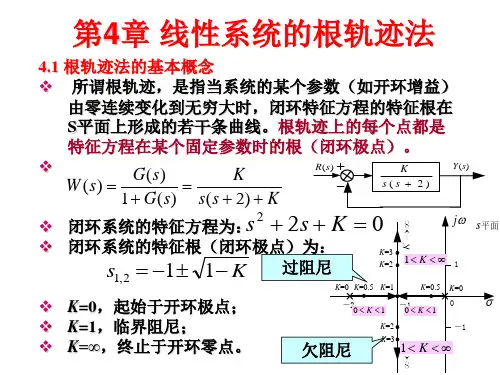
第4章 根轨迹法

第4章 根轨迹法

• 4.4
应用MATLAB绘制根轨迹图
• 使用rlocus命令可以得到连续的单输入单输
出系统的根轨迹。 • （1）Rlocus（num，den）或rlocus（num，
den，k）
• （2）sgrid或sgrid(zeta，wn)
• 解 在图4.11中画出ξ=0.5的射线，与根轨 迹相交得闭环极点的要求位置s0。再画出 Gk(s)的极点到s0的三个向量——
• 得 • 由向量幅值
• 换句话说，如果取K*的值为65，则1+Gk (s) 的一个根将位于s0，另一个根当然是和s0共 轭的。第3个根在何处呢？由根轨迹知道， 第3条根轨迹在负实轴上，在一般情况下， 可以取一试探点，计算相应的K*值，然后 修正试探点直到找出和K*=65相应的点为止。
• ②方法2 根据式(4.14)，求出闭环系统特 征方程。
• 由上式可得
• ③方法3
根据式(4.15)有
• d1在根轨迹上，即为所求的分离点，d2不在根 轨迹上，则舍弃。此系统根轨迹如图4.4。
图4.4
• 以上介绍了9条绘制根轨迹的一般规则。为 了熟练应用上述9条规则，并能绘制复杂系 统根轨迹，下面再举一例说明如何绘制一 个复杂系统的完整根轨迹图。
第4章
• 4.1
• 4.1.1
ቤተ መጻሕፍቲ ባይዱ
根轨迹法
根轨迹的基本概念
根轨迹的定义
• 系统参数（如开环增益K *）由零增加到∞ 时，闭环特征根在S平面移动的轨迹称为该 系统的闭环根轨迹。
• 4.1.2
根轨迹方程
• 既然根轨迹是闭环特征根随参数变化的轨迹，
则描述其变化关系的闭环特征方程就是根轨 迹方程。 • 则根轨迹方程（系统闭环特征方程）为： （4.2）

第四章根轨迹法.

第四章根轨迹法.

9
4.2.1 绘制根轨迹的基本法则 法则 1 根轨迹的分支数和对称性 : 1. 根轨迹对称于实轴(实数根或者复数根) 根轨迹对称于实轴(实数根或者复数根) 2. n阶系统有 条根轨迹 阶方程有 个确定的根,当根由始点 阶系统有n条根轨迹 阶方程有n个确定的根 阶系统有 条根轨迹(n阶方程有 个确定的根, 向终点移动时,必定形成一条根轨迹) 向终点移动时,必定形成一条根轨迹)
24
法则 8 根之和 : 当 n m ≥ 2 时 , 特征方程第二项系数与 K* 无关 , 无论 K* 取 何值 , 开环 n 个极点之和总是等于闭环特征方程 n 个根之和
∑s = ∑ p
i =1 i i =1
n
n
i
(4-25)
25
画出了几种常见的开环零, 在图 4-15 中 , 画出了几种常见的开环零,极点分布及其相应 的根轨迹 , 供绘制概略根轨迹时参考 .
3
4.1.1 根轨迹概念 一, 根轨迹概念 根轨迹简称根迹 , 它是开环系统某一参数从零变到无穷时 , 闭 环系统特征方程的根(闭环极点 在 环系统特征方程的根 闭环极点)在 s 平面上变化的轨迹 . 闭环极点 设控制系统如图4-1所示 设控制系统如图 所示 , 其 闭环传递函数为 C ( s) 2K φ ( s) = = 2 R( s ) s + 2 s + 2 K 显然 , 其特征根为 s1, 2 = 1 ± 1 2 K 其特征根变化如图4-2所示 令 K = 0 → ∞, 其特征根变化如图 所示 . "×"---------表示开环传递函数的极点 × 表示开环传递函数的极点 "°"---------表示开环传递函数的零点 表示开环传递函数的零点 箭头的指向-------表示 增大是根的移动方向 表示K增大是根的移动方向 箭头的指向 表示

第四章 根轨迹

第四章 根轨迹
分离点：两条或两条以上根轨迹分支在s平面上相遇又立即 分开的点。 分离点是特征方程出现重根之处。
∑
n
i=1
1 = d-pi
∑
m
j=1
1 d-zj
求分离点。
也可以根据
用上式求出的解不一定都是分离点，还必须满足特 征方程或用相应的规则来检验。
规则6
• 系统闭环特征方程为
n m
(s p ) K (s z
k
m
n
j 1 j i
j 1
规则7
• 由
( s z
j 1
m
j
) ( s pi ) ( 2k 1)
i 1
n
• 假设在一开环极点pk附近取一点s1, 则
( s1 pk ) s p (2k 1) s1 z j s1 pi
1+K K = -1 0 1 n = ( s -p︱ ) ∏︱
i=1
n ) ∏︱ ( s - z︱ j p︱ s ︱ ∏ j=1 i * *
s - z︱ i ︱ ∏ j
j=1
确定根轨迹上某点对应的K*值
求模求角例题
模值条件与相 角条件的应用
92.49o
2.61
78.8o 66.27o -2
-1.09+j2.07 s2
分离角：根轨迹进入分离点的切线方向与离开分离点的切 线方向之间的夹角。
分离角为
l为进入并离开分离点的根轨迹分支数目。
j
0
实数
共轭复数
如果根轨迹位于实轴上的两个相邻的开环极点（零点） 之间，其中一个可以是无限极点（零点），则在这两个 极点（零点）之间至少存在一个分离点。

第四章 根轨迹法

第四章 根轨迹法
0 0
r 0,1,2,, n m 1
jω
5 3
r 0, 600 r 1, 1800 r 2, 3000
0
σ
五.实轴上的根轨迹 规则五：实轴右侧的开环零、极点个数总和为奇数时， 该实轴段属于根轨迹。
相角条件
( s z j ) ( s pi ) (2r 1)1800
求取分离点与会合点的方法
计算思想：寻找特征方程中k的极值。 闭环特征方程： 1 G ( s ) H ( s ) 0
k ( s z1 )( s z 2 )....( s z m ) k N( s ) G(s) H (s) ( s p1 )( s p2 )....( s pn ) D( s)
根轨迹终止于[s]平面的无穷远处。
闭环特征方程：
( s z1 )( s z 2 )....( s z m ) 1 ( s p1 )( s p2 )....( s pn ) k
当k→∞，得
( s z1 )( s z2 )....( s zm ) 0
即 s z j ( j 1,2,..., m) 闭环极点就是开环零点。 说明根轨迹终止于开环零点。
( s z j ) ( s pi ) (2r 1)1800
j 1 i 1
m
n
r 0,1,2,
按相角条件绘制根轨迹图
具体方法是：在复平面上选足够多的试验点，对每 一个试验点检查它是否满足相角条件，如果是则该 点在根轨迹上，如果不是则该点不在根轨迹上，最 后将在根轨迹上的试验点连接就得到根轨迹图。
k=2 k=0 －2 k=1 －1
K→∞
jω
j k=0 0

第4章根轨迹

第4章根轨迹

j 1 n
0n m
1 K P( s )
1 KP( s) 0
P( s) 2k 1
KP(s) 1
规则2 根轨迹的分支数及起点和终点
K
n
(s p )
i
(s z )
j j 1
起点就是K=0时的s值（s=-pi） ，终 点就是K=∞时的s值（s=-zj） 。
p3
0 符 合 相 角 条 件
设s2如图所示，则
( s2 z1 ) ( s2 p1 ) ( s2 p4 ) ( s2 p5 ) 0 0
2 2k 1 不 满 足 相 角 条 件

例3（例4-2） 设一单位负反馈控制系统如图4-7所示，试绘制 该系统的根轨迹。 S X1 0, S X 2 1, S X 3 2, SO1,2,3 。 ① 起止点： ② 实轴上的根轨迹： j s 平面 无有限零点 ③ 分支数=3，→∞； 时，取0 ④ 渐近线：
(0 1 2) 0 a 1 30 (2k 1) 5 k , , 30 3 3 ⑤ 分离点和会合点： K s(s 1)(s 2)
结论：
实轴上某线段右方的开环零极点数之和为奇数时，该段 为实轴上的根轨迹段。
K 1 s 1 2K s 2 ' s 2 2 例：Gs H s 1 K s 4 s 1 ss 4 ss 4
应绘制Kˊ（根轨迹增益=2×开环增益）的参数根轨迹。 ①起止点： S X1 0, S X 2 4, SO1 2, SO2 。 jj ②实轴上的根轨迹： 规则4 根轨迹的对称性 复变函数等式：
例1续 ： G s H s s 4 10s 3 32s 2 32s Ks K 0 1 列 劳 斯 表 ：4 1 s s 3 10 288 K s 10 9216 156K K 2 s 288 K s0 K

根轨迹的概念

根轨迹的概念

根轨迹的概念特征方程（见传递函数）的根随某个参数由零变到无穷大时在复数平面上形成的轨迹，称为根轨迹。

我们先看下面的例子。

设单位反馈系统的开环传递函数为：当开环放大系数K从零到无穷大变化时，系统的特征根在s平面上怎样分布？解系统有两个开环极点系统的闭环传递函数为系统的特征方程为特征方程的根可见特征根在s平面的位置与K有关。

K=0时，,与开环极点的位置相同。

0<K<1/4时，,均为负实数，分布在0到-1之间，随K从零开始逐渐增大，和也从开环极点的位置开始逐渐接近。

K=1/4时，==-0.5，两个闭环极点重合。

K>1/4时，和都成为共轭复数。

具有相同的负实部，且为常数，而虚部则随K的增加其绝对值也增加。

图3.28给出了系统的特征根在K从零变化到无穷大时，相应位置的变化情况。

这种放大系数K从零到无穷大变化时，特征方程的根在s平面上相应变化的轨迹，称为根轨迹。

根轨迹完整地反映了特征根随参数变化的情况。

根据图3.28的根轨迹图，我们可以知道，在K<1/4时，系统的单位阶跃响应中含有两个指数项函数。

在K=1/4时，两个指数项函数合二为一。

在K1/4时，根轨迹进入复平面，说明系统的单位阶跃响应由单调变化转变为振荡。

从图还可以看出，不论K怎样变化，系统始终是稳定的。

因为全部根轨迹都分布在s平面左半边。

图3.28 特征根随K的变化情况根轨迹的基本条件控制系统的特征方程为(3.145)式中为系统前向通道传递函数，H(s)为系统反馈通道传递函数。

上式可改写为(3.146)将系统的开环传递函数写成零极点形式(3.147)式中K称为根轨迹放大系数或根轨迹增益。

称为开环零点，称为开环极点。

将（3.147）式代入（3.146）式得(3.148)式（3.148）是一个复数方程，可以用复数的幅值和幅角分别表示为(3.149), (3.150)式中是矢量与实轴正方向的夹角，是矢量与实轴正方向的夹角。

我们称式（3.149）为根轨迹的幅值条件，式（3.150）为根轨迹的幅角条件。

根轨迹法的基本概念

根轨迹法的基本概念
渐近线与实轴交点为：
(2k 1)
3
,k 31
0,1 1
, 2
2
2
0231 2 31
4、求分离点：
1
1
d1 d
d
2.47
1 d2
1 d3
j
2.47 3 2 1 0
6、根轨迹的起始角和终止角：
根轨迹的起始角是根轨迹离开开环复数极点处 切线与正实轴的夹角：
m
n
p1 (2k 1) ( p1 zi ) ( p1 p j )
m
(s zi )
1 G(s)H(s) 0
G(s)H(s) K*
i1 n
m
(s pj )
(s zi )
j 1
K * i1 n
1
(s pj )
j 1
m
n
模值条件： (s zi ) (s pj ) (2k 1)
i1
j1
n
s pj
相角条件： K *
j 1 m
s zi
i 1
相角条件是确定根轨迹的充分必要条件。相角条件满足(2k 1) 称为180º根轨迹。
j 1
i 1
n
n
n
(s si ) sn ( si )sn1 (si )
i 1
i 1
i 1
an1s an
n
n
当n m 2 时， si p j
i 1
j 1
4-3 广义根轨迹法
一、参数根轨迹
以非开环增益K*为可变参数的根轨迹，称为参数根 轨迹。
引入等效开环传递函数的概念
G(s)H (s) K * (s z1 ) s(s 2 2s 2)
z1是附加的开环实数零点，其值可在s左半平面内任意选择， 当 z1→∞时，表明不存在有限零点。

第四章 根轨迹法

第四章 根轨迹法
第四章 根轨迹法
4.1 根轨迹法的基本概念 4.2绘制根轨迹的基本条件和规则 绘制根轨迹的基本条件和规则 4.3 特殊根轨迹 4.4 用根轨迹法分析系统性能
4.1 根轨迹法的基本概念
概述: 闭环系统的动态性能与闭环极点在s 概述: 闭环系统的动态性能与闭环极点在s 平面上的位置密切相关， 平面上的位置密切相关 ， 系统的闭环 极点也就是特征方程式的根。 极点也就是特征方程式的根 。 当系统的某 一个或某些参量变化时，特征方程的根 平面上运动的轨迹称为根轨迹 根轨迹。 在s平面上运动的轨迹称为根轨迹。 根轨迹法: 根轨迹法: 直接由开环传递函数求取闭环 特征根的方法. 特征根的方法.
G ( s) H ( s) =
K ∏ (s − z j )
m
∏ (s − p )
i =1 i
j =1 n
其中 K 称为根轨迹增益
z j 是开环零点； 是开环零点；
p i 是开环极点。 是开环极点。
系统的闭环传递函数为
C (s) G (s) = R( s) 1 + G ( s) H ( s)
根轨迹方程（系统闭环特征方程） ⇒ 根轨迹方程（系统闭环特征方程）为
K∏ s − zj
m
∏
i=1
j =1 n
=1 ⇒
K =
∏|s− p ∏|s− z
j =1 i =1 m
n
i
| |
s − pi
j
相角条件:∠G(s)H(s)=±(2k+1)π, k=0,1,2,… 相角条件 ∠ ±
∑ ∠(s − z ) − ∑ ∠(s − p ) = ±奇数倍π
j =1 j i =1 i
n
K=0为根轨迹的起点 为根轨迹的起点 s = pi

根轨迹法特点和方法介绍

根轨迹法特点和方法介绍

n
m
pi zi
a
i 1
j 1
nm
a
(2k1)
nm
渐近线
m
n
(s zi )
a1 p j
G(s)H(s) K*
i1 n
(s pj )
j 1 m
b1 z i
j1
i1
K*
sm sn
b1sm1 L a1sn1 L
bm1s bm an1s an
1G (s)H (s)0
smb 1sm 1Lbm 1sbm1 sna1sn 1Lan 1san K *
2
R D (je ) 32 K * 0 2
ID m (j) 3 2 0
K* 6
基本法则（7）——分离点 d
法则7 分离点 d： d K * = 0 或 ds
（对应重根）
n 1
m1
i1 dpi j1 dzj
当K*从0变到∞时，根轨迹可能出现先会合后分离，这样的点
称分离点。分离点对应重闭环极点。
G (s)H (s)= K * (s-z 1 )(s-z 2 )....(s-z m ) K *> 0 (s-p 1 )(s-p 2)....(s-p n )
系统的闭环特征方程可以表示为：
1+K *(s-z1)(s-z2)....(s-zm)=0 (s-p1)(s-p2)....(s-pn)
以K*为参变量的根轨迹上的每一点都必须满足该方程， 相应地，我们称之为典型根轨迹方程。
G (s)H (s)=
K *(s-z1)
(s-p1)(s-p2)(s-p3)(s-p4)
基于相角条件，在复平面上选足够多的试验点，对每
一个试验点检查它是否满足相角条件，如果是则该点

根轨迹

根轨迹


2

G0 s
K ss 1s 2
2 j s2 2 j
求 s3 ?
4．3广义根轨迹 (前面按根轨迹方程K从0→∞变化时的根轨迹叫常规根轨迹) 除根轨迹增益K变化以外的根轨迹统称为广义根轨迹。 如：参数根轨迹，m>n时的根轨迹，零度根轨迹 一、参数根轨迹 以根轨迹增益K以外的参数为可变参数绘制的根轨迹，称为参数根轨迹。

pi z j
i 1 j 1
n
m
nm
倾角（方向角）为：

2k 1
nm
k 0,1,2,n m 1
5．实轴上的根轨迹仅决定于实轴上的开环极点和开环零点。若实轴上某线段右边的实零、极点总数
为奇数，则该线段是根轨迹，为偶数时不是。 6．根轨迹的分离点与分离角。两条或两条以上根轨迹分支在s平面相遇又立即分开的点，称为根轨 迹的分离点。根轨迹进入分离点的切线方向与离开分离点的切线方向的夹角称为根轨迹的分离角。 m n m 1 ★无零点时， 分离点的坐标d满足方程： 1 1 0
k * k
(s )
=
(s p i ) k * (s z j )
i 1
j 1
n
k (s z i ) (s p j ) j 1
* G i 1
f
h
m
三、根轨迹方程
特征方程：
根轨迹方程
特征方程 1+GH = 0
1 Gs H s 0
1 K
s z
例：已知 G0 s s s 2
K s 4
,确定分离点或会合点,证明根轨迹在实轴外的部分是圆。
n m p a 2k 1 p a z j pa pi i 1 j 1 ia n m z a 2k 1 z a z j z a pi i 1 jj 1 a

根轨迹法基本概念

根轨迹法基本概念

KG0 (s)
则闭环特征方程为:
1 K num 0 den
特征方程旳根随参数K旳变化而变化,即为闭环根轨迹.
项目1:已知系统旳开环传递函数模型为：
K Gk (s) s(s 1)(s 2) KG0(G)
利用下面旳ＭＡＴＬＡＢ命令可轻易地绘制出系统旳根轨迹 >>G=tf(1,[conv([1,1],[1,2]),0]);
引言
A.闭环系统旳稳定性和动态性能 取决于闭环极点特征方程旳根。
B.当待定参数变化时特征根随之变 化，这个根旳变化轨迹就形成根轨迹。
C.用来研究根轨迹旳变化规律以及 和闭环系统性能间旳关系旳措施，称为 控制系统根轨迹分析法。
§4.2 根轨迹旳概念
要求： 1)掌握根轨迹旳概念 2)掌握根轨迹幅值条件和相角条件
2)相角条件是决定根轨迹旳充要条件， s平面上一点若满足相角条件,即为根轨迹 上旳一点。
3)幅值方程用于拟定根轨迹上一点旳K值;
根轨迹点
幅值方程
四. 根轨迹与系统性能
1.稳定性 假如系统特征方程旳根都位于S平面 旳左半部，系统是稳定旳，不然是不稳定旳。若
根轨迹穿越虚轴进入右半S平面，根轨迹与虚轴交
另一种问题是，经过解方程求得旳闭环 极点，是在系统参数一定旳情况下求得旳。 但当系统中旳参数变化时，如开环增益K变化 时，又得重新解方程求根，因而很不以便。
为了处理以上问题，1948年，伊万斯提 出了控制系统分析设计旳根轨迹法。
这种措施是根据反馈控制系统旳开环、闭 环极点传递函数之间旳关系，根据一定旳准 则，直接由开环传递函数旳零、极点，求出 闭环极点。从而，比较轻易旳得到系统旳性能.
要点： 1)根轨迹旳概念 2)闭环系统旳特征根旳根轨迹与开环 传递函数旳关系

自动控制原理第四章根轨迹法

自动控制原理第四章根轨迹法
仿真与实验研究
根轨迹法可用于仿真和实验研究，通过模拟和实验 验证系统的性能和稳定性，为实际系统的设计和优 化提供依据。
根轨迹法的历史与发展
历史
根轨迹法最早由美国科学家威纳于1940年提出，经过多年的 发展与完善，已经成为自动控制领域中一种重要的分析和设 计方法。
发展
随着计算机技术和数值分析方法的不断发展，根轨迹法的应 用范围和精度得到了进一步拓展和提高。未来，根轨迹法有 望与其他控制理论和方法相结合，形成更加完善和高效的控 制系统分析和设计体系。
根轨迹的性能分析
根轨迹的增益敏感性和鲁棒性
通过分析根轨迹在不同增益下的变化情况，可以评估系统的性能和鲁棒性。
根轨迹与性能指标的关系
通过比较根轨迹与某些性能指标（如超调量、调节时间等），可以评估系统的 性能。
04
根轨迹法与其他控制方法的比较
根轨迹法与PID制根轨迹图，直观地分析系统的稳定性、响应速度和超调量等性
特点
根轨迹法具有直观、简便、易于掌握等优点，特别适合用于分析 开环系统的稳定性和性能。
根轨迹法的应用场景
控制系统设计
根轨迹法可用于控制系统设计，通过调整系统参数 ，优化系统的性能指标，如稳定性、快速性和准确 性等。
故障诊断与排除
根轨迹法可用于故障诊断与排除，通过观察系统根 轨迹的变化，判断系统是否出现故障，以及故障的 类型和程度。
在绘制根轨迹时，需要遵循一定 的规则，如根轨迹与虚轴的交点 、根轨迹的分离点和汇合点等。
03
根轨迹分析方法
根轨迹的形状分析
根轨迹的起点和终点
根轨迹的起点是开环极点的位置，而 终点是闭环极点的位置。通过分析起 点和终点的位置，可以判断根轨迹的 形状。
根轨迹的分支数

第4章 根轨迹分析法

第4章 根轨迹分析法

i 1
其余n m,
m
(s zi )
i 1 n
(s pj )
m
(1
m
i 1
pj
(1 s)
zi
n
s
) (s
p
j
)
1 Kg
j 1
j 1
j m 1
此时s ，即无穷远处
8/63
五.实轴上的根轨迹
在实轴上，右方的实数开环极点和实数开环零 点的总和为奇数时，此为根轨迹上点。
GK (s)
m
n
闭环系统特征方程 或根轨迹方程
4/63
GK (s) GK (s) e jGK (s) 1
幅值条件: GK (s) 1 相角条件: GK (s) 180o (2k 1) k 0,1, 2,
或:
m
(s zi )
充要条
K i1 gn
1
件
(s pi )
m
n
j 1
s zi s p j 180o (2k 1) k 0,1,2,
当 nm2
n
n
an1 ( pj ) (sj ) s j 为系统的闭环极点
j 1
j 1
随着根轨迹增益的变化，若一些闭环极点向右移动，则另一些
必向左移动
n
(sj )=(-1)n (a0 Kgb0) j 1
22/63
十条法则：
1.连续性 2.对称性 3.分支数 4.起点、终点 5.实轴上的根轨迹 6.渐近线 7.分离点、会合点 8.出射角、入射角 9.虚轴交点 10.闭环极点的和与积
D(s)N(s) N(s)D(s) 0,3s2 6s 2 0
ss21
0.423 1.577

第四章线性系统的根轨迹法

第四章线性系统的根轨迹法

第四章 线性系统的根轨迹法知识点：1. 根轨迹的概念，2. 绘制根轨迹的法则，3. 其他形式的根轨迹，4. 参数变化时对系统性能的影响。

1. 根轨迹的概念：根轨迹指的是开环传递函数中某一参数变化时，闭环特征根所走过的路径。

注：根：闭环特征方程的根。

1）.开环放大系数与根轨迹增益。

时间常数表达式：()()()()210.210.51k k s s s s G +=++ 尾“1”时，K 叫放大系数零极点表达式：()()()1252g ks s s s k G ⎛⎫+ ⎪⎝⎭=++ 首“1” g k 叫根轨迹增益。

根轨迹：0→+∞所走过的根轨迹增益。

2）.试探法绘制根轨迹。

例子：试求g k 从0→+∞变化时，系统的根轨迹的变化。

解：()()()()()1=0()1kkks C s s s R s s G G G Φ==⇒++2g +0s s k +=1,21s =-±注：,,,%.g k βξσ↑↑↓↑绘制根轨迹使用“X ”表示开环极点，用”o ”表示开环零点，根轨迹用粗实线表示，根轨迹上标有箭头表示g k 增大时，根轨迹移动的方向。

3）.闭环零极点与开环零极点之间的关系。

()()()kS G S H S G =()()1()()G s s G s H s Φ=+令()()()()()()','GHM S M S G S H S N S N S KK==()()()()()()()()'1()()1'GGHM S N S G s s M S M S G s H s N S N S KKKΦ==++()()()()()()'()''GGHM S N S s N S N S M S M S KK KΦ=+①． 闭环零极点由前向通道的零点和反馈通道的极点构成，对于单位负反馈系统的闭环零点就是开环零点。

②． 闭环极点与开环极点，开环零极点及根轨迹都有关系。

第4章 根轨迹法

第4章 根轨迹法

共轭零极点到s1点的相角之和也是零,只有s1右边
的开环零、极点到s1的相角为π ,而相角方程 ：
(s z ) (s p ) (2k 1) (k 0,1,2......).
因而s1的右侧只有奇数个开环零、极点才会满足
相角方程。
z2 p3
S1
m
n
i 1
i
i 1
二、闭环零极点与开环零极点的关系
R(s) G(S) C(s)
H(S)
开环递函数
G( s) H ( s)
G( s) ( s) 1 G( s) H ( s)
闭环传递函数
一般情况下，前向通路传递函数
G( s)
* KG
* (s zi ) KG i 1
a
(s p )
i i 1
渐近线与实轴正 方向的夹角 ： (2k 1)
a
nm
n m i 1 i
45 ,135 .
i
与实轴的交点：
a
p z
i 1
nm 0 (3) (1 j ) (1 j ) 1.25 4
(4)分离点坐标:

i 1
n
1 1 1 1 1 0 则 0 d Pi d d 3 d 1 j d 1 j
a
(s z ) (s z K
*
i
a
c
j
)
(s p ) (s p
i i 1
b
i 1
j 1
d
j
)
j 1
开环系统根轨迹增益
d
i
( s)
K
b i 1
* G

第四章 根轨迹法

第四章 根轨迹法
2 当 K1 a 时，则两根为实数且相等，即
s1 s2 a
。
第四章 根轨迹法
§4-1 根轨迹的基本概念
当 a 2 K1 时，两根成为共轭的复数 根，其实部为
a
，这时根轨迹与实
j
轴垂直并相交于 ( a, j0) 点。
(s+2a)
K1由0向∞变化时的根轨迹，如图4-2 所示。箭头表示K1增大方向。 由图可见： 1) 此二阶系统的根轨迹有两条， K1 0 时分别从开环极点 p1 0 和 p2 2a 出发。
m
| s pi |
i 1
j
1
或
K1
| s pi | | s z j |
j 1 i 1 m
n
(s z
j 1
m
) ( s pi ) 180 (2q 1)
i 1
n
q 0, 1, 2,
在s平面上满足相角条件的点所构成的图形就是闭环系统的根轨迹。 因此，相角条件是决定闭环系统根轨迹的充分必要条件，而幅值条件
D' (s) A' (s) K1B(s) 2(s s1 ) p(s) (s s1 ) 2 p(s) 0
将
A( s ) K1 代入上式，得 B( s)
图4-3 反馈控制系统
G(s) H (s) 1 和 G(s) H (s) 180 (2q 1) q 0, 1, 2,
以上两式是满足特征方程的幅值条件和相角条件，是绘制根轨迹的重 要依据。在s平面的任一点，凡能满足上述幅值条件和相角条件的，就是
系统的特征根，就必定在根轨迹上。
s p1=0 O a
p2=2a

根轨迹

根轨迹

-2
-1
K= 1
-1 -2
K= 2.5 K
动态性能： ① 当 0<K<0.5 时，系统的闭环极点位于负实 轴上，二阶系统处于过阻尼状态，单位阶跃 响应为非周期过程。 ②当K=0.5时，二阶系统处于临界阻尼状态， 单位阶跃响应也为非周期过程。 ③当K>0.5时，系统具有一对共轭复数极点， 处于欠阻尼状态，单位阶跃响应为具有阻尼 的振荡过程。
三、根轨迹方程 1. 开、闭环传递函数的零、极点表达式 控制系统的结构图
R(s) C(s)
其闭环传递函数
G( s) ( s ) 1 G( s) H ( s)
G ( s) H ( s)
式中G(s)H(s)为系统的开环传递函数。
将开环传递函数用其分子、分母多项式方程 根的因式来表示，得 开环传递函数
3.91 根轨迹的基本概念 一、根轨迹的定义 根轨迹：是指系统开环传递函数中某个参数 (如开环增益K)从零变到无穷时，闭环特征 根在s平面上移动所画出的轨迹。 常规根轨迹 ：当变化的参数为开环增益时 所对应的根轨迹。 广义根轨迹 ：当变化的参数为开环传递函 数中其它参数时所对应的根轨迹。
R(s)
s an1 s
n n1

a1 s a0 0
, sn
并设它的n个根为 s1 , s2 ,
则根据代数方程的根与系数的关系可知，有
n si an1 i 1 n ( s ) a i 0 i 1
把系统的传递函数写成
( s z1 )( s z2 ) ( s zm ) G0 ( s ) K ( s p1 )( s p2 ) ( s pn )
1 1 K Kd
一般情况下，两条根轨迹相遇又分开 时，它们的会合角和分离角分别是０º 、 180º 和90º 、-90º ，或者相反。这一规律具 有一般性。可以证明：

根 轨迹法

根 轨迹法

第三章
(五) 《礼记》中说：“入境而问禁，入国而问
俗，入门而问讳。”俗话说“十里不同风、 百里不同俗”“到什么山唱什么歌”，这 些对劳动人民有益的格言都说明尊重各地 不同风俗与禁忌的重要性。尊重习俗原则
上一页 下一页 返回
第三章
1. 仪表是指人的容貌，是一个人精神面貌的
外观体现。一个人的卫生习惯、服饰与形 成和保持端庄、大方的仪表有着密切的关 系。清洁卫生是仪容美的关键，是礼仪的
上一页 下一页 返回
第三章
3. 放松。女性应两膝并拢；男性膝部可分开 一些，但不要过大，一般不超过肩宽。双 手自然放在膝盖上或椅子扶手上。在正式 场合，入座时要轻柔和缓，起座要端庄稳 重，如古人所言的“坐如钟”。若坚持这 一点，那么不管怎样变换身体的姿态，都 会优美、自然。不可随意拖拉椅凳，从椅 子的左侧入座，沉着安静地坐下。女士着
角均等于π。 四、根轨迹的渐近线 五、根轨迹的分离点
当K*由零至无穷大变化过程中，几条根轨迹在s平面某一点 相遇后立即分开，这一点称为分离点。最常见的分离点出现在 实轴上，实轴上的分离点有两种情况：i)实轴上的根轨迹相向 运动，在某一点相遇后进入复数平面，如图4-7的A点；ⅱ)复数 平面内的一对共轭复数根轨迹在实轴上相遇，然后趋向实轴上
上一页 下一页 返回
第三章
2. 服饰是一种文化，反映一个民族的文化素
养、精神面貌和物质文明发展的程度；着 装是一门艺术，能体现个人良好的精神面 貌、文化修养和审美情趣。既要自然得体， 协调大方，又要遵守某种约定俗成的规范 或原则。不但要与自己的具体条件相适应， 还必须时刻注意客观环境和场合上一，页与下时一页间、返回
上一页 返回
§4-3 根轨及草图绘制举例
例4-7 若开环系统传递函数为

第二章 根轨迹法

第二章 根轨迹法
s →∞ j =1 i =1 m n
∑ lim ∠( s − z
j =1 s →∞ m j =1 s →∞
m
j
) − ∑ lim ∠( s − pi ) = (2k + 1)π
i =1 s →∞ n
n
∑ lim ∠s − ∑ lim ∠s = (2k + 1)π
i =1 s →∞
lim[m∠s − n∠s ] = (2k + 1)π
π / 3, k = 0 (2k + 1)π (2k + 1)π ϕa = = = − π / 3, k = −1 n−m 3 π,k =1
与实轴的交点：
σa =
∑ p −∑z
i =1
n
m
1
j =1
j
n−m
0 + ( −1) + ( −2) = = −1 3
j
× −2
× −1
600
i =1 j =1
n
m
∏ (s − z ) ∏ (s − p )
i =1 i j =1 n j
m
1 =− * K
四、实轴上根轨迹所在区段内的右侧，开环零点、极点数 目之和为奇数 例：已知开环传递函数为
K (τs + 1) Gk ( s ) = s (Ts + 1)
τ >s
试确定K（由 0 → ∞ ）变动下的系统根轨迹。
s →∞
ϕ a = ∠s |s→∞ =
(2k + 1)π n−m
证明：根轨迹在趋向无穷远处的渐近线，是一组n-m条以 交点 σ a 为中心，以 σ a 为指向的射线。现构造一个负 反馈系统，令其闭环根轨迹恰为上述射线，则该系统开 环传递函数必为： Ga ( s ) H a ( s ) = K* ( s − σ a ) n−m

第6章 根轨迹

第6章 根轨迹
jω
2. 闭环特征方程实数根 n阶系统有 条根轨迹 阶系统有n条根轨迹 阶系统有 分布在 平面的实轴上。 分布在S 平面的实轴上。 Kr取某一数值时 阶特征方 取某一数值时,n阶特征方 取某一数值时 复数根则成对出现， 复数根则成对出现，实 程有n个确定的根 程有 个确定的根。
s3 s1
0
s5 s2
第二节 绘制根轨迹的基本方法
τ<T 2） ）
(1)开环零、极点分布 开环零、 开环零
p1=0
1 p2= - T z1= τ 1
z1 p2
jω
p 0 1
(2) 实轴上根轨迹段
p1~p2
z1~-∞
τ
-1
-1 T
(3)系统的根轨迹 系统的根轨迹
p1和p2为根轨迹 的起点
z1和-∞为根轨迹 为根轨迹 的终点
Kr (s+ ) G(s)H(s)= 1) s(s+ T
p2
(1) 开环零、极点分布 开环零、
1 p1=0 z1= τ 1 p2= - T
(2) 实轴上根轨迹段
-1 T
p1~z1段: 右侧一个开环极点 p2 ~-∞段：右侧三个开环零极点 段
‫ב‬
jω
z1 p 0 1
τ
-1
(3)系统的 系统的 根轨迹
一、根轨迹 二、根轨迹方程
第一节 根轨迹的基本概念
一、根轨迹
设系统的结构如图 Kr变化时,闭环特征 变化时 闭环特征 极点； Kr 根在s平面上的轨迹 平面上的轨迹: 极点；右半平面为 根在 平面上的轨迹 C(s) 2 s1 Kr 不稳定极点； s2 不稳定极点；虚轴 R(s) =s∞+2s+Kr ω j ↑ -2 0 0 上为临界极点。 上为临界极点。 闭环特征方程式 Kr 1 -1 -1 1 2+2s+K = 0 (2) 0<Kr<1时，系统 时 s 2 Kr=0 1r s1 s -1-j -1+j 2 0 σ -1 有呈过阻尼状态。 有呈过阻尼状态。 -2 特征方程的根 -1 -1+j∞ 系统 Kr (3) 当Kr=1时，-1-j∞ 时 ∞ s1.2 =-1± 1-Kr ∞ 呈临界阻尼状态 。 得相应的闭环特征根值: 得相应的闭环特征根值 (4) 1<Kr<∞时，系统呈欠阻尼状态。 时 系统呈欠阻尼状态。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
S1 1.5 , Z1 1.7 S2,3 4 9.2 j
C (S ) 1 R( S ) (0.01S 2 0.08S 1)
22
系统性能的定性分析
了解闭环零点和闭环实数主导极点对系统性能的影 CI(s) R(s) 1 响非常重要。 5
—
s (5 s 1)
取Td＝0.8
要绘制参数根轨迹，首先要求出等效开环传递函数的极点
2
例8 已知单位负反馈系统的开环传递函数为
1 (s a) G ( s ) 42 s ( s 1)
试绘制以a为参变量的参数根轨迹的大致图形
0a
3
P116 例题4.9 已知具有两个负反馈回路系统如图所示， 试以反馈系数为参变量 绘制根轨迹。
因此，靠近坐标原点的偶极子对动态性能的影响必 须考虑。
偶极子的确定：闭环零、极之间的距离比它们到其他极点的
距离及其自身的模值小一个数量级，这对闭环零、极点构成偶极
子。
18
闭环传递函数
K ( s)
*
(s z
i 1
m
i
)
(s
j 1
n
pj)
单位阶跃输入的响应：
n A0 Ak C ( s) s k 1 s pk


i 1
在绘制广义根轨迹时可将闭环特征方程式进行等 效变换，写成类似标准形式。
K r B( s) 将特征方程式变换： ＋G( s) H ( s)＝ 1 1 ＝0 A( s)
1
例7：设单位反馈系统的开环传递函数为
G (s) K s ( s 1)(Ta s 1)
其中开环增益可自行选定。试分析时间常数 Ta 对系统性能的 影响。
阻尼线cos1 cos1 0.5 600 上 S1, 2 0.33 0.58 j S3 2.33
C (S ) 2 0.53 0.436 2 R( S ) S ( S 1)(S 2) 2 0.53 S 0.66S 0.21 436
P124例4.12
ess 0
( s )
错误
2 ( s 2 2 s 2)
20
P123例4.11
R(S)
+ -
2K S ( S 1)( S 2)
K r 2K
C(S)
Kr G ( s) H s S ( S 1)(S 2)
（1）根轨迹图见P102～1.3例4.1，稳定范围：0<K<3
i 1 ik
14
j 1 n
已知系统的闭环零点、极点定性地分析或定量地估算系统 的性能。
闭环零极点与时间响应的关系
设系统闭环传递函数
系统的闭环极点
单位阶跃响应
20 ( s ) ( s 10)(s 2 2s 2)
p1 10,
p2,3 1 j
h(t ) 1 0.024e10t 1.55et cos(t 129o ) h(t ) 1 1.55et cos(t 129o ) p2,3 1 j 非主导极点 p1 10
4.5 广义（参数）根轨迹 前面讨论的都是以系统的开环根轨迹增益 K r 为 参数的根轨迹，实际上，也可以绘制除 K r 以外 的任何参变量的根轨迹。 m Kr s z j K r B( s ) j 1 1＋G ( s) H ( s)＝1 1＋ n ＝0 A( s) s pi
z0 取 1， 提高开环增益 p0
z0 取 1， 降低开环增益 ，改善动态特性 p0
9
1、附加开环零点的作用 (1) 附加适当的开环零点可以改善系统的稳定性。 设开环传递函数为 *
G( s) H ( s) K ( s z1 ) s ( s 2 2s 2)
z 1 是附加的开环实数零点，其值可在s左半平面内任意选择，当 z1 时，表明不存在有限零点。 令 z 1 为不同的数值，对应的根轨迹见P.118 图4-17所示：
15
近似结果
主导极点
2. 闭环主导极点与闭环偶极子
闭环主导极点（一个或一对）：在闭环极点中离虚轴 最近，而且附近无零点、极点，对稳定系统动态性能 的影响最大，起着主要作用。系统降阶（一、二阶）。
Si i ji
S0 0 j 0
Z i i ji
i 5 0
K r s z j
m j 1
s pi
i 1
n
s z0 s p0
G ( s) H ( s)
K j s 1
m
S Ti s 1
i 1
j 1 n
K Kr
z
i
m
p
j j 1
i 1 n
z0 p0
特征方程式： f (S ) S (S 1) 9 S 9＝0 9 S Kr S 将特征方程式变换：1＋ ＝1＋ ＝0 S ( S 1)＋9 S ( S 1)＋9 4
Kr S Kr S G( S ) H ( S )＝ 2 9 K r S ( S 1)＋9 S S＋9 Kr S Kr S 1 2 1 ( S 0.5 2.95 j )(S 0.5 2.95 j ) ( S ) ＋9 2 4
j

0
j

j

0
2.增加开环零点： 重心向左移，相对稳定性变好。
j

0 0
j

7
3.增加开环偶极子： 在原点附近增加开环偶极子，系 统的动态性能变化不大，稳态性能得到提高。
j
z0 p0
j
o

z0
p0
0

根轨迹局限: (1)无闭环零点信息
(2)表达稳态误差不直观
8
G(s) H ( s)
解：系统开环传递函数 R(S) 9 C (S ) S ( S 1) G(s) E (S ) 1 9 S S ( S 1)
E(S)
9 S (S 1) C (S )
S
9 S ( S 1) 9 S
C (S ) 9 R( S ) S ( S 1) 9 S 9
2
j
Kr 15 0.555 9 39
0.555
-3
0.5 2.95 j
o

可以证明，该系统的根轨迹 是一段以原点为圆心，半径 为3的圆弧。
0.5 2.95 j
3
2 2
2
6
4.6 增加开环零极点对根轨迹的影响 1.增加开环极点： 重心向右移，相对稳定性变差。
从闭环零、极点分布，系统性能的定量估算
(s a ) 2a ( s ) a ( s a)(s 2 2s 2)
(0) 1
简化后
ess 0
1 2a ( s ) 2 a ( s 2s 2)
(0) 1
4-7 用根轨迹分析系统性能 应用根轨迹法，可以迅速确定出系统在某一可变参 数值下的闭环零、极点位置，得到相应的闭环传递函数。 根据闭环零极点分布，确定（估计）系统的性能。 1.闭环零极点分布与单位阶跃响应的定性分析 设闭环传递函数：
C ( s) G(s) R( s) 1 G ( s) H ( s) K r s z j
（a）无开环零点；（b）z1 3 ；（c） z1 2
（d） z1 0
10
11
(2) 附加开环零点的目的，除了改善系统稳定性之外， 还可以改善系统的动态性能。
j j
s1 s3 p3 z1 p2 s2
np
0
s2
1
s1 p2 z1

p3
p1 0

s3
n
结论：只有当附加零点相对原有系统开环极点的位置选 配适当，才有可能使系统的稳定性和动态性能同时得到 明显的改善。 12
c(t ) A0 Ak e pk t
k 1
m * m * K ( zi ) K ( s zi ) i 1 i 1 A0 s n n s ( s p j ) ( p j ) j 1 j 1 s 0
k 1
n
（1）Sk都具有负实部（在S左半平面），系统稳定。
（2）Sk远离虚轴， e sk t 衰减快，上升快，调整短。
（3）Sk共轭极点位于射线 cos1 450，超调量小。 （4）Ak小，动态过程短，C(t ) A0 ,
t
Ak
K r sk z j
m
sk sk si
求分离点或会合点
2
S S 9 Kr S
2
d d S S 9 2S 1S 1 S S 9 Kr 0 2 ds ds S S
2


S 9 0
2
S1 3
(S2 3舍去)
5
S S 9 9 3 9 15 Kr S 3 3 S 3
解：闭环特征方程
s( s 1)(Ta s 1) K 0 [ s ( s 1) K ] Ta s 2 ( s 1) 0 Ta s 2 ( s 1) Ta s 2 ( s 1) 1 0 G1 ( s ) s ( s 1) K s ( s 1) K
m * m * K ( pk zi ) K ( s zi ) i 1 Ak ni 1 ( s pk ) n pk ( pk p j ) s ( s p j ) j 1 j 1 s pk