中梁截面几何特性计算表(原来)
- 格式:doc
- 大小:502.00 KB
- 文档页数:13

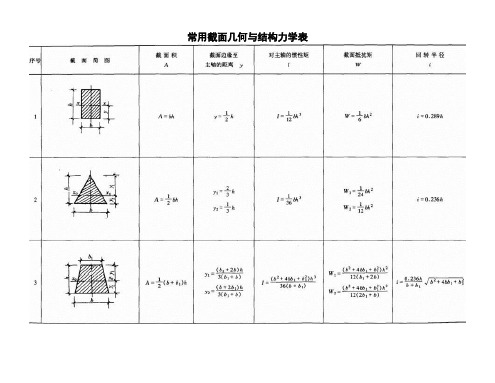
常用截面几何与结构力学表| 1| 2| 3| 4| 5| 6| 7注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
单跨梁的内力及变形表(1)简支梁的反力、剪力、弯矩、挠度| 8| 9| 10 (2)悬臂梁的反力、剪力、弯矩和挠度| 11| 12 (3)一端简支另一端固定梁的反力、剪力、弯矩和挠度| 13| 14 (4)两端固定梁的反力、剪力、弯矩和挠度| 15| 16 (5)外伸梁的反力、剪力、弯矩和挠度| 17| 18| 19等截面连续梁的内力及变形表二跨等跨梁的内力和挠度系数| 20 注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;w =表中系数×ql4/(100EI)。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;w =表中系数×Fl3/(100EI)。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] M B支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mV B左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。

设计资料及构造布置2.1 设计资料2.1.1 桥面跨径及桥宽标准跨径:总体方案选择的结果,采用装配式预应力混凝土箱型梁,跨度25m ,共四跨。
主梁长:伸缩缝采用4cm ,预制梁长24.96m 。
计算跨径:取相邻支座中心间距24.5m 。
桥面净空:20m单侧桥横向布置:0.5⨯2(护栏)+3.75⨯2(两车道)=8.5m2.1.2 设计荷载根据线路的等级,确定荷载等级,由二级公路,设计时速80km/h 可查得: 计算荷载:公路二级荷载。
2.1.3 材料及工艺1)水泥混凝土:主梁、栏杆采用C50号混凝土,桥面铺装采用C50号混凝土。
抗压强度标准值ck f =32.4MPa ,抗压强度设计值cd f =22.4MPa ,抗拉强度标准值tk f =2.65MPa ,抗拉强度设计值td f =1.83MPa ,c E =3.45×410MPa 。
2)预应力钢筋采用(ASTM A416—97a 标准)低松弛钢绞线1×7标准型。
抗拉强度标准值pk f =1860MPa ,抗拉强度设计值pd f =1260MPa ,公称直径15.2mm ,公称面积1392mm ,弹性模量p E =1.95×510MPa 。
2.1.4 设计依据1)《公路桥涵设计通用规范》(JTG D60-2004);2)《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTJ D62-2004);2.2 构造布置2.2.1 主梁间距与主梁片数为使材料得到充分利用,拟采用抗弯刚度和抗扭刚度都较大的箱型截面,按单箱单室截面设计,为减小下部结构的工程数量,采用斜腹式。
施工方法采用先预制,在吊装的方法。
在保证行车道板使用性能—挠度和裂缝控制的前提下,将预制箱梁控制在可以吊装的范围内,整桥横向按6片预制箱梁布置,设计主梁间距均为3.33m,边主梁宽3.23m,中主梁宽3.13m,主梁之间留0.2m后浇段,以减轻吊装重量,同时能加强横向整体性。

①截面几何特性计算
后张法预应力混凝土梁主梁截面几何应根据不同的受力阶段分别计算。
本设计中的T 形梁从施工到运营经历如下三个阶段。
1)主梁预制并张拉预应力根据
主梁混凝土达到设计强度的90%后,进行预应力的张拉,此时管道尚未压浆,所以其截面特性为计入非预应力钢筋影响(将非预应力钢筋换算为混凝土)的净截面,该截面的截面特性计算中应扣除预应力管道的影响。
边梁翼板宽度为1900mm ,中梁翼板宽度为1700mm。
2)灌浆封锚,主梁吊装就位并现浇400mm湿接缝
预应力钢筋张拉完成后并进行管道压浆、封锚后,预应力钢筋能够参与截面受力。
主梁吊装就位后现浇400mm湿接缝,但湿接缝还没有参与截面受力,所以此时的截面特性计算采用计入非预应力钢筋和预应力钢筋影响的换算截面,边梁翼板宽度为1900mm ,中梁翼板宽度为1700mm。
3)桥面及防护栏施工和运营阶段
此时主梁即为全截面参与工作,此时截面特性计算采用计入非预应力钢筋和预应力钢筋影响的换算截面,边梁与中梁翼板宽度为2100mm。
截面几何特性计算可以列表进行,以第一阶段边梁跨中截面为例列表于2-16.
表2-16 边梁第一阶段跨中截面几何特性计算表
注: 54/ 2.010/3.4510 5.797ES S C E E α==⨯⨯=。
同理,可求得其它受力阶段控制截面几何特性如表2-17所示。
表2-17 边梁、中梁各控制截面不同阶段的截面几何特性汇总表
注:p e 为计算截面上钢束重心到截面净矩的距离,p x p e y a =-,其中p a 值见表2-14示。
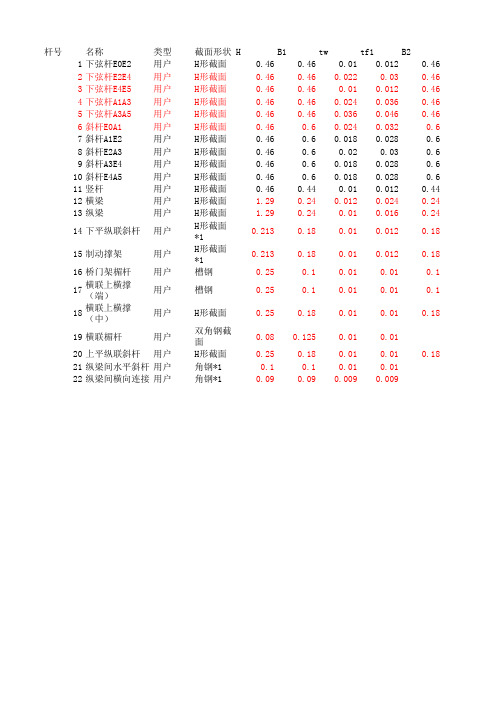
杆号名称类型截面形状H B1tw tf1B2 1下弦杆E0E2用户H形截面0.460.460.010.0120.46 2下弦杆E2E4用户H形截面0.460.460.0220.030.46 3下弦杆E4E5用户H形截面0.460.460.010.0120.46 4下弦杆A1A3用户H形截面0.460.460.0240.0360.46 5下弦杆A3A5用户H形截面0.460.460.0360.0460.46 6斜杆E0A1用户H形截面0.460.60.0240.0320.6 7斜杆A1E2用户H形截面0.460.60.0180.0280.6 8斜杆E2A3用户H形截面0.460.60.020.030.6 9斜杆A3E4用户H形截面0.460.60.0180.0280.6 10斜杆E4A5用户H形截面0.460.60.0180.0280.6 11竖杆用户H形截面0.460.440.010.0120.44 12横梁用户H形截面 1.290.240.0120.0240.24 13纵梁用户H形截面 1.290.240.010.0160.24 14下平纵联斜杆用户H形截面*10.2130.180.010.0120.18 15制动撑架用户H形截面*10.2130.180.010.0120.18 16桥门架楣杆用户槽钢0.250.10.010.010.1 17横联上横撑(端)用户槽钢0.250.10.010.010.1 18横联上横撑(中)用户H形截面0.250.180.010.010.18 19横联楣杆用户双角钢截面0.080.1250.010.0120上平纵联斜杆用户H形截面0.250.180.010.010.18 21纵梁间水平斜杆用户角钢*10.10.10.010.0122纵梁间横向连接用户角钢*10.090.090.0090.009tf2C0.0122-460×300.031-400×240.0122-460×460.0361-368×360.0462-460×120.0321-436×100.0282-460×300.031-400×220.0282-460×360.0281-388×240.0122-600×320.0241-396×240.0160.0122-600×280.0121-404×180.012-600×300.011-400×200.012-600×280.011-404×180.012-600×281-404×182-440×121-436×10。

常用几何截面与结构力学常用公式表
V
max
表示它为相应跨内的最大内力。
常用截面几何与力学特征表中,列出了常用截面的惯性矩、抵抗矩和回转半径等几何及力学特征,这些特征主要用于验算构件截面的承载力和刚度。
其中,惯性矩表示截面对主轴(形心轴)的截面惯性大小,抵抗矩则表示截面抵抗弯曲变形能力的大小。
回转半径则表示截面对扭转的抵抗能力。
单跨梁、简支梁、悬臂梁、一端简支另一端固定梁、两端固定梁和外伸梁等不同类型的梁,都有着不同的反力、剪力、弯矩和挠度等内力和变形特征。
对于等跨连续梁和不等跨连续梁,也有着相应的内力系数表格,可以用于计算相应跨内的最大内力。
在计算中,根据荷载类型的不同,可以使用不同的公式进行计算。
例如,在均布荷载作用下,弯矩M和剪力V可以使
用表格中的系数乘以荷载q进行计算;而在集中荷载作用下,则需要使用表格中的系数乘以荷载F进行计算。
最终得到的
结果可以用于分析和设计相应的结构。
Vmax是荷载在最不利布置时的最大内力。
对于“┌┐”形刚架,内力计算表一和表二分别列出了26、27和28、29两个节点的内力计算结果。
同时,对于“”形刚架,也可以进行内力计算并列出相应的计算表。
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:A dAy I22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:max y IW3.i 称截面回转半径(mm ),其基本计算公式如下:A I i 4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·mV B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
设计资料及构造布置2.1 设计资料2.1.1 桥面跨径及桥宽标准跨径:总体方案选择的结果,采用装配式预应力混凝土箱型梁,跨度25m ,共四跨。
主梁长:伸缩缝采用4cm ,预制梁长24.96m 。
计算跨径:取相邻支座中心间距24.5m 。
桥面净空:20m单侧桥横向布置:0.5⨯2(护栏)+3.75⨯2(两车道)=8.5m2.1.2 设计荷载根据线路的等级,确定荷载等级,由二级公路,设计时速80km/h 可查得: 计算荷载:公路二级荷载。
2.1.3 材料及工艺1)水泥混凝土:主梁、栏杆采用C50号混凝土,桥面铺装采用C50号混凝土。
抗压强度标准值ck f =32.4MPa ,抗压强度设计值cd f =22.4MPa ,抗拉强度标准值tk f =2.65MPa ,抗拉强度设计值td f =1.83MPa ,c E =3.45×410MPa 。
2)预应力钢筋采用(ASTM A416—97a 标准)低松弛钢绞线1×7标准型。
抗拉强度标准值pk f =1860MPa ,抗拉强度设计值pd f =1260MPa ,公称直径15.2mm ,公称面积1392mm ,弹性模量p E =1.95×510MPa 。
2.1.4 设计依据1)《公路桥涵设计通用规范》(JTG D60-2004);2)《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTJ D62-2004);2.2 构造布置2.2.1 主梁间距与主梁片数为使材料得到充分利用,拟采用抗弯刚度和抗扭刚度都较大的箱型截面,按单箱单室截面设计,为减小下部结构的工程数量,采用斜腹式。
施工方法采用先预制,在吊装的方法。
在保证行车道板使用性能—挠度和裂缝控制的前提下,将预制箱梁控制在可以吊装的范围内,整桥横向按6片预制箱梁布置,设计主梁间距均为3.33m,边主梁宽3.23m,中主梁宽3.13m,主梁之间留0.2m后浇段,以减轻吊装重量,同时能加强横向整体性。
史上最全的常用截面几何特性计算公式构件截面的几何性质,如静力矩、形心、轴向惯性矩、极惯性矩、惯性积和主惯性轴位置等,对构件的承载能力有影响,常用于分析构件的弯曲、扭转和剪切。
1.静态力矩:也称为面积力矩或静态表面力矩。
截面对轴线的静力矩等于每个微区的积分乘以整个截面上微区到轴线的距离。
静力矩可以是正的,也可以是负的。
它的维数是长度的三次方。
静力矩的力学意义是:如果有均布载荷作用在截面上,其值表示为单位面积的量,则该载荷在某一轴上的合成力矩等于分布载荷乘以该轴的静力矩。
2、形心:又称面积中心或面积重心,是截面上具有如下性质的点:截面对通过此点任一个轴的静矩等于零。
如果将截面看成一均质等厚板,则截面的形心就是板面的重心。
形心坐标xo、yo的计算公式为:3、惯性矩:反映截面抗弯特性的一个量,简称惯性矩。
截面对某个轴的轴惯性矩等于截面上各微面积乘微面积到轴的距离的平方在整个截面上的积分。
下图所示的面积为A的截面对x、y轴的轴惯性矩分别为:转动惯量总是正的,量纲是长度的四次方。
构件的抗弯能力与轴的惯性矩成正比。
一些典型截面的轴惯性矩可在专业手册中找到。
例如,平行四边形对中心线的惯性矩为4、极惯性矩:反映截面抗扭特性的一个量。
截面对某个点的极惯性矩等于截面上各微面积乘微面积到该点距离的平方在整个截面上的积分。
下图所示面积为A的截面对某点O的极惯性矩为:极惯性矩永远是正的,量纲是长度的四次方。
构件的抗扭能力与惯性矩成正比。
圆形截面相对于其中心的惯性矩为5、惯性积:截面对于两个正交坐标轴的惯性积等于截面上各个微面积乘微面积到两个坐标轴的距离在整个截面上的积分。
面积为A的截面对两个正交坐标轴x、y的惯性积为:惯性积的量纲是长度的四次方。
截面位于坐标系的一、三象限,Ixy为正,位于二、四象限则为负。
6.主惯性轴:使截面惯性积为零的一对正交坐标轴称为截面主惯性轴,简称主轴。
截面对主惯性轴的惯性矩称为主惯性矩。
若两条主惯性轴的交点为质心,则这两条轴称为质心主惯性轴(或称主质心惯性轴)。
中梁截面几何特性计算表(跨中截面)s i i2.1恒载内力计算2.1.1 恒载集度2.1.1.1 预制梁自重a.按跨中截面计,主梁的恒载集度)1(q=m652025.0=⨯16KN/3.b.马蹄抬高,两端加宽所增加的恒载集度q(2)=2.905KN/mc.对边主梁的横隔梁,中横隔梁的体积为:m.1*5972*5.0-.0-3 .0=16.0(**12.0).0228032*1.0125.0*.0m,则同理算得端横隔梁的体积为0.30683')3(q=()253068+⨯/29.96=0.89m5⨯⨯.022280.0KN/对中主梁的横隔梁,'')3(q=2')3(q=1.78mKN/根据以上数据,得到预制梁的恒载集度边梁:q1=q(1)+q(2)+ ')3(q=20.095中梁:q1= q (1)+q(2)+ '')3(q =20.985 2.1.1.2 现浇部分重量a.现浇T 梁翼板恒载集度)5(q =2515.048.0⨯⨯=1.8 m KN /b.对边梁现浇部分横隔梁,一片中横隔梁的体积为:59.10.220.140.16⨯⨯+=0.04773m同理算得一片端横隔梁的体积为85.10.220.220.24⨯⨯+=0.08513m则边梁现浇部分横隔梁的恒载集度为')6(q =()()[]250.085120.04775⨯⨯+⨯/29.96=0.3410m KN /对中梁,')6(q =2')6(q =0.6820m KN /根据以上数据,得到现浇部分恒载集度为)6()5(2q q q += 对边梁,2q =1.8+0.3410=2.141m KN / 对中梁,2q =1.8+0.682=2.482m KN / 2.1.1.3 二期恒载a.铺装8cm 厚的沥青混凝土:23220.08⨯⨯=40.48m KN /5cm 厚的防水混凝土调平层:25240.05⨯⨯=30m KN /将桥面铺装均摊给12片主梁,)7(q ==+123048.40 5.87m KN /b.栏杆和中央分隔带取一侧防撞栏为5m KN /,将两侧的防撞栏和中央分隔带均摊给13片主梁,)8(q =1245⨯=1.67m KN / 根据以上数据,得到二期恒载集度)8()7(3q q q += 对中、边梁,3q =5.87+1.67=7.54m KN /(二)恒载内力计算1.计算恒载弯矩和剪力的公式设x 为计算位置距左边支座的距离,并令a=x/L ,如图主梁弯矩和剪力的计算公式分别为:()q L M 2121ααα-=; ()Lq V αα2-121=2.2 活载内力计算2.2.1 冲击系数和车道折减系数汽车的冲击系数是汽车过桥时对桥梁结构产生的竖向动力效应的增大系数。
对简支梁桥,其基频可采用下列公式估算:ccm EI l f 22π=上式中:c I — 结构跨中截面的截面惯矩l — 结构的计算跨径E — 结构材料的弹性模量c m — 结构跨中处的单位长度质量所以2199.481.9101164.3910267.3813376.58732017106.32.29214.33322=⨯⨯+⨯⨯⨯⨯⨯⨯⨯=f Hz 根据公路桥涵设计通用规范第 4.3.2,当 1.5Hz ≤≤f 14Hz 时,0157.0ln 1767.0-=f μ,则2387.00157.02199.4ln 1767.0=-⨯=μ按公路桥涵设计通用规范第4.3.1条规定,当车道数大于2时,需进行车道折减,6车道的折减系数为0.55,5车道的折减系数为0.60,4车道的折减系数为0.67,3车道的折减系数为0.78,2车道的折减系数为1.00。
2.2.2 计算主梁的荷载横向分布系数 1.2.2.1 跨中的荷载横向分布系数该设计中桥面板之间采用混凝土刚性连接,因此这里采用了刚接梁法来计算荷载的横向分布系数。
a.计算主梁抗扭惯矩I T图2.2.2 I T 计算图式(单位:cm )如图2.2.2所示,翼板的换算平均高度t 1=15+10/4=17.5cm 马蹄的换算平均高度t 3=29+12/2=35cm 对T 梁截面,抗扭惯矩可以近似按下式计算:3i i i m1T t b c I ∑==i上式中:i c —矩形截面的抗扭刚度系数,Ci=1/3×(1-0.63×ti/bi +0.052×(ti/bi)^5)i b —单个矩形截面的宽度i t —单个矩形截面的高度m —梁截面划分成单个矩形截面的个数具体计算见表2.2.2。
计算表②计算抗扭修正系数β对于本桥主梁的间距相同,且主梁为等截面,则得 β=221112Ti ii ii Gl I E a I +∑∑式中:G=0.4E ,L=29.20m ,Ti iI ∑=6×0.00796082.3=0.047765m 4;,a 1=5.10m ,a 2=3.06m ,a 3=1.02m ,a 4=-1.02m ,a 5=-3.06m ,a 6= 5.10 I i =0.21361913m 4 计算得β=0.9711③按修正刚性横梁法计算横向影响线竖标值ηij =1n+β421i ii a ea=∑式中:n=6,521i i a =∑ =2×(5.102+3.062 +1.022)=72.808(m 2)计算结果列于下表中。
④计算荷载横向分布系数1号梁的横向影响线和最不利荷载布置图式如图5所示。
180130180图5 跨中的横向分布系数c m 计算图式(尺寸单位:mm )可变作用(公路—Ⅰ级): 求m cq 对6号梁按照车辆横向排列的规定,两列汽车横向位置如图所示。
边轮离缘石不小于0.5m ,因此,它离6号主梁梁肋的距离为0.8-0.5=0.3m ,四个轮压的合力R=2P ,它的位置离边轮为1.80+0.5*1.30=2.45m ,即离6号梁肋为2.45-0.3=2.15m ,则合力离5号梁肋为0.07m 。
其合力R 的影响线坐标n ,用n4,n5线性内插得n=0.238+(0.3810-0.238)*(2.04-0.07)/2.04=0.376 maxR6=2P*0.376=0.752P= m cq P m cq =0.752桥面为3车道,折减系数为0.78,折减后,m cq =0.752*0.78=0.5866 ⑵支点截面的荷载横向分布系数m 0如图6所示,按杠杆原理法绘制荷载横向影响线并进行布载,6号梁可变作用的横向分布系数计算如下:号3号2号1180130180P1531. 1.000 or图6 支点的横向分布系数0m 计算图式(尺寸单位:mm )可变作用(汽车)m oq =10.502⨯=0.25 ⑶横向分布系数汇总(见表6)1.2.3计算活载内力在活载内力计算中,对于横向分布系数的取值作如下考虑:对中梁,以六号梁为准,计算主梁活载弯矩时,采用全跨统一的横向分布系数m c ,鉴于跨中和四分点剪力影响线的较大坐标位于桥跨中部,故也按不变的m c 来计算。
求支点和变化点截面活载剪力时,由于主要荷载集中在支点附近而应考虑支承条件的影响,按横向分布系数沿桥跨的变化曲线取值,即从支点到4/l 之间,横向分布系数用m 0与m c 值直线插入,其余区段均取m c 值。
对边梁,以中梁来设计。
1.2.3.1计算跨中截面最大弯矩和最大剪力图2.2.7示出跨中截面内力计算图式,计算公式为:()i i c y P m S ∑+=μ1上式中:S —所求截面的弯矩或剪力μ—车辆冲击系数c m —主梁荷载横向分布系数 i P —车道荷载i y —沿桥跨纵向与荷载位置对应的内力影响线坐标值图2.2.7 跨中截面内力计算图式对中梁,弯矩最大时:()()y P q m M k k c +Ω+=μ1max ()()8.98.2168.92.295.05.10257.02387.01⨯+⨯⨯⨯⨯⨯+==3380.18m KN ⋅=V ()()y P m q m k cP k cq 2.11+Ω+μ()()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⨯⨯⨯+⨯⨯-⨯+⎪⎭⎫ ⎝⎛⨯⨯-⨯⨯⨯⨯⨯+=93622.08.3162.18674.09167.05.10752.0904.028.906378.05.22193622.07.36215.10752.02387.01=150.323KN剪力最大时:()()y P q m M k k c +Ω+=μ1()()2.348.2162.345.725.05.1025.02387.01⨯+⨯⨯⨯⨯⨯+==2698.42m KN ⋅=max V ()()y P q m k k c 2.11+Ω+μ=()()5.08.2162.15.06.145.05.10527.02387.01⨯⨯+⨯⨯⨯⨯⨯+=156.87KN 1.2.3.2 计算四分点截面最大弯矩和最大剪力图2.2.8示出四分点截面内力计算图式,当弯矩最大时:()()y P q m M k k c +Ω+=μ1max ()()35.78.21635.72.295.05.10527.02387.01⨯+⨯⨯⨯⨯⨯+==2533.9m KN ⋅=V ()()y P m q m k cP k cq 2.11+Ω+μ()()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⨯⨯⨯+⨯⨯-⨯+⎪⎭⎫ ⎝⎛⨯⨯-⨯⨯⨯⨯⨯+=93622.08.3162.18674.09167.05.10752.0904.028.906378.05.22193622.07.36215.10752.02387.01=252.68图2.2.8 四分点截面内力计算图式剪力最大时()()y P q m M k k c +Ω+=μ1()()2.348.2162.345.725.05.1025.02387.01⨯+⨯⨯⨯⨯⨯+==2245.3m KN ⋅=max V ()()y P q m k k c 2.11+Ω+μ=()()75.08.2162.175.02.2975.05.05.10527.02387.01⨯⨯+⨯⨯⨯⨯⨯⨯+=261.72KN 1.2.3.3 计算变化点截面最大弯矩和最大剪力图2.2.9示出变化点截面内力计算图式图2.2.9 变化点截面内力计算图式当弯矩最大时:()()y P q m M k k c +Ω+=μ1max=V ()()y P m q m k cP k cq 2.11+Ω+μ()()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⨯⨯⨯+⨯⨯-⨯+⎪⎭⎫ ⎝⎛⨯⨯-⨯⨯⨯⨯⨯+=93622.08.3162.18674.09167.05.10752.0904.028.906378.05.22193622.07.36215.10752.02387.01=280.35m KN ⋅当剪力最大时:()()y P q m M k k c +Ω+=μ1()()2.348.2162.345.725.05.1025.02387.01⨯+⨯⨯⨯⨯⨯+==782.54m KN ⋅=max V ()()y P m q m k cP k cq 2.11+Ω+μ()()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⨯⨯⨯+⎪⎪⎪⎭⎫ ⎝⎛⨯⨯-⨯-+⨯⨯⨯⨯⨯+=93622.08.2162.16748.08741.05.10527.08674.025.28.993622.07.265.05.10257.02387.01=282.86KN1.2.3.4 计算支点截面的最大剪力图2.2.10示出支点截面内力计算图式图2.2.10 支点截面内力计算图式=max V ()()y P m q m k cP k cq 2.11+Ω+μ()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯-⨯+⨯⨯⨯⨯⨯+=18.2162.1904.09167.05.10527.0904.028.919.25.05.10527.02387.01=345.19KN2.3 主梁内力组合(1)基本组合(用于承载能力极限状态计算)QK GK d 4M .12M .1M += QK GK d 4V .12V .1V +=(2)短期组合(用于正常使用极限状态计算)μ++=1M 7.0M M QK GK Sμ++=1V 7.0V V QK GK S(3)长期组合(用于正常使用极限状态计算)μ++=1M 4.0M M QK GK Lμ++=1V 4.0V V QK GK L计算结果如表2.2.7所示。