当前位置：文档之家 › 第二讲纳什均衡

第二讲纳什均衡

  • 格式：ppt
  • 大小：430.50 KB
  • 文档页数：51

下载文档原格式

  / 51

合集下载

博弈论纳什均衡

博弈论纳什均衡

博弈论纳什均衡什么是纳什均衡？1、纳什均衡（Nash equilibrium )，又称非合作博弈均衡，是博弈论概念，指的是：一种博弈稳定结果，谁单方改变策略，谁就会损失。

两个囚徒互相揭发，就是一种纳什均衡。

对于每个囚徒来说，如果打破纳什均衡，在对方实施揭发策略时，改变揭发策略，保持沉默，自己就会由判刑2年，变成判刑5年。

也就是说，两个囚徒互相揭发是稳定博弈结果，谁单方改变策略，就会受到损失。

这也就是均衡涵义所在，两个囚徒从利己角度，都不会单方改变策略。

博弈策略稳定，博弈结果也稳定。

之所以命名为纳什均衡，是因为提出者是经济学家、博弈论创始人约翰．纳什。

之所以称为非合作博弈均衡，原因就是：两个囚徒如果合作，互相保持沉默，各自只要坐牢1年；但最终博弈结果，也就是纳什均衡显著特征，是不合作。

2、纳什均衡意义重大。

纳什均衡提出，震动整个经济学界。

诺贝尔经济学奖得主萨缪尔森曾说：“你只要教会鹦鹉说‘需求和供给’，它也是经济学家。

”博弈论专家坎多瑞则说：“这只鹦鹉现在必须多学一个词了，那就是‘纳什均衡’。

”诺贝尔经济学奖得主迈尔森也说：“发现纳什均衡意义，可以和生命科学中发现DNA 双螺旋结构相媲美。

”纳什也因为提出纳什均衡，创立博弈论，而获得1994年诺贝尔经济学家奖。

纳值均衡意义重大，简单来说，就是它对于经济学具有重大意义。

读友们如果了解经济学看不见的手原理，就知道，古典经济学认为，通过市场这只‘看不见的手’调节，个体追求私利行为，会促进集体利益最大化。

但纳什均衡却违反上述原理：两个囚徒分别追求私利行为，并没有促进集体（囚徒整体）利益最大化，反而是损人不利己。

这正是市场失灵软肋之处，通过博弈论视角可以得到合乎逻辑解释，更有条件找到合适解决方案。

从上述这点，读友们可以“一斑窥全豹”，感受到博弈论重要性。

更重要的是，纳什均衡非常普遍，小至个人沟通，中到公司竞争，大到国家往来，都可以观察到。

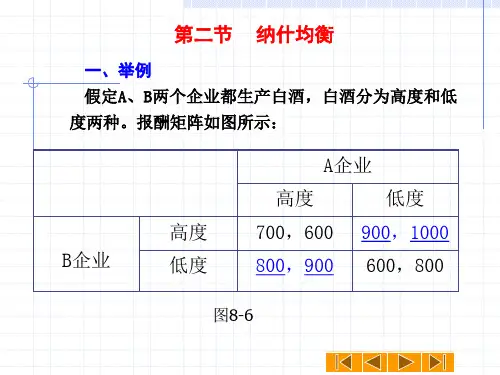
Q2：怎样运用纳什均衡？1、分析囚徒困境。

第2章 Nash均衡

第2章 Nash均衡

剔除劣战略行为
• 在博弈中，如果战略 si′是参与人i的劣战略， 那么参与人i肯定不会选择战略 si′ 。这也就相 当于参与人将战略 si′ 从自己的战略集 Si 中剔 除掉，直接从战略集 Si \{si′} 中选择自己的战 略。参与人的这种选择行为我们称之为剔除 劣战略行为。 • 剔除劣战略行为也是理性参与人选择行为的 基本特征之一。
Control Science and Engineering, HUST All Rights Reserved, 2007, Luo Yunfeng
对经典经济学的冲击
• 古典经济学的创始人亚当·斯密曾经描 述，市场机制这只“看不见的手”，会 引导人们自利的行为促进社会的福利。 博弈论的“囚徒困境”却揭示，非合作 的自利行为可能导致两败俱伤的情景。
现实中的“囚徒困境”
• 见义勇为者常常孤立无缘； • 我国的应试教育制度下，学生的负担、家 长的焦虑； • 军备竞赛 • 价格大战（家电、民航、奶业）
“囚徒困境”的正面效用
• 从消费者的角度，竞争带来降价，得到 实惠。 • 从企业的角度，鼓励竞争，激励企业不 断创新，开发新技术，提升产品质量， 拓展市场，从而赢得市场。
“新产品开发博弈”中的占优战略均衡
• 当市场需求大时，在完全信息静态的“新产品 开发博弈”中，企业1和2都有占优战略“开 发”，因此，博弈的结果为占优战略均衡(开发， 开发)。 企业2
开发
开发
300, 300 0, 800
不开发
800, 0 0, 0
企业1
不开发
Control Science and Engineering, HUST
• 一个战略组合 要成为博 弈的结果，就必须满足：对于所有的参 * 与人，当其他参与人选择战略组合 s 中 * s 给定的战略时，选择 中相应的战略所 得到的支付不小于选择其它战略所得到 的。

第二节 纳什均衡

第二节 纳什均衡

通俗的讲，就是给定你的最优选择，我会选择能 够使我最优的选择，或者说，我选择在给定你的选择 的情况下我的最优选择，你选择了给定我选择情况下 你的最优选择。这种均衡最后到底均衡在哪一点，由 具体情况决定。在存在帕累托改善的情况下，可能会 达到帕累托最优。
在本例中，B企业选择了生产高度白酒，A企业选 择生产低度白酒是一种均衡；B企业选择了生产低度白 酒，A企业选择生产高度白酒也是一种均衡。由于在B 企业选择生产高度白酒，A企业选择生产低度白酒的时 候，A、B两企业的收益都比B企业选择生产低度白酒， A企业选择生产高度白酒时的收益要高，存在着帕累托 改善，因此最后可能会达到帕累托最优，即B企业选择 生产高度白酒，A企业选择生产低度白酒。
二、无纳什均衡的例子 实际上，纳什均衡也是一种特殊情况，并不是所 有的博弈都会产生纳什均衡。例如：在足球比赛中， 罚点球的时候，守门员和罚球者也构成一个博弈，双 方的收益矩阵如下图所示：
守门员
左中右
左 -1，1 1，-1 1，-1
点
球
中 1，-1 -1，1 1，-1
者
右 1，-1 1，-1 -1，1
由于在b企业选择生产高度白酒a企业选择生产低度白酒的时候ab两企业的收益都比b企业选择生产低度白酒a企业选择生产高度白酒时的收益要高存在着帕累托改善因此最后可能会达到帕累托最优即b企业选择生产高度白酒a企业选择生产低度白酒
第二节 纳什均衡
一、举例 假定A、B两个企业都生产白酒，白酒分为高度和低 度两种。报酬矩阵如图所示：
同样，当罚球者判断守门员将向右扑球时，罚 球者将向左或中发球；当罚球者判断守门员将向右 扑球时，罚球者将向右或中发球；当罚球者判断守 门员将向中扑球时，罚球者将向左或右发球。此时 果守门员也选择 了右，罚球者将得 -1，守门员将得 +1；如果守门员 选择了左或者中，罚球者将得 +1，守门员将得 -1。

《博弈论：原理、模型与教程》第02章Nash均衡第03节Nash均衡

《博弈论：原理、模型与教程》第02章Nash均衡第03节Nash均衡

《博弈论：原理、模型与教程》第一部分完全信息静态博弈第2章Nash均衡「 -------------------------------------第2.1节占优行为第2.2节重复剔除劣战略行为第2.3节Nash均衡2.3 Nash 均衡（已精细订正！）1、定义2-5I2、一定理，及其证明I3、简单博弈问题Nash均衡的求解：划线法；箭头法I _________________________________________________________前面两小节分析了理性参与人在博弈中的战略选择行为一行为与剔占优除劣战略行为。

但是，在大多数博弈问题中，参与人的占优战略是不存在的，而且所有参与人同时存在占优战略的情形更是少见；剔除劣战略虽然可以在一定程度上简化博弈问题的求解，但在相当多的博弈中是无法使用重复剔除劣战略的方法求解博弈问题的（如图2-4和图2-6所示的战略式博弈）。

为了完全解决完全信息博弈的求解问题，需要选找新的方法和定义新的博弈解。

探寻博弈问题的解，必须明确：博弈分析是在博弈问题的结构和参与人完全理性为共同知识的假设下进行的，而在该假设下，人们（或博弈论专家）对博弈问题的求解就等同于完全理性的参与人对博弈问题的求解。

因此，可以采用内省式思维分析博弈问题的解。

考察战略式博弈的解。

假设参与人i （i =1,2r ,n）在博弈开始之前对博弈的结果进行预测，并且预测战略组合（s「,sj将成为博弈的结果。

现在的问题是：参与人i的这种预测是否一定就是博弈的真正结果？或者说参与人的预测在什么情况下才是正确的? 参与人i的预测战略组合（s「,s丄）将成为博弈结果，也就意味着参与人i 预测其他参与人的选择为S丄。

在预测其他参与人的选择为S」情况下，参与人i自己的选择S*怎样才是合理的呢？或者说参与人i选择S*应该满足什么样的条件呢？显然，对于理性的参与人i来讲，其选择S*必须满足这样的条件：在其他参与人的选择为S；的情况下，选择S出的所得必须不小于选择其他任何战略的所得，或者说S「必须是使自己的所得最大化的选择。

信息经济学理论之二：纳什均衡

信息经济学理论之二：纳什均衡

信息经济学理论之二：纳什均衡纳什由于引进了合作博弈与非合作博弈的区分, 并为非合作博弈创立了一种均衡概念. 这种均衡概念现在被命名为纳什均衡.纳什均衡理论经典解释：一农户在杀鸡前的晚上喂鸡，不经意地说：快吃吧，这是你最后一顿！第二日，见鸡已躺倒并留遗书：爷已吃老鼠药，你们别想吃爷了，爷他妈也不是好惹的。

当你知道了别人的决定之后，就能做出对自己最有利的决定。

——诺贝尔经济学奖经典理论选编1994年诺贝尔经济学奖的获得者是美国普林斯顿大学的约翰·纳什。

纳什获得诺贝尔经济学奖的原因是他在博奕沦领域的贡献，他提出了“纳什均衡”理论、关于博奕论，流传最广的是一个叫做“囚徒困境”的故事：话说有一天，一个富翁在家中被杀，财物被盗；警方在此案的侦破过程中，抓到两个犯罪嫌疑人张三和李四，并从他们的住处搜出被害人家中丢失的财物。

但是，他们矢口否认曾杀过人，辩称他们只是顺手牵羊偷了点儿东西。

于是警方将两人隔离，分别关在不同的房间进行审讯。

警察分别对张三和李四说，“由于你们的偷盗罪已有确凿的证据，所以可以判你们1年刑期。

但是，我可以和你做个交易。

如果你单独坦白杀人的罪行，我只判你3个月的监禁，但你的同伙要被判10年刑。

如果你拒不坦白，而被同伙检举，那么你就将被判10年刑，他只判3个月的监禁。

但是，如果你们两人都坦白交代，那么，你们都要被判5年刑。

”张三和李四怎么办呢?他们面临着两难的选择——坦白或抵赖。

显然最好的策略是双方都抵赖，结果是大家都只被判一年。

但是由于两人处于隔离的情况下无法串供，按照亚当·斯密的理论，每一个人都是一个“理性的经济人”，都会从利己的目的出发进行选择。

这两个人都会有这样一个盘算过程：假如他招了，我不招，得坐10年监狱，招了才5年，所以招了划算；假如我招了，他也招，得坐5年，他要是不招，我就只坐3个月，而他会坐10年牢，也是招了划算。

综合以上几种情况考虑，不管他招不招，对我而言都是招了划算。

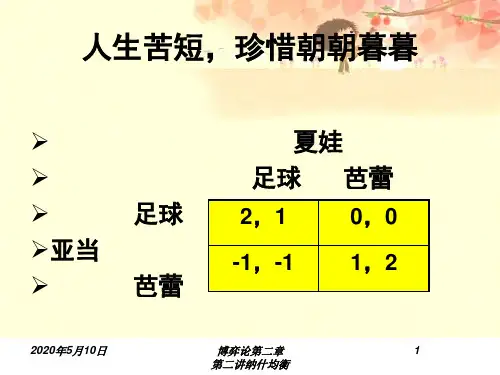
第二讲纳什均衡

第二讲纳什均衡

习题：齐威王田忌赛马矩阵

上中下 上中下
田忌
上下中 中上下 中下上 下中上 下上中
+3，-3 +1，-1 +1，-1 -1，+1 +1，-1
+1，-1 +3，-3 -1，+1 +1，-1 +1，-1
+1，-1 +1，-1 +3，-3 +1，-1 -1，+1
+1，-1 +1，-1 +1，-1 +3，-3 +1，-1
在第二行1 下划线
2015年12月6日
博弈论第二章 第二讲纳什均衡
20
第三节 纳什均衡
三、寻找纳什均衡的方法 （二）相对优势策略划线法 3.设定甲靠左行（第一行） 乙： 1>-1 乙相对优势策略：靠左行
在第一列 1下划线
2015年12月6日
博弈论第二章 第二讲纳什均衡
21
第三节 纳什均衡
四、古诺模型 max i 2.企业i的目标： π1=？，π2=？ 3.企业利润最大化的一阶、二阶条件
1 0 q1 2 0 q2
2015年12月6日
2 1 2 0 2 q1 2 2 2 0 2 q 2
博弈论第二章 第二讲纳什均衡
35
第三节 纳什均衡
27
第三节
纳什均衡
要点：（1）箭 头指向的支付 大；（2）只有 一方单独改变 策略
三、寻找纳什均衡的方法 （三）箭头指向法 2.分析：（适度放牧，过度放牧） （1）给定乙不变，甲改变：0→10 （箭头向上） （2）给定甲不变，乙也不变
2015年12月6日
博弈论第二章 第二讲纳什均衡

第二讲多重纳什均衡

第二讲多重纳什均衡

---------------------------------------------------------------最新资料推荐------------------------------------------------------第二讲多重纳什均衡友军博弈英国支持巴顿支持蒙帅支持巴顿美国支持蒙帅友军博弈特征两个（多个）纳什均衡问题：博弈的最终结果？第三章混合策略纳什均衡第三节多重纳什均衡的选择标准第三节多重纳什均衡的选择标准一、帕累托优势标准：得益更大（一）案例：战争与和平 C 国鹰战略鸽战略鹰战略 A 国鸽战略第三节多重纳什均衡的选择标准一、帕累托优势标准：得益更大（二）纳什均衡的选择标准帕累托优势标准按照支付大小筛选纳什均衡第三节多重纳什均衡的选择标准二、风险优势标准：风险更小？（一）案例：串通作弊博弈学生乙作弊不作弊作弊学生甲不作弊第三节多重纳什均衡的选择标准二、风险优势标准：风险更小（二）分析：偏离损失比较法 1. 甲：单独偏离均衡的损失（1）偏离作弊：9-8=1 （2）偏离不作弊：7-0=7 第三节多重纳什均衡的选择标准二、风险优势标准：风险更小（二）分析：1 / 5偏离损失比较法 2. 乙：单独偏离均衡的损失（1）偏离作弊：9-8=1 （2）偏离不作弊：7-0=7 第三节多重纳什均衡的选择标准二、风险优势标准：风险更小（二）分析：偏离损失比较法3. 偏离损失比较方法：偏离作弊的损失 VS 偏离不作弊的损失 11 ＜77 第三节多重纳什均衡的选择标准二、风险优势标准：风险更小（二）分析：偏离损失比较法 4. 结论（1）偏离（不作弊，不作弊）的损失更大：49 （2）不偏离（不作弊，不作弊）第三节多重纳什均衡的选择标准二、风险优势标准：风险更小（三）纳什均衡的选择标准：风险优势标准比较不同纳什均衡之间的风险状况，风险小的纳什均衡优先第三节多重纳什均衡的选择标准三、聚点均衡（一）案例：城市分组博弈参与人：甲乙策略：把上海、长春、南京、哈尔滨四个城市分成两组，每组 2 个城市支付：甲乙分法相同――奖励 100 元；甲乙分法不同――奖励 0 元---------------------------------------------------------------最新资料推荐------------------------------------------------------第三节多重纳什均衡的选择标准三、聚点均衡（二）聚点均衡 1. 标准使用社会文化习惯、博弈历史等信息达到均衡 1 、 10 、 66 、888 2. 实质规律性第三节多重纳什均衡的选择标准四、相关均衡（一）案例：地域连坐下的产品质量博弈企业乙好产品差产品好产品企业甲差产品第三节多重纳什均衡的选择标准四、相关均衡（二）相关均衡参与人主动设计某种形式的选择机制，形成制度安排，从而确定最终均衡三鹿事件出现后，河北省其他食品企业以后如何做？第三节多重纳什均衡的选择标准五、抗共谋均衡（一）案例：抽象的选择乙左右上甲下乙左右上甲下第三节多重纳什均衡的选择标准五、抗共谋均衡（二）共谋偏离（集体偏离）均衡的激励 1. 如果集体偏离（上，左， A）（1）起因：甲、乙集体偏离，选（下，右， A）（2）结果：甲的支付 01 ，乙的支付 01 （3）结论：甲、乙有集体偏离的动机，（上，左， A）非抗共谋均衡第三节多重纳什均衡的选择标准五、抗共谋均衡（二）共谋偏离（集体偏离）均衡的激励 2. 如果集体偏离（下，右， B）（1）若甲、乙集体偏离，选（上，左， B） -1-2 ， -1-2 （2）若甲、丙集体偏离，选（上，右， A） -1-5 ， 50 （3）若乙、丙集体偏离，选（下，左， A） -1-5 ， 50 （4）结论：缺乏集体偏离的激励，（下，右， B）为抗共谋均衡猎鹿博弈：3 / 5何为抗共谋均衡？乙猎鹿打兔猎鹿甲打兔金无足赤，人无完人人总是要犯错误的，所以要对别人宽容经得起考验的纳什均衡在其他参与人选择了错误策略的情况下，某参与人仍能实现纳什均衡第三节多重纳什均衡的选择标准六、颤抖手精炼均衡Trembling-hand perfect equilibrium （一）颤抖手某一参与人的非蓄意错误博弈偏离均衡路径的原因第三节多重纳什均衡的选择标准六、颤抖手精炼均衡（二）颤抖手均衡 1. 基本思想给定所有参与人均可能犯错误的情况下，如果某一策略组合仍是每一个参与人的最优策略组合，则实现颤抖手均衡第三节多重纳什均衡的选择标准六、颤抖手精炼均衡（二）颤抖手均衡 2. 定义: m――mistake n 人博弈中，对于每一个博弈方 i，存在严格混合策略序列，使下列条件得到满足：（1）尽管每一个博弈方可能犯错误，但错误收敛于零――总有一天能成功穿针引线――功夫不负有心人将一条线穿入针眼，手在不停颤抖，不大可能一下子穿进去但如果试的次数足够大，总是能够成功第三节多重纳什均衡的选择标准六、颤抖手精炼均衡（二）颤抖手均衡 2. 定义：m――mistake n 人博弈中，对于每一个博弈方 i，存在严格混合策略序列，使下列条件得到满足：（2）对于任何可选择的混合策略穿针引线― ― a name=baidusnap0/aB style=‘ color: black; background-color: #ffff66’ 学会宽容/B纳什均衡：---------------------------------------------------------------最新资料推荐------------------------------------------------------ 每一个人都把线穿入针眼宽容：某参与人不能因为其他参与人可能暂时无法把线穿进针眼而故意不把线穿进针眼本章作业 P143-146 1 、 7、 11 、 19 、 20 、21 、 22 、 24 、25 *博弈论第三章第二讲多重纳什均衡 3， 4 1，1 2， 2 4， 3 10 ，10 -10 ， 8 8， -10 -5 ， -5 10 ， 10 -10 ，8 8， -10 -5 ， -5 7， 7 8， 0 0， 8 9， 9 帕累托优势？ 7， 7 8， 0 0， 8 9， 9 7， 7 8， 0 0， 8 9， 9 7， 7 8， 0 0， 8 9，9 7， 7 8， 0 0， 8 9， 9 7，7 8， 0 0， 8 9， 9 -2 ， -2 -2 ，-8 -8 ， -2 4， 4 -2 ， -2 -2 ，-8 -8 ， -2 4， 4 1， 1， -5 -5 ， -5 ， 0 -5 ， -5 ， 0 0， 0，10 丙：A -1 ， -1 ， 5 -5 ， -5 ， 0 -5 ， -5 ， 0 -2 ， -2 ，0 丙：B 4， 4 4， 0 0， 4 10 ， 10 他人不犯错误，你能实现最优；他人犯错误，你仍能实现最优一个人用手抓东西时，手一颤抖，就可能抓不住他想抓的东西：非蓄意错误如何理解？宽容是一种美德 * 博弈论第三章第二讲多重纳什均衡* *div id=loadingADdiv class=ad_boxdiv class=waitingstrong文档加载中. . . /strong 广告还剩em id=adtime/em秒5 / 5。

第二讲纳什均衡

第二讲纳什均衡

美苏军备竞赛
前苏联
扩军 扩军
美 国 －2000 －2000
裁军
－∞ 8000
裁军
－∞
8000
0 0
扩军
百万裁军的论证
• 背景：世界力量的多元化，使得相互制约格局已形成。 背景：世界力量的多元化，使得相互制约格局已形成。各方面的力量都 在发展，绝对的强弱关系让位于相对的强弱关系。 在发展，绝对的强弱关系让位于相对的强弱关系。相对强的一方并不足 于把对方吃掉，相对弱的一方已经有力量做相当的抗争。 于把对方吃掉，相对弱的一方已经有力量做相当的抗争。 • • • 1984年前后，军委主席邓小平同志主持中国人民解放军百万大裁军。 年前后，军委主席邓小平同志主持中国人民解放军百万大裁军。 年前后 博弈双方有三个可供选择的策略：成本为 亿的扩军； 博弈双方有三个可供选择的策略：成本为2000亿的扩军；一个是预算为 亿的扩军 0的不设防策略；一个为成本为500亿美元的有限军备策略 的不设防策略；一个为成本为 的不设防策略 亿美元的有限军备策略 如果都采取有限军备，双方均占不到便宜，盈利为－ 亿美元； 如果都采取有限军备，双方均占不到便宜，盈利为－500亿美元；一个 亿美元 为有限军备，另一个为扩军，则扩军一方获利 亿美元， 为有限军备，另一个为扩军，则扩军一方获利400亿美元，其纯盈利为 亿美元 400－2000＝－ － ＝－1600亿美元，有限军备的一方，损失为 亿美元， 亿美元， ＝－ 亿美元 有限军备的一方，损失为1000亿美元，其纯 亿美元 盈利为－ ＝－1500亿美元；其余同上 亿美元； 盈利为－1000－500＝－ － ＝－ 亿美元
上策均衡法
• 上策均衡：一个博弈的某个策略组合中的所有策略都是 上策均衡： 各个博弈方各自的上策

纳什均衡-文档资料

纳什均衡-文档资料
* 1 * 2 * 3

此为三农户同时独立决定数量时所获得的 稳定结果。任何单方面的擅自改变会使自己受 损。各自得益为784，三农户总收益为2352。
从总体利益的角度来考察公共草地上羊的最 佳数量。设羊的总数为 Q，则总得益为：
精品课程《运筹学》

( 120 Q ) 8 Q=112 P= Q

G = S , S , S ; h , h , h 1 2 n 1 2 n
精品课程《运筹学》
第二节 纳什均衡
S , S , S ; h , h , h 1 2 n 1 2 n 定义8.2.1 在对策 G = 中， 如果有由各个对策方的各选取一个策略组成的 i * * * S , S , S 某个策略组合 中，任一对策方 的策 1 2 n * Si 略为 ，都是对其余策略方策略的组合 * * * * S , S , S S 1 i i 1 n 的最佳策略，即 * * * * * * * * * h ( S , S , S , S , S ) h ( S , S , S , S , S ) i 1 i 1 i i 1 n i 1 i 1 ij i 1 n
精品课程《运筹学》
第二节 纳什均衡
过这个限度，每只羊都无法吃饱，从而羊的产
出就会减少，甚至只能勉强存活或要饿死。假 设这些农户只有夏天才到公共草地放羊，而每 年春天决定养羊的数量，各农户在决定自己养 羊的数量时是不知道其他农户的养羊数量的， 各农户养羊数的决策是同时作出的。假设下面 信息知道的：每只羊的产出（价格）是羊只总 Q q q q p 120 Q 数的减函数， ， , q i 为第 i个农 1 2 3 户饲养羊的数量，每只羊的饲养成本为8元。

《博弈入门》第二章：纳什均衡：理论

《博弈入门》第二章：纳什均衡：理论

努⼒⼯作游⼿好闲努⼒⼯作2,23,0游⼿好闲0,31,1《博弈⼊门》第⼆章：纳什均衡：理论1 策略型博弈策略型博弈是决策者之间相互作⽤的模型。

正是因为相互作⽤,我们称决策者为局中⼈。

每个局中⼈有⼀个可选⾏动的集合。

模型中的每个局中⼈受到所有局中⼈⾏动的影响,⽽不仅是受到她⾃⼰⾏动的影响,从⽽获得局中⼈之间的相互作⽤。

尤其是,每个局中⼈对于⾏动剖⾯⼀-所有局中⼈⾏动的列表(参见17.4节中关于剖⾯的讨论)---都有⾃⼰的偏好。

定义2.1（具有序数偏好的策略型博弈）（具有序数偏好的）策略型博弈由如下要素组成：局中⼈集合对于每个局中⼈，有⼀个⾏动集合对于每⼀个局中⼈，有关于⾏动剖⾯集合的偏好2.2 囚徒困境2.2.1 合作项⽬你和朋友合作-⼀个项⽬。

你们每个⼈可以要么努⼒⼯作要么游⼿好闲。

如果你的朋友努⼒⼯作,⽽你乐意游⼿好闲(如果你也努⼒⼯作的话，项⽬的结局将会好--些，可是其价值的增量对你来讲不值得付出额外的努⼒)。

你喜欢你们俩都努⼒⼯作的结局甚于你们俩都游⼿好闲(在这种情况下,什么都没有完成),对于你,最差的结局是你⼯作很努⼒⽽你的朋友却游⼿好闲(你痛恨被“剥削")。

如果你的朋友有相同的偏好,那么模拟你所⾯对情形的博弈将在图2.2中给出,如你所看到，这个博弈与“囚徒困境”的不同仅在于⾏动的名称。

我们并没有断⾔，两个⼈从事⼀个合作项⽬的情况必定具有“囚徒困境”的结构，只有当局中⼈的偏好与“囚徒困境”中⼀样时才是!例如,如果在其他⼈努⼒⼯作时每个⼈都喜欢努⼒⼯作甚于游⼿好闲,那么“囚徒困境”就不模拟这种情况:局中⼈的偏好与图2.2中给出的偏好不同。

2.2.2 双寡头垄断左图的博弈与“囚徒困境”的不同之处不仅在于局中⼈⾏动的名称，还在于其中两个局中⼈的偏好上有所不同。

右图的博弈与“囚徒困境”的不同之处仅在于局中⼈⾏动的名称。

随机坚持随机1/2（H+L）,1/2(H+L)L,H坚持H,L S,SS>L2.4例证：匹配硬币（⽆冲突博弈）我们研究的求解理论有两个部分。

02-博弈中的纳什均衡与一致预期PPT课件

02-博弈中的纳什均衡与一致预期PPT课件
❖ (3)second-order CKR: (1)+(2)+每个人知道（2）
❖ nth-order CKR: R(b)C(b)R(b)……C(b)R is rational,
报考北大研究生？
.
你知道其他的人的 想法？
10
重复剔除与理性共识
❖ 重复剔除不仅要求每个人是理性的，而且要求每个人知道其 他人是理性的，每个人知道每个人知道每个人是理性的，如 此等等，即理性是“共同知识”（共识）
敌不动，我不动
❖ 例如：乒乓球，生气
.
15
纳什均衡的作用：一致预期
❖ 一致预期：基于信念的选择是合理的；支持 选择的信念是正确的；
❖ 预期的自我实现：如何所有人认为这个结果 会出现，这个结果就会出现。预期是自我实 现的，预期不会错误。如果你认为我预期你 将选择X，你就真的会选择X。
当你知道这样的纳什均衡结果将来会存在，你 会作怎样的当期决策？
甲乙
··1/2
图1 商业位置博弈
.
24
❖ 所以给定甲在1/2处设店，乙在紧靠甲的 左边或右边设店是最优的。反过来，给 定乙在接近1/2处设店，甲的最优选择也 是在1/2附近设店。这样，甲和乙挤在1/2 处设店就是纳什均衡，这就是商业中心 区的形成原理。
❖ 例如：电视台节目；禁娱、禁广告插播、 禁广告植入？
❖ 政策的猛烈炮火，使地产股俨然成为了 近期A股市场的“炮灰”。失守3000点的沪深 股市，地产股悲剧持续演绎。继4月19日房地 产指数下跌7.58%以后，昨日(4月20日)，该指 数再度下跌2.91%。无论是招、保、万、金等 传统的四大天王，还是先前基金青睐的二三 线城市地产股，二级市场上都遭遇了前所未 有的持续打压。

第2章 纳什均衡

第2章 纳什均衡
PA UA = PB δ A类消费者购买商品A A类消费者购买商品 B
PA δ UB = PB
B类消费者购买商品A B类消费者购买商品B
q 用 q A 表示消费者对于产品A的需求量; B 表 示消费者对于产品B的需求量.则 0 PA > PB +δ qA = nA PB δ ≤ PA ≤ PB +δ n +n PA < P δ A B B
为纳什均
衡的充要条件是对任何局中人,支付差为
* * u i ( s i* , s i ) u i ( s i , s i ) ≥ 0
,而与这个差
值是多少无关,由此可导出纳什均衡的一个性质: 纳什均衡的不变性
命题2.1 设 命题
G = N, S1 , , Sn , u1 , , u n
为已知策略型博弈.下不变. 正仿射变换 对 ,令 i∈N
ui' ( s) = δ iui ( s) + Ci ,其中
δ i > 0 ,则G与
' G' = N,S1,,Sn , u1,, u'n 有相同的纳什均衡.
(2)纳什均衡在支付函数的局部变换 局部变换下不变. 局部变换 给定
si ∈S i
定义2.2表明,局中人i的最优化反应映射 ri (s) 仅与 s i 有关. 反应函数 当 ri (s) 为单点集时,称 ri (s ) 为局中人i的最优反应函数 最优反应函数,简称 最优反应函数 反应函数.这时将 ri (s ) 记为 BRi (s i ) . 反应函数
定义2.3 最优反应映射 定义
G的纳什均衡可由以下划线法 划线法求得. 划线法 例2.4在囚徒困境问题中,其支付矩阵为
C C ( 5, 5 ) D ( 8, 0 )

第二讲纳什均衡

第二讲纳什均衡

R3
寻找纳什均衡
参与人B
L C R
参 与 人
U M D
0，4 4，0
3，5
4，0 0，4
3，5
5，3 5，3
6，6
A
公共地的悲剧
公共地的悲剧（tragedy of the commons）是制 度经济学家非常熟悉的例子（Hardin,1968），这个 例子证明，如果一种资源没有排他性的所有权，就 会导致对这种资源的过度使用。 像公海捕鱼就属于这一类问题。 中国一些地区小煤窑的过度发展也属于这类 问题。 公共草地问题证明了纳什均衡常常是低效率 的，最后导致公共草地被过度使用。
三、寻找纳什均衡的方法 （三）箭头指向法 1.（适度放牧，适度放牧） （1）给定乙不变，甲改变：20→30 （箭头向上） （2）给定甲不变，乙改变：20→30 （箭头向左）
第二节
纳什均衡
要点：（1）箭 头指向的支付 大；（2）只有 一方单独改变 策略
三、寻找纳什均衡的方法 （三）箭头指向法 2.（适度放牧，过度放牧） （1）给定乙不变，甲改变：0→10 （箭头向上） （2）给定甲不变，乙也不变
2、纳什均衡一定是在重复剔除严格劣战略过 程中没有被剔除掉的战略组合，但没有被剔除 的战略组合不一定是纳什均衡，除非它是唯一 的。（这句话并不适用于弱劣战略剔除的情况）
第二节
纳什均衡
三、寻找纳什均衡的方法 （一）劣势策略反复消去法 民主党 主动增税 被动增税 2，2 1，4 主动增税 共和党 4，1 3，3 被动增税
第二节
纳什均衡
要点：（1）箭 头指向的支付 大；（2）只有 一方单独改变 策略
三、寻找纳什均衡的方法 （三）箭头指向法 3.（过度放牧，适度放牧） （1）给定乙不变，甲也不变 （2）给定甲不变，乙改变：0→10 （箭头向左）

第二讲(占优均衡、纳什均衡)

第二讲(占优均衡、纳什均衡)

纳什均衡 – 收益占优均衡
• 案例：推与不推博弈
– 吉姆和卡尔开车驶在同一条路上，有棵大树挡住了道路。 两人可以选择都去推树，树会被成功的挪走（每人收益 5）。如果一人推，一人不推，则推的人会受伤（收益 是-10），另一个人要需要将伤者送到医院（收益是0）。 如果两人都不推，就必须掉头驶回（两人收益都为1）。
垃圾处理博弈收益矩阵
甲先生
倾倒
雇卡车
乙先生 倾倒 4000, 4000 5000, 3500 雇卡车 3500，5000 4500，4500
• 在该博弈中，对于甲先生和乙先生，他们最优的战略就是“倾倒垃 圾”，因此即为他们的占优战略。
• 劣战略：如果第二个战略被第一个战略占优，那么第二个战略被 称为劣战略。显然，雇卡车是该博弈的劣战略。
A 40 B 10 A 15 B 15
存在两个以上战略的博弈
• 教科书博弈：
– H和K两位教授都在编写经济教科书。两本书质量相同，但篇 幅长短不同。一般情况下，如果质量一样，教师会选择篇幅 长一点的教科书。当然，每个人都想获得更多的读者，但增 加篇幅需要付出更多的努力。两位作者不想写得太长，只要 能战胜对方就可以了。
协调博弈 (Coordination game)
• 在协调博弈中，只有协调 彼此的战略选择，参与者 才能得到最优的收益。
– 推与不推博弈就是一个协调 博弈。
• 案例：赶集日博弈
– 如果买方和卖方同一天去集 市，交易成功，他们双方都 可获利。但如果不在同一天 去，则交易没法进行，且还 要支付交通费用。
– 请问这两家寡头企业有没有占优战略和占优均衡？ – 该博弈的合作解是什么？ – 两家企业达成了协议进行联合。 – 这对社会效率会有怎样的影响？ – 寡头联合形成垄断（托拉斯），并降低社会效率。在

第2章 Nash均衡【VIP专享】43页PPT

第2章 Nash均衡【VIP专享】43页PPT

谢谢！
பைடு நூலகம்
61、奢侈是舒适的，否则就不是奢侈 。——CocoCha nel 62、少而好学，如日出之阳；壮而好学 ，如日 中之光 ；志而 好学， 如炳烛 之光。 ——刘 向 63、三军可夺帅也，匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里，与其说好 的教师 是幸福 ，不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战，就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
第2章 Nash均衡【VIP专享】
16、人民应该为法律而战斗，就像为 了城墙 而战斗 一样。 ——赫 拉克利 特 17、人类对于不公正的行为加以指责 ，并非 因为他 们愿意 做出这 种行为 ，而是 惟恐自 己会成 为这种 行为的 牺牲者 。—— 柏拉图 18、制定法律法令，就是为了不让强 者做什 么事都 横行霸 道。— —奥维 德 19、法律是社会的习惯和思想的结晶 。—— 托·伍·威尔逊 20、人们嘴上挂着的法律，其真实含 义是财 富。— —爱献 生

纳什均衡

纳什均衡

（-8，0）
（-1，-1）
精品课程《运筹学》
第二节 纳什均衡
对囚徒l来说，囚徒2有坦白和不坦白两种选 择，假设囚徒2选择的不坦白，则对囚徒l来说， 不坦白得益为一l，坦白得益为O，应该选择坦 白；假设囚徒2选择的是坦白，则囚徒1不坦白 得益为一8，坦白得益为一5，他更应该选择坦 白。囚徒2唯一的选择也是坦白。 例8.2.2 设某村庄有3个农户，该村有一片大 家都可自由牧羊的公共草地。由于这片草地的 面积有限，草的数量只能让数量有限的羊吃饱， 如果在此草地上放牧的羊的实际数量超
人的策略集为Si Si1,,Sik ，则他以概率分布
pi pi1, pik 随机在其k 个可选策略中选择的
“策略”称为一个混合策略，其中
精品课程《运筹学》
第二节 纳什均衡
O≤ pij≤1对 k
j=1，…， k都成立，且
pij =1。
j 1
由定义可以看出，纯策略也可看作混合策略。
定义8.2.3 如果一个策略 G =S1,S2,Sn;h1,h2,hn中，
S1*
,
S
* i
,
S
* i1
S
* n
的最佳策略，即
hi
(S1*
, S i*1
,
Si*
,
S
* i1
,
S
* n
)
hi (S1*,Si*1, Sij , Si*1,Sn*)
对任意 S ij Si 都成立则称
S1*
,
S
* 2
,
S
* n
为
一个纯策略纳什均衡。
精品课程《运筹学》
第二节 纳什均衡
例8.2.1 “囚徒的困境” 警察抓住了两个罪犯，但 是警察局缺乏足够的证据指证他们所犯的罪行。如果 罪犯中至少有一人供认犯罪，就能确认罪名成立。为 了得到所需的口供，警察将这两名罪犯分别关押以防 止他们串供或结成攻守同盟，并分别跟他们讲清了他 们的处境和面临的选择：如果他们两人都拒不认罪， 则他们会被以较轻的妨碍公务罪各判1年徒刑；如果两 人中有一人坦白认罪，则坦白者立即释放而另一人将 重判8年徒刑；如果两人都坦白认罪，则他们将被各判 5年监禁。

博弈论与信息经济学-2-1纳什均衡

博弈论与信息经济学-2-1纳什均衡

没有占优战略均衡
(1)：多劳不多得
Baldwin & Meese (1979)
新产品研发与模仿
智猪博弈(2)：多劳反而少得 小猪 按 等待
大猪
按
3, 1
2, 4
等待
7, -1
0, 0
理性与剔除劣战略
最优反应
参与人i对其他参与人选择的战略s−i的最 优反应或最优应对是为其产生最大支付 的战略s*i，即 i(s*i , s−i) i(s’i, s−i)，s’i s*i 如果没有其他战略同样地好，就是严格 最优反应，否则，就是弱最优反应。

弱占优战略



一般地，si*Si 称为参与人i的占优战略， 如果对应所有的si’Si 和所有的s-iS-i， si*是i的弱占优选择，即 ui(si*，s-i)≥ui(si’,s-i)，s-iS-i， si’≠si* 对应地，所有的si’≠si*被称为si*的劣战 略。
占优战略

Sherlock Holmes said, whenever you have eliminated the impossible, whatever remains – no matter how improbable – must be the truth.
占优战略



一般来说，由于每个参与人的效用(支付)是博 弈中所有参与人的战略的函数，因此每个参与 人的最优战略选择依赖于所有其他参与人的战 略选择。 在一些特殊的博弈中，一个参与人的最优战略 可能并不依赖于其他参与人的战略选择，就是 说，不论其他参与人选择什么战略，他的最优 战略是唯一的，这样的最优战略被称为占优战 略(dominant strategy)。——上策 对应地，其他战略称为 “劣战略”（ dominated strategy ）——下策。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1，0 1，3
下 0，4 0，2 2，0
0，4 0，2
左
中
1，0 1，3
严格下策反复消去法
• 智猪博弈
小猪
按 等待
大
按
5，1 4，4
猪
等待 9，－1 0，0
严格下策反复消去法
• 适用面：
– 严格下策反复消去法的适用面比上策均衡要更大些 – 但也有很多博弈问题没有严格下策：田忌赛马、猜硬币、情
侣博弈、交通博弈、石头剪刀布、、、－－此时，该方法失 效。 – 最大的用处：简化博弈
严格竞争博弈和混合策略的引进
一、猜硬币博弈
盖 正面 硬 币 反面 方
猜硬币方
正面
反面
-1， 1
1， -1
1， -1
-1， 1
（1）不存在前面定义的纳什均衡策略组合 （2）关键是不能让对方猜到自己策略－－保持随机性
这类博弈很多，引出混合策略纳什均衡概念
混合策略、混合策略博弈 和混合策略纳什均衡
• 混合策略：在博弈 G {S1, Sn;u1, un} 中，博弈方i 的策略 空间为 Si {si1, s，ik }则博弈方i 以概率分布
• 画出智猪博弈的得益矩阵
“智猪博弈”(boxed pigs)
•
小猪
按 等待
大
按
5，1 4，4
猪
等待 9，－1 0，0
经典博弈之四－－猎人博弈
• 设想在古代的一个地方，有两个猎人。那时候，狩猎是人们的 主要生计。为了简单起见，假设主要的猎物只有两种： 鹿，兔子。 在古代，人类的狩猎手段还比较落后，弓箭威力也有限。在这样的 条件下，我们可以进一步假设，两个猎人一起去猎鹿，才能猎获一 只鹿，如果一个猎人单兵作战，他只能打到4只兔子。如果他打兔 子，你去猎鹿，他可以打到4只兔子，而你一无所获，得0。
得五体投地，她怎么肯放过正宗俄罗斯的芭蕾舞剧《胡桃夹子》？这么说，一
个在家里看电视直播的足球，一个去剧院看芭蕾舞演出不就得了？问题在于他
们是热恋中的情侣，分开各自度过这难得的周末时光，才是最不乐意的事情。
这样一来，他们就面临一场温情笼罩下的“博弈”
• 在情侣博弈中， 我们不妨这样给大海和小丽的“满意程度”赋值：如果大 海看球让小丽一个人去看芭蕾，双方的满意程度都为0；两人一起去看足球， 大海的满意程度为2，小丽的满意程度为1；两人一起去看芭蕾，大海的满意程 度为1，小丽的满意程度为2。应该不会有小丽独自看球而大海独自去看芭蕾的 可能，不过人们还是把它写出来，设想因此双方的满意程度都是－1。
弈
猜
-1， 1
硬
币
1， -1
1， -1 -1， 1
2， 1 0， 0
0， 0 1， 3
课堂习题
• 用划线法求出均衡解
C1
C2
C3
R1
0，4 4，0 5，3
R2 4，0 0，4 5，3
R3 3，5 3，5 6，6
箭头法
• 思路：
– 对博弈中的每一个策略组合进行分析，考察在每个策略组合 处各个博弈方能否通过单独改变自己的策略而增加得益
• 也有时：情侣博弈中，用划线法有两个策略组合同时下面划线，这意味着 两个策略组合中的双方策略都是对对方策略的最佳对策－－都具有内在的 稳定性－－但具体那一个会出现，无法确定。
划线法
1， 0 0， 4
1， 3 0， 2
0， 1 2， 0
囚 徒
-5， -5
0， -8
情 侣
困
-8， 0
境
-1， -1
博
齐威王田忌赛马
Pa 上中下
齐 Pb 上下中 威 Pc 中上下 王 Pd 中下上
Pe 下上中 Pf 下中上
Pg
上 中 下
3，-3 1，-1 1，-1 -1，1 1，-1 1，-1
– 与划线法一样都是基于策略之间的相对优劣关系进行分析的， 所得到的结果也是一致的。
– 如果能，则从所分析的策略组合对应的得益数组引一箭头， 到改变策略后策略组合对应的得益数组
– 最后，只有指向，没有离开的策略组合为均衡解－－稳定－ －没有人愿意单独改变
箭头法
1， 0 0， 4
1， 3 0， 2
0， 1 2， 0
• 假设打到一只鹿，两家平分，每家管10天；打到4只兔子，只能供 一家吃4天。
• 画出得益矩阵
猎人博弈得益矩阵
乙
猎鹿
打兔
10
4
甲 猎鹿 10
0
0
4
打兔 4
4
博弈论故事之五－－高薪养廉
• “高薪养廉”是公务员制度方面的一种理论，我们分 析一下“高薪”为什么能养廉？
• 假设甲乙为一家单位的主任和书记关系密切的国家公 务员，7代表现在政府给他们的高薪。如果两人受贿， 因为串谋而一时不被人发现，他们可以达到9的位置； 而一旦“东窗事发”，他就要被撤职查办， 不受贿一 方得8
pi ( pi1, pik ) 随机在其 k个可选策略中选择的“策略”，
称为一个“混合策略”，0其 中pij 1 j 1对, ,k
都成立，且
pi1 pik 1
• 混合策略扩展博弈：博弈方在混合策略的策略空间（概率
分布空间）的选择看作一个博弈，就是原博弈的“混合策略扩
展博弈）
• 假设行走顺利，每人获益为1，相撞，则获益为－1， • 画出得益矩阵
交通博弈
乙
靠左行
靠右行
靠左行
甲
靠右行
1，1 -1，-1
-1，-1 1，1
经典博弈故事之三－－智猪博弈
• 笼子里面有两只猪，一只比较大，一只比较小。笼子很长，一头 有一个按钮，另一头是饲料的出口和食槽。按一下按钮，将有相当 于10个单位的猪食进槽，但是按按钮以后跑到食槽所需要付出“劳 动”，加起来要消耗相当于2个单位的猪食。问题是按钮和食槽分 置笼子的两端，按按钮的猪付出劳动跑到食槽的时候，坐享其成的 另一头猪早已吃了不少。如果大猪先到，大猪呼啦啦吃到9个单位， 小猪只能吃到1个单位；如果同时到达，大猪吃到7个单位；小猪吃 到3个单位；如果小猪先到，小猪可以吃到4个单位，而大猪吃到6 个单位。
• 静态：博弈方是同时决策的，或者虽然各博弈方决策的 时间不一定真正一致，但他们在做决策时互相不知道其 他博弈方的策略。
• 完全信息静态博弈：各博弈方同时决策，且所有博弈方 对各方得益都了解的博弈。
• 如何求这一类博弈的解呢？－－博弈的结果如何？－－ 博弈各方最终的策略组合？
上策均衡法
• 上策均衡：一个博弈的某个策略组合中的所有策略都是 各个博弈方各自的上策
•博弈方i 的得益：ui
•博弈：G {S1, Sn;u1, un} •纳什均衡：在博弈G {S1, Sn;u1, un} 中，如果由各个博弈 方的各一个策略组成的某个策略组合(si*, sn* ) 中，任一博弈
方i 的策略，都是对其余博弈方策略的组合 (si*, si*1, si*1,...sn* )
博弈方1的混合策略
pA 3 pB 1 pA 2 pB 5
博 弈A 方B 1
博弈方2
C
D
2， 3 5， 2
3， 1 1， 5
博弈方2的混合策略
pC 2 pD 5 pC 3 pD 1
pA+pB=1;
pC+pD=1
策略
得益
博弈方1 （0.8，0.2） 2.6
博弈方2 （0.8，0.2） 2.6
的最佳对策，也即 ui (si*, si*1, si*, si*1,...sn*) ui (si*, si*1, sij , si*1,...sn*)
对任意 si j Si 都成立，则称 (si*, sn* ) 为 G 的一个纳什
均衡
纳什均衡的一致预测性质
•一致预测：
– 如果所有博弈方都预测一个特定博弈结果会出现，所有博弈方都不会 利用该预测或者这种预测能力，选择与预测结果不一致的策略，即没 有哪个博弈方有偏离这个预测结果的愿望，因此预测结果会成为博弈 的最终结果
经典博弈故事之二－－情侣博弈
•
大海和小丽正在热恋。难得的周末又到了，安排什么节目呢？周末晚上，
中国足球队要在世界杯外围赛中和伊朗队做生死之战。大海是个超级球迷，国
内的甲级联赛都不肯放过，何况是不争气的国家队的生死大战？也正好是这个
周末的晚上，俄罗斯一个著名芭蕾舞团莅临该市演出芭蕾舞剧《胡桃夹子》。
丽娟最崇尚钢琴、芭蕾这样的高雅艺术，对斯拉夫民族的歌唱和芭蕾更是崇拜
• 试着用一个得益矩阵来描述大海和丽娟的情侣博弈
情侣博弈的得益矩阵Leabharlann 小丽足球芭蕾
足球
1
2 大
海
芭蕾
－1
－1
0 0
2 1
靠左走还是靠右走
• 在一个没有交通规范的农村小路骑自行车，你应该走 在道路的哪一边？
• 假如别人靠右（左）走，你也 靠右（左）走，则不会 相撞；反之，假如别人靠右（左）走，而你却反其道 而行之，偏要靠左（右）走，则必然相撞。
• 只有，两方均被划线的策略组合，才是稳定的策略－－表明给定一方采用 该策略组合中的策略，则另一方也愿意采用该策略组合中的策略，该策略 组合具有稳定性。
• 但是，许多博弈根本不不存在确定性的结果，划线法失效，比如猜硬币－ －没有一个策略组合是双方同时愿意接受的，这样的博弈根本不可能有可 以预言的博弈结果
• 做法： – 首先找出某博弈人的严格下策，把这个严格下策剔除后，剩下的是一 个不包含已剔除劣策略的新的博弈；然后再剔除这个新的博弈中的严 格下策；继续这个过程，直到没有劣策略存在。如果剩下的策略组合 是唯一的，这个唯一的策略组合就是严格下策反复消去法的均衡
严格下策反复消去法