利息理论实验二

《利息理论》实验教学大纲课程代码：15340016 开课单位：保险系课程总学时：54 学分：3.0 实验学时：9 实验学分：3实验项目数：3课程类别：专业实验课程先修课程：微积分、概率论适用专业：保险（保险实务）一、教学目标金融、保险领域的许多计算问题具有共同的数学特征和模型，大量的计算和分析实践的基础是现金流分析和货币的时间价值（累积和贴现）计算。

本课程的目的是学习如何通过数学模型刻画许多金融领域中遇到的有关利息的计算以及与利息有关的金融产品的定量分析方法，掌握金融数学中以货币时间价值为基础的金融定量分析方法，并为今后对现代金融业务作进一步研究或实务打下坚实的基础。

开设实验课的目的在于将理论与实际相结合，即将保险理论与保险实务紧密地结合在一起，使学生学以致用。

由于许多课程只有通过实验、或通过上机操作才能真正弄清楚，所以说，实验课的开设对培养学生的动手操作能力是必不可少的内容，是保险理论与实务教学的重要组成部分。

本实验课程通过计算机中的Excel或专门的精算软件，解决有关利息的度量、单一支付现值与终值、年金现值与终值的计算、投资决策（NPV、IIR的计算）、摊还表及偿债基金的设计与计算、债券价格的确定及风险的度量等内容，具有综合性的特点。

这些实验课的开设是为了使同学在理论学习的基础上通过计算机实际操作，加深对所学内容的理解，为以后工作和科研提供可以借鉴的实际经验。

二、教学要求课堂讲授：采用多媒体课件，在讲授过程中尽量运用启发式、参与式、情境教学、案例教学等方法与学生形成良性互动。

学生能够了解相关的英语术语，能够学会使用excel进行相关计算。

实验：学生能够在理论学习的基础上，熟练使用计算机中的Excel或专门的精算软件，解决有关利息理论的计算问题。

作业：中国精算师资格考试用书——利息理论中的例题和习题。

三、学时分配四、教学方法采用多媒体课件，在讲授过程中尽量运用启发式、参与式、情境教学、案例教学等方法。

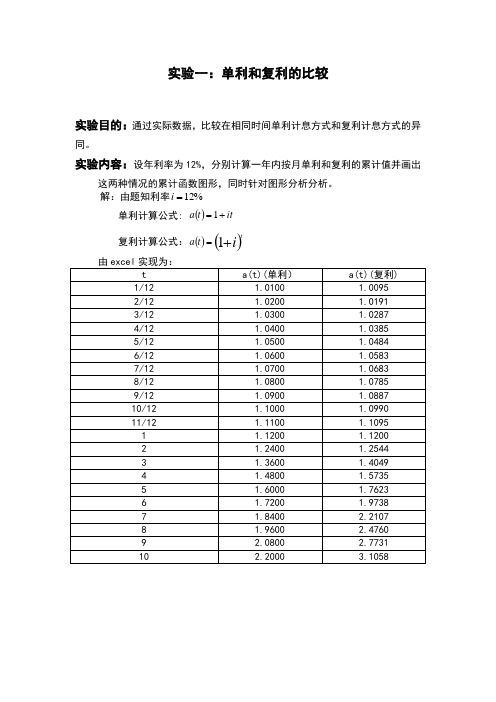
实验一：单利和复利的比较实验目的：通过实际数据，比较在相同时间单利计息方式和复利计息方式的异同。

实验内容：设年利率为12%，分别计算一年内按月单利和复利的累计值并画出这两种情况的累计函数图形，同时针对图形分析分析。

解：由题知利率%12=i单利计算公式: ()itta+=1复利计算公式：()()i tta+=1实验结论:对于一年内的按月累积值，用单利和复利分别计算的累计值基本一致；而按年累计值，随着用单利和复利计算方式的不同，累积值差距越来越大且按相同年份，按复利计算的累积值明显比按单利计算的累积值要高实验二：单贴现、复贴现、连续复贴现的比较实验目的：通过实际数据比较在相同时间内因单贴现、复贴现、连续复贴现的异同点。

实验内容：自行选择贴现率和时间在同一坐标系下画出三个函数的图形并针对图形进行分析。

解：贴现率%8=d ，贴现期为10年单贴现函数：()dt t a -=-11⎪⎭⎫ ⎝⎛≤≤d t 10复贴现函数：()()d t at-=-11⎪⎭⎫ ⎝⎛≤≤d t 10连续贴现函数： ()et a dt--=1⎪⎭⎫ ⎝⎛≤≤d t 10实验结论：在单贴现、复贴现和连续复贴现三种贴现方式下，初始值都为1，在随后每年对应的贴现中复贴现和连续复贴现的值明显高于单贴现的值，连续复贴现的数值要大于复贴现的值。

实验三：净现值方法计算实验内容：一项10年期的投资项目，投资者第一年年初投资10000元，第二年年初投资5000元，其后每年初投资1000元。

该项目预期在最后5年的每年年末有投资收益，其中第5年年末的收益为8000元，其后每年增加1000元。

给出具体的先进流动情况表，画出净现值和利率的图形，利用图形找到收益率。

解：用DCF分析方法得出以下现金流动情况表：由公式()R tno t ti p ∑==ν得到：实验结论：当()0=i p 时的利率i 为收益率，则在上图中可以找出对应收益率约为%9.12。

实验四：收益率的计算实验内容：投资者在第一年年初投资1000元，在第一年年末抽走年初投资的1000元本金，并从该基金中借出1000元，在第二年年末向该基金偿还1155元，求投资者的收益率，画出投资者净现值和利率的图形，并针对图形加以说明。

第二章 年金 部分习题参考答案证明：(1)(1)(1)(1)(1)(1)[]()m nn m m n m n m n v v v v v v i iv v i i a a i i⌝⌝----=---=⨯--=⨯-=⨯-证明：n n n-t t n t t n tttt nnnnn nn t t tt t t t t t t t n na S a a v a a v a =a S v a v a v a v a i v a ia 1111v =====1v v a viv a v v v--+=+----（1-）（1-）（1-）（1-）6. 解：由公式得：mn m+n mva =a a-71118777v a =a a 7.036=9.180 5.153i i=1=0.08299---也即：（1+）解得：7. 设X 可取得的存款额为S,根据题意：5712120.08 0.0818187121000(10.08)1000(10.08)100037.45024 1.0839169.84S S S -=+=+=⨯⨯=12. 解：根据题意，有1010301030101000a 1000a v =a a v K K +-又由于，则上式经整理得：10v =1/21030101030101030101030101111(1)a -a v 10001-v -v (1v )5822111a +a v 1-v +v (1v )91(1)8221800K K ----====--+-=解得：14. 设该永续年金每年支付R ，结合公式: nn a =a v a ∞∞+根据题意该永续年金为三人年金现值之和，即：n n n a a Ra =Rv a 22RR ∞∞++又由于三人所领取的年金现值相等，有:nnn n n 1v a v 2=v a R =R 2i i v =1/3R R ∞- 即，所以，19. 根据题意：22i i 2222222i i 222105105i i 22105i 2i 21051051000=1700011==171=t t t 17t 15=0f()t t 17t 15escart t=f =-0.00117fS S S S t D ⨯++++++-++-+（）（）（）（）（）（）（）（）（）（）-1+（）-1则：令，上式经过整理为：令=根据规则，上式最多有两个正根，而1显然不符合实际，故排除。

利息理论上机实验报告实验1：单利与复利的比较试验目的：通过实际数据，比较相同时间内单利计息方式与复利计息方式的异同点实验内容:设年利率为10﹪，（1）分别给出一年内（按月）单利与复利的累计值和10年内（按年）单利与复利方式下的累计值。

画出两种方式下的累计函数图形，并对图形加以说明。

（2）比较两种计息方式下的年实际利率，画出图形并加以说明。

解：（1）说明：1月=1/12年单利方式下，有a(t)=1+it=1+0.1t复利方式下，有a(t)=（1+i）t=1.1t利用excel计算累计值计算结果如下表利用excel作图如下图形说明：a.横坐标代表时间，纵坐标代表累计值。

b.单利、复利的累计值在1年内的差别不大，很接近。

c.1年后随着时间的推移复利的累计值大于单利的累计值且相差值越来越大。

（2）年实际利率计算：根据a(t)=（1+i）t得i=a(t)1/t-1t/年0.083333333 0.166666667 0.25 0.333333333 0.416666667 0.5 0.583333333 单利年实际利率 0.104713067 0.104260424 0.103812891 0.10337037 0.10293277 0.1025 0.102071971 复利年实际利率 0.1 0.1 0.1 0.1 0.1 0.1 0.1t/年0.666666667 0.75 0.833333333 0.916666667 1 2 3单利年实际利率 0.101648596 0.101229793 0.100815478 0.100405573 0.1 0.095445115 0.091392883 复利年实际利率 0.1 0.1 0.1 0.1 0.1 0.1 0.1t/年 4 5 6 7 8 9 10单利年实际利率 0.087757306 0.084471771 0.081483747 0.078751157 0.076239836 0.073921711 0.071773463 复利年实际利率 0.1 0.1 0.1 0.1 0.1 0.1 0.1利用excel作图如下图形说明：a.横坐标代表时间，纵坐标代表实际利率。

实验一：单利和复利的比较实验1：单利和复利的比较：实验目的：通过实际数据，比较相同时间内单利计息方式和复利计息方式的异同点实验内容：设年利率为10%，（1）分别给出1年内（按月）单利和复利下的累积值和10年内（按年）单利和复利方式下的累积值。

画出两种情况下的累积函数图形，并对图形加以说明。

（2）比较两种计息方式下的年实际利率，画出图形，并加以说明。

解： 实验已知条件：10%i =单利累积函数表达式：()1*,a t i t t Z =+∈ 复利累计函数表达式：()()1,ta t i t Z =+∈（1）、比较1年内（按月）与10年内（按年）按单利和复利计息方式的异同。

（1.1）、根据上面给出的公式并且利用excel 工具，求出了1年内(按月)单利和复利下的累积值，如下表一：表一根据上表我绘制出了如下单利、复利累积函数图，图一：图一：（1.2）、根据上面给出的公式并且利用excel工具，求出了10年内(按年)单利和复利下的累积值，如下表二，并绘制出折线图，图二。

表二：图二：分析：由图一及图二可以看出：在单利和复利两种计息方式下，在1年内的复利方式累积值小于单利方式累计值，并且差别不是很明显；在1年底，两者相同；从第2年开始复利方式的累计值超过单利方式累计值，而且在复利方式下累积值的上升速度远远超过单利累计值的上升速度。

（2）、比较单利、复利两种方式的年实际利率水平： 复利方式下每年的实际利率水平均为10%,n i n N =∈，而单利方式下各年的实际利率水平为：,1*(1)nii n N i n =∈+-，利用excel 工具并且结合上述公式我们计算出10年内各年在单利、复利计息方式下各自的年实际利率数据结果如下表三所示：表三：根据上表绘制出如下图三的折线图：图三：分析：在单利计息方式下，产生的利息为常数，但是实际利率却是随着时间的增加而递减的；而在复利计息方式下，实际利率为常数，即图中蓝线条所示的平行x轴的直线。

《利息理论》习题详解 第一章 利息的基本概念1、解：、解： （1）)()0()(t a A t A =又()25A t t t =++(0)5()2()1(0)55A A t t a t t A \===++ （2）3(3)(2)113(92)232 2.318I A A =-=+-+=+-=（3）4(4)(3)15(113)0.178(3)113A A i A --+===+ 2、证明：、证明： （1）123(1)()(2)(1)(3)(2)()(1)m m m m k I A m A m I A m A m I A m A m I A m k A m k ++++=+-=+-+=+-+=+-+-123123()()()()()m m m m k m m m n I I I I A m k A m n m k A n A m I I I I m n +++++++\++++=+-=+-=++++< 令有（2）()(1)()1(1)(1)n A n A n A n i A n A n --==---()1(1)()(1)(1)n n A n i A n A n i A n \+=-\=+-3、证明：、证明： (1) (1)112123123(1)(0)(0)(2)(0)(0)(0)(3)(0)(0)(0)(0)()(0)(0)(0)(0)(0)k nk i a a a i a a a i a i a a a i a i a i a n a a i a i a i a i \=+=++=+++=+++++第期的单利利率是又(0)1a =123123()1()(0)()1nna n i i i i a n a a n i i i i \=+++++\-=-=++++（2）由于第2题结论成立，当取0m =时有时有12()(0)n A n A I I I -=+++4、解：、解：（1）以单利积累计算）以单利积累计算1205003i =´ 1200.085003i \==´800(10.085)1120\+´=（2）以复利积累计算）以复利积累计算3120500500(1)i +=+0.074337i \=5800(10.074337)1144.97\+=5、解：设原始金额为(0)A 有(0)(10.1)(10.08)(10.06)1000A +++=解得解得 (0)794.1A =6、证明：设利率是i ，则n 个时期前的1元钱的当前值为(1)ni +，n 个时期后的1元钱的当前值为1(1)ni +又22211[(1)](1)20(1)(1)n nnni i i i +-=++-³++ ，当且仅当221(1)(1)1(1)n n n i i i +=Þ+=+，0i =即或者或者n=0n=0n=0时时等号成立。