计量经济学第三版庞浩第七章习题答案

第七章习题（1） 1)PCE=+ 2)PCE=++(2)模型一MPC=;模型二短期MPC=，长期MPC=(1+=(1) 令 2104210321022101001649342α＋α＋＝αβα＋α＋＝αβα＋α＋＝αβ＋α＋α＝αβ＝αβ模型变形为i t u Z Z Z Y ＋＋α＋α＝α＋α2t 21t 10t 0其中4-t 3-t 2-t 1-t 2t 4-t 3-t 2-t 1-t 1t 4-t 3-t 2-t 1-t t 0t 1694432X X X X Z X X X X Z X X X X X Z ＋＋＋＝＋＋＋＝＋＋＋＋＝可得11833.0-17917.0-3123.0-3255.0891012.043210＝β＝β＝β＝β＝β,所以4-t 3-t 2-t 1-t t 11833.0-17917.0-3123.0- 3255.0891012.049234.35-X X X X X Y t ＋＋＝（1）估计t t u Y X Y *1-t 1*t 0**+＋β＋β＝α1）根据局部调整模型的参数关系，有δαα=*,δββ=*,δβ-1=1*,t t u u δ=* 将估计结果带入可得：728324.0=271676.0-1=-1=1*βδ局部调整模型估计结果为：t *864001.0738064.20X Y t ＋＝2）经济意义：销售额每增加1亿元，未来预期最佳新增固定资产投资增加亿元。

3）运用德宾h 检验一阶自相关：在显着水平下，临界值 1.96=h 2α，因为h=＜ 1.96=h 2α，接受原假设，模型不存在一阶自相关性。

（2）做对数变换得到模型：t t u X Y +ln ln ln t *α＋β＝ 在局部调整假定下，估计一阶自回归模型1）根据局部调整模型的参数关系，有αδαln =ln *,δββ=*0,δβ-1=1* 将估计结果带入可得：739967.0=260033.0-1=-1=1*βδ局部调整模型估计结果为：t *ln 22238.145688.1-ln X Y t ＋＝2）经济意义：销售额每增加1%，未来预期最佳新增固定资产投资增加% 3）运用德宾h 检验一阶自相关：在显着水平下，临界值 1.96=h 2α，因为h=＜ 1.96=h 2α，接受原假设，模型不存在一阶自相关性。

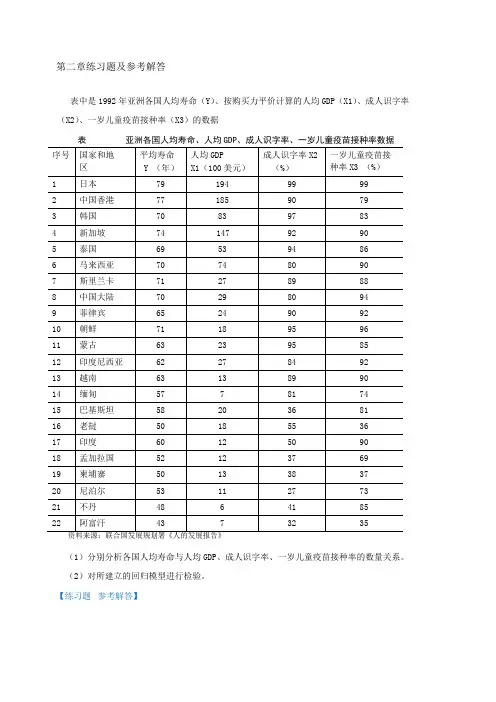
第二章练习题及参考解答表中是1992年亚洲各国人均寿命（Y）、按购买力平价计算的人均GDP（X1）、成人识字率（X2）、一岁儿童疫苗接种率（X3）的数据表亚洲各国人均寿命、人均GDP、成人识字率、一岁儿童疫苗接种率数据（1）分别分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系。

（2）对所建立的回归模型进行检验。

【练习题参考解答】（1）分别设定简单线性回归模型，分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系:1)人均寿命与人均GDP 关系Y i 1 2 X1i u i估计检验结果:2)人均寿命与成人识字率关系3)人均寿命与一岁儿童疫苗接种率关系（2）对所建立的多个回归模型进行检验由人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命回归结果的参数t 检验值均明确大于其临界值,而且从对应的P 值看,均小于,所以人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命都有显着影响.（3）分析对比各个简单线性回归模型人均寿命与人均GDP 回归的可决系数为人均寿命与成人识字率回归的可决系数为人均寿命与一岁儿童疫苗接种率的可决系数为相对说来,人均寿命由成人识字率作出解释的比重更大一些为了研究浙江省财政预算收入与全省生产总值的关系,由浙江省统计年鉴得到以下数据:表浙江省财政预算收入与全省生产总值数据的显着性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2011 年，全省生产总值为32000 亿元，比上年增长%,利用计量经济模型对浙江省2011 年的财政预算收入做出点预测和区间预测(3)建立浙江省财政预算收入对数与全省生产总值对数的计量经济模型,. 估计模型的参数,检验模型的显着性,并解释所估计参数的经济意义【练习题参考解答】建议学生独立完成由12对观测值估计得消费函数为：（1）消费支出C的点预测值；（2）在95%的置信概率下消费支出C平均值的预测区间。

实验一P42第二章第6题=+GDP+Dependent Variable: YMethod: Least SquaresDate: 01/11/08 Time: 09:03Sample: 1985 1998Included observations: 14Variable Coefficient Std.Errort-Statistic Prob.C12596.271244.56710.121010.0000GDP26.954154.1203006.5417920.0000 R-squared0.781002 Meandependent var20168.57Adjusted R-squared 0.762752 S.D. dependentvar3512.487S.E. of regression 1710.865 Akaike infocriterion17.85895Sum squared resid 35124719 Schwarzcriterion17.95024Log likelihood-123.0126 F-statistic42.79505Durbin-Watsonstat0.859998 Prob(F-statistic)0.000028(10.1) ( 6.5), =0.78 =0.76（一）对回归方程的结构分析：是这个样本回归方程的斜率，它表示GDP每增加1亿元，某市将增加26.95的货物运输量；是样本回归方程的截距，它表示不受GDP影响的某市的货物运输量。

（二）统计检验=0.78，说明总离差平方和的78%被样本回归直线解释，有22%未被解释，因此，样本回归直线的拟合优度是可以的。

给出显著水平，查自由度v=14-2=12的t分布表，得临界值，，，固回归系数均显著不为零，回归模型中应包含常数项，GDP对Y有显著影响。

（三）预测2000年的某市货物运输量假如2000年某市以1980年不变价的国内生产总值为620亿元，得到2000年货物运输量的预测值29307.84万吨。

统计学2班第六次作业1、⑴①模型一：t t t PDI A A PCE μ++=21tt PDI E C P 008106.14269.216ˆ+-= t （-6.619723）（67.05920）996455.02=R F=4496.936 DW=1.366654美国个人消费支出受个人可支配收入影响，通过回归可知，个人可支配收入PDI 每增加一个单位，个人消费支出平均增加1.008106个单位。

②模型二：t t t t PCE B PDI B B PCE υ+++=-13211037158.0982382.02736.233ˆ-++-=t t t PCE PDI E C P T （-5.120436）（6.970817） （0.257997）996542.02=R F=2017.064 DW=1.570195美国个人消费支出PCE 不仅受当期个人可支配收入PDI 影响，还受滞后一期个人消费支出PCE t-1自身影响。

⑵从模型一得MPC=1.008106从模型二可得短期MPC=0.982382.从库伊特模型)()1(110---+++-=t t t t t Y X Y λμμλβλα可得1-t PEC 为λ的系数即037158.0=λ因为，长期MPC 即长期乘数为：∑=si iβ，根据库伊特模型)10(0<<=λλββii ，。

当s →∞时，λβλλβλβλβλβββββ-=--==+++=++=∞∞=∞=∑∑111 (00)102210100i ii i 所以长期MPC=02023.1037158.01982382.0=-=MPC2、Y ：固定资产投资 X ：销售额⑴ 设定模型为：t t t X Y μβα++=*，*t Y 为被解释变量的预期最佳值运用局部调整假定，模型转换为：*1*1*0*t t t t Y X Y μββα+++=- 其中：t t δμμδβδββδαα=-===**1*0*,1,,1271676.0629273.010403.15ˆ-++-=t t t Y X Y T （-3.193613） （6.433031） （2.365315）987125.02=R F=690.0561 DW=1.518595t t δμμδβδββδαα=-===**1*0*,1,, ，728324.0271676.011*1=-=-=βδ7381.20728324.010403.15*-=-==δαα，864.0728324.0629273.0*0===δββ∴局部调整模型估计结果为：tt X Y 864.07381.20ˆ*+-= 经济意义：该地区销售额每增加1亿元，未来预期最佳新增固定资产投资为0.846亿元采用德宾h 检验如下0:,0:10≠=ρρH H29728.1114858.0*21121)21.5185951()ˆ(1)21(2*1=--=--=βnVar n d h 在显著性水平05.0=α下，查标准正态分布表得临界值96.1025.02==h h α,因此拒绝原假设96.129728.1025.0=<=h h ，因此接受原假设，说明自回归模型不存在一阶自相关。

第二章简单线性回归模型2.1（1）①首先分析人均寿命与人均GDP 的数量关系，用Eviews 分析：Dependent Variable: YMethod: Least SquaresDate: 12/27/14 Time: 21:00Sample: 1 22Included observations: 22 Variable Coefficient Std. Error t-Statistic Prob. C 56.64794 1.960820 28.88992 0.0000X1 0.128360 0.027242 4.711834 0.0001 R-squared 0.526082 Mean dependent var 62.50000Adjusted R-squared 0.502386 S.D. dependent var 10.08889S.E. of regression 7.116881 Akaike info criterion 6.849324Sum squared resid 1013.000 Schwarz criterion 6.948510Log likelihood -73.34257 Hannan-Quinn criter. 6.872689F-statistic 22.20138 Durbin-Watson stat 0.629074Prob(F-statistic) 0.000134 有上可知，关系式为y=56.64794+0.128360x1②关于人均寿命与成人识字率的关系，用Eviews 分析如下：Dependent Variable: YMethod: Least SquaresDate: 11/26/14 Time: 21:10Sample: 1 22Included observations: 22 Variable Coefficient Std. Error t-Statistic Prob. C 38.79424 3.532079 10.98340 0.0000X2 0.331971 0.046656 7.115308 0.0000 R-squared 0.716825 Mean dependent var 62.50000Adjusted R-squared 0.702666 S.D. dependent var 10.08889S.E. of regression 5.501306 Akaike info criterion 6.334356Sum squared resid 605.2873 Schwarz criterion 6.433542Log likelihood -67.67792 Hannan-Quinn criter. 6.357721F-statistic 50.62761 Durbin-Watson stat 1.846406Prob(F-statistic) 0.000001 由上可知，关系式为y=38.79424+0.331971x2③关于人均寿命与一岁儿童疫苗接种率的关系，用Eviews 分析如下：Dependent Variable: YMethod: Least SquaresDate: 11/26/14 Time: 21:14Sample: 1 22Included observations: 22 Variable Coefficient Std. Error t-Statistic Prob. C 31.79956 6.536434 4.864971 0.0001X3 0.387276 0.080260 4.825285 0.0001 R-squared 0.537929 Mean dependent var 62.50000Adjusted R-squared 0.514825 S.D. dependent var 10.08889S.E. of regression 7.027364 Akaike info criterion 6.824009Sum squared resid 987.6770 Schwarz criterion 6.923194Log likelihood -73.06409 Hannan-Quinn criter. 6.847374F-statistic 23.28338 Durbin-Watson stat 0.952555Prob(F-statistic) 0.000103 由上可知，关系式为y=31.79956+0.387276x3（2）①关于人均寿命与人均GDP 模型，由上可知，可决系数为0.526082，说明所建模型整体上对样本数据拟合较好。

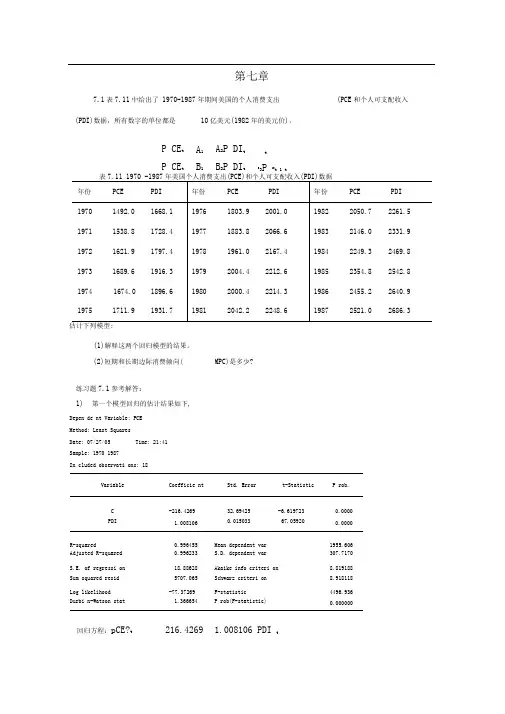
第七章7.1表7.11中给出了 1970-1987年期间美国的个人消费支出 (PCE 和个人可支配收入(PDI)数据，所有数字的单位都是10亿美元(1982年的美元价)。

表7.11 1970 -1987年美国个人消费支出(PCE)和个人可支配收入(PDI)数据年份PCE PDI 年份 PCE PDI 年份 PCE PDI 1970 1492.0 1668.1 1976 1803.9 2001.0 1982 2050.7 2261.5 1971 1538.8 1728.4 1977 1883.8 2066.6 1983 2146.0 2331.9 1972 1621.9 1797.4 1978 1961.0 2167.4 1984 2249.3 2469.8 1973 1689.6 1916.3 1979 2004.4 2212.6 1985 2354.8 2542.8 1974 1674.0 1896.6 1980 2000.4 2214.3 1986 2455.2 2640.9 19751711.91931.719812042.22248.619872521.02686.3估计下列模型:(1)解释这两个回归模型的结果。

练习题7.1参考解答：1) 第一个模型回归的估计结果如下,Depen de nt Variable: PCE Method: Least Squares Date: 07/27/05 Time: 21:41Sample: 1970 1987In cluded observati ons: 18VariableCoefficie ntStd. Errort-StatisticP rob.C -216.4269 32.69425 -6.619723 0.0000 PDI1.0081060.01503367.059200.0000R-squared0.996455 Mean dependent var 1955.606 Adjusted R-squared 0.996233 S.D. dependent var 307.7170 S.E. of regressi on 18.88628 Akaike info criteri on 8.819188 Sum squared resid 5707.065 Schwarz criteri on 8.918118 Log likelihood -77.37269 F-statistic 4496.936 Durbi n-Watson stat1.366654P rob(F-statistic)0.000000回归方程：pCE?t216.4269 1.008106 PDI tP CE t P CE t A 1 B 1 A 2P DI tB 2P DI ttB3P CEt 1 t(2)短期和长期边际消费倾向(MPC )是多少?(32. 69425) ( 0.015033 ) (-6.619723 )(67.05920 )2R =0.996455F=4496.936第二个模型回归的估计结果如下，Dependent Variable: PCE Method: Least Squares Date: 07/27/05Time: 21:51Samp le (adjusted): 1971 1987In cluded observati ons: 17 after adjustme ntsVariable Coefficie nt Std. Error t-Statistic P rob.C -233.2736 45.55736 -5.120436 0.0002 PDI 0.982382 0.140928 6.970817 0.0000 P CE(-1)0.0371580.1440260.2579970.8002R-squared0.996542 Mean dependent var 1982.876 Adjusted R-squared 0.996048 S.D. dependent var 293.9125 S.E. of regressi on 18.47783 Akaike info criteri on 8.829805 Sum squared resid 4780.022 Schwarz criteri on 8.976843 Log likelihood -72.05335 F-statistic 2017.064 Durbi n-Watson stat1.570195 P rob(F-statistic)0.000000回归方程：pcE t233.2736 0.9824PDI t 0.0372PCE 1(45.557 )(0.1409 ) ( 0.1440 )t =(-5.120 )(6.9708 )( 0.258 )R 2=0.9965 F=2017.0642）从模型一得到 MPC=1.008;从模型二得到，短期 要先转换为分布滞后模型才能得到长期边际消费倾向，MPC=0.9824/（ 1+0.0372）=0.9472。

计量经济学 - 庞皓 - 第三版课后答案第二章简单线性回归模型 2.1（1）①首先分析人均寿命与人均GDP的数量关系，用Eviews分析： Dependent Variable: Y Method: Least Squares Date: 12/27/14 Time: 21:00 Sample: 1 22 Included observations: 22Variable Coefficient Std. Error t-Statistic Prob. C 56.64794 1.960820 28.88992 0.0000 X1 0.128360 0.027242 4.711834 0.0001 R-squared 0.526082 Mean dependent var 62.50000Adjusted R-squared 0.502386 S.D. dependent var 10.08889 S.E. of regression 7.116881 Akaike info criterion 6.849324 Sum squared resid 1013.000 Schwarz criterion 6.948510 Log likelihood -73.34257 Hannan-Quinn criter. 6.872689 F-statistic 22.20218 Durbin-Watson stat 0.629074 Prob(F-statistic) 0.000134有上可知，关系式为y=56.64794+0.128360x1②关于人均寿命与成人识字率的关系，用Eviews分析如下： Dependent Variable: Y Method: Least Squares Date: 11/26/14 Time: 21:10 Sample: 1 22 Included observations: 22Variable Coefficient Std. Error t-Statistic Prob. C 38.79424 3.532079 10.98340 0.0000 X2 0.331971 0.046656 7.115308 0.0000 R-squared 0.716825 Mean dependent var 62.50000Adjusted R-squared 0.702666 S.D. dependent var 10.08889 S.E. of regression 5.501306 Akaike info criterion 6.334356 Sum squared resid605.2873 Schwarz criterion 6.433542 Log likelihood -67.67792 Hannan-Quinn criter. 6.357721 F-statistic 50.62761 Durbin-Watson stat 1.846406 Prob(F-statistic) 0.000001由上可知，关系式为y=38.79424+0.331971x2③关于人均寿命与一岁儿童疫苗接种率的关系，用Eviews分析如下：Dependent Variable: Y Method: Least Squares Date: 11/26/14 Time: 21:14 Sample: 1 22 Included observations: 22Variable Coefficient Std. Error t-Statistic Prob. C 31.79956 6.536434 4.864971 0.0001 X3 0.387276 0.080260 4.825285 0.0001 R-squared 0.537929 Mean dependent var 62.50000Adjusted R-squared 0.514825 S.D. dependent var 10.08889 S.E. of regression 7.027364 Akaike info criterion 6.824009 Sum squared resid987.6770 Schwarz criterion 6.923194 Log likelihood -73.06409 Hannan-Quinn criter. 6.847374 F-statistic 23.28338 Durbin-Watson stat 0.952555 Prob(F-statistic) 0.000103由上可知，关系式为y=31.79956+0.387276x3（2）①关于人均寿命与人均GDP模型，由上可知，可决系数为0.526082，说明所建模型整体上对样本数据拟合较好。

统计学2班第六次作业1、⑴①模型一：t t t PDI A A PCE μ++=21t tPDI E C P 008106.14269.216ˆ+-= t （-6.619723）（67.05920）996455.02=R F=4496.936 DW=1.366654美国个人消费支出受个人可支配收入影响，通过回归可知，个人可支配收入PDI 每增加一个单位，个人消费支出平均增加1.008106个单位。

②模型二：t t t t PCE B PDI B B PCE υ+++=-13211037158.0982382.02736.233ˆ-++-=t t tPCE PDI E C P T （-5.120436）（6.970817） （0.257997）996542.02=R F=2017.064 DW=1.570195美国个人消费支出PCE 不仅受当期个人可支配收入PDI 影响，还受滞后一期个人消费支出PCE t-1自身影响。

⑵从模型一得MPC=1.008106从模型二可得短期MPC=0.982382.从库伊特模型)()1(110---+++-=t t t t t Y X Y λμμλβλα可得1-t P E C 为λ的系数即037158.0=λ因为，长期MPC 即长期乘数为：∑=si iβ，根据库伊特模型)10(0<<=λλββi i ，。

当s →∞时，λβλλβλβλβλβββββ-=--==+++=++=∞∞=∞=∑∑111 (001)02210100i ii i所以长期MPC=02023.1037158.01982382.0=-=MPC2、Y ：固定资产投资 X ：销售额⑴ 设定模型为：t t t X Y μβα++=*，*t Y 为被解释变量的预期最佳值运用局部调整假定，模型转换为：*1*1*0*t t t t Y X Y μββα+++=- 其中：t t δμμδβδββδαα=-===**1*0*,1,,1271676.0629273.010403.15ˆ-++-=t t tY X Y T （-3.193613） （6.433031） （2.365315）987125.02=R F=690.0561 DW=1.518595t t δμμδβδββδαα=-===**1*0*,1,, ，728324.0271676.011*1=-=-=βδ7381.20728324.010403.15*-=-==δαα，864.0728324.0629273.0*0===δββ∴局部调整模型估计结果为：tt X Y 864.07381.20ˆ*+-= 经济意义：该地区销售额每增加1亿元，未来预期最佳新增固定资产投资为0.846亿元采用德宾h 检验如下0:,0:10≠=ρρH H29728.1114858.0*21121)21.5185951()ˆ(1)21(2*1=--=--=βnVar n d h 在显著性水平05.0=α下，查标准正态分布表得临界值96.1025.02==h h α,因此拒绝原假设96.129728.1025.0=<=h h ，因此接受原假设，说明自回归模型不存在一阶自相关。

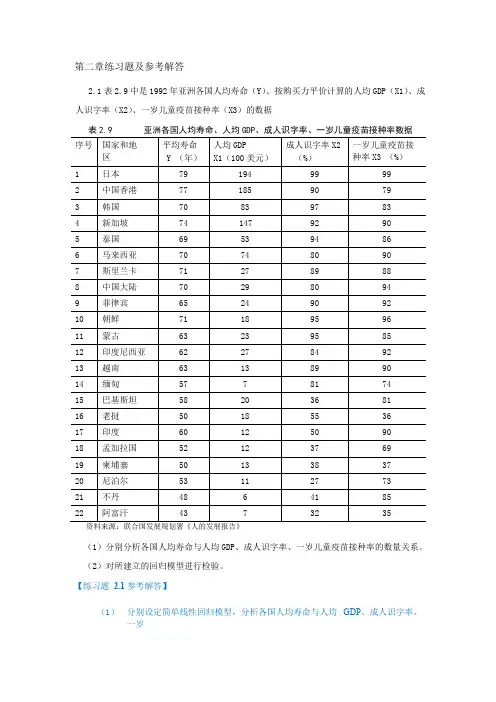
第二章练习题及参考解答2.1表2.9中是1992年亚洲各国人均寿命（Y）、按购买力平价计算的人均GDP（X1）、成人识字率（X2）、一岁儿童疫苗接种率（X3）的数据（1）分别分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系。

（2）对所建立的回归模型进行检验。

【练习题2.1 参考解答】（1）分别设定简单线性回归模型，分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系:1)人均寿命与人均GDP 关系Y i 1 2 X1i u i估计检验结果:2)人均寿命与成人识字率关系3)人均寿命与一岁儿童疫苗接种率关系（2）对所建立的多个回归模型进行检验由人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命回归结果的参数t 检验值均明确大于其临界值,而且从对应的P 值看,均小于0.05,所以人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命都有显著影响.（3）分析对比各个简单线性回归模型人均寿命与人均GDP 回归的可决系数为0.5261 人均寿命与成人识字率回归的可决系数为0.7168 人均寿命与一岁儿童疫苗接种率的可决系数为0.5379相对说来,人均寿命由成人识字率作出解释的比重更大一些2.2为了研究浙江省财政预算收入与全省生产总值的关系,由浙江省统计年鉴得到以下数据:的显著性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2011 年，全省生产总值为32000 亿元，比上年增长9.0%,利用计量经济模型对浙江省2011 年的财政预算收入做出点预测和区间预测(3)建立浙江省财政预算收入对数与全省生产总值对数的计量经济模型,. 估计模型的参数,检验模型的显著性,并解释所估计参数的经济意义【练习题2.2 参考解答】建议学生独立完成2.3 由12对观测值估计得消费函数为：（1）消费支出C的点预测值；（2）在95%的置信概率下消费支出C平均值的预测区间。

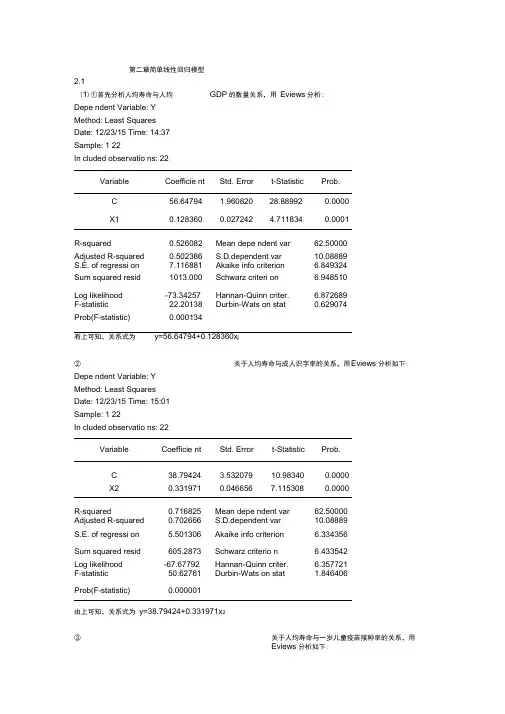
第二章简单线性回归模型2.1(1)①首先分析人均寿命与人均GDP的数量关系，用Eviews分析:Depe ndent Variable: YMethod: Least SquaresDate: 12/23/15 Time: 14:37Sample: 1 22In cluded observatio ns: 22Variable Coefficie nt Std. Error t-Statistic Prob.C 56.64794 1.960820 28.88992 0.0000X1 0.128360 0.027242 4.711834 0.0001R-squared 0.526082 Mean depe ndent var 62.50000Adjusted R-squared 0.502386 S.D.dependent var 10.08889S.E. of regressi on 7.116881 Akaike info criterion 6.849324Sum squared resid 1013.000 Schwarz criteri on 6.948510Log likelihood -73.34257 Hannan-Quinn criter. 6.872689F-statistic 22.20138 Durbin-Wats on stat 0.629074Prob(F-statistic) 0.000134有上可知，关系式为y=56.64794+0.128360x j②关于人均寿命与成人识字率的关系，用E views分析如下: Depe ndent Variable: YMethod: Least SquaresDate: 12/23/15 Time: 15:01Sample: 1 22In cluded observatio ns: 22Variable Coefficie nt Std. Error t-Statistic Prob.C 38.79424 3.532079 10.98340 0.0000X2 0.331971 0.046656 7.115308 0.0000R-squared 0.716825 Mean depe ndent var 62.50000Adjusted R-squared 0.702666 S.D.dependent var 10.08889S.E. of regressi on 5.501306 Akaike info criterion 6.334356Sum squared resid 605.2873 Schwarz criterio n 6.433542Log likelihood -67.67792 Hannan-Quinn criter. 6.357721F-statistic 50.62761 Durbin-Wats on stat 1.846406Prob(F-statistic) 0.000001由上可知，关系式为y=38.79424+0.331971x2③关于人均寿命与一岁儿童疫苗接种率的关系，用Eviews分析如下:Depe ndent Variable: YMethod: Least SquaresDate: 12/23/14 Time: 15:20Sample: 1 22In cluded observatio ns: 22Variable Coefficie nt Std. Error t-Statistic Prob.C 31.79956 6.536434 4.864971 0.0001X3 0.387276 0.080260 4.825285 0.0001R-squared 0.537929 Mean depe ndent var 62.50000Adjusted R-squared 0.514825 S.D.dependent var 10.08889S.E. of regressi on 7.027364 Akaike info criterion 6.824009Sum squared resid 987.6770 Schwarz criteri on 6.923194Log likelihood -73.06409 Hannan-Quinn criter. 6.847374F-statistic 23.28338 Durbin-Wats on stat 0.952555Prob(F-statistic) 0.000103由上可知，关系式为y=31.79956+0.387276x3(2［①关于人均寿命与人均GDP模型，由上可知，可决系数为0.526082，说明所建模型整体上对样本数据拟合较好。

思考题答案第一章 绪论思考题怎样理解产生于西方国家的计量经济学能够在中国的经济理论研究和现代化建设中发挥重要作用答：计量经济学的产生源于对经济问题的定量研究，这是社会经济发展到一定阶段的客观需要。

计量经济学的发展是与现代科学技术成就结合在一起的，它反映了社会化大生产对各种经济因素和经济活动进行数量分析的客观要求。

经济学从定性研究向定量分析的发展，是经济学逐步向更加精密、更加科学发展的表现。

我们只要坚持以科学的经济理论为指导，紧密结合中国经济的实际，就能够使计量经济学的理论与方法在中国的经济理论研究和现代化建设中发挥重要作用。

理论计量经济学和应用计量经济学的区别和联系是什么答：计量经济学不仅要寻求经济计量分析的方法，而且要对实际经济问题加以研究，分为理论计量经济学和应用计量经济学两个方面。

理论计量经济学是以计量经济学理论与方法技术为研究内容，目的在于为应用计量经济学提供方法论。

所谓计量经济学理论与方法技术的研究，实质上是指研究如何运用、改造和发展数理统计方法，使之成为适合测定随机经济关系的特殊方法。

应用计量经济学是在一定的经济理论的指导下，以反映经济事实的统计数据为依据，用计量经济方法技术研究计量经济模型的实用化或探索实证经济规律、分析经济现象和预测经济行为以及对经济政策作定量评价。

怎样理解计量经济学与理论经济学、经济统计学的关系【答：1、计量经济学与经济学的关系。

联系：计量经济学研究的主体—经济现象和经济关系的数量规律；计量经济学必须以经济学提供的理论原则和经济运行规律为依据；经济计量分析的结果：对经济理论确定的原则加以验证、充实、完善。

区别：经济理论重在定性分析,并不对经济关系提供数量上的具体度量；计量经济学对经济关系要作出定量的估计，对经济理论提出经验的内容。

2、计量经济学与经济统计学的关系。

联系：经济统计侧重于对社会经济现象的描述性计量；经济统计提供的数据是计量经济学据以估计参数、验证经济理论的基本依据；经济现象不能作实验，只能被动地观测客观经济现象变动的既成事实，只能依赖于经济统计数据。

第七章习7.1(1)1)PCE=-216.4269+1.008106PDI2)PCE=-233.2736+0.982382PDI+0.037158PEC T -I⑵ 模 型 一 MPC=1.008106;模型 二短期 MPC=0.982382 , 长 期 MPC=0.982382心+0.037158)=0.94727.2(1)a 0馆=a 0+ a.j + a 2令旳=a o + 2a-i +4a 2B 3= a 0 + 3a-| + 9a 2B 4= a 0+ 4% +1&2模型变形为 Y^= a + a 0Z 0t + a -|Z 1t + a 2Z 2t + u iZ °t = X t + X t-1+ X t_2+ X t-3+ X其中乙 t = X t-1 + 2X t-2+3X t-3+ 4X t-4Z 2t =X t-1+4X t-2+9X t-3+16X t-4%= 0.891012 Y t = -35.49234+0.891012X t +0.3255X t 「 -0.3123X t-2-0.17917X t-3 -0.11833X t-4 B 尸-0.118337.3/• r 、r * * ** (1)估计 Y t = a + B °X t + B 1Y t-1 + u t 1 〕根据局部调整模型的参数关系，有 a = S a , B = 3 B , B 1=1-3, u t =3 U t3 = 1-B *1 = 1-0.271676 = 0.728324局部调整模型估计结果为： Y *t = 20.738064+ 0.864001 X t2〕 经济意义：销售额每增加1亿元，未来预期最正确新增固定资产投资增加 0.864001亿元 3〕 运用德宾h 检验一阶自相关：在0.05显着水平下，临界值h ^ =1.96，因为h=1.29728 v h^ =1.96，接受原假设，模型 不存在一阶自相关性。

庞皓计量经济学第三版课后习题及答案顶配庞皓计量经济学第三版课后习题及答案顶配 Last revised by LE LE in 2021第⼆章练习题及参考解答表中是1992年亚洲各国⼈均寿命（Y）、按购买⼒平价计算的⼈均GDP（X1）、成⼈识字率（X2）、⼀岁⼉童疫苗接种率（X3）的数据（1）分别分析各国⼈均寿命与⼈均GDP、成⼈识字率、⼀岁⼉童疫苗接种率的数量关系。

（2）对所建⽴的回归模型进⾏检验。

【练习题参考解答】（1）分别设定简单线性回归模型，分析各国⼈均寿命与⼈均 GDP、成⼈识字率、⼀岁⼉童疫苗接种率的数量关系:1)⼈均寿命与⼈均 GDP 关系Y i 1 2 X1i u i估计检验结果:2)⼈均寿命与成⼈识字率关系3)⼈均寿命与⼀岁⼉童疫苗接种率关系（2）对所建⽴的多个回归模型进⾏检验由⼈均 GDP、成⼈识字率、⼀岁⼉童疫苗接种率分别对⼈均寿命回归结果的参数 t 检验值均明确⼤于其临界值,⽽且从对应的P 值看,均⼩于 ,所以⼈均 GDP、成⼈识字率、⼀岁⼉童疫苗接种率分别对⼈均寿命都有显着影响.（3）分析对⽐各个简单线性回归模型⼈均寿命与⼈均 GDP 回归的可决系数为⼈均寿命与成⼈识字率回归的可决系数为⼈均寿命与⼀岁⼉童疫苗接种率的可决系数为相对说来,⼈均寿命由成⼈识字率作出解释的⽐重更⼤⼀些为了研究浙江省财政预算收⼊与全省⽣产总值的关系,由浙江省统计年鉴得到以下数据:的显着性,⽤规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果 2011 年，全省⽣产总值为 32000 亿元，⽐上年增长 %,利⽤计量经济模型对浙江省 2011 年的财政预算收⼊做出点预测和区间预测(3)建⽴浙江省财政预算收⼊对数与全省⽣产总值对数的计量经济模型,. 估计模型的参数,检验模型的显着性,并解释所估计参数的经济意义【练习题参考解答】建议学⽣独⽴完成由12对观测值估计得消费函数为：（1）消费⽀出C的点预测值；（2）在95%的置信概率下消费⽀出C平均值的预测区间。

欢迎共阅第二章2.2（1）①对于浙江省预算收入与全省生产总值的模型，用Eviews分析结果如下：DependentVariable:YMethod:LeastSquaresDate:12/03/14Time:17:00Sample(adjusted):133（2）当x=32000时，①进行点预测，由上可知Y=0.176124X—154.3063，代入可得：Y=Y=0.176124*32000—154.3063=5481.6617②进行区间预测：Prob(F-statistic) 0.000000①模型方程为：lnY=0.980275lnX-1.918289②由上可知，模型的参数：斜率系数为0.980275，截距为-1.918289③关于浙江省财政预算收入与全省生产总值的模型，检验其显着性：1）可决系数为0.963442，说明所建模型整体上对样本数据拟合较好。

2）对于回归系数的t检验：t（β2）=28.58268>t0.025(31)=2.0395，对斜率系数的显着性检验表明，全省生产总值对财政预算总收入有显着影响。

④经济意义：全省生产总值每增长1%，财政预算总收入增长0.980275%2.4（1）对建筑面积与建造单位成本模型，用Eviews分析结果如下：DependentVariable:YMethod:LeastSquaresDate:12/01/14Time:12:40Sample:112Includedobservations:12Variable Coefficient Std.Error t-Statistic Prob.??X -64.18400 4.809828 -13.34434 0.0000C 1845.475 19.26446 95.79688 0.0000∑x2=∑（X i—X）2=δ2x(n—1)=?1.9894192x(12—1)=43.5357(X f—X)2=(4.5—?3.523333)2当Xf=4.5时，将相关数据代入计算得到：1556.647—2.228x31.73600Yf≤1556.647+2.228x31.73600即Yf的置信区间为（1556.647—478.1231,1556.647+478.1231）第三章3.2１）对出口货物总额计量经济模型，用Eviews分析结果如下：：DependentVariable:YMethod:LeastSquaresDate:12/01/14Time:20:25Method:LeastSquaresDate:12/01/14Time:20:25Sample:19942011Includedobservations:18Variable Coefficient Std.Error t-Statistic Prob.??LNX2 1.564221 0.088988 17.57789 0.0000LNX3 1.760695 0.682115 2.581229 0.0209C -20.52048 5.432487 -3.777363 0.0018R-squared 0.986295 ????Meandependentvar 8.400112AdjustedR-squared 0.984467 ????S.D.dependentvar 0.941530S.E.ofregression 0.117343 ????Akaikeinfocriterion -1.296424Sumsquaredresid 0.206540 ????Schwarzcriterion -1.148029Loglikelihood 14.66782 ????Hannan-Quinncriter. -1.275962F-statistic 539.7364 ????Durbin-Watsonstat 0.686656Prob(F-statistic) 0.000000①由上可知，模型为：LNY=-20.52048+1.564221LNX2+1.760695LNX3②对模型进行检验：1，Sumsquaredresid 55491.07 ????Schwarzcriterion 11.35321Loglikelihood -97.84334 ????Hannan-Quinncriter. 11.22528F-statistic 146.2974 ????Durbin-Watsonstat 2.605783Prob(F-statistic) 0.000000①模型为：Y=0.086450X+52.37031T-50.01638②对模型进行检验：1）可决系数是0.951235，修正的可决系数为0.944732，说明模型对样本拟合较好。

第二章练习题参考解答练习题资料来源:《深圳统计年鉴2002》，中国统计出版社(1)建立深圳地方预算内财政收入对GDP的回归模型；(2)估计所建立模型的参数，解释斜率系数的经济意义；（3）对回归结果进行检验；(4)若是2005年年的国内生产总值为3600亿元，确定2005年财政收入的预测值和预测区间(0.05α=)。

2.2某企业研究与发展经费与利润的数据(单位:万元)列于下表:1995 1996 1997 1998 1999 2000 2001 2002 2003 2004研究与发展经费 10 10 8 8 8 12 12 12 11 11利润额 100 150 200 180 250 300 280 310 320 300 分析企业”研究与发展经费与利润额的相关关系，并作回归分析。

2.3为研究中国的货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相互依存关系，分析表中1990年—2001年中国货币供应量（M2）和国内生产总值（GDP）的有关数据:年份货币供应量(亿元)M2国内生产总值(亿元)GDP1990 1529.31 8598.41991 19349.92 1662.51992 25402.2 26651.91993 34879.8 34560.51994 46923.5 46670.01995 60750.5 57494.91996 76094.9 66850.51997 90995.3 73142.71998 104498.5 76967.21999 119897.9 80579.42000 134610.3 88228.12001158301.994346.4资料来源:《中国统计年鉴2002》，第51页、第662页，中国统计出版社对货币供应量与国内生产总值作相关分析，并说明分析结果的经济意义。

2.4表中是16支公益股票某年的每股帐面价值和当年红利：根据上表资料：（1）建立每股帐面价值和当年红利的回归方程； （2）解释回归系数的经济意义；（3）若序号为6的公司的股票每股帐面价值增加1元，估计当年红利可能为多少？2.5美国各航空公司业绩的统计数据公布在《华尔街日报1999年年鉴》（The Wall Street 1。

第一章绪论参考重点：计量经济学的一般建模过程第一章课后题〔1.4.5〕1.什么是计量经济学计量经济学方法与一般经济数学方法有什么区别答：计量经济学是经济学的一个分支学科，是以提醒经济活动中客观存在的数量关系为内容的分支学科，是由经济学、统计学和数学三者结合而成的穿插学科。

计量经济学方法提醒经济活动中各个因素之间的定量关系，用随机性的数学方程加以描述；一般经济数学方法提醒经济活动中各个因素之间的理论关系，用确定性的数学方程加以描述。

4.建设与应用计量经济学模型的主要步骤有哪些答：建设与应用计量经济学模型的主要步骤如下：(1)设定理论模型，包括选择模型所包含的变量，确定变量之间的数学关系和拟定模型中待估参数的数值范围；(2)收集样本数据，要考虑样本数据的完整性、准确性、可比性和—致性；(3)估计模型参数；(4)检验模型，包括经济意义检验、统计检验、计量经济学检验和模型预测检验。

5.模型的检验包括几个方面其具体含义是什么答：模型的检验主要包括：经济意义检验、统计检验、计量经济学检验、模型的预测检验。

在经济意义检验中，需要检验模型是否符合经济意义，检验求得的参数估计值的符号与大小是否与根据人们的经历和经济理论所拟订的期望值相符合；在统计检验中，需要检验模型参数估计值的可靠性，即检验模型的统计学性质；在计量经济学检验中，需要检验模型的计量经济学性质，包括随机扰动项的序列相关检验、异方差性检验、解释变量的多重共线性检验等；模型的预测检验主要检验模型参数估计量的稳定性以及对样本容量变化时的灵敏度，以确定所建设的模型是否可以用于样本观测值以外的范围。

第二章经典单方程计量经济学模型：一元线性回归模型参考重点：1.相关分析与回归分析的概念、联系以及区别2.总体随机项与样本随机项的区别与联系3.为什么需要进展拟合优度检验4．如何缩小置信区间〔P46〕由上式可以看出〔1〕.增大样本容量。

样本容量变大，可使样本参数估计量的标准差减小；同时，在同样置信水平下，n越大，t分布表中的临界值越小。

计量经济学课后思考题答案-庞皓版提供方法论。

所谓计量经济学理论与方法技术的研究，实质上是指研究如何运用、改造和发展数理统计方法，使之成为适合测定随机经济关系的特殊方法。

应用计量经济学是在一定的经济理论的指导下，以反映经济事实的统计数据为依据，用计量经济方法技术研究计量经济模型的实用化或探索实证经济规律、分析经济现象和预测经济行为以及对经济政策作定量评价。

1.3怎样理解计量经济学与理论经济学、经济统计学的关系？答：1、计量经济学与经济学的关系。

联系：计量经济学研究的主体—经济现象和经济关系的数量规律；计量经济学必须以经济学提供的理论原则和经济运行规律为依据；经济计量分析的结果：对经济理论确定的原则加以验证、充实、完善。

区别：经济理论重在定性分析,并不对经济关系提供数量上的具体度量；计量经济学对经济关系要作出定量的估计，对经济理论提出经验的内容。

2、计量经济学与经济统计学的关系。

联系：经济统计侧重于对社会经济现象的描述性计量；经济统计提供的数据是计量经济学据以估计参数、验证经济理论的基本依据；经济现象不能作实验，只能被动地观测客观经济现象变动的既成事实，只能依赖于经济统计数据。

区别：经济统计学主要用统计指标和统计分析方法对经济现象进行描述和计量；计量经济学主要利用数理统计方法对经济变量间的关系进行计量。

1.4在计量经济模型中被解释变量和解释变量的作用有什么不同？答：在计量经济模型中，解释变量是变动的原因，被解释变量是变动的结果。

被解释变量是模型要分析研究的对象。

解释变量是说明被解释变量变动主要原因的变量。

1.5一个完整的计量经济模型应包括哪些基本要素？你能举一个例子吗？答：一个完整的计量经济模型应包括三个基本要素：经济变量、参数和随机误差项。

例如研究消费函数的计量经济模型：Y++=αuβX其中，Y为居民消费支出，X为居民家庭收入，二者是经济变量；α和β为参数；u是随机误差项。

1.6假如你是中央银行货币政策的研究者，需要你对增加货币供应量促进经济增长提出建议，你将考虑哪些因素？你认为可以怎样运用计量经济学的研究方法？答：货币政策工具或者说影响货币供应量的因素有再贴现率、公开市场业务操作以及法定准备金率。