磁场的安培环路定理

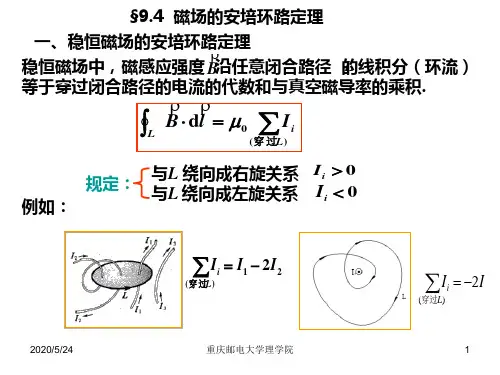
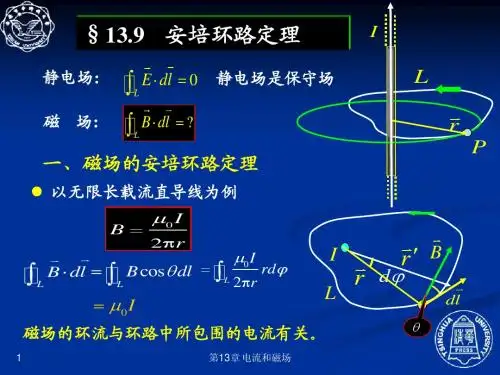
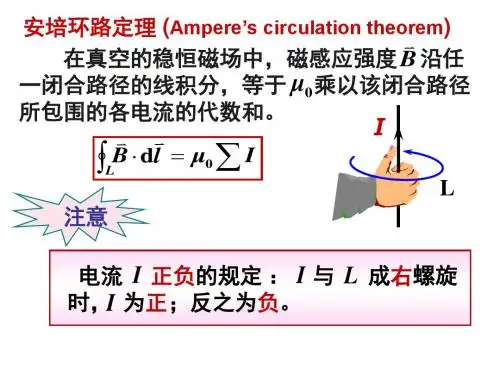
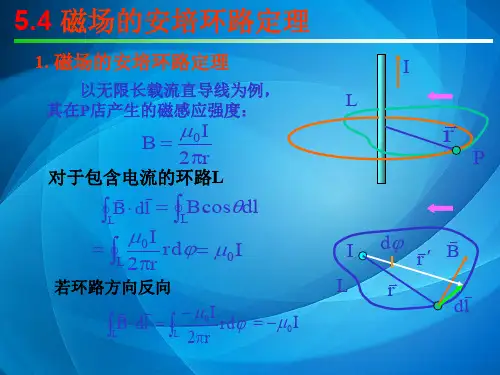
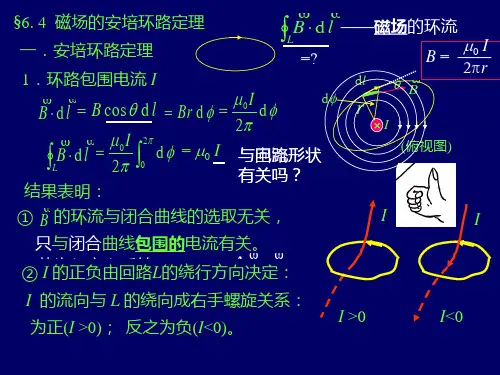
第二十讲： §6.4磁场的安培环路定理一、安培环路定理；是磁场与电流之间相互作用的基本定律之一 1、表述：在稳恒磁场中，B 沿任意闭合回路的积分等于该闭合回路所包围的电流的代数和乘以0μ 。

2、表达式：∑⎰=⋅iI d B 0μ两点说明：①∑i I 虽是闭合回路内所环绕的电流，且满足右手螺旋法则。

但是B 是与闭合回路内外电流有关，即B 是闭合回路内外电流共同作用的结果。

环路外的电流对 d B L ⋅⎰无贡献。

②当B 无对称性时，安培环路定理仍成立，只是B 不能提到积分号外面来，所以，利用安培环路定理不能求解B ，必须利用比-萨定律及叠加原理来进行求解。

二、安培环路定理的应用1、无限长圆柱载流导体的磁场分布∑⎰=⋅iI d B 0μR r ：20122122RIr B r RIr B πμππμπ=⇒=⋅Rr ：rI B I rB πμμπ220202=⇒=⋅☆如果是无限长圆面载流导体的磁场分布∑⎰=⋅iI d B 0μR r ：00211=⇒=⋅B r B πRr ：rI B I rB πμμπ220202=⇒=⋅2、长直载流螺线管内的磁场分布∑⎰=⋅iI d B 0μd B d B d B d B d addccbba⋅+⋅+⋅+⋅=⋅⎰⎰⎰⎰⎰BnIB I ab n ab B abd B 00B μμ=⇒=⇒=⋅⎰电流数密度：单位长度的电流数。

3、载流环形螺线管内的磁场分布∑⎰=⋅iI d B 0μr 2B d B Lπ==⋅⎰⎰d BnII rN B NI r 00022B μπμμπ==⇒=小结：磁场的安培环路定理 作业：P253预习：§6.5 磁场对运动电荷和载流导线的作用第二十讲： §6.4磁场的安培环路定理 作业：P2536-15 （1）a r <，由安培环路定理可得201220122aIrB raI r B πμππμπ==（2）b r a <<rIB Ir B πμμπ220202==（3）c r b <<)(2)()()(222220302222222203b c r r c I B I b c rc b c b r I I r B --=--=⎥⎦⎤⎢⎣⎡---=πμμππμπ（4）0,4=>B c r6-16 （1）如图示，过P 点作一半径为r 的圆形回路，圆心为O ，由安培环路定律可得 rNIB NI u r B πμπ2,200==故绕线环内磁感强度B 的大小与径向距离r 成反比。

磁场安培环路定理证明磁场安培环路定理是电磁学中的一个重要定理，它描述了磁场在电路中的分布和变化规律。

本文将对该定理进行全面详细的证明，包括定义、公式推导、实验验证以及应用等方面。

一、磁场安培环路定理的定义磁场安培环路定理是指：在任意闭合回路上，磁感应强度的积分等于该回路所包围电流的代数和。

即：∮B·dl=μ0I其中，∮B·dl表示沿闭合回路积分的磁感应强度；μ0为真空中的磁导率；I为该回路所包围电流的代数和。

二、公式推导为了证明上述定理，我们需要从麦克斯韦方程组入手，具体如下：1. 静电场高斯定理∮E·dS=Q/ε02. 静电场法拉第定律∮E·dl=-dΦ/dt3. 磁场高斯定理∮B·dS=04. 磁场法拉第定律∮B·dl=μ0I+μ0ε0(dΦE/dt)其中，E为电场强度；B为磁感应强度；S为任意闭合曲面；dl为曲线段微元；dS为曲面微元；Q为该曲面所包围的电荷量；ΦE为电通量；I为该回路所包围电流的代数和。

由于磁场高斯定理中∮B·dS=0，因此我们需要找到一种方法来消去第二个式子中的第二项，即使其等于零。

这时，我们可以利用安培环路定理来实现这一目标。

对于一个任意闭合回路，根据斯托克斯定理可得：∮B·dl=∫(∇×B)·dS其中，∇×B表示磁场强度的旋度运算符。

由于磁场是无旋场，因此有：∇×B=0将上式代入上式中，则有：∮B·dl=0但是，在真空中没有任何电流通过闭合回路时，根据安培定律可知：∮B·dl=μ0I因此，我们可以得到磁场安培环路定理：∮B·dl=μ0I三、实验验证为了验证磁场安培环路定理的正确性，我们可以进行如下实验：1. 实验器材：一个长直导线、一个螺线管、一个万用表和一些导线。

2. 实验步骤：(1) 将长直导线穿过螺线管的中心，将万用表连接到导线两端。

真空中磁场的安培环路定理表达式
磁场的安培环路定理：
一、定义
1、安培环路定理：安培环路定理是物理和电学中一个重要的理论，它指出，在真空中 xyz 三个方向上，通过一定距离或一条环路的一个磁场线时，磁通环 mzmz 与安培数之间存在一种关系。

2、磁场线：磁场线是磁场的一种重要组成部分，每一条磁场线代表不同的磁场值。

二、表达式
安培环路定理表达式为：Mzmz= 2π i Φ，其中Φ是由偶然电磁现象形成的磁场的流过的安培数，i是圆的周长被用于测量的环路的距离。

三、推导
由于磁场力线总是有完整的封闭环路，根据磁感应定律，磁场中心点处将产生磁场，有M0=μ H 的关系，ΔH表示磁感应强度，μ是介质的磁导率，这时环路上的磁感应应该与安培数有关，于是就有了磁场安
培环路定理的表达式：Mzmz= 2π i Φ 。

四、应用
1、安培环路定理用于求解磁场的磁力矢量，可以准确测量磁场的强度、强度的方向以及磁场的变化情况。

2、可以用安培环路定理计算磁力矢量对电磁激励的结果，从而掌握不
同形状、尺寸和构造的电磁设备的性能和特性。

3、也可以用安培环路定理分析及设计空间电磁环境及其对周边子系统
的影响，更好地检测和预测管道、设备的运行状况。

磁场的安培环路定理公式安培环路定理（Ampere's Circuital Law）是电磁学中的一个重要定理，描述了电流所产生的磁场的性质。

该定理是由法国科学家安德烈·玛丽·安培于1826年提出的。

安培环路定理公式可以用来计算闭合曲线上的磁场和电流之间的关系。

安培环路定理可以表述如下：在真空中，闭合曲线上的磁场的环流等于通过该闭合曲线所围成的面内的电流的代数和的N倍，即B·l=μ0·N·I。

其中，B表示磁场强度，单位为特斯拉（T）；l表示闭合曲线的长度，单位为米（m）；μ0表示真空中的磁导率（磁场的常量），约等于4π×10^-7N/A^2；N表示闭合曲线所围成的面内的匝数；I表示通过该闭合曲线所围成的面内的电流，单位为安培（A）。

这个公式表明了闭合曲线上的磁场强度与该闭合曲线所围成的面内电流的代数和成正比。

当电流的方向与闭合曲线所围成的面的法线方向相同时，为正；而当电流的方向与闭合曲线所围成的面的法线方向相反时，为负。

安培环路定理的应用非常广泛。

通过安培环路定理，我们可以计算出闭合曲线上的磁场强度，从而了解电流所产生的磁场的强度和分布情况。

此外，我们还可以通过安培环路定理来计算导线上的磁场，从而提前预测电流的影响范围和磁场的强度。

安培环路定理的一个重要应用是计算长直导线产生的磁场。

对于一根长度为l的直导线，安培环路定理公式可以简化为B=μ0·I/2πr，其中r为距离导线的垂直距离。

另一个应用是计算无限长薄直导线产生的磁场。

在这种情况下，合理的选择闭合曲线为无限大的圆形曲线，通过计算可以得到B=μ0·I/2r，其中r为距离导线的垂直距离。

安培环路定理还可以应用于计算线圈产生的磁场。

对于一个具有N匝的螺线管，安培环路定理的公式可以表示为B·2πr=μ0·N·I，其中B 为螺线管中心处的磁场强度，r为距离螺线管中心的距离。

磁场中的安培环路定理磁场中的安培环路定理是电磁学中的一条重要定理，它描述了磁场中的电流与磁场的相互作用关系。

根据安培环路定理，一个封闭的电流环路所受的磁场力的总和等于该环路所包围的电流的总和乘以真空中的磁导率。

让我们来了解一下什么是磁场。

磁场是由电流或磁体产生的一种力场，它可以对其他电流或磁体施加力。

磁场的强度可以用磁感应强度B来表示，单位是特斯拉(T)。

磁感应强度的方向可以用磁力线来表示，磁力线是磁场中的力线，表示磁场的方向和强度。

在磁场中，当有电流通过一个导线时，该导线周围会形成一个磁场。

根据安培环路定理，沿着一个封闭的回路，该回路内的电流与回路所包围的磁场的相互作用力之和等于回路内电流的总和乘以磁导率的乘积。

这个定理可以用一个简单的公式来表示：∮B·dl=μ0I其中，∮B·dl表示环路所包围的磁场力的总和，μ0表示真空中的磁导率，I表示环路内电流的总和。

安培环路定理的应用非常广泛。

在电磁铁中，安培环路定理可以用来计算铁芯中的磁感应强度。

在计算电感的时候，我们也可以利用安培环路定理来计算电流所产生的磁场。

此外，在电磁感应中，安培环路定理也可以用来计算感应电动势。

为了更好地理解安培环路定理，我们可以通过一个简单的实例来说明。

假设有一个平面圆环，环上有电流I流过。

我们想要计算该圆环所包围的磁场力。

根据安培环路定理，我们可以选择一个闭合的路径，沿着该路径计算环所包围的磁场力的总和。

在这个例子中，我们可以选择圆环的周长作为路径。

然后，我们需要计算路径上的磁场力。

根据安培环路定理，路径上的磁场力等于路径内电流的总和乘以磁导率。

假设路径上的磁感应强度为B，根据安培环路定理，我们可以得到以下等式：B·2πr=μ0I其中，r表示圆环的半径。

通过这个等式，我们可以计算圆环所包围的磁场力。

总结一下，磁场中的安培环路定理是描述磁场中的电流与磁场的相互作用关系的定理。

根据该定理，一个封闭的电流环路所受的磁场力的总和等于该环路所包围的电流的总和乘以真空中的磁导率。

磁场的安培环路定理公式磁场的安培环路定理是电磁学中的重要定理之一，它描述了磁场在闭合回路上的环路积分等于该回路所包围的电流的代数和的性质。

在分析磁场问题时，安培环路定理可以提供一个简便的方法来计算磁场的强度和方向。

安培环路定理的数学表达式为：∮B·dl = μ0·Ienc其中，∮B·dl表示磁场B沿闭合回路的环路积分，μ0是真空中的磁导率，其值约为4π×10^-7 T·m/A，Ienc表示回路所包围的电流的代数和。

通过安培环路定理，可以方便地计算磁场的分布情况。

下面将通过几个具体的例子来说明安培环路定理的应用。

例1：一根直导线的磁场考虑一根无限长的直导线，电流为I，要求计算离导线距离为d处的磁场强度B。

我们可以选择一个以导线为轴的圆形回路，根据安培环路定理，有∮B·dl = μ0·Ienc。

由于回路只包围了一段电流，所以Ienc = I。

回路的环路积分可以通过计算B在回路上的分量得到，由于B的方向在回路上是沿着回路的方向，所以B在回路上的分量为B·2πd，其中2πd是回路的周长。

因此，我们可以得到B·2πd =μ0·I，即B = μ0·I/(2πd)。

这就是直导线产生的磁场强度的公式。

例2：两根平行直导线的磁场考虑两根平行的无限长直导线，电流分别为I1和I2，距离为d，要求计算它们之间的磁场强度B。

同样地，我们可以选择一个以两根导线为边的矩形回路，根据安培环路定理，有∮B·dl = μ0·Ienc。

由于回路包围了两段电流，所以Ienc = I1 + I2。

回路的环路积分可以分为两部分，一部分是沿着左边导线的分量B1在回路上的环路积分，另一部分是沿着右边导线的分量B2在回路上的环路积分。

由于两根导线的方向相反，B1与B2的方向也相反，所以它们的环路积分相加为0。

因此，我们可以得到B1·2d + B2·2d = μ0·(I1 + I2)，即B = μ0·(I1 + I2)/(2d)。