物流选址重心法
- 格式:xlsx
- 大小:15.22 KB
- 文档页数:3

基于重心法的配送中心选址研究配送中心的选址在物流系统中起着至关重要的作用,它直接影响到整个物流网络的效率和运营成本。
因此,基于重心法的配送中心选址成为一种较为常用的研究方法。
本文将探讨基于重心法的配送中心选址研究,并对其优势和应用进行分析。
重心法是一种基于地理位置的定量分析方法,它通过计算分布物体的重心位置来进行空间分析。
在配送中心选址研究中,重心法可以用来确定最佳的配送中心位置,以便最大限度地降低运输距离和成本,并提高物流效率。
在进行基于重心法的配送中心选址研究时,可以按照以下步骤进行:第一步,确定所有潜在的配送点位置。
这些潜在的配送点可以是已经存在的仓库、物流中心或市场,也可以是根据需求和市场分析确定的新的潜在位置。
第二步,收集有关每个潜在配送点的数据。
这些数据可以包括物流流量、运输成本、物流时间等信息。
此外,还可以考虑其他因素,如供应链可行性、市场需求等。
第三步,根据收集到的数据计算每个潜在配送点的重心。
重心是通过计算各点的加权平均值得到的。
具体计算方法可以根据不同的指标进行权重设置,来反映不同指标对于选址的重要程度。
第四步,通过比较不同配送点的重心位置,选择与最终目标最接近的位置作为最佳配送中心位置。
可以使用GIS软件等工具来进行空间分析和可视化。
首先,基于重心法的选址研究基于空间数据的分析,能够直观地反映不同配送点的分布情况和地理位置关系,从而提供客观的选择依据。
其次,基于重心法的选址研究充分利用了已有的数据和信息,通过计算和分析可以从大量的数据中挖掘出有用的信息,为选址决策提供科学依据。
再次,基于重心法的选址研究是一种定量分析方法,可以对不同的配送点进行比较和评估,从而快速选择最佳位置,减少决策时间和成本。
最后,基于重心法的选址研究具有一定的灵活性和适应性,可以根据实际情况进行权重设置和计算方法的调整,从而更好地满足特定需求。
在实际应用中,基于重心法的配送中心选址研究可以用于各种物流系统中,例如电商物流、城市物流等。

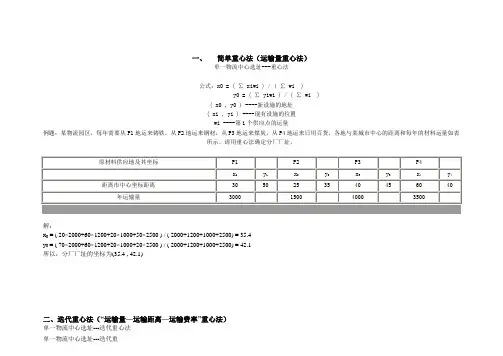
一、简单重心法(运输量重心法)单一物流中心选址---重心法公式:x0 = ( ∑ xiwi ) / ( ∑ wi)y0 = ( ∑ yiwi ) / ( ∑ wi)( x0 , y0 ) ----新设施的地址( xi , yi ) ----现有设施的位置wi ----第i个供应点的运量例题:某物流园区,每年需要从P1地运来铸铁,从P2地运来钢材,从P3地运来煤炭,从P4地运来日用百货,各地与某城市中心的距离和每年的材料运量如表所示。
请用重心法确定分厂厂址。
解:x0 = ( 20×2000+60×1200+20×1000+50×2500 ) / ( 2000+1200+1000+2500) = 35.4y0 = ( 70×2000+60×1200+20×1000+20×2500 ) / ( 2000+1200+1000+2500) = 42.1所以,分厂厂址的坐标为(35.4 , 42.1)二、迭代重心法(“运输量—运输距离—运输费率”重心法)单一物流中心选址---迭代重心法单一物流中心选址---迭代重公式:X = ( ∑Q i R i X i/D i) / ( ∑Q i R i/D i ) Y= ( ∑Q i R i Y i/D i) / ( ∑Q i R i/D i )D i= ( ( X i-X)2+(Y i-Y)2 )1/2F = ∑Q i R i D i(Xi , Yi)----现有目标的坐标位置Qi----运输量Ri----运输费率F----总运费(X , Y)----新仓库的位置坐标Di----现有目标到新仓库的距离解题方法:(1)令Di=1A、求出仓库的初始位置;B、将求出的仓库位置(X,Y)代入Di公式中,求出客户到仓库初始位置的距离;C、计算出仓库初始位置的总运费ΣQiRiDi;( 2 ) 迭代计算:A、将Di代入原公式,求出仓库的新位置坐标(X ,Y);B、将求出的(X ,Y)代入Di公式中求出Di;C、计算出仓库新位置的总运费ΣiQiRiDi…不断迭代,直到求出的仓库位置和总运费越来越接近于不变,即为所得;注意:牵涉到运输费率要用重心法做;但如无费率,又要求用迭代重心法计算,则令费率为1。

重心法选址计算公式物流在物流规划中,选址是一个至关重要的环节。
选址的好坏直接影响到物流运作的效率和成本。
重心法是一种常用的选址计算方法,通过重心法选址计算公式,可以帮助物流规划者找到最优的选址方案。
本文将介绍重心法选址计算公式及其在物流规划中的应用。
重心法选址计算公式是一种基于地理信息的选址计算方法。
它通过对物流需求点的地理位置进行加权平均,找到一个最佳的选址点,使得整个物流网络的运作成本最低。
重心法选址计算公式的基本原理是,通过对各个需求点的地理位置进行加权平均,找到一个最佳的选址点,使得整个物流网络的运作成本最低。
其计算公式如下:重心X坐标 = Σ(需求点X坐标需求量) / Σ需求量。
重心Y坐标 = Σ(需求点Y坐标需求量) / Σ需求量。
其中,需求点X坐标和Y坐标分别表示需求点的地理位置坐标,需求量表示该需求点的物流需求量。
通过这个公式,可以计算出一个最佳的选址点,使得整个物流网络的运作成本最低。
重心法选址计算公式在物流规划中有着广泛的应用。
首先,它可以帮助物流规划者找到最优的物流中心位置,使得整个物流网络的运作成本最低。
其次,它可以帮助物流规划者进行物流网络的优化设计,使得物流运作更加高效和便捷。
此外,重心法选址计算公式还可以帮助物流规划者进行物流需求预测,使得物流运作更加精准和有效。
在实际应用中,重心法选址计算公式需要结合具体的物流需求和地理信息进行计算。
首先,需要对物流需求点的地理位置进行调查和收集,包括需求点的X坐标和Y坐标以及需求量。
然后,根据这些数据,利用重心法选址计算公式进行计算,找到一个最佳的选址点。
最后,需要对选址点进行评估和验证,确保选址方案的可行性和有效性。
在使用重心法选址计算公式进行物流规划时,还需要考虑一些因素。
首先,需要考虑物流需求点的分布情况,以及各个需求点的地理位置和需求量。
其次,需要考虑物流运输的成本和效率,找到一个最佳的选址点,使得整个物流网络的运作成本最低。




基于重心法的物流场所中心选址优化问题的实验总结基于重心法的物流场所中心选址优化问题的实验总结一、引言物流场所中心选址是物流管理中的重要问题之一,合理的选址能够有效降低物流成本、提高物流效率。
本实验采用基于重心法的物流场所中心选址优化方法,通过实验研究其在不同情况下的性能表现。
二、实验设计1. 实验目标:通过选择合适的位置建立物流场所,使得整个物流网络的运输距离最小。
2. 实验环境:使用Python编程语言进行实验设计和模拟。
3. 实验数据:根据真实的物流需求和地理信息,构建了一个包含多个候选地点和需求点的数据集。
4. 实验步骤:a) 初始化候选地点和需求点的坐标信息。
b) 计算每个需求点到所有候选地点的距离,并按照距离从近到远进行排序。
c) 选择一个需求点作为初始中心点,并计算该中心点到其他需求点的距离之和。
d) 依次将其他需求点加入已选择中心点集合,并计算更新后的总距离。
e) 选择总距离最小的中心点集合作为最优解。
三、实验结果1. 实验一:不同候选地点数量下的性能比较a) 设定需求点数量为固定值,分别设置不同数量的候选地点。
b) 运行实验,记录每种情况下的运行时间和最优解。
c) 分析结果发现,随着候选地点数量的增加,运行时间呈线性增长,而最优解的改善效果逐渐减弱。
2. 实验二:不同需求点数量下的性能比较a) 设定候选地点数量为固定值,分别设置不同数量的需求点。
b) 运行实验,记录每种情况下的运行时间和最优解。
c) 分析结果发现,随着需求点数量的增加,运行时间呈指数增长,并且最优解的改善效果也逐渐减弱。
3. 实验三:不同距离权重下的性能比较a) 在计算需求点到候选地点距离时引入权重因素。
b) 设置不同权重值,并运行实验,记录每种情况下的运行时间和最优解。
c) 分析结果发现,在一定范围内增加距离权重可以提高最优解质量,但过大或过小的权重值都会导致最优解的质量下降。
四、实验总结1. 基于重心法的物流场所中心选址优化方法在不同情况下都能够得到较好的结果。

选址重心法模型文章来源:宝库企业管理网更新时间:2007-11-13 16:28:50重心法是一种布置单个设施的方法,这种方法要考虑现有设施之间的距离和要运输的货物量。
它经常用于中间仓库的选择。
在最简单的情况下,这种方法假设运入和运出成本是相等的,它并未考虑在不满载的情况下增加的特殊运输费用。
重心法首先要在坐标系中标出各个地点的位置,目的在于确定各点的相对距离。
坐标系可以随便建立。
在国际选址中,经常采用经度和纬度建立坐标。
然后,根据各点在坐标系中的横纵坐标值求出成本运输最低的位置坐标X和Y,重心法使用的公式是:式中CX--重心的x坐标;Cy--重心的y坐标;Dix--第i个地点的x坐标;Diy--第i个地点的y坐标;Vi--运到第i个地点或从第I个地点运出的货物量。
最后,选择求出的重心点坐标值对应的地点作为我们要布置设施的地点。
重心法:1、现假设有五个工厂,坐标分别为P1(1,2),P2(7,4),P3(3,1),P4(5,5),P5(2,6)。
现要建立一个中心仓库为五个工厂服务。
工厂到中心仓库的运输由载货汽车来完成,运量按车次计算,分别为3,5,2,1,6次每天。
求这个中心仓库的位置。
解:设物流费用与车次数量成正比,则相应的物流费用系数为:3,5,2,1,6。
在坐标轴上标出各个点的相应位置,设总运输费用最低的位置坐标为X和Y,根据重心法的计算方法,可求得中心仓库的坐标。
计算过程如下:(31)(57)(23)(15)(62)613.5883521617(32)(54)(21)(15)(66)69 4.0593521617X Y ⨯+⨯+⨯+⨯+⨯===++++⨯+⨯+⨯+⨯+⨯===++++故所求中心仓库的理论位置在原坐标系里的位置为(3.588,4.059)。
2、 易出莲花超市要在江西省南昌市建立一所地区级中央配送中心,要求该配送中心能够覆盖该地区五个连锁店,连锁店的坐标及每月的销售量数据如表所示,要求求出一个理论上的配送中心的位置。
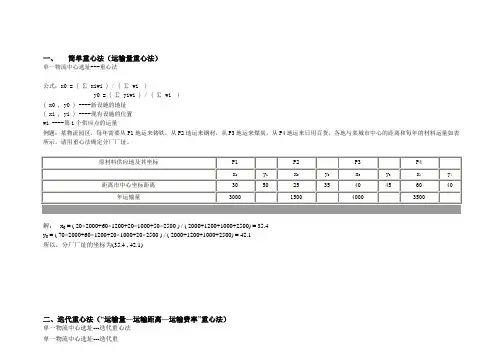
一、简单重心法(运输量重心法)单一物流中心选址---重心法公式:x0 = ( ∑ xiwi ) / ( ∑ wi )y0 = ( ∑ yiwi ) / ( ∑ wi )( x0 , y0 ) ----新设施的地址( xi , yi ) ----现有设施的位置wi ----第i个供应点的运量例题:某物流园区,每年需要从P1地运来铸铁,从P2地运来钢材,从P3地运来煤炭,从P4地运来日用百货,各地与某城市中心的距离和每年的材料运量如表所示。
请用重心法确定分厂厂址。
解:x0 = ( 20×2000+60×1200+20×1000+50×2500 ) / ( 2000+1200+1000+2500) = 35.4y0 = ( 70×2000+60×1200+20×1000+20×2500 ) / ( 2000+1200+1000+2500) = 42.1所以,分厂厂址的坐标为(35.4 , 42.1)二、迭代重心法(“运输量—运输距离—运输费率”重心法)单一物流中心选址---迭代重心法单一物流中心选址---迭代重公式:X = ( ∑Q i R i X i/D i) / ( ∑Q i R i/D i ) Y= ( ∑Q i R i Y i/D i) / ( ∑Q i R i/D i )D i= ( ( X i-X)2+(Y i-Y)2 )1/2F = ∑Q i R i D i(Xi , Yi)----现有目标的坐标位置Qi----运输量Ri----运输费率F----总运费(X , Y)----新仓库的位置坐标Di----现有目标到新仓库的距离解题方法:(1)令Di=1A、求出仓库的初始位置;B、将求出的仓库位置(X,Y)代入Di公式中,求出客户到仓库初始位置的距离;C、计算出仓库初始位置的总运费ΣQiRiDi;( 2 ) 迭代计算:A、将Di代入原公式,求出仓库的新位置坐标(X ,Y);B、将求出的(X ,Y)代入Di公式中求出Di;C、计算出仓库新位置的总运费ΣiQiRiDi…不断迭代,直到求出的仓库位置和总运费越来越接近于不变,即为所得;注意:牵涉到运输费率要用重心法做;但如无费率,又要求用迭代重心法计算,则令费率为1。
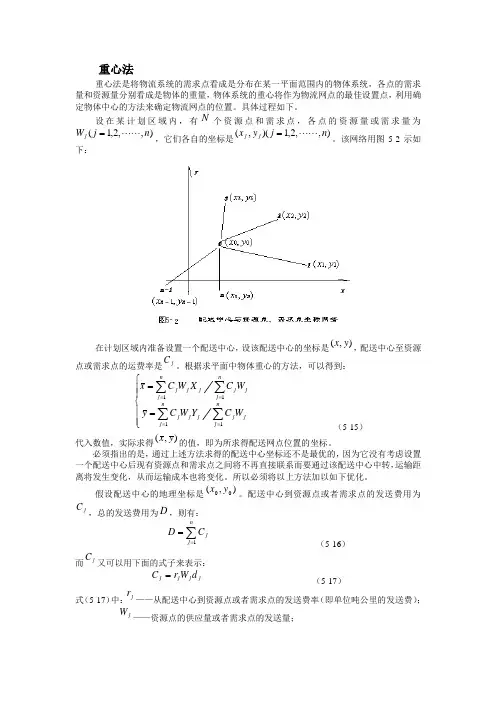
重心法重心法是将物流系统的需求点看成是分布在某一平面范围内的物体系统,各点的需求量和资源量分别看成是物体的重量,物体系统的重心将作为物流网点的最佳设置点,利用确定物体中心的方法来确定物流网点的位置。
具体过程如下。
设在某计划区域内,有N 个资源点和需求点,各点的资源量或需求量为),,2,1(n j W j =,它们各自的坐标是),,2,1)(,(n j y x j j =。
该网络用图5-2示如下:在计划区域内准备设置一个配送中心,设该配送中心的坐标是),(y x ,配送中心至资源点或需求点的运费率是jC 。
根据求平面中物体重心的方法,可以得到:⎪⎪⎩⎪⎪⎨⎧==∑∑∑∑====n j nj j j j j j n j nj j j j j j W C Y W C y W C X W C x 1111 (5-15)代入数值,实际求得),(y x 的值,即为所求得配送网点位置的坐标。
必须指出的是,通过上述方法求得的配送中心坐标还不是最优的,因为它没有考虑设置一个配送中心后现有资源点和需求点之间将不再直接联系而要通过该配送中心中转,运输距离将发生变化,从而运输成本也将变化。
所以必须将以上方法加以如下优化。
假设配送中心的地理坐标是),(00y x 。
配送中心到资源点或者需求点的发送费用为jC ,总的发送费用为D ,则有:∑==nj jC D 1(5-16)而jC 又可以用下面的式子来表示:jj j j d W r C = (5-17)式(5-17)中:j r——从配送中心到资源点或者需求点的发送费率(即单位吨公里的发送费);jW ——资源点的供应量或者需求点的发送量;jd ——从配送中心到资源点或者需求点的直线距离。
其中,jd 也可以写成如下形式:][)(2)(2021j jj y yx x d --=- (5-18)把方程式(5-18)代入(5-17),得到:∑==nj jj j d W r D 1(5-19)从方程式(5-19)和方程式(5-16)可以求得使D 为最小的),(00y x 。
重心法选址项目分析实例答:重心法包括基于需求量的重心法和基于吨距离的重心法等两种方法。
基于需求量的重心解法:把需求量作为考察因素,它的主要步骤是首先将一个经济区域内的各需求点在坐标系中表示,并将各需求点看成一个物理系统,然后将各需求点的需求量视为物体的质量,最后通过求该物理系统的重心来确定物流中心的最佳坐落点。
基于吨距离的重心法解法:因是单一设施选址,物流中心的建设以及运营成本均可以视为固定不变的,而运输费用随距离和货运量而变化,所以可以考虑在不同地点设置的物流中心因距各用户距离变化和需求量而引起运输费用的变化,找出使运输总费用最小的点,并将其作为最佳选址点。
(4)重心法选址计算:x0 = ( 30×2200+70×1800+30×1500+60×2500 ) / ( 2200+1800+1500+2500) = 48.38 y0 = ( 80×2200+70×1800+30×1500+30×2500 ) / (2200+1800+1500+2500) = 52.75所以,分厂厂址的坐标为(48.38 , 52.75)例题二:某汽车公司,每年需要从A ,地运来橡胶,从AZ 地运来玻璃,从A :地运来发动机,从A 、地运来零配件,各地与某城市中心的距离和每年的材料运量如表。
假设城市的中心为原点,各种材料运输费率相同,用重心法确定该公司合理位置。
解:设重心坐标为(X O ,Y O ),则根据重心法公式计算如下:0x =∑∑==4141j j jj jj j W C x W C =29001300150030002900*501300*401500*1003000*45++++++=55.4km; 0y =∑∑==4141j j jj jj j W C y W C =29001300150030002900*801300*101500*703000*60++++++=60.92km 即该公司的合理位置的坐标为(55.4 , 60.92 )。
物流重心法计算公式
物流重心法是一种常用的物流配送路线优化方法,其计算公式如下:
1. 计算各个配送点的重心位置
设某个区域内的n 个点为P1, P2, ..., Pn,其重心位置为P。
对于一个三角形,重心位于三条中线的交点处。
对于一个任意的多边形,可以通过将其分割成若干个三角形,计算每个三角形的重心,然后将这些重心的平均值作为整个多边形的重心。
2. 计算各个配送点到重心位置的距离
设P1, P2, ..., Pn 到重心位置P 的距离分别为d1, d2, ..., dn,则可以通过勾股定理计算出这些距离。
3. 计算各个配送点的权重
设某个点的权重为w,则可以通过以下公式计算出各个点的权重:
w = f(d)
其中,f(d) 是距离与距离之间的函数关系,通常采用的是指数函数或幂函数。
例如,可以采用下面这个公式:w = e^(-d/L)
其中,L 是一个常数,表示距离的衰减速度。
4. 计算各个配送点的总权重
各个配送点的总权重可以通过将各个点的权重相加得到。
5. 确定最优的配送路线
根据各个配送点的总权重,可以确定最优的配送路线。
通常采用的方法是,将各个点按照总权重从大到小排序,然后依次计算出每个点到下一个点的距离和路径,直到确定最优的配送路线。
物流重心法是一种简单有效的物流配送路线优化方法,可以帮助物流公司降低配送成本、提高配送效率,提高客户满意度。
3.1仓库选址3.1.1 重心法求最佳仓库选址的原理重心法是根据几何的方法确定在一个平面或空间内分布有若干的点,求出一点到这若干的点的总距离最短。
重心法是一种模拟方法,它将物流系统中的需求点和资源点看成是分布在某一平面范围内的物流系统,各点的需求量和资源量分别看成是物体的重量,物体系统的重心作为物流网点的最佳设置点,利用求物体系统重心的方法来确定物流网点的位置。
通常重心法可以用于解决仓库的选址、配送中心的选址等问题。
重心法在解决配送中心的选址问题时,它把运输成本看成现有配送点之间的运输距离和运输的货物量的线性函数。
重心法首先要在坐标系中标出各个地点的位置,目的在于确定各点的相对距离。
坐标系采用经度和纬度建立坐标。
这样就确定了各个配送点的具体地理位置。
同时考虑各段运输路线的运输成本。
设拟建的配送中心有N 个需要收件的配送点,它们所在的位置坐标为(i i y x ,),其中i=1,2,···n ,拟建的配送中心的坐标为(x,y),如下图所示:Y根据在中国地图上查找各城市的经纬度得到每个城市的地理坐标(保留小数点后货物从i 地运至配送中心所在地的运输费用是i c ,设i h 为运输费率即单位货物运输单位距离的费用,且假设配送点与配送中心所在地之间的道路为直线,距离为i d ,i w 为运输量。
则i i i i d w h c ⨯⨯=...........................(1) 且i d =22)()(i i y y x x -+- (2)总运输费用H 为: H=i i ni i ni i d w h c ⨯⨯=∑∑==11 (3)由于i d 与配送中心位置(x,y)有关,因此总运输费用是x,y 的函数,将式(2)带入式(3),得:221)()(),(i i i ni i y y x x w h y x H -+-⨯⨯=∑= (4)(1)根据以上公式和案例给定的各个分拨中心的业务量求出配送中心的初始地理坐标(假设一级分拨中心的运输费率为0.05,二级分拨中心的运输费率为0.075)初始坐标:X=111.25585/3.67=30.3149 Y=442.185525/3.67=120.49 (2)计算配送中心在目前初始坐标位置的总运输成本则配送中心在初始坐标的总费用H=3.927671108为求得运输费用最小的配送中心,就变成了对函数H(x,y)求极值的问题,即求(**,y x ),使:H=H(**,y x )min根据函数极值的原理,式(4)分别对x,y 求偏导,令偏导为0,得:0/)(1=-=∂∂∑=i i i ni i d x x w h x H………………………(5) 0/)(1=-=∂∂∑=i i i n i i d y y w h y H………………………(6) 由式(5)和(6)可以求得函数H(x,y)的极值点,由于式(6)是非线性方程组,难以求得**,y x 的表达式,需要用迭代法求解,展开式(5)和(6)得:∑∑===ni iii ni iiiid wh d xw h x 11*// (7)∑∑===ni iii ni iiiid wh d yw h y 11*// (8)(3)求出第一次迭代以后的配送中心的坐标X=189.3623755/6.251962728=30.2884684Y=753.9872233/6.251962728=120.6000829则第一次迭代以后的坐标为(30.2884684,120.6000829)(4)计算配送中心在目前初始坐标位置的总运输成本则配送中心在初始坐标的总费用H=3.860409954其中i d =2*2*)()(i i y y x x -+- ,将式(7)和(8)写成迭代式,有k 次迭代结果表达式:()()∑∑=-=-=ni k i ii ni k i iiid wh d xw h k x 1111*//)( (9)()()∑∑=-=-=ni k i iini k i iiid wh d yw h k y 1111*//)( (10)其中:()2*)1(2*)1(1)()(i k i k k i y y x x d -+-=--- (11)如果k H <1-k H ,说明总运费仍有改进改善的余地,返回步骤(5),继续叠加;否则,说明(()()*1*1,--k k y x )为最佳场址,则停止叠加。
物流系统选址规划设计---重心法课件重心法,即重心最小化法,是一种数学优化方法,适用于物流系统的选址规划设计。
本文将介绍重心法的基本原理及其在物流系统选址规划设计中的应用。
一、重心法的基本原理重心法是在平面或空间中寻找一个点,使得该点到一组点的距离之和最小。
这个点被称为重心,也称为质心或重心点。
重心是物体几何形状的一个量度,它的位置可以通过该物体各点的坐标来计算。
在物流系统选址规划设计中,我们可以应用重心法来确定物流中心的最佳位置。
二、物流系统选址规划设计中的应用1. 收集数据在使用重心法之前,首先需要收集与物流系统有关的数据。
这些数据包括客户地址、货物流动量、货物种类、交通运输工具、在途时间等信息。
通过对这些数据进行分析,确定适宜的物流中心选址。
2. 建立模型在收集到数据之后,需要建立合适的模型。
建模的目的是将复杂的物流网络转化为一个简单的数学模型,方便计算。
通常,物流系统的网络模型可以用图的形式表示,节点表示客户和物流中心,边表示运输线路。
然后,我们可以通过建立目标函数和约束条件来对模型进行优化。
3. 确定重心通过将所有物流节点的位置坐标与其货物流动量相乘,可以得到各节点的质量。
然后,可以通过计算每个节点的质量之和和各节点的坐标之间的加权平均位置,求出物流中心的重心。
4. 评估结果在确定重心之后,需要对结果进行评估。
评估包括评估物流中心的距离、货物的运输成本、交通运输的效率、货物是否按时到达等因素。
评估结果有助于确定物流中心是否最佳,并帮助确定是否需要重新选址。
三、小结重心法是一种简单有效的优化方法,适用于物流系统选址规划设计。
通过收集数据、建立模型、确定重心和评估结果,可以找到最佳的物流中心位置,优化物流系统的效率和效益。
运营管理:什么是重心法选址引言对于一个企业而言,选址是一个至关重要的决策。
选址的好坏将直接影响到企业的运营效益和市场竞争力。
在运营管理中,重心法选址是一种常用的评估方法,通过对各项因素进行综合考量,确定最佳选址方案。
本文将深入探讨什么是重心法选址以及它在运营管理中的应用。
什么是重心法选址重心法选址是一种通过计算区域各点的坐标位置和其所对应的权重,以确定相对最佳选址的方法。
该方法利用各点的坐标和权重,通过数学模型计算出一个具有集中趋势的中心点,即选址重心。
选址重心可以作为选址决策的参考,通常选址越接近重心,表示该选址方案越合适。
重心法选址的优势相比其他选址评估方法,重心法选址具有以下几个明显优势:考虑多个因素重心法选址可以综合考虑多种因素对选址的影响,例如人口密度、交通便利度、竞争对手位置等。
通过权重的设置,不同因素的影响程度可以被合理地量化,从而更加全面地评估选址方案的优劣。
相对容易实施重心法选址的计算相对简单,只需要确定各个因素的权重和其对应的坐标位置即可。
无需复杂的模型和算法,即可得到一个可作为参考的选址重心。
便于可视化展示重心法选址的结果可以直观地以图像形式展示出来。
通过将各点按照其权重绘制在地图上,选址重心可以用一个点表示。
这种可视化展示方式便于决策者进行对比和分析,更容易理解和接受。
重心法选址在运营管理中的应用运营管理中的选址决策直接关系到企业的运营效益和市场竞争力。
重心法选址作为一种常用方法,在运营管理中得到广泛应用。
零售业对于零售业而言,选址是其成功的基石。
通过重心法选址,零售企业能够综合考量人口密度、消费水平、竞争对手分布等因素,确定最佳的店铺选址。
选址重心可以作为零售企业扩张的方向和范围的参考,帮助企业在竞争激烈的市场中占据有利地位。
餐饮业餐饮业也是选址的重点行业之一。
通过重心法选址,餐饮企业可以综合考虑人流量、消费能力、周边竞争等因素,找到最适合开店的位置。
选址重心可以帮助餐饮企业确定开店的区域,从而提高客流量和盈利能力。