当前位置：文档之家 › 5-1向量的内积、长度及正交性

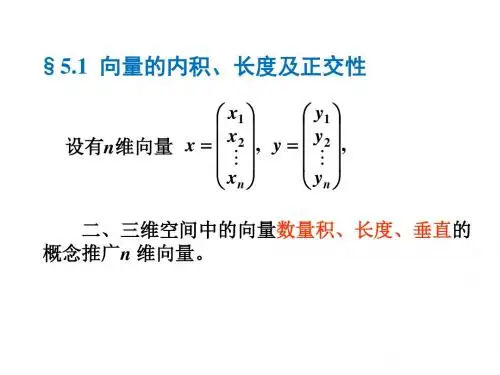
5-1向量的内积、长度及正交性

  • 格式：ppt
  • 大小：812.50 KB
  • 文档页数：48

下载文档原格式

  / 48

合集下载

第一讲：向量的内积、长度和正交性

第一讲：向量的内积、长度和正交性

主讲人：同济大学殷俊锋向量的内积、长度和正交性是线性代数中基本的概念，不仅包含内积、范数等概念，还包括正交向量组、正交规范基、正交矩阵等基本概念，以及将一组线性无关向量组转化为正交规范基的施密特正交化过程。

这些概念对于今后学习矩阵的特征值，以及线性空间等具有非常重要的作用.一、知识要点1、内积、正交定义:给定n 维列向量，定义x 与y 的内积.•内积的性质有交换性、正定性、保持线性运算•施瓦茨不等式•当，则称向量x 与y 是正交的.2(,)(,)(,)≤x y x x y y (,)0=x y 1212(,,,),(,,,)==T T n n x x x x y y y y 1122(,)=+++n n x y x y x y x y2、向量的长度（或范数)定义令称为n 维向量x 的长度（或范数).22212(,),n x x x x x x ==+++x •向量长度的性质有非负性、齐次性和三角不等式•n 维非零向量x 与y 的夹角•当，则称向量x 为单位向量.1=x (),arccos θ=x y x y3、正交向量组、正交基定义正交向量组是一组两两正交的非零向量.定理设n 维向量是一组两两正交的非零向量，则线性无关。

定义设n 维向量是向量空间V 的一个基，如果是两两正交，且都是单位向量，则称是V 的一个规范正交基.12,,,r a a a 12,,,r a a a 12,,,r e e e 12,,,r e e e 12,,,r e e e4、施密特正交化过程设n 维向量是向量空间V 的一个基，则可按照如下步骤将其化为V 的一个规范正交基.步骤：1，正交化令11βα=()()2122111,,αββαβββ=-12,,,r a a a()()()()313233121122,,,,αβαββαββββββ=--()()()()()()121121112211,,,,,,αβαβαββαβββββββββ----=----r r r r r r r r r 121212, , , ,r r r e e e ββββββ===则是V 的一个规范正交基.2：单位化，令12,,,r e e e5、正交矩阵定义设A是一个n阶方阵，如果A T A=E，则称A是正交矩阵，简称正交阵.n 阶方阵A 是正交矩阵A-1=A T;A 的列向量是两两正交的单位向量，即A 的列向量组是R n的标准正交基；A 的行向量是两两正交的单位向量.定义设P是一个正交阵，则线性变换y=Px称为正交变换.6、正交矩阵的性质（1）若A为正交矩阵，则A-1=A T 也为正交阵，且|A|=1或-1；（2）若A和B是正交阵，则AB也是正交阵；（3）正交变换x=Py（P是正交矩阵）保持向量的长度不变.二、教学要求1、理解向量正交、正交基的概念，正交矩阵的概念和性质2、掌握施密特正交化过程的步骤三、例题精讲例1、设140,2,.23λλ-⎛⎫⎛⎫⎪ ⎪===+⎪ ⎪⎪ ⎪-⎝⎭⎝⎭与正交，且，求和a b c a b a c c解：由正交性因此()()()()() ,,,,,λλλ=+=+=a b a a c a a a c a a所以()(),102,5λ-===-a ba a4122(2)02321λ--⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-=--=⎪ ⎪ ⎪⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭c b a例2、试用施密特正交化过程把向量组正交化.()123111,,124139⎛⎫ ⎪= ⎪ ⎪⎝⎭a a a 解：先作正交化()()()()()()111222111132333121122,111,6210,,331113111,,1482410,,,32391113=-⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=-=-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫ ⎪-⎛⎫⎛⎫⎛⎫ ⎪- ⎪ ⎪ ⎪ ⎪=--=--= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ⎪ ⎪⎝⎭b a b a b a b b b b a b a b a b b b b b b再把它们单位化，111222333111,31110,21112.61⎛⎫ ⎪== ⎪ ⎪⎝⎭-⎛⎫ ⎪== ⎪ ⎪⎝⎭⎛⎫ ⎪==- ⎪ ⎪⎝⎭b e b b e b b e b例3、判断矩阵是否为正交阵，并说明理由111231112211132⎛⎫- ⎪ ⎪ ⎪=- ⎪ ⎪ ⎪- ⎪⎝⎭A 解：由于正交矩阵列向量为单位向量且相互正交，而111111,1124913⎛⎫ ⎪ ⎪ ⎪=-=++≠ ⎪ ⎪ ⎪⎝⎭a a 因此，该矩阵不是正交矩阵.例4、设为维向量，，令，证明是对称的正交阵.x 证明：首先证明对称性，()()222,=-=-=-=T T T T T TH E xx E xx E xx H n 1=T x x 2=-T H E xx H ()()()()()2222444444.=--=--=-+=-+=-+=T T T T T T TT T T T TT T H H E xx E xx E xx E xx E xx xx xx E xx x x x x E xx xx E 再证明正交性例5、设都是正交阵，证明也是正交阵.,A B 证明：由题意()===T T T T AB AB B A AB B B E AB ,,==T TA A EB B E AB 所以因此，也是正交矩阵.谢谢！。

5-1 向量的内积、长度及正交性

5-1 向量的内积、长度及正交性

向量的长度 令
2 2 2 || x || [ x, x] x1 x2 xn
||x||称为n维向量x的长度(或范数)
向量的长度的性质 设x y为n维向量 为实数 则 (1)非负性 当x0时 ||x||0 当x0时 ||x||0 (2)齐次性 ||x||||x|| (3)三角不等式 ||xy||||x||||y|| >>>
容易验证b1 b2 br两两正交 且b1 b2 br与a1 a2 ar 等价 把b1 b2 br单位化 即得V的一个规范正交基
e1 1 1 1 b1 e2 b2 er br || b1|| || b2 || || br ||
e1 1 1 2 2 1 1 e2 e3 2 2 0 0 0 0
0 0 0 0 1 1 e4 2 2 1 1 2 2
例2 设a1(1 2 1)T a2(1 3 1)T a3(4 1 0)T 试用施 密特正交化过程把这组向量规范正交化 解 令b1a1
1 1 1 4 5 b2 a2 b1 3 2 1 1 6 1 3 1 [b1, b1] [b1, a2 ] 4 1 1 1 1 5 b3 a3 b1 b2 1 2 1 2 0 0 3 1 3 1 1 [b1, b1] [b2, b2 ] [b1, a3] [b2, a]
施密特正交化方法 设a1 a2 ar是向量空间V中的一个基 取向量组
说明 要找一组两两正交的单位向量e1 e2 er 使e1 e2 er与a1 a2 ar等价 这样一个问题 称为把a1 a2 ar这个 基规范正交化

两个向量内积和正交的定义

两个向量内积和正交的定义

两个向量内积和正交的定义向量是在数学中经常用到的概念，向量的运算方式有点类似于数的运算，但是向量有很多特殊的性质，因此需要了解向量的内积和正交的定义。

一、向量的内积向量的内积是指两个向量的数量积，也被称为点积或标量积，它的定义如下：设有两个n维向量a = (a1, a2, …, an)和b = (b1, b2, …, bn)，它们的内积表示为：a·b = a1b1 + a2b2 + … + anbn。

通过这个公式得到的结果是一个数字，而不是向量，这个数字表示了两个向量的夹角和它们的长度的乘积。

如果a·b = 0，那么这两个向量就被称为正交向量。

二、向量的正交两个向量的正交是指它们之间的夹角为直角，这种关系被称为正交关系。

在三维空间中，我们可以看到两个正交的向量表示的向量平面是一个矩形。

这个矩形的长度是两个向量长度的乘积，宽度则是它们的夹角的正弦值所乘。

在二维空间中，当两个向量垂直时，它们就正交了。

例如，在平面直角坐标系中，两个向量a = (1, 0)和b = (0, 1)是正交向量，它们的内积为0。

三、向量的应用向量的内积和正交在实际应用中有着广泛的应用，例如：1. 在三维计算机图形学中，可以利用向量的内积来计算光照效果。

2. 在机器学习中，向量的内积和正交用于向量的相似性度量，这是非常重要的一个概念。

3. 在物理学中，向量的正交关系被用来计算施加在物体上的力的大小和方向。

四、总结向量的内积和正交是向量的两个重要的概念。

这些概念有着广泛的应用，需要掌握这些概念才能更好地理解一些数学和物理学问题。

我们在应用和研究中，可以通过向量内积和正交，更细致地分析和解决问题，也可以更深入地了解向量及其运算特性。

向量的内积

向量的内积

说明: 内积是两个向量之间的一种运算, 其结果是一个实数, 用 矩阵记号表示, 当x与y都是列向量时, 有 [x, y]=xTy.
向量的内积 设有n维向量x=(x1, x2, , xn)T, y=(y1, y2, , yn)T, 令 [x, y]=x1y1+x2y2+ +xnyn, [x, y]称为向量x与y的内积. 内积的性质 设x, y, z为n维向量, λ为实数, 则 (1)[x, y]=[y, x]; (2)[λx, y]=λ[x, y]; (3)[x+y, z]=[x, z]+[y, z]; (4)当x=0时, [x, x]=0; 当x≠0时, [x, x]>0; (5)[x, y]2≤[x, x][y, y]. ——施瓦茨不等式.
|| y||= yT y = xT PT Px = xT x =|| x|| .
这说明, 经正交变换线段的长度保持不变(从而三角形的 形状保持不变), 这是正交变换的优良特性.
第五章 相似矩阵及二次型
§5.2 方阵的特征值与特征向量
数 学 与 计 算 机 科 学 系
工程技术中的一些问题, 如振动问题和稳定性 问题, 常可归结为求一个方阵的特征值和特征向量 的问题. 数学中诸如方阵的对角化及解微分方程组 的问题, 也都要用到特征值的理论.
1 a2 =ξ1= 0 , 1
0 1 1 1 1 a2 =ξ 2 ξ1 = 1 0= 2 . 1 2 1 2 1 [ξ1, ξ1] [ξ1, ξ 2 ]
正交阵 如果n阶矩阵A满足ATA=E(即A1=AT), 那么称A为正交矩 阵, 简称正交阵. 方阵A为正交阵的充分必要条件是A的列(行)向量都是单 位向量, 且两两正交. n阶正交阵A的n个列(行)向量构成向量空间Rn 的一个规 范正交基. 1 1 1 1 2 2 2 2 1 1 1 1 正交矩阵举例: P = 2 2 2 2 . 1 1 0 0 2 2 0 0 1 1 2 2

本_第17讲_向量的内积、长度及正交性 二次型基本知识

本_第17讲_向量的内积、长度及正交性 二次型基本知识
第3页 页
一、向量的内积
2. 内积的性质 ⑴ [α , β ] = [ β , α ]; ⑵ [ kα , β ] = k[α , β ], k ∈ R; ⑶ [α + β , γ ] = [α , γ ] + [ β , γ ];
[ ⑷ 当 α = 0 时， α ,α ] = 0,
当 α ≠ 0 时，[α ,α ] > 0;
第10页 页
三、向量的正交性
一定线性无关． 定理 正交向量组 α1 ,α2 ,⋯,αr 一定线性无关． 证 设存在 k1 , k2 ,⋯, kr 使
(＊) ＊
k1α1 + k2α2 + ⋯+ krαr = 0, 两两正交， 由α1 ,α2 ,⋯,αr 两两正交，知
T 以α 1 左乘(＊)式两端，得 ＊ 式两端，
二次型基本知识
二次型的概念； 二次型的概念； 二次型的矩阵表示. 二次型的矩阵表示.
一、二次型的概念
含有n个变量 含有 个变量x1, x2, ⋅ ⋅ ⋅, xn的二次齐次函数 个变量 f(x1, x2, ⋅ ⋅ ⋅, xn) = a11x12+a22x22+ ⋅ ⋅ ⋅ +annxn2 +2a12x1x2+2a13x1x3+ ⋅ ⋅ ⋅ +2an−1,, nxn−1xn − − 称为二次型.
两个向量之间的一种运算，其结果是一个数 两个向量之间的一种运算，其结果是一个数， 用矩阵记号表示有 [α , β ] = α T β = β Tα . n≥3维向量的内积是 维向量数量积的推广， 维向量的内积是3维向量数量积的推广 维向量的内积是 维向量数量积的推广， 但是没有3维向量直观的几何意义 维向量直观的几何意义． 但是没有 5. 施密特 施密特(Schimidt)正交化 正交化

向量的内积、长度及正交性

向量的内积、长度及正交性
欧几里得范数
在多维空间中，向量长度可以通过欧几里得范数计算，即 $||vec{a}|| = sqrt{sum_{i=1}^{n} a_i^2}$。
向量模的计算
在数学软件中，如Matlab或Python的NumPy库，可以直接使 用内置函数计算向量长度，如`numpy.linalg.norm()`。
03
02
CHAPTER
向量的长度
向量长度的定义
定义
向量长度是指向量从原点到终点所经 过的距离，通常用符号“||”表示。
几何意义
向量长度等于向量在欧几里得空间中 的模，即以原点为起点、终点为终点 的有向线段的长度。
向量长度的性质
非负性
向量长度总是大于等于0，即对于任意向量$vec{a}$，有 $||vec{a}|| geq 0$。
CHAPTER
向量的正交性
向量正交的定义
两个向量$mathbf{a}$和 $mathbf{b}$正交，当且仅当它们的 内积为零，即$mathbf{a} cdot mathbf{b} = 0$。
正交意味着两个向量在所有方向上都 相互垂直，没有共同的行或列。
向量正交的性质
1
正交向量之间的内积为零，即$mathbf{a} cdot mathbf{b} = 0$。
2
正交向量的点积为零，但不意味着它们的长度为 零。
3
正交向量之间没有共同的行或列，即它们是垂直 的。
向量正交的判断方法
01
检查向量的点积是 否为零
如果$bf{a}$和$mathbf{b}$正 交。
02
检查向量的模长是 否为零
向量的内积、长度及正交性
目录
CONTENTS
• 向量的内积 • 向量的长度 • 向量的正交性 • 向量的应用

第10讲：向量的内积与正交矩阵

方阵A 为正交矩阵的充要条件是 A 的列（行） 向量都是单位向量且两两正交．
正交矩阵的性质: 设A, B 为 n 阶正交矩阵, 则 (1) A－1 = AT 也为正交矩阵 , 且 |A|=1 或－1. (2) AB 也为正交矩阵.
统计软件分析与应用
线性代数A
4.1 向量的内积与正交矩阵
定义: 若 P 为正交阵, 正交变换.
4.1 向量的内积与正交矩阵
§1 向量的内积、长度及正交性
一、内积的定义及性质
定义: n 维向量 x ( x1 , x2 ,L , xn )T , y ( y1 , y2 ,L , yn )T 的内积
[ x, y] x1 y1 x2 y2 xn yn;
若 x, y为列向量, 则 [x, y] xT y.
a2 b1
] ]
b1
,
统计软件分析与应用
线性代数A
4.1 向量的内积与正交矩阵
b3
a3
[b1 , [b1 ,
a3 b1
] ]
b1
[b2 [b2
, ,
a3 b2
] ]
b2
,
br
ar
[b1 , ar ] [b1 , b1 ]
b1
[b2 , ar ] [b2 , b2 ]
b2
L
[br 1 [br1 ,
, ar ] br1 ]
二、向量的长度及性质
定义: n 维向量 x 的长度 ( 或范数 )
x [ x, x] x12 x22 xn2 .
长度的性质： 1. 非负性: x 0; x 0 x 0.
2. 齐次性: 对 R 有 x x .
3. 三角不等式: x y x y .
统计软件分析与应用

【线代课件】5.1向量的内积、长度及正交性


（2）齐次性：lx l x ;
[l x, l x] l[x, l x] l[l x, x] l 2[x, x]
|| l x || [l x,l x] l 2[x, x] | l | [x, x] | l | || x ||
向量的长度
定义：令 || x || [ x, x] x12 x22 xn2
[x + y, z] = [x, z] + [y, z] 当 x = 0（零向量） 时， [x, x] = 0；
当 x ≠ 0（零向量） 时， [x, x] > 0． 施瓦兹（Schwarz）不等式
[x, y]2 ≤ [x, x] [y, y]．
证明：设 x (x1, x2 ,, xn ), y ( y1, y2 ,, yn ) 由(xi z yi )2 0(i 1,2,, n)可得(x1z y1)2 (x2 z y2 )2 (xn z yn )2 0 即(x12 x22 xn2 )z2 2(x1y1 x2 y2 xn yn )z ( y12 y22 yn2) 0
[x, y] = x1 y1 + x2 y2 + … + xn yn = xT y．
内积具有下列性质（其中 x, y, z 为 n 维向量，l 为实数）：
对称性： [x, y] = [y, x]．
[ x, y] x1 y1 x2 y2 y1 x1 y2 x2 [ y, x]
xn yn yn xn
[x, x] = x12 + x22 + … + xn2 ≥ 0
[x, y] = x1 y1 + x2 y2 + … + xn yn = xT y．
内积具有下列性质（其中 x, y, z 为 n 维向量，l 为实数）：

线性代数第五章128


b1 b2 br e1 , e2 , , e r , || b1 || || b2 || || br ||
则e1, e2, · · · , en是向量空间V的一组规范正交基. 由线性无关向量组a1, a2, · · · , ar 构造出正交向量组 b1, b2, · · · , br 的过程称为施密特(Schimidt)正交化过程.
1 0 0 0 0 1 0 0 设 1 0 , 2 0 , 3 1 , 4 0 . 0 0 0 1
又设
1 2 1 2 0 0 0 0 1 2 1 2 , e4 . e1 , e2 , e3 1 2 1 2 0 0 1 2 1 2 0 0 0 ij ( i , j 1, 2, 3, 4). 由于 [e i , e j ] ij 1 i j
2 2 2 [x, x] = x = x1 + x2 + + xn
当|| x ||=1时, 称x为单位向量
3.当|| x || 0, || y || 0 时, n维向量 x 与 y 的夹角： [ x, y] arccos 规定0 . || x || || y || 4.向量 x 与 y 正交定义为： π 当[x, y]=0，也即 θ = .
向量的长度及性质
(1) 非负性: || x || 0, 当且仅当x=0时有|| x || = 0;
(2) 齐次性: || x|| = | | || x ||;
(3) 三角不等式: || x+y || || x || + || y ||.

向量的内积与正交

向量的内积与正交
目录
CONTENTS
• 向量的内积 • 向量的正交 • 向量的内积与正交的应用 • 向量的点积与叉积 • 总结
01
CHAPTER
向量的内积
向量内积的定义
定义
向量内积是两个向量之间的点乘运算，记作$mathbf{A} cdot mathbf{B}$。 其结果是一个标量，表示两个向量之间的角度余弦值与两个向量模的乘积。
几何意义
叉积的几何意义是垂直于两向量所在平面的第三个向量，其模长等于两向量构成的平行四边形的面积。
性质
叉积满足反交换律，即$mathbf{A} times mathbf{B} = -mathbf{B} times mathbf{A}$。
点积与叉积的区别和联系
区别
点积和叉积在定义、几何意义和性质上都有所不同。点积是两向量的内积，结果 是一个标量；叉积是两向量的外积，结果是一个向量。
如果两个向量的方向垂直，则它们正交。
判断两个向量的模长是否 相等
如果两个向量的模长相等，则它们正交。
03
CHAPTER
向量的内积与正交的应用
向量内积在几何中的应用
判断两向量是否垂直
通过计算两向量的内积，若结果为0，则两向量垂直。
计算向量的长度
利用向量内积和向量的模长，可以计算出任意向量的长度。
计算向量的夹角
向量内积的计算方法
坐标表示法
若向量$mathbf{A}$和$mathbf{B}$的坐标分别为$(a_1, a_2, ..., a_n)$和$(b_1, b_2, ..., b_n)$，则$mathbf{A} cdot mathbf{B} = a_1b_1 + a_2b_2 + ... + a_nb_n$。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例4
验证
A
2 1
2
0
2 1 2
0
2 0 1
2 是正交矩阵.
0
1
2 2
解 A 的列向量都是单位向量，且两两正交， 故 A 是正交矩阵.
返回 上页 下页
2. 正交变换
【回顾】从变量 x1, x2, …, xn 到变量 y1, y2, …, ym的
“线性变换”可表示
为
y1 a11x1 a12x2 a1n xn ,
返回 上页 下页
例3
1
1
4
设 R3 的一组基为 1 2 , 2 3 , 3 1
1
1
0
用施密特正交化方法将这组基规范正交化.
解 首先将 1,2,3 正交化：
取
1 2
1;
2
[ 2 [1
, ,
1 1
] ]
1
1 3 1
4 6
1 2 1
5 / 3 5 / 3 ; 5 / 3
即，
是单位向量.
返回 上页 下页
1
2
例1
已知
21,
13,
0
0
计算两个向量单位化后的内积.
解 12 22 (1)2 02 6 14
,
,
1 2 2 (3) (1)1 0 0 6 14
5 2 21
返回 上页 下页
定理 1 向量的内积满足
y2
a21x1
a22x2
a2n xn ,
ym am1x1 am2 x2 amn xn .
y1 a11
即
y2 ym
a21 am1
a12 a22
am2
a1n x1
a2n x2 , 记作 y=Ax.
amn xn
返回 上页 下页
是 V 的一个规范正交基.
例如，
1 2
/ /
3 3
，
2 1/
/3 3
是
R2
的一个规范正交基.
返回 上页 下页
设 1，2， ，r 是向量空间 V 的一组规范正交基， 则向量 在这组基下的坐标向量的第 j 个分量为
[ , j ] ( j 1,2, ,r)
证
x1
设
(1， 2，
基
，
r
)
x2 xr
返回 上页 下页
二、正交向量组、规范正交基
1. 正交向量组
一组两两正交且不含零向量的向量组， 称为非零正交向量组.
定理 3 非零正交向量组是线性无关的.
证 设 1，2， ， s 是非零正交向量组，
即
(非零)
i，i iTi
0
(i, j 1,2, , s)
(正交) i， j iT j 0 (i j)
返回 上页 下页
1
0
解 Ax=O，得基础解系 1 0 , 2 1 .
1
1
1, 2 线性无关，且都与 正交.
再将1, 2 正交化：
1
取
1
1
0
,
1
2
2
[ 2 , [1,
1] 1]
1
1/ 2 1
1/ 2
于是， , 1, 2 是一个非零正交向量组.
返回 上页 下页
三、正交矩阵、正交变换
定义 6 若 A 为正交矩阵，则线性变换 y=Ax 称为正交变换.
正交变换的性质
设： n 维列向量 , 正交变换 A, A (A为正交矩阵)，
则向量的内积与长度以及向量间的夹角都保持不变.
即 A , A , ；
A ；
arccos A , A arccos ,
A A
返回 上页 下页
返回 上页 下页
3. 向量的夹角
定义 3 规定 n 维向量 和 的夹角为 arccos [ , ]
根据定义，如果非零向量 , 的内积 [ , ] 0，则 夹角 =90o ；反之亦然. 因此 定理 2 非零向量 , 正交(或垂直)的充要条件是
[ , ] 0
说明 由于零向量与任何向量的内积为零，因此，也 可以说零向量与任何向量正交.
这是Ax=O 的解空间的一个基本性质.
返回 上页 下页
例2
已知 R3 中的两个向量
1
1 1,
2
1 2
正交，
1
1
求一个非零向量 3，使得1, 2, 3 两两正交.
分析 已知1, 2 相互正交，故只需求出与1, 2 都
正交的一个向量.
以1T
,
T 2
作为行向量构成矩阵
A
1T
T 2
1 1
1 2
证 a11
设
A
a22
an1
a12 a22
an2
a1n
a2n
，按列分块为
(1,2 ,
,n ),
ann
1T
1T1 1T2 1Tn
AT
A
2nTT (1,2,
,n)
2T1 nT1
2T 2
nT 2
2Tn
nT
n
返回 上页 下页
1
2 1
1 2
1
1
2 1
1 2 1
施密特正交化方法：
一组线性无关的非零向量 1，2， ，r
作特定的线性运算
与1，2， ，r 等价的正交单位向量组
返回 上页 下页
施密特正交化方法的基本步骤和思路：
设1，2， ，r 是一组线性无关的非零向量.
① 取 1 1
② 取 2 2 k211
求 k21，使得 2, 1 0，即 2 和 1正交.
, 2 2 2 即 , 2 [ , ][ , ]
(称为Cauchy-Schwarz不等式) 证 参见 附录 1 .
向量长度的性质：
① 0 , 等号成立当且仅当 O；(非负性) ② k k ； (齐次性) ③ (三角不等式)
性质①②显然成立，性质③的证明参见 附录 2 .
x11 x22 x2r
则 [ , j ] [x11 x坐2标2 向量x2r , j ]
x1[1, j ] x2[2, j ] xr[r , j ] 0 0 0 x j[ j , j ] 0 0 x j
返回 上页 下页
3. 施密特(Schimidt)正交化方法
b2
，
规定 和 的内积为
an
bn
, a1b1 a2b2 anbn
(即，对应分量的乘积之和)
返回 上页 下页
说明 (1) 当 和 都为列向量时(一般做法)，
b1
T
(a1,a2 ,
an
)
b2
a1b1 a2b2 anbn
bn
a1
T
(b1 , b2 ,
3
3 1
, ,
1 1
1
3 2
, ,
2 2
2
返回 上页 下页
④ 不断重复以上步骤，直到最后有
r
r
r 1
, ,
1 1
1
r 2
, ,
2 2
2
r
r,
1
r 1
, r1
r
1
通过①②③④的正交化步骤，得到正交向量组：
1，2， ，r (作为习，证明 1，2， ，r 都是非零向量)
最后，再将 1，2， ，r 单位化为 1，2， ，r ，
r
1
返回 上页 下页
再将得到的正交向量组 1，2， ，r 单位化：
1
1 1
,
2
2 2
,
,
r
r r
说明 (1) 正确的顺序是先正交化，再单位化. 这是因为：对一组线性无关的单位向量正交化后, 可能不再是单位向量.
(2) 向量空间的基一般不是规范正交基，但是可以通 过施密特正交化步骤，构造出一组规范正交基，这 称为：对基进行规范正交化.
1. 正交矩阵
定义 5 若 n 阶方阵 A 满足 ATA=E，则 A 为正交矩阵. 根据定义，容易证明如下正交矩阵的性质：
设 A, B 皆为 n 阶正交矩阵，则 ① A1 AT ; ② A1(即 AT) 也是正交矩阵； ③ AB 也是正交矩阵； ④ A 1或1;
返回 上页 下页
定理 4 A为 n 阶正交矩阵的充要条件是：A 的列向量 组是正交单位向量组.
④ [ , ] 0 ，等号成立当且仅当 0 .
返回 上页 下页
2. 向量的长度
a1
定义 2
设
n 维向量
a2 ,
an
规定 的长度(或范数)为
[ , ] a12 a22 an2
说明 (1) 若 1，则称向量 为单位向量.
(2) 任意非零向量 ，可通过长度进行单位化，
25/ 3
1/
3
3
3 3
1/ 2
3
8
0
1 /
2
返回 上页 下页
例4
已知
1 1,
1
求两个向量，与 共同构成非零正交向量组.
解 令矩阵 A T (1, 1, 1)，
建立方程组
Ax
O，即
( 1,
1,
1 )
x1 x2
0.
x3
( Ax O的解与 A 的行向量 T正交，亦即与 正交)
即
j
j j
( j 1,2, ,r)
返回 上页 下页
施密特正交化步骤 小结 ：
首先将线性无关的非零向量组 1，2， ，r 正交化：
令 1 1
2
2
2 1
, ,
1 1
1