当前位置：文档之家 › 导体和电介中的静电场

导体和电介中的静电场

  • 格式：doc
  • 大小：376.00 KB
  • 文档页数：6

下载文档原格式

  / 6

合集下载

大学物理(下)第十章导体和电解质中的静电场(精)

大学物理(下)第十章导体和电解质中的静电场(精)

10-1静电场中的导体Electrostatic field in conductor一、导体的静电平衡1、金属导体的电结构特征：具有大量的自由电子。

2.静电感应：导体在外电场中，其上的电荷重新分布，局部呈带电状态的现象。

3. 静电平衡：自由电子无定向运动，感应电荷稳定 E = E+F F = qE t = -eE导体的静电平衡条件 、严E 1、 导体内部的场强处处为零V （内部电子无运动）。

r2、 导体表面附近紧贴导体外侧处的场强方向垂直 表面（沿表面电子无运动）。

— *■0—Y— *-© Y分布。

导体表面附近的电场 强度的大小与该表面电 荷面密度成正比2）有空腔导体 ＜空腔内无电荷血 ©dd()电荷分布在表面上 问内表面上有电荷吗？ 结论电荷分布在外表面上（内表面无电荷） •导体空腔内包围有电荷 萨肪=（）q 沪_q 当空腔内有电荷时， 内表面因静电感应出现等 值异号的电荷T ，外表面 有感应电荷+?（电荷守恒）2、导体表面电场强度与电荷面密度的关系 帖辰 EdS +II(/、/$+( K ds =—・・•crl, £*1; CT T E T3、孤立导体表面电荷按曲率分布1）导体表面凸出而尖锐的地方（曲率较大）电荷面密度较大2）导体表面平坦的地方（曲率较小）带电导体尖端附近的电场特别大，可使尖端附近的空气发生电离而成为导体产生放电现象，即尖端放电＜电风实验＞f "K1+ + 4尖端放电会损耗电能，还会干扰精密测量和对通讯产生危害；然而尖端放电也有很广泛的应用。

V避雷针〉三、静电屏蔽 1、屏蔽外电场2.屏蔽腔内电场接地空腔导体 将使外部空间不 受空腔内的电场 影响高压带电作业电场影响。

这时,整个空腔导体和腔内的电势也必处 处相等。

例题：点电荷+?处在导体球壳的中心，壳的内外半径分别为乩和心，求电场强度和电势的分布。

解：球壳内表面感应・g ,外表面+? ”二s*0r < : E、・4“ =—£=_^_E4grE,=0/?)< r < R2: E、・4TC r2 =0r>R,i £\・4龙尸=土%例题证明：两平行放置的无限大带电的平行平面金 属板A 和〃相向的两面上电荷面密度大小相等，符号相 反，相背的两面上电荷面密度大小相等，符号相同。

大学物理第九章静电场中的导体电解质课件

大学物理第九章静电场中的导体电解质课件

电场与电解质性质
电解质溶液的介电常数和电导率等性质会影响电场分布。
电场与离子运动
电场对离子产生作用力，使离子发生定向移动，形成电流。
电解质中的电场
在静电场中，电解质中的离子在电场作用下发生定向移动，形成电流。
电流的形成
电流密度与电场强度成正比关系，电场强度越大，电流密度越高。
电流密度与电场强度
电解质的性质如电导率、离子浓度等对电流有重要影响。
实验结论
实验结论与展望
THANKS FOR
WATCHING
感谢您的观看
实验设备与实验原理
实验步骤
1. 将导体放置在静电计的电场中，观察导体是否带电。
2. 将电解质溶液置于电场中，观察电解质溶液的电导率是否发生变化。
实验步骤与实验结果分析
3. 分析实验结果，得出结论。
实验结果分析
1. 导体在静电场中会感应出电荷，表现出静电感应现象。
实验步骤与实验结果分析
2. 电解质溶液在静电场中会发生极化现象，影响其电导率。
3. 通过对比实验结果，可以进一步了解导体和电解质在静电场中的物理特性。
实验步骤与实验结果分析
VS
通过实验观察和分析，可以得出以下结论：导体在静电场中会产生静电感应现象，而电解质溶液则会发生极化现象，影响其电导率。这些现象反映了静电场的性质和导体、电解质的物理特性。
展望
未来可以进一步研究导体和电解质在动态电场中的表现，以及不同类型导体和电解质在静电场中的特性差异。此外，还可以探索导体和电解质在其他物理场中的表现，以更全面地了解其物理性质和应用前景。
静电场中的电荷分布是稳定的，不会发生电流流动。
电场力
电荷在静电场中受到电场力的作用，其大小与电荷量成正比，与电荷到电场中心的距离成反比。

静电场中的导体和电解质

静电场中的导体和电解质

Q + + + + ++ + + + + E= 0 S+ + + + + + + + ++
Q q + + + +++ + +-q + + - E= 0 S + 结论: 电荷分布在导体外表面, 导体 + q + + 内部和内表面没净电荷. + - - + + + + ++ 腔内有电荷q: E 0 q 0

i
结论: 电荷分布在导体内外两个表面,内表面感应电荷为-q. 外表面感应电荷为Q+q.
NIZQ
第 5页
大学物理学 静电场中的导体和电介质
结论: 在静电平衡下,导体所带的电荷只能分布在导体的 表面,导体内部没有净电荷. • 静电屏蔽 一个接地的空腔导体可以隔离内 外电场的影响. 1. 空腔导体, 腔内没有电荷 空腔导体起到屏蔽外电场的作用. 2. 空腔导体,腔内存在电荷 接地的空腔导 体可以屏蔽内、 外电场的影响.
NIZQ
第 3页
大学物理学 静电场中的导体和电介质
• 静电平衡时导体中的电场特性
E内 0
场强:
ΔVab
b
a
E dl 0
• 导体内部场强处处为零 E内 0 • 表面场强垂直于导体表面 E表面 // dS
• 导体为一等势体 V 常量 • 导体表面是一个等势面
S
0 E P dS qi

大学物理导体和电介质中的静电场

大学物理导体和电介质中的静电场
在静电场的作用下，电介质中的 分子会发生极化现象，产生偶极 矩。
极化强度
02
03
极化电荷
极化强度是描述电介质极化程度 的物理量，与电场强度和温度等 因素有关。
由于极化现象，电介质表面会出 现极化电荷，影响外部电场分布。
电介质中的电场分布
电场分布
在电介质中，由于介质的存在，电场分布会发生变化。
01
边界条件
03
电介质中的静电场
电介质的绝缘性质
绝缘性质
电介质通常具有良好的绝缘性能，能够阻止电流通 过。
介电常数
电介质的介电常数是衡量其绝缘性能的重要参数， 介电常数越大，绝缘性能越好。
击穿电压
电介质在一定电压下会发生击穿现象，失去绝缘性 能，击穿电压是衡量电介质耐压能力的指标。
电介质的极化现象
01
极化现象
静电场的定义与特性
01
02
03
04
静电场的定义
由静止电荷产生的电场称为静 电场。
有源场
静电场由电荷产生，电荷是场 源。
无旋场
静电场中不存在旋涡，即电场 线不会闭合。
电场线不闭合
静电场的电场线从正电荷出发 ，终止于负电荷，不会形成闭 合曲线。
02
导体中的静电场
导体的导电性质
80%
金属导体
金属导体中的自由电子在电场作 用下定向移动形成电流。
电场中的电势与电势差
总结词
描述电场中各点电势的高低和变化情况
详细描述
在静电场中，各点的电势是空间位置的函数，其大小与电场强度 和位置有关。电势差则描述了不同位置之间电势的高低差值。在 静电平衡状态下，导体内部电势为零，导体表面附近电势则等于 导体表面电荷密度与一个常数（真空电容率）的乘积。

大学物理第九章(静电场中的导体电解质)课件

大学物理第九章(静电场中的导体电解质)课件
q,r
3. 导体表面邻近处的场强与该处电荷面密度成正比。
ES S / 0
E
高斯面
S
n
E表 σ / ε 0
1 r

r E
+ + +++ + ++ + ++
- + - + 电风
尖端附近的场强特别强, 当场强达到一定程度后, 空气会被击穿,产生尖 端放电现象
Q+q 若腔内有电荷q，则内表 面上电量为-q，外表面上 电量为Q+q，Q为导体空 腔原有电量。
q
-q
S
2. 孤立导体处于静电平衡时，各处的面电荷密度与各 处表面的曲率半径成反比. 证明：设相距很远的导体球，用导线联接 U R U r Q,R Q q 4π ε 0 R 4π ε 0 r
σR r 4 πR 2 σ R 4 πr 2 σ r σr R 4π 0 R 4π 0 r
第九章
导体 绝缘体
静电场中的导体和电介质
半导体
导体: 存在大量的可自由移动的电荷 绝缘体: 没有自由移动的电荷，也称电介质 半导体 :介于上述两者之间
§9-1 静 电 场 中 的 导体
一、导体达到静电平衡的条件和性质 1.静电感应与静电平衡
静电感应——在静电场力作用下，导体中电荷重新分布
的现象。
静电平衡——导体中电荷的宏观定向运动终止，电荷
λ L 2 π 0 L C R2 ΔU ln R1
L
讨论： 1. 电容器之电容和电容器结构，几何形状、尺寸
有关,还与二极板间的介质有关。 若电容器之间充满介质: C r C 0

06静电场中的导体和电解质

06静电场中的导体和电解质

+
- +
（R3 < r < R2 ）
E =0 1
（R2< r < R1 ）
2q E0 = 2 4 or πε
（r > R1 ）
NIZQ
第15页
大学物理学 静电场中的导体和电介质
（2） ）
Uo = ∫
R2
∞
0
v v R3 R2 R1 ∞ E⋅ dl = ∫ + ∫ + ∫ + ∫
0 R3 R2 R 1
Байду номын сангаас
qdr 2qdr Uo = ∫ E2dr + ∫ Eodr = ∫ +∫ 2 2 R3 R R3 4 1 πεor 4 or πε
R2
∞
q 1 1 2q q 1 1 2 − + − + = = 4 o R R 4 oR 4 o R R R πε 3 πε 1 πε 3 2 2 1
O-H+
分子的正、 分子的正、负电荷中心在无外场时 不重合，分子存在固有电偶极矩。 不重合，分子存在固有电偶极矩。
-q H+
+ H2O
=
+q
(2)无极分子： (2)无极分子： 无极分子
H+ H+ C-H+
分子的正、 分子的正、负电荷中心在无外场时 重合。不存在固有分子电偶极矩。 重合。不存在固有分子电偶极矩。
σ3S +σ4S = q2
由静电平衡条件，导体板内 由静电平衡条件，导体板内E=0。 。
σ1 σ2 σ3 σ4 − − − =0 EA = 2εo 2εo 2εo 2εo σ1 σ2 σ3 σ4 EB = + + − =0 2εO 2εO 2εo 2εo

第十章静电场中的导体和电解质剖析

第十章静电场中的导体和电解质剖析
注意: 不论导体带电与否 ，在电场中 最终都将达到静电平衡态。
三 静电平衡条件
+++
+++
E0
+++
+
+
+
E+ 0+
+
E＇ + + +
E0
E
0+ +
E E0 E＇ 0
导体内电场强度 外电场强度 感应电荷电场强度
平 衡
场强 :导体内部 E内=0， E表面 表面
条 件
电势 :导体为等势体，表面为等势面
两球的电荷密度分别为
1
q1
4R12
,
2
q2
4R22
1 R2
2
R1
可见电荷面密度和半径成反比，即曲率半径
愈小（或曲率愈大），电荷面密度愈大。
例 有一外半径 R3和内半径 R2 的金属球壳带电Q，在
球壳内放一半径 R1 的同心金属球带电q，问: 两球体 上的电荷如何分布？球心的电势为多少？(P176 例3)
qi 0
q导体内 0
E dS 0， S2
qi 0
q内表面 q
Qq
S2
q q
S1
结论: 当空腔内有电荷 q 时,内表面因静电感 应出现等值异号的电荷 q ，外表面有感应电
荷 q（电荷守恒）
如果导体本身带电Q，则平衡时外表面带电Q+ q.
(二) 电荷的大小分布（即：面密度σ的大小）
一般情况：面密度σ既与导体自身的带电量和形状有 关，又与其它带电体的电量和分布有关。
解: 球是等势体，球心的电势

静电场中的导体和电解质

静电场中的导体和电解质
1
本章教学基本要求
1、理解导体静电平衡的条件，掌握导体静电平 衡的特点及周围静电场的计算。 2、理解电容的定义，熟练掌握电容器电容的计 算方法及基本步骤。 3、了解电介质的极化过程及特点，掌握有电介 质存在时的高斯定理，理解电场的边界条件 4、理解静电场的能量分布特点，掌握静电场能 量的计算方法。 5、理解电流及电动势的定义。
Q A QB 1 4 2S
QA QB E1 E3 2 0 S
Q A－QB 2 3 2S
QA QB E2 2 0 S
16
例10.2 如图所示，一半径为R1的导体球A，带有电 量q，球外有一内、外半径分别为R2和R3的同心球壳B 带有电量Q。(1)试求球A和球壳B的电势，(2)若用细 导线连接球A和球壳B，再求其电势；(3)若未连接时 使外球接地，此时其电势又是多少？
分析：首先是计算电场强度的分布，然后用电势的 定义来计算就可以了。
17
解 (1)由静电平衡条件可知，导体球和 球壳内的场强为零，电荷均匀分布在 表面上。 根据在球壳B作一高斯面，用高斯定理 可得球壳内表面的感应电荷为-q；由电荷守 恒可得球壳外表面的感应电荷为（q+Q）。 所以空间电场分布有：
q 4 r 2 0 E 0 Qq 2 4 0 r R1 r R2 R2 r R3 r R3
q
R
腔体和腔外的电场强度 和电势分布不随q 位置变化。 腔内的电场强度和电势 分布随q 位置变化。
11
例10.1 一块面积为S的金属大 平板A，带电量为Q，在其附 近平行放置另一块不带电的金 属大平板B，两板间距远小于 板的线度。试求两板表面的电 荷面密度，以及周围空间的场 强分布。 解：设各表面的电荷面密度分别为１、 ２、 ３、 ４ ， 如图所示。 由电荷守恒 可知：

静电场中的导体与电解质.ppt

静电场中的导体与电解质.ppt

C

Q U

4π 0
( R1R2 R2 R1
)
此即孤立球形导体电容的公式。
电容器的串并联：
１. 电容器的并联
C C1 C2
２. 电容器的串联
1 1 1 C C1 C2
例３
11.3 静电场中的电介质
电介质对电容的影响：
C rC0
相对介电常数
空气的相对介电常数近似等于1，其它电介质的相对介电常数均大于1。
4π 0 R
电容是表述导体电学性质的物理量，它与导体是否带电无关。 在国际单位制中，电容的单位为法拉（Farad），符号为F。
1F 106 F 1012pF
电容器的电容：
电容器的电容定义为：两导体中任何一个导体所带的电荷 Q与两 导体间电势差U 的比值，即
CQ U
１.平行板电容器：
11.2 电容·电容器
电容反映了导体的容电本领。这一节我们 先讨论孤立导体的电容，然后讨论电容器及其 电容，最后讨论电容器的联接。
孤立导体的电容：
在真空中，有一半径为R ，电荷为Q 的孤立球形导体，它的电势为
1Q V
4π 0 R
对于在真空中孤立球形导体来说，其电容为
CQ V
Q 1
Q
4π 0 R
电介质的介电常数
0r
电介质的极化：
无极分子
有极分子
综上所述，在静电场中，虽然不同电介质极化的微观 机理不尽相同，但是在宏观上，都表现为在电介质表 面上出现极化面电荷。所以，在静电范围内，就不需 要把这两类电介质分开讨论。
11.4 电介质中的高斯定理及电位移矢量
在静电场中，通过任意闭合曲面的电位移通量等于该闭合曲面内 所包围的自由电荷的代数和，其数学表达式为

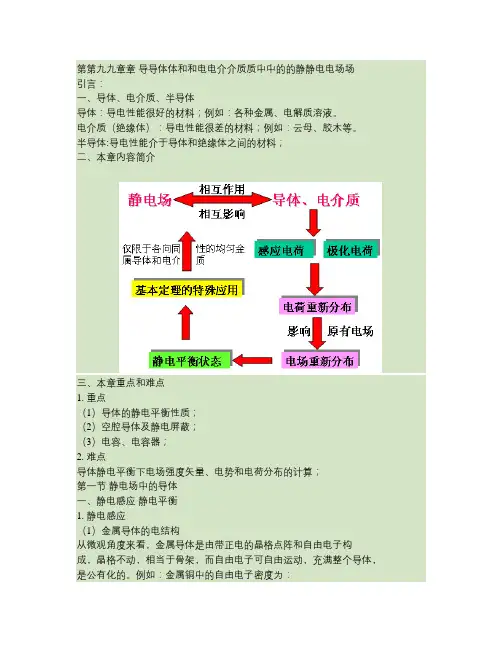
第9章导体和电介质中的静电场(精)

第9章导体和电介质中的静电场(精)

第第九九章章导导体体和和电电介介质质中中的的静静电电场场引言：一、导体、电介质、半导体导体：导电性能很好的材料；例如：各种金属、电解质溶液。

电介质（绝缘体）：导电性能很差的材料；例如：云母、胶木等。

半导体:导电性能介于导体和绝缘体之间的材料；二、本章内容简介三、本章重点和难点1. 重点（1）导体的静电平衡性质；（2）空腔导体及静电屏蔽；（3）电容、电容器；2. 难点导体静电平衡下电场强度矢量、电势和电荷分布的计算；第一节静电场中的导体一、静电感应静电平衡1. 静电感应（1）金属导体的电结构从微观角度来看，金属导体是由带正电的晶格点阵和自由电子构成，晶格不动，相当于骨架，而自由电子可自由运动，充满整个导体，是公有化的。

例如：金属铜中的自由电子密度为：nCu=8⨯1028(m-3)。

当没有外电场时，导体中的正负电荷等量均匀分布，宏观上呈电中性。

（2）静电感应当导体处于外电场E0中时，电子受力后作定向运动，引起导体中电荷的重新分布。

结果在导体一侧因电子的堆积而出现负电荷，在另一侧因相对缺少负电荷而出现正电荷。

这就是静电感应现象，出现的电荷叫感应电荷。

2. 静电平衡不管导体原来是否带电和有无外电场的作用，导体内部和表面都没有电荷的宏观定向运动的状态称为导体的静电平衡状态。

（a）自由电子定向运动（b）静电平衡状态3. 静电平衡条件（静电平衡态下导体的电性质）（1）导体内部任何一点处的电场强度为零；导体表面处电场强度的方向，都与导体表面垂直。

（2）在静电平衡时，导体内上的电势处处相等，导体是一个等势体。

E证明：假设导体表面电场强度有切向分量，即τ≠0，则自由电子将沿导体表面有宏观定向运动，导体未达到静电平衡状态，和命题条件矛盾。

dUdU =0,=0E内=0，Eτ=0dldτ因为，所以，即导体为等势体，导体表面为等势面。

二、静电平衡时导体上电荷的分布1. 实心导体（1）处于静电平衡态的实心导体，其内部各处净电荷为零，电荷只能分布于导体外表面。

第10章导体和电介质中的静电场资料PPT课件

第10章导体和电介质中的静电场资料PPT课件
第十章 导体和电介质中的静电场
(Electrostatic Field in Conductor and Dielectric)
上一章讨论的是真空中的静电场。实际上，在静电场 中总会有导体或电介质的存在，它们受到静电场的作用， 同时也会对静电场产生影响。
本章研究： 1.导体和电介质的静电特性； 2.导体和电介质内外的电场分布； 3.静电场的。
★金属导体的电结构特点： 具有大量的自由电子。当导体不带电、也不受外电场
的作用时，导体内的大量自由电子和晶体格点阵的正电荷 相互中和，导体呈电中性状态。
在电场的作用下，自由电子可以在导体内部移动，因 此电荷很容易在导体内从一处转移到另一处，这就是导体 容易导电的原因。
4
一、静电感应现象： 在导体内部存在电场时，自由电子受电场力作用作定
PQ
场强特点：腔内空间各点的场强处处为零；空腔导体外面空 间电场分布由腔外表面的电荷分布和其它带电体的分布共同 决定。总之，当导体处在外电场中时，空腔导体外的带电体 只会影响空腔导体外表面上的电荷分布，并改变空腔导体外 的电场分布。这些电荷重新分布的结果，最终使导体内部及 空腔内部的场强为零。
EP 0 EQ 0 EO 0
10
3.对孤立导体，则导体表面曲率大的地方（突出而尖锐）， 电荷面密度也大，反之，曲率小的地方也小。
由实验可得以下定性的结论： R1
B
+++++
+ +
A
孤立 导体
C
+++
ABC
●尖端放电现象：带电导体尖端附近的电场特别大，可使
尖端附近的空气发生电离而成为导体产生放电现象，即尖
端放电。

6.1静电场中的导体和电解质

6.1静电场中的导体和电解质

E
上页
下页
3.孤立导体面电荷密度与导体表面曲率有关， 表面曲率越大，面电荷密度越大。 尖端放电现象： 带电导体尖端附近的电场过大，使尖端附近的空 气电离而成为导体产生放电现象。
上页
下页
三.静电屏蔽现象 屏蔽外电场 腔内无带电体的导体放于外电场中
达静电平衡时，导体内和空腔中的场强处处为 零电场线终止于导体的外表面而不进入内腔，空 腔导体可以屏蔽外电场, 使空腔内物体不受外电场 影响.
上页 下页
屏蔽腔内电场 导体空腔内有带电体时，空腔内表面将产生等量 异号电荷。

将导体壳接地，空腔 外的电场消失。
使导体空腔内的物体不受外界影响或利用接地的 空腔导体将腔内带电体对外界影响隔绝的现象称为 静电屏蔽。
上页 下页
例1. 有一块大金属平板，面积为S ，带有总电量 Q ，今在其近旁放置第二块不带电的大金属平板， ① 求静电平衡时，金属板上的电荷分布及周围空 间的电场分布；② 如把第二块金属板接地，情况 又如何？
＇ E
导体达到静电平衡
上页
+ + + + + + + +
E0
' E0 E 0
下页
静电平衡： 导体中电荷的宏观定向运动终止，电荷分布不 随时间改变。 静电平衡条件：导体内部场强处处为零 推论： 导体为一等势体，导体表面是一个等势面
U ab
b
a
E dl 0
导体表面场强垂直于导体表面
上页
下页
例2. 在内外半径分别为R1和 R2 的导体球壳内， 有一个半径为r 的导体小球，小球与球壳同心，让 小球与球壳分别带上电荷量q 和Q，问两球体上的 电荷如何分布？球心的电势为多少？ 解：电荷分布：球壳内表面-q，外 Q+q 表面 Q+q q R2 -q

物理-导体和电介质中的静电场

物理-导体和电介质中的静电场
EA0 EBq 0s EC0
20
[例3] 若A带电q1, B带电q2，求： (1) 图中1，2，3，4 各区域的E和U分布，并画出E ~ r
和U ~ r 曲线.
(2) 若将球与球壳用导线连接，情况如何？
(3) 若将外球壳接地，情况如何？
R3 R2
q q R1
2
11 A
B
3 2A B
4
21Leabharlann q1q2 (1)导体表面 变化，外侧附近场强 E变化， 而 E0 仍然成立。
14
〈2〉无限大带电平面： E20
带电导体表面附近： E0
是否矛盾？
2 1
E
E
S
几何面
sE dS 2ES 0S
如果计及带电面的厚度
式中 1 2 2 1
15
3. 孤立导体 与表面曲率有关 .
1）导体表面凸出而尖锐的地方（曲率较大） 电荷面密度较大
物理-导体和电介质中的静电场
单击此处添加副标题内容
第九章 导体和电介质中的静电场
§9-1 静电场中的导体 一.导体的静电平衡
1.导体 绝缘体 半导体 1)导体：导电能力极强的物体，常见为金属
(存在大量可自由移动的电荷)
2)绝缘体（电介质）：
导电能力极弱或不能导电的物体
3)半导体：导电能力介于上述两者之间的物体
R3
R2
q A q1 qB内 q1 qB外 q1 q2
q1 q1 R 1
1A
E1 0
B
E2
q1
4
0
r
2 2
2
3 4
E3 0
E4
q1 q 2
4
0
r
2 4

第九章 导体和电介质的静电场-wmx剖析

第九章 导体和电介质的静电场-wmx剖析

空腔内部电荷及电场变化会对导体壳的外界产生影响
2. 腔内有带电体 q
▪ 腔内的电场不再为零，其分布
• 与电荷 q电量和分布有关
• 与内表面形状、腔内介质等因素有关
-q q
q
• 与导体外其它带电体的分布无关
这就是说：导体空腔外的电荷对空腔内的电场
及电荷分布没有影响 在腔内仍有： E外表面电荷 E其他带电体 0
1.导体的静电平衡状态 (electrostatice quilibrium)：
指导体内部和表面都没有电荷作宏观的定向运 静电平衡条件(electrostatic equilibrium condition) ：
导体内部电场强度处处为零 这也是静电平衡问题的出发点
油罐内油品蒸汽的击穿场强约为 4.5 102 kV / m 引燃可燃蒸汽的最小放电能量为 0.2mJ
防止静电事故的措施护
减少静电产生 注意消除静电放电
§9-3 电容器(capacitor)的电容(capacity)
• 孤立导体的电容
孤立导体的电容定义为：导体带电量与导体电势的比：
q C V
物理意义：使导体升高单位电势所需的电荷量。 1、电容是导体的客观性质，电容反映了该导体在给定电势
参考“尖端效应及其数学表示”．《大学物理》. 1993. (6).
通过实验人们得到一些定性结论：
在表面凸出的尖锐部分(曲率是正值且较大) 电荷面密度较大， 在比较平坦部分(曲率较小)电荷面密度较小， 在表面凹进部分带电面密度最小。
孤立导体
特殊情况：孤立带电导体球、长直圆柱或大的平板， 它们的面电荷分布是均匀的
S 过导体的内表面上的面元 S 作圆柱形高斯面
E dS 0 设内表面的面电荷密度为

导体和电介质中的静电场

导体和电介质中的静电场
静电平衡时，导体内部的场强为零这一特性在工 程技术上常用作静电屏蔽.用空腔导体可以实现静电屏 蔽，下面分两种情况来分析静电平衡时空腔导体的电 场和电荷分布.
导体和电介质中的静电场
1. 空腔内无电荷的情况
将一腔内无电荷的空腔导体置于静电场中（见图8-28），在 空腔导体内外表面之间作一高斯面S，因为静电平衡时导体内的场 强处处为零，所以通过高斯面的电通量为零.根据高斯定理，高斯 面内电荷的代数和必定为零，说明内表面上的净电荷必然为零.因 为空腔导体内表面没有电荷，所以内表面附近的场强为零，电场 线不可能起于（或止于）内表面.同时，腔内无电荷，在腔内不可 能有电场线的起止点，因此腔内不可能有电场线，即空腔内场强 为零，导体及空腔为等势区域.
图8- 26 导体表面的电场
导体和电介质中的静电场
(3)静电平衡时，孤立导体表面某处的电荷面密度σ与 该处表面曲率有关.导体表面上的电荷分布是个比较复杂的 问题，它不仅与导体的形状有关，还与导体周围的其他物 体有关.但对于孤立的带电导体来说，导体表面突出而尖锐 的地方（曲率较大），电荷面密度较大；表面比较平坦的 地方（曲率较小），电荷面密度较小；表面凹进去的地方 （曲率为负），电荷面密度最小.
一、 导体的静电平衡
金属导体的重要特征是在它的内部有大量的自由电 子.当导体不带电也不受电场力作用时，自由电子做微观 热运动，没有电荷的定向宏观运动，整个导体呈电中性. 将金属导体置于静电场中，金属导体内部大量的自由电子 将受到静电力的作用而产生定向运动，这一运动将改变导 体上电荷的分布.这种电荷分布的改变，反过来影响导体 内部和周围电场的分布.这种电荷和电场的分布一直改变 到静电平衡为止.
导体和电介质中的静电场
高电压的零部件也必须做得十分光滑并尽可能做成球形.相 反，火花放电设备的电极往往做成尖端形状.避雷针就是利用尖 端的电场强度大，空气被电离，形成放电通道，使云地间电流 通过导线流入地下而达到避雷的目的.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

二、导体和电介质中的静电场一、 选择题：1、在一静电场中，作一闭合曲面S ，若有⎰⎰=⋅0s d D ϖϖ，（式中D ϖ为电位移矢量），则S 面内必定：A ：既无自由电荷，也无束缚电荷；B ：没有自由电荷；C ：自由电荷和束缚电荷的代数和为零；D ：自由电荷代数和为零。

[ ]2、一带正电荷的物体M ，靠近一不带电的金属导体N ，N 的左端感应出负电荷，右端感应出正电荷，若将N 的左端接地，如图所示，则（A ） N 上的负电荷入地（B ） N 上的正电荷入地（C ） N 上的电荷不动（D ） N 上所有电荷都入地 [ ]3、在一点电荷产生的静电场中，一块电介质如图放置，以点电荷所在处为球心作一球形闭合面，则对此球形闭合面：（Ａ）高斯定理成立，且可用它求出闭合面上各点的场强；（Ｂ）高斯定理成立，但不能用它求出闭合面上各点的场强；（Ｃ）由于电介质不对称分布，高斯定理不成立；（Ｄ）即使电介质对称分布，高斯定理也不成立。

[ ]4、有一接地的金属球，用一弹簧吊起，金属球原来不带电．若在它的下方放置一电量为q的点电荷，则(A)只有当q>0时，金属球才下移．(B)只有当q<n 时，金属球才下移．(C)无论q 是正是负金属球都下移．(D)无论q 是正是负金属球都不动． [ ]5、在空气平行板电容器中，平行地插上一块各向同性均匀电介质板，如图所示，当电容器充电后，若忽略边缘效应，则电介质中的场强E ϖ与空气中的场强0E ϖ相比较，应有：（A ）0E E 〉， 两者方向相同。

（B ）0E E =， 两者方向相同（C ）E<Eo, 两者方向相同。

（D ）E<Eo ， 两者方向相反。

[ ]6、一球形导体，带电量q ，置于一任意形状的空腔导体中。

当用导线将两者连接后，则与未连接前相比系统静电场能将（A ）增大 （B ）减小 （C ）不变 （D ）如何变化无法确定 [ ]7、将一空气平行板电容器接到电源上充电到一定电压后，在保持与电源连接的情况下，把一快与极板面积相同的各项同性均匀电介质板平行地插入两极板之间，如图所示。

介质板的插入及其所处位置的不同，对电容器储存电能的影响为：(A)储能减少，但与介质板位置无关； (B)储能减少，且与介质板位置有关；(C)储能增加，但与介质板位置无关； (D)储能增加，且与介质板位置有关。

[ ]8、把A ，B 两块不带电的导体放在一带正电导体的电场中，如图所示。

设无限远处为电势零点，A 的电势为U A ，B 的电势为U B ，则（A ） U B >U A ≠0 （B ） U B >U A =0（C ） U B =U A （D ） U B < U A[ ]9.半径为R 的金属球与地连接．在与球心O 相距d =2R 处有一电荷为q 的点电荷．如图所示，设地的电势为零，则球上的感生电荷q '为 (A) 0． (B) 2q ．(C) -2q ． (D) -q ． ［ ］ 10.如图所示，两同心金属球壳，它们离地球很远，内球壳用细导线穿过外球壳上的绝缘小孔与地连接，外球壳上带有正电荷，则内球壳：(A) 不带电荷．(B) 带正电荷．(C) 带负电荷．(D) 内球壳外表面带负电荷，内表面带等量正电荷．［ ］ O R dq11.一带电孤立导体，处于静电平衡时其电荷面密度的分布为σ(x ,y,z )．已知面元d S 处的电荷面密度为σ0>0，如图示，则导体上除d S 面元处的电荷以外的其它电荷在d S 处产生的电场强度的大小为 (A) 00εσ． (B) 002εσ． (C) 00εσ． (D) 002εσ． ［ ］ 12. 图中所示为一带电导体球A ，其上包着一层各向同性的均匀电介质球壳B ．若在介质球壳层中取一闭合面S 1，在介质球壳外取一闭合面S 2，则通过S 1和S 2的电场强度通量Φ1和Φ2及电位移通量ψ1和ψ2之间的关系为(A) Φ1＝Φ2，ψ1＝ψ2．(B) Φ1＝Φ2，ψ1≠ψ2． (C) Φ1≠Φ2，ψ1≠ψ2． (D) Φ1≠Φ2，ψ1＝ψ2．［ ］13. 三个电容器联接如图．已知电容C 1 =C 2 = C 3 ，而C 1、C 2、C 3的耐压值分别为100 V 、200 V 、300 V ．则此电容器组的耐压值为 (E)600 ［ ］14. 一平行板电容器，两板间距离为d ，若插入一面积与极板面积相同而厚度为d / 2 的、相对介电常量为εr 的各向同性均匀电介质板(如图所示)，则插入介质后的电容值与原来的电容值之比C / C 0为 (A) 11+r ε． (B) 1+r r εε． (C) 12+r r εε． (D) 12+r ε． ［ ］二、填空题： 1、一平行板电容器，充电后与电源保持联系，然后使两极板间充满相对介电常数为r ε的各向同性均匀电介质，这时两极板上的电量是原来的____倍，电场强度是原来的____倍，电场能量是原来的_______倍。

2、两个点电荷在真空中相距d 1=7cm 时的相互作用力与在煤油中相距d 2=5cm 时的相互作用力相等，则煤油的相对介电常数εr =----------------------------。

3、已知空气的击穿场强为30 kV / cm ，一平行板空气电容器两极板间距离为1.5cm ，则这平行板电容器的耐压值是：___________。

d /24、在静电场中，电位移线从__________出发，终止于____________.5、一电偶极子放在场强为E的匀强电场中，电偶极矩的方向与电场强度的方向成θ角。

已知作用在电偶极子上的力矩大小为M，则此电偶极子的电矩大小p=_________.6、将一负电荷从无穷远处移到一个不带电的导体附近，则导体内的电场强度________,导体的电势___________. (填增大，不变，减小)7、一空气平行板电容器，两板相距为d，与一电池连接时两板之间相互作用力的大小为F，断开电池后，将两板距离拉开到2d，忽略边缘效应，则两板之间的相互作用力的大小是_________________。

8、如图所示，两块很大的导体平板平行放置，面积都是S，有一定厚度，带电量分别为Q1和Q2。

如不计边缘效应，则A、B、C、D四个表面上的电荷面密度分别为_________、_________、___________、_________。

ε的各向同性电介质中，电位移矢量与场强之间的关系是_______。

9、在相对介电常数为r10、两个点电荷在真空中相距为r1时的相互作用力等于它们在某一“无限大”各项同性均匀电介质中相距为r2时的相互作用力，则该电介质的相对介电常数εr=__________。

11、如图所示，平行板电容器中充有各项同性均匀电介质。

图中画出两组带箭头的线分别表示电力线、电位移线。

则其中（1）为____________，（2）为____________。

12．半径为Ｒ１和Ｒ２的两个同轴金属圆筒，其间充满着相对介电常数为εr的均匀介质。

设两筒上单位长度带电量分别为＋λ和－λ，则介质中的电位移矢量的大小Ｄ＝__________，电场强度的大小Ｅ＝__________。

13．一空气平行板电容器，电容为Ｃ，两极板间距为d 。

充电后，两极板间相互作用力为Ｆ。

则两极板间的电势差为___________，极板上的电荷量大小为____________。

14．一孤立带电导体球，其表面处场强的方向___________________；当把另一带电体放在这个导体球附近时，该导体球表面处场强的方向___________________。

15．分子的正负电荷中心重合的电介质叫做__________________电介质。

在外电场作用下，分子的正负电荷中心发生相对位移，形成_________________。

16．两个电容器1和2，串联以后接上电动势恒定的电源充电。

在电源保持连接的情况下，若把电介质充入电容器2中，则电容器1上的电势差_________________；电容器一级板上的电量___________。

（增大、减小、不变）17. 一导体在外电场中处于静电平衡时，导体上面元d S 的电荷面密度为σ，那么面元d S 所受电场力的大小为______________________________，方向为____________________________．18. 一点电荷q 被放在一个介电常量为ε的有限大各向同性均匀电介质球的中心，则在介质球外距球心为r 处的P 点的场强大小E P ＝____________．19. 描述电介质极化强度的物理量电极化强度P ϖ的定义式是____________，它的物理意义是________________________________________．三、计算题：1、空气中有一半径为R 的孤立导体球，令无穷远处电势为0，试计算：（1）该导体球的电容；（2）球上所带电荷为Q 时储存的静电能；（3）若空气的击穿场强为Eg ，导体球上能储存的最大电荷值。

2、一电容器由两个同轴圆筒组成，内筒半径为a ，外筒半径为b ，筒长都是L ，中间充满相对介电常数为εr 的各向同性均匀电介质。

内、外筒分别带有等量异号电荷+Q 和—Q 。

设b-a<<a, L>>b, 可以忽略边缘效应，求：（1） 圆柱形电容器的电容；（2） 电容器储存的能量。

3、空气中有一半径为R 的孤立导体球。

令无穷远处电势为零，试计算：（1） 该导体球的电容；（2） 球上所带电荷为Q 时储存的静电能；（3） 若空气的击穿场强为Eg ，导体球上能储存的最大电荷值。

4、一球形电容器，内球壳半径为R 1 外球壳半径为R 2 两球壳间充满了相对介电常数为r ε的各向同性均匀电介质，设两球壳间电势差为U 12,求：电容器的电容；（2）电容器储存的能量。

5、两根平行“无限长”均匀带电直导线，相距为d ，导线半径都是R(R<<d)。

导线上电荷密度分别为λλ-+和。

试求该导体组单位长度的电容。

6、一空气平行板电容器，两极板面积均为S ，板间距离为d （d 远小于极板线度），在两极板间平行地插入一面积也是S 、厚度为t （＜d ＝的金属片。

试求：（1） 电容C 等于多少？（2） 金属片放在两极板间的位置对电容值有无影响？7．现有一根单芯电缆，电缆芯的半径为r 1 =15mm ，铅包皮的内半径为r 2 =50mm ，其间充以相对介电常数εr =2.3的各向同性均匀电介质。

求当电缆芯与铅包皮间的电压为U 12=600V 时，长为l=1km 的电缆中储存的静电能是多少？（ε0=8.85×10-12C 2 N -1 m -2）8．两电容器的电容之比为C 1:C 2=1:2。