平行板电容器中介质的受力分析
- 格式:doc
- 大小:235.00 KB
- 文档页数:9



![[详细讲解]平行板电容器中介质的受力分析](https://uimg.taocdn.com/3aab8637dc36a32d7375a417866fb84ae45cc37a.webp)
平行板电容器中介质的受力分析引言: 对于平行板电容器的受力问题,前人大多研究理想情况下平行板电容器的受力,即通过改变电容的大小研究其受力情况。
本文的设想是把电介质放入平行板电容器中电介质在电场的作用下一定会发生变化,必然产生电偶极子,电偶极子在电场中必定会受力,一旦电偶极子受力就会发生位移变化,那么必然存在做功问题,那么就可以从能量角度去分析它的受力,进而得出的两个结果一定是相等的,本文通过例题去检验其确性。
1 介质受力公式的推导(从宏观上理论推导)介质在进入平行板电容器的过程中(假设电量Q 不变),纵向电场使介质极化所做之功转化为介质的极化能,这仍是电容器储能的一部分,根据能量守恒定律,插入介质后电容的静电能应不变,但是由电容器的能量公式W=Q*Q/2C ,当C 增大时,能量却是减少的,矛盾的出现说明我们一定忽略了某些相互作用的存在,为了避开繁琐的力分析,下面,我们将从能量的角度出发,通过数学方法导出平行板电容器中介质的受力的计算公式。
一个平行板电容器,其中部分地充入介质常数为E(p(m),r)(介质常数一般不仅是空间r 的函数,而且还是介质的质量密度p(m)的函数)并且无自由电荷的介质,假设介质沿X 方向作一个无限小位移X ,则电容器的储能变化为22111222W V V vVD EDdV dV EDdVE dV δδδδεε===-⎰⎰⎰⎰ 式(1-1)而 E 0D ρ=-∇Φ∇==则 ()2212VvV VDdv E dV D D E dV δφδδεδδδε=-∇-=-∇Φ+Φ∇-⎡⎤⎣⎦⎰⎰⎰⎰=2212S v V VDd s dV E dV E dV δδρδεδε-Φ+Φ--⎰⎰⎰⎰ 式(1-2)其中在无穷大界面的值为零,而介质中已设自由电荷密度为零。
对于介质给定的一个无限小位移0X,相对于空间的一个固定体积来说,必有:0()m m X vSvdV d s X dV δρρρ=-=-∇∙⎰⎰⎰式(1-3)则 ()()0,x x m mm m m m ρρεδρρεδερδρ∙∇∂∂-=∂∂=∙∇=而()dV E X X E V dV X E V M MM M M M V w ⎰⎰⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂∇∙-⎪⎪⎭⎫ ⎝⎛∂∙∇=∙∇∂∂=ρερρρερρεδ200222121 dV E X dV E X s d X E M M V M v m V M M ⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂∇=⎪⎪⎭⎫ ⎝⎛∂∂∇∙-∙⎪⎪⎭⎫ ⎝⎛∂∂=⎰⎰⎰ρερρερρρε202002212121 式(1-4)A 电量Q 恒定当介质位移0X时,电场对介质作的功等于电容器储能的减少,即2222211()()22m M M M M M M M M M v V F E dV E E E E dVεεεεερρρρρρρρρρ⎡⎤∂∂∂∂∂=∇=∇+∇-∇-∇⎢⎥∂∂∂∂∂⎣⎦⎰⎰B 电压U 恒定电源所作之功一部分转化为电容器的储能,另一部分对介质做功转化为机械能,即有W XF Udq δ-=∙-⎰00X F dq U v∙-⎰=dV E E X MM V)(21220ρερ∂∂∇∙⎰⎰=dC U 2dVE X XF ε∇-∙=∙-⎰20021举例说明:例1 如图所示图1.1一个平行板电容器,带电量为Q ,宽为b ,长为L ,两级板间的距离为 d ,其中部分地冲入电介质常数为ε 的均匀电介质,求介质所受的力。

平行板电容器的动态分析问题平行板电容器是最常见的一种电容器,其结构可以发生变化,因此电容也跟着随之变化。
当我们改变电容器的某个结构时,电容器的电容也随之变化。
从而导致电容器中间的电场强度也会发生变化。
这就引出一种问题,电容器的动态分析问题。
电容器的动态分析问题总体上来说大概分为两类:电压不变的问题和电荷量不变的问题。
一般情况下,题目中的说法是:电压不变(电容器始终接在电源上)电荷量不变(电容器充电完成后,断开电源)如果根据问题的难度再细分:层次1:仅仅分析电容和电荷量(电压)的变化层次2:分析电容和电荷量(电压)的变化,再加上电场强度的变化,而电场强度的变化有两个方法进行比较(U不变的问题中:E=U/d,Q不变的问题中,Q与E成正比(前提是S 不变))层次3:E的变化会导致容器中某点电势的变化(或者电荷在某点电势能的变化)层次4:E的变化会导致容器中液滴所受电场力的变化,进而会产生加速度,根据牛顿第二定律计算加速度;或者容器中国液滴的平衡状态发生变化,从而分析细线角度的变化。
【此题问题本质上只重在分析电场强度的变化问题,因为所需要分析的是力的问题】动态分析问题的处理方法:1.先分析清楚题目给出的是U不变还是Q不变的类型2.找出题目中发生变化的参量,然后分析C的变化(注意正反比关系),Q的变化(U的变化)Q的变化会产生瞬间的充电和放电电流(会判断电流方向)3.再分析E的变化4.如果是平衡问题或者动力学问题需要进行受力分析,写平衡方程或者牛顿第二定律。
典型例题剖析例1:★★【2016 新课标I】一平行板电容器两极板之间充满云母介质,接在恒压直流电源上。
若将云母介质移出,则电容器()A.极板上的电荷量变大,极板间电场强度变大B.极板上的电荷量变小,极板间电场强度变大C. 极板上的电荷量变大,极板间电场强度不变D. 极板上的电荷量变小,极板间电场强度不变 答案:D 解析:由4πr SC kdε=可知,当云母介质抽出时,r ε变小,电容器的电容C 变小;因为电容器接在恒压直流电源上,故U 不变,根据Q CU =可知,当C 减小时,Q 减小。
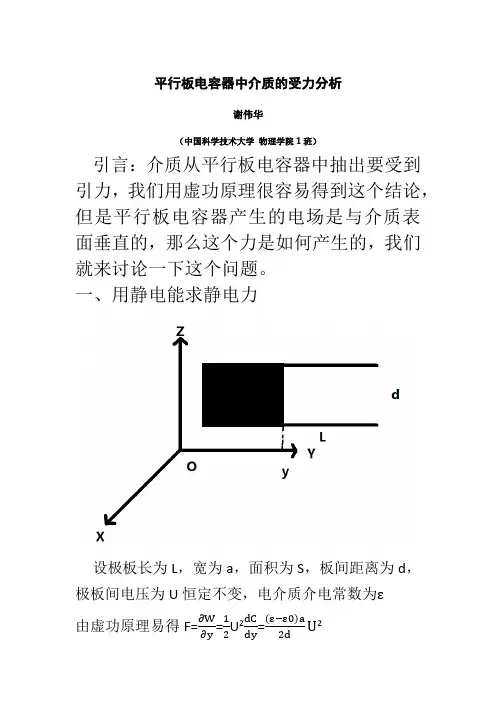
平行板电容器中介质的受力分析谢伟华(中国科学技术大学物理学院1班)引言:介质从平行板电容器中抽出要受到引力,我们用虚功原理很容易得到这个结论,但是平行板电容器产生的电场是与介质表面垂直的,那么这个力是如何产生的,我们就来讨论一下这个问题。
一、用静电能求静电力设极板长为L,宽为a,面积为S,板间距离为d,极板间电压为U恒定不变,电介质介电常数为ε由虚功原理易得F=∂W∂y =12U2dCdy=(ε−ε0)a2dU2用这种方法无法看出这个力从何而来。
所以我们采用下面的方法。
二、用库仑定律求受力电介质在电场中极化成电偶极子,下面先求一个电偶极子在电场中受的力。
设负电荷处电场为为E⃗(r),正电荷处电场为E⃗(r+ l),由于l远小于电介质的线度,所以用泰勒展开得:E⃗(r+l)=E⃗(r)+l x∂∂x E⃗(r)+l y∂∂yE⃗(r)+l z∂∂zE⃗(r)=E⃗(r)+(l·∇)E⃗(r)所以电偶极子受到的合力为(p⃗·∇)E⃗(r)对于一个体积为V的电介质(下面的E都是总电场,因为体电荷元在自身处产生的电场为0)F⃗=∭(P⃗·∇)E⃗dV=(ε−ε0)∭(E⃗·∇)E⃗dV=12(ε−ε0)∭∇E2⃗⃗⃗⃗ dVX与Z方向均为0,所以可以变为1 2(ε−ε0)j∭∂E2⃗⃗⃗⃗⃗∂YdV在极板内部电场是均匀为Ud,外部电场为0,所以只需计算边缘那一部分,且上式积分号内部可化为:ΔE2ΔY ∆V=ΔE2ΔY∆X∆Y∆Z=∆E2∆X∆Z=U2d2∆X∆Z则F⃗=12(ε−ε0)j∬U2d2dXdZ=(ε−ε0)a2dU2j与用静电能求得结果一样。
结论:从计算过程中可以看出,这种力跃迁到0造成的,这产生的原因是电场由Ud是理想化模型的弊端,以致于我们想不明白这个力从何而来。
实际中,电场不可能一下子变成零,边缘处也是有电场的。
所以我们考虑问题应从实际出发,理论只是一个工具,不代表一切。

平行板电容器的动态分析与带电体在电容器中的运动问题一:电容器的动态变化问题 1 两个公式的比较U Q C =kd S C r πε4=公式的特点 定义式,适用于一切电容器 决定式,适合平行板电容器 意义反映容纳电荷的本领反映了影响电容大小的因素2 两类典型的动态变化分析在解题中运用到的公式:C =Q U ; C =εrS 4πkd ;E =Ud3. 解决电容器问题的两个常用技巧(1)在电荷量保持不变的情况下,由E =U d =Q Cd =4πkQεr S知,电场强度与板间距离无关。
(2)针对两极板带电荷量保持不变的情况,还可以认为一定量的电荷对应着一定数目的电场线,如图甲所示;当两极板间距离变化时,如图乙中电场线疏密不变,场强不变;当两极板正对面积变化时,如图丙中电场线变密,场强增大。
【典例1】如图,平行板电容器经开关K 与电池连接,a 处有一带电量非常小的点电荷.K 是闭合的,表示a 点的电势,f 表示点电荷受到的电场力.现将电容器的B 板向下稍微移动,使两板间的距离增大,则A. 变大,f 不变B. 变大,f 变小C.不变,f 不变 D.不变,f 变小【答案】B【解析】由于开关K闭合,且电容器两极板始终与电源的两极相连,故电容器两极板之间的电压U AB 保持不变。
随B极板下移两极板之间的距离增大,根据E=U/d可知两极板之间的电场强度E减小,由于U Aa=Eh Aa,由于电场强度E减小,故U Aa减小,由于U AB=U Aa+U aB,所以U aB增大,由题图可知电源的负极接地,故B极板接地,所以B板的电势为0即U B=0,又U aB=U a-U B,所以U a=U aB增大。
而点电荷在a点所受的电场力f=qE,由于E减小,所以电场力f减小。
故B正确。
故选B。
点睛:本题难度较大,涉及知识面大,需要认真分析.方法是:先找不变量(U AB),再找容易确定的物理量(E和U Aa),最后求出难以确定的量(确定U aB不能用U aB=Eh aB,因为E和h aB一个变大另一个变小).【典例2】如图所示,平行板电容器带有等量异种电荷,与静电计相连,静电计金属外壳和电容器下极板都接地。

⾼中物理:平⾏板电容器的动态分析对平⾏板电容器的有关物理量Q、E、U、C进⾏讨论时,关键在于弄清哪些是变量,哪些是不变量,在变量中哪些是⾃变量,哪些是因变量。
这类问题可分为两种情况来分析:⼀、电容器充电后断开电源,电容器所带电量Q保持不变当极板距离d,正对⾯积S变化时,有:对于电场强度变化,我们还可以认为⼀定量的电荷对应着⼀定数⽬的电场线,若电量不变,则电场线数⽬不变,当两板间距离变化时,场强不变;当两板正对⾯积变化时,引起电场线的疏密程度发⽣了变化,如图1所⽰,电容器的电量不变,正对⾯积减⼩时,场强增⼤。
图1这样,越⼤,电场线就越密,E就越⼤,反之就越⼩;不变时,不管极板间距离如何变化,电场线的疏密程度不变,则E不变。
则此式可知,在电量保持不变的情况下,电场强度与板间的距离⽆关。
例1、⼀平⾏板电容器充电后与电源断开,负极接地,在两极板间有⼀正电荷(电量很⼩)固定在P点,如图2所⽰,E表⽰两板间的场强,U表⽰电容器的电压,W表⽰正电荷在P点的电势能,若保持负极板不动,将正极板移到虚线所⽰的位置,则()图2A.U变⼩,E不变B.E变⼤,W变⼤C.U变⼩,W不变D.U不变,W不变解析:电容器充电后与电源断开,说明电容器带电量不变。
正极板向负极板移近,由可知电容增⼤,由可知,U变⼩,⽽,由此可看出,场强E不变。
因E不变,P点与负极板间的距离不变,可知P点的电势U P不变,那么正电荷的电势能就不变,综上所述,A、C选项正确。
例2、平⾏板电容器两极板与静电计的连接如图3所⽰,对电容器充电,使静电计张开某⼀⾓度,撤去电源后以下说法正确的是()图3A.增⼤两板间距离,静电计指针张⾓变⼤B.减⼩两板间距离,静电计指针张⾓变⼤C.将两板错开⼀些,静电计指针张⾓变⼤D.将某电介质插⼊极板间,静电计指针张开⾓度变⼤解:静电计指针的张⾓反映的是两板之间的电势差的⼤⼩。
由题意可知,撤去电源后电容器所带电量不变。
由电容器的电容决定因素知:若增⼤板间距离,则C变⼩,由知U变⼤,故A正确,B错误。

平行板电容器的动态问题考点归纳在两个相距很近的平行金属板中间夹上一层绝缘物质——电介质(空气也是一种电介质),就组成了一个最简单的电容器,叫作平行板电容器。
我们知道平行板电容器的表达式有定义式Q C U =和决定式4r S C kdεπ=电容器间的电场强度的表达式为对于平行板电容器,如果一个物理量发生了变化,往往会引起其他物理量发生变化,即发生动态变化。
平行板电容器的动态变化问题主要包括电容器始终与电源相连接和电容器充好电后与电源断开两种情况。
两种动态问题的部分情况和所涉考点如下表所示。
一、电容器始终与电源相连接【例1】如图1所示为一个由电源、电流计、平行板电容器、开关S 和导线等组成的电路,平行板电容器水平放置,下极板接地。
开关S 闭合,待电路稳定后,板间P 点有个液滴刚好处于静止状态。
当上极板向上移动一小段距离时,请回答下列问题:(1)电流计中有没有电流流过,有的话方向如何?【解析】电容器两端电压U 不变,由于两极板距离d 的增大导致电容C 减小,根据Q=CU 可知两极板带电量减小,所以电容器放电,电流由b 向a 流过电流计。
(2)液滴动不动,动的话将向哪个方向运动?【解析】电容器两端电压U 不变,两极板距离d 增大,根据U E d=可知电场强度减小,液滴受到的电场力F 减小,所以向下运动。
(3)P 点的电势将发生什么变化? 【解析】因为下极板接地,所以电势为0,则P PO U ϕ'=,假设PO ’的距离为h ,所以P Eh ϕ=,第(2)问已经得出电场强度E 减小,所以P ϕ减小。
(4)若将电流计换成一个二极管,如图2所示,则液滴动不动,动的话向哪个方向移动?【解析】由第(1)问可知,电容器电荷量理应减小,对外放电,但是二极管具有单向导电性,不允许电流自右向左流过.所以电容器带电量不变,根据4r U Q kQ E d Cd Sπε===可知,电场强度不变,液滴受力不受影响,保持不动。

电容器中电介质的作用山东省肥城市第一高级中学 于茂刚 271600高中教材在提到电介质对平行板电容器的电容的影响时,只是通过演示实验就直接得出了结论:当两极板间充满同一种电介质时,电容变大为真空时的r ε倍,即kdS C r πε4= ,r ε 是一个常数,与电介质的性质有关,称为电介质的相对介电常数。
学生只能记住结论,对电介质的特性和电介质对电容的影响机理产生疑惑,就此谈一下电容器中电介质的作用。
电介质不同于金属,电介质的电阻率一般都很高,称为绝缘体,介质中没有(或几乎没有)能够自由移动的电荷,这种电荷叫做束缚电荷。
在电场中静电平衡条件下,电介质的内部仍有电场存在。
在外电场作用下,电介质的表面将出现正负束缚电荷,这就是电介质的极化现象。
如图所示,由于极化,在电介质中的极化电场 E ′(图中方向向左)削弱了没有电介质时的电场 E (图中方向向右)。
由此可见,在两个极板之间的合电场强度的大小比 E 小。
实验和理论证明,在这种情况下,电介质内的合电场强度为E/r ε.如果极板之间充满相对介电常数为r ε的电介质,则极板之间的合电场强度为E/r ε ,这时的电容器在容纳的电荷量一定的情况下,两极板之间的电势差比没有电介质时小,根据 U Q C =,知这时相当于电容器的电容增大了。
两极板间如果不加电介质的话,两极板间会被空气占据,空气有一定的导电能力,因而电容器存储电荷的能力会弱一些,而加入电介质后,电容正负极板的绝缘性能就要比没有电介质时好,也就是存储电荷的能力提高了,所以电容也就升高了, 电容器中间的电介质起到了提高电容容量的作用。
例如:在两极板间相距为d 的平行板电容器中,(1)插入一块厚为d/2的金属大平板(此板与两极板平行),其电容变为原来的多少倍?(2)如果插入一块厚为d/2相对介电常数为r ε的电介质大平板,则又会如何?(3)如果插入一块厚为d 相对介电常数为r ε的电介质大平板,则又会如何?解析:(1)插入一块厚为d/2的金属大平板时,在电场作用下,在金属板处于静电平衡状态,内部电场强度处处为0,整个金属大平板是一个等势体,整个金属大平板上没有电压降,两极板之间的距离缩短为d/2,极板间的电场强度E 未变(因为E ,CdQ d U ==, C 、d 成反比,C 、d 乘积不变,所以E 不变),所以两极板间的电压2'd E U ⋅=,所以根据电容的定义U Q C ==Ed Q 知,此时的电容器的电容变为原来的2倍。

高考中有关平行板电容器的典型问题赏析问题1:电容器的两类基本问题讨论平行板电容器的两类基本问题是:(1)若两极板保持与电源相连,则两极板间电压U不变时,去讨论其它物理量的变化情况;(2)若电容器充电后断开电源,则电容器两极板所带的电荷量Q不变时,去讨论其它物理量的变化情况。
解决此类问题的关键要抓住三个基本关系式:,,。
例1.(2008年重庆理综)如图1所示是某同学设计的电容式速度传感器原理图,其中上板为固定极板,下板为待测物体,在两极板间电压恒定的条件下,极板上所带电量Q将随待测物体的上下运动而变化。
若Q随时间t的变化关系为(a、b为大于零的常数),其图象如图2所示,那么图3、图4中反映极板间场强大小E和物体速率v随t变化的图线可能是()A.①和③B.①和④C.②和③D.②和④解析:平行板电容器上电压U不变。
上板固定下板上下移动,由得,由,得。
所以E—t图线与Q—t图线形状相似。
电容器两板距离,则经时间内,速度,即v与t无关。
因此C项正确,A、B、D项错误。
例2.(2008年宁夏理综)如图5所示,C为中间插有电介质的电容器,a 和b为其两极板,a板接地;P和Q为两竖直放置的平行金属板,在两板间用绝缘线悬挂一带电小球;P板与b板用导线相连,Q板接地。
开始时悬线静止在竖直方向,在b板带电后,悬线偏转了角度α。
在以下方法中,能使悬线的偏角α变大的是()A.缩小a、b间的距离B.加大a、b间的距离C.取出a、b两极板间的电介质D.换一块形状大小相同、介电常数更大的电介质解析:电容器C带电量不变,a、Q两板均接地,电势为零,b、P两板电势相等。
当ab间距离缩小时,电容器C的电容变大,电压U变小。
即b、P两板电势减小,P、Q间电压减小,电场强度E减小,悬线偏角减小,所以A错误,B正确。
取出a、b两极板间电介质时,电容器C的电容变小,电压U变大,悬线偏角增大,所以C正确。
当换一块介电常数更大的电介质时,电容器C的电容变大,电压U变小,悬线偏角减小,所以D错误。
平行板电容器实验的探讨摘要:主要讨论平行板电容器实验原理,静电计对平行板电容器实验的影响。
当距离较小的时候,静电计的电容可以忽略,当距离较大时则影响较大。
另外,还对实验效果进行了分析讨论。
分析了“平行板电容器的电容”演示实验中与静电计指针偏转变化量有关的因素关键词:平行板电容器电容静电计Experimental Parallel Plate Capacitor DiscussionAbstract:This paper analyzed the factors related to the deflection variable of elect remoter pointer in the demonstration experiment of capacity of parallel plate capacitor. Discussed parallel plate capacitor experimental principle, the terms of electrostatic parallel-plate capacitor capacitance. When the smaller distance, or the electrostatic capacitance can be ignored, when the distance is greater when a greater impact. Furthermore, the experimental results were analyzed and discussed.Key words: parallel plate capacitor capacity elect remoter目录1平行板电容器的基本原理 (4)1.1实验装置和方法 (4)1.2实验中的注意事项 (5)2 静电计对电容的影响 (6)2.1 静电计影响的原理分析 (6)2.2 实验过程 (6)2.4结论 (8)3 静电计指针偏转的分析 (9)3.1 θ∆与平行板电容器的电容的变化量∆C 有关 (9)3.2 θ∆与平行板电容器的初始电容C0 有关 (10)3.3 ∆θ与电路中的分布电容有关 (10)3.4 ∆θ与静电计的U -θ显示特性曲线有关 (11)3.5 结论 (11)致谢.............................................................. 错误!未定义书签。
平行板的电场强度一、引言平行板电容器是电学中最基本的电容器之一,其电场强度的计算是电学中的基础知识。
本文将从理论和实验两个方面探讨平行板电容器的电场强度。
二、理论计算平行板电容器的电场强度可以通过高斯定理计算得出。
假设平行板电容器的两个平行板面积为S,距离为d,电容器中充满了电介质,电介质的介电常数为ε,则电场强度E可以表示为:E = σ/ε其中,σ为平行板电容器上的电荷密度,可以表示为:σ = Q/S其中,Q为平行板电容器上的电荷量。
根据电容器的定义,电容量C可以表示为:C = Q/V其中,V为平行板电容器的电势差。
将Q代入σ的公式中,可以得到:σ = CV/S将σ代入E的公式中,可以得到:E = Q/εS = CV/εd因此,平行板电容器的电场强度E与电容量C、介电常数ε以及平行板间距d有关,与平行板面积S无关。
三、实验测量为了验证理论计算的结果,可以进行实验测量。
实验中需要用到电场计和平行板电容器。
首先将平行板电容器连接到电源上,使其充电。
然后将电场计放置在平行板电容器中间,测量电场强度E。
根据电场强度的定义,可以得到:E = F/q其中,F为电场力,q为电荷量。
由于电场力与电荷量成正比,因此可以通过测量电场力和电荷量的比值来得到电场强度。
实验中需要注意的是,平行板电容器的电荷量和电场强度都会随着时间的变化而变化,因此需要在测量前将电容器充电并等待一段时间,使其达到稳定状态。
四、结论通过理论计算和实验测量,可以得到平行板电容器的电场强度与电容量、介电常数和平行板间距有关,与平行板面积无关。
在实际应用中,可以通过改变这些参数来调节电场强度,从而实现不同的电学效果。
五、总结平行板电容器的电场强度是电学中的基础知识,理论计算和实验测量都是非常重要的。
通过本文的介绍,读者可以了解到平行板电容器的电场强度的计算方法和实验测量方法,从而更好地理解电学中的相关知识。
平行板电容器的动态问题分析一 平行板电容器的动态分析问题常见的类型平行板电容器的动态分析问题有两种情况:一是电容器始终与电源连接,此时U 恒定,则Q =CU ∝C ,而C =εr S 4πkd ∝εr d,两板间场强E =U d ∝1d;二是电容器充电后与电源断开,此时Q 恒定,则U =Q C ,C ∝εr S d ,场强E =U d =Q Cd ∝1S。
二.运用电容器定义式与决定式分析电容器相关量变化的思路(1)确定不变量,分析是电压不变还是所带电荷量不变。
(2)用决定式C =εr S 4πkd分析平行板电容器电容的变化。
(3)用定义式C =Q U分析电容器所带电荷量或两极板间电压的变化。
(4)用E =U d分析平行板电容器极板间匀强电场场强的变化。
三.两类动态问题分析比较(1)第一类动态变化:两极板间电压U 恒定不变(2)第二类动态变化:电容器所带电荷量Q 恒定不变四 典题分析1 如图6-3-8所示,平行板电容器与电动势为E 的直流电源(内阻不计)连接,下极板接地。
一带电油滴位于电容器中的P 点且恰好处于平衡状态。
现将平行板电容器的上极板竖直向上移动一小段距离,则( )图6-3-8A.带电油滴将沿竖直方向向上运动B.P点的电势将降低C.带电油滴的电势能将减小D.若电容器的电容减小,则极板带电荷量将增大[尝试解题]上极板向上移动一小段距离后,板间电压不变,仍为E,故电场强度将减小,油滴所受电场力减小,故油滴将向下运动,A错;P点的电势大于0,且P点与下极板间的电势差减小,所以P点的电势降低,B对;两极板间电场方向竖直向下,所以P点的油滴应带负电,当P点电势减小时,油滴的电势能应增加,C错;电容器的电容C=εr S4πkd,由于d增大,电容C应减小,极板带电荷量Q=CE将减小,D错。
[答案] B2.(2012·江苏高考)一充电后的平行板电容器保持两极板的正对面积、间距与电荷量不变,在两极板间插入一电介质,其电容C与两极板间的电势差U的变化情况是( )A.C与U均增大B.C增大,U减小C.C减小,U增大 D.C与U均减小解析:选B 根据平行板电容器电容公式C =εr S 4πkd,在两板间插入电介质后,电容C 增大,因电容器所带电荷量Q 不变,由C =Q U可知,U =Q C减小,B 正确。
平行板电容器中介质的受力分析
谢伟华
(中国科学技术大学物理学院1班)
引言:介质从平行板电容器中抽出要受到引力,我们用虚功原理很容易得到这个结论,但是平行板电容器产生的电场是与介质表面垂直的,那么这个力是如何产生的,我们就来讨论一下这个问题。
一、用静电能求静电力
设极板长为L,宽为a,面积为S,板间距离为d,极板间电压为U恒定不变,电介质介电常数为
由虚功原理易得F==U2=2
用这种方法无法看出这个力从何而来。
所以我们采用下面的方法。
二、用库仑定律求受力
电介质在电场中极化成电偶极子,下面先求一个电偶极子在电场中受的力。
设负电荷处电场为为(),正电荷处电场为,由于l远小于电介质的线度,所以用泰勒展开得:
=
所以电偶极子受到的合力为
对于一个体积为V的电介质(下面的E都是总电场,因为体电荷元在自身处产生的电场为0)
=
X与Z方向均为0,所以可以变为
dV
在极板内部电场是均匀为,外部电场为0,所以只需计算边缘那一部分,且上式积分号内部可化为:
则
与用静电能求得结果一样。
结论:从计算过程中可以看出,这种力
产生的原因是电场由跃迁到0造成的,这是理想化模型的弊端,以致于我们想不明白这个力从何而来。
实际中,电场不可能一下子变成零,边缘处也是有电场的。
所以我们考虑问题应从实际出发,理论只是一个工具,不代表一切。
【参考文献】
【1】胡友秋,《电磁学与电动力学》,科学出版社,2014.6
【2】赵凯华,《电磁学》,高等教育出版社,2006.12。
浅析平行板电容器问题平行板电容器具有以下几个特点:1、两板内侧一定带等量异种电荷取一个上、下底面分别在两板内部的圆柱面作为高斯面,因平行板电容器内的电场线垂直于板面,因此高斯面侧面电通量为零;因为金属板内部电场为零,所以高斯面上、下的电通量也为零。
高斯面总的电通量为零,内部的净电荷必为零,即两板带等量异种电荷。
2、平板行电容器的电容为(真空中)或(介质中)取一个圆柱面作高斯面,一个底面在一块金属板内,另一个底面在两板之间。
设两板间的场强为E,金属板内部的底面和侧面都无电通量,两板之间的底面电通量为。
根据高斯定律应有,可得,因此有即在介质中,故3、当平行板电容器两板带不等量电荷时,两板内侧带等量异种电荷,两板外侧带等量同种电荷。
因为只有这样,两板内部的合场强才为零。
如果两板的电量分别为和,设两板内侧各带电和,外侧各带电,则由电量守恒有可解得对于单个平行板电容器,我们可抓住两种情况,三个公式解决问题。
两种情况:1、电容器始终与电源相连时,电压不变;2、充电后与电源断开,电容器的电量不变。
三个公式:或如果电路中含有多个电容器,该如何求解呢?很多同学不知如何下手,总觉得方程不够,我们通过两题来进行分析。
例、三个相同的电容器连接成如图所示的电路,已知电容器1带电量为Q,上板带正电;电容器2、3原来不带电(1)如果用导线将a、b相连,求C1、C2、、C3各带电多少?(2)如果在上问基础上断开a、b,接通a、c,待稳定后再断开a、c,接通a、b,情况如何呢?(3)如果在上问基础上再将a、d相连,那么C2、、C3又如何呢?分析与解:(1)C1和C2的上板形成一个孤岛,因此①C2的下板和C3的上板也是一个孤岛,因此②再有即③由①②③式可解得(2)断开a、b后,C2的电量不变,C1和C3并联再断开a、c,连接a、b,设三个电容器的电量分别为,C1和C2的上板为一孤岛,所以有④C2的下板和C3的上板也是一个孤岛(注意电荷符号)⑤再有即⑥由④⑤⑥可解得(3)将a、d相连,此时C1被短路,C2和C3并联,应有⑦⑧由⑦ ⑧可解得例:四块面种都为S的导体板A、B、C、D平行放置,间距分别为2d、d、2d,各带有Q、2Q、3Q、4Q的电量,试求:(1)A、D两板间的电势差(2)用导线连接B、D板并接地,试求从接地线流入大地的电量为多大?并求出接地后A、C两板间的电势差(3)除去连接导线和接地线,并抽出B板,然后用导线连接A、D板,再把电势差为的电源的正负极,分别接在板A、C上,试求此后各板上的电量。
平行板电容器中介质的受力分析引言: 对于平行板电容器的受力问题,前人大多研究理想情况下平行板电容器的受力,即通过改变电容的大小研究其受力情况。
本文的设想是把电介质放入平行板电容器中电介质在电场的作用下一定会发生变化,必然产生电偶极子,电偶极子在电场中必定会受力,一旦电偶极子受力就会发生位移变化,那么必然存在做功问题,那么就可以从能量角度去分析它的受力,进而得出的两个结果一定是相等的,本文通过例题去检验其确性。
1 介质受力公式的推导(从宏观上理论推导)介质在进入平行板电容器的过程中(假设电量Q 不变),纵向电场使介质极化所做之功转化为介质的极化能,这仍是电容器储能的一部分,根据能量守恒定律,插入介质后电容的静电能应不变,但是由电容器的能量公式W=Q*Q/2C ,当C 增大时,能量却是减少的,矛盾的出现说明我们一定忽略了某些相互作用的存在,为了避开繁琐的力分析,下面,我们将从能量的角度出发,通过数学方法导出平行板电容器中介质的受力的计算公式。
一个平行板电容器,其中部分地充入介质常数为E(p(m),r)(介质常数一般不仅是空间r 的函数,而且还是介质的质量密度p(m)的函数)并且无自由电荷的介质,假设介质沿X 方向作一个无限小位移X ,则电容器的储能变化为22111222W V V vVD EDdV dV EDdVE dV δδδδεε===-⎰⎰⎰⎰ 式(1-1)而 E 0D ρ=-∇Φ∇==则 ()2212VvV VDdv E dV D D E dV δφδδεδδδε=-∇-=-∇Φ+Φ∇-⎡⎤⎣⎦⎰⎰⎰⎰ =2212SvVVDd s dV E dV E dV δδρδεδε-Φ+Φ--⎰⎰⎰⎰ 式(1-2) 其中在无穷大界面的值为零,而介质中已设自由电荷密度为零。
对于介质给定的一个无限小位移0X ,相对于空间的一个固定体积来说,必有:0()m m X vSvdV d s X dV δρρρ=-=-∇•⎰⎰⎰ 式(1-3)则 ()()00,x x m mm m m m ρρεδρρεδερδρ•∇∂∂-=∂∂=•∇=而()dV E X X E V dV X E V M MM M M M V w ⎰⎰⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂∇•-⎪⎪⎭⎫ ⎝⎛∂•∇=•∇∂∂=ρερρρερρεδ200222121 dV E X dV E X s d X E M M V M v m V M M ⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂∇=⎪⎪⎭⎫ ⎝⎛∂∂∇•-•⎪⎪⎭⎫ ⎝⎛∂∂=⎰⎰⎰ρερρερρρε202002212121 式(1-4)A 电量Q 恒定当介质位移0X 时,电场对介质作的功等于电容器储能的减少,即2222211()()22m M M M M M M M M M v V F E dV E E E E dVεεεεερρρρρρρρρρ⎡⎤∂∂∂∂∂=∇=∇+∇-∇-∇⎢⎥∂∂∂∂∂⎣⎦⎰⎰B 电压U 恒定电源所作之功一部分转化为电容器的储能,另一部分对介质做功转化为机械能,即有W XF Udq δ-=•-⎰00X F dq U v•-⎰=dV E E X MM V)(21220ρερ∂∂∇•⎰⎰=dC U 2dV E X X F ε∇-•=•-⎰20021举例说明:例1 如图所示图1.1一个平行板电容器,带电量为Q ,宽为b ,长为L ,两级板间的距离为 d ,其中部分地冲入电介质常数为ε 的均匀电介质,求介质所受的力。
解:在介质内部,0=∇ε 则 F 内=0,所以介质所受到的力只出现在介质到真空的过度层中,显然作用在极板上下界面的作用大小相等,方向相反,相互抵消。
在侧面上,假定介电常数迅速而连续地从ε降到0ε,略去边缘效应后有:E E E ==21 由上面推导公式可知x Sx x x V e db E e dydz E e dydz dx e X E dV E F )(212121210222200εεεεεεεεε-=∂-=∂∂-=∇-=⎰⎰⎰⎰⎰⎰⎰式(1-5)因为C 总=C 介+C 真=()[]dx b dbx dbxr 11)1(00-+=-+εεεε 式(1-6)则 E=()[]X b Qcd Q R 110-+εε即()[]()()[]xr r x r r e x b d Q e bd x b Q F 2020*******)1(1112-+-=--+=εεεεεεε (0<x<1) 当介质全充入电容器时,由于 0=∇ε,则 0=F 介质不再受横向作用力,这于上面公式推导公式一致的。
例2 如图所示图1.2一个平行板电容器,在宽为 b 长为L , 两板之间距离为 a ,电源电压恒为0U其中部分地充入介电常数为均匀电介质,求电介质受到的力 解 : 上面公式可得dV E X X F dC U ε∇-•=•-⎰⎰200221()()()0000011111r r b x U C ab x x C aεεεε+-⎡⎤⎣⎦=+-++⎡⎤⎣⎦=02000020002200022)1(2)1()1(2100x ab U X F x ab U X F ax b U dydzdx e X E X X F dC U r r r x C C -=•-+•=-∂∂-•=⎰⎰⎰⎰εεεεεεεεε因为介质只能沿 x 方向运动,所以介质受到的合外力只能沿x 方向,即 00>•X F所以,F 只能沿 X 正方向。
则有,x r e ab U F 2)1(020-=εε 2 用库仑定律求插入介质板后介质的受力公式(从微观角度出发)在电场中的电介质要受到电场作用而极化成偶极子(电偶极矩L q p =)。
当偶极子处于电容器中间的均匀场中,如图所示: E q F -=-E qF =+ L q P =E P M ⨯=(A)在均匀电场中的一个偶极子图2.1 偶极子的正端受力一向右的拉力E q ,负端受力 一向左的拉力- Eq 作用在这个位置上的偶极子的净力和力矩都是零。
如图所示(B )作用在偶极子上的力矩是E P M ⨯=图2.2偶极子和电场方向成角度θ,显然受到一个力矩的作用。
取偶极子的中心为原点,故-+⨯-⨯==F r F r M lr )(,2故有是一个和图面垂直的矢量,它的大小是EP M pE lqE Eq Eq M ⨯===+=即θθθθsin sin sin 21sin 21式(2-1)偶极子在图(A )中的方位时,能量最低,把它转到任何其他位置都必须对它做功,现在计算一下,将偶极子从和电场平行的位置转到某角度所需要的功,如图所示:(C) 将偶极子的方位从和电场平行的方向转到图中所表示的方向所作的功是()0cos 1θρ-E图2.3偶极子在图(a )中的方位时,能量最低,把它转到任何其他位置都必须对它做功,现在计算一下,将偶极子从和电场平行的位置转到某个角度0θ 所需要的功,如图(c )所示。
转过无穷小角度 d θ 所需要的功是θmd 。
因此,所做的总功是()00cos 1sin 0θθθθθθ-==⎰⎰pE d pE md将偶极子反转把他倒个头这相当于πθ=0,所需的功等于 2PE 。
偶极子在任何均匀电场中所受的净力,不论其取向如何,显然为零,不均匀的电场中,作用在偶极子的两端的力一般不是正好是大小相等,方向相反的,而是有一净力作用在偶极子上。
当偶极子处于平行板电容器边缘区的不均匀电场中,如图(3 )所示(l r E图2.4组成电极子的两点电荷所在位置的电场强度分别是()r E 和()l r E +则 作用于这个偶极子的力是 ()()r E a l r E a f -+= 式(2-2)由于两点电荷间的距离远小于电介质的线度,故可用泰勒极数开为()()()()()()()()r E l r E r E z lz r E y ly r E x l r E l r E x∇•+=∂∂+∂∂+∂∂+≈+ 因此,作用于这个电偶极子上的力是 ()()()()r E p r E l q f ∇•=∇•= 对于体积为 D V 的电介质,所受的总作用力为⎰∇•=DV E P d F )(式中,表示在 d V 体积内的电偶极矩 dv p p d =,p 是电介质的极化强度矢量E p )(0εε-= ε和 0ε 分别表示电介质的介电常数和真空介电常数在线性均匀介质中 ε 是一定的。
将这些关系带入 E P dF DV ⎰∇•=)(可得()()E dV E dvF ⎰∇•-=0εε 利用矢量恒等式()()dVE F E ,E E E B A A B A B B A B A B A D V 202212)()()()()(∇-=∇•=∇==⨯∇⨯+∇•+⨯∇⨯+∇•=•∇⎰εε于是上式可以写成为则有使式(2-3)这是电介质受力的一般表达式。
在对称情况下,对所有偶极子所受力的力求合力,只有X 方向的合力不为零,因此,上一式可改写为()故在电场强度均匀部分,XE ,dV X E iF D V 0ˆ21220=∂∂∂∂-=⎰εε 式(2-4)0=F若这片电解质左手端远离边缘电场,而右手端均在均匀电场中。
则对X 的积分可写成()()iU d b F ,E j a U E ,dydzE E V iF D ˆ210,ˆˆ212000220εεεε-==⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛--=⎰于是可以得到而左手端是右手端的电场是然而左右左右其中 a 为两极间距离,b 为极板宽度。
当电量Q 一定时, 由(r εεε0=)CQ U UQC ==带入 ()i U d b F ˆ21200εε-= 可以得到下面的式子: ()()[]22211121x Q b d F r -+-=εεε 因此从宏观上和微观上通过数学推倒都是一样的,能量的计算自动把一复杂问题以下子简化,使对问题分析大大减少运算量,这样一来给我们计算复杂问题带来了方便。
从而进一步说明了理论的推导的正确性。
结论:通过对平行板电容器中电介质受力的研究,进一步说明平行板电容器的受力确实是通过电介质的受力来影响的。
以后可以把一个比较复杂的平行板电容器中电介质受力问题通过从能量的角度去分析,这样大大简化了运算过程。
但是因为本文是从数学的角度去推导的,用大量的积分公式,求导公式,有的公式存在假设条件,带有很强理论性,没有通过实验去验证。
参考文献[1] 郭硕鸿.《电动力学》[M]. 北京:高等教育出版社.1979.45.[2] E.M 珀塞尔. 《电磁学(伯克利物理学教程第2卷)》.[M] 北京:科学出版社. 1979372——373.[3] 大学物理编辑部. 《电磁学专辑》[M]. 北京:北京工业出版社.1988. 33. [4] 夏英齐,钱树高.“电容器储能变化和介质受力的问题”[J]. 《物理通报》. 2000(5).14.[5] 张三慧. 《电磁学》[M]. 北京:高等教育出版社.1979. 45[6]. [6] 赵凯华. 《电磁学》[M]. 北京: 高等教育出版社. 1980. 45.[7] 叶鹏,黄遒本.“关于理想平行板电容器充电过程的能量传输问题”[J].《大学物理》 2005. 24(10)57.[8] [美]费曼R P 莱登,R B 桑兹M 费曼.《物理学讲义(第2卷)》.[M] 王子辅译.上海:上海科学技术出版社 .1981.287-290.[9] 蔡圣善, 朱耘 ,徐建军.《电动力学》[M]第2版.北京:高等教育出版社. 2002 35.。