T形截面如何分类
- 格式:ppt
- 大小:307.50 KB
- 文档页数:68








t形截面的分类与判别T形截面是指一个直梁断面形状上部为“横”字形,下部为一竖杆的直梁。
T形截面广泛应用于建筑结构、机械工程等领域,由于其横向稳定性以及易于加工的特点,常常被用作梁、柱、支撑等结构部件,具有重要的实际应用价值。
根据T形截面的特点和性质,可以将其分类为两种:对称T形截面和非对称T形截面。
对称T形截面结构对称,上下翼缘宽度相等,重心与中心轴线重合,是应用最广泛的T形截面。
对称T形截面如图1所示,翼缘宽度分别为BF,重心O位于中心轴线上与下翼缘中心点距离为h/2,纵向面积为A,其惯性矩与截面模量分别为I和W。
在实际应用中,需要根据T形截面的具体情况来选择合适的截面类型和尺寸。
为了便于判别和选择,我们需要对T形截面的性能参数进行计算和分析。
T形截面判别的关键参数包括:纵向截面面积A、惯性矩I、截面模量W、中性轴位置yc、抗弯强度等。
下面我们将对这些参数进行详细介绍。
纵向截面面积A是指T形截面与中心轴线间所有区域的积分面积,用于计算截面受力时的应力和轴力。
其计算公式如下:$$A=B_FL+\frac{(h-2t_f)}{2}t_w$$其中,BF、L、tf和tw分别为图1中所示的尺寸参数,h=L+2tf为截面高度,t为翼缘厚度。
惯性矩I是指T形截面围绕截面中心轴进行转动时所表现出的抵抗力矩的大小,够用于计算截面的扭转刚度和抗弯强度。
其计算公式为:$$W=\frac{B_F}{2}h^2\left(\frac{1}{2}-\frac{t_f}{h}\right)+t_w\left(\frac{B_F} {2}-t_w\right)^2$$中性轴位置yc是指T形截面上下翼缘之间的中性轴线位置,是挖掘截面弯曲特性的关键参数,其计算公式为:$$y_c=\frac{I}{A}\frac{1}{h/2}$$其中,I和A分别为惯性矩和纵向截面面积。
在对称T形截面中,中性轴线位于中心轴线上,即yc=0;而对于非对称T形截面,则需要通过计算求出中性轴位置。


T型截面正截面承载力计算周佳(西南科技大学城市学院土木工程与建筑系,四川绵阳621000)[摘要] 由于T型截面梁具有更经济更轻质的功能,这种构造被广泛用于桥梁工程及大荷载工程,以下根据自己在学习过程中的总结和计算列出一般单筋T型截面梁正截面抗弯承载能力计算的简单过程。
(本文仅错位自己在钢筋混凝土设计课程学习后对一般单筋T型截面梁正截面抗弯承载能力计算过程的总结与复习)[关键词] T型截面梁正截面承载力0 引言T型截面梁由矩形截面梁衍生出来,其截面形式如图1所示。
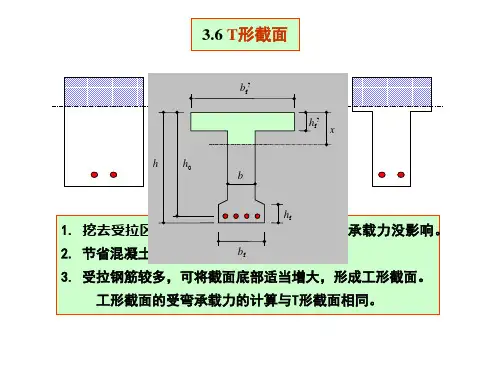
阴影部分面积为混凝土,为减轻自重可以抠除同时基本不会影响该梁的抗弯承载能力。
建筑工程中受弯构件正截面承载力计算的基本假定:1)截面应保持平面;2)不考虑混凝土的抗拉强度;3)给出混凝土受压的应力—应变关系曲线按下列规定取用:图1 图2T型截面梁分为两类(如图2):一类如图2(a):中和轴在翼缘内,即受压区宽度小于等于翼缘厚度。
二类如图2(b):中和轴在翼缘下部,即受压区厚度大于等于翼缘厚度。
给出两类截面梁的判别式文献[1]:2 T 型截面梁正截面抗弯承载力的计算:一、基本公式(一)第一类T 形梁2.第一类T 形梁的基本计算公式这一类梁的截面虽为T 形,但由于中和轴通过翼缘,即'f h x ≤,s y f c A f x b f ='1α⎪⎭⎫ ⎝⎛-'=≤201x h x b f M M f c u α 3.基本公式的适用条件是:1)0h x b ξ≤由于T 形截面的翼缘厚度h f ′一般都比较小,既然x ≤h f ′,因此这个条件通常都能满足,故不必验算。
2)0/bh A s =ρ应不小于min ρ(具体计算时,bh A A s S min min ,ρ=≥)(二)第二类T 形梁1.计算图式2.第二类T 形梁的基本计算公式这一类梁截面的中和轴通过肋部,即x > h f ′,故受压区为T 形。
于是第二类T 形梁正截面受弯承载力的基本计算公式可以写成: s y f f c c A f h b b f bx f ='-'+)(11αα()⎪⎪⎭⎫ ⎝⎛'-'-'+⎪⎭⎫ ⎝⎛-=≤220101f f f c c u h h h b b f x h bx f M M αα3.基本公式的适用条件1)为防止发生超筋破坏,应当满足: 0h x b ξ≤或 b ξξ≤或 y c b s f f bh A //1011αξρ≤=或 ()b b c u bh f M ξξα5.012011-≤2)bhA A s s min min ,ρ=≥由于第二类T 形梁受压区较大,相应受拉钢筋也就较多,故一般均能满足此条件,可不必验算。