第9章 辐射换热计算2013

第九章辐射换热计算复习题1 ．任意位置两表面之间用角系数来计算辐射换热，这对物体表面作了哪些基本假定？2 ．为了测量管道中的气流温度，在管道中设置温度计。

由于温度计头部和管壁之间的辐射换热而引起的测温误差，并提出减少测温误差的措施。

3 ．在安装有辐射采暖板的室内测量空气温度时，为了消除热辐射带来的误差，用高反射率材料分别作筒状和不开口的球壳状遮热罩（图9 一35 ）。

试分析这两种方法的效果，它们测得的温度是否一样，为什么？如将它们的表面涂黑或者刷白，是否影响测温结果？4 ．灰表面间的辐射换热计算式，如果要用于非灰表面（表面的辐射性质与波长有关），你认为应做些什么修改。

5 ．有两平行黑表面，相距很近，它们的温度分别为1000 ℃和500 ℃。

试计算它们的辐射换热量。

当“冷”表面温度增至700 ℃，则辐射换热量变化多少？如果它们是灰表面发射率分别为0.8 和0.5 ，它们的辐射换热量又为多少？6 ．抽真空的保温瓶胆两壁面均涂银，发射率：ε1=ε2=0.02 ，内壁面温度为100 ℃，外壁面温度为20 ℃，当表面积为0 . 25㎡时，试计算此保温瓶的辐射热损失。

7 ．有一微面积dA与另一矩形面积A2相平行，矩形的边长为a、b ，通过dA 法线正对矩形的一角，相距为c，求证：X 1，2=]1111[212222CB arctgC C B C arctg B B +++++π 其中B = a / c ; C=b / c8 ．图9 一36 所示表面间的角系数可否表示为：X 3,(l+2)=X 3,l +X 3,2X (l+2),3=X l,3+X 2,3如有错误，请予更正。

9 ．两宽度分别为a 、b ，长度为无限的平面相交，夹角为θ ，试求角系数Xa ,b =?10 ．试确定图9-37 所示各种情况下的角系数。

11 ．某采暖房间采用立式悬挂辐射采暖板，试求此采暖板和房间各表面间的角系数，房间和采暖板的尺寸见图9-3812.两块平行放置的平板的表面发射率均为0.8，温度分别为t 1=527℃及他t 2=27℃,板间距小于板的宽度与高度。

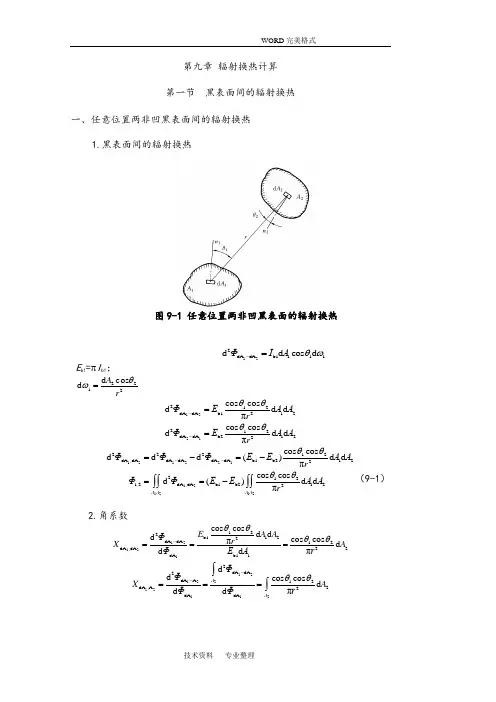
第九章 辐射换热计算 第一节 黑表面间的辐射换热一、任意位置两非凹黑表面间的辐射换热1.黑表面间的辐射换热图9-1 任意位置两非凹黑表面的辐射换热122dA dA b1111d d cos d ΦI A θω-= E b1=πI b1； 2221cos d d rA θω=12212dA dA b1122cos cos d d d πΦE A A r θθ-=21212dA dA b2122cos cos d d d πΦE A A r θθ-=12122122212dA ,dA dA dA dA dA b1b2122cos cos d d d ()d d πΦΦΦE E A A r θθ--=-=- 1212122121,2dA ,dA b1b2122cos cos d ()d d πA A A A ΦΦE E A A r θθ==-⎰⎰⎰⎰ （9-1）2.角系数12121122b1122dA dA 12dA ,dA 22dA b11cos cos d d d cos cos πd d d πE A A Φr X A ΦE A r θθθθ-===12122121122dA dA 2dA A 12dA ,A 22dA dA d d cos cos d d d πA A ΦΦX A ΦΦr θθ--===⎰⎰12121211122dA dAA A121,2122A A1dcos cos1d dπA AA AΦΦX A AΦΦA rθθ--===⎰⎰⎰⎰（9-2a）212212AAA1,2ddπcoscos121212AArAΦΦXAA⎰⎰==-θθ（9-2b）21,212,1AXAX=（9-3）3.辐射空间热阻图9-2 辐射空间热阻21,2b2b112,1b2b12,1)()(AXEEAXEEΦ-=-=（9-4）b1b21,21,211E EΦX A-=Φ1,2=（E b1－E b2）A = σb（T14- T24）A二、封闭空腔诸黑表面间的辐射换热图9-3 多个黑表面组成的空腔图9-4 三个黑表面组成空腔的辐射网络图9-5 例9-1附图：,1,2,,1ni i i i n i j j ΦΦΦΦΦ==++⋅⋅⋅⋅⋅⋅=∑将上式除以i Φ，按角系数定义，可得,1,2,n ,11ni i i i j j X X X X ==++⋅⋅⋅⋅⋅⋅=∑（9-5）∑∑∑∑====-=-==nj nj i j i nj i j i i j i nj j i i A X E A X E A X E E ΦΦ11,bj 1,bi ,bj bi 1,)(∑=-=nj j i j i i A X E A E Φ1,bj bi （9-6）【例9-1】∑=-=311,b 1b11j j j j A X E A E Φ （a ）∑=-=312,b 2b22j j j j A X E A E Φ （b ）0313,b 3b33=-=∑=j j j j A X E A E Φ （c ）02,21,22,11,1====X X X X13,23,1==X X31,313,1A X A X =32,323,2A X A X =213,11,33,223/210.252A r X X X A r ππ==⨯==13,32,31,3=++X X X5.03,3=X033,3b323,2b213,1b13b3=---A X E A X E A X E A E4b b T E σ=2424143T T T +=T 3=415.6K 或者142.6℃1b11b11,11b22,12b33,1344b11b31,3111344311b 244()()()100100473415.61 5.67()()1801.0W 2100100b ΦE A E X A E X A E X A E A E X A A T T T T AC σπ=---=-=-⎡⎤=-⎢⎥⎣⎦⎡⎤=⨯⨯⨯-=⎢⎥⎣⎦【讨论】π411212121=+=+=∑A A A A A AR 4444b1b2121,2()π 5.67 4.73 3.13)1801.0W 4/π4b E E T T ΦRσ--===⨯⨯-=∑（第二节 灰表面间的辐射换热一、有效辐射图9-6 有效辐射示意图图9-7 辐射表面热阻1.有效辐射J 1=ε1E b1＋ρ1G 1=ε1E b1＋（1－α1）G 1 W/m 2（a ）2. 辐射表面热阻11b111111G E G J A Φαε-=-= W/m 2 （b ） 1111b11b111111)(1A J E J E A Φεεεε--=--= W （9-7）二、组成封闭腔的两灰表面间的辐射换热图9-8 两个灰表面组成封闭腔的辐射换热网络图9-9 空腔与内包壁面间的辐射换热22212,1111b2b12,1111A A X A E E Φεεεε-++--=W (9-8a ))11(1)11()(2212,112b 1b 12,1-++--=εεA A X E E A Φ 1,2112()W s b b X A E E ε=- （9-8b ）)11()11(1121,212,1s -+-+=εεεX X1.无限大平行灰平壁的辐射换热A 1=A 2=A ，且X 1,2=X 2,1=1，)(111)(4241b s 212b b12,1T T A E E A Φ-=-+-=σεεε W （9-9）1121s -+=εεε2.其中一个表面为平面或凸表面的辐射换热)11(1)(22112b 1b 12,1-+-=εεA A E E A Φ W (9-10)A 2 >>A 1，且ε2的数值较大Φ1,2=ε1 A 1（E b1-E b2）W （9-11）三、封闭空腔中诸灰表面间的辐射换热1.网络法求解图9-10三个灰表面组成封闭腔辐射换热网络图9-11 例9-4附图图9-12 例题9-5附图节点1013,11312,1121111b1=-+-+-A X J J A X J J A J E εε （a ）节点2 011123,22321,2212222b2=-+-+--A X J J A X J J A J E εε （b ）节点3 011132,33231,3313333b3=-+-+--A X J J A X J J A J E εε （c ）【例9-4】X 1,2= X 2,1=0.38X 1,3=X 2,3=1-X 1,2=1-0.38=0.62计算网络中的各热阻值：A 1=A 2=π⨯0.32=0.283m 21.14283.02.02.011111=⨯-＝－A εε m -23.5283.04.04.011222=⨯=-－A εε m -23.9283.038.01112,1=⨯=A X m -27.5283.062.011123,213,1=⨯==A X A X m -2流入每个节点的电流总和等于零07.53.91.141b3121b1=-+-+-J E J J J E 07.53.93.52b3212b2=-+-+-J E J J J E 202447731067.5484b1=⨯⨯==-T E b σW/m 235445001067.5484b2=⨯⨯==-T E b σW/m24593001067.5484b3=⨯⨯==-T E b σW/m 2J 1=5129 W/m 2 J 2=2760W/m 2b1111112024451291072W 114.1E J ΦA εε--===- b22222235442760148W 1 5.3E J ΦA εε--===-312()(1072148)1220W ΦΦΦ=-+=-+=-【例9-5】1.1411111=-=A R εεm -23.512222=-=A R εεm -23.9112,12,1==A X R m -27.5113,13,23,1===A X R R m -2E b1=20244W/m 2 E b2=3544W/m 2∑++++=23,23,12,11111R R R R R R =14.1+5.243.57.57.513.911=+++m -2b1b21,2202443544682W 24.5E E ΦR --===∑J 1=E b1－Φ1,2⨯R 1=20244－682⨯14.1=10627.8 W/m 2J 2=E b2＋Φ1,2⨯R 2=3544＋682⨯5.3=7185.6 W/m 2J 3=（J 1+J 2）/2=8893.2 W/m 2J 3=G 3=E b3=σ b T 341/41/4b3388893.2629K5.6710b E T σ-⎛⎫⎛⎫=== ⎪⎪⨯⎝⎭⎝⎭2. 值解法图9-13 例9-6（a ）（b ）附图及其辐射换热网络∑==ni i j i i j j A X J G A 1,j j εα=∑=-+=ni i j i i j j j j j j A X J A E A J 1,b )1(εε（9-12）∑∑===ni i j i j n i i j i i X J A A X J 1,1,b ,1(1)nj j j j i j i i J E J X εε==+-∑（9-13）4b 1,11j j j j jni i j i T J X J σεεε⎥⎥⎦⎤⎢⎢⎣⎡-=--∑=（9-14）4111,121,231,31,b 1114212,122,232,32,b 2221,12,231()()111()()11n n n n n n n J X J X J X J X T J X J X J X J X T J X J X J X εσεεεσεε-+++⋅⋅⋅+=--+-++⋅⋅⋅+=--⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅++4,3,b 1()()11n n n n n n n J X T εσεε⎫⎪⎪⎪⎪⎬⎪⎪⎪+⋅⋅⋅+-=⎪--⎭ （9-15）ii i i i i A J E Φεε--=1b i =1，2，…n （9-16）【例9-6】1,11,21,31,400.150.540.31X X X X ====、、、；2,12,22,32,40.2500.500.25X X X X ====、、、；3,13,23,33,40.270.140.320.27X X X X ====、、、；4,14,24,34,40.310.150.540X X X X ====、、、；4432198.267.5931.054.015.010⨯⨯=---J J J J 4432183.267.5425.05.0525.0⨯⨯=--+-J J J J4432186.267.5427.068.414.027.0⨯⨯=-+--J J J J 4432184.267.55.15.254.015.031.0⨯⨯=+---J J J JJ 1=440.45 W/m 2； J 2=370.28 W/m 2； J 3=382.69 W/m 2 ; J 4=380.80 W/m 2。

传热学V 第九章辐射传热的计算辐射传热是热传导和对流传热之外的另一种重要的能量传递方式。

当两个物体具有不同的温度时，它们之间会通过辐射传热来交换能量。

在传热学的研究中，辐射传热的计算是一个非常重要的课题。

辐射传热的基本原理辐射传热是指物体之间通过电磁波的辐射而进行的能量传递。

辐射传热的基本原理可以通过斯特藩-玻尔兹曼定律来描述，该定律表明辐射传热的速率与物体的温度的四次方成正比。

辐射传热的计算需要考虑一些关键因素，如辐射传热系数、温度差异、表面特性等。

这些因素的综合作用会影响辐射传热的速率和总的传热量。

辐射传热的计算方法黑体辐射计算对于黑体表面，其辐射传热只与温度有关，与表面的其他特性无关。

在计算黑体辐射传热时，可以使用斯特藩-玻尔兹曼定律，计算辐射传热速率的公式为：$$ q = \\varepsilon \\sigma A (T_1^4 - T_2^4) $$其中，q表示单位时间内通过辐射传热的热量，$\\varepsilon$表示辐射率（0 ≤ $\\varepsil on$ ≤ 1），$\\sigma$表示斯特藩-玻尔兹曼常数（$5.67 \\times10^{-8}$ W/m2·K4），A表示面积，T1和T2分别表示两个物体的温度。

灰体辐射计算对于灰体表面，辐射传热除了与温度有关外，还受到表面的发射率的影响。

灰体的辐射传热速率可以表示为：$$ q = \\varepsilon \\sigma A (T_1^4 - T_2^4) $$这里，$\\varepsilon$表示发射率（0 ≤ $\\varepsilon$ ≤ 1），其他符号的意义与黑体辐射计算相同。

辐射换热器的计算在工程应用中，辐射传热经常在换热器中发生。

换热器的辐射传热计算一般通过计算表面间的辐射热交换量来完成。

换热器表面的总辐射传热率可以表示为：$$ q = \\sum(\\varepsilon \\sigma A (T_1^4 - T_2^4)) $$其中，$\\sum$表示对所有表面的求和。

第九章 辐射换热计算重点：角系数的特点、性质及其计算，表面热阻、空间热阻及有效辐射的概念，两个及多个漫灰表面辐射换热的计算方法，辐射换热的强化与削弱，气体辐射的特点。

影响辐射换热的因素有：表面温度、表面的几何特性（大小、形状）、表面的相对位置，表面的辐射性质。

本章只对黑体表面和漫灰表面作分析。

第一节 黑表面间的辐射换热1-1 任意位置两非凹黑表面间的辐射换热 一、两黑表面间的辐射换热设有两个任意放置的非凹黑体表面，面积分别为1A 、2A ，温度分别为1T 、2T 。

从表面上分别取微元面积1dA 、2dA ，两者的距离为r ，两表面的法线与连线r 间的夹角分别为：1θ，2θ。

微面积1dA 投射到微元面积2dA 的辐射能为：111cos 121ωθd dA I b dA dA ⋅⋅⋅=Φ-黑体服从兰贝特定律：11b b I E ⋅=π ⇒ 21221c o sc o s 121dA dA rE b dA dA ⋅⋅⋅⋅=Φ-πθθ 2221cos rdA d θω=同理，从微面积2dA 投射到微元面积1dA 的辐射能为：21221cos cos 212dA dA r E b dA dA ⋅⋅⋅⋅=Φ-πθθ微面积1dA 和2dA 之间的辐射换热量为：21221cos cos 2121dA dA rE E b b dA dA ⋅⋅⋅⋅-=Φπθθ）（、 黑体表面1A 和2A 之间的辐射换热量为：⎰⎰⎰⎰⋅⋅⋅⋅-=Φ=Φ122112212122121cos cos A A b b A A dA dA dA dA r E E πθθ）（、、二、角系数（angle factor or view factor ）角系数：表示一表面发出的辐射能中直接落到另一表面上的百分数。

21、X —称为1A 对2A 的角系数，表示1A 辐射的能量落到2A 上的百分数。

12、X —称为2A 对1A 的角系数角系数中的第一个角码指发射体，第二个角码指受射体。