我的笔记(传热学第八章) - 辐射换热的计算
- 格式:docx
- 大小:806.36 KB
- 文档页数:10


第八章1.什么叫黑体?在热辐射理论中为什么要引入这一概念?2.温度均匀得空腔壁面上的小孔具有黑体辐射的特性,那么空腔内部壁面的辐射是否也是黑体辐射?3.试说明,为什么在定义物体的辐射力时要加上"半球空间"及"全部波长"的说明? 4.黑体的辐射能按波长是怎样分布的?光谱吸收力λb E 的单位中分母的"3m "代表什么意义?5.黑体的辐射按空间方向是怎样分布的?定向辐射强度与空间方向无关是否意味着黑体的辐射能在半球空间各方向上是均匀分布的?6.什么叫光谱吸收比?在不同光源的照耀下,物体常呈现不同的颜色,如何解释? 7.对于一般物体,吸收比等于发射率在什么条件下才成立?8,说明灰体的定义以及引入灰体的简化对工程辐射传热计算的意义.9.黑体的辐射具有漫射特性.如何理解从黑体模型(温度均匀的空腔器壁上的小孔)发出的辐射能也具有漫射特性呢? 黑体辐射基本定律8-1、一电炉的电功率为1KW ,炉丝温度为847℃,直径为1mm 。
电炉的效率为0.96。
试确定所需炉丝的最短长度。
解:5.67×341096.010*******⨯=⎪⎭⎫ ⎝⎛+dL π得L=3.61m8-2、直径为1m 的铝制球壳内表面维持在均匀的温度500K ,试计算置于该球壳内的一个实验表面所得到的投入辐射。
内表面发射率的大小对这一数值有否影响?解:由40100⎪⎭⎫⎝⎛=T C E b =35438 W/2m 8-3、把太阳表面近似地看成是T=5800K 的黑体,试确定太阳发出的辐射能中可光所占的百分数。
解:可见光波长范围是0.38~0.76m μ40100⎪⎭⎫⎝⎛=T C E b =64200 W/2m可见光所占份额()()()%87.44001212=---=-λλλλb b b F F F8-4、一炉膛内火焰的平均温度为1500K ,炉墙上有一着火孔。
试计算当着火孔打开时从孔向外辐射的功率。
该辐射能中波长为2m μ的光谱辐射力是多少?哪种波长下的能量最多?解:40100⎪⎭⎫⎝⎛=T C E b =287W/2m ()310/51/1074.912m W e c E T c b ⨯=-=-λλλT =1500K 时,m m 121093.1-⨯=λ8-5、在一空间飞行物的外壳上有一块向阳的漫射面板。






第八章1.什么叫黑体在热辐射理论中为什么要引入这一概念2.温度均匀得空腔壁面上的小孔具有黑体辐射的特性,那么空腔内部壁面的辐射是否也是黑体辐射3.试说明,为什么在定义物体的辐射力时要加上"半球空间"及"全部波长"的说明 4.黑体的辐射能按波长是怎样分布的光谱吸收力λb E 的单位中分母的"3m "代表什么意义5.黑体的辐射按空间方向是怎样分布的定向辐射强度与空间方向无关是否意味着黑体的辐射能在半球空间各方向上是均匀分布的6.什么叫光谱吸收比在不同光源的照耀下,物体常呈现不同的颜色,如何解释 7.对于一般物体,吸收比等于发射率在什么条件下才成立8,说明灰体的定义以及引入灰体的简化对工程辐射传热计算的意义.9.黑体的辐射具有漫射特性.如何理解从黑体模型(温度均匀的空腔器壁上的小孔)发出的辐射能也具有漫射特性呢 黑体辐射基本定律8-1、一电炉的电功率为1KW ,炉丝温度为847℃,直径为1mm 。
电炉的效率为。
试确定所需炉丝的最短长度。
解:×341096.010*******⨯=⎪⎭⎫ ⎝⎛+dL π得L=8-2、直径为1m 的铝制球壳内表面维持在均匀的温度500K ,试计算置于该球壳内的一个实验表面所得到的投入辐射。
内表面发射率的大小对这一数值有否影响解:由40100⎪⎭⎫⎝⎛=T C E b =35438 W/2m 8-3、把太阳表面近似地看成是T=5800K 的黑体,试确定太阳发出的辐射能中可光所占的百分数。
解:可见光波长范围是~m μ40100⎪⎭⎫⎝⎛=T C E b =64200 W/2m可见光所占份额()()()%87.44001212=---=-λλλλb b b F F F8-4、一炉膛内火焰的平均温度为1500K ,炉墙上有一着火孔。
试计算当着火孔打开时从孔向外辐射的功率。
该辐射能中波长为2m μ的光谱辐射力是多少哪种波长下的能量最多解:40100⎪⎭⎫⎝⎛=T C E b =287W/2m ()310/51/1074.912m W e c E T c b ⨯=-=-λλλT =1500K 时,m m 121093.1-⨯=λ8-5、在一空间飞行物的外壳上有一块向阳的漫射面板。


传热学第8章-辐射换热的计算第⼋章辐射换热的计算重点内容:辐射空间热阻及⿊体表⾯间的辐射传热计算分析⽅法。
影响辐射换热的因素:物体表⾯的温度,表⾯形状及尺⼨,表⾯间相对位置,表⾯的辐射及吸收特性。
分析中的假定:物体表⾯⑴为恒温表⾯;⑵为漫-灰表⾯;⑶之间⽓体为透明体。
任何换热均有阻⼒,辐射换热也不例外,但其热阻形式与导热和对流换热有所不同,它包括仅与表⾯间⼏何因素有关的空间热阻和仅与表⾯辐射及吸收特性有关的表⾯热阻两⼤类。
因此,辐射换热计算中最有效、应⽤最普遍的⽅法是封闭空腔⽹络法。
这⾥将分析⿊体表⾯间的辐射换热并引出空间热阻,并讨论如何应⽤封闭空腔⽹络法进⾏⿊体表⾯间辐射换热的分析计算。
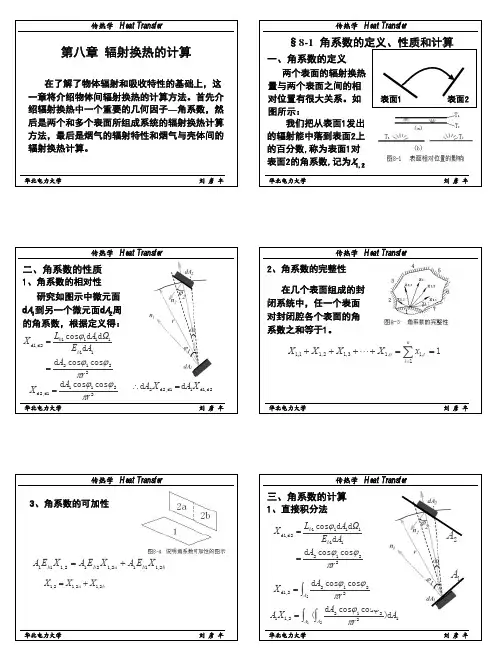
§ 8-1 ⾓系数的定义、性质及计算前⾯讲过,热辐射的发射和吸收均具有空间⽅向特性,因此,表⾯间的辐射换热与表⾯⼏何形状、⼤⼩和各表⾯的相对位置等⼏个因素均有关系,这种因素常⽤⾓系数来考虑。
⾓系数的概念是随着固体表⾯辐射换热计算的出现与发展,于 20 世纪 20 年代提出的,它有很多名称,如,形状因⼦、可视因⼦、交换系数等等。
但叫得最多的是⾓系数。
值得注意的是,⾓系数只对漫射⾯ ( 既漫辐射⼜漫发射 ) 、表⾯的发射辐射和投射辐射均匀的情况下适⽤。
1. ⾓系数的定义在介绍⾓系数概念前,要先温习两个概念. (1)投⼊辐射:单位时间内投射到单位⾯积上的总辐射能,记为 G 。
(2) 有效辐射:单位时间内离开单位⾯积的总辐射能为该表⾯的有效辐射,参见图 8-1 。
包括了⾃⾝的发射辐射 E 和反射辐射 r G 。
G 为投射辐射。
下⾯介绍⾓系数的概念及表达式。
(1) ⾓系数:有两个表⾯,编号为 1 和 2 ,其间充满透明介质,则表⾯ 1 对表⾯ 2 的⾓系数 X 1,2 是:表⾯ 1 直接投射到表⾯2(8—1)同理,也可以定义表⾯ 2 对表⾯ 1 的⾓系数。
从这个概念我们可以得出⾓系数的应⽤是有⼀定限制条件的,即漫射⾯、等温、物性均匀(2) 微元⾯对微元⾯的⾓系数如图8-2所⽰,⿊体微元⾯d A1对微元⾯d A2的⾓系数记图8-1为(8—2b )(3) 微元⾯对⾯的⾓系数(8—3a )微元⾯dA2对⾯(8—3b )(4) ⾯对⾯的⾓系数⾯A 1(8—4a )(8—4b )2. ⾓系数性质根据⾓系数的定义和诸解析式,可导出⾓系数的代数性质。
第八章 辐射换热的计算§8-1 角系数的定义、性质及计算❖ 两个表面之间的辐射换热量与两个表面之间的相对位置有很大关系❖ a 图中两表面无限接近,相互间的换热量最大;b 图中两表面位于同一平面上,相互间的辐射换热量为零。
由图可以看出,两个表面间的相对位置不同时,一个表面发出而落到另一个表面上的辐射能的百分数随之而异,从而影响到换热量。
一. 角系数的定义角系数是进行辐射换热计算时空间热组的主要组成部分。
定义:把表面1发出的辐射能中落到表面2上的百分数称为表面1对表面2的角系数,记为X 1,2。
二. 角系数的性质❖ 研究角系数的性质是用代数法(代数分析法)求解角系数的前提: 假定:(1)所研究的表面是漫射的(2)在所研究表面的不同地点上向外发射的辐射热流密度是均匀的 1、角系数的相对性❖ 一个微元表面到另一个微元表面的角系数11211112,11cos b A dA dA b A I d d dA dA XdA E d θ⋅⋅⋅Ω==⋅由发出的落到上的辐射能由发出的辐射能两微元表面角系数的相对性表达式: 2、角系数的完整性对于由几个表面组成的封闭系统,据能量守衡原理,从任何一个表面发射出的辐射能必全部落到封闭系统的个表面上。
因此,任何一个表面对封闭腔各表面的角系数之间存在下列关系:注:若表面1为非凹表面时,X 1,1 = 0;若表面1为凹表面,X 1,1≠ 0 3、角系数的可加性注意,利用角系数可加性时,只有对角系数符号中第二个角码是可加的,对角系数符号中的第一个角码则不存在类似的关系。
从表面2上发出而落到表面1上的辐射能,等于从表面2的各部分发出而2212,cos cos 21rdA X dA dA πθθ⋅⋅=1221,2,1dA dA dA dA X dA X dA ⋅=⋅1,13,12,11,1=++++n X X X X落到表面1上的辐射能之和。
三、角系数的计算方法 1、直接积分法按角系数的基本定义通过求解多重积分而获得角系数的方法2、代数分析法利用角系数的相对性、完整性及可加性,通过求解代数方程而获得角系数的方法称为代数分析法。
第八章 辐射换热的计算§8-1 角系数的定义、性质及计算两个表面之间的辐射换热量与两个表面之间的相对位置有很大关系a 图中两表面无限接近,相互间的换热量最大;b 图中两表面位于同一平面上,相互间的辐射换热量为零。
由图可以看出,两个表面间的相对位置不同时,一个表面发出而落到另一个表面上的辐射能的百分数随之而异,从而影响到换热量。
一. 角系数的定义角系数是进行辐射换热计算时空间热组的主要组成部分。
定义:把表面1发出的辐射能中落到表面2上的百分数称为表面1对表面2的角系数,记为X 1,2。
二. 角系数的性质研究角系数的性质是用代数法(代数分析法)求解角系数的前提: 假定:(1)所研究的表面是漫射的(2)在所研究表面的不同地点上向外发射的辐射热流密度是均匀的 1、角系数的相对性一个微元表面到另一个微元表面的角系数两微元表面角系数的相对性表达式:11211112,11cos b A dA dA b A I d d dA dA X dA E d θ⋅⋅⋅Ω==⋅由发出的落到上的辐射能由发出的辐射能2212,cos cos 21r dA X dA dA πθθ⋅⋅=1221,2,1dA dA dA dA X dA X dA ⋅=⋅2、角系数的完整性对于由几个表面组成的封闭系统,据能量守衡原理,从任何一个表面发射出的辐射能必全部落到封闭系统的个表面上。
因此,任何一个表面对封闭腔各表面的角系数之间存在下列关系:注:若表面1为非凹表面时,X 1,1 = 0;若表面1为凹表面,X 1,1≠ 0 3、角系数的可加性注意,利用角系数可加性时,只有对角系数符号中第二个角码是可加的,对角系数符号中的第一个角码则不存在类似的关系。
从表面2上发出而落到表面1上的辐射能,等于从表面2的各部分发出而落到表面1上的辐射能之和。
三、角系数的计算方法 1、直接积分法按角系数的基本定义通过求解多重积分而获得角系数的方法2、代数分析法利用角系数的相对性、完整性及可加性,通过求解代数方程而获得角系数的方法称为代数分析法。
3、几何分析法§8-2 被透明介质隔开的两固体表面间的辐射换热 一、两黑体表面组成的封闭腔间的辐射换热计算1,13,12,11,1=++++n X X X X如图8-7所示,黑表面1和2之间的辐射换热量为二、两漫灰表面组成的封闭系统的辐射换热计算 1、有效辐射(1)投入辐射:单位时间内投射到单位面积上的总辐射能,记为G 。
(2)有效辐射:单位时间内离开单位面积的总辐射能为该表面的有效辐射,记为J 。
有效辐射包括:自身射辐射E 、投入辐射被反射辐射的部分考察表面温度均匀、表面辐射特性为常数的表面1(如图8-8所示)。
根据有效辐射的定义,表面1的有效辐射有如下表达式:Gρ的部分的部分到达表面到达表面的热辐射的热辐射发出表面发出表面1221)(212,111,2222,1112,1↓↓-=-=Φb b b b E E X A X E A X E A在表面外能感受到的表面辐射就是有效辐射,它也是用辐射探测仪能测量到的单位表面积上的辐射功率w/m2。
从表面1外部来观察,其能量收支差额应等于有效辐射J1 与投入辐射G1之差,即从表面内部观察,该表面与外界的辐射换热量应为: 上两式联立,消去G 1,得到J 与表面净辐射换热量之间的关系:注意:式中的各个量均是对同一表面而言的,而且以向外界的净放热量为正值。
2、两灰表面组成的封闭腔的辐射换热定义系统黑度(或称为系统发射率)三种特殊情形(1) 表面1为凸面或平面,此时,X 1,2=1,于是(2) 表面积A 1比表面积A 2小得多,即A 1/A 2→ 0 于是111111111G E G E G J q b αεα-=-=-=111qE G α=-⇒⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-+=1111112212,112,1εεεA A X X s ⎪⎪⎭⎫ ⎝⎛-+=11112211εεεA A s 1εε=s(3) 表面积A 1与表面积A 2相当,即A 1/A 2→ 1 于是 举例(1) 两平行平壁间的辐射换热(2) 空腔与内包壁间的辐射换热讨论练习:某房间吊装一水银温度计读数为15,已知温度计头部发射率(黑度)为0.9,头部与室内空气间的对流换热系数为20,墙表面温度为10,求该温度计的测量误差。
如何减小测量误差?12A A A==1221X X =,,1221X X =,,111121-+=εεεs ⎪⎪⎭⎫ ⎝⎛-++⎪⎪⎭⎫ ⎝⎛--=Φ11111)(2212,112112,1εεA A X E E A b b ⎪⎪⎭⎫ ⎝⎛-+=11112211εεεA A s 1121,21122()111b b A E E A A εε-Φ=⎛⎫+- ⎪⎝⎭§8-3 多表面系统辐射换热的计算 1.势差与热阻 据有效辐射的计算式又据两个表面的净换热量为利用上述两个单元格电路,可以容易地画出组成封闭系统的两个灰体表面间辐射换热的等效网络,如图所示。
根据等效网络,可以立即写出换热量计算式:这种把辐射热阻比拟成等效的电阻从而通过等效的网络图来求解辐射换热的方法成为辐射换热的网络法。
应用网络法求解多表面封闭系统辐射换热问题的步骤:(1)画出等效的网络图。
(2)列出节点的电流方程(3)求解上述代数方程得出节点电势。
(4)按公式 确定每一个表面的净辐射换热量。
1,2111,2222,111,212()A J X A J X A X J J Φ=-=-12121111,222111b b E E A A X A εεεε-Φ=--++1bi iii i i E J A εε-Φ=-2.网络法的应用举例以图(a)所示的三表面的辐射换热问题为例画出图(b)的等效网络图3. 两个重要特例a 有一个表面为黑体。
黑体的表面热阻为零。
其网络图见图8-14a。
b 有一个表面绝热,即该表面的净换热量为零。
其网络图见图8-14b 和8-14c,§8-4 辐射换热的强化与削弱强化辐射换热的主要途径有两种:(1) 增加发射率; (2) 增加角系数。
削弱辐射换热的主要途径有三种:(1) 降低发射率; (2) 降低角系数; (3) 加入遮热板。
所谓遮热板,是指插入两个辐射换热表面之间以削弱辐射换热的薄板,其实插入遮热板相当于降低了表面发射率。
本节主要讨论这种削弱辐射换热的方式。
辐射表面和金属板的温度、吸收比如图所示。
为讨论方便,设平板和金属薄板都是灰体,并且稳态时有:可见,与没有遮热板时相比,辐射换热量减小了一半。
§8-5 气体辐射本节将简要介绍气体辐射的特点、换热过程及其处理方法。
在工程中常见的温度范围内 ,CO2和 H2O 具有很强的吸收和发射热辐射的本领,而其他的气体则较弱,这也是本节采用这两种气体作为例子的原因。
1 气体辐射的特点(1) 气体辐射对波长具有选择性。
它只在某谱带内具有发射和吸收辐射的本领,而对于其他谱带则呈现透明状态。
如图8-16所示。
(2) 气体的辐射和吸收是在整个容积中进行的,因而,气体的发射率和吸收比还与容器的形状和容积大小有关。
⎪⎪⎩⎪⎪⎨⎧==-=⇒-=-=2,33,12,1212,1232,3313,1)(21)()(q q q E E q E E q E E q b b s b b s b b s εεε2 气体辐射的衰减规律当热辐射进入吸收性气体层时,因沿途被气体吸收而衰减。
为了考察辐射在气体内的衰减规律,如图8-17所示,我们假设投射到气体界面 x = 0 处的光谱辐射强度为Lo ,通过一段距离x 后,该辐射变为Lx 。
再通过微元气体层 d x 后,其衰减量为dLx 。
理论上已经证明,dLx/Lx 与行程 d x 成正比,设比例系数为K ,则有进行积分可得(1)式中,负号表示吸收,K 为光谱衰减系数,m -1,它取决于其体的种类、密度和波长.(2)式(Beer 定律)中,s 是辐射通过的路程长度,常称之为射线程长。
从上式可知,热辐射在气体内呈指数规律衰减。
3 气体辐射的光谱吸收比、光谱发射率 对于气体,反射率为零4 气体的发射率1)确定气体的发射率2)利用 计算气体的发射辐射。
(还与气体的温度和气体得分压力有关)与射线程长s 关系密切,而s取决s K s eL L λλλ-=0,,x K L L x xd d ,,λλλ-=4g g T A σε=Φgε于气体容积的形状和尺寸。
如图8-18所示。
3)为了使射线程长均匀,人们引入了当量半球的概念,其半径就是等效的射线程长,见图8-19所示。
在缺少资料的情况下,任意几个形状气体对整个包壁的平均射线程长可按下式计算:式中,V 为气体容积,m 3;A 为包壁面积,m 2。
图8-18 气体对不同地区的辐射图8-19 半球内气体对球心的辐射5 气体的吸收比在其体发射率和吸收比确定后,气体与黑体外壳之间的辐射换热公式为:AV s 6.3=αααα∆-+=**2222CO CO O H O H g C C wb g g b g E E q ,,αε-=。