期末复习(一)复数与导数(教师)
- 格式:doc
- 大小:1.09 MB
- 文档页数:11

复数导数知识点总结1. 复数导数的基本概念在微积分中,导数描述了函数在某一点的变化率。
对于一元函数而言,导数是函数在某一点的斜率。
而对于多元函数(即含有多个自变量的函数),我们就需要引入复数导数来描述其变化率。
复数导数是一个复数,它包括了函数在所有自变量方向上的变化率信息。
对于一个多元函数f(x1, x2,...,xn),它的复数导数可以表示为:∂f/∂x1 * i + ∂f/∂x2 * j + ... + ∂f/∂xn * k其中,∂f/∂x1、∂f/∂x2、...、∂f/∂xn 分别表示函数f在x1、x2、...、xn方向上的偏导数。
i、j、k分别是三维空间中的基本单位向量。
这样,函数f在某一点的复数导数就包含了其在所有自变量方向上的变化率信息。
2. 复数导数的性质与一元函数的导数类似,复数导数也具有一些基本性质。
其中包括线性性、链式法则、乘积法则、商规法则、复合函数求导、隐函数求导等。
这些性质是复数导数计算和应用的基础,对于求解复杂问题至关重要。
3. 复数导数的计算方法在实际应用中,我们经常需要计算多元函数的复数导数。
复数导数的计算方法包括了偏导数、全导数、梯度、方向导数等。
偏导数是多元函数在某一点上的各个自变量方向上的导数,它是复数导数的基本成分。
全导数是多元函数在某一点上的所有自变量方向上的导数,它由偏导数组成。
梯度是多元函数在某一点上最大的变化率以及变化的方向,它是函数的复数导数。
方向导数是多元函数在某一点上沿着某一给定方向的导数,它可以用梯度的方向与给定方向的夹角来表示。
这些方法为我们计算多元函数的复数导数提供了有效的工具。
4. 复数导数的应用复数导数在物理学、工程学、经济学等领域有着广泛的应用。
在物理学中,复数导数可以用来描述质点在空间中的运动轨迹,以及场和电路中的变化率。
在工程学中,复数导数可以用来描述材料的变形、结构的变化以及系统的响应。
在经济学中,复数导数可以用来描述市场的供求关系以及货币的流动。

数学复数高考知识点总结一、复数的概念和表示方法1.1 复数的定义复数是由实数和虚数构成的数,一般形式为a+bi,其中a为实部,bi为虚部,i为虚数单位,满足i²=-1。
1.2 复数的表示方法复数可以用直角坐标系和极坐标系表示。
在直角坐标系中,复数z=a+bi可以表示为有序数(a,b),其中a为实部,b为虚部;在极坐标系中,复数z=a+bi可以表示为z=r(cosθ+isinθ),其中r为模,θ为幅角。
1.3 复数的加减法复数的加减法与实数的加减法类似,实部与实部相加减,虚部与虚部相加减。
1.4 复数的乘法复数的乘法可利用分配律和i²=-1进行计算,即(a+bi)×(c+di)=ac+adi+bci+bdi²=(ac-bd)+(ad+bc)i。
1.5 复数的除法复数的除法需要将除数与被除数同时乘以共轭复数,然后利用分配律进行计算。
1.6 复数的共轭复数z=a+bi的共轭是z的实部不变,虚部取负数,即z的共轭为a-bi。
1.7 复数的模和幅角复数z=a+bi的模是z距离原点的长度,又可以表示为|z|=√(a²+b²);复数z的幅角是z与正实轴之间的夹角,一般取在-π<θ≤π的区间内。
1.8 二次根式对于复数z=a+bi,其二次根式为±√z=±(√r)(cos(θ/2)+isin(θ/2)),其中r为z的模,θ为z 的幅角。
二、复数的应用2.1 复数的几何意义复数可以表示平面上的点,实部代表横坐标,虚部代表纵坐标;复数的模代表点到原点的距离,复数的幅角代表点与正实轴之间的夹角。
2.2 解析式解析式是指利用复数形式的代数式表示函数值,在一些复杂的数学问题中,可以利用复数的解析式简化计算。
2.3 需解方程部分方程的解需要引入复数,如一元二次方程的解可能为复数,解方程时需考虑复数根的情况。
2.4 矩阵计算在一些特定矩阵的计算中,可能出现复数,需要利用复数的运算规则进行计算。

复数的知识点总结一、复数概述复数是数学中的一个重要概念,它由实数和虚数部分组成。
虚数单位i定义为i² = -1,其中i是一个虚数。
复数可表示为a + bi的形式,其中a是实数部分,bi 是虚数部分。
二、复数运算1. 复数加法和减法复数的加法和减法按照实部和虚部分别进行运算,即将实部相加或相减,并将虚部相加或相减。
例如,给定复数z₁ = a₁ + b₁i和z₂ = a₂ + b₂i,它们的和可以表示为z₁ + z₂ = (a₁ + a₂) + (b₁ + b₂)i,差可以表示为z₁ - z₂ = (a₁ - a₂) + (b₁ - b₂)i。
2. 复数乘法复数乘法采用分配律和虚数单位的平方等于-1的性质进行计算。
例如,给定复数z₁ = a₁ + b₁i和z₂ = a₂ + b₂i,它们的乘积可以表示为z₁ * z₂ = (a₁ * a₂ - b₁ * b₂) + (a₁ * b₂ + a₂ * b₁)i。
3. 复数除法复数除法是将分子和分母同乘以分母的共轭,并利用虚数单位的平方等于-1的性质进行计算。
例如,给定复数z₁ = a₁ + b₁i和z₂ = a₂ + b₂i,它们的除法可以表示为z₁ / z₂ = ((a₁ * a₂ + b₁ * b₂) / (a₂² + b₂²)) + ((a₂ * b₁ - a₁ * b₂) / (a₂² + b₂²))i。
三、复数的共轭和模1. 复数的共轭复数的共轭是保持实部相同而虚部变号的操作。
复数a + bi的共轭可以表示为a - bi,其中a是实部,b是虚部。
2. 复数的模复数的模是复数到原点的距离,可以用勾股定理计算。
复数a + bi的模可以表示为√(a² + b²)。
四、复数的指数形式和三角形式1. 复数的指数形式复数可以用指数形式表示为re^(iθ),其中r是模,θ是辐角。
2. 复数的三角形式复数的三角形式是指使用三角函数表示复数。
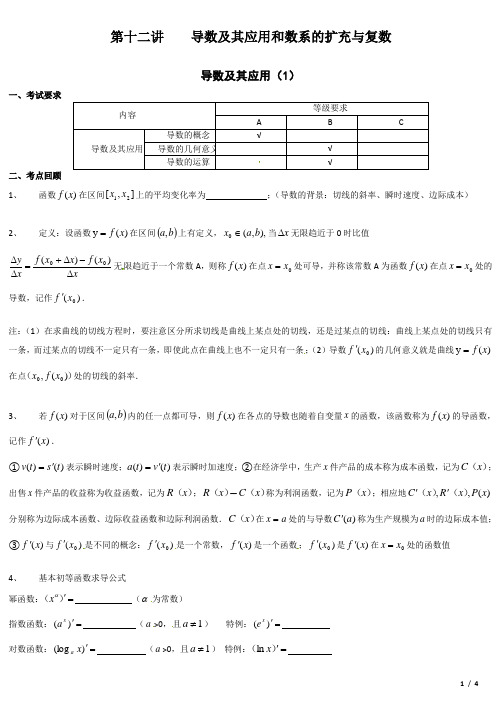
第十二讲 导数及其应用和数系的扩充与复数导数及其应用(1)一、考试要求内容等级要求A B C 导数及其应用导数的概念√ 导数的几何意义 √ 导数的运算√二、考点回顾 1、 函数)(x f 在区间],[21x x 上的平均变化率为 ;(导数的背景:切线的斜率、瞬时速度、边际成本)2、定义:设函数)(y x f =在区间()b a ,上有定义,),,(0b a x ∈当x ∆无限趋近于0时比值xx f x x f x y ∆-∆+=∆∆)()(00无限趋近于一个常数A ,则称)(x f 在点0x x =处可导,并称该常数A 为函数)(x f 在点0x x =处的导数,记作)(0x f '.注:(1)在求曲线的切线方程时,要注意区分所求切线是曲线上某点处的切线,还是过某点的切线:曲线上某点处的切线只有一条,而过某点的切线不一定只有一条,即使此点在曲线上也不一定只有一条;(2)导数)(0x f '的几何意义就是曲线)(y x f =在点)()(,00x f x 处的切线的斜率.3、若)(x f 对于区间()b a ,内的任一点都可导,则)(x f 在各点的导数也随着自变量x 的函数,该函数称为)(x f 的导函数,记作)(x f '.①)()(t s t v '=表示瞬时速度;)()(t v t a '=表示瞬时加速度;②在经济学中,生产x 件产品的成本称为成本函数,记为)(x C ;出售x 件产品的收益称为收益函数,记为)(x R ;)(x R —)(x C 称为利润函数,记为)(x P ;相应地)(,,x P x R x C )()(''分别称为边际成本函数、边际收益函数和边际利润函数.)(x C 在a x =处的与导数)(a C '称为生产规模为a 时的边际成本值;③)(x f '与)(0x f '是不同的概念:)(0x f '是一个常数,)(x f '是一个函数;)(0x f '是)(x f '在0x x =处的函数值 4、基本初等函数求导公式幂函数:=')(αx (α为常数) 指数函数:=')(xa (a >0,且1≠a ) 特例:=')(xe对数函数:=')(log x a (a >0,且1≠a ) 特例:=')(x ln正弦函数:=')(sin x 余弦函数:=')(cos x导数及其应用(2)一、考试要求内容等级要求AB C导数及其 应用 导数的运算√ 利用导数研究函数的单调性和极值√ 导数在实际问题中的应用√二、考点回顾(1)导数与函数的单调性:若()0f x '>,则()f x 为增函数;若()0f x '<,则()f x 为减函数;若()0f x '=恒成立,则()f x 为常数函数;若()f x '的符号不确定,则()f x 不是单调函数.(2)利用导数求函数单调区间的步骤:①求()f x ';②求方程()0f x '=的根,设为12,,n x x x ;③12,,n x x x 将给定区间分成n+1个子区间,再在每一个子区间内判断()f x '的符号,由此确定每一子区间的单调性.(3)求函数()y f x =在某个区间上的极值的步骤:(i )求导数()f x ';(ii )求方程()0f x '=的根0x ;(iii )检查()f x '在方程()0f x '=的根0x 的左右的符号:”左正右负”⇔()f x 在0x 处取极大值;”左负右正”⇔()f x 在0x 处取极小值.特别提醒:①0x 是极值点的充要条件是0x 点两侧导数异号,而不仅是()0f x '=0,()0f x '=0是0x 为极值点的必要而不充分条件.②给出函数极大(小)值的条件,一定要既考虑0()0f x '=,又要考虑检验”左正右负”(“左负右正”)的转化,否则条件没有用完,这一点一定要切记!(4)求函数()y f x =在[,a b ]上的最大值与最小值的步骤:①求函数()y f x =在(,a b )内的极值;②将()y f x =的各极值与()f a ,()f b 比较,其中最大的一个为最大值,最小的一个为最小值.特别注意:①利用导数研究函数的单调性与最值(极值)时,要注意列表!②要善于应用函数的导数,考察函数单调性、最值(极值),研究函数的性态,数形结合解决方程不等式等相关问题.(5)导数的三大应用:①求斜率:在曲线的某点有切线,则求导后把横坐标代进去,则为其切线的斜率; ②有关极值:就是某处有极值,则把它代入其导数,则为0;③单调性的判断: ()0f x '>,)(x f 单调递增;()0f x '<,)(x f 单调递减,和一些常见的导数的求法.数系的扩充与复数一. 复数的定义1. 复数的定义:形如的数叫复数,叫复数的实部,叫复数的虚部全体复数所成的集合叫做复数集,用字母C表示。

欢迎阅读、复数的概念(1) 它的平方等于1,即i 21 ;(2) 实数可以与它进行四则运算,进行四则运算时,原有加、乘运算律仍然成立. (3) i 与一1的关系:i 就是1的一个平方根,即方程x 2 1的一个根,方程x 2 1的另一个根是-i .(4) i 的周期性:・4n 34nii , i 1 .通常用字母z 表示,即z a bi(a ,b R),把复数表示成a bi 的形式,叫做复数的代 数形式.对于复数a bi(a ,b R),当且仅当b 0时,复数a bi (a ,b R)是实数a ;当b 0时,复数z a bi 叫做虚数;当a 0且b 0时,z bi 叫做纯虚数;当且仅当a b 0时, z 就是实数0 6.复数集与其它数集之间的关系:N 荷Z Q 荷R C知识内容1. 虚数单位i:2. 数系的扩充:复数bi实数a(b 0)纯虚数bi(a虚数 a bi(b 0)- '非纯虚数a0)bi(a 0)3. 复数的定义:形如a bi(a ,b R)的数叫复数,a 叫复数的实部,b 叫复数的虚部.全体复数所成的集合叫做复数集,用字母C 表示 4. 复数的代数形式:5. 复数与实数、虚数、纯虚数及0的关系:欢迎阅读7. 两个复数相等的定义:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等•这就是说, 如果 a , a ,b, d , c , d R ,那么 a bi c di a c , b d二、复数的几何意义1. 复平面、实轴、虚轴:复数z a bi(a,b R)与有序实数对a ,b 是一一对应关系.建立一一对应的关系.点Z 的横坐标是a ,纵坐标是b ,复数z a bi(a,b R)可用点Z a ,b 表示,这个建立了直角坐标系来表示复数的平面叫做复平面,也叫高斯平面, 叫做虚轴.实轴上的点都表示实数.2..对于虚轴上的点要除原点外,因为原点对应的有序实数对为数是z 0 0i 0表示是实数.除了原点外,虚轴上的点都表示纯虚数.这就是复数的一种几何意义.也就是复数的另一种表示方法,即几何表示方法.三、复数的四则运算1. 复数Z i 与Z 2的和的定义:2. 复数z ,与z 2的差的定义:3. 复数的加法运算满足交换律 :乙 Z 2 Z 2 乙4. 复数的加法运算满足结合律 :(Z zj Z 3Z (Z 2 Z 3)5. 乘法运算规则:'l1 \ \ ;设 z 1 a bi , z 2 c di (a 、 b 、c 、dR )是任意两个复数,那么它们的积z 1z 2 a bic diac bdbc ad i其实就是把两个复数相乘,类似两个多项式相乘,在所得的结果中把 i 2换成1,并且把实部与虚部分别合并.两个复数的积仍然是一个复数. 6. 乘法运算律:(1) Z i Z 2 Z 3 Z 1Z 2 Tz (2) (z zj Z 3 z 亿 Z 3) (3) Z 1 Z 2 Z 3 Z 1Z 2 Z 1Z 3x 轴叫做实轴,y 轴0,0,它所确定的复7.复数除法定义:欢迎阅读记为:(a bi) c di 或者 c di 8. 除法运算规则:设复数 a bi (a 、b R ),除以 c di(c ,d R),其商为 x yi ( x 、y R ), 即(a bi) c di x yi ■/ x yi c di cx dy dx cy icx dy dx cy i a bi.((a bi) c di ac bd bc ad.--------------- ------------------- i2 . 22 . 2 1c d c d点评:①是常规方法,②是利用初中我们学习的化简无理分式时, 都是采用的分母有理化思想方法,而复数c di 与复数c di ,相当于我们初中学习的.3 「2的对偶式\3 2,它们之积2 2为1是有理数,而 c di c di c d 是正实数•所以可以分母实数化•把这种方法叫做分 母实数化法.ac 由复数相等定义可知 cx dx dy a ,解这个方程组,得cy by 于是有:(abi) c diac bd bc ad ic 2d 2c 2d 2i②利用c di cdi 2 c d 2于是将a di的分母有理化得原式a bi (a bi)(c di) [ac bi ( di)](bc ad)ic di(cdi)(c di)2cd(ac bd) (bc ad)iac bd bc ad .2 c 2 d2 2c d 2 ci . dx bdc 2d 2 bcad , c 2 d 2满足c di x yia bi 的复数 x yi (x 、yR )叫复数a bi 除以复数c di 的商,9. 共轭复数:当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数。

高中数学导数和复数教案一、导数1. 定义:导数是函数在某一点处的变化率,表示函数在该点的斜率。
2. 导数的符号表示:函数 f(x) 在点 x 处的导数表示为 f'(x),读作 f prime of x。
3. 导数的计算方法:- 利用定义法:导数 f'(x) = lim(h->0) [f(x+h) - f(x)] / h- 利用基本导数法则:常数规则、幂规则、指数函数规则、三角函数规则等- 利用求导法则:和差法则、乘法法则、商法则、链式法则等4. 导数的应用:求函数的极值、切线、凹凸性以及函数图像的特征等。
二、复数1. 复数的定义:复数是由实部和虚部组成的数,形式为 a + bi,其中 a 和 b 都是实数,i 是虚数单位,满足 i^2 = -1。
2. 复数的运算:- 复数的加减法:(a + bi) + (c + di) = (a + c) + (b + d)i- 复数的乘法:(a + bi)(c + di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad + bc)i- 复数的除法:(a + bi) / (c + di) = (ac + bd) / (c^2 + d^2) + (bc - ad)i / (c^2 + d^2)3. 复数的共轭:复数 a + bi 的共轭是 a - bi,记作 a - bi。
4. 复数的模和幅角:复数 a + bi 的模是 |a + bi| = sqrt(a^2 + b^2),幅角是 arg(a + bi) = arctan(b/a)。
5. 复数的指数形式:复数 a + bi 可以表示为re^(iθ) 的指数形式,其中 r 为模,θ 为幅角。
教学目标:掌握导数的概念与计算方法,了解导数在函数中的应用;理解复数的定义和运算规则,掌握复数的模、幅角和指数形式。
教学过程:1. 导数的概念和计算方法的介绍,包括常见导数的基本规则和应用。
导 数 知识要点1. 导数(导函数的简称)的定义:设0x 是函数)(x f y =定义域的一点,如果自变量x 在0x 处有增量x ∆,则函数值y 也引起相应的增量)()(00x f x x f y -∆+=∆;比值xx f x x f x y ∆-∆+=∆∆)()(00称为函数)(x f y =在点0x 到x x ∆+0之间的平均变化率;如果极限x x f x x f x yx x ∆-∆+=∆∆→∆→∆)()(limlim0000存在,则称函数)(x f y =在点0x 处可导,并把这个极限叫做)(x f y =在0x 处的导数,记作)(0'x f 或0|'x x y =,即)(0'x f =xx f x x f x yx x ∆-∆+=∆∆→∆→∆)()(limlim 0000. 注:①x ∆是增量,我们也称为“改变量”,因为x ∆可正,可负,但不为零.②以知函数)(x f y =定义域为A ,)('x f y =的定义域为B ,则A 与B 关系为B A ⊇. 2. 函数)(x f y =在点0x 处连续与点0x 处可导的关系:⑴函数)(x f y =在点0x 处连续是)(x f y =在点0x 处可导的必要不充分条件. 可以证明,如果)(x f y =在点0x 处可导,那么)(x f y =点0x 处连续. 事实上,令x x x ∆+=0,则0x x →相当于0→∆x .于是)]()()([lim )(lim )(lim 000000x f x f x x f x x f x f x x x x +-+=∆+=→∆→∆→).()(0)()(lim lim )()(lim )]()()([lim 000'0000000000x f x f x f x f xx f x x f x f x x x f x x f x x x x =+⋅=+⋅∆-∆+=+∆⋅∆-∆+=→∆→∆→∆→∆⑵如果)(x f y =点0x 处连续,那么)(x f y =在点0x 处可导,是不成立的. 例:||)(x x f =在点00=x 处连续,但在点00=x 处不可导,因为xx x y ∆∆=∆∆||,当x ∆>0时,1=∆∆x y ;当x ∆<0时,1-=∆∆xy ,故x yx ∆∆→∆0lim不存在. 注:①可导的奇函数函数其导函数为偶函数.②可导的偶函数函数其导函数为奇函数.3. 导数的几何意义:函数)(x f y =在点0x 处的导数的几何意义就是曲线)(x f y =在点))(,(0x f x 处的切线的斜率,也就是说,曲线)(x f y =在点P ))(,(0x f x 处的切线的斜率是)(0'x f ,切线方程为).)((0'0x x x f y y -=-4. 求导数的四则运算法则:''')(v u v u ±=±)(...)()()(...)()(''2'1'21x f x f x f y x f x f x f y n n +++=⇒+++=⇒''''''')()(cv cv v c cv u v vu uv =+=⇒+=(c 为常数))0(2'''≠-=⎪⎭⎫⎝⎛v v u v vu v u 注:①v u ,必须是可导函数.②若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导. 例如:设x x x f 2sin 2)(+=,xx x g 2cos )(-=,则)(),(x g x f 在0=x 处均不可导,但它们和=+)()(x g x fx x cos sin +在0=x 处均可导.5. 复合函数的求导法则:)()())(('''x u f x f x ϕϕ=或x u x u y y '''⋅= 复合函数的求导法则可推广到多个中间变量的情形.6. 函数单调性:⑴函数单调性的判定方法:设函数)(x f y =在某个区间内可导,如果)('x f >0,则)(x f y =为增函数;如果)('x f <0,则)(x f y =为减函数. ⑵常数的判定方法;如果函数)(x f y =在区间I 内恒有)('x f =0,则)(x f y =为常数.注:①0)( x f 是f (x )递增的充分条件,但不是必要条件,如32x y =在),(+∞-∞上并不是都有0)( x f ,有一个点例外即x =0时f (x ) = 0,同样0)( x f 是f (x )递减的充分非必要条件.②一般地,如果f (x )在某区间内有限个点处为零,在其余各点均为正(或负),那么f (x )在该区间上仍旧是单调增加(或单调减少)的. 7. 极值的判别方法:(极值是在0x 附近所有的点,都有)(x f <)(0x f ,则)(0x f 是函数)(x f 的极大值,极小值同理)当函数)(x f 在点0x 处连续时,①如果在0x 附近的左侧)('x f >0,右侧)('x f <0,那么)(0x f 是极大值; ②如果在0x 附近的左侧)('x f <0,右侧)('x f >0,那么)(0x f 是极小值.也就是说0x 是极值点的充分条件是0x 点两侧导数异号,而不是)('x f =0①. 此外,函数不可导的点也可能是函数的极值点②. 当然,极值是一个局部概念,极值点的大小关系是不确定的,即有可能极大值比极小值小(函数在某一点附近的点不同).注①: 若点0x 是可导函数)(x f 的极值点,则)('x f =0. 但反过来不一定成立. 对于可导函数,其一点0x 是极值点的必要条件是若函数在该点可导,则导数值为零. 例如:函数3)(x x f y ==,0=x 使)('x f =0,但0=x 不是极值点.②例如:函数||)(x x f y ==,在点0=x 处不可导,但点0=x 是函数的极小值点.8. 极值与最值的区别:极值是在局部对函数值进行比较,最值是在整体区间上对函数值进行比较.注:函数的极值点一定有意义. 9. 几种常见的函数导数:I.0'=C (C 为常数) x x cos )(sin '= 2'11)(arcsin xx -=1')(-=n n nx x (R n ∈) x x sin )(cos '-= 2'11)(arccos xx --=II. x x 1)(ln '=e x x a a log 1)(log '= 11)(arctan 2'+=x x x x e e =')( a a a x x ln )('= 11)cot (2'+-=x x arcIII. 求导的常见方法: ①常用结论:xx 1|)|(ln '=. ②形如))...()((21n a x a x a x y ---=或))...()(())...()((2121n n b x b x b x a x a x a x y ------=两边同取自然对数,可转化求代数和形式.③无理函数或形如x x y =这类函数,如x x y =取自然对数之后可变形为x x y ln ln =,对两边求导可得xx x x x y y x y y x x x y y +=⇒+=⇒⋅+=ln ln 1ln '''复 数 知识要点1. ⑴复数的单位为i ,它的平方等于-1,即1i 2-=. ⑵复数及其相关概念:① 复数—形如a + b i 的数(其中R b a ∈,); ② 实数—当b = 0时的复数a + b i ,即a ; ③ 虚数—当0≠b 时的复数a + b i ;④ 纯虚数—当a = 0且0≠b 时的复数a + b i ,即b i.⑤ 复数a + b i 的实部与虚部—a 叫做复数的实部,b 叫做虚部(注意a ,b 都是实数) ⑥ 复数集C —全体复数的集合,一般用字母C 表示. ⑶两个复数相等的定义:00==⇔=+∈==⇔+=+b a bi a R d c b a d b c a di c bi a )特别地,,,,(其中,且. ⑷两个复数,如果不全是实数,就不能比较大小.注:①若21,z z 为复数,则 1若021 z z +,则21z z - .(×)[21,z z 为复数,而不是实数] 2若21z z ,则021 z z -.(√)②若C c b a ∈,,,则0)()()(222=-+-+-a c c b b a 是c b a ==的必要不充分条件.(当22)(i b a =-,0)(,1)(22=-=-a c c b 时,上式成立)2. ⑴复平面内的两点间距离公式:21z z d -=.其中21z z ,是复平面内的两点21z z 和所对应的复数,21z z d 和表示间的距离. 由上可得:复平面内以0z 为圆心,r 为半径的圆的复数方程:)(00 r r z z =-. ⑵曲线方程的复数形式:①00z r z z 表示以=-为圆心,r 为半径的圆的方程. ②21z z z z -=-表示线段21z z 的垂直平分线的方程.③212121202Z Z z z a a a z z z z ,)表示以且( =-+-为焦点,长半轴长为a 的椭圆的方程(若212z z a =,此方程表示线段21Z Z ,).④),(2121202z z a a z z z z =---表示以21Z Z ,为焦点,实半轴长为a 的双曲线方程(若212z z a =,此方程表示两条射线). ⑶绝对值不等式:设21z z ,是不等于零的复数,则①212121z z z z z z +≤+≤-.左边取等号的条件是),且(012 λλλR z z ∈=,右边取等号的条件是),(012 λλλR z z ∈=. ②212121z z z z z z +≤-≤-.左边取等号的条件是),(012 λλλR z z ∈=,右边取等号的条件是),(012 λλλR z z ∈=. 注:n n n A A A A A A A A A A 11433221=++++- . 3. 共轭复数的性质:z z = 2121z z z z +=+a z z 2=+,i 2b z z =-(=z a + b i ) 22||||z z z z ==⋅2121z z z z -=- 2121z z z z ⋅=⋅2121zz z z =⎪⎪⎭⎫ ⎝⎛(02≠z ) n n z z )(= 注:两个共轭复数之差是纯虚数. (×)[之差可能为零,此时两个复数是相等的] 4 ⑴①复数的乘方:)(...+∈⋅⋅=N n z z z z znn②对任何z ,21,z z C ∈及+∈N n m ,有 ③n n n n m n m n m n mz z z z z z z z z2121)(,)(,⋅=⋅==⋅⋅+注:①以上结论不能拓展到分数指数幂的形式,否则会得到荒谬的结果,如1,142=-=i i 若由11)(212142===i i 就会得到11=-的错误结论.②在实数集成立的2||x x =. 当x 为虚数时,2||x x ≠,所以复数集内解方程不能采用两边平方法.⑵常用的结论:1,,1,,143424142=-=-==-=+++n n n n i i i i i i i)(,0321Z n i i i i n n n n ∈=++++++i iii i i i i -=+-=-+±=±11,11,2)1(2 若ω是1的立方虚数根,即i 2321±-=ω,则 . 5. ⑴复数z 是实数及纯虚数的充要条件:)(0,01,1,,121223Z n n n n ∈=++=++===++ωωωωωωωωωω①z z R z =⇔∈.②若0≠z ,z 是纯虚数0=+⇔z z .⑵模相等且方向相同的向量,不管它的起点在哪里,都认为是相等的,而相等的向量表示同一复数. 特例:零向量的方向是任意的,其模为零. 注:||||z z =.6. ⑴复数的三角形式:)sin (cos θθi r z +=.辐角主值:θ适合于0≤θ<π2的值,记作z arg . 注:①z 为零时,z arg 可取)2,0[π内任意值. ②辐角是多值的,都相差2π的整数倍. ③设,+∈R a 则πππ23)arg(,2arg ,)arg(,0arg =-==-=ai ai a a . ⑵复数的代数形式与三角形式的互化: )sin (cos θθi r bi a +=+,22b a r +=,rb r a ==θθsin ,cos . ⑶几类三角式的标准形式:)]sin()[cos()sin (cos θθθϑ-+-=-i r i r)]sin()[cos()sin (cos θπθπθθ+++=+-i r i r)]sin()[cos()sin cos (θπθπθθ-+-=+-i r i r)]2sin()2[cos()cos (sin θπθπθθ-+-=+i r i r7. 复数集中解一元二次方程:在复数集内解关于x 的一元二次方程)0(02≠=++a c bx ax 时,应注意下述问题: ①当R c b a ∈,,时,若∆>0,则有二不等实数根ab x 22,1∆±-=;若∆=0,则有二相等实数根abx 22,1-=;若∆<0,则有二相等复数根a i b x 2||2,1∆±-=(2,1x 为共轭复数).②当c b a ,,不全为实数时,不能用∆方程根的情况.③不论c b a ,,为何复数,都可用求根公式求根,并且韦达定理也成立. 8. 复数的三角形式运算:)]sin()[cos()sin (cos )sin (cos 212121222211θθθθθθθθ+++=+⋅+i r r i r i r)]sin()[cos()sin (cos )sin (cos 212121222211θθθθθθθθ-+-=++i r r i r i r棣莫弗定理:)sin (cos )]sin (cos [θθθθn i n r i r n n +=+。
数学导数复数知识点总结在本文中,我们将对导数的复数知识点进行详细总结,包括复数的定义、复数函数的导数、复数函数的全微分与全导数,以及一些相关的应用和例题。
一、导数的复数定义1.1 复数的定义在正式介绍导数的复数知识点之前,我们有必要先来回顾一下复数的概念。
复数是由一个实数部分与一个虚数部分组成的数,通常表示为 a+bi,其中a和b都是实数,而i是虚数单位,满足i²=-1。
因此,复数可以看作是实数与虚数的结合,是一个具有一定规律和性质的数。
而复数函数就是以复数为自变量和因变量的函数,例如f(z)=z²+1,其中z是复数。
1.2 复数的运算对于复数的运算,我们可以通过实部和虚部的运算,实现加减乘除等操作。
例如,对于复数z1=a1+b1i和z2=a2+b2i,它们的和、差、积、商分别为z1+z2=(a1+a2)+(b1+b2)i,z1-z2=(a1-a2)+(b1-b2)i,z1*z2=(a1a2-b1b2)+(a1b2+a2b1)i,z1/z2=(a1a2+b1b2)/(a2²+b2²)+((a2b1-a1b2)/(a2²+b2²))i。
通过这些运算,我们可以得到两个复数的和、差、积、商,这为后续导数的复数知识点打下了基础。
1.3 导数的复数定义在实数情况下,我们知道导数的定义是函数在某一点的极限。
而对于复数函数,我们同样可以根据实数的导数定义来给出复数函数导数的定义。
设f(z)是z的一个函数,如果存在复数w,使得对于任意给定的ε>0,存在另一个正数δ,当|z-z0|<δ时,|f(z)-w|<ε成立,则称f(z)在z=z0处有极限w,记作limz→z0f(z)=w。
如果函数f(z)在z0处有极限w,且对于z0的任何邻域内的点z≠z0,都有limz→z0(f(z)-f(z0))/(z-z0)=w,则称f(z)在z0处可导,并称w是f(z)在z0处的导数。
复数的考点知识点归纳总结复数的考点知识点归纳总结复数是基础数学中的重要概念,广泛应用于数学、物理、工程等领域。
掌握复数的概念、性质和运算规则对于建立数学思维、解决实际问题具有重要意义。
本文将从复数的基本概念、运算法则和实际应用等方面进行归纳总结。
一、复数的基本概念1. 复数的定义:复数是由实部和虚部组成的数,形式为a+bi,其中a为实数部分,bi为虚数部分,i为虚数单位,满足i²=-1。
2. 复数的实部和虚部:复数a+bi中,a为实部,bi为虚部。
3. 复数的共轭复数:设复数z=a+bi,其共轭复数记为z*,则z*的实部与z相同,虚部的符号相反。
4. 复数的模:复数z=a+bi的模定义为|z|=√(a²+b²)。
5. 复数的辐角:复数z=a+bi的辐角定义为复数与正实轴正半轴的夹角,记作arg(z)。
6. 三角形式:复数z=a+bi可以写成三角形式r(cosθ+isinθ),其中r为模,θ为辐角。
二、复数的运算法则1. 复数的加法和减法:复数的加法和减法运算与实数类似,实部与实部相加减,虚部与虚部相加减。
2. 复数的乘法:复数的乘法运算使用分配律和虚数单位的性质,即(a+bi)(c+di)=(ac-bd)+(ad+bc)i。
3. 复数的除法:复数的除法运算需要将分子分母同时乘以共轭复数,即(a+bi)/(c+di)=[(a+bi)(c-di)]/[(c+di)(c-di)]。
4. 复数的乘方和开方:复数的乘方和开方运算需要使用三角函数的性质和欧拉公式,即z^n=r^n[cos(nθ)+isin(nθ)],√z=±√r[cos(θ/2)+isin(θ/2)]。
三、复数的性质和应用1. 复数的性质:复数具有加法和乘法的封闭性、交换律、结合律、分配律等性质。
2. 复数平面:复数可以用平面上的点来表示,实部为横坐标,虚部为纵坐标,构成复数平面。
3. 复数与向量:复数可以看作是向量的延伸,复数的运算有时可以用向量的加法和旋转来理解。
复数知识点复习咱今儿来好好复习复习复数这个知识点,这玩意儿在数学里可重要着呢!先来说说啥是复数。
复数啊,就像是数学世界里的“神秘嘉宾”,它由实部和虚部组成。
比如说,3 + 4i ,这里的 3 就是实部,4i 就是虚部。
记得我之前教过一个学生小明,他一开始对复数那是一头雾水。
有一次做作业,他把复数的运算弄了个乱七八糟。
我就问他:“小明啊,你咋把这简单的复数都给搞晕啦?”小明愁眉苦脸地说:“老师,我觉得这复数太抽象了,我搞不明白。
”我笑着告诉他:“别着急,咱们慢慢来。
”咱先看看复数的加法。
复数的加法就跟合并同类项差不多。
比如说,(2 + 3i) +(1 + 2i) ,那就是实部相加 2 + 1 = 3 ,虚部相加 3i +2i = 5i ,最后结果就是 3 + 5i 。
这多简单,就像你把一堆苹果和一堆梨分别加起来一样。
再说说复数的减法。
其实和加法原理差不多,就是实部减实部,虚部减虚部。
举个例子,(5 + 4i) (2 + 2i) ,那就是 5 2 = 3 ,4i 2i= 2i ,结果就是 3 + 2i 。
然后是复数的乘法。
这个可得仔细点,(a + bi)(c + di) = ac +adi + bci + bdi²。
因为 i²=-1 ,所以化简一下就好啦。
比如说,(2+ 3i)(1 + 2i) ,算出来就是 2×1 + 2×2i + 3i×1 + 3i×2i = 2 + 4i +3i + 6i²= 2 + 7i 6 =-4 + 7i 。
复数的除法稍微有点麻烦,得先把分母实数化。
比如说,(2 +3i)÷(1 + 2i) ,分子分母同时乘以分母的共轭复数 1 2i ,然后按照乘法法则计算就行啦。
咱再回过头来说说小明。
经过我这么一番耐心讲解,小明慢慢开窍了。
后来有一次测验,他在复数的题目上做得可好了,还跑来跟我炫耀:“老师,我现在觉得复数也没那么难嘛!”我笑着拍拍他的肩膀说:“对呀,只要用心,啥都能学会!”总之,复数这部分知识,只要多练习,多琢磨,就一定能掌握好。
期末复习(一)复数与导数班级: 姓名:复数1. 若复数22(3)(56)i m m m m -+-+(R m ∈)是纯虚数, 则m 的值为 ( ) A .0 B .2 C .0或3 D .2或3 2.在复平面内,复数21i i-+对应的点位于( )DA .第一象限B . 第二象限C .第三象限D .第四象限 3.i 为虚数单位,则=⎪⎭⎫ ⎝⎛-+201111i i ( )AA.i -B.1-C.iD.14.若a ,b ∈R ,i 是虚数单位,且(2)i 1i a b +-=+,则a b +的值为 ( )D A.1 B.2 C. 3 D. 45.设ii z 21+=,则复数=_z ( )DA. i --2B. i +-2C. i -2D.i +2 6.a 为正实数,i 为虚数单位,2=+ii a ,则=a ( )BA .2 B. CD .1 7.已知复数z =||z = ( )A . 14B .12C .1D .28.复数1z i =+,z 为z 的共轭复数,则1z z z --=( ) B A .-2i B .-i C .i D .2i 9.若x C ∈,则方程||13x i x =+-的解是( )CA122+B 124,1x x ==-C 43i -+D122-10.|34|2z i ++≤,则||z 的最大值为( B )A 3B 7C 9D 5 11.已知方程|2||2|z z a --+=表示等轴双曲线,则实数a 的值为( A ) A± BCD12.复数1cos sin ,(2)z i ααπαπ=++<<的模是( B ) A 2cos2αB 2cos2α- C 2sin2αD 2tan2α-13.复平面上,方程558z z --+=的曲线是( )A .双曲线B .双曲线的左支C .双曲线的右支D .一个点149.对任意复数()i ,R z x y x y =+∈,i 为虚数单位,则下列结论正确的是 A .2z z y -= B .222z x y =+ C .2z z x -≥ D .z x y ≤+15.复数2i 1ia +-在复平面内所对应的点在虚轴上,那么实数a = . 216.的值等于__ ___.17.若z ∈C 且22i 1z +-=,则22i z --的最小值是_____.18.已知复数1z 满足1(2)(1)1z i i -+=-(i 为虚数单位),复数2z 的虚部为2,且12z z ⋅是实数,求2z .解: 1(2)(1)1z i i -+=-⇒12z i =-………………(4分)设22,z a i a R =+∈,则12(2)(2)(22)(4)z z i a i a a i =-+=++-,……(12分)∵ 12z z R ∈,∴ 242z i =+ ………………(12分)19. 已知x 是实数,y 是纯虚数,且满足i y y i x )3()12(--=+-,求x 与y .思路分析:因为y 是纯虚数,所以可设)0,R (≠∈=b b bi y ,代入等式,把等式的左、右两边都整理成bi a +形式后,可利用复数相等的充要条件得到关于x 与b 的方程组,求解后得x 与b 值.解答:设)0R (≠∈=b b bi y 且代入条件并整理得i b b i x )3()12(-+-=+-由复数相等的条件得⎩⎨⎧-=-=-3112b b x 解得⎪⎩⎪⎨⎧-==234x b ∴.4,23i y x =-= 20.设复数2(1)3(1)2i i z i++-=+ ,且21z az b i ++=+,求实数,a b 的值。
解: ,将 代入得, 即∴由两复数相等的定义得 解得 .∴所求实数 。
21.已知复数z 满足23()z z i z ai a R ⋅+⋅=+∈ ,且z 的对应点在第二象限,求a 的取值范围。
解:设 ,。
由 得①对应点在第二象限,故有②又由①得③由③得,即 ,∴ ,∴④于是由②,④得, 即再注意到a<0,故得 即所求a 的取值范围为22..已知关于t 的一元二次方程)R ,(,0)(2)2(2∈=-++++y x i y x xy t i t(1)当方程有实根时,求点),(y x 的轨迹方程. (2)求方程的实根的取值范围.思路分析(1)本题方程中有y x t 、、三个未知数由复数相等的充要条件能得到两个等式,而结论是要求动点),(y x 的轨迹方程,联想到解析几何知识,求),(y x 的轨迹方程就是求关于y x 、的方程,于是上面的两个等式正是轨迹方程的参数形式,消去参数t ,问题得解(2)由上面解答过程中的②知0=+-t y x 可看作一条直线,由③知2)1()1(22=++-y x 是一个圆,因此求实根t 的范围可转化为直线与圆有公共点的问题.解答(1)设实根为t ,则0)(2)2(2=-++++i y x xy t i t 即0)()22(2=-++++i y x t xy t t根据复数相等的充要条件得⎩⎨⎧=-+=++)2(0)1(0222y x t xy t t由(2)得x y t -=代入(1)得02)(2)(2=+-+-xy x y x y即2)1()1(22=++-y x (3)∴所求点的轨迹方程为2)1()1(22=++-y x ,轨迹是以(1,-1)为圆心,2为半径的圆.(2)由(3)得圆心为(1,-1),半径2=r ,直线与圆有公共点,则22)1(1≤+--t,即22≤+t ∴04≤≤-t ,故方程的实根的取值范围为[]0,4-.导数1.若曲线2y x ax b =++在点(0,)b 处的切线方程是10x y -+=,则( ) A 1,1a b == B 1,1a b =-= C 1,1a b ==- D 1,1a b =-=-【解析】A :本题考查了导数的几何意思即求曲线上一点处的切线方程 ∵2x y x aa='=+=,∴ 1a =,(0,)b 在切线10x y -+=,∴ 1b =2.若曲线12y x -=在点12,a a -⎛⎫ ⎪⎝⎭处的切线与两个坐标围成的三角形的面积为18,则a =(A )64 (B )32 (C )16 (D )8 【答案】A【命题意图】本试题主要考查求导法则、导数的几何意义、切线的求法和三角形的面积公式,考查考生的计算能力.. 【解析】332211',22y xk a--=-∴=-,切线方程是13221()2y aax a ---=--,令0x =,1232y a-=,令0y =,3x a =,∴三角形的面积是121331822s a a -=⋅⋅=,解得64a =.故选A.3.已知点P 在曲线41xy e =+上,α为曲线在点P 处的切线的倾斜角,则α的取值范围是( ) (A)[0,4π) (B)[,)42ππ(C ) 3(,]24ππ(D) 3[,)4ππ解析:选D.2441212x xxxxey ee e e'=-=-++++,12,10x xe y e'+≥∴-≤< ,即1tan 0α-≤<,3[,)4παπ∴∈4.如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t 时刻五角星露出水面部分的图形面积为()()()00S t S =,则导函数()'y S t =的图像大致为【答案】A【解析】本题考查函数图像、导数图、导数的实际意义等知识,重点考查的是对数学的探究能力和应用能力。
最初零时刻和最后终点时刻没有变化,导数取零,排除C ;总面积一直保持增加,没有负的改变量,排除B ;考察A 、D 的差异在于两肩位置的改变是否平滑,考虑到导数的意义,判断此时面积改变为突变,产生中断,选择A 。
5.(2012年高考(新课标理))已知函数1()ln(1)f x x x=+-;则()y f x =的图像大致为( )【解析】选B()ln(1)()1()010,()00()(0)0x g x x x g x xg x x g x x g x g '=+-⇒=-+''⇒>⇔-<<<⇔>⇒<=得:0x >或10x -<<均有()0f x < 排除,,A C D6.(2012年高考(浙江理))设a >0,b >0.( )A .若2223aba b +=+,则a >bB .若2223aba b +=+,则a <b C .若2223aba b-=-,则a >b D .若2223aba b-=-,则a <b【答案】A【解析】若2223a ba b+=+,必有2222a ba b +>+.构造函数:()22x f x x =+,则()2ln 220xf x '=⋅+>恒成立,故有函数()22x f x x =+在x >0上单调递增,即a >b 成立.其余选项用同样方法排除.7.(2012年高考(重庆理))设函数()f x 在R 上可导,其导函数为()f x ',且函数(1)()y x f x '=-的图像如题(8)图所示,则下列结论中一定成立的是( )A .函数()f x 有极大值(2)f 和极小值(1)fB .函数()f x 有极大值(2)f -和极小值(1)fC .函数()f x 有极大值(2)f 和极小值(2)f -D .函数()f x 有极大值(2)f -和极小值(2)f 【答案】D【解析】2,10x x <-->,由(1)()0()0x f x f x ''->⇒>,函数()f x 为增;21,10x x -<<->,由(1)()0()0x f x f x ''-<⇒<,函数()f x 为减;12,10x x <<-<,由(1)()0()0x f x f x ''->⇒<,函数()f x 为减; 2,10x x >-<,由(1)()0()0x f x f x ''-<⇒>,函数()f x 为增.【考点定位】判断函数的单调性一般利用导函数的符号,当导函数大于0,则函数为增,当导函数小于0则函数递减.8.(2012年高考(陕西理))设函数()xf x xe =,则( )A .1x =为()f x 的极大值点B .1x =为()f x 的极小值点C .1x =-为()f x 的极大值点D .1x =-为()f x 的极小值点解析:()(1)x f x x e '=+,令()0,f x '=得1x =-,1x <-时,()0f x '<,()xf x xe =为减函数;1x >-时,()0f x '>,()x f x xe =为增函数,所以1x =-为()f x 的极小值点,选D.9.(2012年高考(山东理))设0a >且1a ≠,则“函数()xf x a =在R 上是减函数 ”,是“函数3()(2)g x a x =-在R 上是增函数”的 ( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【解析】若函数x a x f =)(在R 上为减函数,则有10<<a .函数3)2()(x a x g -=为增函数,则有02>-a ,所以2<a ,所以“函数x a x f =)(在R 上为减函数”是“函数3)2()(x a x g -=为增函数”的充分不必要条件,选A.10.(2012年高考(湖北理))已知二次函数()y f x =的图象如图所示,则它与x 轴所围图形的面积为 ( )A .2π5B .43C .32D .π2考点分析:本题考察利用定积分求面积.解析:根据图像可得: 2()1y f x x ==-+,再由定积分的几何意义,可求得面积为12311114(1)()33S x dx x x --=-+=-+=⎰.11.(2012年高考(福建理))如图所示,在边长为1的正方形OABC中任取一点P,则点P 恰好取自阴影部分的概率为A.14B .15C .16D .17【答案】C【解析】31221211)()1326S x dx x x S ==-==⎰正阴影,故16P =,答案C【考点定位】本题主要考查几何概型的概率和定积分,考查推理能力、计算求解能力.12.(2012年高考(大纲理))已知函数33y x x c =-+的图像与x 轴恰有两个公共点,则c =( )A .2-或2B .9-或3C .1-或1D .3-或1答案A【命题意图】本试题主要考查了导数在研究三次函数中的极值的运用.要是函数图像与x轴有两个不同的交点,则需要满足极佳中一个为零即可.【解析】因为三次函数的图像与x 轴恰有两个公共点,结合该函数的图像,可得极大值或者极小值为零即可满足要求.而2()333()(1)f x x x x '=-=-+,当1x =±时取得极值 由(1)0f =或(1)0f -=可得20c -=或20c +=,即2c =±. 13.设函数()1f x x x=-,对任意x [1,∈+∞),f(mx)+mf(x)<0恒成立,则实数m 的取值范围是________ 【答案】m<-1【解析】本题主要考查了恒成立问题的基本解法及分类讨论思想,属于难题。