风管管件展开图教程
- 格式:doc
- 大小:992.00 KB
- 文档页数:31

在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22.5°的角,即∠AOK、∠KOC、∠COD与∠DOE。
通风管道的展开下料步骤通风管道的部件很多,比如弯头,料斗、旋风分离器等,它们的结构有一点复杂,并不像矩形风管,很简单能做出长宽高厚,所以要想精确地把这些加工制作出来,必要先学会展开成金属板材上的下料图形,下面苏州饶丰机电一起看看几种通风除尘、气力输送风网常用部件的展开方法。
一、弯头多节弯头俗称虾米腰, 是用来改变通风管道方向及其它装置的配件。
按其断面形状,可分为圆形、方形(或矩形) 两种。
从理论上说,弯头的形状为圆环面,是不展曲面,在实际构形设计当中,为了便于展开加工,只好改为分节的办法,将圆环面改为圆柱面。
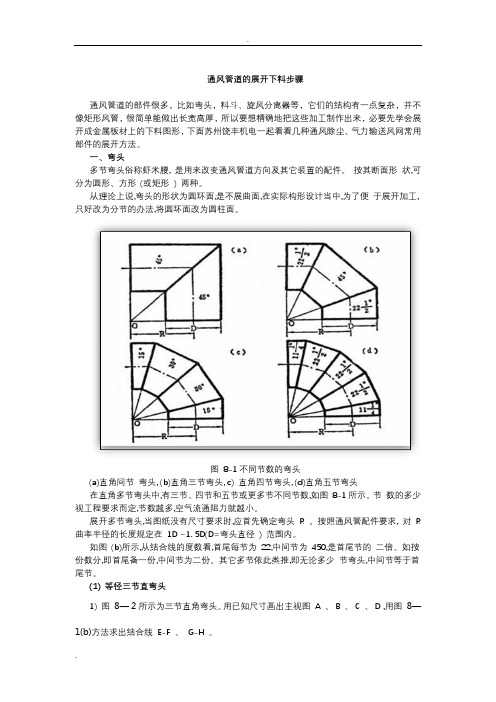
图8-1不同节数的弯头(a)直角间节弯头, (b)直角三节弯头, c) 直角四节弯头, (d)直角五节弯头在直角多节弯头中,有三节、四节和五节或更多节不同节数,如图8-1所示。
节数的多少视工程要求而定,节数越多,空气流通阻力就越小。
展开多节弯头,当图纸没有尺寸要求时,应首先确定弯头R 。
按照通风管配件要求, 对R 曲率半径的长度规定在1D ~1. 5D(D=弯头直径) 范围内。
如图(b)所示,从结合线的度数看,首尾每节为22,中间节为450,是首尾节的二倍。
如按份数分,即首尾备一份,中间节为二份。
其它多节依此类推,即无论多少节弯头,中间节等于首尾节。
(1) 等径三节直弯头1) 图8— 2所示为三节直角弯头。
用已知尺寸画出主视图A 、B 、C 、D ,用图8—1(b)方法求出结合线E-F 、G-H 。
2) 6等分断面半圆周1…… 7, 由各点向上作垂线, 与G — H 结合线相交点1…… 7,再由各点作F-H 的平行线,在E-F 结合线交1” …… 7” 。
3) 作C — D 的延长线,在延长线上截取E 1— E 2等于断面圆周展开长度,均分12等分, 由各点作上垂线, 与G — H 结合线上各点所引的水平线对应相交点10…… 70…… 10,将各点连圆滑曲线,即得尾节(首节) 的展开图。
4) 作△ EOG 的平分钱I — J 并延长(中节基准线) , 在延长线上以7…… 1…… 7的顺序截取(因尾节咬口缝在G — C 处, 考虑咬口缝过厚的影响, 中节咬口缝应与前咬口错开(中节改在F — H 面) ,以避免咬口缝过厚带来加工困难。

管道弯头展开放样图作法在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22.5°的角,即∠AOK、∠KOC、∠COD与∠DOE。

管道弯头展开放样图作法在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一.一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯(1)按已知1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
ﻫ尺寸画出立面图,如图3-3所示。
ﻫ(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
ﻫ(3)由各等分点作侧管中心(4)线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
ﻫ作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
ﻫ(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3—3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4直角弯展开图二、虾壳弯的展开放样ﻫ虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:ﻫ(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。


管道弯头展开放样图作法在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22.5°的角,即∠AOK、∠KOC、∠COD与∠DOE。
常用管件放样展开图【管工干货】概述在管道工程中看懂图,下准料是十分重要的,下料过程大致可分为放样,作展开图,画线,切割,等步骤。
其中放样和作展开图是下料过程的关键。
依照实物或施工图的要求,按正投影原理把需要制作的管子,管件等形状画到放样平台,钢板或油毡纸上的操作称为放样,所画出的图形称为放样图。
将管子,管件等物体的表面按其实际形状和大小,摊平在一个平面上,称为管子,管件等物体的展开,展开后所得到的平面图形,称为该物体的表面展示图。
管子,管件等物体展开的方法,有计算法和作图法,一般施工现场多采用作图法。
无论制品的外形如何复杂、都可以用这两种方法来展开。
在作图展开法中,按其作图方法的不同,又可分为放射线法,平行线法和三角形法等,本编章介绍的常用展开图主要有弯头,三通、大小头,就是采用常用的平行线法和放射线法。
展开下料的壁厚处理钢管都有一定的壁厚,分内径,外径和平均直径。
在展开下料过程中,如果取错管径,作出来的展开图及管件的下料会产生较大的误差。
因此在展开下料前必须根据具体情况决定用外径还是用内径。
解决这个问题的过程称为壁厚处理。
凡壁厚(板厚)大于1.5mm的,均应进行壁厚处理。
圆管类下料展开长度计算用钢板卷制的管展开长度的计算,钢板在卷成圆管时,里面受压缩短、外面受拉伸长,中性层不变。
因此应按中径计算圆管展开长度。
同时制作展开图的样板也有厚度,因此样板的周长也应考虑这个因素。
即L=π(d+t)。
异径三通管壁厚处理异径三通小管径端的展开周长按管径中径即π(d+t),开孔端展开周长则按小管径内径计算,即πd。
等径三通管及虾节弯头展开周长以管子外径计算即πD式中L=圆周长,π=圆周率(3.14.16),d=管子内径,t=管壁厚度,D=管子外径。
几种常用的几何作图法作垂线(十字平分线)①、作已知AB直线上一点O的垂线作法②、以O为圆心,任意长为半径画弧,在AB直线上交于C,D两点。
③、分别以C、D为圆心,以任意长半径画弧,(但必须大于CO 或DO),相交于E,F两点。
在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个°的角,即∠AOK、∠KOC、∠COD与∠DOE。
管道弯头展开放样图作法在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22.5°的角,即∠AOK、∠KOC、∠COD与∠DOE。
第一节展开原理1.展开放样的基本思路1) 什么是展开放样所谓展开,实际是把一个封闭的空间曲面沿一条特定的线切开后铺平成一个同样封闭的平面图形。
它的逆过程,即把平面图形作成空间曲面,通常叫成形过程。
实际生产工作中,往往是先设计空间曲面后再制作该曲面,而这个曲面的制造材料大都是平面板料。
因此,用平板做曲面,先要求得相应的平面图形,即根据曲面的设计参数把平面坯料的图样画出来。
这一工艺过程就叫展开放样。
实际工作中,有人把它简称为展开,也有人把它简称为放样,本书中采用前者的说法。
2) 展开的基本思路----换面逼近图2-1-0 换面逼近示意图如图2-1-0,我们按预先设定的经纬网络把曲面网格化,并在曲面上任取其一个四角面元abcd(A、B、C、D为其四个顶点,a、b、c、d为其四条边界弧线)。
连接它的四个顶点A、B、C、D和对角点B、C,将得到一个与四角面元abcd对应的四边形ABCD以及组成四边形ABCD的两个平面三角形△ABC和△BCD。
为了简化我们的研究,我们以三角形△ABC和△BCD代替对应的四角面元abcd,其中直线段AB、AC、CD、DB与a、b、c、d四条弧线分别对应。
对所有的网格都做同样的替代处理,我们就可以得到一个与曲面贴近的,由众多三角平面元构成的多棱面。
多棱面与原曲面当然会存在差别,但是,只要网格数目足够多,他们的误差可以足够小,小到我们允许的公差范围内。
把曲面换成与之相近、由小平面组成的多棱面,再用多棱面的展开图去近似替代该曲面的理论展开图,这就是换面逼近的基本思路。
多棱面的展开是容易的,只要在同一平面上把这些小平面元按相邻位置和共用边逐个画出来就得到了多棱面的展开图。
需要指出的是,如何网格化是个中关键,这一部分将在讲展开方法时详细介绍。
以上讲的是三角平面元替换,其实我们也可以采用其他形状的小平面来换面逼近。
如梯形、六边形等等。
更进一步,我们还可以用简单曲面,如圆柱面、正锥面等来作类似的替换。
实践证明,这样的替换逼近效果更好,既简化了手续,又保证了精度。
以下图例,可资说明。
2.换面逼近的几个例子第一个例子是共顶点三角形替换。
请看图2-1-1。
换面逼近的大致步骤如下:图2-2-1 共顶点三角形替换首先分割:将圆锥底圆分外分为12等分,等分点为A、B、C、D、E、F、G、H、I、J、K、L;然后以过锥顶0与各分点的素线为界线将此圆锥面分为12个共一顶点的三角锥面元;其次换面:用平面三角形△0AB、△0BC、△0CD、…△0KL、△0LA替代对应的三角锥面元;就总体而言,这种替换,也可以理解为用一个12棱锥的外表面来代替圆锥面;然后展开:在同一平面上把这些三角形按照共用边和共用顶点逐个画出来,这样就得到了12个共同一顶点并呈放射状分布的三角形组成的平面图形;我们用这个平面图形模拟、逼近圆锥的理想展开曲面。
当然,这只是一个近似展开图形,但是他们之间的误差是可以控制的,例如我们只要增加底圆的等分点数N,其替代误差随着N的增加而减小,以至小到允许的公差范围以内。
以上即所谓共顶点三角形换面逼近。
就工艺而言,这是一个可行的方法;从精度来看,关键是N的确定,实际中,N根据误差大小、布点方式、加工工艺和材料性质等因素通过实践选择。
在各种锥面的展开中,我们都采用这种换面逼近的思路,久而久之,便形成了一个成熟的展开方法。
由于它的展开图线由以顶点为中心呈放射状布置,我们通常把它叫做放射线展开法。
第二个例子是梯形替换。
这是一个用梯形面元替换对应曲面元的例子图2-1-2 梯形替换如图2-1-2 所示,本图系斜口圆柱面展开时进行换面逼近的示意图。
象圆锥面展开的思路一样,用以取得圆柱微面元的方式仍然是素线分割,但此时的素线已不再相交而是相互平行了。
由此得到的微面元是四角曲面,对应的平面图形是梯形。
如图所示,我们是用梯形AA′BB′去替换四角微面元AA′BB′,逐个替换以后,整个斜口圆柱面的展开将用其内接12边形为底面的12棱柱面的展开去近似它。
以上即所谓梯形换面逼近。
从这个思路出发,在展开放样中已形成了成熟的平行线展开法。
第三个例子是三角形替换,请看图图2-1-3。
图2-1-3 三角形替换图中斜口大小头上下口均为圆,但直径不同;上口圆中心在下口圆面的投影与下口圆中心同心;此外上下口所在平面之间有15°夹角。
需要展开的是以上、下口圆为边界的周边蒙面。
本例是这样换面和逼近的:首先,将上下口圆分别以对称中面为基准各自等分为12等分,然后一上一下,依次连接各等分点,由此得到24条直线,即图中aA、Ab、bB、Bc、cC、Cd、dD…La、aA;之后分别用每条直线和下口圆心确定的平面分割蒙面,得到24个三角曲面元;同时也得到与之对应的24个平面三角形,即图中△aAb、△AbB、△bBc、△BcC…△lLa、△LaA;其中12个三角形都有一条边长度为上口圆周长的1/12,而另外12个三角形都有一条边长度为下口圆周长的1/12;为了简化蒙面的展开,我们再将这24个三角形逐个替换对应的三角曲面元,换言之,我们用一个多棱面来近似大小头蒙面的展开。
这样替换的结果无疑存在误差,但它的误差是可以控制的,例如增大等分点的数目就是减小误差的途径,不管你给出的公差多小,总可以设法使误差不超过你的公差范围。
最后展开。
选定一个切开线,如图中Aa,并以之作为起始线在同一平面内逐个画出△aAb、△bAB、△Bbc、△cBC…△lLa、△Ala。
这24个三角形共同组成了正确的近似展开图形。
以上即所谓三角形换面逼近。
从这个思路出发,在展开放样中已形成了成熟的三角形展开法。
第四个例子是曲面替换。
(如图2-1-4)所谓曲面替换是在换面逼近时,直接用已知的、易展开曲面(如圆柱面、正圆锥面)的曲面元去替代复杂曲面的对应曲面元,以取得更好的逼近效果,从而使复杂曲面的展开工作更简便,更快捷。
图2-1-4 曲面替换本图以24条经线与24纬线分划球面,得到的曲面元是由相邻的两条经线和相邻的两条纬线所围成球面元。
对这些曲面元,我们分别进行平面元(梯形面元+三角面元)替换、柱面元替换和锥面元替换。
图中虚线线部分,采用椭圆柱面元替换。
即以一个经线处为原来弧线,纬线处由同一纬线两端点所连直线,长半径为球半径的椭圆柱面元去替代球面元;图中粗线部分采用了平面替换,即用球面元四个顶点连线组成的梯形替代了球面元,它的四边都是直线;图中细线部分则采用了锥面替换,即以一个上下纬线为上下圆的圆锥台面去替代球面元,这个锥面元的四边,上下仍为弧线,对应的经线处则已变成了直线;略作比较,不难发现锥面替换、椭圆柱面替换比梯形替换逼近程度高。
对于前述的共点三角形替换和梯形替换,我们实际展开中不采用底圆等分点间的弦长而是采用弧长,就是贯彻曲面替换思想的结果。
上述各种换面逼近在整个换面逼近过程中除替换面不同以外,其他情况类似,大同小异,兹不赘述。
需要强调的是:实际展开中,对同一曲面的替换面元不必采用同一类型,而是根据曲面的结构特点和简捷方便的展开原则灵活地混用各种替换面元。
3. 展开放样的一般过程设计图是展开放样的依据,其表示方式是视图。
众所周知,视图上小面元的形状及其组成线段是实物形状、实际组成线段在该视图上的投影,它们的长度不一定反映实际长度。
而画展开图必须是1:1的实际长度,因此,怎样通过各视图上线段的投影去求得线段的实长是展开放样至关重要的第一步。
求实长常用的方法,一是选择与实际线段平行、投影反映实长的投影面(先看基本视图,后选向视图),在该面视图上对应量取;二是通过相互关联的几个视图上对应投影之间的函数关系去设法求得。
二者可以通过几何作图,也可以通过计算求得。
第二步,画展开图。
展开的重点是画展开曲线,即展开图样的边线。
展开曲线是一般平面曲线,要画这种曲线,通常先在图纸上求出曲线上一定数量的、足以反映其整体形状的点;之后再圆滑连接各点,得出所求曲线“近似版”。
此版尽管是近似的,却可以设法达到事先要求的准确度,因为曲线的准确性跟点的数量有关,越多越准。
展开时,为了作图的方便,点的布置通常采用等分的办法;在曲线变化急剧的区域,适当插入一些更细的分点,以求得事半功倍的效果。
第二节展开放样的基本要求与方法1.展开三原则展开三原则是展开时必须遵循的基本要求。
1) 准确精确原则:这里指的是展开方法正确,展开计算准确,求实长精确,展开图作图精确,样板制作精确。
考虑到以后的排料套料、切割下料还可能存在误差,放样工序的精确度要求更高,一般误差≤0.25㎜。
2) 工艺可行原则:放样必须熟悉工艺,工艺上必须通得过才行。
也就是说,大样画得出来还要做的出来,而且要容易做,做起来方便,不能给后续制造添麻烦;中心线、弯曲线、组装线预留线等以后工序所需的都要在样板上标明。
3) 经济实用原则:对一个具体的生产单位而言,理论上正确的并不一定是可操作的,先进的并不一定是可行的,最终的方案一定要根据现有的技术要求、工艺因素、设备条件、外协能力、生产成本、工时工期、人员素质、经费限制等等情况综合考虑,具体问题具体分析,努力找到经济可行,简便快捷、切合实际的经济实用方案,绝不能超现实,脱离现有工艺系统的制造能力。
2.展开三处理展开三处理是实际放样前的技术处理,它根据实际情况,通过作图、分析、计算来确定展开时的关键参数,用以保证制造精度。
1) 板厚处理上面所说的空间曲面是纯数学概念的,没有厚度,但实际中的这种面只存在于有三度尺寸的板面上。
是板料就会有厚度,只不过是厚度有厚有薄而已。
板料成形加工时,板材的厚度对放样有没有影响?答案是肯定的,不可能没有影响;板材的厚度越大,影响越大,而且随着加工工艺的不同,影响也不同。
下面先看两个例子。
⑴我们把L×b×δ的一块钢条弯曲成曲率为R的圆弧条时,发现上面(弧内侧)的长度变短了,下面(弧外侧)的长度变长了。
根据连续原理,其中间一定存在一个既不伸长也不缩短的层面。
这个层面我们叫它中性层。
那么,这个中性层的位置在哪里呢?实践证明,中性层的位置跟加工的工艺和弯曲的程度有关。
如采用一般的弯曲工艺,当R>8δ时,中性层的位置在板料的中间。
这一客观事实给我们的启示是:如果设计了这样一个圆弧条要我们加工,加工前的展开料长应该按中径上的对应弧段计算。
显然,该圆弧条的展开长度是L。
如此类推,倘要用厚度为δ钢板卷制一个圆筒,其展开长度应按中径计算,即L=πφ。
这是一个很重要的结论,因为按中径展开,更准确一点,按中性层展开就是我们钣厚处理的基本原则。
请注意,图2-2-1中没有给出尺寸数值的单位。
未标单位不是没有单位,而是采用默认单位。
机械制造行业默认的单位是毫米。
图中长度314没有标明单位,按默认值,其单位就是毫米。
以后均应如此,恕不重述。