自动控制原理胡寿松第四版课后答案

1 请解释下列名字术语:自动控制系统、受控对象、扰动、给定值、参考输入、反馈。

解:自动控制系统:能够实现自动控制任务得系统,由控制装置与被控对象组成; 受控对象:要求实现自动控制得机器、设备或生产过程扰动:扰动就是一种对系统得输出产生不利影响得信号、如果扰动产生在系统内部称为内扰;扰动产生在系统外部,则称为外扰。

外扰就是系统得输入量。

给定值:受控对象得物理量在控制系统中应保持得期望值参考输入即为给定值、反馈:将系统得输出量馈送到参考输入端,并与参考输入进行比较得过程。

２请说明自动控制系统得基本组成部分。

解:作为一个完整得控制系统,应该由如下几个部分组成:①被控对象: 所谓被控对象就就是整个控制系统得控制对象;②执行部件: 根据所接收到得相关信号,使得被控对象产生相应得动作;常用得执行元件有阀、电动机、液压马达等。

③给定元件: 给定元件得职能就就是给出与期望得被控量相对应得系统输入量(即参考量);④比较元件: 把测量元件检测到得被控量得实际值与给定元件给出得参考值进行比较,求出它们之间得偏差、常用得比较元件有差动放大器、机械差动装置与电桥等。

⑤测量反馈元件:该元部件得职能就就是测量被控制得物理量,如果这个物理量就是非电量,一般需要将其转换成为电量。

常用得测量元部件有测速发电机、热电偶、各种传感器等;⑥放大元件: 将比较元件给出得偏差进行放大,用来推动执行元件去控制被控对象。

如电压偏差信号,可用电子管、晶体管、集成电路、晶闸管等组成得电压放大器与功率放大级加以放大。

⑦校正元件: 亦称补偿元件,它就是结构或参数便于调整得元件,用串联或反馈得方式连接在系统中,用以改善系统得性能、常用得校正元件有电阻、电容组成得无源或有源网络,它们与原系统串联或与原系统构成一个内反馈系统。

３请说出什么就是反馈控制系统,开环控制系统与闭环控制系统各有什么优缺点？解:反馈控制系统即闭环控制系统,在一个控制系统,将系统得输出量通过某测量机构对其进行实时测量,并将该测量值与输入量进行比较,形成一个反馈通道,从而形成一个封闭得控制系统;开环系统优点:结构简单,缺点:控制得精度较差;闭环控制系统优点:控制精度高,缺点:结构复杂、设计分析麻烦,制造成本高、4 请说明自动控制系统得基本性能要求。

dx(t ) d 2 x(t ) p(t ) f kx(t ) m dt dt 2
移项整理，得系统的微分方程为
m
d 2 x(t ) dx(t ) f kx(t ) p(t ) 2 dt dt
2-2 试列写图 2-2 所示机械系统的运动微分 方程。 解：由牛顿第二运动定律，不计重力时，得
是非电量，一般需要将其转换成为电量。常用的测量元部件有 测速发电机、热电偶、各种传感器等； ⑥ 放大元件： 将比较元件给出的偏差进行放大，用来推动执行元件去控制被 控对象。如电压偏差信号，可用电子管、晶体管、集成电路、 晶闸管等组成的电压放大器和功率放大级加以放大。 ⑦ 校正元件： 亦称补偿元件，它是结构或参数便于调整的元件，用串联或反 馈的方式连接在系统中，用以改善系统的性能。常用的校正元 件有电阻、电容组成的无源或有源网络，它们与原系统串联或 与原系统构成一个内反馈系统。
CsUC1 ( s) CsUC 2 ( s) U R 2 ( s) R2
（1 ） （2 ） （3 ）
U i ( s) U o ( s) CsUC 2 ( s) R1
（4 ）
整理得传递函数为
U o (s) R1R2C 2 s 2 R1Cs U i ( s) Cs 2 1 1 R1R2C 2 s 2 ( R1 2 R2 )Cs 1 R1 R2 R1R2Cs
（3） F ( s)
2 s 2 5s 1 s( s 2 1)
s 1 1 2 ( s 2)( s 5) s 2 s 5
1 2 ] s2 s5
解： （1 ） F ( s )
L1[ F ( s)] L1[
1 2 ] 2 L1[ ] s2 s5 e2t 2e5t L1[

用电技术专业方向）
先修课程： 高等数学、大学物理、积分变换、电路、数字电子技术、模拟电子技术
一、课程性质、目的和任务
本课程为电气工程及其自动化专业的主要专业基础课程之一，目的是使学生掌握负反馈控制原理、控
制系统数学模型的建立和系统性能分析、设计的基本方法，培养学生分析和设计自动控制系统性能的基本
能力并能满足其它后续专业课程对自动控制理论知识的需要。
制系统的性能。了解开环零、极点对系统性能的影响。
5．熟悉频率分析法分析控制系统性能的方法 熟悉典型环节频率特性的求取以及频率特性曲线，掌握系统开环对数频率特性曲线、极坐标曲线绘制
的基本方法。了解根据开环对数频率特性曲线分析闭环系统性能的方法。熟悉用奈奎斯特稳定判据判断系
1
《自动控制原理》电子教案
统稳定性的方法。掌握稳定裕度的计算方法。 6．熟悉控制系统校正的方法 了解串联超前校正、串联滞后校正的校正装置设计的基本原理和方法。 7．熟悉非线性控制系统的分析方法 了解非线性控制系统的特点和常见非线性特性。熟悉非线性控制系统的描述函数法。
熟悉系统微分方程的建立，拉氏变换及其应用。掌握系统传递函数的定义及求取，系统动态结构图 的建立及其简化以及系统不同传递函数的定义及求取。
1．控制系统微分方程的建立 2．非线性数学模型的线性化 3．控制系统的传递函数 4．典型环节的传递函数 5．控制的动态结构图及变换 6．信号流图及梅逊公式 7．反馈控制系统的传递函数 （三）自动控制系统的时域分析法 熟悉控制系统的时域指标，一阶系统的单位阶跃响应、斜坡响应以及性能指标的求取。掌握典型二阶 系统的单位阶跃响应以及性能指标的求取。掌握劳斯稳定判据分析系统的稳定性方法。熟悉控制系统稳态 误差分析以及稳态误差、误差系数的求取。 1． 控制系统性能指标的定义 2．一阶系统性能分析 3．二阶系统性能分析 4． 欠阻尼二阶系统的时域分析和指标计算 5． 高阶系统的时域分析、闭环主导极点和高阶系统的降阶

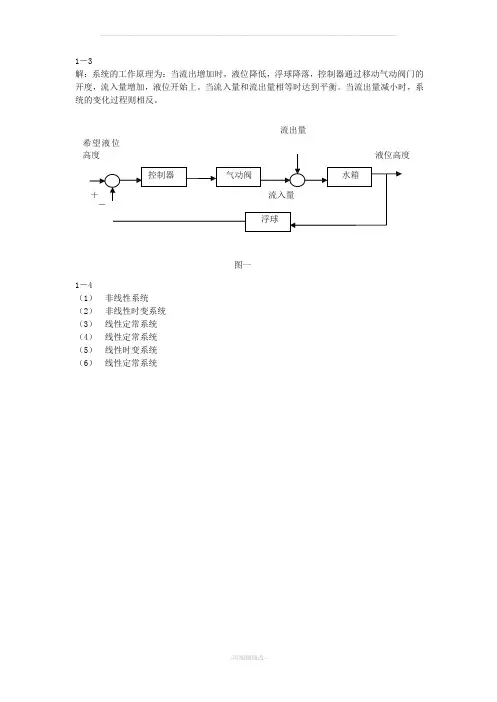
1－3解：系统的工作原理为：当流出增加时，液位降低，浮球降落，控制器通过移动气动阀门的开度，流入量增加，液位开始上。

当流入量和流出量相等时达到平衡。

当流出量减小时，系统的变化过程则相反。

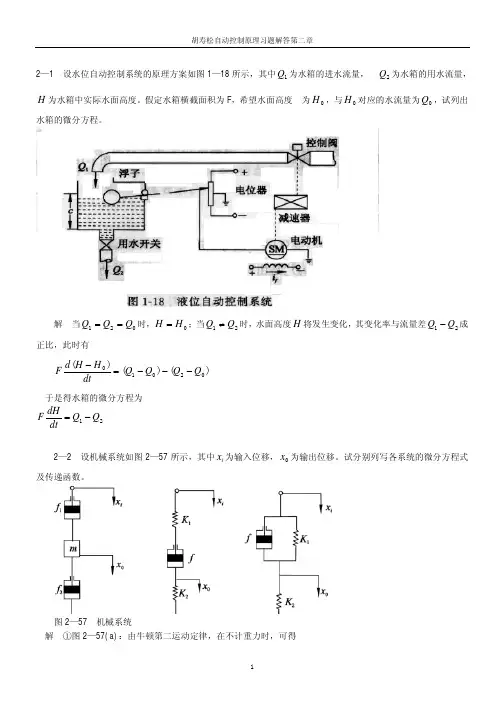
流出量希望液位图一1－4（1）非线性系统（2）非线性时变系统（3）线性定常系统（4）线性定常系统（5）线性时变系统（6）线性定常系统2 2-1 解：显然，弹簧力为 k x (t ) ，根据牛顿第二运动定律有：F (t ) − kx (t ) = m移项整理，得机械系统的微分方程为：d 2 x (t ) dt 2m d x (t ) + kx (t ) = F (t ) dt 2对上述方程中各项求拉氏变换得：ms 2 X (s ) + kX (s ) = F(s )所以，机械系统的传递函数为：G (s ) = X (s ) =F (s )1ms 2 + k2-2 解一：由图易得：i 1 (t )R 1 = u 1 (t ) − u 2 (t ) u c (t ) + i 1 (t )R 2 = u 2 (t ) du c (t )i 1 (t ) = Cdt由上述方程组可得无源网络的运动方程为：C ( R + R ) du 2 (t ) u (t ) = CRdu 1 (t ) u (t )1 2 dt+ 2 2+ 1 dt对上述方程中各项求拉氏变换得：C (R 1 + R 2 )sU 2 (s ) + U 2 (s ) = CR 2 sU 1 (s ) + U 1 (s )所以，无源网络的传递函数为：G (s ) = U 2 (s )=U 1 (s )1 +sCR 21 + sC (R 1 +R 2 )解二（运算阻抗法或复阻抗法）：U (s ) 1 + R 2 1 + R Cs2 = Cs = 2U (s ) R + 1 + R 1 + ( R + R )Cs 1 1 21Cs22-5 解：按照上述方程的顺序，从输出量开始绘制系统的结构图，其绘制结果如下图所示：依次消掉上述方程中的中间变量 X 1 , X 2 , X 3 , 可得系统传递函数为：C (s ) = R (s )G 1 (s )G 2 (s )G 3 (s )G 4(s )1 + G2 (s )G3 (s )G 6 (s ) + G 3 (s )G4 (s )G5 (s ) + G 1 (s )G 2 (s )G 3 (s )G 4 (s )[G 7 (s ) −G 8 (s )]2-6 解：①将G1 (s) 与G1 (s) 组成的并联环节和G1 (s) 与G1 (s) 组成的并联环节简化，它们的等效传递函数和简化结构图为：G12 (s) = G1(s) + G2(s)G34 (s) = G3(s) −G4(s)②将G12 (s), G34 (s) 组成的反馈回路简化便求得系统的闭环传递函数为：2-7 解：C(s)=R(s)G12(s)1 + G12(s)G34(s)=G1(s) + G2(s)1 + [G1(s) + G2(s)][G3(s) −G4(s)]由上图可列方程组：[E(s)G1 (s) −C(s)H2(s)]G2(s) = C(s)R(s) −H1(s)C(s)G2(s)= E(s)联列上述两个方程，消掉E(s) ，得传递函数为：C(s)= R(s)G1(s)G2(s)1 + H1(s)G1(s) + H2(s)G2(s)联列上述两个方程，消掉C(s) ，得传递函数为：E(s)= R(s)1 + H2(s)G2(s)1 + H1(s)G1(s) + H2(s)G2(s)1 2 22 32-8 解：将①反馈回路简化，其等效传递函数和简化图为： 0.4G (s ) = 2s + 1 = 1 +0.4 * 0.5 2s + 11 5s + 3将②反馈回路简化，其等效传递函数和简化图为：1G (s ) =s + 0.3s + 1= 5s + 321 + 0.45s +4.5s+ 5.9s + 3.4(s + 0.3s + 1)(5s + 3)将③反馈回路简化便求得系统的闭环传递函数为：0.7 * (5s + 3)Θo (s)= 5s 3 + 4.5s 2 + 5.9s + 3.4 =3.5s + 2.1Θi (s) 1 + 0.7 * Ks(5s + 3)5s 3+ (4.5 + 3.5K )s2+ (5.9 + 2.1K )s + 3.42 5s3-3 解：该二阶系统的最大超调量：σp =e−ζπ/1−ζ2*100%当σp= 5% 时，可解上述方程得：ζ= 0.69当σp= 5% 时，该二阶系统的过渡时间为：ts≈3ζwn所以，该二阶系统的无阻尼自振角频率w n 3-4 解：≈3ζts=30.69* 2= 2.17由上图可得系统的传递函数：10 * (1 + Ks)C (s)= R(s)s(s + 2)1 +10 * (1 + Ks)s(s + 2)==10 * (Ks +1)s + 2 * (1 +5K )s +10所以w n =10 ，ζw n =1+5K⑴若ζ= 0.5 时，K≈0.116所以K≈0.116 时，ζ= 0.5⑵系统单位阶跃响应的超调量和过渡过程时间分别为：σp =e−ζπ/1−ζ2*100% =e−0.5*3.14/1−0.52*100%≈16.3%ts= 3ζwn =30.5 *≈1.910⑶加入(1 + Ks )相当于加入了一个比例微分环节，将使系统的阻尼比增大，可以有效地减小原系统的阶跃响应的超调量；同时由于微分的作用，使系统阶跃响应的速度（即变w 2 1 2 p化率）提高了，从而缩短了过渡时间：总之，加入 (1 + Ks ) 后，系统响应性能得到改善。

与题中给出的 G s 表达式对比可得： a 5,b 5,c 5
则系统约当型状态方程为
9-8 已知矩阵
试求 A 的特征方程、特征值、特征向量，并求出变换矩阵将 A 对角化。 解：A 的特征方程为 则 A 的特征值为 特征向量为
7 / 46
圣才电子书

使 A 对角化矩阵为
9 / 46
圣才电子书 十万种考研考证电子书、题库视频学习平台

9-12 已知线性系统状态转移矩阵
试求该系统的状态阵 A 。
解：该系统的状态阵 A 为
9-13 已知系统状态方程 试求系统传递函数 G（s）。
解：由式 G s c sI A1 b 可得系统传递函数为
圣才电子书 十万种考研考证电子书、题库视频学习平台

第 9 章 线性系统的状态空间分析与综合 9-1 已知电枢控制的直流伺服电机的微分方程组及传递函数为
（1）设状态变量
输出量 y=θm，试建立其动态方程；
（2）设状态变量
试建立其动态方程；
确定两组状态变量间的变换矩阵 T。
6S 4S
8 3
1
2S 5 S2 4S
3
1
3 2
1 1 S 1 2
1 S 3
其可控标准型为
由对偶原理知其可观标准型为
对角型为ቤተ መጻሕፍቲ ባይዱ
9-7 已知系统传递函数
6 / 46
圣才电子书 十万种考研考证电子书、题库视频学习平台

试求约当型（A 为约当阵）动态方程。 解：设传递函数分解为部分分式
解：由系统结构图可知
图 9-3 系统结构图
整理得系统动态方程为
变换形式可得系统动态方程为
4 / 46
圣才电子书 十万种考研考证电子书、题库视频学习平台

6
胡寿松自动控制原理习题解答第二章
在该点附近用泰勒级数展开近似为：
y
=
f
(
x0
)
+
df (x) dx
x0
(
x
−
x0
)
即 ed − Ed0 cosα 0 = K s (α − α 0 )
其中 K s
=
ded dα
α =α
= −Ed 0 sinα 0
2-9 若某系统在阶跃输入r(t)=1(t)时，零初始条件下的输出响应 c(t) = 1 − e−2t + e−t ，试求系统的传递函数和脉冲
K 2 x0 = f (x& − x&0 )
消去中间变量 x，可得系统微分方程
f (K1
+
K
2
)
dx0 dt
+
K1K2 x0
=
K1 f
dxi dt
对上式取拉氏变换，并计及初始条件为零，得系统传递函数为
ቤተ መጻሕፍቲ ባይዱ
X 0 (s) =
fK1s
X i (s) f (K1 + K2 )s + K1K2
③图 2—57(c)：以 x0 的引出点作为辅助点，根据力的平衡原则，可列出如下原始方程：
K 2 (xi − x0 ) + f 2 (x&i − x&0 ) = f1 (x&0 − x&) （1）
K1x = f1 (x&0 − x&) （2）
所以 K 2 (xi − x0 ) + f 2 (x&i − x&0 ) = K1x （3）
对（3）式两边取微分得

《自动控制原理》电子教案
自动控制原理
电子教案
《自动控制原理》电子教案
《自动控制原理》课程教学大纲
课程编号： 课程名称：自动控制原理 英文名称：Automatic Control Theory 课程类型:：专业基础必修课 总 学 时：64 学 学 时：64 分：4 讲课学时：56 上机学时：8
适用对象：电气工程及其自动化专业（电力系统及自动化、电力系统继电保护、电网监控技术、供 用电技术专业方向） 先修课程： 高等数学、大学物理、积分变换、电路、数字电子技术、模拟电子技术
大纲制订人：杨志超 大纲审定人：李先允 制订日期：2005 年 6 月
7
《自动控制原理》电子教案
自动控制原理授课计划（64 学时）
2．利用 MATLAB 程序绘制控制系统阶跃响应曲线、计算性能指标，讨论开环放大倍数对闭环系统响 应速度、稳定性和稳态误差的影响 。 （验证性实验） 2 学时
3． 利用 MATLAB 程序绘制控制系统的 Nyquist 曲线、 Bode 图， 计算控制系统的幅值裕度和相位裕度。 （验证性实验） 4．利用 MATLAB 软件设计控制系统（设计性实验） 2 学时 2 学时
六、实验报告要求
每次上机实验必须提交实验报告。实验报告由实验原理、实验内容、仿真程序、实验数据记录及分析 处理等内容组成。
七、考核方式与成绩评定标准
实验成绩：预习 10%、上机操作 50%、报告 40%
八、教材及主要参考资料
教 材： 《自动控制理论实验指导书》 ，王芳、杨志超编写，2007 年 参考书：《自动控制原理》，国防工业出版社，王划一主编，2001 年 《基于 MATLAB 的系统分析与设计》-控制系统，楼顺天、于卫编著，西安电子科技大学出 版社，1999 年 《MATLAB 控制系统设计与仿真》，赵文峰编著，西安电子科技大学出版社，2002 年

自动控制原理 (胡寿松著) 科学出版社课后答案《自动控制原理》是胡寿松编著的一本关于自动控制原理的教材。

本书系统地介绍了自动控制的基本原理、方法和技术，适用于自动化、电气、机械等相关专业的本科生和研究生学习使用。

本书一共分为十一章，包括控制系统基础、传递函数与系统的时域特性、系统的频域特性、稳定性分析、根轨迹法、频率响应法、校正器设计、状态空间法、观测器设计、控制系统设计以及非线性系统控制等内容。

每一章都有相应的习题，用于检测学生对所学知识的掌握情况。

第一章：控制系统基础1. 控制系统的定义和分类。

控制系统是指通过对被控对象进行测量和判断，从而对被控对象进行控制的一种系统。

根据被控对象的特性和控制方式的不同，控制系统可以分为连续控制系统和离散控制系统。

2. 控制系统的基本组成。

控制系统由被控对象、测量元件、判断元件、执行元件和反馈元件组成。

3. 控制系统的基本特性。

控制系统的基本特性包括稳定性、灵敏度、精度和动态性能等。

第二章：传递函数与系统的时域特性1. 传递函数的定义和性质。

传递函数是描述控制系统输入和输出之间关系的函数。

传递函数具有线性性、时不变性和因果性等性质。

2. 系统的时域特性。

系统的时域特性包括阶跃响应、冲击响应和频率响应等。

第三章：系统的频域特性1. 频域特性的概念。

频域特性是指系统对不同频率的输入信号的响应情况。

2. 振荡特性的判据。

系统振荡的判据是极点的实部为零和虚部不为零。

第四章：稳定性分析1. 稳定性的定义。

稳定性是指系统在无穷远时间内对于有限输入的响应趋于有限。

2. 稳定性的判据。

稳定性的判据包括判别函数法、根轨迹法和Nyquist稳定判据等。

第五章：根轨迹法1. 根轨迹的概念和性质。

根轨迹是描述传递函数极点随参数变化而运动轨迹的图形。

2. 根轨迹的绘制方法。

根轨迹的绘制方法包括定性法和定量法。

第六章：频率响应法1. 频率响应的概念和性质。

频率响应是指系统对不同频率的输入信号的响应情况。

ui − u0 = uC
iC = C
du C dt
i R1 =
uC R1
du d (u i − u 0 ) u i − u 0 u u 0 = (iC + i R1 ) R2 = C C + C R2 = C + R2 R1 dt R1 dt
整理得：
CR2
胡寿松自动控制原理习题解答第二章
2—1
设水位自动控制系统的原理方案如图 1—18 所示，其中 Q1 为水箱的进水流量，
Q2 为水箱的用水流量，
H 为水箱中实际水面高度。假定水箱横截面积为 F，希望水面高度 为 H 0 ，与 H 0 对应的水流量为 Q0 ，试列出
水箱的微分方程。
解
当 Q1 = Q2 = Q0 时， H = H 0 ；当 Q1 ≠ Q2 时，水面高度 H 将发生变化，其变化率与流量差 Q1 − Q2 成
正比，此时有
F
d (H − H 0 ) = (Q1 − Q0 ) − (Q2 − Q0 ) dt
于是得水箱的微分方程为
F
dH = Q1 − Q2 dt
2—2 设机械系统如图 2—57 所示，其中 xi 为输入位移， x0 为输出位移。试分别列写各系统的微分方程式
及传递函数。
图 2—57 机械系统 解 ①图 2—57(a)：由牛顿第二运动定律，在不计重力时，可得
[f
1
= f1 f 2 s + ( f1 K 2 + K1 f 2 ) s + K1 K 2 X i ( s)
2
[
f 2 s 2 + ( f1 K 2 + K1 f1 + K1 f 2 ) s + K1 K 2 X 0 ( s)

k 2 = 0.311
3-6 ξ = 1.43 ω n = 24.5 3-7 k1 = 1.44 3-8 (a) ξ = 0 ω n = 1 系统临界稳定 s+1 (b) Φ ( s ) = 2 ξ = 0.5 ω n = 1 (c) 3-9 (1)
G( s ) = s +s+1 1 Φ1
(b) R 2C C u ( t ) + ( RC + 2 RC )u ( t ) + u ( t ) 1 2 o 2 1 o o
= RC 1 C 2 u i ( t ) + 2 RC 1 u i ( t ) + u i ( t )
2-5(1) 运动模态: 运动模态: e
(2-5题~2-10题) 题 题 0.5 t
C(s ) G 1G 2 G 3 = R ( s ) 1 + G 1 H 1 + G 2 H 2 + G 3 H 3 + G 1 H 1G 3 H 3
C(s ) G 1G 2G 3 = G4 + R (s ) 1 + G 2 H 1 G 1G 2 H 1 + G 2G 3 H 2
(f)
C(s) (G 1 + G 3 )G 2 = R(s ) 1 + G 1G 2 H 1
2-3(a) R1 R2C1C 2 uo ( t ) + ( R1C1 + R2C 2 + R1C 2 )uo ( t ) + uo ( t )
m xo ( t ) = f1[ xi ( t ) - xo ( t )] - f 2 xo ( t )
= R1 R2C1C 2 ui ( t ) + ( R1C1 + R2C 2 )ui ( t )

大纲制订人：杨志超 大纲审定人：李先允 制订日期：2005 年 6 月
7
《自动控制原理》电子教案
自动控制原理授课计划（64 学时）
4．频率法反馈校正的基本原理和方法（选讲）
（七）非线性控制系统 了解非线性系统与线性系统的区别，了解非线性特性和非线性系统的主要特征，学会非线性系统的描 述函数分析方法，了解非线性系统的相平面分析法（选讲） 。
3
《自动控制原理》电子教案
1． 非线性系统的基本概念 2． 典型非线性特性、非线性系统的主要特征 3． 描述函数定义、应用条件和求取方法 4． 应用描述函数分析非线性系统的稳定性 5． 非线性系统自激振荡分析和计算 6． 介绍非线性系统相平面分析法（选讲）
二、本课程实验的基本理论与实验技术知识
采用 MATLAB 软件上机进行实验，就是利用现代计算机硬件和计算机软件技术，以数字仿真技术为核 心，实现对自动控制系统基本理论和分析方法的验证以及控制系统设计。 通过上机实验，使学生在 MATLAB 软件的基本使用、编程调试、仿真实验数据的获取、整理、分析以 及实验报告的撰写等基本技能得到训练。
三、实验方法、特点与基本要求
本课程实验采用计算机 MATLAB 软件仿真方法，其特点是利用 MATLAB 软件丰富的功能函数、灵活的编 程和调试手段以及强大的人机交互和图形输出功能，可以实现对控制系统直观和方便的分析和设计。 本课程实验的基本要求是， 使学生对 MATLAB 软件有一个基本的了解， 掌握 MATLAB 软件中基本数组和 矩阵的表示方法，掌握 MATLAB 软件的基本绘图功能，学会 MATLAB 软件中自动控制理论常用函数的使用， 学会在 MATLAB 软件工作窗口进行交互式仿真和使用 M_File 格式的基本编程方法，初步掌握利用 MATLAB 软件进行控制系统设计，让学生得到撰写报告的基本训练。

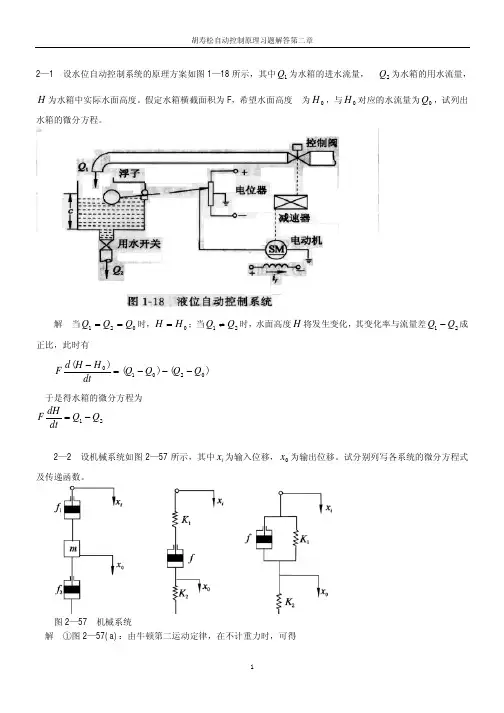
1－3解：系统的工作原理为：当流出增加时，液位降低，浮球降落，控制器通过移动气动阀门的开度，流入量增加，液位开始上。

当流入量和流出量相等时达到平衡。

当流出量减小时，系统的变化过程则相反。

流出量希望液位图一1－4（1）非线性系统（2）非线性时变系统（3）线性定常系统（4）线性定常系统（5）线性时变系统（6）线性定常系统2 2-1 解：显然，弹簧力为 kx (t ) ，根据牛顿第二运动定律有：F (t ) − kx (t ) = m移项整理，得机械系统的微分方程为：d 2x (t ) dt 2m d x (t ) + kx (t )= F (t ) dt2对上述方程中各项求拉氏变换得：ms 2 X (s ) + kX (s ) =F (s )所以，机械系统的传递函数为：G (s ) = X (s ) =F (s )1ms 2+k2-2 解一：由图易得：i 1 (t )R 1 = u 1 (t ) − u 2 (t ) u c (t ) + i 1 (t )R 2 = u 2 (t ) du c (t )i 1 (t )= Cdt 由上述方程组可得无源网络的运动方程为：C ( R + R ) du 2 (t ) u (t ) = CRdu 1 (t ) u (t )1 2 dt+ 22 + 1 dt 对上述方程中各项求拉氏变换得：C (R 1 + R 2 )sU 2 (s ) + U 2 (s ) = CR 2 sU 1 (s ) + U 1 (s )所以，无源网络的传递函数为：G (s ) = U 2 (s ) =U 1 (s )1 + sCR 21 + sC (R 1 +R 2 ) 解二（运算阻抗法或复阻抗法）：U (s ) 1 + R 2 1 + R Cs2 = Cs =2U (s ) R + 1 + R 1 + ( R + R )Cs 1 1 21Cs22-5 解：按照上述方程的顺序，从输出量开始绘制系统的结构图，其绘制结果如下图所示：依次消掉上述方程中的中间变量 X 1 , X 2 , X 3 , 可得系统传递函数为：C (s ) = R (s )G 1 (s )G 2 (s )G 3 (s )G 4(s )1 + G2 (s )G3 (s )G 6 (s ) + G 3 (s )G4 (s )G5 (s ) + G 1 (s )G 2 (s )G 3 (s )G 4(s )[G 7 (s ) − G 8 (s )]2-6 解：①将G1 (s) 与G1 (s) 组成的并联环节和G1 (s) 与G1 (s) 组成的并联环节简化，它们的等效传递函数和简化结构图为：G 12 (s) = G1(s) + G2(s)G 34 (s) = G3(s) −G4(s)②将G12 (s), G34 (s) 组成的反馈回路简化便求得系统的闭环传递函数为：2-7 解：C(s)=R(s)G12(s)1 + G12(s)G34(s)=G1(s) + G2(s)1 +[G1(s) + G2(s)][G3(s) −G4(s)]由上图可列方程组：[E(s)G1 (s) −C(s)H2(s)]G2(s) = C(s)R(s) −H1(s)C(s)G2(s)= E(s)联列上述两个方程，消掉E (s) ，得传递函数为：C(s)= R(s)G1(s)G2(s)1 + H1(s)G1(s) + H2(s)G2(s)联列上述两个方程，消掉C (s) ，得传递函数为：E(s)= R(s)1 + H2(s)G2(s)1 + H1(s)G1(s) + H2(s)G2(s)1 22 23 2-8 解：将①反馈回路简化，其等效传递函数和简化图为： 0.4G (s ) =2s + 1 =1 +0.4 * 0.5 2s + 15+ 3将②反馈回路简化，其等效传递函数和简化图为：1 G (s ) = s + 0.3s + 1 = 5s + 3 21 + 0.4 5s + 4.5s + 5.9s + 3.4(s + 0.3s + 1)(5s + 3)将③反馈回路简化便求得系统的闭环传递函数为：0.7 * (5s +3)Θo (s)= 5s 3 + 4.5s 2 + 5.9s + 3.4=3.5s + 2.1Θi (s) 1 +0.7 * Ks(5s +3)5s3+ (4.5 +3.5K )s 2+ (5.9 + 2.1K )s +3.42 5s3-3 解：该二阶系统的最大超调量：σp =e−ζπ/1−ζ2*100%当σp= 5% 时，可解上述方程得：ζ=0.69当σp= 5% 时，该二阶系统的过渡时间为：ts≈3ζwn所以，该二阶系统的无阻尼自振角频率w n 3-4 解：≈3ζts=30.69*2= 2.17由上图可得系统的传递函数：10 * (1 + Ks)C (s)= R(s)s(s + 2)1 +10 * (1 +Ks)s(s + 2)==10 * (Ks +1)s + 2 * (1 +5K )s +10所以w n =10 ，ζwn=1 +5K⑴若ζ= 0.5 时，K ≈0.116所以K ≈0.116时，ζ= 0.5⑵系统单位阶跃响应的超调量和过渡过程时间分别为：σ p = e−ζπ / 1−ζ2*100% = e−0.5*3.14 /1−0.52*100% ≈ 16.3%t s =3 ζw n= 3 0.5 *≈ 1.910⑶ 加入 (1 + Ks ) 相当于加入了一个比例微分环节，将使系统的阻尼比增大，可以有效地减小原系统的阶跃响应的超调量；同时由于微分的作用，使系统阶跃响应的速度（即变w 212p化率）提高了，从而缩短了过渡时间：总之，加入 (1 + Ks ) 后，系统响应性能得到改善。

4-3设单位反馈控制系统开环传递函数如下，试概略绘出相应的闭环根轨迹图（要求确定分离点坐标d ）：（2） (1)()(21)K s G s s s +=+ 解：（1）系统开环传递函数为： */2(1)(1)()(0.5)(0.5)K s K s G s s s s s ++==++，*/2K K = （2）p1=0，p2=-0.5，z1=-1. n=2,m=1根轨迹有2条分支(3) n-m=1 1条渐近线，负实轴；（4）实轴上的根轨迹：（-∞,-1）(-0.5,0)(5) 分离点坐标计算如下：(0.5)0(1)s dd s s ds s =⎡⎤+=⎢⎥+⎣⎦ 220.50d d ++=，解方程得：1 1.7d =-，20.3d =-。

根轨迹如下图所示：Matlab:G=zpk([-1],[0 -0.5],1);figure;rlocus(G)4-4 已知单位反馈控制系统开环传递函数如下，试概略画出相应的闭环根轨迹图（要求算出起始角Pi θ）：（2）*(20)()(1010)(1010)K s G s s s j s j +=+++-解：(1)有三个极点：10p =，21010p j =-+，31010p j =--，有一个零点 120z =-。

(2) n=3，根轨迹有3条分支，m=1，有n-m=2趋于无穷远处； 渐近线交点： 111010*********n m iji j a p z j j n m σ==----++===--∑∑ 渐近线与实轴夹角：0,(21)(21)23311,2a k k k n m k πππϕπ⎧=⎪++⎪===⎨--⎪=⎪⎩(3) 实轴上根轨迹：(-20, 0)；(4) 起始角221212312(21)()()()180(101020)(1010)90180451359000p p p k p z p p p p j j θπθθ=++∠--∠--∠-=︒+∠-++-∠-+-︒=︒+︒-︒-︒=︒=-=︒根轨迹如下图所示：(Matlab:G=zpk([-20],[0 -10-10i -10+10i],1);figure;rlocus(G);) 4-5 设单位反馈控制系统的开环传递函数如下，要求：（1）确定*()(1)(10)K G s s s s =++产生纯虚根的开环增益。

自动控制原理—勘误表1. 自动控制的一般概念1.1 P7：图1-6给出的系统中无开环控制器(扰动补偿)。

1.2 P18：1-7题第一问后，改为“对于图1-21按用水量扰动设计的补偿装置(开环控制)，当冷水温度变化时，出口热水温度如何变化？原补偿装置能否补偿这个温度变化？”1.3 P18：1-8题，“…生产过程中，在最佳湿度条件下出粉率最高，因此…”。

2. 控制系统的数学模型 2.1 P21：图2-2中， 2.2 P21：16行，“…，e C 是反电动势系数。

”2.3 P21：23行，“电动机轴上的转动惯量；)(t M c 是作用在电动机轴上的负载力矩。

”2.4 P23：式(2-17)，…211z z M c +ω； 式(2-20)，c c M z z M 21='。

2.5 P23：图2-5中，应标出测速电机的电压t u 极性，+接地。

2.6 P56：“(2)由系统结构图绘制信号流图”叙述混乱，注意听课。

2.7 P56：图2-41(a)是据方框图2-23(h)绘制的。

图中s M 应改为m s M M -。

2.8 P56：倒2行，“…精简节点的数目，尽可能(方便)地省去只有一个输出的节点。

例如，图2-41(b)中的节点m M 。

”删除后续部分。

2.9 P68：倒2行，“…2/T t e -”2.10 P71：题2-9中，t t e e t c --+-=221)(。

2.11 P72：图2-63中，1K -和2K -都改为K -。

2.12 P73：题2-23的表格中，1行11列的250改为230。

2.13 P74：题2-23中，“(2)若该对象可用具有延迟的二阶惯性环节…时间常数1T 和2T 。

”2.14 P74：题2-24的表格中，2行4列的0.045改为0.04；)(t y 改为)(v y 。

3. 线性系统的时域分析法3.1 P85：图3-9(a)中，n ζω应改为n ζω-。

图3-9中增加说明：(a)01<<-ζ (b)1-<ζ (c)10<<ζ (d)0=ζ (e)1=ζ(f)1>ζ3.2 P95：图3-20下一行，0.004改为0.002。

=
0.04 s 2
1 + 0.24s
+1
C (s)
=
0.04 s 2
10 6s + 10
R(s) 1 + G(s)H (s) 1 + 20 10
6s + 10 20s + 5
E(s) =
10
=
10
R(s) 1 + G(s)H (s) 1 + 20 10
6s + 10 20s + 5
=
(6s
200(20s + 5) + 10)(20s + 5) +
200
=
200(20s + 5) 120s 2 + 230s + 250
U 0 (s) + U i (s) R0
U1 (s) R0
U 2 (s) R0
式（1）（2）（3）左右两边分别相乘得
9
胡寿松自动控制原理习题解答第二章
U0 (s)
= − Z1 Z 2 R2 即
U 0 (s) + U i (s) R0 R0 R0
U 0 (s) + U i (s) = − R03
U0 (s)
正比，此时有
F
d(H − dt
H0)
=
(Q1
−
Q0 )
−
(Q2
−
Q0 )
于是得水箱的微分方程为
F
dH dt
= Q1 − Q2
胡寿松自动控制原理习题解答第二章
图 2-58 电网络与机械系统
1
解：（a）：利用运算阻抗法得： Z1
=
R1

4-1 设单位反馈控制系统的开环传递函数 1)(+=∗s K s G试用解析法绘出∗K 从零变到无穷时的闭环根轨迹图，并判断下列点是否在根轨迹上： （－２＋ｊ０）， （０＋ｊ１）， （－３＋ｊ２） 解：有一个极点：（－1＋ｊ０），没有零点。

根轨迹如图中红线所示。

（－２＋ｊ０）点在根轨迹上，而（０＋ｊ１）， （－３＋ｊ２）点不在根轨迹上。

4-2 设单位反馈控制系统的开环传递函数 )12()13()(++=s s s K s G 试用解析法绘出开环增益K 从零增加到无穷时的闭环根轨迹图。

解：系统开环传递函数为)2/1()3/1()2/1()3/1(2/3)(++=++=s s s K s s s K s g G 有两个极点：（0＋ｊ０），（－1/2＋ｊ０），有一个零点（-1/3，j0）。

根轨迹如图中红线所示。

4-3 已知开环零、极点分布如图4-28所示，试概略绘出相应的闭环根轨迹图。

图4-28 开环零、极点分布图4-4 设单位反馈控制系统开环传递函数如下，试概略绘出相应的闭环根轨迹图(要求确定分离点坐标d)：　 (1) )15.0)(12.0()(++=s s s Ks G解：系统开环传递函数为)2)(5()2)(5(10)(++=++=s s s K s s s Ks g G 有三个极点：（0＋ｊ０），（－2＋ｊ０），（－5＋ｊ０）没有零点。

分离点坐标计算如下：051211=++++d d d 3解方程的010142=++d d 7863.31−=d ，d 88.02−=取分离点为88.0−=d根轨迹如图中红线所示。

（2） )12()1()(++=s s s K s G解：系统开环传递函数为)5.0()1()5.0()1(2/)(++=++=s s s K s s s K s g G有两个极点：（0＋ｊ０），（－0.5＋ｊ０），有一个零点（－1＋ｊ０）。

分离点坐标计算如下：115.011+=++d d d 解方程的05.022=++d d 7.11−=d ，d 29.02−=取分离点为7.11−=d ，29.02−=d 根轨迹如图中红线所示。