模糊神经网络讲义
- 格式:pdf
- 大小:771.25 KB
- 文档页数:17


模糊神经网络第一篇:模糊神经网络的基本原理及应用模糊神经网络是一种最早应用于模糊理论和神经网络理论的融合体,是一种新型的人工智能技术。
模糊神经网络的基本原理是将模糊理论和神经网络理论相结合,通过神经元与模糊集之间的映射建立模糊神经网络,实现数据处理和分类识别的功能。
模糊神经网络由输入层、隐含层和输出层三层组成,输入层接收输入数据,隐含层对输入数据进行加工处理,输出层根据隐含层提供的输出结果进行数据分类和识别。
整个模型的训练过程是通过反向传播算法实现,用来更新神经元之间权值的调整,进而提高分类和识别的准确度。
模糊神经网络在模式识别、图像处理、智能控制、时间序列预测等许多领域得到广泛应用,其应用具有许多优点。
例如,在模式识别领域,其能够对样本数据的模糊性进行精细化处理,提高识别精度;在智能控制领域,其能够通过学习和反馈调整策略,提高自适应控制效果,还能够模拟人的认知过程,具有较高的仿真能力,从而实现全面协调的规划与决策。
尽管模糊神经网络具有许多优点,但是和其他神经网络一样,其存在一些缺点。
例如,网络模型设计难度大,需进行繁琐的参数优化和实验验证;模型训练过程中存在局部最优问题,可能导致模型的收敛速度较慢,所以在实际应用过程中,需要充分考虑它们的优缺点来选择合适的模型。
综上所述,模糊神经网络在人工智能领域的应用具有广泛的前景,因为其能够克服传统的困难,更好地解决问题。
在未来,我们将不断地研究模糊神经网络的性能优化和应用扩展,为促进人工智能理论与应用的融合做出更大的贡献。
第二篇:模糊神经网络的案例分析及实现方法模糊神经网络是人工智能领域重要的一类算法之一,它在图像处理、数据挖掘、机器学习等领域得到了广泛的应用。
下面我们以智能交通管理为例,介绍模糊神经网络的具体应用过程。
模糊神经网络在实现智能交通管理中,主要可以实现车辆流量监测、拥堵监测、交通信号优化等功能。
其中,车辆拥堵监测是模糊神经网络在智能交通管理中的应用较为广泛的方向。


模糊神经网络的研究及其应用模糊神经网络是一种结合了模糊逻辑和神经网络的先进技术,它在许多领域中都得到了广泛的应用。
在本文中,我们将介绍模糊神经网络的基本概念、特点、理论研究以及实际应用,最后对未来发展进行展望。
模糊神经网络是一种基于模糊逻辑理论的多层前馈网络,它通过模拟人脑神经元的连接方式来实现分类和识别等功能。
与传统的神经网络相比,模糊神经网络具有以下特点:模糊化输入:将输入数据转换为模糊量,使网络能够更好地处理不确定性和非线性问题。
采用模糊规则:模糊神经网络采用模糊规则进行计算,这些规则可以很好地描述现实世界中的模糊现象。
双重迭代:模糊神经网络需要进行模式识别和参数优化双重迭代过程,以实现网络性能的优化。
模糊神经网络在许多领域中都得到了广泛的应用,以下是其中的几个典型例子:图像处理:模糊神经网络可以应用于图像分类、图像增强、图像恢复等方面,提高图像处理的效果和速度。
语音识别:模糊神经网络可以应用于语音信号的特征提取和分类,提高语音识别的准确率和鲁棒性。
自然语言处理:模糊神经网络可以应用于文本分类、情感分析、机器翻译等方面,提高自然语言处理的效果和效率。
控制领域:模糊神经网络可以应用于系统建模、控制优化等方面,提高控制系统的稳定性和鲁棒性。
模糊神经网络的理论研究主要集中在以下几个方面:模糊逻辑的研究:模糊逻辑是模糊神经网络的基础,因此对模糊逻辑的研究是十分必要的。
主要研究内容包括模糊集合、模糊关系、模糊推理等方面的研究。
神经网络的研究:神经网络是模糊神经网络的核心,因此对神经网络的研究也是十分必要的。
主要研究内容包括神经元的数学模型、神经网络的训练算法、神经网络的稳定性等方面的研究。
模糊神经网络的建模和优化:模糊神经网络的建模和优化是提高其性能的关键。
主要研究内容包括网络结构的选取、参数的优化、训练算法的设计等方面的研究。
模糊神经网络在实际应用中已经取得了显著的成果,以下是其中的几个例子:电力系统的负荷预测:通过建立基于模糊神经网络的负荷预测模型,可以对电力系统的负荷进行准确预测,提高电力系统的稳定性和安全性。
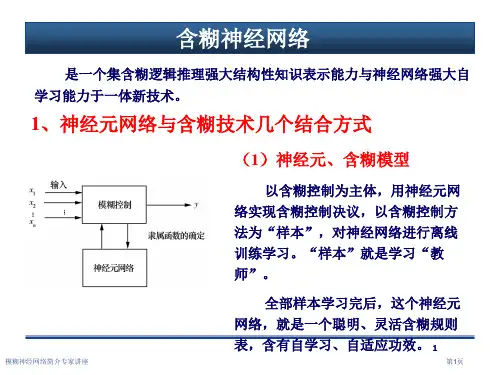




模糊神经网络(备课笔记)预备知识复杂的东西是难以精确化的,这使得人们所需要的精确性和问题的复杂性间形成了尖锐的矛盾。
正如模糊数学的创始人L.A.Zadeh(查德)教授(美国加利福尼亚大学)所说:“当系统的复杂性增加时,我们使它精确化的能力将减小。
直到达到一个阈值,一旦超越它,复杂性和精确性将相互排斥。
”这就是著名的“互克性原理”。
该原理告诉我们,复杂性越高,有意义的精确化能力就越低;而复杂性意味着因素众多,以致人们往往不可能同时考察所有因素,只能把研究对象适当简化或抽象成模型,即抓住其中的主要部分而忽略掉次要部分。
当在一个被压缩了的低维因素空间考虑问题时,即使本来是明确的概念,也会变得模糊起来。
或者某些抽象简化模型本身就带有概念的不清晰,如“光滑铰链”这个力学模型,什么叫“光滑”、什么叫“粗糙”就没有一个明确的定义,客观上两者之间没有绝对分明的界限;主观上,决策者对此类非程序化决策做出判断时,主要是根据他的经验、能力和直观感觉等模糊概念进行决策的。
或者判断一个人的好坏,本来有很多因素,比如人品、性格、相貌等,现在简化改成一个综合评价:好、坏、一般等,都是根据个人爱好或者个人经验等模糊概念进行判断的。
在科学发展的今天,尤其在工程研究和设计领域中,这些模糊性问题就无法回避了,要求对数据进行定量分析,那如何对其进行定量分析呢?1965年,Zadeh教授发表一篇论文“模糊集合”(Fuzzy sets),所谓模糊集合就是指边界不清的集合。
提出用“隶属函数”(menbership function)这一概念来描述现象差异中的中间过渡,突破了德国人Cantor创立的古典集合论中属于或不属于的绝对关系,标志着模糊数学的诞生。
Zadeh认为应该重新把模糊性和精确性统一在一起,因为在现实生活中复杂事物要绝对精确是不可能的,实际上只是把所谓的不准确程度降低到了无关重要的程度。
他这篇论文第一次引人注目地提出了模糊性问题,给出了模糊概念的定量表示法,标志着模糊数学的诞生。


模糊神经网络(备课笔记)参考书:杨纶标,高英仪。
《模糊数学原理及应用》(第三版),广州:华南理工大学出版社彭祖赠。
模糊数学及其应用。
武汉:武汉科技大学胡宝清。
模糊理论基础。
武汉:武汉大学出版社王士同。
模糊系统、模糊神经网络及应用程序设计。
《模糊系统、模糊神经网络及应用程序设计》本书全面介绍了模糊系统、模糊神经网络的基本要领概念与原理,并以此为基础,介绍了大量的应用实例及编程实现实例。
顾名思义,模糊神经网络就是模糊系统和神经网络的结合,本质上就是将常规的神经网络(如前向反馈神经网络,Hopfield神经网络)赋予模糊输入信号和模糊权值。
选自【模糊神经网络P17】预备知识复杂的东西是难以精确化的,这使得人们所需要的精确性和问题的复杂性间形成了尖锐的矛盾。
正如模糊数学的创始人L.A.Zadeh(查德)教授(美国加利福尼亚大学)所说:“当系统的复杂性增加时,我们使它精确化的能力将减小。
直到达到一个阈值,一旦超越它,复杂性和精确性将相互排斥。
”这就是著名的“互克性原理”。
该原理告诉我们,复杂性越高,有意义的精确化能力就越低;而复杂性意味着因素众多,以致人们往往不可能同时考察所有因素,只能把研究对象适当简化或抽象成模型,即抓住其中的主要部分而忽略掉次要部分。
当在一个被压缩了的低维因素空间考虑问题时,即使本来是明确的概念,也会变得模糊起来。
或者某些抽象简化模型本身就带有概念的不清晰,如“光滑铰链”这个力学模型,什么叫“光滑”、什么叫“粗糙”就没有一个明确的定义,客观上两者之间没有绝对分明的界限;主观上,决策者对此类非程序化决策做出判断时,主要是根据他的经验、能力和直观感觉等模糊概念进行决策的。
或者判断一个人的好坏,本来有很多因素,比如人品、性格、相貌等,现在简化改成一个综合评价:好、坏、一般等,都是根据个人爱好或者个人经验等模糊概念进行判断的。
在科学发展的今天,尤其在工程研究和设计领域中,这些模糊性问题就无法回避了,要求对数据进行定量分析,那如何对其进行定量分析呢?1965年,Zadeh教授发表一篇论文“模糊集合”(Fuzzy sets),所谓模糊集合就是指边界不清的集合。
提出用“隶属函数”(menbership function)这一概念来描述现象差异中的中间过渡,突破了德国人Cantor 创立的古典集合论中属于或不属于的绝对关系,标志着模糊数学的诞生。
Zadeh认为应该重新把模糊性和精确性统一在一起,因为在现实生活中复杂事物要绝对精确是不可能的,实际上只是把所谓的不准确程度降低到了无关重要的程度。
他这篇论文第一次引人注目地提出了模糊性问题,给出了模糊概念的定量表示法,标志着模糊数学的诞生。
模糊数学是使模糊现象定量化的应用数学分支学科。
由于它突破了传统数学绝不允许模棱两可的约束,使那些与数学毫不相关的学科都可能用定量化和数学化加以描述和处理,从而显示其强大的生命力。
在模糊评价中,最基本和使用最多的是隶属度和隶属函数。
隶属度表示元素u属于模糊集合U的程度;也就是对模糊集合的判断是用元素对此集合的从属程度大小来表达的。
模糊系统模糊逻辑控制系统,简称模糊控制系统或模糊系统,是一种基于模糊数学理论的新型控制方法。
模糊控制由于模仿人对复杂事物的抽象思维方式,利用模糊信息处理对被控对象执行控制。
所以,它不需要知道系统的精确数学模型。
对不确定的非线性的系统来说是一种有效的控制途径。
但是,模糊控制对信息的简单模糊化导致系统的控制精度下降。
为了提高精度,往往要在模糊化时增加模糊量的个数,或者,增大控制规则集。
这样会使控制规则搜索范围的扩大、搜索时间增加、降低了决策的速度,则影响了动态过程的品质。
因此,隶属函数和控制规则的优化是提高品质的关键,在本质上,是对模糊控制中的知识进行正确性校正。
一般地说,模糊系统是指那些与模糊概念和模糊逻辑有直接关系的系统,主要由模糊化接口、知识库、模糊推理机、反模糊化接口四部分组成。
1、模糊化(Fuzzification),输入变量模糊化,即把确定的输入转化成为由隶属度描述的模糊集。
模糊化接口主要将检测输入变量的精确值根据其模糊度划分和隶属度函数转换成合适的语言值(即模糊值)。
模糊划分尚未有一种确定的唯一的方法。
它是根据经验而进行划分的。
对于一个论域而言,模糊度的划分过少,很明显语言变量就会粗糙,这样对于一个控制系统来说,其控制质量就产生不良影响。
如果划分的模糊集过多,则变量的检测和控制精度就越高,但是形成的控制规则就会过多,进行模糊推理就会占用大量的处理时间和过程;在采用模糊关系运算时,也会产生庞大的关系矩阵,从而关系运算就变得麻烦,产生的控制表也会庞大而占据较多内存。
一般情况下为了尽量减少模糊规则数,可对于检测和控制精度要求高的变量划分多(例如5一7个)的模糊度,反之则划分少(例如3个)的模糊度。
当完成变量的模糊度划分后,需定义变量各模糊集的隶属函数。
每个划分的梯形隶属度函数如图:2、知识库(knowledge base)知识库中存贮着有关模糊控制器的一切知识,包含了具体应用领域中的知识和要求的控制目标,它们决定着模糊控制器的性能,是模糊控制器的核心。
例如数据库、规则库等等。
(1)此数据库不是计算机软件中数据库的概念,它存贮着有关模糊化、模糊推理、解模糊的一切知识,如模糊化中的输入变量各模糊集合的隶属函数定义,以及模糊推理算法,反模糊化算法,输出变量各模糊集合的隶属函数定义等。
(2)模糊规则库是由若干模糊推理规则组成的,模糊控制规则是根据人的思维方式对一个被控系统执行控制而总结出来的带有模糊性的控制规则。
如专家经验等。
3、模糊推理机(Fuzzy Inference Engine)模糊推理机的功用在于:根据模糊逻辑法则把模糊规则库中的模糊“if-then”规则转换成某种映射。
模糊推理,这是模糊控制器的核心,模拟人基于模糊概念的推理能力。
4. 反模糊化(defuzzification),清晰化,即把输出的模糊量转化为实际用于控制的清晰量。
神经网络(Neural Network,简称NN)是由众多简单的神经元连接而成的网络。
尽管每个神经元结构、功能都不复杂,但网络的整体动态行为极为复杂,可组成高度非线性动力学系统,从而可表达许多复杂的物理系统。
神经网络的研究从上世纪40年代初开始,目前,在世界范围已形成了研究神经网络前所未有的热潮。
它已在控制、模式识别、图像和视频信号处理、金融证券、人工智能、军事、计算机视觉、优化计算、自适应滤波和A/D变换等方面获得了应用。
模糊系统(Fuzzy System,简称FS)是仿效人的模糊逻辑思维方法设计的系统,方法本身明确地说明了系统在工作过程中允许数值量的不精确性存在。
模糊数学自1965年诞生至今已有40多年的历史,它在理论上还处于不断发展和完善中。
它是用精确的数学理论研究人类思维的模糊性,其最基本的概念是隶属度。
用隶属度来描述某一对象或称为元素属于某一论域者称为集合的程度,这样既能准确描述人类思维中的模糊性,又能被计算机理解。
目前,它已广泛应用于计算机科学、自动控制、系统工程、环保、机械、管理科学、思维科学、社会科学等领域。
模糊系统与神经网络的区别与联系(1)从知识的表达方式来看模糊系统可以表达人的经验性知识,便于理解,而神经网络只能描述大量数据之间的复杂函数关系,难于理解。
(2)从知识的存储方式来看模糊系统将知识存在规则集中,神经网络将知识存在权系数中,都具有分布存储的特点。
(3)从知识的运用方式来看模糊系统和神经网络都具有并行处理的特点,模糊系统同时激活的规则不多,计算量小,而神经网络涉及的神经元很多,计算量大(4)从知识的获取方式来看模糊系统的规则靠专家提供或设计,难于自动获取.而神经网络的权系数可由输入输出样本中学习,无需人来设置。
因此将两者结合起来,在处理大规模的模糊应用问题方面将表现出优良的效果。
模糊集理论和神经网络虽都属于仿效生物体信息处理机制以获得柔性信息处理功能的理论,但两者所用的研究方法不同。
神经网络着眼于大脑的微观网络结构,通过学习、自组织化和非线性动力学理论形成并行分析方法,可处理语言化的模式信息,而模糊集理论则着眼于可用语言和概念作为代表大脑的宏观功能,按人为引入的隶属度函数,逻辑处理包含有模糊性的语言信息。
模糊逻辑具有模拟人脑抽象思维的特点,而神经网络具有模拟人脑形象思维的特点,对二者结合将有助于从抽象和形象思维两方面模拟人脑的思维特点,是目前实现智能控制的重要形式。
目前,FS和NN的结合主要有模糊神经网络和神经模糊系统。
神经模糊系统是以NN为主,结合模糊集理论。
它将NN作为实现FS 模型的工具,即在NN的框架下实现FS或其一部分功能。
神经模糊系统虽具有一些自己所具有而NN不具备的特性,但它没有跳出NN的框架。
神经模糊系统从结构上来看,一般是四层或五层的前向神经网络。
模糊神经网络是神经网络的模糊化。
即以模糊集、模糊逻辑为主,结合NN方法,利用NN的自组织性,达到柔性信息处理的目的。
目前,FS理论和NN结合主要应用于商业及经济估算、自动检测和监视、机器人及自动控制、计算机视觉、专家系统、语音处理、优化问题、医疗应用等方面,并可推广到工程、科技、信息技术和经济等领域。
模糊神经网络进入20世纪80年代以后,模糊理论体系得到逐步完善,模糊技术在工业控制应用中取得巨大成功,特别是神经网络研究热潮的再一次兴起,许多人很自然地把目光投向模糊逻辑系统与神经网络的结合这一重要方向。
在20世纪80年代末至90年代初,模糊逻辑系统与神经网络融合问题开始真正引起学术界的关注。
近年来,这两类方法日趋融合,已成为智能控制方法。
人工神经网络按其运行过程中信息流向可以分为前向网络和反馈型网络两大类。
前向网络通过许多具有简单处理能力的神经元的相互组合使整个网络具有复杂的非线性逼近能力,反馈型网络通过网络神经元状态的变迁最终稳定于平衡状态,得到联想存储或优化计算的结果。
感知器、自适应线性元件和BP网络等属于前向网络,而Hopfield网络则属于反馈型网络。
按学习方式神经网络又可分为有监督学习、无监督学习和强化学习三类。
有监督学习需要包含已知输入和输出的样本训练集,学习系统根据已知输出与实际输出之间的差值来调节系统参数。
在无监督学习中,学习系统完全按照数据的某些统计规律来调节自身结构和参数,是一种自组织的过程。
强化学习介于前两种学习方式之间,外界环境对系统输出结果只给出评价信息(奖或惩)而不给出正确答案,学习系统通过强化那些受奖的动作来改善自身性能。
神经网络具有非线性映射能力、学习能力、并行处理能力和容错能力,模糊逻辑具有处理不确定性的能力,二者在复杂工业对象的建模和控制领域已经得到了广泛的应用。
目前,单纯使用神经网络控制技术的研究有停滞不前的趋势。