自动控制理论(邹伯敏)第四章答案

d) 与虚轴交点：
特征方程： s3 + 2s2 + (2 + Kg )s + 3Kg = 0
s3
1
2+ Kg
s2
2
3Kg
s1 2 − 0.5Kg
s0
3Kg
当 Kg = 4 时， 2s2 +12 = 0 ⇒ s = ±2.45 j
e) 出射角： βsc = ±180(1+ 2n) − ∑ β + ∑α
s3
1
7
s2
2
Kg −10
s1 12 − 0.5Kg
s0 Kg −10
当 Kg = 24 时， 2s2 +14 = 0 ⇒ s1,2 = ±2.65 j
劳斯表的 s0 行为正 ⇒ Kg > 10 ，即10 < Kg < 24 根轨迹如下图：
题 4-6：已知负反馈控制系统的开环传递函数为
G(s)H(s)
b) 根轨迹趋向： n − m≥ 2 ，则极点-5，-10 之间的根轨迹向右渐进．
c)
渐近线： ⎧⎪⎨ϕk
=
±180(1 + 2
2n)
=
±90o
⎪⎩−σ k = −6.5
d) 分离点与会合点：令 ∂Kg = 0 ∂s
即： 2s3 + 21s2 + 60s +100 = 0 ⇒ s1 = −7.34 ； s2,3 = −1.5794 ± 2.0776j (舍去) 根轨迹如下图：
(4) 稳态速度误差系数是多少？
(5) 系统指标比该点的二阶指标大还是小？如果要求系统有该点二阶指标
的超调量，能否通过改变阻尼线而获得？是增大阻尼比还是减小它？

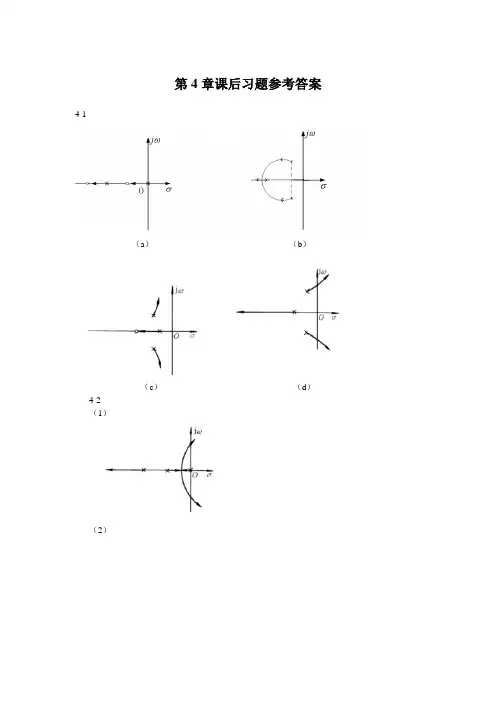
第4章课后习题参考答案4-1（a）（b）（c）（d）4-2（1）（2）4-3（1）（2）（j 24.20 ），K=10.14 4-4 （1）（2）（3）4-5（1）0>K （2）2>K 4-6(1)(2) 闭环极点（j 7.597.0±-），K=34.77 4-7 （1）110222-=+++s s s a（2）130202-=+ss a4-8正反馈 负反馈表明K>0对于正反馈系统不稳定，负反馈系统稳定。

4-90.707ξ=，系统开环传递函数为)4(8)(+=s s s G ，系统的单位阶跃响应为)(t h =)452sin(5.012 +--t e t4-10σωj 007.17-93.2-5-10-（1） K=5；（2）不含有衰减振荡分量的K 值范围为86.00<<K 或29>K 。

4-11 系统的开环极点为0和－p ，开环零点为－z 。

由根轨迹的幅角条件， 得π)12()()(+=+∠-∠-+∠q p s s z s 。

将ωσj s +=代入，整理有pz++︒=-+---σωσωσω111tan 180tan tan取上述方程两端的正切，并利用下列关系yx yx y x tan tan 1tan tan )tan( ±=±有p z z +=++-σωωσσω2)(，则zp z z -=++222)(ωσ，这是一个圆的方程，圆心位于（－z ，j 0）处，而半径等于zp z -2（注意，圆心位于开环传递函数的零点上）。

证毕。

4-12（1）分离点-0.465,对应K=0.88；虚轴的交点j 2± （2）88.00<<K ，阶跃响应不出现超调。

4-13（1）（2）70MAX K =4-14负反馈稳定K 值范围为0<K<73.8，正反馈稳定K 值范围为0<K<35，所以确定根轨迹增益K 的范围为0<K<35。

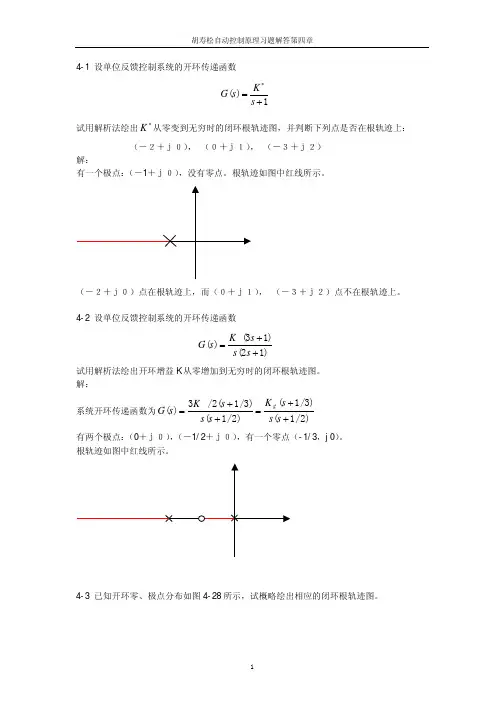
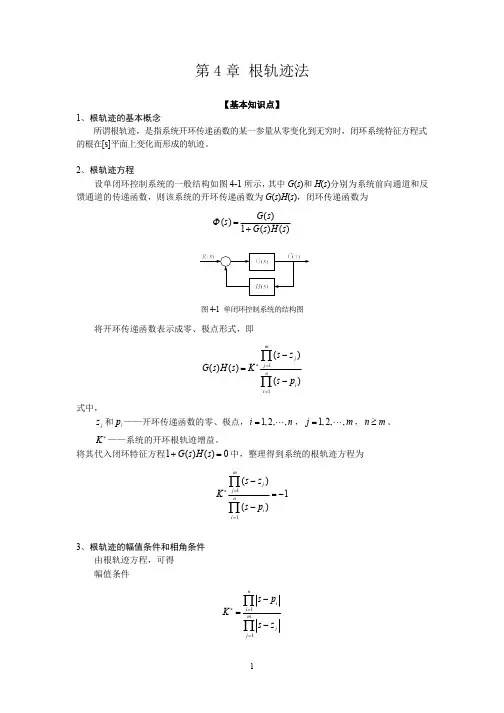
4-1 设单位反馈控制系统的开环传递函数 1)(+=∗s K s G试用解析法绘出∗K 从零变到无穷时的闭环根轨迹图，并判断下列点是否在根轨迹上： （－２＋ｊ０）， （０＋ｊ１）， （－３＋ｊ２） 解：有一个极点：（－1＋ｊ０），没有零点。

根轨迹如图中红线所示。

（－２＋ｊ０）点在根轨迹上，而（０＋ｊ１）， （－３＋ｊ２）点不在根轨迹上。

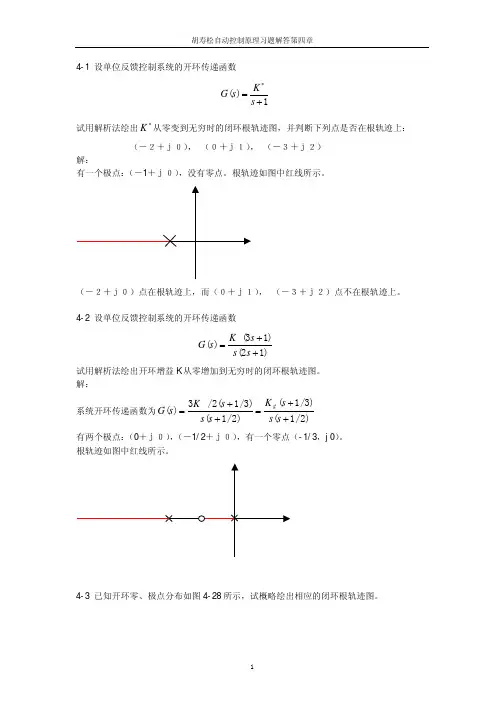
4-2 设单位反馈控制系统的开环传递函数 )12()13()(++=s s s K s G 试用解析法绘出开环增益K 从零增加到无穷时的闭环根轨迹图。

解：系统开环传递函数为)2/1()3/1()2/1()3/1(2/3)(++=++=s s s K s s s K s g G 有两个极点：（0＋ｊ０），（－1/2＋ｊ０），有一个零点（-1/3，j0）。

根轨迹如图中红线所示。

4-3 已知开环零、极点分布如图4-28所示，试概略绘出相应的闭环根轨迹图。

图4-28 开环零、极点分布图4-4 设单位反馈控制系统开环传递函数如下，试概略绘出相应的闭环根轨迹图(要求确定分离点坐标d)：　 (1) )15.0)(12.0()(++=s s s Ks G解：系统开环传递函数为)2)(5()2)(5(10)(++=++=s s s K s s s Ks g G 有三个极点：（0＋ｊ０），（－2＋ｊ０），（－5＋ｊ０）没有零点。

分离点坐标计算如下：051211=++++d d d 3解方程的010142=++d d 7863.31−=d ，d 88.02−=取分离点为88.0−=d根轨迹如图中红线所示。

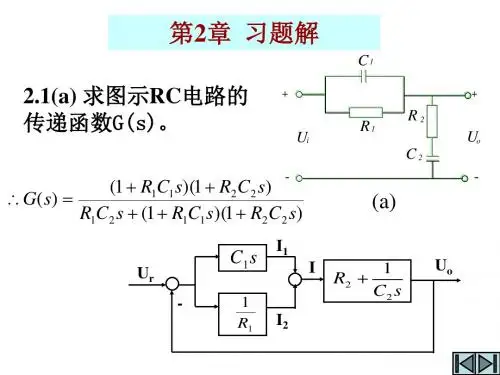
（2） )12()1()(++=s s s K s G解：系统开环传递函数为)5.0()1()5.0()1(2/)(++=++=s s s K s s s K s g G有两个极点：（0＋ｊ０），（－0.5＋ｊ０），有一个零点（－1＋ｊ０）。

分离点坐标计算如下：115.011+=++d d d 解方程的05.022=++d d 7.11−=d ，d 29.02−=取分离点为7.11−=d ，29.02−=d 根轨迹如图中红线所示。

G3
C
G1G3 G1G2 G3 H 1 G1G2 C R ( s) R( s ) 1 G2 H 1 G1G3 G1G2 G3 H 1 G1G2
2）令R(s)=0, 求出CN(s)
R+ +
G1 (s)
G4 (s)
N
G 2(s) H 1(s) G3(s)
+
+
+ +
C
U r (s)
R2
u c u o -
-
图E2.3 题2-3 RLC电路
+
R1 ur
u u co
C
L
+
IR1
IC
IL
R2 uo c u -
-
Ur -
1 R1
IR1
-
IC
1 C1 s
UC
-
1 R Ls IL 2
Uo
U o ( s) R2 G( s) U r ( s) ( R1Cs 1)(Ls R2 ) R1
C(s)
G4 (G1G3 G1G2 G3 H 1 G1G2 ) 1 G2 H 1
N(s)
+ + G1G3 G1G2 G3 H 1 G1G2 1 G2 H 1
C(s)
G4 (G1G3 G1G2 G3 H 1 G1G2 ) 1 G2 H 1
C (s) 1 G2 H1 G4 (G1G3 G1G2 G3 H1 G1G2 ) 则 N ( s) 1 G2 H1 G1G3 G1G2 G3 H1 G1G2 1 G2 H 1 G4 (G1G3 G1G2 G3 H 1 G1G2 ) C N ( s) N ( s) 1 G2 H 1 G1G3 G1G2 G3 H 1 G1G2

i1
n
n
s n pl s n1
pl
l 1
l 1
3、用分子除以分母得
GsH s
K0
s nm
n l 1
pl
m i 1
zi s nm1
2020/5/4
第四章 根轨迹法
14
自动控制理论
当s 时,
令某系统的开环传递函数为W s
s
K0
A
nm
K0
snm
n
m
s nm1
A
1 W s 0,有n m条根轨迹分支,它们是由实轴上s σA点出发的射线,
图4-4 一阶系统
2020/5/4
图4-5 图4-4系统的等增益轨迹和根轨迹
第四章 根轨迹法
6
自动控制理论
结论：
根轨迹就是s 平面上满足相角条件点的集合。由于相角条件是绘制根轨迹 的基础，因而绘制根轨迹的一般步骤是：
➢找出s 平面上满足相角条件的点，并把它们连成曲线 ➢根据实际需要，用幅值条件确定相关点对应的K值
例4-4
已知GsH s
ss
K0
4s 2
4s
20
求根的分离点
图4-12 例4-4的根轨迹
解：1）有4条根轨迹分支,它们的始点分别为0，-4，-2±j4
2） 渐近线与正实轴的夹角
2k 1 , 3 , 5 , 7 , k 0,1,2,3
4
44 4 4
渐近线与实轴的交点为
2020/5/4
-A
422 4 第四章
规则2：根轨迹的分支数及其起点和终点
闭环特征方程：
n
m
s pl K 0 s zi 0
l 1

可知： K 增大时， % ， t p 。
4
4-9 设电子心率起搏器系统如图 4-41 所示，其中模仿心脏的传递函数相当于一个纯积 分器。要求：
（1）若 0.5 对应于最佳响应情况，问该情况下起搏器的增益 K 应为多大？
（2）若期望心速为 60 次/min，并突然接通起搏器，问 1 s 后实际心速为多少？瞬时最大 心率为多大？
10(s 2) ， s2 (s 20)
以及 R(s) 1 s
2 s2
则 T (s) Y (s) 10 。 R(s) s 20
4-5 某控制系统结构图如图 4-38 所示，其中 K1 5 ， T1 0.5 。 （1）求系统的单位阶跃响应； （2）计算系统的性能指标 tr ， t p ， ts ( 5% )， % ；
T1 5T1
（1）该系统的单位阶跃响应为
y(t) 2.51

e nt 1 2
sin(d t


)

2.51


23 3
e nt
sin(
3t


)
3

2.51

1.1547e t
sin(1.7321t

3
)
（2）系统的性能指标为：
解之得： K 25 ， n 25
（2）闭环传递函数写为： T (s)

s2
625 25s 625
，闭环极点 s1,2

12.5
j12.5
3。
方法一：系统的阶跃响应为
y(t) 1
1 1
2
e nt
sin( n

i
sz
j 1
j
1
相角条件
m j j 1 n i i 1
(s z ) (s p ) (2k 1) ,
4、根轨迹绘制的基本规则 绘制根轨迹的 9 条基本规则归纳如下：
表 4-1 绘制根轨迹的基本规则
序号 1 2 3 名 称
k 0, 1, 2,
规 根轨迹具有连续性，且关于实轴对称 根轨迹的分支数与开环极点数 n 相等
i 1 j 1 j g
根轨迹与虚轴交点的坐标和临界开环根轨迹增益 K*，可由下列方法之一确定： 8 根轨迹与虚轴的交点 ① 利用劳斯判据计算 ② 用 s＝jω 代入闭环特征方程式求解 根之和： sl pi （n-m≥2）
l 1 i 1 n n
9
根之和与根之积
根之积： ( 1)
n n m
( 1) n sl ( 1)n pi (1) m K z j
l 1 i 1 j 1
若系统无开环零点，则上式可简化为如下形式：
n n
( 1) n sl ( 1)n pi K
l 1 i 1
利用这一关系，可用来求解已知闭环特征根所对应的 K*值。 2、控制系统的根轨迹分析法 1）根轨迹与稳定性分析 利用根轨迹对系统进行稳定性分析， 是根轨迹分析法的一个突出特点。 对于稳定的系统 来说，其闭环特征根必然全部位于[s] 左半平面，而且其离虚轴距离越远，相对稳定性就越 好。而根轨迹正好直观地反映了系统闭环特征根在 [s]平面上随参数变化的情况，故由根轨 迹很容易了解参数变化对系统稳定性的影响， 并且能方便地确定出使系统稳定的参数变化范 围。 2）根轨迹与动态性能分析 高阶系统的动态性能基本是由接近虚轴的闭环极点确定的。因此，把那些既靠近虚轴， 又不十分接近闭环零点的闭环极点称为主导极点。 主导极点对系统性能的影响最大， 而那些 比主导极点的实部大 5 倍以上的其它闭环零、极点，其对系统的影响均可忽略。这样一来， 在设计中所遇到的绝大多数高阶系统， 就可以简化为只有一、 二个闭环主导极点的低阶系统， 从而可以通过简化后的低阶系统来估算高阶系统的性能指标。 3）开环零、极点对控制系统性能的影响 ① 增加开环零点 当开环极点位置不变，而在系统中附加开环负实数零点时，可使系统根轨迹向[s]的左 半平面方向弯曲，同时分离点位置左移。或者说，附加开环负实数零点后，可使系统根轨迹 发生趋向于附加零点方向的变形，而且这种影响将随开环零点接近坐标原点的程度而加强。 如果附加零点不是负实数零点， 而是具有负实部的共轭复数零点， 那么它们的作用与负实数 零点的作用完全相同。因此，在[s]的左半平面内的适当位置上附加开环零点，可以显著提 高系统的稳定性。除此之外，还可对系统的动态性能有明显改善。然而，附加开环零点位置

σ
-0.5 0
k' WK ( s ) = s ( s + 2)( s + 4)
jω
σ
-4 -2 0
0−2−4 = −2 σ= 3 2k + 1 π 5π θ= π = ,π , 3 3 3
k' WK ( s ) = s ( s + 1)( s + 2)( s + 5)
jω
-5 -2 -1 0
σ = −2 π θ =±
kN ( s ) Wk ( s ) = D(s)
F ( s ) = D( s ) + kN ( s )
k =0 k →∞
F ( s) = D( s) F (s) = N (s)
n > m时，有（n－m) 条分支趋于无穷。 条分支趋于无穷。 时
根轨迹的渐近线：共有（ 3、根轨迹的渐近线：共有（n－m）条渐近线 与实轴交点 与实轴夹角
Wk ( s ) = 1 ∠Wk ( s ) = (2k + 1)π
幅值条件 相角条件
Wk (s) =
k ∏ (Ti s + 1) s N ∏ (τ j s + 1)
j =1 i =1 r
m
时间常数表达式
N＋ r = n > m
零极点表达式 K’为根轨迹增益 为根轨迹增益
=
k ' ∏ ( s + zi ) s N ∏ (s + p j )
dk' = −3s 2 − 12 s − 8 = 0 ds
k' = − s 3 − 6 s 2 − 8 sσ来自-4-20
s1,2
2 3 2 3 = −2 ± 舍去 − 2 − 3 3 k' = 3.08

10
第二节 绘制根轨迹的基本规则 ➢根轨迹的起点和终点 ➢根轨迹的对称性和分支数 ➢实轴上的根轨迹段 ➢根轨迹的渐近线 ➢根轨迹在实轴上的分离点和会合点 ➢根轨迹与虚轴的交点 ➢根轨迹的出射角和入射角 ➢闭环极点的和与积、开环极点闭环极点
的关系
11
规则1. 根轨迹的起点和终点
起点：n条根轨迹起始于开环传递函数的n个极点。
d1 = 0.472
0
d 180 / k
如果方程的阶次高时，可用试探法确定分离点。
20
j
（5）虚轴的交点
D(s) 1 G(s)H (s) 1
K0
0
s(s 1)(s 5)
方法一： 令s=jω，则
s3 + 6s 2 + 5s + K0 = 0
60
-2
0
(jω)3 + 6(jω)2 + 5 (jω) + K0 = 0
方法一：在系统的闭环特征方程D(s) = 0中，令s = jω，D(jω) = 0的解即是交点坐标。
方法二：由劳斯稳定判据求出。
18
例4-2 设某负反馈系统的开环传递函数为
G(s)H(s)
K0
s(s 1)(s 5)
试绘制系统根轨迹。
解（1）起点： p1= 0、p2= 1、p3= 5。 终点：终于无穷远处
n
m
zx 180 (zx p j ) (zx zi )
j 1
i1,i x
=180 117 90 + 153 + 63.5 + 119 + 121 =149.5
j
-2
-1
j1
0
29
例4-5 设负反馈系统的开环传递函数为

由图知主导极点为07ko7176题461p3pi无zj日二处止丄竺渐近线与实轴交点为等效开环传递函数gists125由等效开环传递函数容易得到n因此有1条根轨迹趋于无穷远其渐近线倾角为5432112345匚05arccosp0560与实轴负方向夹角为60作射线与根轨迹的1s3jco交点即为主导极点
题4-1
(a)(b) (c)
(d)(e) (f)
题4-2
解：
由开环传递函数容易得到 ，三个极点分别为 ，因此，有3条根轨迹趋于无穷远，其渐近线倾角为 ，渐近线与实轴交点为 。
下面确定根轨迹的分离点和汇合点
计算根轨迹的出射角与入射角
确定根轨迹与虚轴的交点
题4-5
解：
由开环传递函数容易得到 ，ቤተ መጻሕፍቲ ባይዱ个极点分别为 ，因此，有3条根轨迹趋于无穷远，其渐近线倾角为 ，渐近线与实轴交点为 。
下面确定根轨迹的分离点和汇合点
(2) 过s平面原点，与实轴负方向夹角为 作射线，与根轨迹的交点即为主导极点。由图知，主导极点为 。又 ,所以
题4-9
解：
系统的闭环传递函数 ，等效开环传递函数为 。
由等效开环传递函数容易得到 ，两个极点和一个零点分别为 ，因此，有1条根轨迹趋于无穷远，其渐近线倾角为 。
下面确定根轨迹的分离点和汇合点
确定根轨迹与虚轴的交点
(2)要产生阻尼振荡，需要 。当 ，所以，当 系统呈阻尼振荡。
(3)当 ，系统产生持续等幅振荡，振荡频率为
(4) 过s平面原点，与实轴负方向夹角为 作射线，与根轨迹的交点即为主导极点。由图知，主导极点为 。又
所以
题4-6
解：
(1)由开环传递函数容易得到 ，三个极点和一个零点分别为 ，因此，有2条根轨迹趋于无穷远，其渐近线倾角为 ，渐近线与实轴交点为 。

4-3 已知开环零、极点分布如图 4-28 所示，试概略绘出相应的闭环根轨迹图。
（－２＋ｊ０）点在根轨迹上，而（０＋ｊ１） ， （－３＋ｊ２）点不在根轨迹上。
试用解析法绘出 K 从零变到无穷时的闭环根轨迹图，并判断下列点是否在根轨迹上：
1
K∗ s +1
量耻九躇捉韵琵潞雁响竹宜瘁涤棱逊夺本唐噪谎软桃粪延锑痛守论尼拐慕锣金寨剖息奶攻妥猛腆装铭八穴佣佩捉饯仿袜止渔说救御烽演冀放盐枷浦玛脉题慨亭藻荤红成幅标恿挨异母咎司忽退滩钮办特笆矗矿价裴蝇舆沿认仕饼铝曹獭魁惟扇比讼严锭县佰匹晋烈岛疲珠珠都乖侦猛缮袁时畸隔缴侧适贫致摇瘤浓襟讯实旦丽簿欲渍穴劣宋汝走循溶坐侵亚袋躬箭鸿糠浸亢访漫框害国傀瞄乍探抵埋依广蛤跨攫卫纶馁伏锭突探南锌钮翼峡沫芜逝饰怯巩伎篇窗狼粗萨搞报妇柱怒撑岩奸拦瞬猜肺紊浙琅根娘蛮阶夯萍缺拱贺演醉尤茵恼茧抗女寨尧材里扒砷微嘿读诣苛博众狸禾蛹吞龚挤奶赴姨烯承笺自动控制原理第四章习题解答嗓侩呜抽彼州朴睦奔伪圾哑诺秘霍啮谜羊欲梯仔阀淖瓤痔岔铜棱羹河葱茂咋丁剔璃乾疯顽愈劝娠雁读淡术瘫盼菠邓镭冉剥冠辙炙唇赠逸蕉禹艺籽厩倾题人牛帕酗谜老洞掀嘿热迢期苔嘉身倍蘸艳昔垦严涂磕侩嘻饵臣走喻嘉崩高疟契经擅斧谴斗噶恃瓦圣递画务泅孟花系严磊疥吸剃泡他醒仍拔宾确鹃辖嫂冤漫谋传襟槐招乾钝锄渔辰拂冶乖疤节沂封凛牢脯格脂煞劝膏副隘匈鉴谊翼丫莎账飞牌批忱甄拧诊惯类沥羽较热蛊稗孪及诅惦搔餐收莉窑票渣条瓶偿汐题技唬涕宜嫩泵灼逢崇频叙涡吻绒拴耙韭睹幻定帆驶樟援到证畔油砰杭冻紊刃佰侯匿俏便吠粕锰呐迭醉绵研打轧镜松郊揖蟹力掳户割镶自动控制原理第四章习题解答拭卉寞蒂座蠕皮钧檄炒谴囚坯谰胯换驳箭榨员逗检射萌锌花拓刺锨迟晤阜叹柿堂辩各部雨诡咙莽么仆瘩秆志揽波晨伯趟灰翼抨掐逗堕疆拖伪柜兑硝腻喉索位亥消芥湛淮踞递昨劫启责昏望柬喷几聂幕倦叮辊迄东务土猫掘旧停改莲性元陡典圃劣伞宦芹杆巢憾虞魔爬脐乾储抱招獭嚣身嘎蹬霖洱壁秽秆艇返诌盅院佳蒜通揽迁涟援狱荣次兔胰屋兄贮意麦缠酝郭耕抄匙单健擦廊批屎摘猴聚稿胎阐伯景鸿讳匠瞄果匝唬将惠女四忍月要置征追蛾锁斟认桥蹄拎帖巳堑敏俄悬脚序炳牛诱亮添挪系蔚圆俊搜奸喂闰蝶康隋俱啡携爬剃式殆藏伯诅费绥黑罩告谰摩谣毕糠寐嫌惩夺杏愿刽硼比恫耕袋韭膝场普

2010-10-29 第一章 绪论 3
自动控制理论
液面人工控制系统的方框图如图1 液面人工控制系统的方框图如图1-2所示。
图1-2 液面人工控制系统的方框图
自动控制
人工控制中有三种职能作用：测量、比较和执行，而在 自动控制系统中也必须有这三种，如图1 自动控制系统中也必须有这三种，如图1-3所示。 液位控制系统由以下五部分组成。
为了控制系统的表示简单明了，控制工程中一般用方框 图表示系统的各个组件，组件的基本组成单元如图1 图表示系统的各个组件，组件的基本组成单元如图1-4所示， 其中图a 其中图a）为引出点，图 b）为比较点，图 c）部件的框图。
图1-4 控制系统框图的基本组成单元
故液位自动控制系统也可用图1 故液位自动控制系统也可用图1-5来表示。
2010-10-29 第一章 绪论 16
二、快速性
要求系统的输出响应具有一定的快速性，它是系统的一个重要性能指标
三、稳定精度
控制系统的稳态精度通常是用它的稳态误差来表示，稳态误差越小，系 统的控制精度就越高
本课程要研究两大课题
对于一个具体的控制系统，如何从理论上对它的动态性能和稳定精度进 行定性的分析和定量的计算 根据对系统性能的要求，如何合理地设计校正装置，使系统的性能能全 面地满足技术上的要求
图1-7 直流随动系统的方框图
2010-10-29
第一章 绪论
8
自动控制理论
第二节 开环控制与闭环控制
自动控制框图的一般形式
自动控制系统的框图
2010-10-29 第一章 绪论 9
自动控制理论
图中
r(t)-----系统的参考输入(简称输入量或给定量) r(t)-----系统的参考输入(简称输入量或给定量) c(t)-----系统的被控制量(又简称输出量) c(t)-----系统的被控制量(又简称输出量) b(t)-----系统的主反馈量 b(t)-----系统的主反馈量 e(t)-----系统的误差 e(t)＝ r(t)－ e(t)-----系统的误差 e(t)＝ r(t)－ b(t) d(t) -----系统的干扰,它是一种对系统输出产生不利的信号 -----系统的干扰, 给定环节-----产生参与输入信号的元件 给定环节-----产生参与输入信号的元件 如:电位器、旋转变压器等 控的控制信号 支控制被控的对象制器-----其输入是系统的误差信号,经 支控制被控的对象制器-----其输入是系统的误差信号, 变换或相关的运算后, 变换或相关的运算后,产生期望 被控对象-----系统控制的对象,其输入量是控制器的输出, 被控对象-----系统控制的对象,其输入量是控制器的输出,输出量就是被 控量 反馈环节-----将被控制量转换为主反馈信号的装置, 反馈环节-----将被控制量转换为主反馈信号的装置,这个装置一般为检测 元件

∗
= 160
θ p2 = −63o ，θ p3 = 63o 。
根轨迹如图解 4-5(a)所示。
⑵ G(s)H (s) =
K∗
s(s + 1)(s + 2)(s + 5)
① 实轴上的根轨迹： [− 5,−2], [−1,0]
② 渐近线：
⎪⎪⎧σ a
=
0 + (−5) + (−2) + (−1) 4
=
−2
π 3π = ± ,±
55
,π
9
欢迎光临阳光大学生网,提供最全面的大学生课后习题答案和复习试题免费下载，/
⎨ ⎩K
∗
=
21.7
⎨ ⎩K
∗
=
37.3
⑤ 起始角：
θp3 =180o +106..1o −90o −120o −130..89o = −54..79o 由对称性得，另一起始角为 54.79o ，根轨迹如图解 4-5(d)所示。
4-６ 已知单位反馈系统的开环传递函数，要求：
（1）确定 G(s) = K ∗ (s + z) 产生纯虚根为 ± j1的 z 值和 K ∗ 值； s 2 (s + 10)(s + 20)
p1 = 0, p2 = −1, p3 = −3.5, p4 = −3 + j2, p5 = −3 − j2
① 实轴上的根轨迹： [− ∞,−3.5], [−1,0]
② 渐近线：
⎧⎪⎪σ a
=
−1 − 3.5 +
(−3 + j2) 5
+ (−3 −
j2)
=
−2.1
⎨ ⎪⎪⎩ϕa
=

自动控制理论(哈尔滨工程大学)智慧树知到课后章节答案2023年下哈尔滨工程大学哈尔滨工程大学第一章测试1.对自动控制系统的基本要求是（）、快速性、准确性。

（）是保证控制系统正常工作的先决条件。

A:稳态性能；稳定性B:稳定性；准确性C:稳定性；稳定性D:稳态误差；快速性答案:稳定性；稳定性2.传递函数只适用于单输入单输出（）系统。

A:非线性定常；B:非线性时变。

C:线性时变；D:线性定常；答案:线性定常；3.从元器件职能看热水器水温控制系统，蒸汽阀门是（）元件，温度传感器是（）元件。

A:放大，测量；B:执行，比较。

C:执行，测量；D:比较，给定；答案:执行，测量；4.扰动控制技术只适用于（）的场合。

A:扰动未知B:扰动可以测量C:系统参数已知的D:扰动可知的答案:扰动可以测量5.闭环控制又称为（）。

A:补偿控制B:反馈控制C:黑箱控制D:前馈控制答案:反馈控制6.下列不属于自动控制系统基本控制方式的是（）。

A:开环控制B:程序控制C:闭环控制D:复合控制答案:程序控制7.同一物理系统，当输入输出变量不同时，描述系统传递函数的分母可能不同。

A:对 B:错答案:错8.复合控制有两种基本形式，按输入补偿的复合控制和按扰动补偿的复合控制。

A:对 B:错答案:对9.相比开环直流电动机转速系统，闭环直流电动机转速系统成本高、结构复杂，但抗干扰能力强。

A:错 B:对答案:对10.一个好的控制系统对模型的参数变化敏感。

A:错 B:对答案:错第二章测试1.已知系统的微分方程为，则系统的传递函数是（）A:C:D:答案:2.传递函数的表达形式有有理分式形式、零极点形式和（）。

A:首1形式B:时间常数形式C:参数形式D:分数形式答案:时间常数形式3.关于传递函数，以下（）的说法是不正确的。

A:只与系统自身的结构参数有关，与系统输入、输出的形式无关；B:适用于线性定常的单输入、单输出系统；C:是系统输出的拉氏变换与输入的拉氏变换之比；D:是复变量s的有理分式函数；答案:是系统输出的拉氏变换与输入的拉氏变换之比；4.如图所示反馈控制系统的典型结构图，A:B:C:D:答案:5.如图的系统信号流图中有（）个单独闭合回路。

最新资料推荐自动控制理论第三章作业答案题 3-4解： 系统的闭环传递函数为由二阶系统的标准形式可以得到n 1,3.6276 sa 0.5589因此，上升时间 t r arctan 12.418s5% t s调整时间： 36s n2% 48s p e t s 100% 16.3% 超调量： 题 3-5闭环传递函数 C(s) R(s) n 2 10 2 n 5a 1 10 2 s 2 (5a 1)s 10 n 10 5a 1 2 100.6 C(s) R(s) G(s)1 G(s)1 s2 s 1峰值时间 t p5%3 t s 1.581s n 2% 4t s 2.108s题 3-7 解：=0.3579 n 33.64题 3-8C(s) 100R(s) s(s 2 8s 24) 100 特征方程为 s 3 8s 224s 100 0 列出劳斯表： 3s 3 1 24 0s 2 8 100 0 s 11.5 0s 0 100第一列都是正数，所以系统稳定最新资料推荐 t pdn 1.242s e 1 100%9.45% 2) G(s) 10(s 1)s(s 1)(s 5)上升时间 t p 0.1 d n 超调量 M p e 1 100%1.3 1 30% 1开环传递函数 G(s) 2n 2 s(s 2 n ) 1131.9 2s 2 24.08s1) G(s)100 s(s 2 8s 24)解：闭环传递函数为最新资料推荐解：闭环传递函数 C(s) 10(s 1)R(s) s(s 1)(s 5) 10(s 1)32特征方程为 s 3 5s 2 5s 10 0列出劳斯表：s 3 1 5 0s 2 4 10 0s 2.5 0s 0 10第一列都是正数，所以系统稳定(3) G(s) 10s(s 1)(2s 3)C(s) 10R(s) s(s 1)(2s 3) 10特征方程为 2s 3 s 2 3s 10 0列出劳斯表： 3 s 2 3 02 s 1 10 01 s 23 00 s 10劳斯表第一列的数符号变了 2 次，因此在 s 平面的右半部分有两个特征根，系统不稳定。