当前位置：文档之家 › 2014最新人教版二次函数复习课件

2014最新人教版二次函数复习课件

  • 格式：ppt
  • 大小：723.50 KB
  • 文档页数：36

下载文档原格式

  / 36

合集下载

二次函数复习ppt课件

二次函数复习ppt课件
点坐标是（1/2，1） ； （2）若抛物线y = a (x+m) 2+n 开口向下，顶点在第四象限，则 a ＜刀
3.求下列二次函数的开口方向,对称轴,顶点坐标.
y=x2 - 2x + 3 y= -2x2 - 4x - 6
解:y=x2-2x+1+2 =(x-1)2+2
y
o
x
a <0,b 0<,c 0. =
y
5.抛物线y=ax2+bx+c(a≠0)的图象经过原点,
且它的顶点在第三象限，则a、b、c满足
的条件是：a >0,b 0>,c 0. =
o
x
6.二次函数y=ax2+bx+c中，如果a>0，b<0，c<0，
那么这个二次函数图象的顶点必在第 四象限
y 先根据题目的要求画出函数的草图，再根据 图象以及性质确定结果（数形结合的思想）
二次函数复习
6.二次函数的应用
1. 如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有 二道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围； (2)当x取何值时所围成的花圃面积最大，最大值是多少？
解：(1) ∵ AB为x米、篱笆长为24米
x
7.已知二次函数的图像如图所示，下列结论： ⑴a+b+c=0 ⑵a-b+c﹥0 ⑶abc ﹥0 ⑷ b=2a 其中正确的结论的个数是（ D） A 1个 B 2个 C 3个 D 4个
y
-1 0 1
x
要点：寻求思路时，要着重观察抛物线的开口方 向，对称轴，顶点的位置，抛物线与x轴、y轴的 交点的位置，注意运用数形结合的思想。

二次函数复习课第一课时PPT

二次函数复习课第一课时PPT
二次函数复习课第一课时 PPT
本节课为二次函数复习课的第一课时，将重点回顾二次函数的定义及基本形 式，并介绍二次函数的图像特征和性质。
二次函数的图像特征
对称性
二次函数的图像以顶点为对称轴对称。
顶点坐标
顶点坐标为(x,y)，其中y为二次函数的最 小值（当开口向上时）或最大值（当开口 向下时）。
开口方向
焦点
焦点是图像上的特殊点，与 抛物线的形状有关。
对称轴
对称轴是二次函数图像的对 称线，通过顶点且垂直于准 线。
二次函数的变形与图像
1
垂直方向缩放
通过改变二次系数a的绝对值，可以
水平方向平移
2
改变二次函数图像的形状与开口大 小。
通过改变二次函数中x的常数项或线
性项，可以使图像左右移动。
3
对称轴变化
通过改变二次函数中x的线性项，可 以改变图像关于y轴的对称轴位置。
3
注意事项
注意事项包括仔细阅读题目、画出 准确的图像以及验证计算结果等。
二次函数的应用举例
抛物线轨迹
抛物线轨迹的运动可以用二次函数来描述， 如投射运动、弹道等。
面积与最大值
通过优化二次函数来求解相关问题，如求最 大面积。
二次函数拟合及其应用
拟合
通过将实际数据点与二次函数图像相拟合， 可以预测用于经济学、物理 学、工程学等领域中的数据模型和问题求 解。
二次函数的常见错误及纠错方法
1
常见错误
常见错误包括图像方向、顶点坐标
纠错方法
2
计算错误等。
纠错方法包括通过复习基本概念、
练习题目以及请教老师等。
当二次系数a为正数时，图像开口向上； 当a为负数时，图像开口向下。

2014最新人教版二次函数复习课件

2014最新人教版二次函数复习课件

）2-8 状相同，其解析式为 y=0.5（x-16 。
5、若x为任意实数，则二次函数y=x2+2x+3的函
数值y的取值范围是
y≥2 。
6、抛物线y=2x2-4x-1是由抛物线y=2x2-bx+c向 左平移1个单位，再向下平移2个单位得到的， 则b= 8 ，c= 3。
7、已知抛物线y=2x2+bx+8的顶点在x轴上， 则b= ±8。
（7）已知二次函数y=x2+bx+c的顶点坐标（1，-2），求 b，c的值
（8）已知二次函数y=x2+4x+c的顶点坐标在x轴上， 求c的值 （9）已知二次函数y=x2+4x+c的顶点坐标在直线y=2x+1 上，求c的值
如何求抛物线解析式常用的三种方法
1、已知抛物线上的三点，通常设解析式为 2+bx+c(a≠0) y=ax ________________ 一般式 2、已知抛物线顶点坐标（m, k），通常 设抛物线解析式为_______________ y=a(x+m)2+k(a≠0) 3、已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为y=a(x-x _____________ 1)(x-x2) (a≠0) 4.公式法
1 1 1 = AO ·OC + （OC+ED） ·OE+ EB ·ED 2 2 2 1 1 1 = × 1×3+ × （3+4） × 1+ × 3-1 ×4 =9 2 2 2
y
7.如图，已知直线 y= x+3与X轴、y轴分别交于点 B、C，抛物线y= -x2+bx+c 经过点B、C，点A是抛物线 与x轴的另一个交点。 （3）若点P在直线 BC上且

二次函数(复习课)课件

二次函数(复习课)课件
详细描述
伸缩变换包括横向伸缩和纵向伸缩。横向伸缩是指将图像在x轴方向上进行放大或缩小，纵向伸缩是指将图像在y轴方向上进行放大或缩小。具体来说，对于函数y=ax^2+bx+c，若图像在x轴方向上放大k倍，则新的函数为y=a(kx)^2+b(kx)+c；若图像在y轴方向上放大k倍，则新的函数为y=a(x)+b(x)/k+ck。通过这两种伸缩变换，我们可以得到原函数的放缩版函数。
02
二次函数的解析式
总结词
二次函数的一般形式是 $y = ax^2 + bx + c$，其中 $a neq 0$。
详细描述
一般式是二次函数的基本形式，它包含了二次函数的最高次项、一次项和常数项。通过一般式可以明确地看出函数的开口方向和开口大小，由系数 $a$ 决定。
VS
二次函数的顶点形式是 $y = a(x - h)^2 + k$，其中 $(h, k)$ 是函数的顶点坐标。
总结词
实际应用问题
总结词
与其他函数的综合
总结词
与几何图形的结合
01
02
03
04
05
06
总结词
详细描述
总结词与图像关系
这类问题需要探讨二次函数的系数与图像之间的关系，如开口大小、对称轴位置等。
一题多解法
这类问题通常有多种解法，需要灵活运用二次函数的性质和图像，寻找最简便的解法。
详细描述
二次函数具有对称性，其对称轴为直线$x = -frac{b}{2a}$。此外，二次函数的开口方向由系数$a$决定，当$a > 0$时，开口向上；当$a < 0$时，开口向下。顶点坐标为$left(-frac{b}{2a}, fleft(-frac{b}{2a}right)right)$。

二次函数复习课件PPT

二次函数复习课件PPT

个单位,再向 平移
个单位可
得到抛物线 y=3(x+2)2 -3.
16、将函数y＝－3（x－1）2－1的图象 (1) 沿y轴翻折后得到的函数解析式_____. (2) 沿X轴翻折后得到的函数解析式_____. (3) 沿原点旋转180°后得到的函数解析式
_____. (4) 沿顶点旋转180°后得到的函数解析式
解: y ax2 bx c
a x2 b x c 提取二次项系数
a x2
a a
b x b 2 b 2 a 2a 2a
c a
配方:加上再减去一 次项系数绝对值一 半的平方
a
x
b 2a
2
4ac b2 4a2
整理:前三项化为平方形 式,后两项合并同类项
a x
y的 最值
增减性
在对称 在对称 轴左侧 轴右侧
y=ax2
a＞0 向上 y轴
（0，0）
最小值 是0
y随x的增 y随x的增 大而减小 大而增大
a＜0 向下
y轴
（0，0）
最大值 y随x的增 是0 大而增大
y随x的增 大而减小
y=ax2+c
a＞0 向上 a＜0 向下
y轴 y轴
（0，c）
最小值 是C
y随x的增 y随x的增 大而减小 大而增大
4a
➢当a>0时，抛物线的开口向上，顶点 是抛物线上的最低点；
➢当a<0时，抛物线的开口向下，顶点 是抛物线上的最高点.
二次函数关系式的常见形式：
一般式：y=ax2+bx+c 顶点式：y=a(x+m)2+k
交点式：y=a(x-x1)(x-x2)
确定二次函数的解析式时，应该根据 条件的特点，恰当地选用一种函数表达式.

二次函数复习课课件

二次函数复习课课件

提升习题
提升习题1
已知二次函数$f(x) = ax^2 + bx + c$在区间$(m,n)$上 单调递增，求$a, b, c$的取值范围。
提升习题2
已知二次函数$f(x) = ax^2 + bx + c$在区间$(m,n)$上 有两个不同的零点，求$a, b, c$的取值范围。
综合习题
综合习题1
伸缩变换
总结词
伸缩变换是指二次函数的图像在平面内沿x 轴或y轴方向进行缩放。
详细描述
伸缩变换包括横向和纵向的缩放。横向缩放 是指图像在x轴方向上缩小或放大，纵向缩 放是指图像在y轴方向上缩小或放大。在伸 缩变换过程中，二次函数的解析式会相应地 乘以或除以一个大于0的常数。例如，将二 次函数y=ax^2+bx+c的图像沿x轴方向缩 小k倍，解析式变为y=a(x/k)^2+b(x/k)+c；
二次函数的性 质
总结词
二次函数具有开口方向、对称轴、顶点 和与坐标轴交点等性质。
VS
详细描述
二次函数的性质包括开口方向、对称轴、 顶点、与坐标轴交点等。根据系数$a$的 正负，抛物线有不同的开口方向：当$a > 0$时，抛物线开口向上；当$a < 0$时， 抛物线开口向下。对称轴为直线$x = frac{b}{2a}$，顶点坐标为$left(frac{b}{2a}, fleft(frac{b}{2a}right)right)$。与y轴的交点 为$(0, c)$，与x轴的交点可以通过求解方 程$ax^2 + bx + c = 0$得到。
沿y轴方向缩小k倍，解析式变为 y=ax^2+bx/k+c/k。
对称变换

【人教版】2014中考数学复习方案：二次函数的图象与性质(二)(29张PPT)

【人教版】2014中考数学复习方案：二次函数的图象与性质(二)(29张PPT)
考点聚焦 归类探究 回归教材 中考预测
第15讲┃二次函数的图象与性质(二)
(1)二次函数的图象是抛物线，是轴对称图形，充 分利用抛物线的轴对称性，是研究利用二次函数的性 质解决问题的关键． (2)已知二次函数图象上几个点的坐标，一般用待 定系数法直接列方程(组)求二次函数的解析式． (3)已知二次函数图象上的点(除顶点外)和对称轴 ，便能确定与此点关于对称轴对称的另一点的坐标．
解
(3)从图象和(1)(2)中可知，二次函数y＝x2＋2x的图
象与x轴有两个交点，交点的坐标分别为(0，0)，(－2，0)， 方程x2＋2x＝0有两个根0，－2； 二次函数y＝x2－2x＋1的图象与x轴有一个交点，交点坐标为 (1，0)，方程x2－2x＋1＝0有两个相等的实数根1； 二次函数y＝x2－2x＋2的图象与x轴没有交点，方程x2－2x＋
探究四 二次函数的图象与性质的综合运用
命题角度： 二次函数的图象与性质的综合运用．
例5 [2013· 内江] 已知二次函数y＝ax2＋bx＋c(a>0)的 图象与x轴交于A(x1，0)，B(x2，0)(x1<x2)两点，与y轴 交于点C，x1，x2是方程x2＋4x－5＝0的两根． (1)若抛物线的顶点为D，求S△ABC∶S△ACD的值； (2)若∠ADC＝90°，求二次函数的解析式．
解
(1)二次函数y＝x2＋2x，y＝x2－2x＋1，y＝x2－2x＋
2的图象与x轴分别有两个交点，一个交点，没有交点．
(2)一元二次方程x2＋2x＝0有两个根0，－2；方程x2－2x＋1
＝0有两个相等的根1，验证略；方程x2－2x＋2＝0没有实数
根．
考点聚焦
归类探究
回归教材
中考预测
第15讲┃二次函数的图象与性质(二)

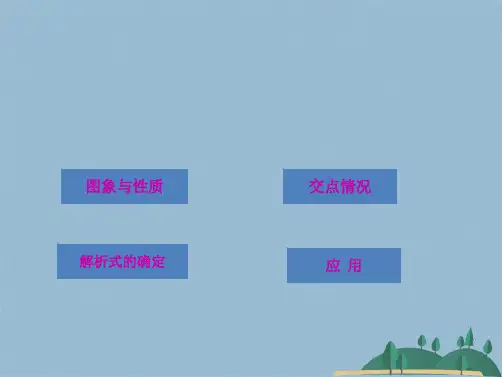
二次函数复习(共36张PPT)

二次函数复习(共36张PPT)

y=ax2+bx+c的图 方程ax2+bx+c=0
象和x轴交点
的根
b2-4ac
有两个交点
方程有两个不相等的 b2-4ac>0
实数根
只有一个交点
方程有两个相等的 b2-4ac=0
实数根
没有交点
方程没有实数根 b2-4ac<0
函数的图象
y
.
. ox
y
o
x
y
o
x
根据下列表格中二次函数y＝ax2+bx+c的自变量与函数 值的对应值，判断方程ax2+bx+c =0
(4)函数的自变量x的取值范围：任意实数
当二次函数表示某个实际问题时,还必须根据题意确定自变量的取值范
围.
二次函数的一般形式:
• 函数y＝ax2＋bx＋c
– 其中a、b、c是常数 – 切记：a≠0 – 右边一个x的二次多项式（不能是分式或根式）
二次函数的特殊形式：
当b＝0时， y＝ax2＋c 当c＝0时， y＝ax2＋bx 当b＝0，c＝0时， y＝ax2
向上
直线X=-h
（-h，k）
a ＜ 0 向下
图象的平移规律：
对于抛物线y=a(x+h)2+k的平移有以下规律： (1)、平移不改变 a 的值； (2)、h决定图象沿x轴方向左右平移，左+右— (3)、k决定图象沿y轴方向上下平移，上+下—
知识运用
（坐1标）是抛物线,图(y0象=,0过)x32 第2的开口向一象、,限对上二称；轴是
二次函数 开 口 方 向 对 称 轴 顶 点 坐 标
y = ax 2
a ＞ 0 向上 直线X=0 a ＜ 0 向下 （或y轴）

第22章《二次函数》复习课PPT课件(人教版)

第22章《二次函数》复习课PPT课件(人教版)
形？若存在，求点N的坐标；若不存在，请说明理由
三、课堂练习
N M
N
重视知识归纳； 重视基本概念； 重视典型题型； 重视每日小练； 重视错题整理； 避免盲目大意。
九年级数学
第22章 《二次函数》 复习（2）
定形图 性 义式象 质
坦洲实验中学初三数学
一、知识回顾
归纳知识：
（1）开a口的向符上号：由抛物a线>0的开口y 方向确定
开口向下
（2）c的符号：
a<0
o
x
由抛物线与y轴的交点位置确定.
交点在y轴正半轴
c>0
y
交点在y轴负半轴
c<0
交点是坐标原点
c=0
ox
∴ OE=DE=1.5 即D(1.5,-1.5)
设直线OD为y=kx,代入D点坐标得y= -x
令x2-2x-3 = -x
二、典型例题
证明: b2-4ac=[-(2m-1)]2-4×1×(m2-m-2) =4m2-4m+1-4m2+4m+8 =9
即b2-4ac ＞0 ∴ 抛物线与x轴有两个不同的交点
三、课堂练习
C
一次函数y=ax+b经过的象限与a, b符号关系 A选项，经过一二四象限， a＜0, b＞0 B选项，经过一二三象限，a＞0, b＞0 C选项，经过一三四象限， a＞0, b＜0 D选项，经过一三四象限，a＞0, b＜0
三、课堂练习
·B
A2
6
三、课堂练习
-1·
·5
与x,y轴交点
-5·
二、典型例题
解：令x=0,解得y=m2-m-2 令y=0,得x2-(2m-1) x+m2-m-2=0 [x-(m-2)][x-(m+1)]=0

初三数学复习《二次函数》(专题复习)PPT课件

初三数学复习《二次函数》(专题复习)PPT课件

面积问题
面积问题
在二次函数中，可以通过求函数与坐标轴的交点来计算图形的面积。例如，当函数与x轴交于两点时 ，可以计算这两点之间的面积；当函数与y轴交于一点时，可以计算这一点与原点之间的面积。这些 方法在解决实际问题时非常有用，例如在计算利润、产量等方面。
求解方法ቤተ መጻሕፍቲ ባይዱ
求出二次函数与x轴和y轴的交点坐标，然后根据这些坐标计算图形的面积。对于更复杂的问题，可能 需要使用积分或其他数学方法来求解。
05
综合练习与提高
基础练习题
巩固基础 覆盖全面 由浅入深
基础练习题主要针对二次函数的基本概念、性质和公 式进行设计，旨在帮助学生巩固基础知识，提高解题的 准确性和速度。
基础练习题应涵盖二次函数的各个方面，包括开口方 向、顶点坐标、对称轴、与坐标轴的交点等，确保学生 对二次函数有全面的了解。
题目难度应从易到难，逐步引导学生深入理解二次函 数，从简单的计算到复杂的综合题，逐步提高学生的解 题能力。
初三数学复习《二次函数》(专题复习)ppt课 件
目录 Contents
• 二次函数的基本概念 • 二次函数的解析式 • 二次函数的图像与性质 • 二次函数的实际应用 • 综合练习与提高
01
二次函数的基本概念
二次函数的定义
总结词
理解二次函数的定义是掌握其性 质和图像的基础。
详细描述
二次函数是形式为$f(x) = ax^2 + bx + c$的函数，其中$a, b, c$是 常数，且$a neq 0$。这个定义表 明二次函数具有两个变量$x$和 $y$，并且$x$的最高次数为2。
03
二次函数的图像与性质
开口方向
总结词：根据二次项系数a的正负判断开口方向 a>0时，开口向上

二次函数阶段专题复习课件ppt

二次函数阶段专题复习课件ppt

详细描述
根据二次函数的单调 性，判断函数在某个 区间的单调性；
根据二次函数的奇偶 性，判断函数的奇偶 性并求出函数的对称 轴；
根据二次函数的周期 性，求函数的周期并 观察图像的变化规律 。
综合练习题及答案
详细描述
根据二次函数与实际问题的综合 应用，解决实际问题并求出最优 解；
总结词：二次函数与其他知识点 的综合应用
求二次函数的最大值或最小值的方法是：先确定函数的对称 轴，再根据a的符号确定最大值或最小值的坐标，最后代入函 数解析式计算最大值或最小值。
02
知识点详解
二次函数的表达式及求解
表达式
$y = ax^{2} + bx + c$
求法
通过已知的三个点或顶点及对称轴可求得 $a$、$b$、$c$的值，进而得到二次函数 的表达式
2023
二次函数阶段专题复习课 件ppt
目 录
• 知识点概述 • 知识点详解 • 经典例题解析 • 易错点及应对策略 • 练习题及答案
01
知识点概述
什么是二次函数
1
二次函数是指形如`y = ax^2 + bx + c`（其中a 、b、c为常数，且a≠0）的函数。
2
二次函数的图像是一个抛物线，其顶点坐标为(b/2a,c-b^2/4a)，对称轴为x=-b/2a。
二次函数与实际问题的结合
要点一
总结词
要点二
详细描述
了解二次函数与实际问题的联系，能 够建立数学模型并解决实际问题。
二次函数与实际问题结合广泛，如最 优化问题、经济问题、物理问题等。 通过对实际问题的分析，可以更好地 理解二次函数的应用价值。
要点三
示例题目

第1讲二次函数的图象和性质复习课件(共39张PPT)

第1讲二次函数的图象和性质复习课件(共39张PPT)
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
第二种是在瑞典本国流行的说法．在诺贝尔立遗嘱期 间，瑞典最有名望的数学家就是米塔格·勒弗列尔，诺贝尔 很明白，如果设立数学奖，这项奖金在当时必然会授予这位 数学家，而诺贝尔很不喜欢他．所以诺贝尔不设立数学奖．
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
从函数图象中获取信息 a的作用：决定开口的方向和大小． (1)a＞0开口向上，a＜0开口向下； (2)a越大，抛物线的开口越小． b的作用：决定顶点的位置． 左(对称轴在y轴左边) 同(a，b同号) 右(对称轴在y轴右边) 异(a，b异号) c的作用：决定抛物线与y轴交点的位置． 上(抛物线与y轴的交点在y轴正半轴)
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
【解析】 ①∵图象与x轴的交点A，B的横坐标分别为－1，3， ∴AB＝4， ∴对称轴 x＝－2ba＝1， 即2a＋b＝0， 故①错误； ②根据图示可知，当x＝1时，y＜0，即a＋b＋c＜0， 故②错误； ③∵点A的坐标为(－1，0)， ∴a－b＋c＝0，且b＝－2a， ∴a＋2a＋c＝0，即c＝－3a， 故③正确；
大师导航 归类探究 自主招生交流平台 思维训练
第一章 二次函数
第1讲 二次函数的图象和性质
全效优等生
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
诺贝尔为什么没有设数学奖 诺贝尔奖在全世界有很高的地位，许多科学家梦想着能 获得诺贝尔奖．数学被誉为“科学女皇的骑士”却得不到每年由 瑞典科学院颁发的诺贝尔奖，过去没有，将来也不会有．因为 瑞典著名化学家诺贝尔留下的遗嘱中没有提出设立数学奖．对 此，外界流传着两种说法． 第一种是在法国和美国流行的说法．与诺贝尔同时期的 瑞典著名数学家米塔格·勒弗列尔曾是俄国彼得堡科学院的外 籍院士，后来又是前苏联科学院的外籍院士．米塔格·勒弗列 尔曾侵犯过诺贝尔的夫人，诺贝尔对他非常厌恶．为了对他所 从事的数学研究进行报复，所以诺贝尔不设立数学奖．

二次函数复习课精选教学PPT课件

二次函数复习课精选教学PPT课件
感谢父母给了我生命和无私的爱； 感谢老师给了我知识和看世界的眼睛；
感谢朋友给了我友谊和支持； 感谢完美给了我信任和展示自己能力的机会；
感谢邻家的小女孩给我以纯真无邪的笑脸； 感谢周围所有的人给了我与他人交流勾通时的快乐； 感谢生活所给予我的一切，虽然并不全都是美满和幸福;
感谢天空，给我提供了一个施展的舞台 感谢大地，给我无穷的支持与力量； 感谢太阳，给我提供光和热；
想一想
什么叫做二次函数？你能举例说明吗？
一般地，形如y=ax2+bx+c(a、b、c是常数，且a≠0)的 函数叫做x的二次函数。
注意：
1、x是自变量，y是用x的二次整式表示的. y是x的二次函数。 2、 a≠0，但b、c可以为0。 3、通过恒等变形，可以化为y=ax2+bx+c这种形式的函数，
它也可为y=a(x-h)2+k 或y=a(x-x1)(x-x2)的形式。
2a
4a
当a＞0时y有最大值
当x b 时,最大值为 4ac b2
2a
4a
二次函数y=ax2+bx+c的其它性质
⑴a的符号决定开口方向：a＞0开口向上，a＜0开口向下
⑵ a、b的符号决定对称轴位置： a、b同号对称轴偏在y轴左侧 a、b异号对称轴偏在y轴右侧
⑶c决定y轴的交点的位置：当x=0时，y＝c；即(0,c) 当c＞0时 交y轴正半轴， c＜0交y轴负半轴．
x=0
式
y =a(x-h)2 a＞0向上
x =h
a＜0向下
(0,0) (0,k) (h,0)
当a＞0时在对 称轴的左侧y 随x的增大而 减小在对称轴
的右侧y随x的 增大而增大
当x=0时y最大（小）值是０ 当x=0时y最大（小）值是k 当x =h时y最大（小）值是０

2014年秋新人教版九年级上《二次函数》复习ppt课件

2014年秋新人教版九年级上《二次函数》复习ppt课件

=0;④8a+c<0;⑤9a+3b+c<0,其中结论正确
的是
.(填入正确结论的序号)
第22页，共38页。
【自主解答】∵抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,
∴一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根,
∴b2-4ac>0,即b2>4ac,①是正确的.
∵抛物线的开口方向向上,∴a>0;
C.y=3(x-1)2+2
D.y=2x2
【解析】选D.函数y=3x2的图象平移后,二次项系数仍然是3,不可
能变为2,所以D选项中二次函数的图象不能通过函数y=3x2的图象
平移得到.
第6页，共38页。
2.(2013·衢州中考)抛物线y=x2+bx+c的图象先向右平移2个单位,再向
下平移3个单位,所得图象的函数解析式为y=(x-1)2-4,则b,c的值为
方,与x轴有交点,有部分在x轴下方,所以y>0,y=0,y<0都有可能.
所以正确的共有4个,选B.
第11页，共38页。
【主题升华】
图象形状 顶点坐标 开口及最值
b,c,b2-4ac
抛物线y=ax2+bx+c(a≠0)
b 4ac b2
( ,
)
2a 4a
a>0↔向上↔最小值4ac b2
4a
a<0↔向下↔最大值4ac b2
第25页，共38页。
1.(2013·昭通中考)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则 下列结论中正确的是( ) A.a>0 B.3是方程ax2+bx+c=0的一个根
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

y
B（3，0）
x
解：令y=0，则 –x+3=0，x=3， ∴B（3，0）， 令x=0， 则y=3， ∴C（0，3）， 得 -9+3b+c=0 解得 b=2 c=3 c=3 ∴ y= -x2+2x+3
｛
｛
7.如图，已知直线 y= D（1，4） （0，3） x+3与X轴、y轴分别交于点 C 2 B、C，抛物线y= -x +bx+c 经过点B、C，点A是抛物线 A B（3，0） 与x轴的另一个交点。 x （-1，0）o （1，0） E （1）求抛物线的解析式； （2）若抛物线的顶点为D，求四边形ABDC 的面积； 解：S四边形ABDC=S△AOC+S梯形OEDC+S △EBD
2a 4ac b 2 y最小 ) 4a a>0，x≤-b/2a,y
b 直线x 2a b 4ac b 2 ( , ) 2 a 4 a b a 0,当x ,
x≥-b/2a,y随x增大 而增大
2.二次函数图象的画法
对称轴直线x= y
b 2a
b ( , c) a
x1 O x2
（4）b2-4ac的符号： a、b同号 a、b异号 b=0
由抛物线与x轴的交点个数确定
与x轴有两个交点 与x轴有一个交点 与x轴无交点 b2-4ac>0 b2-4ac=0 b2-4ac<0
（1）已知y=ax2+bx+c的图象如图所示,
＜ a___0,
＞ ＞ b____0, c_____0, abc____0 ＜
（7）已知二次函数y=x2+bx+c的顶点坐标（1，-2），求 b，c的值
（8）已知二次函数y=x2+4x+c的顶点坐标在x轴上， 求c的值 （9）已知二次函数y=x2+4x+c的顶点坐标在直线y=2x+1 上，求c的值
如何求抛物线解析式常用的三种方法
1、已知抛物线上的三点，通常设解析式为 2+bx+c(a≠0) y=ax ________________ 一般式 2、已知抛物线顶点坐标（m, k），通常 设抛物线解析式为_______________ y=a(x+m)2+k(a≠0) 3、已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为y=a(x-x _____________ 1)(x-x2) (a≠0) 4.公式法
2
平移
对称 轴
y=ax2
b 4ac b 2 y a x 2a 4a
直线x=0 直线x=-m (0,0)
a>0当 x=0,y最小 =0
顶点 坐标 最值
增减 性
(-m,0)
a>0当x=m,y最小=0
a>0，x≤-m,y随x 增大而减小 x≥- 随x增大而减小
m,y随x增大而增大
问题1 建立如图所示的直角坐标系， 求抛物线的解析式； 问题2这位同学身高1.7 m,若 3.5m 在这次跳投中，球在头顶上 方0.25 m处出手，问：球出 手时，他跳离地面的高度是 多少？
o 2.5m 4 m
3.05 m
x
2.你知道吗？平时我们在跳绳时，绳甩到最高处的形 状可近似的看为抛物线，如图所示，正在甩绳的甲、 乙两名学生拿绳的手间距为4米，距地面均为1米，学 生丙、丁分别站在距甲拿绳的手水平距离1米、2.5米 处，绳子甩到最高处时，刚好通过他们的头顶，已知 学生丙的身高是1.5米，请你算一算学生丁的身高。
函数解析式是
y=2(x+2)2-3
。
（6）已知二次函数y=x2-4x-5 ， 求下列问题
①开口方向
②对称轴
④怎样平移
③顶点坐标
⑤x在什么范围，y随x 增大而增大 ⑦当x为何值时，y>0
③最值
⑥与坐标轴的交点坐标
⑧与x轴的交点坐标为A,B,与y轴的交点为C,则 2-8 S∆ABC= y=-2(x+1) . ⑨在抛物线上是否存在点P,使得S∆ABP是∆ABC面积的2 倍,若存在，请求出点P的坐标，若不存在，请说明 理由
顶点式
交点式或两根式
如何求下列条件下的二次函数的解析式:
1.已知一个二次函数的图象经过点
（0，0），（1，﹣3），（2，﹣8）。
2.已知二次函数的图象的顶点坐标为 （－2，－3），且图象过点（－3，－2）。 3.已知二次函数的图象的对称轴是直线x=3,
并且经过点(6,0),和(2,12) 4.矩形的周长为60，长为x，面积为y，则y关于 x的函数关系式 。
S△PAC=
1 2
y
（0，3）
C A
P
o
B（3，0） Q
x
S △PAB，求P的坐标；
（4）第（3）题改为在直线y= -x+3上是否存在 1 点P，使S△PAC= S △PAB？若存在，求出点P 2 的坐标；若不存在，说明理由。答案一样吗？
P
y （ 0， 3） C A
y （ 0， 3） C P
（3，0） A B x o
(2) y=-2x2-2是由 y=-2x2 向 下 平移 2 (3) y=-2(x-2)2+3是由 y=-2x2 向右 平移 ，再向 上 平移 3 个单位得到 个单位得到
2 个单位
(4) y=2x2+4x-5是由 y=2x2向 左 平移 1 个单位，再 向 下 平移 7 个单位得到 (5) y=2x2向左平移2个单位，再向下平移3个单位得到
）2-8 状相同，其解析式为 y=0.5（x-16 。
5、若x为任意实数，则二次函数y=x2+2x+3的函
数值y的取值范围是
y≥2 。
6、抛物线y=2x2-4x-1是由抛物线y=2x2-bx+c向 左平移1个单位，再向下平移2个单位得到的， 则b= 8 ，c= 3。
7、已知抛物线y=2x2+bx+8的顶点在x轴上， 则b= ±8。
如何判别a、b、c、b2-4ac，2a+b，a+b+c的符 号
（1）a的符号：由抛物线的开口方向确定
a>0 开口向上 a<0 开口向下 （2）C的符号： 由抛物线与y轴的交点位置确定. c>0 交点在x轴上方 交点在x轴下方 经过坐标原点 c<0 c=0
（3）b的符号： 由对称轴的位置确定 对称轴在y轴左侧 对称轴在y轴右侧 对称轴是y轴
解:（1）由题意，x=1时，y=2；x=2时，y=2+4=6,分别代入 y=ax2+bx,得a+b=2,4a+2b=6, 解得:a=1,b=1, ∴y=x2+x. （2）设g＝33x-100-x2-x,则 g=-x2+32x-100=-(x-16)2+156. 由于当1≤x≤16时，g随x的增大而增大，故当x=4时，即第4年可 收回投资。
c x
2 b 4 ac b 顶点坐标 （ ， ） 4a 2a
与X轴
b 4ac b 2 （ ， ） 4a 2a
与Y轴的交点坐标及它 关于对称轴的对称点
(0, c)
b ( , c) a
(1) y=2(x+2)2是由 y=2x2 向 左平移 2 个单位得到
6.某商场将进价40元一个的某种商品按50元一个售出 时，能卖出500个，已知这种商品每个涨价一元，销量 减少10个，为赚得最大利润，售价定为多少？最大利 润是多少？ 分析：利润=（每件商品所获利润）× （销售件数）
设每个涨价x元， 那么
（1）销售价可以表示为
（50+x）元（x≥ 0，且 为整数）
8、已知y=x2-（12-k）x+12，当x＞1时，y随 x的增大而增大，当x＜1时，y随x的增大而减 小，则k的值为
10
。
综合应用
(中考必考题）
1. 如图，有一次,我班某同学在距篮下4m处 跳起投篮，球运行的路线是抛物线，当球运 行的水平距离2.5m时，达到最大高度3.5m， 然后准确落入篮圈。已知篮圈中心到地面的 y 距离为3.05m.
2014最新人教版九年级上册数学
二 次 函 数 复 习
乌市第58中 郭云舒
一、二次函数概念
形如y=ax2+bx+c (a,b,c是常数，a≠0) 的函 数叫做二次函数
其中二次项为ax2，一次项为bx，常数项c 二次项的系数为a，一次项的系数为b，常数项c
练习：1、y=-x² ，y=2x² -2/x，y=100-5
x² , y=3 x² -2x³ +5,其中是二次函数的有____个。 2.当m_______时,函数y=(m+1)χ - 2χ+1 是二次函 数？
二.二次函数图象
y=ax2+k 顶点式 y=a(x+m)2 y=a(x+m)2+k 直线x=-m (-m,k)
a>0当x=m,y最小=k
一般式 y=ax2+bx+c
Q
o
Q
B （ 3， 0 x

（14）（2014 •乌鲁木齐）在平面直角坐标系 xOy中，抛物线y=mx² -2x与x轴正半轴交于点 A，顶点为B.
(3) ∵墙的可用长度为8米
∴ 0<24－4x ≤8
4≤x<6
∴当x＝4m时，S最大值＝32 平方米
5.某企业投资100万元引进一条产品加工生产线，若不 计维修、保养费用，预计投产后每年可创利33万。该 生产线投产后，从第1年到第x年的维修、保养费用累 计为y(万元)，且y=ax2+bx,若第1年的维修、保养 费用为2万元，到第2年为6万元。 （1）求y的解析式； （2）投产后，这个企业在第几年就能收回投资？