当前位置：文档之家 › 第5章晶体定向和结晶符号

第5章晶体定向和结晶符号

  • 格式：ppt
  • 大小：916.50 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

晶体定向和晶体学符号

晶体定向和晶体学符号

a=b<>c
唯一的L4或Li4为 z 轴; 相互垂直的L2, 或相互
垂直的对称面法线, 或适当的晶棱为 x, y 轴； z 轴直立， y 轴左右水平，x 轴前后水平。
3. 正交（斜方）晶系晶体定向
晶格常数为: a = b = g = 90 °

a<>b<>c
三个相互垂直的L2为 z, x, y 轴; 或L2为z轴, 相互垂直的对称面法线为 x, y 轴 z 轴直立， y 轴左右水平，x 轴前后水平
OP在a1, a2, a3轴的垂直投影OA, OB, OC
t= -( u+v ) OA+OB=-5/2+(-1)=-7/2=-OC 满足：
还可以证明： OA+OB+OC=3/2 OP 求密布氏指数首先求出晶向上任一结点 在四轴的垂直投影； 然后将前3个指数分别乘以2/3； 再和第四个数值化为最小整数即为密布 氏指数。 -5/2, -1, 7/2, 0，晶向指数为[5270]
（ 2 ）轴角：两个结晶轴正向 之夹角。用a，b，g 表示。
结晶轴选择原则
符合晶体本身的对称 适宜的对称元素作为结晶轴
适宜的晶棱方向作为结晶轴
尽量使得晶轴之间夹角为90
晶体定向的几个基本概念
（ 3 ）轴单位：晶体坐标系中结晶轴的长度单位。是相应 晶体点阵中平行于晶轴的行列上相邻节点间距。用a, b, c分 别表示x轴、y轴、z轴的轴单位。 （4）轴率：结晶轴的轴单位之连比。用a:b:c 表示。 （5）晶体几何常数：轴率a:b:c和轴角a，b，g的合称。表 示晶体坐标系特征的一组参数，用以区分不同的晶系。
晶面族
z
（001）
用{h k l}表示对称性联系的一组晶面， 称为晶面族Family of planes.
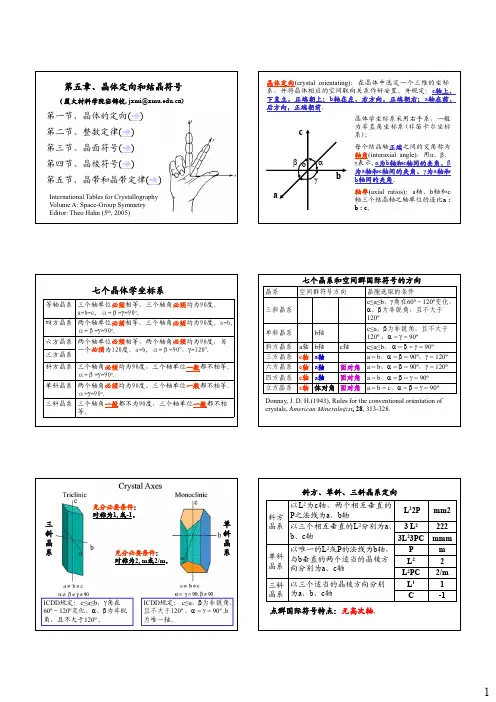
第五章 晶体定向和结晶符号

第五章 晶体定向和结晶符号

第五章、晶体定向和结晶符号（厦大材料学院宓锦校, jxmi@)第一节、晶体的定向(Î)第二节、整数定律(Î)第三节、晶面符号(Î)第四节、晶棱符号(Î)第五节、晶带和晶带定律(Î)International Tables for Crystallography V olume A: Space-Group Symmetry Editor: Theo Hahn (5th , 2005)三斜晶单斜晶充分必要条件：对称为1, 或-1。

充分必要条件系系ICDD 规定：c ≤a ≤b ，γ角在60º～120º变化，α、β为非锐：对称为2, m 或2/m 。

ICDD 规定：c ≤a ，β为非锐角，且不大于120º ，α= γ= 90º ,b四方晶系斜方晶系充分必要条件：对称为mm2, 222 或mmm 。

充分必要条件：有且仅有一个四次轴(4,或-4)。

三方晶系六方晶系充分必要条件：有且仅充分必要条件：有且仅有一个三次轴(3,或-3)。

立方晶系充分必要条件：有四个三次轴(3,或-3)。

René Just Haüy(1743.2.28-1822.6.3)Miller IndexA treatise oncrystallography,W. H. Miller•The points of intersection of a plane with the latticeaxes are located;(取平面与空间格子坐标轴的交点)•The reciprocals of these values are taken to obtain theMiller indices;(以这些坐标轴的倒数为米氏指数)•The planes are then written in the form (h k l)where h= 1/x, k = 1/y and l = 1/z;(并写在圆括号内表示)•Miller Indices are always enclosed in ( );cz These points define aplane with intercepts 2a 3b , 6c (A’’, B’’, C’’) and a Miller index of (321)h : k : l =a /OX :b /OY :c /OZ = a /2a : b /3b : c /6c =1/2 : 1/3 : ab1/6= 321Notation(符号)William Hallowes Miller (1801 -1880) British Mineralogist andCrystallographer•In 1839, wrote a paper, “treatise on Crystallogrphy” in which he introduced •Lattice points are not enclosed –100(点阵点不加括号)•Lines, such as axes directions, are shown in square brackets, [100]is the a axis;(直线用方括号表示)•Direction from the origin through 102 is [102] ;the concept now known as the Miller Indices.U:V:T:W=(2u-v):(2v-u):(-u-v):3wU+V+T=0u:v:w=(U-T):(V-T):W如a轴方向[100]在四轴坐标系中表示为[2-1-10]；b轴方向[010]则表示为[-12-10]；d轴方向[-1-10]则表示为[-1-120]；[011](011)(1-11)[0](100)(01-1)(0-11)(11-1)()[uvw ]晶带的晶面晶带方程魏斯定律。

结晶学与矿物学课件-晶体定向、晶面符号和晶带定律

结晶学与矿物学课件-晶体定向、晶面符号和晶带定律

根據這一規律，我們可以由若干已知面或晶帶推導 出晶體上一切可能的晶面的位置。
在晶體定向、投影和運算中，晶帶和晶帶定律得到 了廣泛的應用。
晶帶定律和整數定律分別以不同的形式闡述了晶面 (面網)與晶核(行列)相互依存的幾何關係。
(2)軸角 系指晶軸正端之間的夾角，它 們分別以α (Y∧Z)、β (Z∧X)和γ(X∧Y)表 示。等軸、四方和斜方晶系晶軸為直角
坐標α＝β＝γ＝90。；在三方和六方晶系 中α＝β＝90，γ＝120。(X軸和Y軸正端 夾角)，單斜晶系中一軸傾斜從而使α＝γ ＝90，β＞90。三斜晶系中三晶軸彼此斜 交，α≠β≠γ≠90。
確定晶棱符號的方法如下：
將晶Байду номын сангаас平移，使之通過晶軸的交點、然後在 其上任一點，取座標（x、y、z），並以軸長 來度量，即求得晶棱符號： (x/a):(y/b):(z/c)=r:s:t，晶棱符號採用[ ]表 示，即[ rst]。
2．晶帶
由布拉維法則可知，晶面是網面密度較大的 面網，所以晶體上所出現的實際晶面為數是 有限的；相應地，晶面的交棱也應當是結點 分佈較密的行列，這種行列的方向也是為數 量不多的，所以晶體上的許多晶棱常具有共 向的方向而相互平行。
交棱相互平行的一組晶面的組合，稱為一個 晶帶。
通過晶體中心的直線cc，晶棱與之平行，稱 該晶帶的晶帶軸；該組晶棱的符號也就是該 晶帶軸的符號。
3、晶帶定律
晶體是一個封閉的幾何多面體，每一晶面與其它晶 面相交，必有兩個以上的互不平行的晶棱。因此， 晶體上任一晶面至少屬於兩個晶帶。這一規律稱為 晶帶定律。它也可以這樣來表述，即：任意二晶棱 (晶帶)相交必可決定一個可能晶面．而任意二晶面 相交必可決定一可能晶棱(晶帶)。
(3)軸長與軸率 晶軸系格子構造中的行列， 該行列上的結點間距稱為軸長。X、Y、Z軸 上的軸長分別以a、b、c表示。由於結點間 距極小(以nm計)，需藉X射線分析方能測定。 根據晶體外形的宏觀研究不能定出軸長， 但應用幾何結晶學的方法可以求出它們的 比率a：b：c，這一比率稱為軸率。
04-晶体定向和结晶符号(结晶学与矿物学)

04-晶体定向和结晶符号(结晶学与矿物学)

10
第五章 晶体定向及结晶符号
5-2. 2 各晶系的定向法则
三方和六方晶系的四轴定向:
U +
-
+ 120
O
Z U
Y
90 O
Y
+
X
-
X
11
第五章 晶体定向及结晶符号
七大晶系晶体常数特点：
等轴晶系： α=β=γ=90°, a = b = c 四方晶系： α=β=γ=90°, a = b ≠c 三方、六方晶系：α=β= 90°, γ=120°, a = b ≠ c
三方和六方晶系的四轴定向: 选择唯一的高次轴作为直立结晶轴c轴，在垂直c轴 的平面内选择三个相同的、即互成60°交角的L2或 P的法线，或适当的显著晶棱方向作为水平结晶轴， 即a轴、b轴以及d轴(U轴)
共有12个点群: 晶格常数为: α=β= 90°, γ=120°, a = b ≠ c c轴直立，b轴左右水平，a轴前后水平偏左30°
过坐标原点而平行于(h k l)平面的方程为： hx+ky+lz=0 因(h k l)晶面属于[r s t]晶带, 故直线[r s t]上的任一点均满足平面 方程, 即用r, s, t替代x, y, z, 便得到上述的晶带方程
28
第五章 晶体定向及结晶符号
5.6. 晶带符号和晶带定律
晶带定律的应用
8
第五章 晶体定向及结晶符号
5-2. 2 各晶系的定向法则
三斜晶系的定向:
共有2个点群: 1, -1
晶格常数为: α ≠ β ≠ γ ≠ 90 °, a ≠ b ≠ c 适当的晶棱为a, b, c轴 大致上c轴直立，b轴左右，a轴前后
9
第五章 晶体定向及结晶符号
5第五讲 晶体定向及结晶符号

5第五讲 晶体定向及结晶符号


第五章 晶体定向及结晶符号
2．晶带：
交棱相互平行的一组晶面的组合称为晶带。晶带由多个晶面组 成，一个晶面可属于多个晶带。 晶带轴：假象的直线，平行晶带公共交棱方向并通过晶体中 心的直线。该晶带轴符号同与之平行的晶棱符号相同。 晶带定律：任意两晶棱（晶带）相交比可决定一个可能晶 面，任意两个晶面相交比可决定一个可能晶棱（晶带）。
3．晶面符号书写方法（按结晶轴顺序）： 三轴定向（XYZ）— （hkl） 四轴定向（XYUZ）— （hkil）
注意： 若晶面与晶轴负半轴相交，晶面指数上加负号。
4．晶面指数规律和特点：
（1）截距系数越大指数越小；当晶面与晶轴平行时，指数 为0。 （2）一般式中字母和数字不能同时混用，但可出现0和系数， 如（hk0）。 （3）三、六方晶系晶面指数前三位代数和为0。
第五章 晶体定向及结晶符号
思考题：
1、模型上形态相同的晶面符号有何规律？ 2、在低级晶族的各晶系中（001）与Z轴的关系如何（垂直、 斜交）？ 3、在等轴晶系中（1）与XYZ轴等截距相交的晶面有哪些？晶 面符号特点（2）与二个结晶轴等截距相交与另一晶轴 平行的晶面有哪些？晶面符号？
第五章 晶体定向及结晶符号
第五章 晶体定向及结晶符号
3. 对称型的国际符号 对称型只列出所有对称要素，标明了各要素的数量，但 不能表达所有要素的空间方位。 以一定的原则制定更为简单的符号代替简单的对称型罗 列，表达数量和方位，即国际符号和圣弗利斯符号。 国际符号：由Hermann和Mauguin创立，所以也称HM符号。


3.顺序 x，y，z 或x，y，u，z 4.一般形式 （hkl）或（hkil）
Z
A
c a
O b Y
X
chap5-晶体定向与结晶符号

chap5-晶体定向与结晶符号


八面体个晶面的米勒指数
例2：确定四方柱各晶面的晶面符号。
对称型：L44L25PC 晶轴选择：L4为Z轴；2L2为XY轴 晶体几何常数： a=b≠c ， α=β=γ=90o 。
X
Y
四方柱水平晶轴的两种选择
第一种选择 晶面在XYZ上的截距： OH,OH, ∞； h:k:l =a/OH:a/OH:c/∞ =1:1:0
Z(+) Y(+) X(+)
U(-)
六方柱晶轴的选择
六方柱水平晶轴的两种选择
第一种选择： h:k:i:l =a/OH : 0 : a/OH : 0 =1:0:1:0 晶面符号： (1010) (1010)
(0110) (1100)
Y(+)
(1100) X(+) (0110)
(1010)
U(-)
晶体外形不可能知道轴单位，但根据对称性可知道 轴单位之间的比值关系，即： a:b:c 例如：等轴晶系的 a:b:c =? 四方晶系的 a:b:c =?
⑵轴率：轴单位的连比a:b:c，称为轴率。
轴率通常以b的长度为单位长度，写成以 b为1的连比式。例如橄榄石的轴率为 0.46575:1:0.58651。
三个不共面的行列方向是一致的。
为什么? 因为空间格子中三个不共面的行列也 是根据晶体的对称性,人为地画出来的。而晶 轴也是根据晶体的对称性,人为地选出来的。 晶体的内部对称与晶体的宏观对称是一致的,
所以晶轴与三个行列就是一致的。
2.四轴定向
三方及六方晶系采取四轴定向。
• 对称特点：有且只有一个L3或L6或Li6。
• • • • 晶轴：行列; 晶面：面网 晶面截晶轴于结点 截距系数为整数 截距系数之比为整数比
结晶学与矿物学 第五章 晶体定向与晶体符号

结晶学与矿物学 第五章 晶体定向与晶体符号

三晶棱符号晶带与晶带符号晶棱符号edgesymbol表征晶棱直线方向的符号晶棱符号晶带zone交棱相互平行的一组晶面的组合称为一晶面符号不仅用于表征晶体外部形晶面符号不仅用于表征晶体外部形态特征还用于表征矿物的解理裂开态特征还用于表征矿物的解理裂开矿物中包裹体的分布矿物切片矿物矿物中包裹体的分布矿物切片矿物光性及晶体内部结构等与晶体方向有关光性及晶体内部结构等与晶体方向有关的内容应当重点掌握
结晶轴的安置及晶体常 数特征
c 轴 直 立 b 轴 左 右 水 平 a轴前后水平， a=b≠c α=β=γ=90º
L44P
L44L2 Li42L22P L44L25PC
两个相互垂直的P的法线分别为a轴和b 轴. (⊥P ——X,Y)
两个互相垂直的L2分别为a轴和b轴. (2L2——X,Y)
六 方 和 三 方 晶 系
制定国际符号的规则：
（1）Ln ——1,2,3,4,6。
Lin ——1, 2, 3, 4, 6。 （2）P —— m。
（3）若P与Ln或Lin垂直，则两者用“－”或“/”隔开。
如：L2PC-----2/m（ ），L4PC-----4/m（ ）。 （4）按一定顺序列出一定方向的对称要素，省略等同的和 派生的要素。
晶面符号特点
4.1 截距系数越大，晶面指数（ ？ ）
4.2 晶面与晶轴平行时，指数为（ ？）
4.3 字母和数字不能混用，0除外 4.4 三、六方晶系，晶面指数前三位代数和（？）
三、晶棱符号、晶带与晶带符号
1. 晶棱符号edge symbol
表征晶棱（直线）方向的符号
晶棱符号 2. 晶带zone
交棱相互平行的一组晶面的组合，称为一 个晶带
5.对称型国际符号
本章结束 第六章
晶体教程第五章晶体定向与结晶符号

晶体教程第五章晶体定向与结晶符号

晶体教程第五章晶体定向与结晶符号第五章晶体定向和结晶符号只要在生长时有足够的自由空间，晶体必然会长成由许多晶面和晶棱包围的几何多面体。

在晶体上，所有的晶面、晶棱和角顶，它们的分布都是对称的。

但除此而外，晶面和晶棱之间还有另一方面的几何关系，表现在晶面和晶棱相截或平行时，都可以用确定的数学形式来表征彼此间的空间取向关系。

为了表达这种关系，首先需要在晶体中建立起一个坐标系，这就是晶体定向。

所谓晶体定向，就是要在晶体上选择合理的三维坐标系，包括在晶体上选择坐标轴和确定各坐标轴的度量单位两项工作。

在此基础上，就可以进一步确定晶面符号和晶棱符号，用数学的方式来表示各个晶面或晶棱在晶体上的方向，并反映出它们彼此间的几何关系。

其中，平行于同一晶棱的若干晶面，特别称之为一个晶带。

而整数定律则是进行上述这些工作的依据。

在本章中，首先讨论晶体定向的原则，以便在晶体中建立起一个三维坐标系，在此基础上，分别叙述晶面符号和晶棱符号的构成。

最后，再讲述整数定律以及有关晶带的问题。

第一节结晶轴和晶体几何常数一、结晶轴的概念和选择原则⒈结晶轴的概念晶体中的坐标轴称结晶轴，简称晶轴。

晶轴是几根假想的直线，沿着与晶体对称有关的限定方向穿过理想晶体，相交在晶体中心。

⒉晶轴的选择原则晶轴的选择不是任意的。

首先，晶轴的选择要符合晶体自身的对称性，因此，要优先选择对称轴和对称面的法线方向。

若晶体无对称轴和对称面或其数目不够时，则选合适的晶棱方向，在选择晶棱做晶轴时，可以设想将其平移至晶体中心。

其次，在满足上述条件的前提下，应使晶轴尽可能互相垂直或近于垂直，并使轴单位尽可能相等，即使a=b=c α=β=γ=90°。

⒊晶轴的安置及名称三轴定向：除三方晶系、六方晶系以外的晶体，均采用X、Y、Z 三轴定向。

X、Y、Z晶轴的安置是：Z轴直立，上端为正；X轴前后，前端为正；Y 轴左右，右端为正。

轴角：X、Y、Z晶轴正端之间的夹角为轴角。

分别用α（Y∧Z）、β（Z∧X）、γ（Y∧Z）表示，如图5-1。

高职结晶学 五、晶体定向和结晶学符号

高职结晶学 五、晶体定向和结晶学符号


三轴定向晶体 h:k:l=a/OH : b/OK : c/OL 四轴定向晶体 由于a＝b＝d≠c h:k:i:l=a/OH : a/OK : a/OI : c/OL
crystallography
例1：确定立方体和八面体各晶面的晶面 符号。 对称型：3L44L36L29PC 晶轴选择：3L4为XYZ轴 晶体几何常数：a＝b＝c； α＝β＝γ＝90o
锆石 a=b≠c， α=β=γ=90o, a:c=1:0.6407
crystallography
三方、六方晶系（四轴定向）


对称特点：有且只有一个L3或L6或Li6。 选轴原则：选择唯一的高次轴作为直立结晶轴z轴，在垂 直 z 轴的平面内选择三个相同的、即互成60°交角的L2或 P的法线，或适当的显著晶棱方向作为水平结晶轴，即x 轴、 y 轴以及 U轴 晶体几何常数：a=b≠c，α=β=90o ，γ=120o 。
方解石（三方）
a:c=1:0.8543
crystallography
3)斜方晶系 对称特点：L2和P的总数不少于三个。 选轴原则：有3 L2时，以3L2为X、Y、Z轴； 在 L22P中，以L2为Z轴， 2P法线为X、Y轴。 晶体几何常数：a≠b≠c，α=β=γ=90o
十字石 a:b:c=0.4734:1:0.6828
crystallography
3.整数定律
晶面在各晶轴上的截距系数之比，恒为 简单整数比。
crystallography
晶轴：行列 晶面：面网 截距系数为整数 截距系数之比为整数比

crystallography
Z
c
a1 a4
X
b1 b2 b3 b4 Y
a3
晶体定向和结晶符号

晶体定向和结晶符号

实验2. 晶体定向和结晶符号一、目的要求掌握不同晶系晶轴选择的原则，确定模型中单形的名称及其符号。

二、基本原理为了获得晶体形态的完整描述，需要确切地表示晶面在空间的相对位置。

在晶体学中，确定晶面在空间的位置是按晶体的对称特征选择坐标系，将晶体按对称特征放置于该坐标系中(晶体定向)，再以一种符号表示法表示出晶面在空间的位置。

晶体定向就是给晶体选择坐标轴(晶轴)和确定坐标轴上的轴单位。

在七个晶系中，有五个晶系（立方、四方、斜方、单斜、三斜）采用三轴定向，即选择交于晶体中心的三条直线，它们分别记为a、b、c轴(或X、Y、Z轴)。

相应b与c间轴角为α，a与c间轴角为β，a与b间轴角为γ。

三方、六方晶系一般采用四轴定向，即在ab平面上增加了一个d轴，使水平面三轴间正向的轴角形成120°，以满足该类晶系对称性的要求。

晶体放置的取向原则是要反映晶体的对称性，从晶体的外形上讲，对称轴、倒转轴、对称面的法线及晶棱是与晶体构造中的行列重合的，因此晶体与坐标轴的相对取向按对称轴、倒转轴、对称面的法线、晶棱的优先顺序作晶轴方向。

轴单位是晶轴上的单位长度。

由于所选定的晶轴都是格子构造中的行列方向，所以晶轴的轴单位就是该行列的结点间距。

a、b、c轴上的轴单位分别以a o、b o、c o表示，有时也直接用a、b、c表示，其间比率a：b：c称为轴率(或称轴单位比)。

轴率a：b：c和轴角α、β、γ合称为晶体几何常数。

在晶体定向的基础上，我们就可以确定晶体各种结晶几何参数在空间的位置。

表示这些参数在空间位置所用的符号称为结晶符号，结晶符号主要有晶面符号、晶向符号、单形符号和晶带符号。

表示晶面在空间位置的符号称为晶面符号。

晶面符号有几种，通常多采用米氏符号，又称米勒指数或晶面指数，是英国学者米勒(W．H．Miller)于1839年提出。

本实验通过在晶体模型上确定米勒指数和单形符号，达到掌握晶体定向和确切表示晶面族在空间的相对位置的方法。

第五章晶体定向和结晶符号

第五章晶体定向和结晶符号

⑴晶轴的选择是与晶体的 格子构造一致的，晶面是面 网，晶轴是行列，晶面截晶 轴于结点，或者晶面平移后 截晶轴于结点（平移后各晶 轴上的截距系数之比不变， 所以晶面符号不变）。所以 如果以晶轴上的结点间距a、 b、c作为度量单位，则晶面 在晶轴上的截距系数之比必 为整数比。
⑵如图所示，平行Z轴的一组面网截X轴于a1点，截Y轴分 别于b1、b2、b3、b4……bn点，网面密度a1b1＞a1b2＞ a1b3＞……a1bn，它们在X、Y轴上的截距系数之比则 分别为1︰1、1︰2、1︰3……1︰n，显然，网面密度 越大，晶面在晶轴上的截距系数之比越简单。
例六：L2PC，单斜晶系，国际符号中只有一个 位，代表Y轴方向，其方向上有2/m所以这一对 称型的国际符号为2/m。
3、根据国际符号判断所属晶系
（参照P19，表2）
❖⑴根据低级晶族的对称特点判断其晶系，无2 或m的为三斜晶系；2或m不多于一个的为单斜晶 系；2或m多于一个的为斜方晶系。
❖⑵中级晶族：首位是4或 4者为四方晶系；首 位是3或 3者为三方晶系；首位是6或 6 者为六方
以L6、Li6、L3为Z轴，以垂直Z轴并彼此相交 为120°的三个L2或P法线为X、Y、U轴；当 无L2或P时，X、Y、U轴平行晶棱选取
a = b≠c α=β=90°γ=120°
以相互垂直的3L2为X、Y、Z，在L22P对称 a≠b ≠ c
型中以L2为Z轴，以2P法线为X、Y轴
α=β=γ=90°
以L2或P的法线为Y轴，以垂直Y轴的主要晶 a≠b ≠ c
❖晶带轴：通过晶体中心且平行晶带上晶棱方向的直线。
2、晶带符号：表示晶带空间方位的符号。
因为每一个晶带都有一个晶带轴，所以晶带通常用晶 带轴来表示。而晶带轴平行于晶棱，所以晶带符号通常是 以晶棱符号来代替的。一般用〔rst〕表示，r︰s︰t为晶棱 在三个坐标轴上的坐标系数比。

第五章-晶体定向和结晶符号


X
School of Materials Science and Engineering
第5章 晶体定向与结晶符号
5.2 各晶系晶轴的选择及晶体几何常数特点
三轴定向选择结晶轴的一般顺序 有四次轴时，优先选择四次轴； 四次轴不够或没有时，选择L2； L2不够或没有时，选择P的法线； P不够或没有时，选择合适晶棱方向； 在以上的选择中，除单斜晶系优先考虑Y轴之外，
法线为X、Y轴。 晶体几何常数： a≠b≠c，α=β=γ=90o
3L2 3PC
β X
L2 =Z
L2 2P
Z α Y γ
School of Materials Science and Engineering
第5章 晶体定向与结晶符号
5.2 各晶系晶轴的选择及晶体几何常数特点
⑷ 单斜晶系 对称特点
School of Materials Science and Engineering
主要教学内容
第5章 晶体定向与结晶符号
晶体定向的概念* 结晶轴与晶体几何常数* 各晶系晶轴的选择及晶体几何常数特征* 晶面符号* 整数定律 晶棱符号和晶带符号* 晶带定律 对称型的国际符号* 对称型的圣佛利斯符号
School of Materials Science and Engineering
⑴ 米氏晶面符号的构成
第5章 晶体定向与结晶符号
米氏晶面符号的一般形式 三轴定向：(hkl)，晶面指数按X,Y, Z顺序排列。
h:k:l=a/OH : b/列。
5.2 各晶系晶轴的选择及晶体几何常数特点
选择晶轴的原则： ① 晶轴的选择要符合晶体自身的对称性； ② 优先选择对称轴；对称轴不够或没有时选对称

05 晶体定向和结晶学符号


晶面符号的一般式： 晶面符号的一般式： 三轴定向： 顺序排列。 三轴定向：(hkl)，按X、Y、Z顺序排列。 ， 、 、 顺序排列 四轴定向： 四轴定向：(hkil)，按X、Y、U、Z、顺序 ， 、 、 、 、 排列。 排列。 四轴定向中， 四轴定向中， h +k +i = 0 ,即h、k、i 中 即 、 、 只有两个是独立的， 只有两个是独立的，故一般式又可写作 (h k · l)。 。
⑸三斜晶系
对称特点：只有 对称特点：只有L1和C。 。 选轴原则：以三根合适的晶棱方向为X、 选轴原则：以三根合适的晶棱方向为 、 Y、Z轴。 、 轴 晶轴安置： 轴直立 轴直立， 轴左右并向右 晶轴安置：Z轴直立，Y轴左右并向右 下倾斜， 轴前后并向前下倾斜 轴前后并向前下倾斜。 下倾斜， X轴前后并向前下倾斜。 晶体几何常数： 晶体几何常数：a≠b≠c，α≠β≠γ≠90o 。 ，
三轴定向选择结晶轴的一般顺序是： 三轴定向选择结晶轴的一般顺序是： 有四次轴时，优先选择四次轴； 有四次轴时，优先选择四次轴； 四次轴不够或没有时，选择L 四次轴不够或没有时，选择L2； 不够或没有时，选择P的法线； L2不够或没有时，选择P的法线； 不够或没有时，选择合适晶棱方向； P不够或没有时，选择合适晶棱方向； 在以上的选择中， 在以上的选择中，除单斜晶系优先考虑 轴之外， 优先考虑Z Y轴之外，其余皆 优先考虑Z轴。
立方体 已知晶面在XYZ轴上的截距为： 轴上的截距为： 已知晶面在 轴上的截距为 OH ，∞ ，∞； ； h:k:l＝a/OH : a/∞ : a/∞＝1:0:0； ＝ ＝ ； 米氏符号： 米氏符号：(100)。 。
八面体 已知晶面在XYZ轴上距： 轴上距： 已知晶面在 轴上距 OH=OK=OL； ； h:k:l = a/OH : a/OH : a/OH =1:1:1； ； 米氏符号： 米氏符号：(111)。 。

4第四讲第五章晶体定向晶面符号和晶带定律

根据这一规律，我们可以由若干已知面或晶带推导 出晶体上一切可能的晶面的位置。
在晶体定向、投影和运算中，晶带和晶带定律得到 了广泛的应用。
晶带定律和整数定律分别以不同的形式阐述了晶面 (面网)与晶核(行列)相互依存的 晶带。
通过晶体中心的直线cc，晶棱与之平行，称 该晶带的晶带轴；该组晶棱的符号也就是该 晶带轴的符号。
3、晶带定律
晶体是一个封闭的几何多面体，每一晶面与其它晶 面相交，必有两个以上的互不平行的晶棱。因此， 晶体上任一晶面至少属于两个晶带。这一规律称为 晶带定律。它也可以这样来表述，即：任意二晶棱 (晶带)相交必可决定一个可能晶面．而任意二晶面 相交必可决定一可能晶棱(晶带)。
确定晶棱符号的方法如下：
将晶棱平移，使之通过晶轴的交点、然后在 其上任一点，取坐标（x、y、z），并以轴长 来度量，即求得晶棱符号： (x/a):(y/b):(z/c)=r:s:t，晶棱符号采用[ ]表 示，即[ rst]。
2．晶带
由布拉维法则可知，晶面是网面密度较大的 面网，所以晶体上所出现的实际晶面为数是 有限的；相应地，晶面的交棱也应当是结点 分布较密的行列，这种行列的方向也是为数 量不多的，所以晶体上的许多晶棱常具有共 向的方向而相互平行。
2、晶面符号
1．晶面符号的概念 晶体定向后，晶面在空间的相对位置即可根据 它与晶轴的关系予以确定。这种相对位置可以 用一定的符号来表征。表征晶面空间方位的符 号．称为晶面符号 晶面符号有多种型式，通常所采用的是米氏符 号，系英国人米勒尔(W．H．Miller)所创。 米氏符号用晶面在三个晶轴上的截距系数的倒 数比来表示。
2．晶面在晶轴上截距系数之比为简单整数比。 晶面指数一般是小整数。这是因为晶面在晶面上 的截距系数之比为简单整数比。

第五章晶体定向与结晶符号

3个平行双面 a{100}, b{010}, c{001} 3个斜方柱 m{hk0}, dh0l}, k{0kl} 1个斜方双锥 e{hkl}
3.单形符号举例
萤 石（757）
立方体｛100｝ 八面体｛111｝ 菱形十二面体｛110｝
注意:
①米氏符号中某个数为0时，表示 该晶面与相应的晶轴平行。
②同一米氏符号中，晶面指数越 大，表示晶面在相应结晶轴上的截 距系数越小。
③由于晶轴有正、负方向之分， 因此，若相交于晶轴负端，则在晶 面指数上加“－” 。
注意:
④晶面指数是截距系数的倒数 比，一般不超过6。
⑤同一米氏符号中，晶面指数 越大，表示晶面在相应的结晶轴上 的截距系数越小；在轴单位相等的 情况下，还表示相应截距的绝对长 度越短，而晶面本身与该结晶轴的 夹角则越大。
a1∶b1=1∶1 a1∶b2=1∶2 a1∶bn=1∶n
网面密度越大,晶面在晶轴上的截距系 数之比愈简单.根据布拉维法则可知,晶面在 晶轴上的截距系数之比为简单整数比.
4.晶面指数写法
⑴.三轴定向的晶系
对三轴定向的晶系而言：晶面
指数按X、Y、Z轴的顺序排列。 如果能确定具体数字时，用阿
拉伯数字表示，如果不能确定具 体数字时，用h、k、l表示。
如:（110）（hkl）（hko）
⑵四轴定向的晶系
对四轴定向的晶体而言： 晶面指数按X、Y、U、Z轴顺 序排列，一般写作（hkil）。
四轴定向的晶系晶面指数写法
不能确定数字， 但能判定指数大小 时，i ＞h＞k，l固 定表示Z轴指数；
晶面指数的前三 个指数的代数和为 零，即h + k + I = 0。
(321)即为HKL晶 面的米氏符号。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

三、六方晶系的晶轴
5
⑶轴单位和轴率
轴单位是晶轴上的单位长，是晶轴所在行列上的 结点间距。X、Y、Z轴上的轴单位分别以a、b、c表示， 或者以a0、b0、c0表示。
由于结点间距很小（以nm计），需借助X射线分 析方能测定，根据晶体外形不能确定轴单位的真实长 度，但应用几何结晶学的方法可以求出它们的比率， 即a︰b︰c，这一比率称为轴率。
以L6、Li6、L3为Z轴，以垂直Z轴并彼此相交 为120°的三个L2或P法线为X、Y、U轴；当 无L2或P时，X、Y、U轴平行晶棱选取
a = b≠c α=β=90°γ=120°
以相互垂直的3L2为X、Y、Z，在L22P对称 a≠b ≠ c
型中以L2为Z轴，以2P法线为X、Y轴
α=β=γ=90°
以L2或P的法线为Y轴，以垂直Y轴的主要晶 a≠b ≠ c
7
2、晶轴选择与各晶系晶体常数特点
晶轴选择的原则： ⑴应符合晶体所固有的对称性。因此，晶轴 应优先与对称轴或对称面的法线重合；若无对 称轴和对称面，则晶轴可平行主要晶棱选取。 ⑵在上述前提下，应尽可能使晶轴相互垂直 或趋于垂直，并使轴单位趋于相等。即尽可能 使α＝β＝γ＝90°，a＝b＝c。
各晶系的对称特点不同，选择晶轴的方法及其晶 体常数特点也不一样。
13
⑵如图所示，平行Z轴的一组面网截X轴于a1点，截Y轴分 别于b1、b2、b3、b4……bn点，网面密度a1b1＞a1b2＞ a1b3＞……a1bn，它们在X、Y轴上的截距系数之比则 分别为1︰1、1︰2、1︰3……1︰n，显然，网面密度 越大，晶面在晶轴上的截距系数之比越简单。
❖根据布拉维法则，因此， 晶面在晶轴上的截距系数之 比为简单整数比。这一规律 被称为整数定律。 ❖晶面指数一般是小的整数， 晶面符号中最常见的指数为 1和0，其次为2和3，超过3 的很少。
10
例：晶面HKL在晶轴上的截距分别为2a、3b、 6c，则截距系数的倒数比为1/2︰1/3︰1/6＝ 3︰2︰1，去其比例符号，加上小括号，即为 该晶面的米氏符号（321）。
晶面符号图解
11
晶面符号的括号内数字称为晶面指数。晶面指数 是按照X、Y、Z轴顺序排列的，一般式写作（hkl）； 如果晶面与晶轴的负端相交，则在其相应的指数上 加“－”。 而对于三方、六方晶系，晶面指数按照X、Y、U、
棱方向为Z及X轴
α=γ=90° β＞ 90°
以不在同一平面内的三个主要晶棱方向为X、 a ≠ b ≠ c
Y、Z轴
α ≠ β ≠ γ ≠ 90°
9
二、晶面符号
1、晶面符号的概念和写法 晶体定向后，晶面在空间的相对位置即可
根据它与晶轴的关系予以确定。表示晶面空 间方位的符号称为晶面符号。
通常所采用的是米氏符号，是英国人米勒 尔在1839年所创。米氏符号是用晶面在结晶 轴上的截距系数的倒数比来表示的。
晶轴分别以X轴（前端为“＋”，后端为“－”）、Y轴 （右端为“＋”左端为“－”）和Z轴（上端为“＋”， 下端为“－”）表示，或称a、b、c轴。对于三方和六方晶 系要增加一个U轴（前端为“－”，后端为“＋”）。
4
⑵轴角：晶轴正端之间的夹角。分别以α
（Y∧Z）、β（Z∧X）、γ（X∧Y）表示。
晶轴及轴角
14
三、单形符号
单形符号简称形号：是指在单形中选择一代表晶面， 将其晶面指数用“｛｝”括起来，用以表征组成该单形 的一组晶面的结晶学取向的符号。
同一单形的各个晶面与晶轴都有着基本相同的相对位置。如立 方体的每一晶面都与一个晶轴垂直而与另外两个晶轴平行，八面体 的每一晶面都截三个晶轴等长。因此，同一单形的各个晶面的指数 的绝对值不变，而只有排列顺序和正负号的区别。如八面体的各晶 面符号为（111）、（1 1 1）、（11 1）、（ 111）、（1 1 1 ）、 （ 1 1 1）、（ 1 1 1 ）、（ 1 1 1 ）。
由四方柱和四方双 锥组成的两个聚 形，对称型均为L44L25PC
2
一、晶体定向
晶体定向的概念 晶轴选择与各晶系晶体常数特点
3
1、晶体定向的概念
晶体定向：在晶体上选择坐标系统。即选定坐标轴 （晶轴）和确定各晶轴上轴单位之比（轴率）。
⑴晶轴：是交于晶体中心的三条直线，晶轴的选择 不是任意的，应与格子构造中的行列平行，并一般 应与对称轴、对称面的法线或晶棱重合。
8
各晶系选择晶轴的原则及晶体常数特点
晶系
选轴原则
晶体常数特点
等轴 晶系
四方 晶系
三、 六方 晶系
斜方 晶系
单斜 晶系
三斜 晶系
以相互垂直的L4、Li4或L2为X、Y、Z轴
a = b=c α=β=γ=90°
以个Y轴LL42平或或行LPi的晶4为法棱z线轴选为，取X以、垂Y直轴Z；轴当并无相L互2或垂P直时的，两X、αa==β=bγ≠=c90°
第五章 晶体定向与结晶符号
一、晶体定向 二、晶面符号 三、单形符号 四、晶带及晶带符号 五、对称型的国际符号 六、各晶系晶体定向及常见单形符号
（自学）
1
在研究晶体形态时，仅确定其对称型和有哪些单形 组成，仍不能获得晶体的具体形态。因此，必须进 一步确定各单形在空间的相对位置，这就需要在晶 体上选定一坐标系统，并用一定的数学符号表示晶 面、晶棱等在空间的方位，这就是晶体定向和结晶 符号所要解决的内容。
Z轴的顺序排列，一般式写作（hk i l），而且h＋k
＋ i ＝0。
如果晶面平行于某晶轴，那么它在该晶轴上的截距 系数为∞，则其晶面指数就是1/∞＝0。例如，与X、 Y轴平行，与Z轴相交的晶面，其晶面符号为 （001）。
12
2、晶面在晶轴上截距系数之比为简单的整数比
⑴晶轴的选择是与晶体的 格子构造一致的，晶面是面 网，晶轴是行列，晶面截晶 轴于结点，或者晶面平移后 截晶轴于结点（平移后各晶 轴上的截距系数之比不变， 所以晶面符号不变）。所以 如果以晶轴上的结点间距a、 b、c作为度量单位，则晶面 在晶轴上的截距系数之比必 为整数比。
例如，中级晶族晶体中只有一个高次轴，以高次轴 为Z轴，通过高次轴的作用可以可使X、Y轴重合，因此 轴单位a＝b≠c，轴率a︰c因晶体的种类而异。
6
⑷晶体常数：轴率a︰b︰c和轴角α、β、γ
称为晶体常数。
晶体常数是表征晶体坐标系统的一组基 本参数。它与晶体内部结构研究中晶胞的参 数（或格子参数）一致，如果轴单位和轴角 已知，就可以知道晶胞的形状和大小。