15整式的乘除与因式分解知识结构图-学生版

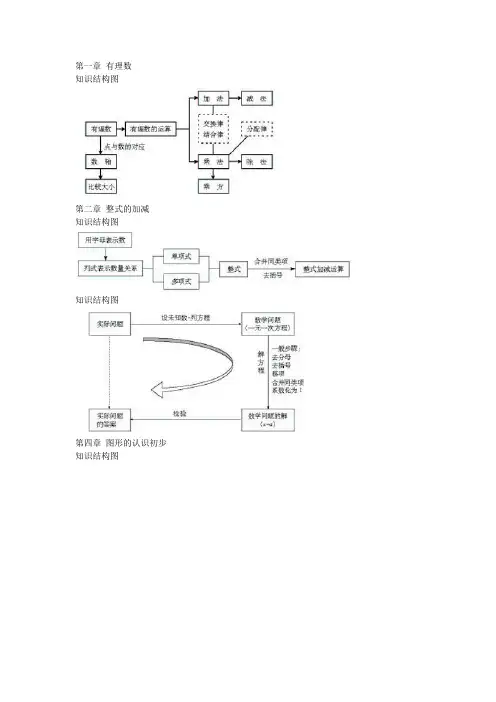
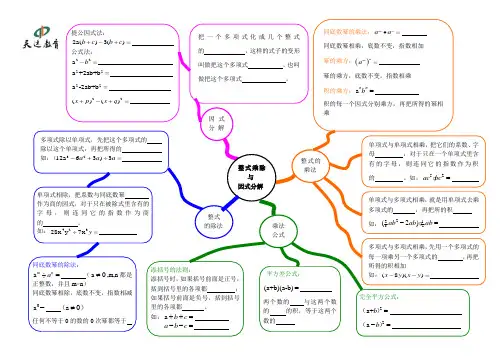
同底数幂的乘法：m n a a •= 同底数幂相乘，底数不变，指数相加 幂的乘方：()n m a = 幂的乘方，底数不变，指数相乘 积的乘方：a n nb = 积的每一个因式分别乘方，再把所得的幂相乘同底数幂的除法：a m n a ÷= （a 0≠,m,n 都是正整数，并且m>n ）同底数幂相除，底数不变，指数相减0a = a 0≠（）任何不等于0的数的0次幂都等于整式的乘法单项式与单项式相乘，把它们的系数、字母 ，对于只在一个单项式里含有的字母，则连同它的指数作为积的 。

如：52ac bc =g单项式与多项式相乘，就是用单项式去乘多项式的 ，再把所的积如：22132(2)ab ab ab -=g多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的 ，再把所得的积相加如：(8)()x y x y --= 乘法 公式平方差公式：(a+b)(a-b)=两个数的 与这两个数的 的积，等于这两个数的完全平方公式：2a+b =（） 2a b -=（）添括号的法则：添括号时，如果括号前面是正号，括到括号里的各项都 ；如果括号前面是负号，括到括号里的各项都 。

如：a b c ++=a b c --=单项式相除，把系数与同底数幂 作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的 。

如：42328x y 7x y ÷=整式 的除法多项式除以单项式，先把这个多项式的 除以这个单项式，再把所得的 如：3212a 63)3a a a -+÷=（把一个多项式化成几个整式的 ，这样的式子的变形叫做把这个多项式 。

也叫做把这个多项式 。

因式分 解整式乘除与 因式分解提公因式法：2a()3()b c b c +-+=公式法：22a b -=22a +2ab+b = 22a -2ab+b =22()()x p x q +-+=。

一张带你梳理整式的乘除知识内
容
一、思维导图工具
想要绘制整式的乘除思维导图通常可以使用迅捷思维导图工具进行，这款工具带有android、web、win等多种版本，可通过手机、电脑、排版等设备用软件会在线的方式制作思维导图，并提供有诸多和学习相关的思维导图模板供以参考，详情可通过“思维导图软件”一文了解。

二、画整式的乘除思维导图
通过“思维导图简单画法”一文可以了解到，思维导图通过递进式结构将零散且存在关联的内容串联到一起，有序地梳理发散性内容。

将思维导图运用到学习中梳理整式的乘除同样是用层层递进的方式有序梳理。

至于整式的乘除思维导图绘制方法通常可以梳理为以下多个步骤：
1、首先通过迅捷思维导图的任意版本创建一份“空白思维导图”；
2、接着把需要梳理的主题录入到编辑器的“中心节点”，即整式的乘除；
3、随后以层层递进的方式围绕“中心节点”梳理与之相关的“分支内容”，即有序梳理整式的乘除相关知识内容；
4、后续还可以通过插入素材、图标、概要、关系线等功能进一步完善知识内容，亦或使用一键美化、样式、主题等功能适当美化导图；
5、当整式的乘除思维导图绘制完毕后，将其“保存”至账号云端或“导出”至设备本地即可。

三、整式的乘除思维导图模板
当然了，除了通过思维导图编辑器依序梳理整式的乘除知识内容外，还可从迅捷画图模板库中套用整式的乘除思维导图模板，以便快速绘图。

新课标人教版初中数学八年级上册第十五章《整式的乘除与因式分解》简介人教版《义务教育课程标准实验教科书?数学》第十五章是“整式的乘除与因式分解”。

本章的主要内容是整式的乘除运算、乘法公式以及因式分解。

本章内容建立在已经学习了的有理数运算、列简单的代数式、一次方程及不等式、整式的加减运算等知识的基础上。

整式的乘除运算和因式分解是基本而重要的代数初步知识，这些知识是以后学习分式和根式运算、函数等知识的基础，在后续的数学学习中具有重要意义，同时，这些知识也是学习物理、化学等学科及其他科学技术不可缺少的数学基础知识.本章共安排了4个小节，教学时间约需13课时（供参考）：15.1 整式的乘法4课时15.2 乘法公式2课时15.3 整式的除法2课时15.4 因式分解3课时数学活动小结2课时一、教科书内容和课程学习目标（一）本章知识结构框图（二）教科书内容本章共包括4节15.1 整式的乘法整式的乘法是整式四则运算的重要组成部分。

本节分为四个小节，主要内容是整式的乘法，这些内容是在学生掌握了有理数运算、整式加减运算等知识的基础上学习的。

其中，幂的运算性质，即同底数幂的乘法、幂的乘方和积的乘方是整式乘法的基础，教科书把它们依次安排在前三个小节中，教学中应适当复习幂、指数、底数等概念，特别要弄清正整数指数幂的意义。

在学生掌握了幂的运算性质后，作为它们的一个直接应用，教科书在第四小节安排一般整式乘法的教学内容。

首先是单项式与单项式相乘，由于进行单项式与多项式、多项式与多项式相乘的前提是熟练地进行单项式与单项式相乘，因此，对于单项式与单项式相乘的教学应该予以充分重视。

在学生掌握了单项式与单项式相乘的基础上，教科书利用分配律等进一步引入单项式与多项式相乘、多项式与多项式相乘，这样使整式乘法运算的教学从简到繁，由易到难，层层递进。

15.2乘法公式本节分为两个小节，分别介绍平方差公式与完全平方公式。

乘法公式是整式乘法的特殊情形，是在学习了一般的整式乘法知识的基础上学习的，运用乘法公式能简化一些特定类型的整式相乘的运算问题，教科书在本节开始首先指出了这一点。

整式的乘除jpeg文件后，粘贴在这里；如果提交到平台，则需要使用图片导入的功能。

）主题单元学习目标（说明：依据新课程标准要求描述学生在本主题单元学习中所要达到的主要目标）知识与技能：1、理解并会进行同底数幂乘法、幂的乘方、积的乘方和同底数幂除法。

2、了解并记住零指数幂、负指数幂的意义。

3、理解整式乘法法则（包括乘法公式），能熟练进行整式的乘法。

4、以整式乘法法则为基础理解整式除法法则，并会进行整式除法运算。

过程与方法：1、类比数的运算，通过观察和体会、运用幂的意义，最终得到以字母为底数的幂的运算法则。

室或多媒体教室。

其他纸、笔学习活动设计第一课时同底数幂的乘法活动一：试试看：(1)下面请同学们根据乘方的意义做下面一组题：①23×25＝（2×2×2）（2×2×2×2×2）②=＿＿＿＿＿＿＿＿＿＿＿＿＿=③a3．a4=＿＿＿＿＿＿＿＿＿＿＿＿＿=a( )(2)根据上面的规律，请以幂的形式直接写出下列各题的结果：102×103= 104×105= 10m×10n= (1／10)m×（1／10）n=活动二：猜一猜：当ｍ，ｎ为正整数时候，=（a×a×a×…×a）（a×a×a×…×a）．＝（a×a×a×…×a）＝（）个（）个（）个即am·an= (m、n都是正整数)活动三：同底数幂的乘法法则：同底数幂相乘运算形式：（同底、乘法）运算方法：（底不变、指加法）当三个或三个以上同底数幂相乘时，也具有这一性质，用公式表示为 am·an·ap = am+n+p （m、n、p都是正整数）活动四：练习1. 下面的计算是否正确? 如果错，请在旁边订正（1）．a3·a4=a12 （2）．m·m4=m4 (3)．a2·b3=ab5 （4）．x5+x5=2x10（5）．3c4·2c2=5c6 （6）．x2·xn=x2n (7)．2m·2n=2m·n （8）．B4·b4·b4=3b42．填空：（1）x5 ·（）=x 8 （2）a ·（）=a6x k （3）x · x3（）= x7 （4）xm ·（）＝x3m（5）x5·x( )=x3·x7=x( ) ·x6=x·x( ) （6）an+1·a( )=a2n+1=a·a( )活动五：例1．计算（1）(x+y)3 · (x+y)4 （2）-x2·（-x6）（3）（a-b）3(b-a)5 （4）a3m·a2m-1（m是正整数）活动六：变式训练．计算（1）(-7)3(-7)8（2）(-6)267（3）. 53 (-5)5 (-5)4 （4）（b-a）2(a-b)（5）（a-b）(b-a)4 （6）xn·xn+1+x2n·x （ｎ是正整数）回顾小结1．同底数幂相乘法则要注重理解“同底、相乘、不变、相加”这八个字．2．解题时要注意a的指数是1．3．解题时，是什么运算就应用什么法则．同底数幂相乘，就应用同底数幂的乘法法则；整式加减就要合并同类项，不能混淆．4．-a2的底数a，不是-a．计算-a2·a2的结果是-(a2·a2)=-a4，而不是(-a)2+2=a4．5．若底数是多项式时，要把底数看成一个整体进行计算[／评价要点1、能熟练进行幂的运算。

&单项式与多项式相乘的乘法法则 ：单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的整式的乘除与因式分解基本知识点、整式的乘除:合并同类项：把多项式中的同类项合并成一项，叫做合并同类项3x 2y -2xy + xy 2 -4x 2y +2x 3 +10xy-2x 3 =同底数幕的乘法法则：a m - a n =a m+n （m, n 是正整数）.例如：a 3a积的乘方的法则：（a b ） m =a m b m （m 是正整数）.积的乘方，等于把积的每一个因式分别乘方，再把所得的幕相乘5、同底数幕的除法法则：a m + a n =a m-n （a M 0, m n 都是正整数，并且同底数幕相除，底数不变，指数相减.规定：a 0 =1 （a 工0） 例如：a 3 rn a =6、单项式乘法法则单项式与单项式相乘， 把它们的系数相乘、 相同字母的幕分别相加,因式。

7、单项式除法法则单项式相除，把系数与同底数幕分别相除作为商的因式，对于只在被除式里含有的字母，则连同它的指数 作为商的一个因式.例如：3a - a =2 2 ;a +a =1、 2、 同底数幕相乘, 底数不变，指数相加3、 幕的乘方法则 :（a m ）n =a mn（m ，n 是正整数）.幕的乘方，底数不变，指数相乘 例如：（a 2）3；(x 5)2 = ；(a 4)3-(a 3)。

4、 例如：（ab ）3 =;(-2a 2b)3 = ;(—5a 3b 2)2 = 其余字母连同它的指数不变， 作为积的2x ”3y(―2x 2y)(5xy 2) (3xy)2 <-2xy 2) , 2,\3 / 2,\2 (—a b) (a b)24x 2 y 斗(一 6xy ) (6X108 片(3"05)积相加.9、多项式乘法法则：多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加.10、多项式除以单项式的除法法则：多项式除以单项式，先把这个多项式的每一项除以这个单项式，再把所得的商相加. (8a 2 -4abF( -4a)2a 2c--b 2C L - c2 丿211、整式乘法的平方差公式 ：（a+b ）（ a-b ）= a 2-b 2. 两个数的和与这两个数的差的积，等于这两个数的平方差(-3 + x)(-3-x) =2 2 2 2 2 212、整式乘法的完全平方公式 ：(a+b) =a +2ab+b , (a-b) =a -2 ab+b .两数和（或差）的平方，等于它们的平方和，加 （或减）它们的积的2倍.例如：（2a+5b 2 =(-ab +22 =二、因式分解:m(a +b +c)2x(—2x-3y +5) -3ab(5a - ab + 2b 2)(X + 2)(x-6)(2x -3y)(x -2y +1) (a + b^a 2 -ab+ b 2) (6 xy + 5 X 户 X ； (20a 4 b- 45a 2b ^5a 2 b 例如：(4a — 1) (4a+1)= (3a — 2b) (2b+3a)=1、提公共因式法(1 )、如果一个多项式的各项含有公因式 ，那么就可以把这个公因式提出来 ，从而将多项式化成两个因式乘积的形式.这种分解因式的方法叫做提公因式法女0:ab + ac = a (b+ c)(2)、概念内涵：① 因式分解的最后结果应当是“积”② 公因式可能是单项式，也可能是多项式；③提公因式法的理论依据是乘法对加法的分配律 ，即:ma + mb-mc=m(a+ b-c)练习2、公式法.：3、分组分解法:如： am +a n +bm +b n = a(m + n) +b(m + n) = (a + b)(m + n)(2)、概念内涵：分组分解法的关键是如何分组 ，要尝试通过分组后是否有公因式可提 ，并且可继续分解，分组后是否可利用 4 xy - yX 2 +x 3 2 " 3 , + 12x +4x m(a -1) + n(a — 1)(1 )、平方差公式: a 2 - b 2 = (a + b)(a - b)x 2 -1 4a 2 —9b 2 16x 2 -(y + z)2 (a+2b)2 -(2a-b)2(2)、完全平方公式: a 2 +2ab +b 2 = (a + b)2a 2 - 2ab + b 2 = (a - b)2 m 2 -4m +49x 2 +6xy + y 2 16x 2 +24x + 9(a + b)2 -12(a + b) + 36公式法继续分解因式.(3)、注意：分组时要注意符号的变化4、“十字相乘法”：即式子 x +(p+q)x+pq 的因式分解.X +(p+q)x+ pq=(x+ p)(x+q).有些二次三项式，可以把第一项和第三项的系数分别分解为两个数之积，然后借助画十字交叉线的方法, 把二次三项式进行因式分解，这种方法叫十字相乘法。

整式知识结构图1. 由数与字母的乘积组成的代数式叫做单项式，单独的一个数或一个字母也是单项式。

如：等都是单项式。

2. 单项式的系数、次数，单项式中的数字因数叫做单项式的系数。

如的系数分别是5，，单项式ab的系数是“1”，单项式的系数是。

单项式中，所有字母的指数的和叫做单项式的次数，如单项式叫5次单项式，叫做三次单项式。

3. 多项式及多项式的次数。

几个单项式的和叫做多项式，在多项式中，每个单项式叫多项式的项，不含字母的项叫常数项。

多项式里，次数最高项的次数，就是这个多项式的次数。

如多项式是一个四次三项式。

多项式是一个七次二项式。

4. 多项式的升幂排列和降幂排列：把一个多项式按某一字母的指数从大到小的顺序排列起来，叫做这个多项式按这个字母降幂排列。

把一个多项式按某一字母的指数从小到大的顺序排列起来，叫做这个多项式按这个字母升幂排列。

由于多项式的项包括它前面的性质符号，因此在排列时，需带符号一起移动，在含有两个或两个以上字母的多项式，按某一字母排列时，要特别注意按哪一个字母排列。

5. 整式的概念单项式和多项式统称为整式6. 同类项的概念：所含字母相同，并且相同字母的次数也相同的项叫做同类项，几个常数项也是同类项。

判断几个单项式（或同一个多项式的项）是不是同类项有两个条件（1）所含有的字母相同（2）相同字母的指数分别相同。

只有这两个条件同时具备了才能说它们是同类项。

同类项与其系数无关，与字母的顺序无关。

7. 合并同类项合并同类项的法则：把同类项的系数相加，所得的结果作为系数，字母和字母的指数保持不变。

合并同类项的具体步骤：第一步：准确地找出同类项第二步：利用分配律，把同类项的系数加在一起（用小括号），字母和字母的指数不变。

第三步：写出合并结果。

8. 去括号和添括号去括号法则：括号前是“+”号，把括号和它前面的“+”号去掉，括号里各项都不变符号。

括号前是“－”号，把括号和它前面的“－”号去掉。

括号里各项都改变符号。