2021届云南省曲靖市二中、大理新世纪中学2018级高三上学期一模考试文科综合地理试卷及答案

2018年云南省高中毕业生复习统一检测语文试题一、现代文阅读（35分）（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1～3题。

当今世界，各国经济发展深度融合，单一国家已经难以独自面对全球性经济问题的挑战。

改革开放以来，中国经济快速发展，为世界经济发展注入了强劲动力和活力。

应对当前经济全球化面临的问题和挑战，需要中国智慧、中国方案。

在世界格局大变革大调整的关键时期，中国倡导和推动“一带一路”建设。

“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称。

“一带一路”贯穿欧亚大陆，东边连接亚太经济圈，西边进入欧洲经济图。

无论是发展经济、改善民生，还是应对危机、加快调整，许多沿线国家同我国有着共同利益。

历史上，陆上丝绸之路和海上丝绸之路就是我国同中亚、东南亚、南亚、西亚、东非、欧洲经贸和文化交流的大通道，“一带一路”是对古丝绸之路的传承和提升，获得了国际社会的广泛认同。

“一带一路”建设不是为了另起炉灶，更不是为了针对谁，而是对现有国际机制的有益补充和完善，目标是实现合作共赢、共同发展。

中国推进“一带一路”建设，不是要一家唱独角戏，而是欢迎各方共同参与；不是要谋求势力范围，而是支持各国共同发展；不是要营造自己的后花园，而是建设各国共享的百花园。

“一带一路”建设的实践表明，这一伟大创举是对传统区域经济一体化模式的超越与创新。

它致力于推动基础设施建设和互联互通，加强经济政策协调和发展战略对接，促进协同联动发展，实现共同繁荣。

它坚持共商共建共享原则，开创发展新机遇、谋求发展新动力、拓展发展新空间，帮助各参与国打破发展瓶颈、缩小发展差距、共享发展成果。

各参与国是平等贡献者、受益者，甘苦与共、命运相连，携手应对经济全球化面临的问题和挑战。

“一带一路”建设有利于构建相互尊重、公平正义、合作共赢的新型国际关系，打造对话不对抗、结伴不结盟的伙伴关系。

中国愿在和平共处五项原则基础上，发展同所有“一带一路”建设参与国的友好合作关系，中国愿同世界各国分享发展经验，但不会干涉他国内政，不会输出社会制度和发展模式，更不会强加于人。

2021年曲靖一中高三语文一模试题及答案一、现代文阅读（36分）(一)现代文阅读I(9分)阅读下面的文字，完成各题。

欢喜简平我怎么可能会喜欢这样一个寒冷而绝望的冬天呢？那痛楚是割裂着心的锐利的冰凌，那绝望如漫漫冬夜里连一颗幽暗的星子都没有。

时至年末，偶尔有一些零星的爆竹声，人们和这世界一起准备进入下一个年轮。

可我却翻不动我的日历——从胃癌切除手术室出来，我就觉得太阳再也不会升起来了。

可是，母亲来了，她帮我把12月的日历翻到最后一张，然后，在大理石台历架上换上了全新的日历芯子，那封面上标着鲜红的纪年：2012年。

母亲坐在我的床头，用平静的声音对我说：“人生来就是要受苦的，但再苦也要走过去，而且总是走得过去的。

你看，新的一年就要到来了，所有的日子都在前面一天天等着你呢。

”也就是从那个12月开始，母亲每周三都早早地来到我的住处。

她来时总是两只手都提着沉沉的袋子，里面装满了刚刚买好的蔬菜、瓜果，有时还装着报纸和书籍。

我怕她累着了，让她每次都坐出租车过来，但她不肯，说这点东西她提得动。

所以，母亲还是每每乘公交车来，路上要倒几趟车，来回至少得两个多小时。

一进门，母亲就忙乎起来，一边跟我聊天，一边拣菜、洗菜，然后去厨房煲汤做菜，稍有空隙，还帮我打扫屋子。

这个时候，我就会停止无穷无尽的销蚀灵魂的妄念，在颠簸的气流里上下乱飞的风筝便也静止在了空中。

从此，每个周三成了我心里企盼的节日。

每当听见母亲用钥匙转动门锁的声音，我心里就欢喜得像是燃放起了焰火，那焰火在彻骨的寒冷中美丽绽放，将凛冽染上了一层明亮和温暖。

我感觉那一天心情特别平和，特别安宁。

我真的又可以站立起来了，可以趴在窗前看外面的天与地了。

原本因为恐惧和焦虑，我如同一只被蒙住眼睛的惊慌的小鸟，哪怕飞得再高，也看不见连绵的山脉和澎湃的海洋了。

那天，下雪了，江南的雪花不是完整的一朵朵的，谁都无法相信它会聚起来，可偏偏不多时，雪就把房顶、树枝和路径覆盖住了，白色皑皑，一派纯净。

云南省曲靖市第二中学2021届高三第一次模拟考试数学（文）试题(本卷满分150分，考试时间120分钟)注意事项：1.答卷前，考生务必用黑色碳素笔将自己的姓名、准考证号填写在答题卡上.2.回答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮檫干净后，再涂选其他答案标号.回答非选择题时，将答案写在答题卡上.写在试卷上无效.3.考试结束后，将本试卷和答题卡一并交回.第Ⅰ卷（选择题，共60分）一、选择题：本大题共12小题,每小题5分,在每小题的四个选项中只有一个是正确的。

1.若复数i Z i Z -=+=2,321，则21Z Z -在复平面内对应的点位于 A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.若集合}01|{≤≤-=x x A ，}0)1(log |{2≤-=x x B ，则=B AA.}11|{<≤-x xB.}11|{≤<-x xC.}0{D.}11|{≤≤-x x3.已知P (1,3)在双曲线x 2a 2－y 2b2＝1()a >0，b >0的渐近线上, 则该双曲线的离心率为A.10B.2C. 5D.3 4.“a=1”是“直线ax+2y-8=0与直线x+（a+1）y+4=0平行”的 A. 充要条件 B. 充分而不必要条件C. 必要而不充分条件D.既不充分也不必要条件 5.函数x e x f xln )(=在点))1(,1(f 处的切线方程是A ．)1(2-=x e yB ．1-=ex yC ．)1(-=x e yD ．e x y -= 6.已知a ，b 是非零向量，且向量a ，b 的夹角为3π，若向量||||a b p a b =+，则||p = A ．2+ B37.执行如图所示的程序框图，为使输出的数据为63， 则判断框中应填入的条件为 A.4i ≤ B.5i ≤C.6i ≤D.7i ≤ （第7题图）8.已知数列{}a n 的前n 项和为S n , 通项公式a n ＝log 2n ＋1n ＋2 (n ∈N *), 则满足不等式S n <－6的n 的最小值是A.62B.63C.126D.127 9.在ABC ∆中，C B A 、、的对边分别为c b a 、、，其中ac b =2,且B C sin 2sin =,则其最小角的余弦值为 A.42-B.42C.825 D.4310.右图为一个正四面体的侧面展开图，G 为BF 的中点，则 在原正四面体中，直线EG 与直线BC 所成角的余弦值为 A.33B.36C.63 D.633（第10题图）11.本周星期日下午1点至6点学校图书馆照常开放, 甲、乙两人计划前去自习, 其中甲连续自习2小时, 乙连续自习3小时．假设这两人各自随机到达图书馆, 则下午5点钟时甲、乙两人都在图书馆自习的概率是A.19B. 16C.13D. 1212.已知双曲线)0,0(12222>>=-b a b y a x 的两顶点分别为21,A A ，F 为双曲线的一个焦点，B 为虚轴的一个端点,若在线段BF 上（不含端点）存在两点21,P P，使得221211A P A A P A ∠=∠2π=，则双曲线的渐近线斜率k 的平方的取值范围是A.)215,1(+ B.)213,1(+ C.)215,0(+ D.)213,23(+ 第Ⅱ卷（非选择题，共90分）二、填空题：（本题共4个小题，每个小题5分，共20分）13. 已知圆C 1：(x －a )2＋y 2＝1与圆C 2：x 2＋y 2－6x ＋5＝0外切, 则a 的值为 .14. 已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为 .15.若变量x ，y 满足31031102x y x y y --≥⎧⎪+-≤⎨⎪≥⎩，且y ax z -=的最小值为1-，则实数a 的值为 .16.在平面直角坐标系xOy 中，点),(00y x P 在单位圆O 上，设α=∠xOP ，且)43,4(ππα∈．G F EDC BA若1312)4cos(-=+πα，则0x 的值为 . 三、解答题：（本大题共6个小题，共70分） 17.（本题12分）已知函数))(12(sin 2)62sin(3)(2R x x x x f ∈-+-=ππ（1）求函数)(x f 的最小正周期；（2）求使函数)(x f 取得最大值的x 的集合．18. （本题12分）某产品的三个质量指标分别为x ，y ，z ，用综合指标S ＝x ＋y ＋z 评价该产品的等级. 若S ≤4，则该产品为一等品. 现从一批该产品中，随机抽取10件产品作为样本，其质量指标列表如下：产品编号 A 1 A 2 A 3 A 4 A 5 质量指标(x ，y ，z ) (1,1,2) (2,1,1) (2,2,2) (1,1,1) (1,2,1)产品编号 A 6 A 7 A 8 A 9 A 10 质量指标(x ，y ，z )(1,2,2) (2,1,1) (2,2,1) (1,1,1) (2,1,2)(1) 利用上表提供的样本数据估计该批产品的一等品率； (2) 在该样本的一等品中，随机抽取2件产品， ①用产品编号列出所有可能的结果；②设事件B 为“在取出的2件产品中，每件产品的综合指标S 都等于4”，求事件B 发生的概率．19.（本题12分）如图, 已知三棱柱ABC －A ′B ′C ′的侧棱垂直于底面, AB ＝AC , ∠BAC ＝90, 点M , N 分别是A ′B 和B ′C ′的中点. (1) 证明：MN ∥平面AA ′C ′C ；(2) 设AB ＝λAA ′，当λ为何值时，CN ⊥平面A ′MN ，试证明你的结论.20.（本题12分）如图, 已知抛物线C ：y 2＝x 和⊙M ：(x －4)2＋y 2＝1, 过抛物线C 上一点H (x 0，y 0) (y 0≥1)作两条直线与⊙M 分别相切于A 、B 两点, 分别交抛物线于E 、F 两点. (1) 当∠AHB 的角平分线垂直x 轴时, 求直线EF 的斜率； (2) 若直线AB 在y 轴上的截距为t , 求t 的最小值.21.（本题12分）设x m =和x n =是函数21()ln (2)2f x x x a x =+-+的两个极值点，其中m n <，a R ∈. (1) 求()()f m f n +的取值范围； (2) 若2a e e≥-,求()()f n f m -的最大值. 请考生在第22,23题中任选一题作答如果多做，则按所做的第一题计分 22. （本题10分）选修4-4：坐标系与参数方程已知在直角坐标系xOy 中, 圆C 的参数方程为 ⎩⎪⎨⎪⎧x ＝3＋2cos θ，y ＝－4＋2sin θ(θ为参数).(1) 以原点为极点, x 轴正半轴为极轴建立极坐标系, 求圆C 的极坐标方程； (2) 已知A (－2, 0), B (0, 2), 圆C 上任意一点M , 求△ABM 面积的最大值. 23. （本题10分）选修4-5：不等式选讲已知函数f (x )＝k －||x －3, x ∈R 且f (x ＋3)≥0的解集为[]－1，1.(1) 求k 的值；(2) 若a , b , c 是正实数, 且1ka ＋12kb ＋13kc ＝1, 求证：19a ＋29b ＋39c ≥1.云南省曲靖市第二中学2021届高三第一次模拟考试数学（文）试题参考答案一．选择题1.A2.A3.A4.A5.C6.D7.B8.C9.C 10.C 11.B 12.A 二．填空题13.0或6 14.π29 15. 2 16. 2627-17. (1) f(x)=3sin(2x －π6)+1－cos2(x －π12)= 2[32sin2(x －π12)－12 cos2(x －π12)]+1 =2sin[2(x －π12)－π6]+1= 2sin(2x －π3) +1 ∴ T=2π2=π(2) 当f(x)取最大值时, sin(2x －π3)=1, 有 2x －π3 =2k π+π2即x=k π+ 5π12(k ∈Z)∴所求x 的集合为{x ∈R|x= k π+ 5π12 , (k ∈Z)}.18.(1)产品编号A1A2A3A4A5A6A7A8A9A10S4463454535其中S ≤4的有A 1，A 2，A 4，A 5，A 7，A 9，共6件，故该样本的一等品率为＝0.6，从而可估计该批产品的一等品率为0.6. ------4分(2)①在该样本的一等品中，随机抽取2件产品的所有可能结果为{A 1，A 2}，{A 1，A 4}，{A 1，A 5}，{A 1，A 7}，{A 1，A 9}，{A 2，A 4}，{A 2，A 5}，{A 2，A 7}，{A 2，A 9}，{A 4，A 5}，{A 4，A 7}，{A 4，A 9}，{A 5，A 7}，{A 5，A 9}，{A 7，A 9}，共15种 ----9分②在该样本的一等品中，综合指标S 等于4的产品编号分别为A 1，A 2，A 5，A 7，则事件B 发生的所有可能结果为{A 1，A 2}，{A 1，A 5}，{A 1，A 7}，{A 2，A 5}，{A 2，A 7}，{A 5，A 7}，共6种．所以P (B )＝. ----12分19.(1)取A ′B ′的中点E ，连接ME ，NE .因为点M ，N 分别是A ′B 和B ′C ′的中点，所以NE ∥A ′C ′，ME ∥AA ′，又A ′C ′面AA ′C ′C ，AA ′面AA ′C ′C ， 所以ME ∥平面AA ′C ′C ，NE ∥平面AA ′C ′C ， 所以平面MNE ∥平面AA ′C ′C ，因为MN 平面MNE ，所以MN ∥平面AA ′C ′C . 6分(2)连接BN ，设A ′A ＝a ，则AB ＝λa ，由题意知BC ＝2λa ，NC ＝BN ＝a 2＋12λ2a 2，∵三棱柱ABC －A ′B ′C ′的侧棱垂直于底面，∴平面A ′B ′C ′⊥平面BB ′C ′C ， ∵AB ＝AC ，点N 是B ′C ′的中点，∴A ′N ⊥平面BB ′C ′C ，∴CN ⊥A ′N .要使CN ⊥平面A ′MN ，只需CN ⊥BN 即可，∴CN 2＋BN 2＝BC 2，2⎝ ⎛⎭⎪⎫a 2＋12λ2a 2＝2λ2a2∴ λ＝2，∴当λ＝2时，CN ⊥平面A ′MN . 12分 20．(1)法一：∵当∠AHB 的角平分线垂直x 轴时，点H (4，2)， ∴k HE ＝－k HF ，设E (x 1，y 1)，F (x 2，y 2)， ∴y H －y 1x H －x 1＝－y H －y 2x H －x 2，∴y H －y 1y 2H －y 21＝－y H －y 2y 2H －y 22，∴y 1＋y 2＝－2y H ＝－4， k EF ＝y 2－y 1x 2－x 1＝y 2－y 1y 22－y 21＝1y 2＋y 1＝－14. 6分法二：∵当∠AHB 的角平分线垂直x 轴时，点H (4，2)，∴∠AHB ＝60°，可得k HA ＝3，k HB ＝－3，∴直线HA 的方程为y ＝3x －43＋2， 联立方程组⎩⎨⎧y ＝3x －43＋2，y 2＝x ，得3y 2－y －43＋2＝0， ∵y E ＋2＝33，∴y E ＝3－63，x E ＝13－433. 同理可得y F ＝－3－63，x F ＝13＋433，∴k EF ＝－14. 6分(2)法一：设点H (m 2，m )(m ≥1)，HM 2＝m 4－7m 2＋16，HA 2＝m 4－7m 2＋15.以H 为圆心，HA 为半径的圆方程为：(x －m 2)2＋(y －m )2＝m 4－7m 2＋15，① ⊙M 方程：(x －4)2＋y 2＝1.②①－②得：直线AB 的方程为(2x －m 2－4)(4－m 2)－(2y －m )m ＝m 4－7m 2＋14. 当x ＝0时，直线AB 在y 轴上的截距t ＝4m －15m(m ≥1)，∵t 关于m 的函数在[1，＋∞)单调递增，∴t min ＝－11. 12分 法二：设A (x 1，y 1)，B (x 2，y 2)，∵k MA ＝y 1x 1－4，∴k HA ＝4－x 1y 1， 可得，直线HA 的方程为(4－x 1)x －y 1y ＋4x 1－15＝0， 同理，直线HB 的方程为(4－x 2)x －y 2y ＋4x 2－15＝0，∴(4－x 1)y 20－y 1y 0＋4x 1－15＝0，(4－x 2)y 20－y 2y 0＋4x 2－15＝0， ∴直线AB 的方程为(4－y 20)x －y 0y ＋4y 20－15＝0， 令x ＝0，可得t ＝4y 0－15y 0(y 0≥1)，∵t 关于y 0的函数在[1，＋∞)单调递增，∴t min ＝－11. 12分21.函数()f x 的定义域为(0,)+∞,21(2)1()(2)x a x f x x a x x-++'=+-+=.依题意,方程2(2)10x a x -++=有两个不等的正根m ,n (其中m n <).故2(2)40020a a a ⎧+->⇒>⎨+>⎩, 并且2,1m n a mn +=+=. 所以,221()()ln ()(2)()2f m f n mn m n a m n +=++-++2211[()2](2)()(2)1322m n mn a m n a =+--++=-+-<- 故()()f m f n +的取值范围是(,3)-∞- (Ⅱ)解:当2a ≥-时,21(2)2a e e +≥++.若设(1)nt t m =>,则222()11(2)()22m n a m n t e mn t e++=+==++≥++.于是有111()(1)0t e t e t e t e te+≥+⇒--≥⇒≥222211()()ln ()(2)()ln ()()()22n n f n f m n m a n m n m n m n m m m -=+--+-=+--+-2222111ln ()ln ()ln ()22211ln ()2n n n m n n m n m m m mn m m n t t t-=--=-=--=--构造函数11()ln ()2g t t t t =--(其中t e ≥),则222111(1)()(1)022t g t t t t -'=-+=-<.所以()g t 在[,)e +∞上单调递减,1()()122e g t g e e≤=-+.故()()f n f m -的最大值是1122e e -+ .22.(1)圆C 的参数方程为⎩⎪⎨⎪⎧x ＝3＋2cos θ，y ＝－4＋2sin θ(θ为参数)所以普通方程为(x －3)2＋(y ＋4)2＝4，∴圆C 的极坐标方程：ρ2－6ρcos θ＋8ρsin θ＋21＝0. 5分 (2)设点M (3＋2cos θ，－4＋2sin θ)，则点M 到直线AB ：x －y ＋2＝0的距离为d ＝|2cos θ－2sin θ＋9|2，△ABM 的面积S ＝12×|AB |×d ＝|2cos θ－2sin θ＋9|＝⎪⎪⎪⎪⎪⎪22sin ⎝ ⎛⎭⎪⎫π4－θ＋9， 所以△ABM 面积的最大值为9＋2 2. 10分 23.(1)因为f (x )＝k －||x －3，所以f (x ＋3)≥0等价于： 由||x ≤k 有解，得k ≥0，且其解集为{} |x －k ≤x ≤k又f (x ＋3)≥0的解集为[]－1，1，故k ＝1. 5分 (2)由(1)知1a ＋12b ＋13c＝1，又a ，b ，c 是正实数，由均值不等式得a ＋2b ＋3c ＝(a ＋2b ＋3c ) ⎝ ⎛⎭⎪⎫1a ＋12b ＋13c ＝3＋a 2b ＋a 3c ＋2b a ＋2b 3c ＋3c a ＋3c 2b ＝ 3＋⎝ ⎛⎭⎪⎫a 2b ＋2b a ＋⎝ ⎛⎭⎪⎫a 3c ＋3c a ＋⎝ ⎛⎭⎪⎫2b 3c ＋3c 2b ≥3＋2＋2＋2＝9，当且仅当a ＝2b ＝3c 时取等号．也即19a ＋29b ＋39c ≥1. 10分。

秘密★启用前2021届高三第一次模拟考试文科综合试卷历史部分24.成书于战国末期的《吕氏春秋》,用拼凑式的做法把诸子百家思想综合起来,并不追求-一个内在的思想系统,成为“兼儒墨,合名法”“于百家之道无不贯通”的“杂家”代表作。

这A.体现了政治统--的趋势B.重振了百家争鸣的气象C.反映了学术创新的停滞D.阻碍了社会经济的转型25.下表为不同史籍对汉代儿童生活状态的叙述。

据此能够被认定的汉代史实是A.儿童教育受到社会广泛重视B.农牧业发展不平衡较为突出C.儿童参与生产活动较为普遍D.技术进步推动小农经济发展26.唐朝实行三省六部制并进- -步完善;元朝以中书省总领百官,尚书省时置时废,门下省不再设置;明太祖废中书省,六部直接对皇帝负责。

这一变化反映了A.宰相的权力不断削弱B.政治制度的质变性质C.少数民族政权的特殊性D.监督制约机制的削弱27.《明史●食货志》记载:“总括一州县之赋役,量地计丁,丁粮毕输于官,-岁之役,官为佥募。

力差,则计其工食之费,量为增减;银差,则计其缴纳之费,加以增耗。

凡额办派……并为一条,皆计亩征银。

”对此理解正确的是A.不侵犯地主官僚利益B.有利于商品经济发展C.简化税制以杜绝腐败D.免征徭役为农民减负28.右图为1893年汉口租界工部局设立的汉口书信馆(Ha-nkowLocalPost0ffice，即汉口商埠邮局)发行的邮票,图上是一位挑运茶叶的农民。

这可以用来说明A.租界当局主导了武汉的近代化B.茶叶贸易在汉口具有独特地位C.个体劳动仍是生产活动的主体D.中西文化融合成为了社会主流29.五四运动爆发后,胡适认为学生的爱国运动特别是采用白话文宣传,对新文化运动有很大的推动和促进作用,使之从校园传播到了全国。

晚年却认为五四运动是对新文化运动的一个“政治性干扰”。

胡适这一变化主要由于A.历史解释需要不断被重构B.五四运动反帝爱国的性质C.阶级立场和意识形态决定D.救亡和启蒙相互矛盾冲突30.右图是画家丰子恺的漫画。

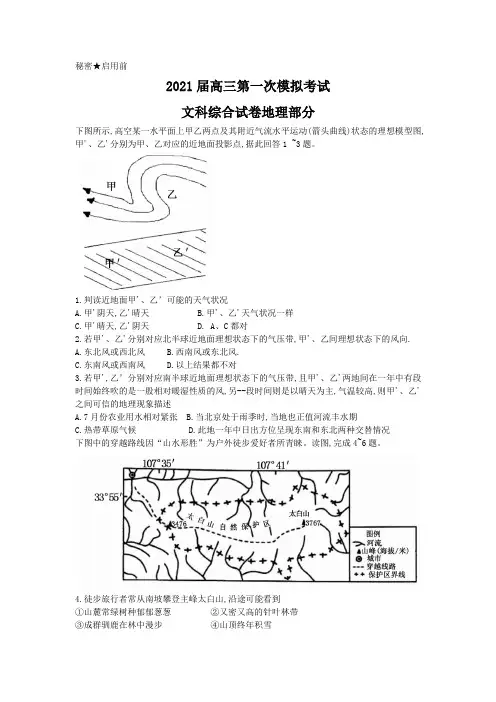
秘密★启用前2021届高三第一次模拟考试文科综合试卷地理部分下图所示,高空某一水平面上甲乙两点及其附近气流水平运动(箭头曲线)状态的理想模型图,甲'、乙'分别为甲、乙对应的近地面投影点,据此回答1 ~3题。

1.判读近地面甲'、乙’可能的天气状况A.甲'阴天,乙'晴天B.甲'、乙'天气状况一样C.甲'晴天,乙'阴天D. A、C都对2.若甲'、乙'分别对应北半球近地面理想状态下的气压带,甲'、乙间理想状态下的风向.A.东北风或西北风B.西南风或东北风.C.东南风或西南风D.以上结果都不对3.若甲',乙’分别对应南半球近地面理想状态下的气压带,且甲'、乙'两地间在一年中有段时间始终吹的是一股相对暖湿性质的风,另--段时间则是以晴天为主,气温较高,则甲'、乙'之间可信的地理现象描述A.7月份农业用水相对紧张B.当北京处于雨季时,当地也正值河流丰水期C.热带草原气候D.此地一年中日出方位呈现东南和东北两种交替情况下图中的穿越路线因“山水形胜”为户外徒步爱好者所青睐。

读图,完成4~6题。

4.徒步旅行者常从南坡攀登主峰太白山,沿途可能看到①山麓常绿树种郁郁葱葱②又密又高的针叶林带③成群驯鹿在林中漫步④山顶终年积雪A.①②B.③④C.①③D.②④5.从安全角度考虑，图示线路较适合的徒步旅行时段是A.2月B.12月.C.7月D.9月6.图中的穿越线路主要经过A.鞍部B.山谷C.山脊D.山坡坡耕地.上的种植方式主要有两种:一种是横坡垄作,即垄的方向和坡向垂直;一种是顺坡垄作，即垄的方向和坡向平行。

下图示意两种种植方式。

读图,完成7~8题。

7.我国的坡耕地大多采用横坡垄作,其主要原因A.可充分利用坡度，提高排水效果B.可充分利用光照,提高产品质量C.便于机械化生产,降低生产成本.D.可减轻水土流失，便于保水保肥8.下列国家的坡耕地最适合顺坡垄作是A.英国B.印度C.日本D.马来西亚纽约是美国东部最大的海港。

2021届云南省曲靖市二中、大理新世纪中学2018级高三上学期一模考试理科综合物理参考答案14.【答案】B【解析】小球受重力、挡板弹力F1和斜面弹力F2,将F1与F2合成为F,如图所示：小球一直处于平衡状态,三个力中的任意两个力的合力与第三个力等值、反向、共线,故F 1和F2合成的合力F一定与重力等值、反向、共线。

由图可知,当F1的方向沿斜面向上时最小,最小为：1sin301000.550F G N,故B正确,ACD错误。

15.【答案】B【解析】A．光电效应是原子吸收光子向外释放电子的现象,A错误；B．饱和光电流的强度随入射光强度的增强而增强,B正确；C．逸出功与金属本身的特点有关,与外界因素无关,C错误；D．由于不可见光的频率有的比可见光大,有的比可见光小,由光电效应方程k E hv W=-知产生光电子的初动能无法比较,D错误。

16.【答案】D【解析】A.卫星沿轨道2从A 运动到B 的过程中,地球对卫星的引力做负功,卫星的动能减小,线速度减小,故A 错误；B.卫星运动过程中万有引力产生加速度,卫星沿轨道2经过A 时和沿轨道1经过A 时的加速度一样,故B 错误；C.由222Mm G mr r T π=（）,解得：T =可知,3T =,故C 错误； D.根据开普勒第三定律可知,232223T T =（）,因此,2T =,因此卫星从A 点沿轨道2运动到B点所用时间为222T t ==,故D 正确。

17.【答案】D【解析】运动过程中系统中只有弹簧弹力做功,系统机械能守恒,由于挡板P 的弹力对小球A 有向右的冲量,因此系统动量不守恒,选项A 错误；在冲量作用下小球B 获得的初动能E k 0＝12mv 20＝12m,当小球A 将要离开挡板P 时弹簧处于原长,由机械能守恒定律知此时小球B 的动能E k ＝E k 0,由动量定理知挡板P 对小球A 的冲量等于系统动量的改变量,即I A ＝mv 0－(－mv 0),解得I A ＝2I,选项B 错误；从初始到小球A 将要离开挡板,小球A 一直静止,则挡板P 对小球A 不做功,选项C 错误；A 离开挡板后,弹簧压缩至最短或拉伸到最长时系统弹性势能最大,此时A 、B 速度相等,则有mv 0＝I ＝(m ＋m)v ′及E p ＝12mv 20－12×2mv ′2,解得E p ＝I 24m ,选项D 正确． 18.【答案】A 【解析】A ．当三角形闭合回路进入磁场一半时,即这时等效长度最大为2L ,这时感应电动势最大。

2021届云南省曲靖市二中、大理新世纪中学2018级高三上学期一模考试文科综合参考答案1.C2.B3.B考查热力环流及大气环流。

甲、乙位于高空,甲´、乙´为分别对应的地面,空气的运动发生在甲、乙、甲´、乙´之间。

甲´为高气压（带）,高压控制下天气晴朗天气。

乙´为低气压（带）,低压控制下阴雨天气。

第1题C选项正确。

甲´、乙´之间的风带可能是北半球的信风带、西风带、极地东风带,风向组合都是东北风和西南风。

第2题B选项正确。

甲´、乙´两地间吹相对暖湿性质的风,是西风,以晴天为主是受高气压控制,甲´、乙´之间为南半球地中海气候。

第3题B选项正确。

4.A5.D6.C4.根据图中的经纬度（或者主峰太白山)可判定图示区域为秦岭山地。

南坡为亚热带季风气候,山麓为亚热带常绿阔叶林,①正确；随着海拔升高,山腰处热量逐渐降低,降水逐渐增加,形成针叶林带,②正确；驯鹿是苔原气候的动物,不可能出现在秦岭南坡,③错误；根据气温垂直递减率,太白山没有永久积雪（该纬度夏季最高温30℃以上,因此山峰海拔至少5000米才能有永久积雪）,④错误。

故选A项。

5.冬季气温低、积雪厚度大,不适宜徒步旅行,可排除A、B项；7月正处于雨季,地面湿滑,滑坡、泥石流等地质灾害多发,较危险,排除C项；9月雨季已过且气温较高,比较适宜徒步穿越。

故选D项。

6.读图可知,图中的河流大多发源于穿越线路附近,且经过了最高峰太白山,因此可以判定穿越线路为山脊。

故选C项。

7.D 8.A7.考查地理环境对农业生产的影响,顺坡垄不利于保水保土,易发生水土流失（灌溉不便）一般分布在降水频率高(经常降雨）,强度小（少暴雨或每次降雨量较小）,降水量季节分配较均匀的地区,横坡垄作具有保水的特点,可以减缓水土流失,一般分布在降水不足或降水季节变化大的地区。

我国大部分地区处于季风气候区,降水的季节分配不均,采用横坡垄耕作可以减少水土流失,保持土壤的水分和肥力,D正确,故选D。

2018年云南省曲靖市高考数学一模试卷（文科）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知复数z =5i i−1（i 为虚数单位），则复数z 在复平面内对应的点位于（ ）A.第四象限B.第三象限C.第二象限D.第一象限2. 已知全集U ＝R ，集合A ＝{x|y =√lnx}，集合B ＝{y|y =x 12}，那么A ∩(∁U B)＝（ ）A.⌀B.(0, 1]C.(0, 1)D.(1, +∞)3. 计算机是将信息转换成二进制进行处理的．二进制即“缝二进一”，如${1101_{（2）}}表示二进制数,将它转化成十进制形式是{1\times 2^{3}+ 1\times 2^{2}+ 0\times 2^{1}+ 1\times 2^{0}}{13},那么将二进制数{1010_{（2）}}$转化成十进制形式是（ ） A.13 B.10 C.15 D.184. 已知向量a →=(√3, 0)，b →=(0, −1)，c →=(k, √3)，若(a →−2b →)⊥c →，则k ＝（ ）A.2B.−2C.32D.−325. 若a ＝(12)34，b ＝(34)12，c ＝log 23，则a ，b ，c 大小关系是（ ）A.a <b <cB.b <a <cC.b <c <aD.c <b <a6. 若在区间[−3, 3]内任取一个实数m ，则使直线x −y +m ＝0与圆(x −1)2+(y +2)2＝4有公共点的概率为（ ） A.13 B.35C.√23D.2√237. 如图是计算13+15+17+⋯+117的值的一个流程图，其中判断框内应填入的条件是（ ）A.i ≥8B.i >8C.i >9D.i ≤98. 已知某几何体的三视图如图所示，则该几何体的体积为（ ）A.6+4√2B.12C.4+4√2D.49. 递增的等比数列{a n }的每一项都是正数，设其前n 项的和为S n ，若a 2+a 4＝30，a 1a 5＝81，则S 6＝（ ） A.121 B.−364 C.364 D.−12110. sin(−2055∘)＝（ ） A.√6−√24B.−√2+√64C.√2+√64D.√2−√6411. △ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若C =π3，c =√7，b ＝3a ，则△ABC 的面积为（ ） A.3√34B.2−√34C.√2D.2+√3412. 若关于x 的不等式x 2+kx −1>0在[1, 2]区间上有解，则k 的取值范围是（ ）A.(−∞, 0)B.(−32, 0) C.[−32, +∞)D.(−32, +∞)二、填空题（每题5分，满分20分，将答案填在答题纸上）若“x >a ”是“x 2−5x +6≥0”成立的充分不必要条件，则实数a 的取值范围是________．实数x ，y 满足约束条件{x ≤√2yy ≤2√2≤x ≤2√2，则z ＝x +2√2y 的最大值为________．抛物线y 2=2ax(a >0)的焦点为F ，其准线与双曲线y 24−x 29=1相交于M ，N 两点，若∠MFN =120∘，则a =________．棱长为a 的正四面体ABCD 的四个顶点都在同一个球面上，若过棱AB 作四面体的截面，交棱CD 的中点于E ，且截面面积是3√2，则四面体外接球的表面积是________．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）若数列{a n}是递增的等差数列，它的前n项和为T n，其中T3＝9，且a1，a2，a5成等比数列．（1）求{a n}的通项公式；（2）设b n=1a n a n+1，数列{b n}的前n项和为S n，求S n．央视传媒为了解央视举办的“朗读者”节目的收视时间情况，随机抽取了某市名30观众进行调查，其中有12名男观众和18名女观众，将这30名观众收视时间编成如图所示的茎叶图（单位：分钟），收视时间在35分钟以上（包括35分钟）的称为“朗读爱好者”，收视时间在35分钟以下（不包括35分钟）的称为“非朗读爱好者”．（1）若采用分层抽样的方法从“朗读爱好者”和“非朗读爱好者”中随机抽取5名，再从这5名观众中任选2名，求至少选到1名“朗读爱好者”的概率；（2）若从收视时间在40分钟以上（包括40分钟）的所有观众中选出男、女观众各1名，求选出的这两名观众时间相差5分钟以上的概率．如图，在三棱柱ABC−A1B1C1中，P、Q分别是AA1、A1C1的中点．（1）设棱BB1的中点为D，证明：C1D // 平面PQB1（2）若AB＝2，AC＝AA1＝AC1＝4，∠AA1B1＝60∘，且平面AA1C1C⊥平面AA1B1B，求三棱锥P−QA1B1的体积．如图，已知椭圆C:x2a2+y2b2=1(a>b>0)的左焦点为F(−1, 0)，过点F做x轴的垂线交椭圆于A，B两点，且|AB|＝3．（1）求椭圆C的标准方程：（2）若M，N为椭圆上异于点A的两点，且直线AM，AN的倾斜角互补，问直线MN的斜率是否为定值？若是，求出这个定值；若不是，请说明理由．函数f(x)＝xe x−ax+b的图象在x＝0处的切线方程为：y＝−x+1．（1）求a和b的值；（2）若f(x)满足：当x>0时，f(x)≥x2+m，求实数m的取值范围．[选修4-4：坐标系与参数方程]在平面直角坐标系xOy中，已知曲线C:{x=√3cosαy=sinα（α为参数）；在以原点O为极点，x轴的非负半轴为极轴建立的极坐标系中，曲线C1的极坐标方程为ρ＝2(0≤θ≤π)，射线l的极坐标方程为θ＝a0（a0∈[0, π2]）（1）写出曲线C的极坐标方程和曲线C1的直角坐标方程；（2）若射线l与曲线C1、C分别相交于A、B两点，求|AB|的取值范围．[选修4-5：不等式选讲]已知函数f(x)＝|2x−1|+|2x+3|．（1）解不等式f(x)<5；（2）若不等式f(x)−t<0的解集为空集，记实数t的最大值为a，求实数a的值．参考答案与试题解析2018年云南省曲靖市高考数学一模试卷（文科）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.【答案】D【考点】复数的代数表示法及其几何意义【解析】直接利用复数代数形式的乘除运算化简，求出z的坐标得答案．【解答】∵z=5ii−1=5i(−1−i)(−1+i)(−1−i)=52−52i，∴z=52+52i，∴复数z在复平面内对应的点的坐标为(52,52)，位于第一象限．2.【答案】A【考点】交、并、补集的混合运算【解析】可解出集合A＝[1, +∞)，B＝[0, +∞)，然后进行交集、补集的运算即可．【解答】解lnx≥0得x≥1；∴A＝[1, +∞)，B＝[0, +∞)；∴∁U B＝(−∞, 0)；∴A∩(∁U B)＝⌀．3.【答案】B【考点】进位制【解析】根据题中二进制数化为十进制数的方法计算即可．【解答】根据题意得：1×23+0×22+1×21+0×20＝8+0+2+0＝10，4.【答案】B【考点】数量积判断两个平面向量的垂直关系【解析】由已知向量的坐标求得a→−2b→的坐标，再由向量垂直与数量积的关系列式求得k值．【解答】∵a→=(√3, 0)，b→=(0, −1)，∴a→−2b→=(√3,2)，又c→=(k, √3)，且(a→−2b→)⊥c→，∴√3k+2√3=0，即k＝−2．5.【答案】A【考点】对数值大小的比较【解析】利用指数函数与对数函数的单调性即可得出．【解答】∵a＝(12)34<(12)12<b＝(34)12，c＝log23>1，则a<b<c，6.【答案】C【考点】几何概型计算（与长度、角度、面积、体积有关的几何概型）直线与圆的位置关系【解析】利用圆心到直线的距离小于等于半径可得到直线与圆有公共点，可求出满足条件的m，最后根据几何概型的概率公式可求出所求．【解答】∵直线x−y+m＝0与圆(x−1)2+(y+2)2＝4有公共点，∴√2≤2，解得−1≤m≤3，∴在区间[−3, 3]内任取一个实数m，使直线x−y+m＝0与圆(x−1)2+(y+2)2＝4有公共点的概率为−3+2√2−(−3)6=√23．7.【答案】B【考点】程序框图【解析】模拟程序的运行，可得框图中i的值为9时判断框中的条件应该满足，算法结束，由此得到判断框中的条件．【解答】框图首先给累加变量S赋值为0，给循环变量i赋值1．执行S＝0+13，i＝1+1＝2，判断，判断框中的条件不满足，执行S＝0+13+15，i＝2+1＝3，判断，判断框中的条件不满足，执行S＝0+13+15+17，i＝3+1＝4，判断，判断框中的条件不满足，…执行S=13+15+17+⋯+117，i＝8+1＝9，此时，由题意，应该满足判断框内的条件，跳出循环，输出S的值为S=13+15+17+⋯+117，可得判断框内应填入的一个条件为i>8？8.【答案】D【考点】由三视图求体积【解析】首先根据三视图，把几何体进行复原，最后求出几何体的体积．【解答】根据三视图，复原后的几何体为：底面为四边形ABCD，AE⊥底面ABCD，所以：V=13∗12(2+4)∗2∗2=4．9.【答案】C【考点】等比数列的前n项和【解析】设每一项都是正数的递增的等比数列{a n}的公比为q>1，由a2+a4＝30，a1a5＝81＝a2a4，联立解出，再利用通项公式与求和公式即可得出．【解答】设每一项都是正数的递增的等比数列{a n}的公比为q>1，∵a2+a4＝30，a1a5＝81＝a2a4，联立解得a4＝27，a2＝3．∴3q2＝27，解得q＝3．∴a1×3＝3，解得a1＝1．则S6=36−13−1=364．10.【答案】C【考点】运用诱导公式化简求值【解析】由题意利用利用诱导公式，化简所给的式子，可的结果．【解答】sin(−2055∘)＝sin(−6×360∘+105∘)＝sin105∘＝cos15∘＝cos(45∘−30∘)＝cos45∘cos30∘−sin45∘sin30∘=√22∗√32+√22∗12=√6+√24，11.【答案】A【考点】余弦定理【解析】由已知及余弦定理可求a，b的值，进而根据三角形的面积公式即可计算得解．【解答】∵C=π3，c=√7，b＝3a，∴由余弦定理c2＝a2+b2−2abcosC，可得：7＝a2+b2−ab＝a2+9a2−3a2＝7a2，解得：a＝1，b＝3，∴S△ABC=12absinC=12×1×3×√32=3√34．12.【答案】D【考点】函数的零点与方程根的关系利用导数研究函数的单调性【解析】用分离常数法得出不等式k>1x−x在x∈[1, 2]上成立，根据函数f(x)=1x−x在x∈[1, 2]上的单调性，即可求出k的取值范围．【解答】关于x的不等式x2+kx−1>0在区间[1, 2]上有解，∴kx>1−x2在x∈[1, 2]上有解，即k>1x−x在x∈[1, 2]上成立；设函数f(x)=1x−x，x∈[1, 2]，∴f′(x)=−1x2−1<0恒成立，∴f(x)在x∈[1, 2]上是单调减函数，且f(x)的值域为[−32, 0]，要k>1x−x在x∈[1, 2]上有解，则k>−32，即实数k的取值范围为(−32, +∞)．二、填空题（每题5分，满分20分，将答案填在答题纸上） 【答案】 [3, +∞) 【考点】充分条件、必要条件、充要条件 【解析】求出不等式的等价条件，结合充分不必要条件的定义进行求解即可． 【解答】由x 2−5x +6≥0得x ≥3或x ≤2，若“x >a ”是“x 2−5x +6≥0”成立的充分不必要条件， 则a ≥3，即实数a 的取值范围是[3, +∞)， 【答案】 6√2【考点】 简单线性规划 【解析】画可行域，判断z 为目标函数的几何意义，平移直线过A 时z 有最大值． 【解答】画实数x ，y 满足约束条件{x ≤√2yy ≤2√2≤x ≤2√2可行域如图， 满足约束条件的是图中阴影部分，其中A(2√2, 2)． z 为目标函数z ＝x +2√2y ，画直线0＝x +2√2y ， 平移直线过A(2√2, 2)点时z 有最大值6√2． 【答案】3√2613【考点】 双曲线的特性 【解析】利用抛物线方程求出准线方程，然后代入双曲线方程求出M ，利用∠MFN =120∘，转化求解即可． 【解答】抛物线y 2=2ax(a >0)的焦点为F(a2, 0)， 准线方程为x =−a2，代入双曲线的方程可得y 2=4(1+a 236)=4+a 29，可设M(−a 2, √4+a 29)，∠MFN =120∘， 可得tan ∠MFN 2=tan60∘=√4+a29a=√3，解得a =3√2613， 【答案】 18π【考点】球的体积和表面积 【解析】棱长为a 的正四面体，其正四面体外接球半径为√64a ．过棱AB 作四面体的截面，交棱CD 的中点于E ，可得ABE 是等腰三角形，AB ＝a ，EB ＝EA =√32a ，可得截面面积是3√2=12a ×√22a ，解得a ，从而求解外接球的表面积．【解答】过棱AB 作四面体的截面，交棱CD 的中点于E ，可得ABE 是等腰三角形， ∵ AB ＝a ，EB ＝EA =√32a ，可得截面面积是3√2=12a ×√22a ，解得：a =2√3．由正四面体外接球半径为√64a ．即外接球半径R =3√22． 外接球的表面积S ＝4πR 2＝18π．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 【答案】数列{a n }是递增的等差数列，公差设为d(d >0)， T 3＝9，即a 1+a 2+a 3＝9，即有3a 1+3d ＝9，即a 1+d ＝3， 又a 1，a 2，a 5成等比数列，可得a 22＝a 1a 5，即有(a 1+d)2＝a 1(a 1+4d)， 解得a 1＝1，d ＝2，则a n ＝1+2(n −1)＝2n −1；b n =1a n a n+1=1(2n −1)(2n +1)=12(12n−1−12n+1)，前n 项和为S n =12(1−13+13−15+⋯+12n−1−12n+1)=12(1−12n+1)=n2n+1．【考点】等差数列与等比数列的综合 数列的求和 【解析】（1）公差设为d(d >0)，运用等差数列的通项公式和等比数列中项性质，解方程可得首项和公差，即可得到所求通项公式； （2）求得b n =1an a n+1=1(2n−1)(2n+1)，运用裂项相消求和，化简即可得到所求和．【解答】数列{a n}是递增的等差数列，公差设为d(d>0)，T3＝9，即a1+a2+a3＝9，即有3a1+3d＝9，即a1+d＝3，又a1，a2，a5成等比数列，可得a22＝a1a5，即有(a1+d)2＝a1(a1+4d)，解得a1＝1，d＝2，则a n＝1+2(n−1)＝2n−1；b n=1a n a n+1=1(2n−1)(2n+1)=12(12n−1−12n+1)，前n项和为S n=12(1−13+13−15+⋯+12n−1−12n+1)=12(1−12n+1)=n2n+1．【答案】根据茎叶图，有“朗读爱好者”12人，“非朗读爱好者”18人，用分层抽样的方法，每个人被抽到的概率是P=530=16；∴选中的“朗读爱好者”有12×16=2人，记为B、C，“非朗读爱好者”有18×16=3人，记为1、2、3；记A：至少有一名是“朗读爱好者”被选中，基本事件有BC，B1，B2，B3，C1，C2，C3，12，13，23共10个；满足事件A的有BC，B1，B2，B3，C1，C2，C3共7个，∴则P(A)=710；收视时间在40分钟以上的男观众分别是41，42，44，47，51，女观众分别是40，41，现要各抽一名，则有：(41、40)，(41、41)，(42、40)，(42、40)，(44、40)，(44、41)，(47、40)，(47、41)，(51、40)，(51、41)共10种情况．收视时间相差5分钟以上的有：(47、40)，(47、41)，(51、40)，(51、41)共4种情况．故收视时间相差5分钟以上的概率P=410=25．【考点】茎叶图【解析】（1）根据茎叶图，用分层抽样法求得所抽到的人数，用列举法求出基本事件数，计算所求的概率值；（2）用列举法计算所求的基本事件数，求对应的概率值．【解答】根据茎叶图，有“朗读爱好者”12人，“非朗读爱好者”18人，用分层抽样的方法，每个人被抽到的概率是P=530=16；∴选中的“朗读爱好者”有12×16=2人，记为B、C，“非朗读爱好者”有18×16=3人，记为1、2、3；记A：至少有一名是“朗读爱好者”被选中，基本事件有BC，B1，B2，B3，C1，C2，C3，12，13，23共10个；满足事件A的有BC，B1，B2，B3，C1，C2，C3共7个，∴则P(A)=710；收视时间在40分钟以上的男观众分别是41，42，44，47，51，女观众分别是40，41，现要各抽一名，则有：(41、40)，(41、41)，(42、40)，(42、40)，(44、40)，(44、41)，(47、40)，(47、41)，(51、40)，(51、41)共10种情况．收视时间相差5分钟以上的有：(47、40)，(47、41)，(51、40)，(51、41)共4种情况．故收视时间相差5分钟以上的概率P=410=25．【答案】证明：连接AD，∵D是BB1的中点，P是AA1的中点，可由棱柱的性质知AP // DB1，且AP＝DB1，∴四边形ADB1P是平行四边形．∴AD // PB1．∵P、Q分别是AA1、A1C1的中点．∴AC1 // PQ．∴平面AC1D // 平面PQB1．∴C1D // 平面PQB1；在面AA1C1C内作QM⊥AA1于点M，∵平面AA1C1C⊥平面AA1B1B，∴QM⊥平面AA1B1B，∴QM=√3．∵A1P＝A1B1＝2，∠AA1B1＝60∘，∴△PA1B1是边长为2的正三角形．∴S△PA1B1=√3．∴V P−QA1B1=13S△PA1B1∗QM=13×√3×√3=1．【考点】柱体、锥体、台体的体积计算直线与平面平行【解析】（1）连接AD，可得AP // DB1，且AP＝DB1，四边形ADB1P是平行四边形，进一步得到AC1 // PQ，从而平面AC1D // 平面PQB1，可得C1D // 平面PQB1；（2）在面AA1C1C内作QM⊥AA1于点M，结合已知可得QM⊥平面AA1B1B，求出QM，进一步求出△PA1B1是边长为2的正三角形．再由体积公式计算得答案．【解答】证明：连接AD，∵D是BB1的中点，P是AA1的中点，可由棱柱的性质知AP // DB1，且AP＝DB1，∴四边形ADB1P是平行四边形．∴AD // PB1．∵P、Q分别是AA1、A1C1的中点．∴AC1 // PQ．∴平面AC1D // 平面PQB1．∴C1D // 平面PQB1；在面AA1C1C内作QM⊥AA1于点M，∵平面AA1C1C⊥平面AA1B1B，∴QM⊥平面AA1B1B，∴QM=√3．∵A1P＝A1B1＝2，∠AA1B1＝60∘，∴△PA1B1是边长为2的正三角形．∴S△PA1B1=√3．∴V P−QA1B1=13S△PA1B1∗QM=13×√3×√3=1．【答案】由题意可知c＝1，令x＝−c，代入椭圆可得y=±b2a，所以2b2a=3，又a2−b2＝1，两式联立解得：a2＝4，b2＝3，∴x24+y23=1；由（1）可知，F(−1, 0)，代入椭圆可得y=±32，所以A(−1,32)，因为直线AM，AN的倾斜角互补，所以直线AM的斜率与AN的斜率互为相反数；可设直线AM方程为：y=k(x+1)+32，代入x24+y23=1得：(3+4k2)x2+4k(3+2k)x+4k2+12k−3＝0，设M(x M, y M)，N(x N, y N)，因为点A(−1,32)在椭圆上，所以−1⋅x M=4k2+12k−33+4k2，x M=−4k2+12k−33+4k2，y M=kx M+k+32，又直线AM的斜率与AN的斜率互为相反数，在上式中以−k代替k，可得x N=−4k2−12k−33+4k2，y N=−kx N−k+32所以直线MN的斜率k MN=y M−y Nx M−x N=k(x M+x N)+2kx M−x N=−12，即直线MN的斜率为定值，其值为−12．【考点】椭圆的离心率【解析】（1）根据题意，分析可得c的值，进而分析可得2b2a=3，由椭圆的几何性质分析可得a、b的值，代入椭圆的方程即可得答案；（2）根据题意，设直线AM方程为：y=k(x+1)+32，M(x M, y M)，N(x N, y N)，将直线AM的方程与椭圆联立，分析可得(3+4k2)x2+4k(3+2k)x+4k2+12k−3＝0，由根与系数的关系分析可得答案．【解答】由题意可知c＝1，令x＝−c，代入椭圆可得y=±b2a，所以2b2a=3，又a2−b2＝1，两式联立解得：a2＝4，b2＝3，∴x 24+y 23=1；由（1）可知，F(−1, 0)，代入椭圆可得y =±32，所以A(−1,32)，因为直线AM ，AN 的倾斜角互补，所以直线AM 的斜率与AN 的斜率互为相反数； 可设直线AM 方程为：y =k(x +1)+32，代入x 24+y 23=1得：(3+4k 2)x 2+4k(3+2k)x +4k 2+12k −3＝0，设M(x M , y M )，N(x N , y N )，因为点A(−1,32)在椭圆上， 所以−1⋅x M =4k 2+12k−33+4k 2，x M =−4k 2+12k−33+4k 2，y M =kx M +k +32，又直线AM 的斜率与AN 的斜率互为相反数，在上式中以−k 代替k ，可得x N =−4k 2−12k−33+4k 2，y N =−kx N −k +32所以直线MN 的斜率k MN =y M −yNx M−x N=k(x M +x N )+2kx M −x N =−12，即直线MN 的斜率为定值，其值为−12．【答案】∵ 函数f(x)＝xe x −ax +b 的图象在x ＝0处的切线方程为：y ＝−x +1， ∴ f′(x)＝(x +1)e x −a ， ∴ {f(0)=b =1f ′(0)=1−a =−1，解得a ＝2，b ＝1．∵ f(x)满足：当x >0时，f(x)≥x 2+m ， ∴ m ≤xe x −x 2−2x +1，令g(x)＝xe x −x 2−2x +1，x >0，则g′(x)＝(x +1)e x −2x −2＝(x +1)(e x −2)， 设g′(x)＝0，x >0，则e x ＝2，从而x ＝ln2， 当x ∈(0, ln2)时，g′(x)<0， 当x ∈(ln2, +∞)时，g′(x)>0；∴ 函数g(x)在(0, ln2)上单调递减，在(ln2, +∞)上单调递增， ∴ g(x)min ＝g(ln2)＝1−ln 22， ∵ m ≤xe x −x 2−2x +1恒成立， ∴ m ≤g(x)min ＝1−ln 22，∴ 实数m 的取值范围是：(−∞, 1−ln 22]． 【考点】利用导数研究函数的最值利用导数研究曲线上某点切线方程 【解析】（1）由函数f(x)＝xe x −ax +b 的图象在x ＝0处的切线方程为：y ＝−x +1，利用导数的几何意义列出方程组，能求出a ，b ．（2）推导出m ≤xe x −x 2−2x +1，令g(x)＝xe x −x 2−2x +1，x >0，则g′(x)＝(x +1)(e x −2)，利用导数性质求出g(x)min ＝g(ln2)＝1−ln 22，由m ≤xe x −x 2−2x +1恒成立，得到m ≤g(x)min ，由此能求出实数m 的取值范围．【解答】∵ 函数f(x)＝xe x −ax +b 的图象在x ＝0处的切线方程为：y ＝−x +1， ∴ f′(x)＝(x +1)e x −a ， ∴ {f(0)=b =1f ′(0)=1−a =−1，解得a ＝2，b ＝1．∵ f(x)满足：当x >0时，f(x)≥x 2+m ， ∴ m ≤xe x −x 2−2x +1，令g(x)＝xe x −x 2−2x +1，x >0，则g′(x)＝(x +1)e x −2x −2＝(x +1)(e x −2)， 设g′(x)＝0，x >0，则e x ＝2，从而x ＝ln2， 当x ∈(0, ln2)时，g′(x)<0， 当x ∈(ln2, +∞)时，g′(x)>0；∴ 函数g(x)在(0, ln2)上单调递减，在(ln2, +∞)上单调递增， ∴ g(x)min ＝g(ln2)＝1−ln 22， ∵ m ≤xe x −x 2−2x +1恒成立， ∴ m ≤g(x)min ＝1−ln 22，∴ 实数m 的取值范围是：(−∞, 1−ln 22]． [选修4-4：坐标系与参数方程] 【答案】∵ 曲线C:{x =√3cosαy =sinα （α为参数），∴ 消去参数α得曲线C 的直角坐标方程为x 23+y 2=1．∴ C 的极坐标方程为：ρ2=31+2sin 2θ．∵ 曲线C 1的极坐标方程为ρ＝2(0≤θ≤π)，∴ 曲线C 1的直角坐标方程为：x 2+y 2＝4(y ≥0)． 将θ＝a 0（a 0∈[0, π2]）与曲线C 、C 1的方程分别联立， 可得ρ1=√31+2sin 2a 0，ρ2＝2，∴ |AB|＝|ρ1−ρ2|＝|2−√31+2sin 2a 0，∵ a 0∈[0, π2]，∴ |AB|的取值范围是[2−√3, 1]． 【考点】圆的极坐标方程参数方程与普通方程的互化 【解析】（1）曲线C 消去参数α得曲线C 的直角坐标方程为x 23+y 2=1．由此能求出C 的极坐标方程；由曲线C 1的极坐标方程为ρ＝2(0≤θ≤π)，能求出曲线C 1的直角坐标方程．（2）将θ＝a 0（a 0∈[0, π2]）与曲线C 、C 1的方程分别联立，求出ρ1=√31+2sin 2a 0，ρ2＝2，从而|AB|＝|ρ1−ρ2|＝|2−√31+2sin 2a 0，由a 0∈[0, π2]，能求出|AB|的取值范围．【解答】∵ 曲线C:{x =√3cosαy =sinα （α为参数），∴ 消去参数α得曲线C 的直角坐标方程为x 23+y 2=1．∴ C 的极坐标方程为：ρ2=31+2sin 2θ．∵ 曲线C 1的极坐标方程为ρ＝2(0≤θ≤π)，∴ 曲线C 1的直角坐标方程为：x 2+y 2＝4(y ≥0)． 将θ＝a 0（a 0∈[0, π2]）与曲线C 、C 1的方程分别联立， 可得ρ1=√31+2sin a 0，ρ2＝2，∴ |AB|＝|ρ1−ρ2|＝|2−√31+2sin 2a 0，∵ a 0∈[0, π2]，∴ |AB|的取值范围是[2−√3, 1]． [选修4-5：不等式选讲] 【答案】f(x)={ −4x −2x ≤−324−32<x <124x +2x ≥12 ； ∴ 由f(x)<5得，{x ≤−32−4x −2<5，或{−32<x <124<5，或{x ≥124x +2<5；解得：−74<x <34；∴ 原不等式的解集为：(−74,34)；由f(x)−t <0的解集为⌀知，t ≤f(x)min ； 由（1）知f(x)的最小值为4； ∴ t ≤4，且a 是t 的最大值； ∴ a ＝4． 【考点】函数的最值及其几何意义 绝对值不等式的解法与证明 【解析】（1）讨论x 的取值，去绝对值号得出f(x)={−4x −2x ≤−324−32<x <124x +2x ≥12 ，从而可由f(x)<5得到三个不等式组，解不等式组即可得出f(x)<5的解集；（2）据题意可得到t ≤f(x)min ，而由|2x −1|+|2x +3|≥4即得出f(x)的最小值为4，从而得出a ＝4． 【解答】f(x)={−4x −2x ≤−324−32<x <124x +2x ≥12 ；∴ 由f(x)<5得，{x ≤−32−4x −2<5，或{−32<x <124<5，或{x ≥124x +2<5；解得：−74<x <34；∴ 原不等式的解集为：(−74,34)；由f(x)−t <0的解集为⌀知，t ≤f(x)min ； 由（1）知f(x)的最小值为4； ∴ t ≤4，且a 是t 的最大值； ∴ a ＝4．。