历年来北大自主招生数学试题

自主招生数学试题及答案一、选择题（每题5分，共20分）1. 若函数f(x) = x^2 - 4x + 3，求f(2)的值。

A. 1B. 3C. 5D. 7答案：B2. 已知等差数列{a_n}的首项a_1 = 3，公差d = 2，求a_5的值。

A. 13B. 15C. 17D. 19答案：A3. 计算定积分∫(0到1) x^2 dx的值。

A. 1/3B. 1/2C. 2/3D. 1答案：B4. 设A = {1, 2, 3}，B = {3, 4, 5}，求A∩B的值。

A. {1, 2}B. {3}C. {4, 5}D. 空集答案：B二、填空题（每题5分，共20分）5. 已知函数f(x) = 2x - 1，求f(-1)的值。

答案：-36. 计算等比数列1, 2, 4, ...的第5项。

答案：167. 已知圆的半径为5，求圆的面积。

答案：25π8. 已知向量a = (3, 4)，向量b = (-4, 3)，求向量a与向量b的点积。

答案：-7三、解答题（共60分）9. 已知函数f(x) = x^3 - 6x^2 + 11x - 6，求f(x)的导数。

答案：f'(x) = 3x^2 - 12x + 1110. 已知直线l1: y = 2x + 1和直线l2: y = -x + 3，求两直线的交点坐标。

答案：交点坐标为(1, 3)11. 已知圆心在原点，半径为5的圆，求圆的方程。

答案：x^2 + y^2 = 2512. 已知函数f(x) = x^2 - 6x + 8，求函数的最小值。

答案：函数的最小值为2，当x = 3时取得。

高校自招数学试题及答案一、选择题（每题4分，共40分）1. 下列哪个数是无理数？A. 0.33333…（循环）B. πC. √2D. 1答案：B、C2. 已知函数f(x) = 2x - 3，求f(5)的值。

A. 7B. 4C. 1D. 2答案：A3. 若a > b > 0，下列不等式中正确的是：A. a^2 > b^2B. a + b > 2√(ab)C. a/b > b/aD. a^3 > b^3答案：D4. 已知等差数列的首项为1，公差为2，求第10项的值。

A. 19C. 17D. 16答案：A5. 圆的半径为5，求圆的面积。

A. 25πB. 50πC. 75πD. 100π答案：B6. 已知三角形ABC，∠A = 90°，AB = 3，AC = 4，求BC的长度。

A. 5B. 6C. 7D. 8答案：A7. 函数y = x^2 - 4x + 4的顶点坐标是什么？A. (2, 0)B. (-2, 0)C. (2, 4)D. (-2, 4)答案：A8. 已知正弦函数sin(x)的周期为2π，求余弦函数cos(x)的周期。

B. 2πC. 4πD. 8π答案：B9. 根据勾股定理，直角三角形的斜边长度是两直角边长度的平方和的平方根。

设a和b是直角边，c是斜边，下列哪个表达式是正确的？A. c = √(a^2 + b^2)B. a = √(c^2 + b^2)C. b = √(c^2 - a^2)D. c = √(b^2 - a^2)答案：A10. 已知一个数列的前三项为1, 1, 2，且每一项都是前两项的和，求第5项的值。

A. 4B. 5C. 6D. 7答案：C二、填空题（每题4分，共20分）11. 根据二项式定理，展开式(a + b)^3的通项公式是________。

答案：T_{r+1} = C_{3}^{r}a^{3-r}b^{r}12. 如果一个函数是奇函数，那么f(-x)等于________。

2020年北京海淀区北京大学自主招生数学试卷（金秋营）-学生用卷一、综合题（本大题共5小题）1、【来源】 2020年北京海淀区北京大学自主招生（金秋营）第1题对于非负实数a 1，a 2，⋯，a n ，考虑如下2n 个实数i 1a 1+i 2a 2+⋯+i n a n ，其中i k =±1，1⩽k ⩽n ，记S 为这2n 个数中所有正数之和，在∑a n n i=1=1的条件下，求S 的最小值．2、【来源】 2020年北京海淀区北京大学自主招生（金秋营）第2题在△ABC 中，D 为BC 的中点，E ，F 分别为BC ⌢，BAC ⌢中点，取△ABC 外接圆ω，△ADE 外接圆与射线AB ，AC 交于点J ，K ，△ADF 外接圆与射线AB ，AC 交于点L ，M ，证明：若AD 、JK 、LM 共点，则JM 、LK 交点在ω上．3、【来源】 2020年北京海淀区北京大学自主招生（金秋营）第3题数列{a n }满足：a 0=2，a 1=5，a n+1=5a n −a n−1，n ⩾1，已知a m |a 2n−2+a 2n−1，求证：3|m ，3|n ．4、【来源】 2020年北京海淀区北京大学自主招生（金秋营）第4题求k 的最小值，使得将7×7方格挖去k 个格后，剩余图形不存在T 字形（T 字形指一个方格与其相邻的三个方格有公共边构成的图形）．5、【来源】 2020年北京海淀区北京大学自主招生（金秋营）第5题△ABC 内部取一点O ，直线AO ，BO ，CO 分别交对边于D ，E ，F ，若四边形AEFO ，BDFO ，CDEO 都有内切圆，求证：O 在△ABC 内心和垂心所在直线上．1 、【答案】暂无;2 、【答案】暂无;3 、【答案】暂无;4 、【答案】暂无;5 、【答案】暂无;。

1.（2007清华）对于集合2M R ⊆（表示二维点集），称M 为开集，当且仅当0,0P M r ∀∈∃>，使得{}2P R PP r M ∈<⊆⎰。

判断集合{}(,)4250x y x y +->⎰与集合{}(,)0,0x y x y ≥>⎰是否为开集，并证明你的结论。

2，（2009北大）已知,cos cos 21x R a x b x ∀∈+≥-恒成立，求max ()a b +3，（2009清华）已知,,0x y z >，a 、b 、c 是x 、y 、z 的一个排列。

求证：3a b c x y z ++≥。

4，（2006清华）已知a ，b 为非负数，44M a b =+，a+b=1，求M 的最值。

5，（2008北大）实数(1,2,i i a i b i ==满足123a a a b b b ++=++，122313122313a a a a a a bb b b bb ++=++，123123min(,,)min(,,)a a a b b b ≤。

求证：12312m a x (,,)m a x (,,)a a a b b b ≤。

6，（2009清华）试求出一个整系数多项式110()n n n n f x a x a x a --=+++…，使得()0f x =有一根为7，（2009清华）x>0,y>0,x+y=1,n 为正整数，求证：222112n n n xy -+≥8，（2007北大） 已知22()5319653196f x x x x x =-++-+，求f(1)+f(2)+…＋f(50)。

9，（2006清华）设正三角形1T 的边长为a ，1n T +是n T 的中点三角形，n A 为n T 除去1n T +后剩下三个三角形内切圆面积之和，求1lim n k n k A →∞=∑。

10，（2008北大）数列{}1n n a ∞=定义如下：1234561,2,3,a a a a a a ======……（1） 给定自然数n ，求使l a n =的L 的范围；（2） 令221m m l l b a ==∑，求3limm m b m →∞。

2016北大自主招生数学试卷A1、函数的单调递增区间为（ ）（A ） （B ） （C ） （D ）前三个答案都不对 【解析】B函数的定义域为，设，其单调递增区间为，单调递减区间为，且单调递减，因此的单调递增区间为.2、对于任意给定的所在平面上的点满足，，的面积相等，则这样的点的个数是（ ）（A ）1 （B ）3 （C ）5 （D ）前三个答案都不对 【解析】D为△的重心，或者四点构成平行四边形.3、圆内接四边形中，，则它的外接圆直径为（ ） （A ）170 （B ）180 （C ）（D ）前三个答案都不对 【解析】A注意到，即，故由余弦定理可得解得，故外界圆直径为，.4. 正方体的8个顶点中任取3个构成三角形，则三角形是等腰三角形的概率为（ ） （A ）（B ） （C ） （D ）前三个答案都不对 【解析】B 由题意易知只有对角面上的三角形不是等腰三角形故 ()()20.5log 2f x x x =-++11,2æö-ç÷èø122æöç÷èø，12æö+¥ç÷èø，()f x ()1,2-()()2212g x x x x =-++-<<11,2æö-ç÷èø122æöç÷èø，()()0.5log f x g x =()()20.5log 2f x x x =-++122æöç÷èø，ABC D P PAB D PBC D PAC D P P ABC ,,,A B C P ABCD 136,80,150,102AB BC CD DA ====222215013610280-=-222215080136102+=+222222cos 2cos BD BC DC BC DC C BA DA BA DA AA C pì=+-×=+-×í+=î2A C p==BD 170BD =1247383864417P ´=-=C5、已知，为整系数多项式且，则 的各项系数之和为（ ）（A ）8 （B ）4 （C ）2 （D ）前三个答案都不对 【解析】A易知为二次多项式，设，代入得，对照系数可得，解得则各项系数之和为8.6、设，则的取值范围为（）（A ） （B ） （C ） （D ）前三个答案都不对 【解析】B，即即，.7、实系数方程的根都不是实数，其中两个根的和为，另两根的积为，则等于（ ）（A ）11 （B ）13 （C ）15（D ）前三个答案都不对 【解析】C()234f x x x =-+()g x ()()432318506948f g x x x x x =++++()g x ()g x ()2g x Ax Bx C =++()()()()22234f g x Ax Bx CAxBx C =++-+++2223361836506693448A AB B AC A BC B C C ì=ï=ïï+-=íï-=ïï-+=î134A B C =ìï=íï=î()g x ()0,2x p Î2=x 02p æöç÷èø，2p p æöç÷èø，32p p æöç÷èø，2=cos sin 2cos sin x xx x-=cos 0x >sin 0x <4320x ax bx cx d ++++=2i +56i +b故由韦达定理可得，8、54张扑克牌，将第1张扔掉，第2张放到最后，第3张扔掉，第4张放到最后，依次下去，最后手上只剩下一张牌，则这张牌在原来的牌中从上面数的第几张（ ） （A ）30 （B ）32 （C ）44 （D ）前三个答案都不对 【解析】C第一轮依次剩下的倍数，，，…，，第二轮依次剩下的倍数，，，…，，（最后一张扔掉54，开始第三轮）第三轮依次剩下模8余4的数，，，，，，，，（第四轮以扔掉4开始） 第四轮剩下的数，12，28，44， 第五轮剩下的数，12，44 最后剩下44.9、的个位数字为（ ）（A ）1 （B ）3 （C ）5 （D ）前三个答案都不对 【解析】C易知数字为一个奇数，可以被5整除.10、设为有限集合，为的子集，且对每个，都有，则一定有中某个元素在至少多少个中出现（ ）（A ）403 （B ）404 （C ）2016 （D ）前三个答案都不对 【解析】B由抽屉原理，可知选B11、四个半径为1的球两两相切，则它们的外切正四面体的棱长为（ ）（A ） （B ） （C ） （D ）前三个答案都不对 【解析】B()4a z w z w =-+++=-()()b zz zw zw zw zw ww z w z w zw zw =+++++=++++15=()()c zzw zzw zww zww zw z w zw z w =+++=+++8=61d zwzw =-=-22454448524122028364452()()()()23201621212121+++×××+S 122016,,,A A A ×××S i 15i A S ³S iA (21+(21(22+由棱长为的正四面体的内切球半径为, 设由四个球心所构成的正四面体为,其棱长为，内切球半径设大四面体的内切球半径为，则，则大四面体的棱长12、空间中点集定义如下：，，则由中的点组成的图形的体积等于（ ） （A ）（B ） （C ） （D ）前三个答案都不对 【解析】C 对于每一个，易得，，.故一定，我们考虑极限情况故为三维分别为的长方体，.13、满足等式的正整数的个数为（ ）（A ）0 （B ）1001 （C ）2002 （D）前三个答案都不对 【解析】D答案为4002，由,即, 即 于是,即,故要求,即,14、已知对任意，方程在上至少有一个根，则 等于（ ）（A ）1 （B ）2（C ）3 （D ）前三个答案都不对 【解析】B取，此时，故至少一个属于，a1234O O O O 2r ¢r 116r r ¢=+=+126a ö+=+÷÷ø(){}3,,|381nnnn A x y z xy z =Î++£R 1n n A A ¥==!A 14121n A 1x £1y £1z £+1n n A A Í1n n A A ¥==!(){}3lim ,,|1,81,1n A x y z x y z ==Σ££R A 12,2,41V =2002n éé=ëën 2002200120021´=<20022001200220011´<<´+20022001é=´ë200220012002n é´´=ë2001n é=ë200120011n n £<+2001n 4002n £[]122016,,0,4x x x ×××Î201612016i i x x a =-=å[]0,4a 1220162x x x ====!2x a -=2,2a a +-[]0,4若，综合只能，若，综合只能，排除C 取，此时，此时只能.综合可知选B.15、已知关于的方程有两个不同的非零整数根，则有可能等于（ ） （A ）一个素数 （B ）2的非负整数次幂 （C ）3的非负整数次幂 （D ）前三个答案都不对 【解析】D 方程为，设整数根为，由韦达定理的知识可得. 且，，此时，排除A 由平方数模3余0或者1，可得C 错误.由平方数模4余0或者1，且，知余至少一个模4余1或者2.则要是2的幂只能，与矛盾.16. 用表示距离，则的值为（ ） （A ）1015056 （B ）1017072 （C ）1019090 （D ）前三个答案都不对 【解析】B先考虑的解的个数，由，知当满足，会使得，其个数为，这个片段的和刚好为，则刚好需要个这个片段， 所以17、已知对于实数，存在实数，满足，，则这样的实数 的个数为（ ）（A ）1 （B ）3 （C ）无穷个 （D ）前三个答案都不对 【分析】[]20,4a +Î[]0,2a Î[]20,4a -Î[]0,2a Î1210080x x x ====!1009101020164x x x ====!42x x a +-=2a =x 21x ax b ++=22a b +210x ax b +-+=,m n ,a b ÎZ ()a m n =-+1b mn -+=()()22222222111a b m n m n m n +=+++=++m n ¹21m +21n +1m n ==m n ¹n a 121112016na a a ++×××+=n n a k =221124k k k æö+=++ç÷èøn ()()22111k k n k k -+-+££+n a k =2k 2100824620171017072x =++++=L a ,b c 3333a b c abc --=()22a b c =+a 3333a b c abc ++-()()333a b c ab a b c =++-++()()()223a b c a b a b c c ab éù=+++-++-ëû()()222a b c a b c ab bc ca =++++---【解析】B 由因式分解常见公式， 可得 故要么，此时，解得或；要么，此时，此时解得或18、三角形的三个顶点分别对应复数，已知，则三角形的面积与其最长边长的平方的比等于（ ） （A ）（B ） （C ） （D ）前三个答案都不对 【解析】A由，得到，且由余弦定理可得，故最长边为19.将这100个数分成3组满足第一组中各数之和是102的倍数，第二组中各数之和是203的倍数，第三组中各数之和是304的倍数，则满足上述要求的分组方法数为（ ） （A ）1 （B ）3 （C ）6 （D ）前三个答案都不对 【解析】D 设三组之和分别为，，，,则，易得，结合是正整数，； 同样的得到,,又，得到，显然不可能.20、已知，，则的值为（ ） A. 0 B. 1 C. 不确定 D. 三个均不正确 【解析】A()()3332223a b c abc a b c a b c ab bc ca ++-=++++---()()33322203a b c abc a b c a b c ab ac bc =---=--++++-a b c =+()22a b c =+0a =2a =2220a b c ab ac bc ++++-=()()()222102a b a c b c éù++++-=ëûb c a ==-0a =4a =-ABC 123,,z z z 213112z z i z z -=+-ABC 1516112213112z z i z z -=+-c =cos A =sin A =2a b =c =21sin 2ABC S bc A b D ==1,2,,100×××102x 203y 304z *,,x y z ÎN 1022033045050x y z ++=5050102203505010222031304304x y z ---´-´=£z 15z £22y £42x £()101235050x y z x y z +++++=101|x y z ++2016x y z ++=11112016x y z ++=()()()201620162016x y z ---由已知可得，，即,2016x y z ++=12016xy yz zx xyz ++=()2016xyz xy yz zx =++()()()201620162016x y z ---()()23201620162016xyz xy yz zx x y z =-+++++-0=。

北京大学 2023 年优秀中学生寒假学堂数学试题说明：本试题为考生回忆版，共 20 题，每题 5 分，考试时间 60 分钟。

1．设复数,,a b c 满足2223330,3a b c a b c a b c ++=++=++=，则202320232023a b c ++的值为A ．0B ．3C ．2023D ．其它三个答案都不对2．方程组2223334,6,10x y z x y z x y z ++=++=++=的解的个数为A ．0B ．3C ．6D ．其它三个答案都不对3．设三角形ABC 的三个顶点为复平面上的三点123,,z z z ，满足1231231223310,82i,1510i z z z z z z z z z z z z =++=+++=+，则三角形ABC 内心的复数坐标z 的虚部所在区间为A ．(0.0,5) C ．(1,2)B ．(0,0.5)D ．其它三个答案都不对4．若P 是三角形ABC 的外心，0,120PA PB BC C λ++==︒∠，则实数λ的值为B ．其它三个答案都不对2A ． -1C ． −3D ．12-5．在四面体ABCD 中，面ABC 与面BCD 成60︒的二面角，顶点A 在BCD 的投影H 是三角形BCD 的垂心，G 是三角形ABC 的重心，若4,AH AB AC ==，则GH 的长度是ABC ．其它三个答案都不对D6．过单位正方体1111ABCD A B C D -对角线1BD 做截面，则截面面积的最小值为A．3B．4C ．其它三个答案都不对D ．627．已知直线l 与双曲线22221(0)x y b a a b-=>>两支分别交于点,P Q ，O 为原点，若OP OQ ⊥，则O 到直线l 的距离为A ．abb a-B ．2ab b a -C ．其它三个答案都不对D8．在三角形ABC 中，444222,,,2(),72AB c AC b BC a a b c c a b A ===++=+∠=︒，则B ∠=A ．其它三个答案都不对B ．63︒C ．45︒D ．60︒9．设222121011133520212023S =+++⋅⋅⋅ ，则[]S 的值为A ．251B ．252C ．其它三个答案都不对D ．25310．过椭圆22221(0)x y a b a b+=>>左焦点1F 做倾角为60︒的直线l 交椭圆与,A B 两点，若2AF BF =，则椭圆的离心率为A ．34B ．23C ．其它三个答案都不对D ．1211．以一个正方体的顶点为顶点构成的棱锥的个数为A ．其它三个答案都不对B ．104C ．106D ．10812．已知函数:f →R R 的图像关于点3(,0)4-中心对称且3()(),(1)1,(0)22f x f x f f =-+-==-，则(1)(2)(2022)f f f +++ 的值为A ．其它三个答案都不对B ．6-C ．6D ．013．已知数列{}n a 满足12111,1,,2n n n a a a a a n +-===+≥，则2020202320212022a a a a ⋅-⋅的值为A ．1-B ．1C ．2-D ．其它三个答案都不对14．对于任意的实数z ，方程组22,231,x ay z xy z z +=⎧⎨=++⎩有实数解(,)x y ，则参数a 的变化范围是A ．[4,0)-B ．[2,2)-C ．其它三个答案都不对D ．[0,4)15．以一个给定正2022边形的4个顶点为顶点的梯形称为好梯形，好梯形的个数为A ．100910101011⋅⋅B ．100810091010⋅⋅C ．100010111012⋅⋅D ．其它三个答案都不对16．已知圆内接四边形的边长为2,6,4AB BC CD DA ====，则四边形ABCD 的面积为A．B．C．D ．其它三个答案都不对17．设π,(0,)2x y ∈，则222211cos sin sin cos x x y y+的最小值为A ．8B ．10C ．9D ．其它三个答案都不对18.设=2023,x y =20232023，且y nn n=a x ,x n=b y ，则（ ）A.∃N ∈ n ∀n >,N a n <b ,n +a b n <∀n > ∀∈n ,n a b C. ++，使得nB.D. 其它三个选项<均不对19.数列{a }n 满足a 012=1,=2,a a =6且+32+1=7n n n n a a a a +5++，记k =(2023)!，则a k −1模 ） B.13179的余数为（ A.166C.1D.其它三个选项均不对20.有六件货物，其中两件为次品，其余四件合格，每次从中抽取一件检验后不放回，求恰好需要四次检验就能确定出次品的概率.2023年北京大学优秀中学生寒假学堂数学测试题答案1.解：因为2222()2220a b c a b c ab bc ca ab bc ca ++=+++++⇒++=且3332223()()=1a b c abc a b c a b c ab bc ca abc ++-=++++---⇒从而我们有=001a b c ab bc ca abc ++⎧⎪++=⎨⎪=⎩由韦达定理知,,a b c 是方程310x -=的三个根.由于20231(mod 3)≡，所以202320232023=0a b c a b c ++++=故选择A .2.解：类似于上题，我们可以得到=452x y z xy yx zx xyz ++⎧⎪++=⎨⎪=⎩从而,,x y z 是方程324520t t t -+-=的三个根，注意到322452(1)(2)t t t t t -+-=--从而,,x y z 是1,1,2的一个排列，即原方程组的解有3组，故选择B .3.解：不失一般性，设10z =，则1212+=8+21510z z i z z i=+，从而有23=532z z i=+，不妨设23,z z 对应的点为A 和B ，内心为I ，从而有5,13,8OA OB AB ===且3Im()()OA z OA AB OB r ⋅=++⋅所以105138r =++于是我们有510100.5165169594r <=<<=++++从而选择B 4.解：设AB 的中点为D ，则2PA PB PD +=.由0PA PB PC λ++=，有20PD PC λ+= 所以向量,PD PC共线，又P 是ABC ∆外心，故PA PB PD AB =⇒⊥，从而CD AB ⊥，因为120ACB ∠=，所以120APB ∠=，即四边形APBC 是棱形，于是2PA PB PD PC+== 所以20PD PC PC PC λλ+=+= 所以1λ=-，故选择A .5.设平面AHD 交BC 于F ，则BC DF ⊥，从而BC ADF ⊥面，于是BC AF ⊥，这说明AFH ∠为平面ABC 与平面BCD 成的二面角，即60AFH ∠=.在ABC ∆中，由AB AC =可知BF CF =，从而G 在AF 上且13GF AF =.在直角三角形AHF 中，4AF =，所以FH AF GF ===.在GFH ∆中，由余弦定理可得2221122cos 27GH GF FH GH HF AFH =+-⋅∠=从而9GH ==，故选择B6.解：由对称性，我们只需要考虑截面与面1AD 的交线交线段1AA 于E 的情形.注意到截面面积1112BD A BED F S S S BD d ∆===⋅=四边形其中d 为点E 到线段1BD 的距离.要使得截面面积S 最小，只需要考虑1AA 上的点到1BD 的距离d 最小.取E 为1AA 的中点，易得1OE BD ⊥，且1OE AA ⊥，此时d OE =为异面直线1AA 到1BD 的距离，为d 的最小值且min 122d EF ==.于是截面面积min min 2622S ===故选择D .7.解：不妨设OP m OQ n ==，且POx θ∠=。

2018年北京大学自主招生数学试卷选择题共20小题：在每小题的四个选项中，只有一项符合题目要求，请把正确选项的代号填在表格中，选对得5分，选错扣1分，不选得0分。

1. 把实数2018)335(+=a 写成十进制小数，则a 的十分位、百分位和千分位上数字之和等于（ C ） A.0 B. 9 C. 27 D. 前三个答案都不对解答：记2018(5b =−，容易知道b 是一个很小的正数，进一步，0.00001b <.由二项式展开，容易知道20182018*(5(5a b N +=++−∈，从而a 是一个正整数减去一个很小的正数，从而a 的十分位、百分位和千分位上数字都是9. 答案C.2. 已知b a ≠，1)()(22=+=+c a b c b a ，则abc b a c −+)(2的值为（ A ）A. 2B. 1C. 0D. 前三个答案都不对解法一：由22()()()()()0()()0a b c b a c ab a b c a b a b a b ab bc ca +=+⇒−+−+=⇒−++=，又a b ≠，所以0ab bc ca ++=，2()1()1()11a b c a ab ca a bc abc ∴+=⇔+=⇔−=⇒=−，2()()()22c a b abc c ca cb abc c ab abc abc ∴+−=+−=−−=−=。

解法二:记()21ab c +=……①，()21b a c +=……②，①-②有()()()()2200ab a b c a b a b ab c a b −+−=⇔−++=⎡⎤⎣⎦，由b a ≠，()()0ab c a b ab c a b ++=⇔=−+，从而原式=22()2c a b abc +=−.另一方面，由21b c a +=……③，21a c b+=……④，④-③有 222211a b a b a b b a −=−⇒=+，与()ab c a b =−+比较可知道11c abc ab=−⇒=−， 从而原式=22()22c a b abc +=−=. 答案A. 3. 设1,0≠>a a ，函数14)(2−−=x xa ax f 在区间[-1,2]上的最小值为-5，则a 的取值范围是（ C ）A. 221≥=a a 或 B. 210≥<<a a 或 C .2210≥<<a a 或 D. 前三个答案都不对解答：()22()4125x x x f x a a a =−−=−−，则()22xa −在[]1,2x ∈−时的最小值为0，即当[]1,2x ∈−时，xa 的取值范围包含2，根据指数函数的单调性，有()()(21220210a a a a a a ⎛⎫−−≤⇔−≥ ⎪⎝⎭， 考虑到0a >，可得2210≥<<a a 或. 答案C. 4. 设n S 为一等差数列的前n 项和，已知2501510==S S ，，则n nS 的最小值是（ D ）A. -25B. -36C. -48D. 前三个答案都不对 解答：由等差数列常用性质：n S n ⎧⎫⎨⎬⎩⎭是等差数列，且10010S =，155153S =，可知()1103n S n n =−，则 ()21110(202)36n nS n n n n n =−=−⋅⋅−，根据均值不等式可知7n =时，n nS 有最小值-49. 答案D.5. 以梯形ABCD 的下底BC 上一点为圆心做半圆，此半圆与这个梯形的上底AD 和两腰AB 、CD 都相切，则 |AB|+|CD|-|BC|的值（ D ）A. 为正B. 为负C. 可正可负D. 前三个答案都不对 解答：当ABCD 特别接近矩形时，12AB CD BC r ===，可知|AB|+|CD|-|BC|无限趋近于0；事实上，当ABCD 四点共圆的时候，可以证明|AB|+|CD|-|BC|=0（1985年IMO 几何问题）； 另一方面，当A,D 重合，也就是ABCD 退化成一个三角形时，明显有|AB|+|CD|-|BC|大于零.从而|AB|+|CD|-|BC|的值可零可正. 答案D.6. 在ABC ∆中，0tan tan tan >++C B A 是ABC ∆为锐角三角形的（ C ）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 前三个答案都不对 解答： 根据三角形中的常用恒等式tan tan tan tan tan tan A B C A B C ++=⋅⋅，可知tan ,tan ,tan 0A B C >，从而ABC ∆为锐角三角形，反之亦然. 答案C.7. 满足对任意实数a ，b 都有)()()(b f a f b a f +=+和)()()(b f a f ab f =的实函数)(x f 的个数是（ B ）A. 1B. 2C.无穷多D. 前三个答案都不对解答： 容易猜测满足题意的实函数)(x f 只有两个：()f x x =或()0f x =. 事实上，有柯西方程可知()f x kx =（这样说并不严谨，只有证明了()f x 单调性或者连续性之后才能严谨地证明()f x kx =，事实上，不难借助两个条件方程证明：当()f x 不恒等于零时，其一定是单调递增的），代入()()()f x x f x f x ⋅=⋅ 有2k k = ，从而0,1k =. 答案B.8. 设函数t t t f 2)(2+=，则点集{})()(2)()(|),(y f x f y f x f y x ≥≤+且所构成的图形的面积是（ B ）A. 4πB. 2πC. πD. 前三个答案都不对解答：平面区域问题()()()()22222222114f x f y x x y y x y +≤⇔+++≤⇔+++≤；()()()()222220f x f y x x y y x y x y ≥⇔+≥+⇔−++≥；如图，画出平面区域后可知，满足两个不等式的区域是两个圆心角为90的扇形， 并且扇形半径为2.所以区域面积为2π. 答案B.9. 不等式122>+yx 且3,3≥≥y x 的正整数解),(y x 的个数是（ D ） A. 3B. 4C. 6D. 前三个答案都不对解答：本质上是不定方程问题:()()()22120224xy x y x y x y+>⇒−+<⇒−−<, 所以()()()()()()2,21,1,1,2,2,1,1,3,3,1x y −−=，所以正整数解),(y x 的个数是5. 答案D. 10. 设数列{}1≥n a n 的首项20191=a ，前n 项和n S =n a n 2，则2018a 的值为（ C ）A.20191B.20181 C. 10091D. 前三个答案都不对解答：n S =n a n 2，1n S +=()211n n a ++，作差可得()()22111112n n n n n n n a S S n a n a n a na ++++=−=+−⇒+=，()()()111211222019n n n n a n n a a +⇒++=+==⋅⋅=⋅，所以2018220191.201820191009a ⋅==⋅ 答案C.11. 在ABC ∆中，AB=13，AC=15，BC=14，AD 为边BC 上的高，则ABD ∆和ACD ∆的内切圆圆心之间的距离为（ D ）A. 2B. 3C. 5D. 前三个答案都不对解答：根据AD 垂直BC 于D,且AB=13，AC=15，BC=14，容易根据勾股数的性质求得：BD=5，CD=9，AD=12， 则三角形ABD 的内切圆半径为5121322+−=，三角形ACD 的内切圆半径为1291532+−=，则ABD ∆和ACD ∆的内切圆圆心之间的距离为d ==答案D.12. ABC ∆的内角A ，B ，C 的对边分别为c b a ,,，满足3cos cos c A b B a =−，则BAtan tan 等于（ A ） A. 2B. 1C.21D. 前三个答案都不对 解答：根据正弦定理 ()11sin cos sin cos sin sin 33A B B A C A B −==+展开可得，24tan sin cos sin cos 233tan AA B B A B=⇒=. 13. 设实数y x ,满足1422=+y x ，则1243−+y x 的取值范围为（ B ）A. [)+∞,0B. []13212132-12+， C. []13212,0+ D. 前三个答案都不对 解答：记()(),2cos ,sin x y θθ=，则()34126cos 4sin 121212x y θθθϕ⎡+−=+−=+−∈−+⎣，答案B.14. 过椭圆14922=+y x 上一点M 做圆222=+y x 的两条切线，过切点的直线与坐标轴交于Q P ,两点，O为坐标原点，则POQ ∆面积的最小值为（ B ）A.21 B.32 C.43 D. 前三个答案都不对解答：记()220000,,194x y M x y +=，则由切点弦的性质00:2PQ x x y y +=，则00220,,,0P Q y x ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭，000012222POQS x y x y ∆==，另一方面2200001943x y x y =+≥=，所有0022.3POQ S x y ∆=≤ 答案B.15. 设正实数b a ,满足1=+b a ，则3271ba +的最小值为（ A ） A.2131347+ B. 2131555+ C. 218D. 前三个答案都不对解答：记1a b =−，3127,1u b b =+− 则()241811du db b b =−−，令()2418101du db bb =−=−，根据 10,0a b b =−>>，则()29912b b b −+=−⇒=（舍负），代入可得3271ba +的最小值为 2131347+. 答案A.16. 在正方体1111D C B A ABCD −中，动点M 在底面ABCD 内运动且满足M DD A DD 11∠=∠,则动点M 在底面ABCD 内的轨迹为（ A ）A. 圆的一部分B. 椭圆的一部分C. 双曲线一支的一部分D. 前三个答案都不对 解答：1145DD M DD A ∠=∠=，从而1DM DD =，答案A.17. 已知21,F F 是椭圆与双曲线的公共焦点，P 是椭圆与双曲线的一个交点，且321π=∠PF F ，则椭圆与双曲线的离心率的倒数之和的最大值为（ D ）A. 32B. 3C.331D. 前三个答案都不对解答：设椭圆和双曲线的短半轴（虚半轴）分别为12,b b ，则由常用面积结论：122212tancot33F PF S b b ππ∆==，于是22213b b =，记两曲线的半焦距为c ，则两条曲线的离心率的倒数之和1211e e +==12111e e +=≤= 答案D.18. 设三个实数c b a ,,组成等比数列，c b a c 320+≤>且，则实数acb 2−的取值范围是（ B ） A. ⎥⎦⎤ ⎝⎛∞161-，B. ⎥⎦⎤ ⎝⎛∞91-，C. ⎥⎦⎤ ⎝⎛∞81-， D. 前三个答案都不对解答：由2,0b ac c =>，可知0a > ，则()()223231233110b ca b c q q q q a a≤+⇒≤+=+⇒−+≥， 所以13q ≥或1q ≤− . 进一步， 222max2111111222483489b c q q q a −⎛⎫⎛⎫=−=−−+=−−+= ⎪ ⎪⎝⎭⎝⎭，所以实数a c b 2−的取值范围是 ⎥⎦⎤ ⎝⎛∞91-，. 答案B. 19. 设实函数0,)(2≠++=a c bx ax x f ，定义)2))((()(),()(11≥==−n x f f x f x f x f n n ，已知方程x x f =)(1无实根，则方程x x f =)(2018的实根个数是（ A ）A. 0B. 2018C. 4036D. 前三个答案都不对解答：方程x x f =)(1无实根，则1()f x x >恒成立或1()f x x <恒成立，进而()11()()f f x f x x >>或()11()()f f x f x x <<恒成立，依次类推，()20172017()()f f x f x x >>>或()20172017()()f f x f x x <<<恒成立，从而方程x x f =)(2018没有实根. 答案A.20. 三棱锥ABC P −中，底面ABC 是以A ∠为直角的直角三角形，PA 垂直于底面ABC ，且AC AB PA +=，则三个角CPA BPC APB ∠∠∠与,的和是（ C ）A. 60°B. 75°C. 90°D. 前三个答案都不对解答：记,,APB BPC CPA αγβ∠=∠=∠=，则tan tan 1αβ+=；所以()sin cos sin cos 1sin cos cos cos cos αββααβαβαβ+=⇒+=，另一方面，对二面角B PA C −−用二面角余弦定理可知，cos cos cos cos 0sin sin 2λαβπαβ−==，从而cos cos cos λαβ=，所以()sin cos αβγ+=，又因为,,αβγ都是锐角，所以2παβγ+=−，所以答案C.。

2016年北京大学自主招生测试数学学科1. 求()212log 2x x -++的单调增区间。

2. 圆内接四边形ABCD 满足AB =80，BC =102，CD =136，DA =150，求直径。

3. 四个半径为1的球两两相切，求其外切正四面体的棱长为（ ）A.2+B.2+C.4+D.以上均错4. 已知实数x ，y ，z 满足1112016,2016x y z x y z++=++=，求(2016)(2016)(2016)x y z ---=( )A.1B.0C.-1D.以上全错5. 设x ，y ，z 3R ∈，求方程381n n n x y z ++≤，当n →+∞时确定的几何体的体积为________。

6. 正方体八个顶点中任取3个，求能构成等腰三角形的概率________。

7. 设n a的整数，若112016n k k a ==∑，求n =________。

8. 若方程21x ax b ++=有两个不同的非零整数根，则22a b +可能为________。

A. 素数B. 2的非负整数次幂C. 3的非负整数次幂9. 2002n ⎡⎡=⎣⎣有________个正整数解。

10. 实数a ，b ，c 满足33323,2(),,,a b c abc a b c a b c N --==+∈，这样的a 有_________个。

11. 232016(21)(21)(21)...(21)++++的个位数字为（ ）A.1B.3C.5D.以上均错12. 实系数方程4320x ax bx cx d ++++=有四个非实数根，其中两个之和为2+i ，另外两个之积5+6i ，b =________。

13. 若△ABC 的三个顶点对应复数为z 1，z 2，z 3，且满足213112z z i z z -=+-，则△ABC 的面积与其最长边的平方之比为________。

14. 将1~100这100个正整数分成三组，使第一组和为102的倍数，第二组和为203的倍数，第三组和为304的倍数。

2019年北京大学自主招生数学试题2019年清华大学自主招生数学试题2019年中国科学技术大学自主招生数学试题4．记3cos(),4cos()36x t y t =+-=++，则22x y +的最大值为__________。

5．设点0(1,0)P ，i OP (i =1,2,3…)绕原点按顺时针旋转θ得到向量i OQ ， i Q 关于y 轴对称点记为1 i P +，则2019P 的坐标为__________。

．，且．已知，且9．将△D 1D 2D 3的各中点连线，折成四面体ABCD ，已知12233112,10,8D D D D D D ===，求四面体ABCD 的体积。

10．求证：对于任意的在R 上有仅有一个解0x =11．已知(1)求证：存在多项式()p x ，满足cos (cos )n p θθ=；(2)将()p x 在R [x ]上完全分解。

2019年中国科学技术大学自主招生数学试题参考答案2.B红色曲线为y =sin 2x ,蓝色曲线为y =-cos 3x综上，知：00100110cos sin cos sin 01sin cos sin cos x x x y y y θθθθθθθθ---⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪ ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭那么222(,)P x y 满足：200020002cos sin 10sin cos 01x x x x y y y y θθθθ--⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭这也就说明了20,P P 重合。

故2019P 坐标为(cos ,sin )θθ--6.首先将递推公式两侧取倒数，则：112(1)11112(1)n n n n nn x n x x x x ++++=⇔-=+累加，即：21122(1)n n n k k x x n n =-=⇒=+∑裂项求和，则：2019112019*********k k x ==-=∑7.如图所示，我们定义a ~b 表示复数a 和b之间的边11z z -+是纯虚数，表明0~(z-1)与0~(z+1)垂直，进而说明|z~(z-1)|=|0~z|=|z~(z+1)|=1故||1z =，进一步，我们设cos sin z i θθ=+则222222222|3|(cos 2cos 3)(sin 2sin )cos 2cos 96cos 6cos 22cos cos 2sin 2sin 2sin 2sin 116cos 2812cos 8cos 53z z cos θθθθθθθθθθθθθθθθθθ++=++++=++++++++=++=++≥等号成立条件为1cos 3θ=-8.9.简解：由题意，易知四面体ABCD为等腰四面体，将其嵌入长方体后割补法即可图示蓝色边框为等腰四面体，黑色为被嵌入的长方体答案：410.首先，我们定义()()n f x 代表函数()f x 的n 阶导数令0()!kn x k x f x e k ==-∑注意到()()1n x f x e =-在R 上单调递增，故其在R 上仅有一根x =0，从而(1)()1n x f x e x -=--在R 上有最小值，即(1)(1)()(0)0n n f x f --≥=进而2(2)()12n x x f x e x -=---在R 上单调递增以此类推，可知：(2)()n k f x -在R 上单调递增，仅有一根x =0(21)()n k f x --在R 先减后增，且恒为非负实数，且仅有一根x =0综上，不论n 取何值，0()!knx k x f x e k ==-∑在R 上仅有一根x =011.本题考察内容十分清晰，旨在考察Chebyshev 多项式（1）采取归纳法证明，若对于不同的n ，存在满足题设的多项式，则记其为()n p x 首先，当1n =时，存在多项式1()p x x=其次，当2n =时，存在多项式22()21p x x =-我们假定命题在2,1n n --的情形下成立，下面考察n 的情形cos cos[(1)]cos(1)cos sin(1)sin 1cos(1)cos [cos cos(2)]2n n n n n n n θθθθθθθθθθθ=-+=-⋅--⋅=-⋅+--进而有cos 2cos cos(1)cos(2)n n n θθθθ=---即12()2()()n n n p x xp x p x --=-因为12(),()n n p x p x --都是多项式，所以()n p x 也是多项式。

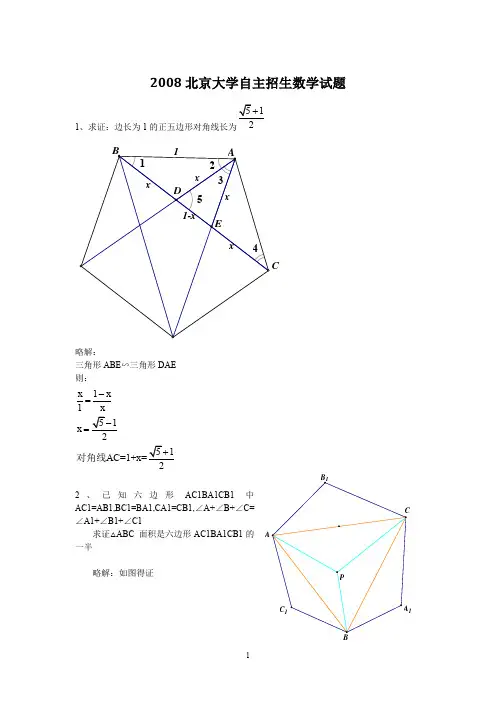
2010年北大自主招生试题（理科）数学：1.AB为正五边形边上的点，证明：AB最长为（根5+1）/2(25分)2.AB为y=1-x^2上在y轴两侧的点，求过AB的切线与x轴围成面积的最小值。

(25分)3.向量OA与OB已知夹角，|OA|=1，|OB|=2，OP=tOA，OQ=（1-t）OB，|PQ|在t0是取得最小值，问当0<t0<1/5时，夹角的取值范围。

(25分)4.存不存在0<x<π/2，使得sinx,cosx,tanx,cotx为等差数列。

(25分)化学：1.Ca在空气中燃烧的固体产物溶于水，放热，放出有臭味的气体，写出方程式。

2.同样浓度下，醋酸和氨水的电离程度相同，但氢氧化铝可以完全溶于醋酸，却不能溶于氨水，问这能说明氢氧化铝的什么性质？3.和水一样，酯也可以在氨中发生氨解反应，写出RCOOR’的氨解反应方程式。

4.不同于水溶液，在液氨的环境中，“不活泼”金属可以将“活泼”金属置换出来，如Mg+NaI=MgI+Na，解释为什么可以发生这样的反应。

5．Fe，Cu溶于稀硝酸，剩余固体为以下情况时，溶液中可能的阳离子：（1）不剩余固体（2）剩余固体为Cu(3）剩余固体为Fe，Cu（4）可不可能剩余的固体只有Fe，为什么？6．已知C（s），氢气（g），乙醇（l）的燃烧热为394kJ/mol，286kJ/mol，1367kJ/mol，由这些可以知道哪些数据？7．在发烟硝酸H2SO4•SO3中，2molI2和3molI2O5生成I2（SO4）3，I2（SO4）3溶于水生成I2和I2O4，写出以上两个方程式。

8.测定溶液中Iˉ的方法，当Iˉ太少时可用增大倍数的方法，第一种：用氯气将Iˉ氧化为HIO3，后除去多余氯气，用KI还原HIO3后测定Iˉ的量；第二种：用IO4ˉ将Iˉ氧化为IO3ˉ，加入一种物质阻止IO4ˉ和Iˉ反应，用KI还原IO3ˉ后测定Iˉ的量。

问以上两种方法分别将Iˉ扩大了多少倍？物理：1．光滑平面，两个相隔一定距离的小球分别以Vo（左）和0.8Vo（右）反向匀速运动，它们中间有两个小球1在左侧m，2在右侧2m，中间有一压缩的弹簧，弹性势能为Ep，当弹性势能全部释放后（1）求小球1，2的速度（2）若小球1能追上左边的以Vo运动的球，而小球2不能追上右边以0.8Vo运动的球，求m的取值范围。

2014年北京大学自主招生数学试题1. 圆心角为3π的扇形面积为6π，求它围成圆锥的表面积. 2. 将10个人分成3组，一组4人，两组每组3人，共有几种分法. 3. 2()2()(),(1)1,(4)733a b f a f b f f f ++===,求()2014f . 4.2()lg(2)f x x ax a =-+的值域为R ，求a 的取值范围.5. 已知1x y +=-，且,x y 都为负实数，求1xy xy+的取值范围. 6. 22()arctan14x f x C x +=+-在11,44⎛⎫- ⎪⎝⎭上为奇函数，求C 的值. 一、求证：tan3Q ∉二、已知实系数二次函数()f x 与()g x ，()()f x g x =和()()30f x g x +=有两重根，()f x 有两相异实根，求证：()g x 没有实根.三、1213,a a a 是等差数列，{}113i j k M a a a i j k =++≤<<≤，问：7160,,23是否同在M 中，并证明你的结论.四、()01,2,,i x i n >=，且11n i i x ==∏，求证1)1)nn i i x =≥∏.答案1．π7； 2．2100； 3．4027)2024(12)(=⇒-=f x x f ； 4．1 00≥≤⇒≥∆a or a ；5．⎪⎭⎫⎢⎣⎡+∞,417；6．2arctan 0)0(-=⇒=C f 一、求证：Q ∉︒3tan解：若Q aab Q a ∈-=︒=⇒∈=︒2126tan 3tan ，Q ab b a c ∈-+=︒=⇒19tan Q bc cb d ∈-+=︒=⇒115tan 52518tan 41518sin 2-=︒⇒-=︒ 于是Q d d ∈-=⇒=-=︒233215tan ，从而矛盾。

二．实系数二次函数)(),(x g x f ，)()(x g x f =和0)()(3=+x g x f 有两重根，)(x f 有两相异根，求证：)(x g 无实数根。

北大自主招生数学试题一、下列哪个数列不是等差数列？A. 1, 3, 5, 7, ...B. 2, 4, 8, 16, ...C. 10, 8, 6, 4, ...D. -1, 0, 1, 2, ...（答案：B）二、若复数z满足(1+i)z=2i，则z等于？A. 1-iB. 1+iC. -1+i（答案）D. -1-i三、设函数f(x) = x3 - 3x2 + 2，则f(x)的极小值点为？A. x = 0B. x = 1C. x = 2（答案）D. x = 3四、在三角形ABC中，若sinA:sinB = 3:4:5，则cosC的值为？A. 1/5B. -1/5（答案）C. 3/5D. 4/5五、已知向量a = (1, 2)，b = (2, 1)，则向量a与b的夹角θ的余弦值为？A. √5/5B. 2√5/5（答案）C. 1/√5D. -1/√5六、设集合A = {x | x2 - 5x + 6 = 0}，B = {x | x2 - ax + a - 2 = 0}，若B是A的子集，则a的取值范围是？A. a = 2或a = 3或a = 5B. a = 3或a = 5（答案）C. a = 2或a = 5D. a = 2或a = 3七、已知圆C的方程为x2 + y2 - 2x - 5 = 0，直线l的方程为2x - y - 1 = 0，则圆心C到直线l的距离为？A. √5B. 2√5/5C. √5/5（答案）D. 3√5/5八、若实数x, y满足约束条件x + y ≤ 2, x - y ≤ 1, x ≥ 0，则z = 2x + y的最大值为？A. 2B. 3C. 4D. 5（答案）九、设函数f(x) = ex - e(-x)，则不等式f(x + 2) < f(1 - x)的解集为？A. (-∞, 3/2)B. (-3/2, +∞)（答案）C. (-∞, -1/2)D. (1/2, +∞)十、已知矩阵A = [1 2; 3 4]，向量β = [5; 6]，若向量α满足Aα = β，则α为？A. [-1; 2]B. [2; -1]（答案）C. [1; 1]D. [-2; 1]。

自主招生数学试题及答案一、选择题（每题5分，共30分）1. 下列哪个选项不是正整数？A. 0B. 1C. 2D. 3答案：A2. 如果函数\( f(x) = x^2 - 4x + 3 \)，那么\( f(2) \)的值是多少？A. -1B. 1C. 3D. 5答案：A3. 圆的面积公式是？A. \( \pi r^2 \)B. \( 2\pi r \)C. \( \pi d \)D. \( \pi r \)答案：A4. 已知\( \sin(\alpha) = \frac{3}{5} \)，且\( \alpha \)在第一象限，求\( \cos(\alpha) \)的值。

A. \( \frac{4}{5} \)B. \( \frac{1}{5} \)C. \( -\frac{4}{5} \)D. \( -\frac{1}{5} \)答案：A5. 以下哪个数是无理数？A. \( \sqrt{2} \)B. 1.5C. 0.333...D. 1答案：A6. 一个等差数列的首项是3，公差是2，第10项是多少？A. 23B. 21C. 19D. 17答案：B二、填空题（每题3分，共15分）1. 一个直角三角形的两条直角边分别为3和4，斜边的长度是______。

答案：52. 函数\( g(x) = 2x - 1 \)的反函数是______。

答案：\( g^{-1}(x) = \frac{x + 1}{2} \)3. 一个数的平方根是4，这个数是______。

答案：164. 已知\( \tan(\theta) = 3 \)，求\( \sin(\theta) \)的值（假设\( \theta \)在第一象限）。

答案：\( \frac{3\sqrt{10}}{10} \)5. 一个等比数列的首项是2，公比是3，第5项是多少？答案：162三、解答题（每题25分，共50分）1. 解不等式：\( |x - 5| < 4 \)。