自主招生北大2011数学测试试题

()()1132，(123x +的交点的直线方程()()1132得⎧⎪⎪⎨⎪⎪⎩252x x -++解析：因为222cos 2a b c C ab +-=22222a b a b ab +⎛⎫+- ⎪⎝⎭≥()2231422a b ab ab +-= 312422ab ab ab⋅-≥12=，当且仅当a b =时，""=成立，又因为()0,C π∈，所以060C ∠≤。

所以211212CC CC r r C C -=-<，由双曲线的定义，C 的圆心的轨迹是以1C ，2C 为焦点、实轴长为12r r -的双曲线；所以211212CC CC r r C C -=+<，由双曲线的定义，C 的圆心的轨迹是以1C ，2C 为焦点、实轴长为12r r +的双曲线；21121212点、实轴长为12r r -的双曲线；所以211212CC CC r r C C -=+=或211212CC CC r r C C +=+=，所以C 的圆心的轨迹是过1C ，2C 的直线（除直线与圆1C 、2C 的交点外）；所以211212CC CC r r C C -=-<，由双曲线的定义，C 的圆心的轨迹是以1C ，2C 为焦点、实轴长为12r r -的双曲线（圆1C 、2C 的交点除外）；21121212实轴长为12r r +的椭圆（圆1C 、2C 的交点除外）；所以211212CC CC r r C C -=-=或2112CC CC r r +=-，所以C 的圆心的轨迹是过1C ，2C 的直线（除直线与圆1C 、2C 的交点外）；（ⅱ）若C 与1C 内切，2C 外切，则11CC r r =-，22CC r r =+，所以211212CC CC r r C C +=+>，所以C 的圆心的轨迹是以1C ，2C 为焦点、实轴长为12r r +的椭圆（两圆1C 、2C 的交点除外）；（ⅰ）若C 与1C ，2C 都内切，则11CC r r =-，22CC r r =-，所以211212CC CC r r C C +=->，所以C 的圆心的轨迹是以1C ，2C 为焦点、实轴长为12r r -的椭圆；（ⅱ）若C 与1C 内切，2C 外切，则11CC r r =-，22CC r r =+，所以211212CC CC r r C C +=+>，所以C 的圆心的轨迹是以1C ，2C 为焦点、实轴长为12r r +的椭圆。

绝密★使用完毕前2011年普通高等学校招生全国统一考试数学（理）（北京卷）本试卷共5页，150分。

考试时间长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题 共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）已知集合P=｛x ︱x 2≤1｝,M=｛a ｝.若P ∪M=P,则a 的取值范围是（A ）(-∞, -1] （B ）[1, +∞） （C ）[-1，1] （D ）（-∞，-1] ∪[1，+∞） （2）复数212i i-=+（A ）i（B ）-i（C ）（D ）4355i--4355i -+（3）在极坐标系中，圆ρ=-2sin θ的圆心的极坐标系是(A)(B) (C) (1,0)(1,)2π(1,2π-(D)(1，)π（4）执行如图所示的程序框图，输出的s 值为（A ）-3 （B ）-12（C ）13（D ）2（5）如图，AD ，AE ，BC 分别与圆O 切于点D ，E ，F ，延长AF 与圆O 交于另一点G 。

给出下列三个结论：AD+AE=AB+BC+CA ；○1回归往日精品，再现今日辉煌AF·AG=AD·AE○2③△AFB ～△ADG 其中正确结论的序号是（A ）①② （B ）②③ （C ）①③ （D ）①②③（6）根据统计，一名工作组装第4件某产品所用的时间（单位：分钟）为（A ，C 为常数）。

已知工人组装第4件产品用时30分钟，组装第A 件产品用时15分钟，那么C 和A 的值分别是（A ）75，25 （B ）75，16 （C ）60，25 （D ）60，16 (7)某四面体的三视图如图所示，该四面体四个面的面积中，最大的是(A) 8 (B) (C)10 (D) （8）设,，,.记为平行四边形()0,0A ()4,0B ()4,4C t +()(),4D t t R ∈()N t ABCD 内部（不含边界）的整点的个数，其中整点是指横、纵坐标都是整数的点，则函数的值域为()N t（A ） （B ） {}9,10,11{}9,10,12（C ） （D ） {}9,11,12{}10,11,12第二部分 （非选择题 共110分）二、填空题共6小题，每小题5分，共30分。

2011年北京四中自主招生考试数学试卷一、选择题（共6小题，每小题5分，满分30分）1．（5分）已知＜cosA＜sin80°，则锐角A的取值范围是（）A．60°＜A＜80°B．30°＜A＜80°C．10°＜A＜60°D．10°＜A＜30°2．（5分）实数b满|b|＜3，并且有实数a，a＜b恒成立，a的取值范围是（）A．小于或等于3的实数B．小于3的实数C．小于或等于﹣3的实数D．小于﹣3的实数3．（5分）x1，x2是方程x2+x+k=0的两个实根，若恰x12+x1x2+x22=2k2成立，k的值为（）A．﹣1B．或﹣1C．D．﹣或1 4．（5分）代数式的最小值为（）A．12B．13C．14D．115．（5分）掷一枚质地均匀的正方体骰子，骰子的六个面上分别刻有1至6六个数．连续掷两次，掷得面向上的点数之和是3的倍数的概率为（）A．B．C．D．6．（5分）1×2+2×3+3×4+…+99×100=（）A．223300B．333300C．443300D．433300二、填空题（共6小题，每小题5分，满分30分）7．（5分）多项式6x3﹣11x2+x+4可分解为．8．（5分）已知点P（x，y）位于第二象限，并且y≤2x+6，x、y为整数，则点P 的个数是．9．（5分）已知⊙O的半径OA=1，弦AB、AC的长分别是、，则∠BAC的度数是．10．（5分）方程（2007x）2﹣2006×2008x﹣1=0的较大根为a，方程x2+2006x ﹣2007=0的较小根为b，则a﹣b=．11．（5分）已知x=，则x3+12x的算术平方根是．12．（5分）如图，Rt△ABC中，∠BCA=90°，∠BAC=30°，AB=6．△ABC以点B 为中心逆时针旋转，使点C旋转至AB边延长线上的C′处，那么AC边转过的图形（图中阴影部分）的面积是．三、解答题（共5小题，满分60分）13．（12分）现将一个表面涂满红色的正方体的每条棱十等分，此正方体分割成若干个小正方体．在这些小正方体中，求：（1）两面涂有红色的小正方体的个数；（2）任取一个小正方体，各面均无色的小正方体的概率；（3）若将原正方体每条棱n等分，只有一面涂有红色的小正方体的个数．14．（12分）已知x、y均为实数，且满足xy+x+y=17，x2y+xy2=66，求：代数式x4+x3y+x2y2+xy3+y4的值．15．（12分）在直角△ABC中，∠C=90°，直角边BC与直角坐标系中的x轴重合，其内切圆的圆心坐标为P（0，1），若抛物线y=kx2+2kx+1的顶点为A．求：（1）求抛物线的对称轴、顶点坐标和开口方向；（2）用k表示B点的坐标；（3）当k取何值时，∠ABC=60°？16．（12分）如图，OA和OB是⊙O的半径，并且OA⊥OB．P是OA上的任意一点，BP的延长线交⊙O于点Q，点R在OA的延长线上，且RP=RQ．（1）求证：RQ是⊙O的切线；（2）求证：OB2=PB•PQ+OP2；（3）当RA≤OA时，试确定∠B的取值范围．17．（12分）平面上有n个点（n≥3，n为自然数），其中任何三点不在同一直线上．证明：一定存在三点，以这三点作为顶点的三角形中至少有一个内角不大于．2011年北京四中自主招生考试数学试卷参考答案一、选择题（共6小题，每小题5分，满分30分）1．D；2．C；3．A；4．B；5．C；6．B；二、填空题（共6小题，每小题5分，满分30分）7．（x﹣1）（3x﹣4）（2x+1）；8．6；9．15°或75°；10．2008；11．2；12．9π；三、解答题（共5小题，满分60分）13．；14．；15．；16．；17．；。

（ⅰ）若 C 与 C1 ， C2 都外切，则 CC1 r1 r ， CC2 r2 r ，所以 CC1 CC2 r1 r2 ； 若 C 与 C1 ， C2 都内切，则 CC1 r r1 ， CC2 r r2 ，所以 CC2 CC1 r1 r2 ； 所以 CC2 CC1 r1 r2 C1C2 ，由双曲线的定义， C 的圆心的轨迹是以 C1 ， C2 为焦点、实轴长为 （ⅱ）若 C 与 C1 内切， C2 外切，则 CC1 r r1 ， CC2 r2 r ， r1 r2 的双曲线； 所以 CC2 CC1 r1 r2 ；若 C 与 C1 外切， C2 内切，则 CC1 r r1 ， CC2 r r2 ， 所以 CC1 CC2 r1 r2 ；所以 CC2 CC1 r1 r2 C1C2 ，由双曲线的定义， C 的圆心的轨迹是以
值为何？ 解 由 a7 a3 4d 可得公差 d 4 , 从而 a1 21 . 令 21 4( x 1) 0 得 x 6.25 , 故 {an } 从第 7 项开 始为正, 所以 {S n } 的最小项为 S6 66 . 4. 在 ABC 中， a b 2c ，求证： C 60 . 证 根据正弦定理有 sin A sin B 2sin C , 从而有
2011 年北约等十三校联考自主招生数学试卷 厦门一中徐小平
1. 已知平行四边形的其中两条边长为 3 和 5，一条对角线长为 6，求另一条对角线长. 解一 (引理) 平行四边形的对角线平方和等于四边的平方和. 另一对角线长为
2(32 52 ) 62 4 2 . C B 解二 如图, 设 AB 3 , AD 5 , BD 6 , 则据余弦定理有 2 2 2 2 AB AD cos A AB AD BD 2 , 于是 AC 2 DC 2 AD 2 2 DC AD cos CDA D A 32 52 2 AB AD cos A 32 , 从而 AC 4 2 . 2 2 2. 求过抛物线 y 2 x 2 x 1 和 y 5 x 2 x 3 的交点的直线方程. 解 由上述两方程消去二次项可得 6 x 7 y 1 0 , 此即为过两抛物线交点的直线方程. 3. 在等差数列 {an } 中， a3 13, a7 3 ，数列 {an } 的前 n 项和为 S n ，求数列 {S n } 的最小项，并指出其

Ａ ２１； Ｂ ２０； Ｃ １９； Ｄ １８ ４．解法 １ 根 据ａ＋ｂ≥２ｃ，并 运 用 正 弦 定 理 得 ｓｉｎ Ａ＋ｓｉｎ Ｂ≥２ｓｉｎ Ｃ，则
４ｓｉｎ２Ｃｃｏｓ２Ｃ ＝２ｓｉｎ Ｃ≤ｓｉｎ Ａ＋ｓｉｎ Ｂ＝
的方程．
｛ｙ＝２ｘ２ －２ｘ－１，
解法 ２ 联 立 方 程 组
消去 ｙ＝－５ｘ２ ＋２ｘ＋３．
２ ０１１×｜ｘ－２ ０１１１｜＝｜ｘ－１｜＋（｜ｘ－２１｜＋｜ｘ－２１｜）＋
（｜ｘ－３１｜＋｜ｘ－３１｜＋｜ｘ－３１｜）＋ … ＋
（｜ｘ－２ ０１１１｜＋｜ｘ－２ ０１１１｜＋ … ＋｜ｘ－２ ０１１１｜）＝
（｜ｘ－１｜＋｜ｘ－２０１ １１｜）＋（｜ｘ－２１｜＋｜ｘ－２ ０１１１｜）＋
（｜ｘ－２１｜＋｜ｘ－２ ０１１１｜）＋（｜ｘ－３１｜＋｜ｘ－２ ０１１１｜）＋
其２ 个交点为Ａ（ｘ１ ，ｙ１ ）、Ｂ（ｘ２ ，ｙ２ ）．代入点 Ａ 的坐
标
得
烄ｙ１ 烅 烆ｙ１
＝２ｘ１２ －２ｘ１ －１， ＝－５ｘ２１ ＋２ｘ１ ＋３．
① ②
①×５＋②×２ 得 ７ｙ１ ＝－６ｘ１ ＋１，即 ６ｘ１ ＋７ｙ１ －１
＝０．同理得 ６ｘ２ ＋７ｙ２ －１＝０．
所以，两交点 Ａ、Ｂ 都在直线６ｘ＋７ｙ－１＝０ 上，
（｜ｘ－３１｜＋｜ｘ－２ ０１１１｜）＋ …
（※）
其中共有（１＋２＋３＋ … ＋２ ０１１）÷２＝５０３×２ ０１１
解法２ 设等差数列｛ａｎ｝的公差为ｄ，则３＝ａ７ ＝ ａ３ ＋４ｄ＝－１３＋４ｄ，解得ｄ＝４＞０，则通项
ａｎ＝ａ３ ＋（ｎ－３）ｄ＝４ｎ－２５． 令 ａｎ ＝４ｎ－２５＜０，得 正 整 数 ｎ≤６，则
ａ１ ＜ａ２ ＜…＜ａ５ ＜ａ６ ＜０＜ａ７ ＜…， Ｓ１ ＞Ｓ２ ＞…＞Ｓ５ ＞Ｓ６ ＜Ｓ７ ＜Ｓ８ ＜…． 所以，数列Ｓ１ ，Ｓ２ ，…中的第 ６ 项最小，最小值为

2011年普通高等学校招生全国统一考试数学（文）（北京卷） 本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题 共40分）一、 选择题共8小题，每小题5分，共40分。

在每小题列出四个选项中，选出符合题目要求的一项。

（1） 已知全集U=R ，集合{}21P x x =∣≤，那么U P =ð(A)(,1-∞-) (B)(1,+∞) (C)（-1，1) (D)()()11-∞,-,+∞（2）复数212i i-=+ (A)i (B )i - (C)4355i -- (D)4355i -+ （3）如果1122log log 0x y <<，那么（A ）1y x << (B)1x y << (C)1x y << (D)1y x <<（4）若p 是真命题，q 是假命题，则（A ）p q ∧是真命题 (B)p q ∨是假命题题 (C)p ⌝是真命题 (D)q ⌝是真命（5）某四棱锥的三视图如图所示，该四棱锥的表面积是 (A)32(B)16+(C)48(D)16+（6）执行如图所示的程序框图，若输入A 的值为2，则输出的P 值为(A)2(B)3(C)4(D)5（7）某车间分批生产某种产品，每批的生产准备费用为800元。

若每批生产x 件，则平均仓储时间为8x 天，且每件产品每天的仓储费用为1元。

为使平均到每件产品的生产准备费用与仓储费用之和最小，每批应生产产品（A ）60件 (B)80件 （C ）100件 （D ）120件（8）已知点()()0,2,2,0A B 。

若点C 在函数2y x =的图象上，则使得ABC 的面积为2的点C 的个数为（A ）4 (B)3 (C)2 (D)1第二部分（非选择题 共110分）二、填空题共6小题，每小题5分，共30分。

（9）在ABC 中，若15,,sin 43b B A π=∠==，则a = . （10）已知双曲线2221(0)y x b b-=>的一条渐近线的方程为2y x =，则b = .（11）已知向量),(01),(a b c k ==-=2a b -与c ，共线，则k = .（12）在等比数列{}n a 中，若141,4,2a a ==则公比q = ； 12n a a a ++⋯+= .数 若关于x 的方程()f x k = 有两个不同的实（13）已知函根，则实数k 的取值范围是 . （14）设(0,0),(4,0),(4,3),(,3)(A B C t D t t +∈R )。

２ 即方程ｘ ｘ＋ ｘ）＝ｘ ＋ｐ ｆ（ ｑ－ｘ ０ 也只有一根 ， ０＝ ２ ２ ， ， 只有一根 又 ０ ∴ｐ －４ ｘ ｑ＋４ ｐ －４ ｑ ＝ ０， ０ ＝０ ２ ， 故 ｘ ＋ｐ 则 ∴ｘ ｘ ＋ｑ ＝ ０ 只有一根 ｘ ＝ ０， ０ ＝０
Ｇ（
ｘ １ ＋ｘ ２ ＋ｘ ３ ， ３
ｙ １ ＋ｙ ２ ＋ｙ ３ ）＝ Ｇ（ ） ， 而 ０， ０ ３ ） ， 故 Ｂ Ｃ 的外心 为 Ｏ（ ０， ０ △Ａ ， 为正三角形 Ａ Ｂ Ｃ △
０．
２ ２ 从而 ４ ｘ ４ ｘ ｐ －４ ｑ）＜ ０， ｐ － １ ＝－ （ ２ ≤－ （ ， 故ｘ ４ ｘ ． ｑ）＜ ０， １ ＜０ ２ ＜０ 因此 ， ｘ ｘ ． ｐ ＝－ （ ｑ ＝ｘ １ ＋ｘ ２） １ ２ ＞０ ＞ ０， ， ， 综合以上情况可得 ： 问题得证 ． ｐ ≥ ０ｑ ≥ ０ 点评 此题研究的其实是复合方程问题 ， 一 般解决的方法 是 代 数 法 ， 此法对恒等变形的要求 还有数 形 结 合 的 思 想 方 法 也 是 解 决 这 类 题 较高 ， 目的很好工具 ， 有时更显 得 形 象 直 观 ． 在历年的名 这种 题 型 出 现 比 较 多 ， 以下两 校自主招生试题中 ， 例供同学们参考 ： （ 已知 １． ２ ０ ０ ８年上海交通大学自主招生试题 ） （ ） ， 函数 ｆ（ 且ｆ（ ｘ） ｘ２ ＋ ｂ ｘ＋ ｃ ａ ≠０ ｘ） ＝ａ ＝ｘ 无 ］＝ ｘ 是否有实数根 ？ 实根 ， 试判断 ｆ［ 证明你 ｘ） ｆ（
２ ａ ， ） ， 设切线与 ｘ 轴的交点为 Ｑ ， 则得 Ｑ（ ０ ｘ ０ ２ ａ ｃ＋ ２ Ｆ１Ｑ ｘ ｃ ｘ０ ＋ａ ｅ ｘ０ ＋ａ ０ ∴ ＝ ２ ＝ ２ ＝ Ｆ２Ｑ ｅ ｘ０ －ａ ａ ｃ ｘ０ －ａ ｃ－ ｘ ０ Ｐ Ｆ１ ， ＝ Ｐ Ｆ２ 又由三角形内角平分线定理逆定理知 ， Ｐ Ｑ平

2011 年普通高等学校招生全国统一考试 数学（文）（北京卷）
本试卷共 5 页，150 分。考试时长 120 分钟。考生务必将答案答在答题卡上，在试卷上作答无 效。考试结束后，将本试卷和答题卡一并交回。
第一部分（选择题 共 40 分）
一、选择题共 8 小题，每小题 5 分，共 40 分。在每小题列出四个选项中，选出符合题目要求的一项。
55
(D) 4 3 i 55
【解析】： i 2 1 2i
(i 2)(1 2i) (1 2i)(1 2i)
i 2i2 2 4i 1 4i2
i 2(1) 2 1 4(1)
4i
i
，选
A。
（3）如果 log 1 x log 1 y 0 ，那么 (
2
2
（A） y x 1 (B) x y 1
（6）执行如图所示的程序框图，若输入 A 的值为 2，则输出的 P 值为( )
(A)2
(B)3 (C)4 (D)5
【答案】C
第 1页 （共 7页）
【解析】执行三次循环，S 1 A 2 成立， p 11 2 ，S 1 1 1 1 3 ，S 3 A 2
P 22
2
成立， p 2 1 3 ， S 3 1 3 1 11 ， S 11 A 2 成立， p 3 1 4
y
2x ，则 b
.
【答案】2
第 2页 （共 7页）
【解析】：由
x2
y2 b2
1得渐近线的方程为 x2
y2 b2
0y
bx
即
y
bx ，由一条渐近线的方程
为 y 2x 得b 2
（11）已知向量 a ( 3,1),b (0 1), c (k, 3) 。若 a 2b 与 c ，共线，则 k =

2011年“北约”13校联考自主招生数学试题2012年北约自主招生数学试题1、求x 的取值范围使得12)(-+++=x x x x f 是增函数；2、求1210272611=+-+++-+x x x x 的实数根的个数；3、已知0)2)(2(22=+-+-n x x m x x 的4个根组成首项为41的等差数列，求n m -；4、如果锐角ABC ∆的外接圆的圆心为O ，求O 到三角形三边的距离之比；5、已知点)0,2(),0,2(B A -，若点C 是圆0222=+-y x x 上的动点，求ABC ∆面积的最小值。

6、在2012,,2,1Λ中取一组数，使得任意两数之和不能被其差整除，最多能取多少个数？7、求使得a x x x x =-3sin sin 2sin 4sin 在),0[π有唯一解的a ； 8、求证：若圆内接五边形的每个角都相等，则它为正五边形；9、求证：对于任意的正整数n ，n )21(+必可表示成1-+s s 的形式，其中+∈N s2012年自主招生北约联考数学试题解答2013年北约自主招生数学试题解析12312为两根的有理系数多项式的次数最小是多少？解析：显然，多项式23()(2)(1)2f x x x ⎡⎤=---⎣⎦2和312-于是知，2和312为两根的有理系数多项式的次数的最小可能值不大于5. 若存在一个次数不超过4的有理系数多项式432()g x ax bx cx dx e =++++，其两根分别为和1,,,,a b c d e不全为0，则：420(42)(2020a c eg a c e b db d++=⎧=++++=⇒⎨+=⎩(1(7)(232(630g a b c d e a b c d a b c=-+----+++++702320a b c d ea b c d+---=⎧⇒⎨+++=⎩即方程组：420(1)20(2)70(3)2320(4)630(5)a c eb da b c d ea b c da b c++=⎧⎪+=⎪⎪+---=⎨⎪+++=⎪++=⎪⎩，有非0有理数解.由（1）+（3）得：110a b c d++-=（6）由（6）+（2）得：1130a b c++=（7）由（6）+（4）得：13430a b c++=（8）由（7）-（5）得：0a=，代入（7）、（8）得：0b c==，代入（1）、（2）知：0d e==.于是知0a b c d e=====，与,,,,a b c d e不全为0矛盾.所以不存在一个次数不超过4的有理系数多项式()g x和1-和1为两根的有理系数多项式的次数最小为5.2．在66⨯的表中停放3辆完全相同的红色车和3辆完全相同的黑色车，每一行每一列只有一辆车，每辆车占一格，共有几种停放方法？解析：先从6行中选取3行停放红色车，有36C种选择.最上面一行的红色车位置有6种选择；最上面一行的红色车位置选定后，中间一行的红色车位置有5种选择；上面两行的红色车位置选定后，最下面一行的红色车位置有4种选择。

5
答案： 1、 不妨设角 ADC 为 a,那么角 ABC=π-a。 由余弦定理可得 AC=根号（9+16-24cosa)=根号(1+4+4cosa) 从而可解出 cosa=5/7.即有 sina=2(根号 6)/7. 代入 cosa=5/7,可得 AC=根号（55/7). 所以圆的半径就是 AC/2sina. 2、设 13=a1+md,25=a1+nd,41=a1+kd. 那么我们可得 a1+(m+499(k+m-2n))d=2009. 而实际上这道题是有漏洞的，因为 (m+499(k+m-2n))可能是负的，也就是当这是递减的等差数列的时候，那么 2009 就不在这个 数列中了。 3、 挺简单，设 a=tanx+（根 3）,b=cotx+(根号 3）,假设均为有理数。 那么由(a-（根号 3） ） （b-（根号 3） ）=1 可得（a+b）根号 3=ab+2.若 a+b 非零，除过来就矛盾了。 所以必有 a+b=0，此时 ab+2 也是 0. 显然与 a，b 是有理数矛盾。 4、b=0 的时候可知得有|a|≤1.,此时 a+b≤1.下面考虑 b 不等于 0 的情况。 代入+1 和-1 后得出的式子可以化成|a|≤b+1.....(1)（必有 b≥-1) 对称轴的位置是 x=-a/4b.当对称轴在[-1,1]外的时候 那么 1≤|-a/4b|≤(b+1)/4|b|. 分类讨论后就可以得出 b≤1/3.此时 a+b≤b+1+b≤5/3. 若对称轴在[-1,1]内，则可得 a^2≤8（b-b^2)......(2) 这里注意到(b+1)^2-8(b-b^2)=(3b-1)^2≥0.故只需要(2)式成立,就必有 (1)式也成立。此时用柯西不等式 (a+b-1/2)^2≤（a^2+8(b-1/2)^2)(1+1/8)≤9/4 那么就有了 a+b≤2.等号成立的充要条件是 a=4/3,b=2/3,易验证这是成立的. 比较三种情况，显然 2 是 a+b 的最大值， 5、设优秀有 a 人，及格 b 人，不及格 c 人。 则 a+b+c=333 ① 6a+4b+0c≤1000（这里都取各层次里的最少人，故用小于等于） 即 6a+4b≤1000 即 3a+2b≤500 由①得 2a+2b=666-2c 即 a+666-2c≤500 即 a+166≤2c 若 a≥167 则这 167 人至少共解出 167*6=1002 道题，矛盾 故 a≤166 故 a+166≤166+166≤2c 即 c≥166 所以 c≥166≥a 即不及格得人数大于等于优秀的人数

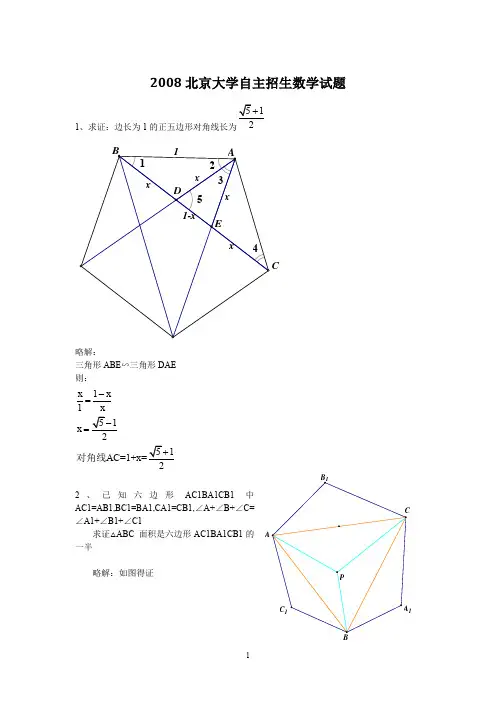
2014年北京大学自主招生数学试题1. 圆心角为3π的扇形面积为6π，求它围成圆锥的表面积. 2. 将10个人分成3组，一组4人，两组每组3人，共有几种分法. 3. 2()2()(),(1)1,(4)733a b f a f b f f f ++===,求()2014f . 4.2()lg(2)f x x ax a =-+的值域为R ，求a 的取值范围.5. 已知1x y +=-，且,x y 都为负实数，求1xy xy+的取值范围. 6. 22()arctan14x f x C x +=+-在11,44⎛⎫- ⎪⎝⎭上为奇函数，求C 的值. 一、求证：tan3Q ∉二、已知实系数二次函数()f x 与()g x ，()()f x g x =和()()30f x g x +=有两重根，()f x 有两相异实根，求证：()g x 没有实根.三、1213,a a a 是等差数列，{}113i j k M a a a i j k =++≤<<≤，问：7160,,23是否同在M 中，并证明你的结论.四、()01,2,,i x i n >=，且11n i i x ==∏，求证1)1)nn i i x =≥∏.答案1．π7； 2．2100； 3．4027)2024(12)(=⇒-=f x x f ； 4．1 00≥≤⇒≥∆a or a ；5．⎪⎭⎫⎢⎣⎡+∞,417；6．2arctan 0)0(-=⇒=C f 一、求证：Q ∉︒3tan解：若Q aab Q a ∈-=︒=⇒∈=︒2126tan 3tan ，Q ab b a c ∈-+=︒=⇒19tan Q bc cb d ∈-+=︒=⇒115tan 52518tan 41518sin 2-=︒⇒-=︒ 于是Q d d ∈-=⇒=-=︒233215tan ，从而矛盾。

二．实系数二次函数)(),(x g x f ，)()(x g x f =和0)()(3=+x g x f 有两重根，)(x f 有两相异根，求证：)(x g 无实数根。

自主招生数学试题及答案一、选择题（每题5分，共30分）1. 下列哪个选项不是正整数？A. 0B. 1C. 2D. 3答案：A2. 如果函数\( f(x) = x^2 - 4x + 3 \)，那么\( f(2) \)的值是多少？A. -1B. 1C. 3D. 5答案：A3. 圆的面积公式是？A. \( \pi r^2 \)B. \( 2\pi r \)C. \( \pi d \)D. \( \pi r \)答案：A4. 已知\( \sin(\alpha) = \frac{3}{5} \)，且\( \alpha \)在第一象限，求\( \cos(\alpha) \)的值。

A. \( \frac{4}{5} \)B. \( \frac{1}{5} \)C. \( -\frac{4}{5} \)D. \( -\frac{1}{5} \)答案：A5. 以下哪个数是无理数？A. \( \sqrt{2} \)B. 1.5C. 0.333...D. 1答案：A6. 一个等差数列的首项是3，公差是2，第10项是多少？A. 23B. 21C. 19D. 17答案：B二、填空题（每题3分，共15分）1. 一个直角三角形的两条直角边分别为3和4，斜边的长度是______。

答案：52. 函数\( g(x) = 2x - 1 \)的反函数是______。

答案：\( g^{-1}(x) = \frac{x + 1}{2} \)3. 一个数的平方根是4，这个数是______。

答案：164. 已知\( \tan(\theta) = 3 \)，求\( \sin(\theta) \)的值（假设\( \theta \)在第一象限）。

答案：\( \frac{3\sqrt{10}}{10} \)5. 一个等比数列的首项是2，公比是3，第5项是多少？答案：162三、解答题（每题25分，共50分）1. 解不等式：\( |x - 5| < 4 \)。

2011年北约自主招生数学试题1、已知平行四边形两边长分别是3和5，一条对角线是6．求另一条对角线的长度．2、求过抛物线22221,523y x x y x x =--=-++两交点的直线方程．3、等差数列1237,,13, 3..n a a a a n S ⋅⋅⋅=-=满足这个数列的前项和为数列12,⋅⋅⋅S S 中哪一项最小？并求出这个最小值．4、在2,60.ABC a b c C ∆+≥∠≤中，如果证明5、是否存在四个正实数，它们两两乘积分别是2，3，5，6，10，16．6、设12C C 和是平面上两个不重合的固定圆周．设C 是该平面上的一个动圆，它与12C C 和均相 切．问：C 的圆心轨迹是何种曲线？证明你的结论．7、求12120111.x x x -+-+⋅⋅⋅+-的最小值2【参考答案】1、解答：设平行四边形为ABCD ，且6,3,5===AC BC AB ，易得：51cos -=∠ABC ，所以151cos =∠BAC ，24,321515322592==⨯⨯⨯-+=BD BD ． 2、解答：设两条抛物线额交点为),(),,(2211y x B y x A ，联立两条抛物线的方程⎩⎨⎧++-=--=32512222x x y x x y ，消去2x 得：167+-=x y ，B A ,两点的坐标均满足这个方程，所以直线AB 的方程为0176=-+y x ．3、解答：方法一：因为公差4437=-=a a d ，所以03,01,21761>=<-=-=a a a ，所以6S 最小，最小值666-=S ； 方法二：8234232322222-⎪⎭⎫ ⎝⎛-=-=n n n S n ，当6=n 时，n S 的最小值为666-=S ． 4、解答：方法一、在ABC ∆中，由余弦定理得： 21848233222cos 22222222=≥-+=⎪⎭⎫ ⎝⎛+-+≥-+=ab ab ab ab b a ab b a b a ab c b a C ，因为函数x y cos =在),0(π上单调递减，所以3π≤C ． 方法二、依题意得：2cos 2sin 42cos 2sin 2sin 2sin sin B A B A B A B A C B A ++≥-+⇔≥+， 212cos ≤+B A ，因为函数x y cos =在),0(π上单调递减，所以33232πππ≤⇒≥+⇒≥+C B A B A ． 5、解答：假设存在满足题意的四个正实数d c b a ,,,，且假定d c b a <<<<0，依题意得：16,10,3,2====cd bd ac ab ，由前两个式子得32=c b ，由后两个式子得85=c b ，矛盾，所以不存在满足题意的四个数．6、解答：设⊙1C 的半径为1r ，⊙2C 的半径为2r ，⊙C 的半径为r ，且假定21r r ≥．（1）当21r r =时，①若⊙1C 与⊙2C 外离，当⊙C 与⊙1C 、⊙2C 均外切或均内切时，点C 的轨迹是21C C 的中垂线；当⊙C 与⊙1C 、⊙2C 一个外切一个内切时，点C 的轨迹是以21,C C 为焦点，实轴长为21r r +的双曲线； ②若⊙1C 与⊙2C 外切，当⊙C 与⊙1C 、⊙2C 均外切或均内切时，点C 的轨迹是21C C 的中垂线（除去21C C 的中点）；当⊙C 与⊙1C 、⊙2C 一个外切一个内切时，点C 的轨迹是直线21C C （除去21C C 的中点）； ③若⊙1C 与⊙2C 相交，此时⊙C 必与⊙1C 、⊙2C 均外切或均内切，点C 的轨迹是两圆公共弦在圆外部分的两条射线．（2）当21r r >时，①若⊙1C 与⊙2C 外离，当⊙C 与⊙1C 、⊙2C 均外切或均内切时，点C 的轨迹是以21,C C 为焦点，实轴长为21r r -的双曲线；当⊙C 与⊙1C 、⊙2C 一个外切一个内切时，点C 的轨迹是以21,C C 为焦点，实轴长为21r r +的双曲线；②若⊙1C 与⊙2C 外切，当⊙C 与⊙1C 、⊙2C 均外切或均内切时，点C 的轨迹是以21,C C 为焦点，实轴长为21r r -的双曲线（除去⊙1C 与⊙2C 的切点）；当⊙C 与⊙1C 、⊙2C 一个外切一个内切时，点C 的轨迹是直线21C C （除去点21,C C 及⊙1C 与⊙2C 的切点这三个点）；③若⊙1C 与⊙2C 相交，当⊙C 与⊙1C 、⊙2C 均外切或均内切时，点C 的轨迹是以21,C C 为焦点，实轴长为21r r -的双曲线（除去⊙1C 与⊙2C 的两个交点）；当⊙C 与⊙1C 、⊙2C 一个外切一个内切时，点C 的轨迹是以21,C C 为焦点，长轴长为21r r +的椭圆（除去⊙1C 与⊙2C 的两个交点）；④若⊙1C 与⊙2C 内切，当⊙C 与⊙1C 、⊙2C 均外切或均内切时，点C 的轨迹是直线21C C （除去⊙1C 与⊙2C 的切点）；当⊙C 与⊙1C 、⊙2C 一个外切一个内切时，点C 的轨迹是以21,C C 为焦点，长轴长为21r r +的椭圆（除去⊙1C 与⊙2C 的两个切点）；⑤若⊙1C 内含⊙2C ，且不同心，当⊙C 与⊙1C 内切、与⊙2C 外切时，点C 的轨迹是以21,C C 为焦点，长轴长为21r r +的椭圆；当⊙C 与⊙1C 、⊙2C 均内切时，点C 的轨迹是以21,C C 为焦点，长轴长为21r r -的椭圆；⑥若⊙1C 内含⊙2C ，且同心，当⊙C 与⊙1C 内切、与⊙2C 外切时，点C 的轨迹是以1C 为圆心，半径为221r r +的圆；当⊙C 与⊙1C 、⊙2C 均内切时，点C 的轨迹是以1C 为圆心，半径为221r r -的圆． 7、解答：首先设12n a a a ≤≤≤，12()||||||n f x x a x a x a =-+-++-．由绝对值的最高理论知， n 为奇数时，当12n x a +=时，()f x 有最小值；n 为偶数时，当122,n n x a a +⎡⎤∈⎢⎥⎣⎦任何值时，()f x 有最小值． 于是分解之，20111111111()|1|||||||||||||||2233320112011f x x x x x x x x x =-+-+-+-+-+-++-++-个， 共有： 201220111+2+2011==20230662⨯个断点（包括多重）． 设123456111,,,23a a a a a a ======202306612011a =． 因为202306610115332=． 现在求1011533a 和1011534a 的值．设10115331a t =，则121011533t +++≥， 1211011533t +++-<．可得1422t =．且1011533101153411422a a ==，故11422x =时，()f x 的值最小．111111491()112114221423120111832.142214221422142214231422711f =-+-⨯++-⨯+⨯-++⨯-=。

Ｃ
图１
Ａ Ｂ于 点Ｄ、Ｅ．
～ ～ ～ ～ ～ ～ ～ ～ ～ ～ ～ ～ ～ ～ ～ ～ ～ ～ ～ ～ ～ ～ ～ ～ ～
２ ． ４
０＜２＜ ３ ２
在 Ｒｔ ＡＣＭ Ｐ 中， ＣＰＭ ＝ ９ 。 ／ ０
・ ．
（Ｊ。 △ＡＭ Ｅ ∽ ／ＥＮ ， ３ ・ ’ ＿ ｋ
．
一
‘ｓｎ／ＣＭ Ｐ － Ｃ Ｐ ｉ
．
． １＝ ＺＢ Ａ Ｏ ．。 Ｏ ＡＣ ＝ ＯＣ Ａ ， ． ． ． ’
’ ．
ＣＳ 一ｃｓ ￣＋２ ） Ｏ ２ ｏ（ ４
２
・ ． ．
ＡＯ ＝ ＯＣ ，ＡＥ ＝ Ｏ Ｅ ， Ａ ＡＯ Ｅ ￣ ／ Ａ ＣＯ ＇ ， ＡＣ ＝ 丽Ｃ Ｏ （ ＝ ） Ａ Ｅ
…
．
・
・
．
①
’ ・
Ｙ ０ 一 ５ 盖
函数关 系式 为 ＝ 一２ ＋５ 定义域为 １ ０
，
解得 ｋ ＝０舍去）ｋ ＝８ ｌ （ ，２ ．
。 ． ．
・
．
．
综 卜所 述 ：ＡＰ 的 长 为 ２ ２或 ４ ． ２
２１ 年第 ９ ０１ 期
数 学教 学
９３ －９
《 ｓ ＝ｓ （ ） ｓ （＋ ． ＝ ｉ ２ ｎ ｉ ＋ ・ｉ ， ）…⑤ ｎ ｎｙ 由于ｓ （ ） ｓ （ ） ｉ（ ） ｉ ￣＋ ・ｉ ￣＋ ＝ｓ ￣＋ ・ ｎ ｎ ｎ ｓ（ ｉ ￣一３ ） ｉ（ ） ｓ （￣＋ ＝ ｎ 一 ＝ｓ ￣＋ ・ｉ ３ ） ｎ ｎ
一
发现这个问题有多种解法． 如图 １ 已知 △ 中， ） ， Ｂ （是三角形 内一点， ＝ 满 足： ＢＡＯ ＝ Ｃ ／ ＡＯ ＝ Ｃ ＢＯ ＝ （， ＝ ） 求证： △ＡＢ Ｃ三边成等比数列． 法一： 如图２ 过点Ｏ作 Ｃ的平行线交Ｂ ， 、

绝密★使用完毕前2011年普通高等学校招生全国统一考试数学（理）（北京卷）本试卷共5页，150分。

考试时间长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题 共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）已知集合P=｛x ︱x 2≤1｝,M=｛a ｝.若P ∪M=P,则a 的取值范围是（A ）(-∞, -1] （B ）[1, +∞） （C ）[-1，1] （D ）（-∞，-1] ∪[1，+∞）（2）复数212i i-=+ （A ）i （B ）-i （C ）4355i -- （D ）4355i -+ （3）在极坐标系中，圆ρ=-2sin θ的圆心的极坐标系是 (A) (1,)2π (B) (1,)2π- (C) (1,0) (D)(1，π)（4）执行如图所示的程序框图，输出的s 值为（A ）-3（B ）-12（C ）13（D ）2（5）如图，AD ，AE ，BC 分别与圆O 切于点D ，E ，F ，延长AF 与圆O 交于另一点G 。

给出下列三个结论：○1AD+AE=AB+BC+CA ；○2AF ·AG=AD ·AE③△AFB ～△ADG其中正确结论的序号是（A ）①② （B ）②③（C ）①③ （D ）①②③ （6）根据统计，一名工作组装第4件某产品所用的时间（单位：分钟）为（A ，C 为常数）。

已知工人组装第4件产品用时30分钟，组装第A 件产品用时15分钟，那么C 和A 的值分别是（A ）75，25 （B ）75，16 （C ）60，25 （D ）60，16(7)某四面体的三视图如图所示，该四面体四个面的面积中，最大的是(A) 8 (B) 62 (C)10 (D) 82（8）设()0,0A ,()4,0B ，()4,4C t +,()(),4D t t R ∈.记()N t 为平行四边形ABCD 内部（不含边界）的整点的个数，其中整点是指横、纵坐标都是整数的点，则函数()N t 的值域为（A ）{}9,10,11 （B ）{}9,10,12（C ）{}9,11,12 （D ）{}10,11,12第二部分 （非选择题 共110分）二、填空题共6小题，每小题5分，共30分。

２ｓ＝口ｌ＋ａ２＋口３＋ｂｌ＋ｂ２＋ｂ３，
形
＝
舞ＡＣＢＡＢＡ慧ＣＢ麓ＡＣ ＝／缓二Ｃ
。，
。／
ｌ／
Ｄｋ
：：：．？日 ＼、Ｅ。．・。
＼Ｉ，・’
，‘１
．。．
ＢＡ 。，
。
口２丁，６２丁，
．ａｌ一口２
ｂＩ—ｂ２
Ｂ Ａ ＋￡ Ａ Ｂ Ｃ ＋￡Ｃ ．，二 Ｃ
即证｛一（口Ｉ＋口２＋ｂＩ＋６２）一（口ｌ＋ｄ２＋口，＋
ａ 口ｌ ａ 口２
２丁＋口，
２丁一口＇
【百１８９】＋１＝１３分，而北方最高分的最大值为６＋ｎ
万方数据
１４
中’？善ｉ：．７（２００ｓ年第２期・高中版）
南方球队内部比赛总得分ＣⅢ２
，１２
・解题研究・
＝１３６，
一ｌ＝１１分＜１３分，
．・．
冠军在南方队
北方球队内部比赛总得分ｃ２＝２８，
北方胜南方得分＝３０—２８＝２， 北方球队最高得分＝７＋２＝９， 因为９×１７＝１５３＜２７０， 所以南方球队中至少有一支得分超过９分． 冠军在南方球队中．综上所述，冠军是一支南方 球队． 点评这道试题要注意突破口的选择，也需要 耐心和比较强的推理、分析能力． ５．（理科）０一ｘｙｚ坐标系内ｘｏｙ平面系内０≤，，≤ ２一石２绕），轴旋转一周构成一个不透光立体在点 （１，０，１）设置一光源，在ｘｏｙ平面内有一以原点为圆 心的圆ｃ被光照到的长度为２霄，求曲线Ｃ上未被照 到的长度．
ｃ：＋。＋ｎ（肛＋９）≥召，ｃ：≤Ａ，
即３ｎ２—２２ｎ一３６。＜０．
‘．・
’Ｂ＝９Ａ，
．・．ｃ：＋９＋ｎ（，ｌ＋９）≥Ｂ＝９Ａ１＞９ｃ：，
（１）
，’２
又总分为乞Ⅲ有１０Ｉ乞小钴厶（１）得厅＝６或８．

2011年普通高等学校招生全国统一考试数学（文）（卷） 本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题 共40分）一、 选择题共8小题，每小题5分，共40分。

在每小题列出四个选项中，选出符合题目要求的一项。

（1） 已知全集U=R ，集合{}21P x x =∣≤，那么U P =(A)(,1-∞-) (B)(1,+∞) (C)（-1，1) (D)()()11-∞,-,+∞ （2）复数212i i-=+ (A)i (B )i - (C)4355i -- (D)4355i -+ （3）如果1122log log 0x y <<，那么（A ）1y x << (B)1x y << (C)1x y << (D)1y x <<（4）若p 是真命题，q 是假命题，则（A ）p q ∧是真命题 (B)p q ∨是假命题题 (C)p ⌝是真命题 (D)q ⌝是真命（5）某四棱锥的三视图如图所示，该四棱锥的表面积是 (A)32(B)16+162(C)48(D)16322+（6）执行如图所示的程序框图，若输入A 的值为2，则输出的P 值为(A)2(B)3(C)4(D)5（7）某车间分批生产某种产品，每批的生产准备费用为800元。

若每批生产x 件，则平均仓储时间为8x 天，且每件产品每天的仓储费用为1元。

为使平均到每件产品的生产准备费用与仓储费用之和最小，每批应生产产品（A ）60件 (B)80件 （C ）100件 （D ）120件（8）已知点()()0,2,2,0A B 。

若点C 在函数2y x =的图象上，则使得ABC 的面积为2的点C 的个数为（A ）4 (B)3 (C)2 (D)1第二部分（非选择题 共110分）二、填空题共6小题，每小题5分，共30分。

（9）在ABC 中，若15,,sin 43b B A π=∠==，则a =. （10）已知双曲线2221(0)y x b b-=>的一条渐近线的方程为2y x =，则b =. （11）已知向量(3,1),(01),(,3)a b c k ==-=。