非线性动力学练习题
- 格式:doc
- 大小:166.50 KB
- 文档页数:6



练习题1:质点运动学和动力学一、判断题(每题2分,共20分)1.物体做匀速圆周运动,由于速率大小不变,所以加速度为零。
(×)2.质点的位置矢量方向不变,质点一定作直线运动。
(√)3. 物体匀速率运动,加速度必定为零。
( × )4. 对于一个运动的质点,具有恒定速率,但可能有变化的速度。
( √ )5. 物体作曲线运动时,一定有加速度,加速度的法向分量一定不等于零。
( √ )6.质点运动经一闭合路径,保守力对质点作的功为零。
(√)7.一个系统如果只受到保守内力的作用,此系统机械能守恒。
(√)8.质量为 M 的木块静止在光滑水平面上,一质量为 m的子弹水平地射入木块后又穿出木块,则在子弹射穿木块的过程中,子弹和木块组成的系统动量守恒。
(√)9. 子弹分别打在固定的软和硬的两块木块内,则木块受到的冲量相同,但硬木块的平均作用力大。
(√)10. 一对内力作功之和必为零。
(×)二、选择题(每题2分,共20分)1.当物体的加速度不为零时,则:( B )(A)对该物体必须做功;(B)对该物体必须施力,且合力不会为零;(C)它的速率必然增大;(D)它的动能必然增大。
2. 质点在O−xy平面内运动,其运动方程为r⃗=2ti⃗+(4−t2)j⃗ (SI),则当t=2S时,质点的速度是 ( A )(A) (2i ⃗−4j ⃗)m s ⁄ (B) (−2i ⃗)m s ⁄ (C) (−4j ⃗)m s ⁄ (D) (2i ⃗+4j ⃗)m s ⁄3、下列几种运动形式,哪一种运动是加速度矢量a ⃗⃗保持不变的运动?( C )。
A 、单摆运动;B 、匀速度圆周运动;C 、抛体运动;D 、以上三种运动都是a ⃗⃗保持不变的运动。
4. 一个质点在做圆周运动时,则有( B )(A) 切向加速度一定改变,法向加速度也改变;(B) 切向加速度可能不变,法向加速度一定改变;(C) 切向加速度可能不变,法向加速度不变;(D) 切向加速度一定改变,法向加速度不变。

(2009江苏高考)航模兴趣小组设计出一架遥控飞行器,其质量m =2kg,动力系统提供的恒定升力F =28N。
试飞时,飞行器从地面由静止开始竖直上升。
设飞行器飞行时所受的阻力大小不变,g取10m/s2o(1)第一次试飞,飞行器飞行5 = 8s时到达高度H = 64m。
求飞行器所阻力f的大小(2)第二次试飞,飞行器飞行0 = 6s时遥控器出现故障,飞行器立即失去升力,求飞行器能达到的最人高度h(3)为了使飞行器不致坠落到地面,求E行器从开始下落到恢复升力的最长时间【答案】(1)第一次飞行中,设加速度为如。
飞行器做匀加速运动,H由牛顿第二定律F - mg - / = ma x解得f = 4N(2)第二次飞行中,设飞行器失去升力时的速度为耳,上升的高度为S]飞行器匀加速运动* =扌如£设失去升力后的速度为血,上升的高度为S2 由牛顿第二定律mg + / = ma2^1 = a1^2解得/i = S] + S2 = 42m(3)设失去升力下降阶段加速度为。
3;恢复升力后加速度为。
4,恢复升力时速度为巾由牛顿第二定律mg - f = ma3F + f _ mg = ma4且±+± = h2。
3 2a4“3 = a3^3解得S =(或2.1s)如图所示,质量为m的物体A,从底线/为定值的斜面顶点从静止开始向下滑动,已知物体与斜面的动摩擦因数为“。
问Q角为何值吋,下滑的时I'可最短,等于多少?【答案】由受力分析可知,物体的加速度a = g(sina - /^cosa),物体下滑的位移s = l/cosa0物体做匀加速运动,由运动学公式s=^at2可得41g(sin2a —“cos2a—“)有三角函数知识,当a = |arctan 时,严最小,即时闫最短。
(2009山东高考)某物体做直线运动的st 图象如图甲所示,据此判断图乙(F 表示物最短吋间为tmin = I 机 yj g(Jl+“2-“)(2011北京卷)“蹦极”就是跳跃者把一端固定的 长弹性绳绑在踝关节等处,从儿十米高处跳下的一种极限 运动。


非线性物理试题及答案一、单项选择题(每题2分,共10分)1. 非线性光学中,光的二次谐波产生属于:A. 线性效应B. 非线性效应C. 量子效应D. 热效应答案:B2. 以下哪项不是非线性动力学系统的特点?A. 存在混沌现象B. 系统行为对初始条件敏感C. 系统行为可预测D. 存在分叉现象答案:C3. 非线性系统方程中,以下哪项是正确的?A. \( \frac{dx}{dt} = ax \)B. \( \frac{dx}{dt} = ax^2 \)C. \( \frac{dx}{dt} = ax + bx^2 \)D. \( \frac{dx}{dt} = ax + bx^3 \)答案:D4. 非线性系统中,孤立波解是指:A. 波形随时间不变B. 波形随时间变化C. 波形随空间变化D. 波形随时间和空间变化答案:A5. 非线性物理中,Bose-Einstein凝聚态描述的是:A. 电子气B. 费米子气C. 光子气D. 玻色子气答案:D二、填空题(每题2分,共10分)1. 在非线性光学中,光的____效应可以产生频率为原始光频率两倍的光。
答案:二次谐波2. 非线性动力学系统中的____现象是指系统在某些参数变化时,会出现多种可能的行为模式。
答案:分叉3. 非线性系统的方程通常包含____项,这使得系统的行为复杂化。
答案:非线性4. 非线性系统中的____波是一种在传播过程中保持形状不变的波。
答案:孤立5. 在非线性物理中,____凝聚态是一种在低温下,玻色子粒子聚集在最低能态的现象。
答案:Bose-Einstein三、简答题(每题5分,共20分)1. 简述非线性物理中孤子的概念及其物理意义。
答案:孤子是一种在非线性介质中传播的波,它能够保持其形状和速度不变,即使在与其他孤子相遇时也不会发生能量交换。
孤子的物理意义在于它们展示了非线性系统中的局部化波解,这在光学、流体力学等领域有重要的应用。
2. 解释非线性动力学系统中的混沌现象及其特点。


即non-linear 是指输出输入既不是正比例也不是反比例的情形。
如宇宙形成初的混沌状态。
自变量与变量之间不成线性关系,成曲线或抛物线关系或不能定量,这种关系叫非线性关系。
“线性”与“非线性”,常用于区别函数y = f (x)对自变量x的依赖关系。
线性函数即一次函数,其图像为一条直线。
其它函数则为非线性函数,其图像不是直线。
线性,指量与量之间按比例、成直线的关系,在空间和时间上代表规则和光滑的运动;而非线性则指不按比例、不成直线的关系,代表不规则的运动和突变。
如问:两个眼睛的视敏度是一个眼睛的几倍?很容易想到的是两倍,可实际是 6-10倍!这就是非线性:1+1不等于2。
非线性关系虽然千变万化,但还是具有某些不同于线性关系的共性。
线性关系是互不相干的独立关系,而非线性则是相互作用,而正是这种相互作用,使得整体不再是简单地等于部分之和,而可能出现不同于"线性叠加"的增益或亏损。
激光的生成就是非线性的!当外加电压较小时,激光器犹如普通电灯,光向四面八方散射;而当外加电压达到某一定值时,会突然出现一种全新现象:受激原子好像听到“向右看齐”的命令,发射出相位和方向都一致的单色光,就是激光。
迄今为止,对非线性的概念、非线性的性质,并没有清晰的、完整的认识,对其哲学意义也没有充分地开掘。
线性:从相互关联的两个角度来界定,其一:叠加原理成立;其二:物理变量间的函数关系是直线,变量间的变化率是恒量。
在明确了线性的含义后,相应地非线性概念就易于界定:其—,“定义非线性算符N(φ)为对一些a、b或φ、ψ不满足L(aφ+bψ)=aL(φ)+bL(ψ)的算符”,即叠加原理不成立,这意味着φ与ψ间存在着耦合,对(aφ+bψ)的*作,等于分别对φ和ψ*作外,再加上对φ与ψ的交叉项(耦合项)的*作,或者φ、ψ是不连续(有突变或断裂)、不可微(有折点)的。
其二,作为等价的另—种表述,我们可以从另一个角度来理解非线性:在用于描述—个系统的一套确定的物理变量中,一个系统的—个变量最初的变化所造成的此变量或其它变量的相应变化是不成比例的,换言之,变量间的变化率不是恒量,函数的斜率在其定义域中有不存在或不相等的地方,概括地说,就是物理变量间的一级增量关系在变量的定义域内是不对称的。

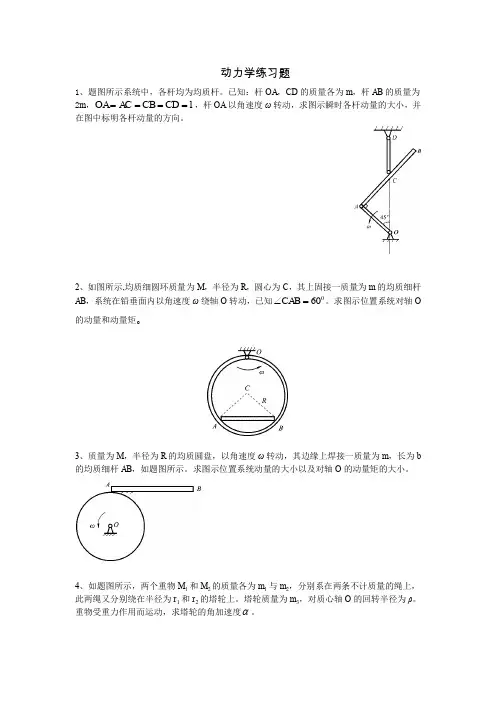
动力学练习题1、题图所示系统中,各杆均为均质杆。
已知:杆OA ,CD 的质量各为m ,杆AB 的质量为2m ,l CD CB AC OA ====,杆OA 以角速度ω转动,求图示瞬时各杆动量的大小,并在图中标明各杆动量的方向。
2、如图所示,均质细圆环质量为M ,半径为R ,圆心为C ,其上固接一质量为m 的均质细杆AB ,系统在铅垂面内以角速度ω绕轴O 转动,已知060=∠CAB 。
求图示位置系统对轴O 的动量和动量矩。
3、质量为M ,半径为R 的均质圆盘,以角速度ω转动,其边缘上焊接一质量为m ,长为b 的均质细杆AB ,如题图所示。
求图示位置系统动量的大小以及对轴O 的动量矩的大小。
4、如题图所示,两个重物M 1和M 2的质量各为m 1与m 2,分别系在两条不计质量的绳上,此两绳又分别绕在半径为r 1和r 2的塔轮上。
塔轮质量为m 3,对质心轴O 的回转半径为ρ。
重物受重力作用而运动,求塔轮的角加速度α。
5、如题图所示的卷扬机,轮B,C的半径分别为R,r,对通过点O1,O2的水平轴的转动惯量分别为J1,J2,物体A重P,在轮C上作用一常转矩M。
试求物体A上升的加速度。
6、在图示机构中,鼓轮A和圆盘B为均质,重量各为P,半径均为R,物体C重为Q,轮A上作用一矩为M的常值力偶,试求此瞬时系统中物块C的加速度及轮A上绳子的拉力。
7、均质圆柱体的质量为m1、半径为R,沿固定水平面作纯滚动;重物B的质量为m2;定滑轮D质量不计;弹簧的弹性系数为k,初始时弹簧长度为其原长L0的一半,系统从静止无初速释放。
试求重物下降h=2L0时的速度和加速度以及水平段绳索拉力。
8、图示机构中,沿斜面纯滚动的圆柱体O'和鼓轮O为均质物体,质量均为m,半径均为R。
绳子不能伸缩,其质量略去不计。
粗糙斜面的倾角为θ,不计滚动摩擦。
如在鼓轮上作用一常力偶M。
求:(1)鼓轮的角加速度;(2)绳索的拉力;(3)轴承O的水平反力。
动力学问题1.一质量为M 的探空气球在匀速下降,若气球所受浮力F 始终保持不变,气球在运动过程中所受阻力仅与速率有关,重力加速度为g .现欲使该气球以同样速率匀速上升,则需从气球吊篮中减少的质量为A.)(2g F M - B.gFM 2-C.g FM -2 D.02.两个分别带有电荷量Q 和+3Q 的相同金属小球(均可视为点电荷),固定在相距为r 的两处,它们间库仑力的大小为F 。
两小球相互接触后将其固定距离变为2r ,则两球间库仑力的大小为A .112FB .34FC .43FD .12F3.用一根长1m的轻质细绳将一副质量为1kg的画框对称悬挂在墙壁上,已知绳能承受的最大张力为10N,为使绳不断裂,画框上两个挂钉的间距最大为(g取210m/s)A.3m2B.2m2C.1m2D.3m44.在无风的情况下,跳伞运动员从水平飞行的飞机上跳伞,下落过程中受到空气阻力,下列描绘下落速度的水平分量大小x v、竖直分量大小y v与时间t的图像,可能正确的是5.如图所示,一块橡皮用细线悬挂于O点,用铅笔靠着线的左侧水平向右匀速移动,运动中始终保持悬线竖直,则橡皮运动的速度(A)大小和方向均不变(B)大小不变,方向改变(C)大小改变,方向不变(D)大小和方向均改变6.如图所示,置于水平地面的三脚架上固定着一质量为m的照相机.三脚架的三根轻质支架等长,与竖直方向均成30 角,则每根支架中承受的压力大小为(A)13mg(B)23mg(C)36mg(D)239mg7.如图所示,石拱桥的正中央有一质量为m 的对称楔形石块,侧面与竖直方向的夹角为α,重力加速度为g ,若接触面间的摩擦力忽略不计,旵石块侧面所受弹力的大小为A .2sin mg αB .2s mgco αC .1tan 2mg αD .1t 2mgco α8.将一只皮球竖直向上抛出,皮球运动时受到空气阻力的大小与速度的大小成正比。
下列描绘皮球在上升过程中加速度大小a与时间t关系的图象,可能正确的是9.如图所示,一夹子夹住木块,在力F 作用下向上提升。
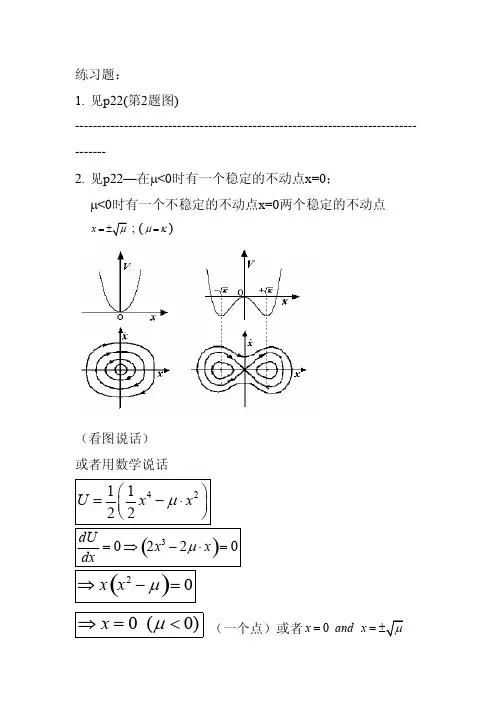
2017-2018学年秋季学期《非线性动力学》课程作业考虑如下非线性动力学系统稳定性:30x x x x δβ+-+= (δ≠0) (1)上式可化为如下二维平面非线性系统:3x yy y x x δβ=⎧⎨=-+-⎩(δ≠0) (2) 容易看到:当0β≤ 时,存在唯一奇点(0,0);当0β> 时,存在三个奇点:(0,0), )(),系统的导算子(雅克比矩阵)为:2013J xβδ⎡⎤=⎢⎥--⎣⎦下面依次分析:1.当0β< 时系统存在唯一奇点(0,0),此时奇点处的导算子为1J βδ⎡⎤=⎢⎥-⎣⎦其特征值为λ=1.1当0δ≥> 时,奇点导算子的特征值:10λ=<,20λ=< 此时,奇点(0,0)是稳定奇点.令1β=- ,3δ= ,分别以(-5,-5),(5,5),(-3,-10),(3,10)为起始点,可以画出四条轨迹组成的相图,如下:由相图可以看到,0δ≥>时 (0,0)为稳定焦点.1.2当0δ≤-< 时,奇点导算子的特征值:10λ=>,20λ=>此时,奇点(0,0)是不稳定奇点.令1β=- ,3δ=- ,以奇点(0,0)附近特定点为初始点可以画出此时的相图,如下:由相图中可以看到,轨迹从起始点(0.1,-0.2)以远离奇点(0,0)的方向螺旋发散,因此当0δ≤-<时,(0,0)是不稳定焦点。
1.3当δ-<<(δ≠0)时,奇点导算子的特征值:2i δλ=-可以看到,在δ-<<δ由负到正,特征值将沿复平面的上方或下方穿过虚轴,即发生Hopf 分叉。
当0δ-<<时,特征值实部恒为正,奇点(0,0)为不稳定奇点. 取1β=- ,1δ=-,以奇点(0,0)附近特定点为初始点可以画出此时的相图:显然,0δ-<<时,奇点(0,0)为不稳定焦点。
当0δ<<(0,0)为稳定奇点. 取1β=- ,1δ=,以(-3,-10)为初始点可以画出此时的相图:由相图可知,0δ<<(0,0)为稳定焦点.综上所述,在β<0的条件下,δ<0时,奇点(0,0)为不稳定焦点,δ>0时,奇点(0,0)为稳定焦点。
六、平衡点的静态分叉1. 分叉概念分叉:当任意小的参数变化使结构不稳定的动力系统相轨迹拓扑结构发生突然的变化,这种变化称为分叉。
结构稳定性:若动力系统受到小扰动后产生的新动力系统与原动力系统拓扑轨道等价,则称此系统具有结构稳定性(1973年由Andronov A A 和Pontryagin L S 首先研究)。
说明:(1)由于动力系统仅仅是物理模型的一个精确的近似,若一个系统是结构不稳定的,则一个小的扰动将显著改变系统的解的结构。
若系动力系统是结构稳定的,则由近似或实验误差造成的小误差可以全然不管,此时,模型系统的解等价或拓扑共轭于实际解;(2)古典动力系统大多是结构不稳定的,如研究气象学的Lorent 系统。
拓扑轨道等价:以同胚变换将一动力系统相轨迹变换为另一动力系统的相轨迹,则这两个动力系统称为拓扑轨道等价。
若稳定焦点拓扑等价于稳定结点;而结点、中心、鞍点之间不是拓扑等价的。
同胚:单值连续且其逆也单值连续的变换。
静态分叉:研究0),(=p u f 解的数目和稳定性随参数的变化。
平衡点静态分叉:研究平衡点的产生(或消失)、时变状态(如周期轨线、同宿或异宿轨线)的出现等,属于局部分叉范畴。
动态分叉:静态分叉之外的分叉,如闭轨分叉。
(1)一维动力系统11),(R P p R U u p u f u⊆∈⊆∈=,, (1)平衡点0),(00=p u f ,下面研究平衡点附近解对参数的关系。
对参数求导数得到0=+p uf dpduf (2)若0),(00≠p u f u ,则可解出),(),(000010p u f p u f dpdu p u p p -=-=(3)由隐函数定理知,在00=p 的邻域中存在唯一解。
隐函数定理结论:只要函数f 连续且u f 在),(00p u 非奇异,则方程0),(=p u f 的解在),(00p u 附近存在且唯一,而且解)(p u 曲线局部可以用p 作为参数表示。
[定义1] 设n n R R R f →⨯:连续且0),(00=p u f 。
2013“非线性振动”练习题1、简述绘制相轨线的原理及其作用。
2、用小参数摄动法求X+ = £X2X(£• « 1)的一阶近似解。
3、用多尺度法或均值法求(第三章16)X + CD^X = £X3{£ « 1)的一阶近似解。
4、用多尺度法求周期激励范德波尔方程x + co^x = £(1 一x2)x + F coscot. x(0)= A + —7. x(0) = 0的非共振解。
5、设运动微分方程为x + = -ex2 + Feos cot (s « 1)试求的主共振解。
6、简述非线性单自由度保守系统自由振动的主要特点及与线性系统的区别。
7、简述非线性单自由度系统在简谐激励下的强迫振动特点。
8、简述自激振动产生的主要原因及其特点。
9、以两自由度非线性系统为例,简述非线性多自由度系统振动的主要特点。
10、简述分岔和混沌的概念。
(考试从中选取5题)1、简述绘制相轨线的原理及其作用。
答:绘制相轨迹线的原理如下:将系统的动力学方程X4/(X,X)=0转化为以状态变量表示的状态方程组y=x7(1)y=/(x>y)在利用I:式消去微分dt,得到y和x的关系式红心凹⑵dx y这个式子所确定的平面(x,y)上的各点的向量场,就构成了相轨迹族。
绘制相轨迹线的方法有两种,第一是等倾线法。
等倾线法的原理如下,令方程(2)右边等于常数C,得到(x,y)相平面内以C为参数的曲线族/(x,y)+Cy=O (3)(3)称作相轨迹的等倾线族,族内每一曲线上的所有点所对应的由方程(2)确立的向量场都指向同一方向。
第二种方法是李纳法。
其原理如下:适当选择单位使弹簧的系数为1,设单位质量的阻尼力为-©(y),则有f(x,y)=x+e(y)..相轨迹微分方程为空=W(y) ⑷dx y在平而上做辅助曲线x=0(y)。
此辅助曲线即上述零斜率号倾线,过某个相点P (x,y) 作x轴的平行线与辅助曲线交与R点,再过R点作y轴的平行线与x轴交于S点,连接PS, 将向量亦逆时针旋M 9()度后的方向就是方程(4)确宦的相轨迹切线方向"相轨迹线可以帮助我们总性地了解系统在不同初始条件卜的运动全貌。
非线性物理试题及答案一、选择题(每题5分,共20分)1. 在非线性动力学中,下列哪一项不是系统表现出混沌行为的特征?A. 周期轨道B. 敏感依赖于初始条件C. 拓扑混合D. 奇异吸引子2. 非线性光学中的自聚焦现象是由于以下哪种非线性效应?A. 克尔效应B. 拉曼散射C. 布里渊散射D. 瑞利散射3. 在非线性波动方程中,哪一类波可以被视为孤波?A. 正弦波B. 余弦波C. 锯齿波D. 冲击波4. 以下哪个方程不是描述非线性系统的典型方程?A. 洛伦兹方程B. 范德波尔方程C. 薛定谔方程D. 麦克斯韦方程二、填空题(每题5分,共20分)1. 非线性系统的一个关键特性是它们可以表现出_________,即使在没有外部扰动的情况下。
2. 在非线性系统中,当系统参数变化时,系统的行为可能会发生_________,导致系统从一个稳定状态跳跃到另一个稳定状态。
3. 非线性系统中的_________现象是指系统在某些参数值附近表现出周期性行为,而在其他参数值附近则表现出混沌行为。
4. 非线性动力学中的_________是指系统状态随时间演化的轨迹在相空间中形成的闭合曲线。
三、简答题(每题10分,共30分)1. 简述非线性系统与线性系统的主要区别。
2. 解释什么是分岔,并给出一个分岔的例子。
3. 描述孤波的概念,并说明它在物理现象中的应用。
四、计算题(每题15分,共30分)1. 考虑一个一维非线性波动方程:\[ \frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2} + \alpha u \frac{\partial u}{\partial x} \] 其中,\( u(x,t) \) 是波形,\( c \) 是波速,\( \alpha \) 是非线性系数。
求该方程的孤波解。
2. 给定一个非线性系统的动态方程:\[ \frac{d^2 x}{dt^2} + \beta \frac{dx}{dt} + \omega_0^2 x + \gamma x^3 = 0 \]其中,\( \beta \)、\( \omega_0 \) 和 \( \gamma \) 是常数。
2013 “非线性振动” 练习题
1、简述绘制相轨线的原理及其作用。
2、用小参数摄动法求
)1(220<<=+εεωx x x x
的一阶近似解。
3、 用多尺度法或均值法求 (第三章16)
)1(320<<=+εεωx x x
的一阶近似解。
4、 用多尺度法求周期激励范德波尔方程
0)0(,)0(,cos )1(220220=-+=+-=+x F A x t F x x x x ω
ωωεω 的非共振解。
5、 设运动微分方程为
)1(cos 220<<+-=+εωεωt F x x x
试求0ωω≈的主共振解。
6、 简述非线性单自由度保守系统自由振动的主要特点及与线性系
统的区别。
7、 简述非线性单自由度系统在简谐激励下的强迫振动特点。
8、 简述自激振动产生的主要原因及其特点。
9、 以两自由度非线性系统为例,简述非线性多自由度系统振动的
主要特点。
10、 简述分岔和混沌的概念。
(考试从中选取5题)
1、简述绘制相轨线的原理及其作用。
答:绘制相轨迹线的原理如下:
将系统的动力学方程...
+(x,)=0x f x 转化为以状态变量表示的状态方程组 ..==-(x,y)
y x
y f (1)
在利用上式消去微分dt,得到y x 和的关系式 ,=-dy f dx y
(x y ) (2) 这个式子所确定的平面(x,y )上的各点的向量场,就构成了相轨迹族。
绘制相轨迹线的方法有两种,第一是等倾线法。
等倾线法的原理如下,令方程(2)右边等于常数C ,得到(x,y)相平面内以C 为参数的曲线族
(x,y)+Cy=0f (3)
(3)称作相轨迹的等倾线族,族内每一曲线上的所有点所对应的由方程(2)确定的向量场都指向同一方向。
第二种方法是李纳法。
其原理如下:
适当选择单位使弹簧的系数为1,设单位质量的阻尼力为-(y)ϕ,则有f(x,y)=x+(y)ϕ。
相轨迹微分方程为
+(y)=-dy x dx y
ϕ (4) 在平面上做辅助曲线=-(y)x ϕ 。
此辅助曲线即上述零斜率等倾线,过某个相点 P (x,y )作x 轴的平行线与辅助曲线交与R 点,再过R 点作y 轴的平行线与x 轴交于S 点,连接PS ,将向量PS →
逆时针旋转90度后的方向就是方程(4)确定的相轨迹切线方向。
相轨迹线可以帮助我们定性地了解系统在不同初始条件下的运动全貌。
当系统是强非线性振动的时候,近似解析法(如小参数摄动法,多尺度法)不再适用,此时可以采用相轨迹法来研究。
(相轨迹线的作用)
非线性动力学主要研究非线性振动系统周期振动规律(振幅,频率,相位的变化规律)和周期解的稳定条件。
其研究内容主要有:保守系统中的稳定性及轨道扩散问题;振动的定性理论;非线性振动的近似解析方法;非线性振动中混沌的控制和同步问题;随机振动系统和参数振动系统问题等。
2、用小参数摄动法求
)1(220<<=+εεωx x x x
的一阶近似解。
解:此处取一阶近似解201=++O()x x x εε (1)
设 222200=+=-D D ωωεωωε即 (2)
此处D 为调谐参数 并设=F K ε (3)
将(1)(2)(3)代入系统动力学方程中则有
....
22010101++(-D )(x +x )=-(x +x )+cos x x K t εωεεεεεω (4)
考虑到ε两边同次幂的系数相等,于是有
..0200..1221100:+=0
(5a):+=Dx -x +cos (5b)x x x x K t
εωεωω 由(5a )可得 0=cos +Bsin x A t t ωω (6)
将(6)代入(5b )中有
22
..2
11+=DA cos +sin -(1+cos 2)-(1-cos 2)-ABsin2+cos 22A B x x t DB t t t t K t ωωωωωωω(7)
为了消去久期项,必有使得cos t ω和sin t ω的系数都为0 于是有
DA+=0
=0
K DB (8) 于是有 A =-=-=0K F B D D ε (9)
解(7) (9) 可得
22
11222=R cos +sin +-+cos 226A A x t R t t ωωωωω
(10) 由初始条件 .
11(0)=0 (0)=0x x (11)可得 2
122==03A R R ω (12)
222
1222=cos +cos 2-362A A A x t t ωωωωω
(13)
所以,方程的主共振解为
222222=cos +cos -+cos 2326A A A x A t t t ωωωεωωω⎛⎫ ⎪⎝⎭
(14) 这里A =-(D )F D ε
其中为调谐参数(15)
3、用多尺度法或均值法求
)1(320<<=+εεωx x x
的一阶近似解。
4、用多尺度法求周期激励范德波尔方程
0)0(,)0(,cos )1(220220=-+=+-=+x F A x t F x x x x ω
ωωεω 的非共振解。
5、设运动微分方程为
)1(cos 220<<+-=+εωεωt F x x x
试求0ωω≈的主共振解。
6、简述非线性单自由度保守系统自由振动的主要特点及与线性系统的区别。
答:特点:
(1)恢复力与位移不成线性比例或阻尼力与速度不成线性比例
(2)非线性单自由度保守系统自由振动的机械能守恒
(3)系统的周期与初始条件有关。
(4)保守系统的微分方程形式如:。
其中p (u) 是仅依赖于系统位移u 的非线性有势力。
(5)。
区别:线性振动只适用于小运动范围 ,超过此范围,就变成非线性振动。
7、简述非线性单自由度系统在简谐激励下的强迫振动特点。
答:非线性单自由度系统在简谐激励下的强迫振动有以下特点:
(1)
非线性单自由度系统在简谐激励下的强迫振动微分方程为: +F(t)
F (t )为正弦时为简谐激励。
上式为弱非线性,有周期解。
(2)振幅与激励频率在一定关系下发生突跳现象。
(3)在非线性系统中,当干扰力频率在派生系统固有频率附近变化,而受迫振动振幅很大时,发生主共振。
一定条件下还会发生超谐共振、亚谐共振、组合共振等非主共振现象。
9、以两自由度非线性系统为例,简述非线性多自由度系统振动的主要特点。
答:多自由度系统的非线性振动,除两自由度系统之外,很少有精确解。
多采用数值方法为近似分析方法。
在某些条件下,存在内共振现象、 饱和现象、周期激励下不存在周期运动的现象。
在两自由度时:(1)内共振现象,以弹簧摆有限振动为例,
经过计算得到:弹簧的伸长和摆动均为有界,而两种运动的幅值交替增减,能量不断在两种振动形式之间交换,变种现象称为内共振。
(2)受迫振动中的饱和现象,以船舶在海浪作用为例,
),,(20x x t f x x ε
ω=+l
g x x l x x l x x m k x g x l x x =+-=+=-=+022120221220220122221201122ωωωωω
(3)受拍振动中的无周期响应现象,
无周期运动。
)cos(2)
cos(2,22212222202211211111201121θωαμωθωαμω+++-=++++-=+t F x x x x t F x x x x x :x x 振动方程可写为为仰俯角
为横摇角设。
x x F F 这就是所谓饱和现象能量渗透到饱和幅值就不再增加后超过某一临界值但当仰俯振动的幅值也增加随着激励幅值的增加
开始激发仰俯振动时且从纵向拍击船舶当海浪频率即若存在内共振,),(,,,,
,)0(2,12210201
02=≈≈ωωωω)cos(2)cos(2222122222022112111112011θωαμωθωαμω+++-=++++-=+t F x x x x t F x x x x x 0102012)(ωωωω≈≈且存在内共振即主共振当。