当前位置：文档之家 › 第二章2传递函数

第二章2传递函数

  • 格式：ppt
  • 大小：706.50 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

第2章 2.3传递函数

第2章 2.3传递函数
K ∏ (τ i s + 1) ∏ τ i2 s 2 + 2ρiτ i s + 1
i =1 i =1 l 1 ( m−l ) 2
G(s ) =
(
)
∏ (T s +1) ∏ (T
h j j =1 j =1
1 ( n −h ) 2
2 2 j
s + 2ξ jT j s + 1
)
注意！
K 传递系数或 静态增益，常 数项归一
C (s) (s G( s ) = R(s)
C(s) b0 s + b1s + ⋯ + bm−1s + bm = n n −1 R(s) a0 s + a1s + ⋯ + an−1s + an
m
m−1
2.3传递函数
一 定义与性质 [性质] （1）传递函数的概念只适用于线性定常 系统，它是在零初始条件下定义的。 （2）传递函数是复变量 S 的有理分式函 数，即： ≥ m；各系数均为实数。 n 是系统元件参 数的函数 物理系统的固有特性是因果性；若m>n, 则这是物理不可实现的系统。
C (s) 1 = 2 2 传递函数： G ( s ) = R ( s ) T s + 2ξ Ts + 1
ω n2 1/T 2 = = 2 2ξ 1 s + 2ξω n s + ω n2 2 s + s+ 2 T T
R(s)
ωn ：无阻尼 无阻尼
ζ ：阻尼比
22
1 T 2 s 2 + 2ξ Ts + 1
振荡环节方框图
C(s)
自然振荡频率
2.3传递函数

《自动控制原理》第2章 线性系统的传递函数

《自动控制原理》第2章 线性系统的传递函数

+
anc(t)
=
b0
dm dtm
r(t)
+
b1
d m−1 d t m −1
r(t)
++
bm−1
d dt
r(t)
+
bmr(t)
(m n)
设r(t), c(t)及各阶导数在t=0时的值均为零(零初始条件)， 则对方程两端求拉氏变换，可得系统的传递函数
Ch2 控制系统的数学模型
◼ 传递函数的一般形式：
Ch2 控制系统的数学模型
第二章 控制系统的数学模型
Ch2 控制系统的数学模型
本章内容
❖ 引言 ❖ 物理系统的微分方程 ❖ 拉氏变换与拉氏反变换 ❖ 线性系统的传递函数 ❖ 方框图及其等效变换 ❖ 信号流图与Mason公式*
Ch2 控制系统的数学模型
2.3 线性系统的传递函数
一. 传递函数的定义
Ux(s) =
I
(s) − I2(s) sC1
(2)
I 2 (s)
=
Ux
(s) −Uo(s) R2
(3)
U o (s)
=
I 2 (s) sC2
(4)
Ch2 控制系统的数学模型
I (s) = Ui (s) −U x (s) (1) R1
Ui _
I
1/R1
Ux
Ux(s) =
I
(s) − I2(s) sC1
Uo (s)
Ui (s) （b）
I(s) Uo (s)
Ch2 控制系统的数学模型
I(s)
（c）
Uo (s)
Ui (s)
I(s)
－ Uo (s) （d）

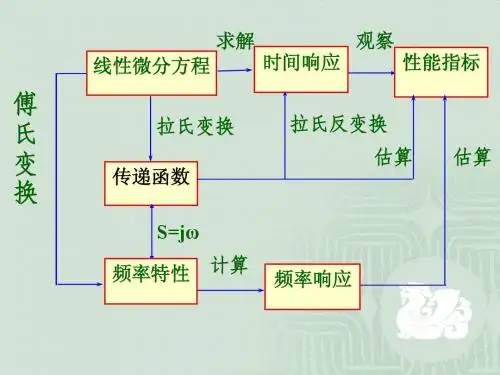
第二章2传函

第二章2传函

n
n 1
y(t)为系统的输出，r(t)为系统输入，则零初 始条件下，对上式两边取拉氏变换，得到系 统传递函数为：
b0 s m b1s m1 bm1s bm Y ( s) G ( s) n n 1 R( s) a0 s a1s an1s an
d Cm lim ( s s1 ) F ( s ) Cm 1 lim [( s s1 ) m F ( s )] s s1 s s1 ds
m
Cm j
1 dj lim j [( s s1 ) m F ( s )] j! s s1 ds
1 d ( m 1) C1 lim ( m 1) [( s s1 ) m F ( s )] (m 1)! s s1 ds f (t ) L1[ F ( s )] Cm Cm 1 m 2 m 1 [ t t (m 1)! (m 2)! C2t C1 ]e s1t
线性微分方程
性能指标
傅 氏 变 换
拉氏变换
传递函数 S=jω
频率特性
计算
频率响应
拉氏反变换
按定义求拉氏反变换很困难，一般常用部分分 式法计算：
F (s )
分解
部分分式
查表
原函数
F (s ) 的一般形式为 B ( s ) b0 s m b1s m 1 bm 1s bm F (s) n A( s ) s a1s n 1 an 1s an
Uo ( s) [例] 求如图所示电路的传递函数 U i ( s )
C i1 R1 i2 R2
[解]：解法一：列出回路电压方程和输 出节点方程
1 i1dt R1i1 R1i2 ui R2 i2 uO

第二章 传递函数-梅逊公式

第二章 传递函数-梅逊公式
第二章 自动控制系统的数学模型
2.3 传递函数与系统动态结构图
2.3.1 传递函数的定义
设系统的标准微分方程为
an
dnc(t) dt n
a n1
dn1c(t) dt n 1
……
a1
dc(t) dt
a0c(t)
bm
dmr(t) dt m
bm1
d m 1r ( t ) dt m1
……
b1
dr(t) dt
点
上图所示的是
G(s)
(s
(s 1)(s 2) 3)(s 2 2s
2)
的零、极点分布图。
2.2 传递函数
比
比例环节（无惯性环节）： c(t)=kr(t)
例
传递函数：G(S)=C(S)/R(S)=k
c(t)
环
阶跃响应：R(S)=1/S
r(t)
节
C(S)=kR(S)=k/S C(t)=k
0
方框图： R(S) k/s C(S)
3
传
递
积分调节器：
C
在A点列方程可得：
函 数
Ur(t)
R
i2
i1
A
Uc(t) i2=i1, i1=Uc(t)/R Uc(t)=1/C∫i2(t)dt=1/(RC)∫Uc(t)dt
设RC＝T（积分时间常数），则有：Uc(t)=1/T∫Uc(t)dt
拉氏变换后为：Uc(S)=1/(TS)Uc(S)
5）传递函数具有正、负号（输入量和输出量的变化方向）。
6）传递函数的单位是输出量的单位与输入量的单位之比。
m
(s z j )
7）传递函数可以写成
G(s)
Kg
j1 n

自控理论 2-2传递函数

自控理论 2-2传递函数

当 ui ( t ) = 1( t )时,
− t 1 −1 τs 则u0 ( t ) = L ⋅ =e τ τs + 1 s 1
图2-8 RC电路 电路
当 τ << 1 时，可近似认为 G ( s ) ≈ τs
5. 振荡环节
d 2 c( t ) dc( t ) 2 T + 2ζT + c( t ) = Kr ( t ) 2 dt dt
运放 2
U 2 ( s ) τs + 1 G2 ( s) = = U 1 ( s) Ts
( 2 − 38)
式中
τ = R3C
T = R2C
功放
U a ( s) G3 ( s) = = K2 U 2 ( s)
( 2 − 39)
附:电枢控制直流电动机的微分方程 电枢控制直流电动机的微分方程
dmc d 2n dn TaTm 2 + Tm + n = K u ua − K m (Ta + mc ) dt dt dt La ; 电磁时间常数 Ta = Ra 传递系数 1 Ku = Ce 机电时间常数 Tm Km = J ( 2 − 10)
m m −1
∏ (s − z
j =1 n i =1
m
j
)
∏ (s − p )
i
式中
z j ( j = 1 , 2 L m )为传递函数的零点； 为传递函数的零点； p i ( i = 1 , 2 L n )为传递函数的极点； 为传递函数的极点； K 1 = b0 为传递系数或根轨迹增 益。
② 时间常数表达式
n≥m
当初始条件均为零时，两边取拉氏变换 当初始条件均为零时，
(s

第二章-系统的传递函数方框图及其简化.

第二章-系统的传递函数方框图及其简化.

系统闭环传递函数
GB (s)
X o (s) Xi (s)
由图可知
X i (s) E(s) G(s)
B(s)
H (s)
X o (s)
E(s) Xi (s) B(s) Xi (s) Xo(s)H (s) Xo(s) G(s)E(s) G(s)[Xi (s) Xo(s)H (s)]
G(s)Xi (s) G(s)Xo(s)H (s) 由此可得：
GK (s) G(s)H (s) E(s)
无量纲.
系统闭环传递函数
GB (s)
X o (s) Xi (s)
注意:我们所指的前向通道的传递函数、反馈回路的
传递函数和开环传递函数都是针对一个闭环系统而
言的。它们都是闭环系统的一部分。系统闭环传递
函数是闭环系统的传递函数。看一个传递函数是什
么具体类型，要从定义出发，而不能只看其符号。
8.分支点和相加点之间等效规则
X1(s)
X1(s) X2(s)
X 2 (s)
X1(s) X2(s)
X1(s)
X 2 (s)
X1(s) X2(s)
X1(s) X2(s)
X 2 (s)
一般应避免分支点和相加点之间的相互移动
三、方框图简化的一般方法 （法1）
1.确定系统的输入量和输出量.若作用在系统上的输 入量或输出量有多个,则必须分别对每一输入量,逐个 进行方框图的简化,以求得各自的传递函数. 2.若方框图中有交叉连接,则利用分支点或相加点的 移动规则,将交叉消除,简化成无交叉的多回路方框图 的形式.(大回路套小回路) 3.对多回路方框图,按照先里后外的顺序依次对各个 回路进行简化. 4.写出系统的传递函数.
Ua (s) 0

第二章 2-2传递函数

第二章 2-2传递函数
6
3
为了方便，常把传递函数分解为一次因式的乘积，
式（2-51）中的K常称为传递函数的增益或传递系 数（放大系数）。
4
二、传递函数的零、极点
式（2-52）中zj (j=1.2……m)为分子多项式的根，称为传 递函数的零点。 Pi(1.2……n)为分母多项式的根，称为传递函数的极点。 传递函数的零、极点可以是实数或零，也可以是复数，由 于传递函数分子、分母多项式的系数都是实数，故若有复数 零极点时，它们必是成对共轭的。 传递函数的分母多项式就是相应微分方程式 (2-49)的特 征多项式，令该分母多项式等于零，就可得到相应微分方程 的特征方程。 在特征方程中，s最高阶次等于输出量最高阶导数的阶次， 如果s的最高阶次等于n，这种系统就称为n阶系统。
1
一、传递函数的定义：线性定常系统在零初始条件下， 输出量的拉氏变换与输入量的拉氏变换之比，称为该系 统的传递函数。
若线性定常系统的微分方程为：
在初始条件为零时，对（2-49）进行拉氏变换，得
2
根据传递函数的定义，描述该线性定常 系统的传递函数为：
可见，传递函数是由系统微分方程经拉氏变换而引出的。 系统输入、输出及传递函数之间的相互关系可用下图表示， 输出是由输入经过G(s)的传递而得到的，因此称G(s)为传递 函数。因为传递函数是在零初始条件下定义的，故在初始条 件为零时，它才能完全表征系统的动态性能。
§2-2传递函数
控制系统的微分方程，是时域中描述系统动态性能的数 学模型，求解微分方程可以得到在给定外界作用及初始条 件下系统的输出响应，并可通过响应曲线直观地反映出系 统的动态过程。 但系统的参数或结构形式有变化，微分方程及其解都会 同时变化，不便于对系统进行分析与研究。 根据求解微分方程的拉氏变换法，可以得到系统的另一 种数学模型 ——传递函数。 它不仅可以表征系统的动态特性，而且可以方便地研究 系统的参数或结构的变化对系统性能所产生的影响。 在经典控制理论中广泛应用的根轨迹法和频率法，就是 在传递函数基础上建立起来的。

2第二章 2控制系统的传递函数模型

2第二章 2控制系统的传递函数模型

(S Z
i 1 n j 1
m
i
)
(S P )
j
Zi (i=1,2,…,m) 是分子多项式的根，称为传递函数的零点
pj (j=1,2,…,n) 是分母多项式的根，称为传递函数的极点
K *=b0/a0
称为传递函数的传递系数（根轨迹增益）
传递函数的零极分布图
为了更直观、更形象地 p2 × p1× z1
4、理想微分环节
微分方程 c(t)= Tdr(t)/dt 传递函数 G(s)=Ts 特点： 输出量正比输入量变化的速度，能 预示输入信号的变化趋势。 实例：集成运放的微分运算，测速发电 机输出电压与输入角度间的传递函数即为 微分环节。
5、一阶微分环节（或称比例微分环节）
微分方程 c(t)= Tdr(t)/dt + r(t) 传递函数 G(s)=Ts+1 特点： 输出量既包含与输入量成正比的量， 又包含输入信号的变化趋势。 实例：集成运放的比例微分运算等。
0 1 n 1 n
G( s)

例1、试求RC无源网络的传递函数
uo(s)/u (s)
i
解答：
RC网络的微分 方程表示为
Ui
R1
R2
i (t ) C 1
C2
Uo
d 2 uo ( t ) duo ( t ) R1 R2 C 1C 2 ( R1C 1 R1C 2 R2 C 2 ) 2 dt dt uo ( t ) ui ( t )
主要内容：
第一讲、 时域数学模型
第二讲、 复域数学模型 第三讲、 方框图与信号流图
本章要求：
一、了解控制系统数学模型的建立方法及数学 模型的表示形式。 二、掌握控制系统时域、复域数学模型的建立

2-2 传递函数及方块图

2-2 传递函数及方块图
2－2
传递函数
传递函数 是经典控制最基本，最重要的概念之一。 1. 定义：线性定常系统在初始条件为零时，输出量的拉氏变
换和输入量的拉氏变换之比。 设：输入----r(t)，输出----c(t)，则传递函数：
L[c(t)] C(s) G(s) L[r(t)] R(s)
式中：C(s)=L[c(t)]——输出量的拉氏变换式 R(s)=L[r(t)]——输入量的拉氏变换式。 那么 C(s)=R(s)G(s) 控制系统的时间响应c(t)等于C(s)的拉氏反变换：
19
2－3
方块图
4、误差传递函数 a) 在控制量作用下系统的误差传递函数： 假设N(s)＝0，则
E ( s ) R( s ) C ( s ) H ( s ) C ( s) H ( s) 1 R(s) R( s ) R( s )
G1 ( s)G2 ( s) H ( s) 1 1 1 G1 ( s)G2 ( s) H ( s) 1 G1 (s)G2 ( s) H ( s)
C(s) G(s) R(s) 1 G(s)H(s)
结论： 具有负反馈结构环节传递函数等于前向通 的传递函数除以1加（若正反馈为减）前向通道与反 馈通道传变换方式 A +
原方块图 + B C + B + C A BC
等效方块图
A
+ + C
+ _
A BC
1
比较点交换
X1 (s) X 2 (s) C(s)
所以
G(s)
C(s) X 1 (s) X 2 (s) X 1 (s) X 2 (s) R(s) R(s) R(s) R(s)
G 1 (s) G 2 (s)

2第二节传递函数

2第二节传递函数

第二节控制系统的传递函数传递函数是经典控制理论中最重要的数学模型之一。

利用传递函数，在系统的分析和综合中可解决如下问题：不必求解微分方程就可以研究初始条件为零的系统在输入信号作用下的动态过程。

可以研究系统参数变化或结构变化对系统动态过程的影响，因而使分析系统的问题大为简化。

可以把对系统性能的要求转化为对系统传递函数的要求，使综合问题易于实现。

一、传递函数的基本概念令初始值为零，将上式求拉氏变换，得)()...()()...(01110111s X b s b s b s b s Y a s a s a s a m m m m n n n n ++++=++++----当传递函数和输入已知时，Y (s )=G (s ) X (s )。

通过拉氏反变换可求传递函数的定义：线性定常系统在零初始条件下输出量的拉氏变换与输入量的拉氏变换之比。

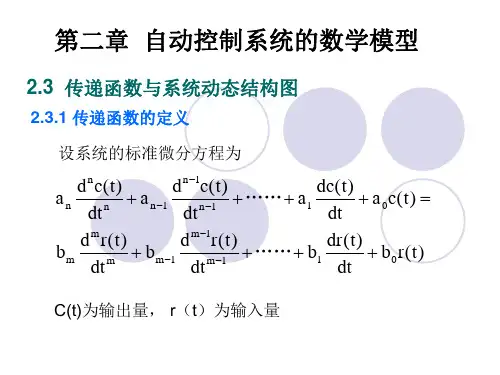
01110111......)()()(a s a s a s a b s b s b s b s X s Y s G n n n n m m m m ++++++++==----称为元件和系统的传递函数)~0,~0(,m j n i b a j i ==式中：x (t ) —输入，y (t )—输出为常系数)()(...)()()()(...)()(01)1(1)(01)1(1)(t x b t x b t x b t x b t y a t y a t ya t y a m m m m n n n n +'+++=+'+++----设系统或元件的微分方程为：[关于传递函数的几点说明]⏹传递函数的概念适用于线性定常系统，它与线性常系数微分方程一一对应。

且与系统的动态特性一一对应。

⏹传递函数不能反映系统或元件的学科属性和物理性质。

物理性质和学科类别截然不同的系统可能具有完全相同的传递函数。

而研究某传递函数所得结论可适用于具有这种传递函数的各种系统。

⏹传递函数仅与系统的结构和参数有关，与系统的输入无关。

第二章 (2.1,2.2)控制系统的微分方程、传递函数

第二章 (2.1,2.2)控制系统的微分方程、传递函数

拉氏变换的重要应用——解线性定常微分方程

求微分方程的拉氏变换，注意初值！！
求出 C ( s ) 的表达式 拉氏反变换，求得 c (t )
例1 已知系统的微分方程式，求系统的输出响应。
d 2c(t ) dc(t ) 2 2c(t ) r(t ) 2 dt dt d2 解： 在零初态下应用微分定理： 2 s 2
+
i (t )
R
–
u (t )
+
i (t )
u (t ) i (t ) R
du ( t ) 1 i (t ) dt C
di (t ) u (t ) L dt
电容
C
–
u (t )
+
ቤተ መጻሕፍቲ ባይዱi (t )
电感
u (t )
–
L
机械系统三要素的微分方程
设系统输入量为外力，输出量为位移
d 2 x (t) m f (t) 2 dt
d uc (t ) duc (t ) LC RC uc (t ) ur (t ) 2 dt dt
2
3．机械位移系统
输入量为外力: F (t ) 输出量为位移: y (t )
dy 2 (t ) 依据牛顿定律： F m dt 2
dy (t ) d y (t ) F (t ) ky (t ) f m 2 dt dt
d 2 y (t ) dy (t ) m f ky (t ) F (t ) 2 dt dt
微分方程结构一致 二阶线性定常微分方程
不同形式的物理环节和系统可以建立相同形式的数学模型。
系统微分方程由输出量各阶导数和输 入量各阶导数以及系统的一些参数构成。 n阶线性定常系统的微分方程可描述为：

2第二节传递函数解析

2第二节传递函数解析

第二节控制系统的传递函数传递函数是经典控制理论中最重要的数学模型之一。

利用传递函数，在系统的分析和综合中可解决如下问题：不必求解微分方程就可以研究初始条件为零的系统在输入信号作用下的动态过程。

可以研究系统参数变化或结构变化对系统动态过程的影响，因而使分析系统的问题大为简化。

可以把对系统性能的要求转化为对系统传递函数的要求，使综合问题易于实现。

一、传递函数的基本概念令初始值为零，将上式求拉氏变换，得)()...()()...(01110111s X b s b s b s b s Y a s a s a s a m m m m n n n n ++++=++++----当传递函数和输入已知时，Y (s )=G (s ) X (s )。

通过拉氏反变换可求传递函数的定义：线性定常系统在零初始条件下输出量的拉氏变换与输入量的拉氏变换之比。

01110111......)()()(a s a s a s a b s b s b s b s X s Y s G n n n n m m m m ++++++++==----称为元件和系统的传递函数)~0,~0(,m j n i b a j i ==式中：x (t ) — 输入，y (t ) — 输出为常系数 )()(...)()()()(...)()(01)1(1)(01)1(1)(t x b t x b t x b t x b t y a t y a t ya t y a m m m m n n n n +'+++=+'+++----设系统或元件的微分方程为：[关于传递函数的几点说明]⏹传递函数的概念适用于线性定常系统，它与线性常系数微分方程一一对应。

且与系统的动态特性一一对应。

⏹传递函数不能反映系统或元件的学科属性和物理性质。

物理性质和学科类别截然不同的系统可能具有完全相同的传递函数。

而研究某传递函数所得结论可适用于具有这种传递函数的各种系统。

3第二章(举例2)传递函数及结构图变换

3第二章(举例2)传递函数及结构图变换

K ( i s 1) ( l s 2 l l s 1) s
v
s
e
s
(T j s 1) (Tk s 2 k Tk s 1)
2 2 j 1 k 1
i 1 d
l 1 e
积分环节
惯性环节
振荡环节
延迟环节
环节是根据微分方程划分的，不是具体的物理
装置或元件。
C 2 ( s) G2 ( s)R( s)
2. 并联结构的等效变换
• 等 效 变 换 证 明 推 导
R(s) G1(s) G2(s)
C1(s)

C(s)

C2(s)
C ( s ) [G 1 ( s ) G 2 ( s )] R ( s ) C (s) R(s) G1 ( s ) G 2 ( s )
K ——环节的放大系数 T ——环节的时间常数 ——环节的阻尼比
d x r (t ) dt
2
2
2
dx r ( t ) dt
x r ( t )]
1 两个串联的一阶微分环节
延滞环节 例1：水箱进水管的延滞 传递函数：
G (s) X c (s) X r (s) e
s
运动方程式：
出值。
延迟环节从输入开始之初，在0 ~τ时间内没 有输出，但t=τ之后，输出完全等于输入。
水箱进水管的延滞
系统函数方块图
系统函数方块图是一种数学模型，采用
它将更便于求传递函数，同时能形 象直观地表明输入信号在系统或元 件中的传递过程。
1.
串联结构的等效变换（１）
• 串联方块图
R(s)
G1(s)
传递函数
传递函数的概念与定义

《自动控制原理》第2章线性系统的传递函数

《自动控制原理》第2章线性系统的传递函数

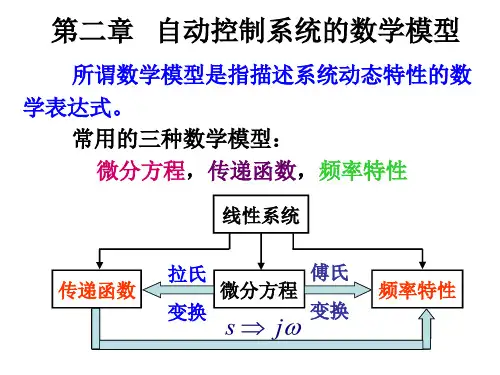
《自动控制原理》第2章线性系统的传递函数线性系统是指系统的输出与输入之间存在线性关系的系统。

线性系统的传递函数是描述系统输入输出之间关系的一种数学表示方法。

在线性系统中，传递函数是一个复变函数，通常表示为H(s)，其中s是复变数，表示Laplace变换域中的复频率。

传递函数可以通过对系统的微分方程进行Laplace变换得到。

传递函数的形式可以根据系统的特点进行表示。

例如，对于一个惯性系统，其传递函数可以表示为H(s)=k/(Ts+1)，其中k是系统的增益，T是系统的时间常数。

传递函数的分子表示系统的输出与输入之间的增益关系，分母表示系统的动态响应特性。

通过传递函数，我们可以分析系统的频率响应特性。

频率响应可以通过将复变数s替换为jω，其中j是虚数单位，ω是真实频率。

通过计算传递函数在不同频率下的幅频特性和相频特性，我们可以了解系统对不同频率的输入信号的响应情况。

另外，传递函数还可以用于系统的稳定性分析。

对于一个线性时不变系统，如果其传递函数的分母没有极点位于劣半平面，即实部为负的复数域中，那么系统是稳定的。

通过分析传递函数的极点位置，我们可以判断系统的稳定性。

在实际应用中，我们可以利用传递函数进行系统的设计和控制。

例如，对于给定的控制要求，我们可以通过选择合适的传递函数参数，来设计满足要求的控制器。

控制器的设计过程可以通过将传递函数相乘或串联、并联等操作来实现。

总结起来，线性系统的传递函数是描述系统输入输出关系的一种数学表示方法。

通过传递函数，我们可以分析系统的频率响应和稳定性，并进行系统的设计和控制。

掌握传递函数的理论和应用，对于理解和应用自动控制原理具有重要意义。

以上是关于《自动控制原理》第2章线性系统的传递函数的1200字以上的介绍。

希望对读者理解和学习该章节内容有所帮助。

《自动控制原理》第二章传递函数

《自动控制原理》第二章传递函数

输出信号的拉氏变换 传递函数 = 输入信号的拉氏变换 零初始条件
C ( s) G(s) = R( s)
autocumt@ 1 中国矿业大学信电学院
一、 传递函数的定义和主要性质
设线性定常系统由下述n阶线性常微分方程描述： 设线性定常系统由下述n阶线性常微分方程描述：
dn d n −1 d a 0 n c (t ) + a1 n −1 c (t ) + ⋅ ⋅ ⋅ + a n −1 c (t ) + a n c (t ) dt dt dt d m −1 d dm = b0 m r (t ) + b1 m −1 r (t ) + ⋅ ⋅ ⋅ + bm −1 r (t ) + bm r (t ) dt dt dt
autocumt@
15
中国矿业大学信电学院
自动控制原理
4、振荡环节
特点：包含两个独立的储能元件，当输入量发生变化时，两个 包含两个独立的储能元件，当输入量发生变化时， 包含两个独立的储能元件 储能元件的能量进行交换，使输出带有振荡的性质。 储能元件的能量进行交换，使输出带有振荡的性质。
z1 n 2 (t) = n1 (t) z2
G(s) = N 2 (s) z1 = =K N1 (s) z 2
传递函数： 传递函数：
autocumt@
9
中国矿业大学信电学院
其它一些比例环节
自动控制原理
R2 R1
r (t )
Ec
R
c (t )
ic (t )
r1
r2
r (t )
c(t )
C
例：积分电路 积分电路
i1 (t )
R1

控制工程基础4-第2章 (数学模型-2：传递函数)

控制工程基础4-第2章 (数学模型-2：传递函数)
第三节 传递函数
拉氏变换可以简化线性微分方 程的求解。还可将线性定常微分方 程转换为复数S域内的数学模型— 传递函数。
一、传递函数的概念
二、典型环节的传递函数
一、 传递函数概念
输入
输入拉氏 变换
设一控制系统 r(t) c(t) 系统 G(S)
R(S)
输出 输出拉氏 变换
C(S)
传递函数的定义：
零初始条件下，系统输出量拉氏变换与系 统输入量拉氏变换之比。
R(s)
G1(s)+G2(s)
C(s)
+ G2(s) C2(s)
n C1(s)=R(s)G1(s) C2(s)=R(s)G2(s) G (s)=Σ Gi (s) n个环节的并联 i=1 C(s)=C1(s)+C2(s) =R(s)G1(s)+R(s)G2(s) C(s) =G (s)+G (s) G(s)= R(s) 1 等效 2
2） 传递函数取决于系统的结构和参数， 与外施信号的大小和形式无关。
3） 传递函数为复变量S 的有理分式。
4） 传递函数是在零初始条件下定义 的，不能反映非零初始条件下系统的运 动过程。
二、 基本环节的传递函数
不同的物理系统，其结构差别很 大。但若从系统的数学模型来看，一 般可将自动控制系统的数学模型看作 由若干个典型环节所组成。研究和掌 握这些典型环节的特性将有助于对系 统性能的了解。
结构图特点
• 结构图是方块图与微分方程（传函）的结合。一方面它直观反映了整 个系统的原理结构（方块图优点），另一方面对系统进行了精确的定 量描述（每个信号线上的信号函数均可确定地计算出来） • 能描述整个系统各元部件之间的内在联系和零初始条件下的动态性能， 但不能反映非零条件下的动态性能 • 结构图最重要的作用：计算整个系统的传函 • 对同一系统，其结构图具有非唯一性；简化也具有非唯一性。但得到 的系统传函是确定唯一的. • 结构图中方块≠实际元部件，因为方框可代表多个元件的组合，甚至 整个系统

自动控制理论第二章传递函数_图文

自动控制理论第二章传递函数_图文
解：前向通路4条 独立回路3个
§2.6 一般反馈控制系统
传递函数的各种术语 误差传函 扰动传函 一般控制作用
1. 一般控制系统
前向通道传函 闭环系统的开环传函 系统闭环传递函数 系统在给定作用下的输出
1、由系统输入到系统输出端的信号通路定义为系统 前向主通路(道)[简称主通路或前向通路]
②方框：表示输入、输出信号之间的传递 关系。
③引出点(测量点)：表示信 号引出或测量位置，从同一 点引出的信号完全相同。
④比较点(综合点)：表示两个或两个以上 的信号，在该点相加、减。注意，比较点 处信号的运算符号必须标明正(+)、负(-)， 一般不标者取正号。同时进行运算的信号 必须具有相同的量纲。
梅逊公式
回路总增益 (闭环传函)
第i条前向通 道余子式
第i个前向 通道增益
特征式
例：三级RC滤波网络如
图所示，求传递函数G(s)。
解： 前向通路1条 独立回路5个
两两不接触回路6个
三三不接触回路 特征式 余子式 传递函数
例：试求取图示系统的传递函数
解：前向通路3条
独立回路2个
例：系统结构图如图所示，试求其传递函数
积分器框图
特性：调节系统稳态误差，也称为无差 环节。
电压的传递函数
三、纯微分环节
定义：环节的输出响应正比于输入信号的变化率 。
微分方程 传递函数
测速发电机
四、惯性环节
定义：环节的输出不能立即复现输入，而是经过 一定时间后才能复现输入的变化。
微分方程
传递函数
运算放大器
五、振荡环节
定义：在输入作用下，环节输出响应随时间变化的 过渡过程总是在某一稳定值上下出现衰减振荡，而 最终趋于稳定值。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
6 3 2 1 X (s) 2 s ( s 5 s 6) s 2 s 3 s
2t
jik03
u (t )
t
x(t ) L1[ X ( s )] （查表）
x (t ) x s (t ) 3e
2e
3 t
1 (t≥0)
7
Page: 8
1 0.8 0.6 0.4 0.2 0 t 0 0.5 1 1.5 2 2.5 3 3.5 4 瞬 态 响 应 -3 e 2 t + 2 e - 3 t
Page: 1
复习：线性系统微分方程的一般形式
( n) ( n 1) an xo (t ) an1 xo (t ) a1 x o (t ) a0 xo (t )
( m) ( m1) bm xi (t ) bm1xi (t ) b1x i (t ) b0 xi (t )
L[ xi (t )] X i ( s)
an s a1s a0
例:
Hale Waihona Puke dxo (t ) T xo (t ) kxi (t ) dt
L:
TsX o ( s ) X o ( s ) kX i ( s ) (Ts 1) X o ( s ) kX i ( s )
jik03
1．多项式分式形式 X o ( s ) bm s m b1s b0 G( s) X i ( s ) an s n a1s a0 2．零极点增益形式 分子、分母首一化，再分解因式
Page: 16
K bm / a n 系统增益 零极点增益形式：
N ( s) ( s z1 )( s z2 )( s zm ) G( s ) K K D( s ) ( s p1 )( s p2 )( s pn )
jik03 5
Page: 6
特点：
（1）解的各项系数: 指数: （2）只有瞬态响应，稳态响应=0； 2.5 x Z (t) （3）初始条件变化 2 只改变各组成项的系数。 瞬 态 响 应
1.5 1 0.5 0 0 0.5 1 1.5 2 2.5 3 3.5 4
8 e -2 t - 6 e -3 t
若
L[ f1 (t )] F1 ( s) ， L[ f 2 (t )] F2 ( s)
则
L[af1 (t ) bf 2 (t )] aF1 ( s) bF2 ( s)
d L[ f (t )] sF ( s ) f (0) dt
jik03 3
（2）微分性质
Page: 4
dn L[ n f (t )] dt s n F ( s ) s n 1 f (0) s n 2 f (0) sf ( n 2) (0) f ( n 1) (0)
常用机电相似系统：力—电压相似系统, 力—电流相似系统
jik03
c1s c2 s ( 1)( 1) k1 k2 G( s ) c1s c2 s c1s ( 1)( 1) k1 k2 k2 1 对比： R1 c1 R2 c2 C1 k1
1 C2 k2
15
五．传递函数的表达形式
K
( s zi )
) ( s p j jik03
j 1 i 1 n
m
( n m)
16
传递函数的零点：-zi(i=1,2,…m) 传递函数的极点：-zj(j=1,2,…n),（特征根） 3．典型环节形式 分子、分母“末1化”，再分解因式
K (1s 1) G( s) s(T1s 1)(T 2 s 2 2Ts 1)
F (s) L[ f (t )] :
拉氏变换将原函数变换成象函数
(3)拉氏逆变换将象函数变换成原函数 f(t)=L-1[F(s)]
(4)s的量纲是时间的倒数[T]-1 F(s)的量纲? jik03
2
Page: 3
(5)要求:会查表，会使用。 熟悉几个最简单函数的拉氏变换。
3．最简单的性质：
（1）叠加性质
t0 0 (t ) (t )dt 1 0 t0 0 1 L 变换: sX ( s) 3 X ( s) 2 2 s 1 2 3 X ( s) 2 s ( s 1) s 1 s 1
L[ (t )] 1
0
t
x(t ) L1[ X ( s )] （查表）
17
Page: 18
（2）多项式与零极点形式的转换 [Z,P,K]=tf2zp(num,den) [num,den]=zp2tf(Z,P,K) 小结： 1.微分方程的拉氏算子解法; 2.系统的响应就是微分方程的解 总响应x(t) =零输入响应xZ(t)+零状态响应xs(t) =瞬态响应+稳态响应
X o (s) L[ xo (t )] 3.传函的的定义（零初始条件） G(s) X i (s) L[ xi (t )]
x (t )
xs ( t )
稳 态 响 应
1
2 1.5 1 0.5 0 0
瞬 态 响 应 5 e -2 t-4 e -3 t 稳 态 响 应 +1
1
2
3
4
t
4．总响应[复合运动]
总响应x(t)= 零输入响应xZ(t)+零状态响应xs(t) =瞬态响应+稳态响应 前例:x(t ) x Z (t ) x S (t )
(i ) a x ( t ) b x i i (t ) j 0 ( j) j o i 0 n m
§2.2 传递函数
一.拉氏变换
1.定义
F (s) L[ f (t )]
jik03

0
f (t )e dt
1
st
Page: 2
2.讨论：
(1)零初始条件。 (2) f(t)∶原函数，时间域。 F(s)∶象函数，复数域。S=σ+jω且σ>0。
3．零状态响应 [强迫运动]
稳 态 响 应
0 t
初始条件(状态)=0，输入≠0 微分方程的特解，包括瞬态响应和稳态响应
jik03 6
Page: 7
x (t ) 5x (t ) 6x(t ) 6， 例 2.8 求解 (0) 0 初始条件 x(0) 0 ， x
t0 1 1 解：单位阶跃函数 u (t ) t0 0 1 0 L[u (t )] s 6 2 s X ( s ) 5sX ( s ) 6 X ( s ) L变换: s
Page: 17
组成环节：
4．传递函数相互转换的MATLAB命令 （1）多项式形式的表达 num=[bm bm-1 … b1 b0]; den=[an an-1 … a1 a0]; g=tf(num,den) （2）零极点形式的表达 Z=[z1;z2];P=[p1;p2+j*p3; p2-j*p3];K=k; d=zpk(Z,P,K) jik03
s X ( s) sx(0) x (0) 5sX ( s) 5x(0) 6 X ( s) 0
代入初始条件用部分分式法展开
X (s) 2 s 12 8 6 ( s 2 5 s 6) s 2 s 3
1
解： L变换:
2
x(t ) L [ X ( s)] （查表） 2t 3t (t 0) x(t ) x Z (t ) 8e 6e
(8e 2t 6e 3 t ) (3e 2t 2e 3t 1)
(5e 2t 4e 3t ) 1 jik03
8
Page: 9
例 2.9 求解 x (t ) x(t ) t 2 (t )， 初始条件x(0) 3
(t )
解：单位脉冲函数δ(t)
x(t ) (e
t
t 1) (2e
jik03
t
3e ) = 6e
t
t
+
(t 1)
9
Page: 10
特点：
(1)只有一个特征根， 只有一项瞬态响应6e-t； 两项稳态响应，t 和 -1; (2)系统的初值≠初始条件（状态）. δ(t)改变了系统的初始条件（状态）
8 x ( t) 7 6 5 瞬态响应 6 e - t 4 3 稳 态 响 应 2 1 0 0 1 2 3 4 5 6
X o ( s) k G( s) X i ( s) Ts 1
11
Page: 12
2.讨论
(1)传递函数的分母是系统特征多项式， 分子反映系统与外界的关系。
(2) X o (s) G(s) X i (s) 时域函数
Xi (s) G(s) X o( s)
xo (t ) L1[ X o (s)] L1[G(s) X i (s)]
例：求传递函数
Page: 14
四．相似性原理 相似系统： 能用形式相同的数学模型来描述的两个系统； 相似量： 在微分方程或在传递函数中占有相同 位置的物理量。
ui (i2 i1 )R1 uo
1 (i2 i1 ) R1 i1dt C1 1 uo i2 R2 i2 dt C2
4.由微分方程求传递函数的方法： p s
5. 传函的零点、极点（系统微分方程的特征根）； 1 x ( t ) L [G(s) X i (s)] 6.输出的时域表示： o
1
t -1
t
7
8
三. 传递函数
(an p n a1 p a0 ) xo (t ) (bm p m b1 p b0 ) xi (t ) (n m)
作拉氏变换（在零初始条件下） p s
jik03
10