探究串并联电路中电流的规律

《探究串、并联电路中电流的规律》教学设计一、对本节的分析本节教材是在同学初步了解电路和电流的概念及认识了串联电路和并联电路的特点、会正确运用电流表的基础上，通过老师提出问题后，由同学进行科学的猜想、设计试验方案、动手试验收集数据、对数据进行分析争论、初步领悟科学试验的方法。

二、教学目标1.知识与技能〔1〕会用电流表测串联电路和并联电路中的电流。

〔2〕通过试验讨论掌控串、并联电路中电流的规律。

2.过程与方法学会提出问题，提出猜想，设计方案，试验验证，分析论证，评估沟通的探究方法。

3.情感、立场与价值观〔1〕培育同学乐于用试验事实解决问题的习惯，让同学体验解决物理问题的喜悦。

〔2〕培育同学实事求是，尊敬自然规律的科学立场。

〔3〕使同学有将自己的见解公开并与他人沟通的愿望，认识沟通与合作的重要性。

〔4〕体会物理规律本身具有的深刻的美学特征。

三、教学重点、难点1.教学重点：在试验中探究串、并联电路中电流的规律2.教学难点：组织、指导同学在探究过程中，仔细观测、分析、得出正确结论。

四、教法：科学探究法争论法五、教学突破让同学经受科学探究过程，学习科学探究方法，培育同学的探究精神，实践技能以及创新意识。

六、教学具预备1.老师：电路示教板2.同学：电池组1个，开关1个，2.5V的灯泡2个，3.8V的灯泡2个，电流表3个，导线假设干，数据记录卡1张七、教学过程〔一〕创设情境导入新课上课前在黑板上挂上一串小彩灯，并使之发光。

【师问】：请大家认真观测这一串彩灯，你想提出什么问题？生：这些小彩灯有的亮，有的暗。

通过这些小彩灯的电流相等吗？它们是怎样连接的？师：谁上来试一试？生：把其中一个小灯泡旋下来后，其他灯都不亮了，说明这串小彩灯就是串联。

【师问】：彩灯间是串联，那么通过的电流是否相等，就是今日这节课所要探究的内容。

【师问】：把任意两个灯泡连接到电路中，请问两小灯泡的连接方式有几种？请大家分别画出这两种电路图。

【老师提出问题】：大家猜想一下在串联电路中，通过灯泡L1和L2的电流之间又有什么样的关系呢？并联电路中干路电流和各之路电流之间什么关系呢？〔二〕进行新课一是探究串联电路电流规律1.同学们大胆的提出自己的猜想并给出恰当的理由〔1〕由于我们的串联在电路中灯泡一样亮，我们猜想串联电路电流到处相等。

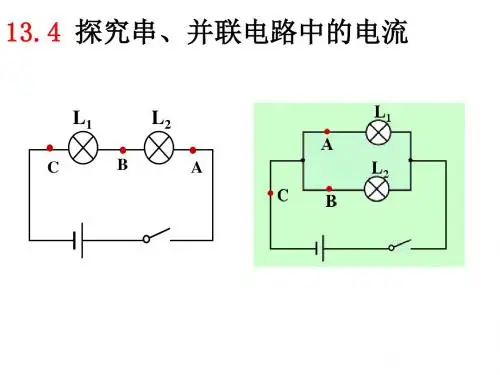
探究串并联电路中电流的规律知识和技能基本要求：探究串并联电路中电流的规律；训练连接电路和使用电流表的技能知识要点：科学探究活动的大致程序是：提出问题→猜想与假设→设计实验→进行实验→分析和论证→评估与交流过程：1、电路图2、器材：两节干电池，一只电流表，两只小灯泡，一只开关，导线若干3、步骤：一）探究串联电路中的电流①照图甲那样连好电路，断开开关。

②把电流表接在A点，经检查无误闭合开关，记下电流值I A。

③把电流表先后改接在电路中的B处和C处，分别测出两处电流I B、I C。

④比较I A、I B和I C可得出：I A=I B=I C。

二）探究并联电路中的电流①照图乙那样连好电路，断开开关。

②把电流表接在干路上的A点，经检查后确定无误再闭合开关，记下电流表的示数I A。

③把电流表分别改接在支路中的B、C处，分别测出两处电流I B、I C。

④将I A与I B+I C进行比较可得出：I A=I B+I C。

结论：串联电路中各处的电流相等，并联电路中干路上的电流等于各支路中的电流之和。

典型例题：例1、把较大的电灯与较小的电灯串联后接入电路中，如果通过较小电灯的电流是0.4A，那么通过较大电灯的电流将（）A、大于0.4AB、小于0.4AC、等于0.4AD、无法确定解：根据探究在串联电路中电流的特点：电流处处相等。

答案：C例2、如图所示的电路甲和乙中，电流表A1、A2、A3的示数分别是I1、I2和I3。

分析数据可得出两点结论：（1）并联电路的干路电流_________各支路电流之和，用符号关系式表示为___________；（2）___________电路中处处电流相等，用符号关系式表示为___________。

分析：根据在串联电路中电流处处相等，在并联电路中干路电流等于各支路电流之和。

解：（1）等于，I3＝I1+I2（2）串联，I1＝I2＝I3例3、如图所示电路，通电后，电流表A1、A2、A3的示数分别为I1、I2、I3，则各表示数关系是（）A、I1=I2+I3B、I1=I2=I3C、I1＜I2＜I3D、I1＞I2＞I3解：因为灯L1、L2、L3是并联的，而A1串联在干路上，测得的电流为总电流，A2是测L2、L3的总电流，A3是测L3支路中的电流，根据并联电路中干路上的电流等于各支路上电流之和可知I1＞I2＞I3。

探究串、并联电路中电流的规律教学过程一、导入新课1、在串联电路中〔如上图〕，A、B、C三点的电流有什么关系？2、在并联电路中〔如上图〕，A、B、C三点的电流有什么关系？二、进行新课学习内容一：探究串联电路中各点电流关系〔1〕、学生猜测： I A=I B=I C I A>I B>I C…………〔2〕、设计实验：把电流表分别接入串联电路中的A、B、C三点〔作出对应的电路图共三个〕，闭合开关，测出对应的电流值并记录在下面的表格中。

A点的电流I A B点的电流I B C点的电流I C 第一次测量第二次测量第三次测量〔3〕、换用的小灯泡，再次测量各点的电流，把测量结果记录在上表〔4〕、分析与论证：电流表在A、B、C三处的示数是相等的，即I A=I B=I C，换用另外两个灯泡，也得出相同的实验结果〔5〕、得出结论：在串联电路中，电流处处相等即I=I1=I2实验中的考前须知按画好的电路图连接电路时，应先开关。

连接好电路后，要先用开关，观察电流表指针偏转情况，确认无误后，再进行实验操作。

要更换的灯泡进行屡次实验，是为了。

串联电路电流规律的理解学习内容二：探究并联电路中电流规律〔1〕、学生猜测： I A=I B＋I C I A>I B>I C …………〔2〕、把电流表分别接入串联电路中的A、B、C三点〔作出对应的电路图共三个〕，闭合开关，测出对应的电流值并记录在下面的表格中。

A点的电流I A B点的电流I B C点的电流I C 第一次测量第二次测量第三次测量〔3〕、换用的小灯泡，再次测量各点的电流，把测量结果记录在上表〔4〕、分析与论证：电流表在C处的示数等于在A处和B处的示数之和，即I C=I A+I B，换用另外两个灯泡，也得出相同的实验结果〔5〕、得出结论：在并联电路中，干路的电流等于各支路的电流之和即I=I1＋I2训练题1.如下图，开关由闭合到断开，电流表A1、A2的示数I1、I2的变化〔〕A．I1变小，I2变大 B．I1不变，I2变大C．I1变大，I2变小 D．I1不变，I2变小1.某同学在使用电流表测量通过某一灯泡的电流的实验，闭合开关后，发现电流表的指针偏转到右图所示的位置，于是他立即断开开关.那么：〔1〕测量时产生这种现象的原因是 ； 〔2〕该同学为了完成实验,下一步应该采取的措施是 。

串联并联电路中的电流规律知识点串联电路和并联电路是电学中两个基本的连接方式，它们都有自己的电流规律。

下面我将分别介绍串联电路和并联电路中的电流规律知识点。

串联电路中的电流规律：1.串联电路中的电流是相等的：在串联电路中，电流只有一条路径可走，因此电流在整个串联电路中是相等的。

这意味着无论是穿过电源、电阻还是其他元件，电流的强度都保持不变。

2.元件电压之和等于电源电压：在串联电路中，电流通过电源、电阻和其他元件时会有不同的电压降。

根据基尔霍夫电压定律，串联电路中的元件电压之和等于电源电压。

换句话说，电源提供的电压等于电路中各个元件所消耗的电压之和。

3.串联电阻的总阻值等于各个电阻的阻值之和：在串联电路中，电阻是按照顺序连接的，因此串联电路的总阻值等于各个电阻的阻值之和。

这可以通过欧姆定律来证明，即总电阻等于总电压除以总电流。

并联电路中的电流规律：1.并联电路中的电流分流：在并联电路中，电流可以选择不同的路径流过。

根据基尔霍夫电流定律，电流在分流点分成相应的分支电流，然后汇聚到一起。

每一个分支电流的强度之和等于总电流。

2.元件电压相等：在并联电路中，元件具有相同的电压。

这是因为并联电路中，各个元件之间是平行连接的，它们在两个端点之间具有相同的电势差，从而保持相等的电压。

3.并联电阻的总阻值等于各个电阻的倒数之和的倒数：在并联电路中，电阻是平行连接的。

根据欧姆定律，电阻越小，电流越大。

因此，并联电路的总阻值等于各个电阻的倒数之和的倒数。

需要注意的是，串联电路和并联电路之间有一些明显的差异。

在串联电路中，电流是相等的，而电势差随电阻的不同会有变化。

而在并联电路中，电压是相等的，而电流随电阻的不同而分流。

这些规律使得串联电路和并联电路在不同的应用中具有不同的特性和用途。

同时，需要注意的是以上所述的电流规律均适用于理想的电路情况，现实中的电路中可能存在一些非理想特性，如电阻的内部电阻、线路的电容和电感等，这些都可能对电流规律产生一定的影响。

探究串、并联电路中电流的规律》电流规律学《探究串、并联电路中电流的规律》在我们的日常生活中，电无处不在。

从照明的电灯到驱动各种电器的电源，电路的作用至关重要。

而要深入理解电路，就必须探究其中电流的规律。

今天，让我们一起来探索串、并联电路中电流的那些神秘规律。

首先，我们来了解一下什么是串联电路。

串联电路就像是一条单一的道路，电流只有一条路径可走。

想象一下，把几个灯泡一个接一个地连接起来，通过的电流就必须依次经过每个灯泡，这就是串联电路。

在串联电路中，电流的规律是：电流处处相等。

这是为什么呢？我们可以这样来理解，电流就好比是水流，在一个没有分支的管道中，无论在哪个位置，水的流量都是一样的。

同样的道理，在串联电路中，由于电流没有其他的分支路径，所以通过每个元件的电流大小都是相同的。

为了更直观地验证这个规律，我们可以进行一个简单的实验。

准备一个电源、几个不同阻值的电阻、一个电流表和若干导线。

将电阻依次串联起来，然后把电流表接入电路的不同位置，你会发现无论电流表接在哪里，显示的电流数值都是相同的。

接下来，我们再看看并联电路。

并联电路就像是多条道路并行，电流有多个分支可以选择。

比如家庭中的各个电器，它们通常都是并联在电路中的。

在并联电路中，电流的规律是：干路电流等于各支路电流之和。

这又该怎么理解呢？还是用水流来打比方，假设水流从一个主管道分流到几个支管道，那么主管道中的水流量就等于各个支管道水流量的总和。

在并联电路中，电流从电源的正极出发，分成若干支路，然后在负极汇合，所以干路中的电流就是各个支路电流的总和。

同样，我们可以通过实验来验证。

按照电路图连接好电源、电阻（组成并联电路）和电流表，分别测量干路和各支路的电流，你会发现干路电流的数值恰好等于各支路电流数值之和。

了解了串、并联电路中电流的规律，对我们的生活和学习有什么实际的帮助呢？在家庭电路中，我们知道各个电器是并联的，所以当我们同时使用多个电器时，干路中的电流会增大。

探究串、并联电路的电流规律通过实验探究得出串并联电路中的电流规律，即串联电路中电流处处相等，并联电路中干路上电流等于各支路中的电流之和。

具体要求：会根据需要确定各器件的连接方式，会画电路图；电流表会正确使用，包括调零，选择适当的量程（大小量程的5倍数量关系），注意“＋”、“－”接线柱，读数时，要明确量程与分度值；在接、拆电路时，必须断开开关；为了使实验结论具有普遍性，应换用不同规格的灯泡进行多次实验，测出多组数据，会分析实验数据，得出结论。

下面举例说明：例1 某新型手电筒由电池，开关和三粒相同的LED 灯珠连接而成，工作时每粒灯珠都正常发光且电压都为U 。

为探究三粒灯珠的连接方式，小明从正在发光的手电筒中取下其中一粒灯珠，发现另外两粒灯珠不亮，则手电筒中三粒灯珠是_______联的，手电筒正常工作时通过三粒灯珠的电流_______（相等/不相等）．解析：“取下其中一粒灯珠，发现另外两粒灯珠不亮”，说明用电器工作是相互影响的，所以，三粒灯珠是串联，而串联电路中电流处处相等．答案：串；相等．例2 在图甲所示的电路中，闭合开关S 后，两个电流表的指针指在图乙所示的同一位置，则电灯L 2中的电流I 2= ______A 。

解析：本题的关键是确定量程。

并联电路中干路上电流大于支路上电流，现指针指在同一位置，所以，干路上的电流表使用的是大量程，电流为1A ，L 1支路上电流表使用的是小量程，电流为0.2A ，根据并联电路中的电流规律，I 2=I －I 1=0.8A ． 答案：0.8．例3 如图，电流表A 的示数为1.5A ，电流表A 1的示数为0.8A ，电流表A 2的示数为1.2A ，试求通过L 1，L 2，L 3的电流分别是_____A 、_____A 和______A ．解析：根据“去表法”（把电流表当作导线）可知，三个灯泡是并联的，其中A 1表测得是L 2和L 3的电流，A 2表测得是L 1和L 2的电流，A 表测得是L 1、L 2和L 3的电流，即总电流。

探究串、并联电路中电流的规律》电流路径析《探究串、并联电路中电流的规律——电流路径析》在我们日常生活和学习中，电无处不在。

从点亮的灯泡到运行的电器，电路的作用不可或缺。

而要深入理解电路的工作原理，探究串、并联电路中电流的规律是关键。

其中，对电流路径的分析更是重中之重。

首先，让我们来认识一下什么是串联电路。

串联电路就像是一条单一的通道，电流只有一条路径可走。

想象一下，有几个小灯泡依次连接在一起，电流就如同水流一样，依次流过每个灯泡，没有其他的岔路可选择。

在串联电路中，电流的路径是非常明确和单一的。

假设我们有一个由电池、两个灯泡和导线组成的串联电路。

当电池接通时，电流从电池的正极出发，经过第一个灯泡，然后经过第二个灯泡，最后回到电池的负极。

在这个过程中，电流的大小始终保持不变。

这是因为在串联电路中，通过每个元件的电流是相等的。

为什么会这样呢？我们可以这样理解，电流就像一群人在排队通过一个狭窄的通道，无论这个通道中有多少个关卡，通过每个关卡的人数都是一样的。

所以，在串联电路中，只要其中一个元件出现问题，比如一个灯泡灯丝烧断了，整个电路就会断路，电流无法通过，所有的元件都无法工作。

接下来，我们再看看并联电路。

并联电路则像是一个有多个分支的道路系统，电流有多条路径可以选择。

还是以灯泡为例，如果几个灯泡的两端分别连接在一起，然后再与电源相连，这就是并联电路。

在并联电路中，电流会分成几路分别通过各个支路。

比如有两个支路，电流会根据支路的电阻大小分配。

电阻小的支路，电流通过的量就大；电阻大的支路，电流通过的量就小。

但无论如何，总电流等于各支路电流之和。

举个例子，如果一个并联电路中有两个支路，一个支路上连接着一个电阻较小的灯泡，另一个支路上连接着一个电阻较大的灯泡。

当电源接通时，电流从电源正极出发，一部分电流会流向电阻较小的灯泡所在的支路，另一部分电流会流向电阻较大的灯泡所在的支路，最后所有的电流在电源负极汇合。