陕西省商洛市商南县鹿城中学2017-2018年度数学必修一第一次月考数学试题(无答案)

2017——2018学年度下学期高一年级第一次月考数学试题考试时间：120分钟 满分：150分第Ⅰ卷 （客观题 共60分）一、选择题（共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1.2=αrad 的终边在（ ） A.第一象限 B.第二象限 C.第三象限 D.第四象限2.cos300°=（ ） A.21 B.21- C.23 D.23- 3.已知α为第三象限角，则2α所在的象限是（ ） A ．第一或第二象限 B ．第二或第三象限 C ．第一或第三象限 D ．第二或第四象限 4.设a=sin1,b=cos1,c=tan1,则a,b,c 的大小关系是（ ）A.a<b<cB.a<c<bC. b<a<cD.b<c<a 5.函数)4tan(x y -=π的定义域是（ ）A.⎭⎬⎫⎩⎨⎧∈≠R x x x ,4πB.⎭⎬⎫⎩⎨⎧∈-≠R x x x ,4π C.⎭⎬⎫⎩⎨⎧∈∈+≠R x Z k k x x ,,4ππ D.⎭⎬⎫⎩⎨⎧∈∈+≠R x Z k k x x ,,43ππ 6.已知正弦函数f(x)的图像过点），（m 37π，则m 的值为（ ） A ．2 B ． C ．23D ．1 7.要得到函数)62sin(2)(π+=x x f 的图象，可将x y 2sin 2=的图象向左平移（ ）A.6π个单位 B.3π个单位 C.4π个单位 D.12π个单位 8.设α是第二象限角，且35cos ,32m 3sin +-=+-=m m m αα，则m 的值为（ ） A.532<<m B.910 C.910或2 D. 2 9.函数的图象大致为（ ）10.将函数()sin 26f x x π⎛⎫=- ⎪⎝⎭的图象向右平移12π个单位后得到的图象的一条对称轴是 （ ） A. 4x π=B. 38x π=C. 512x π=D. 724x π= 11.在一个港口，相邻两次高潮发生的时间相距12h ，低潮时水深9m,高潮时水深为15m. 每天潮涨潮落时，该港口水的深度y(m)关于时间t(h)的函数图象可以近似地看成函数k wt A ++=)sin(y ϕ的图象，其中24t 0≤≤，且t=3时涨潮到一次高潮，则该函数的解析式可以是（ ） A. 12t 6sin3y +=πB.12t 6sin-3y +=πC.12t 12sin3y +=πD.12123cosy +=t π12.设函数y=f(x)的定义域为D ，若任取D x x ∈21,，当a x x 221=+时，b x f x f 2)()(21=+,则称点（a,b)为函数y=f(x)图象的对称中心.研究函数1sin )(3++=x x x f 的某一个对称中心，并利用对称中心的上述定义，可得到f(-2015)+f(-2014)+...+f(2014)+f(2015)=( ) A.0 B.4030 C.4028 D.4031第Ⅱ卷（主观题 共90分）二、填空题（共4小题，每小题5分，共20分）13.若3tan =α，则2cos sin ）（αα+= ． 14.一个扇形的弧长与面积的数值都是5，则这个扇形中心角的弧度数为 ．15.函数R x y ∈+=),43x -sinπ（的单增区间是 ．（原创）16.设)22,0)(wx sin3)(πϕπϕ<<->+=w x f （的图象关于直线32π=x 对称，它的周期是π，则下列叙述（1）f(x)的图象过点)21,0(；（2）f(x)的一个对称中心是)0,125(π；（3）f(x)在]32,12[ππ上是减函数；（4）将f(x ）的图向右平移ϕ个单位得到函数y=3sinwx 的图象。

商南县高级中学2017-2018学年度第一学期高三年级第一次模拟考试数学（理科）试题命题人：审题人：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题）两部分，考试时间120分钟,满分150分.考生应首先阅读答题卡上的文字信息，然后在答题卡上作答，在试卷上作答无效,交卷时只交答题卡。

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题）两部分.考生根据要求作答,分别答在答题卡（Ⅰ卷）和答题卡(Ⅱ卷）上．第Ⅰ卷（选择题)注意事项：1.答第Ⅰ卷前，考生务必先将自己的姓名、准考证号、考试科目涂写在答题卡上。

2.选择题答案使用2B铅笔填涂,每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动,用橡皮擦干净后，再选涂其它答案标号.在试题卷上作答无效.3.本卷共12小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项符合题目要求。

一．选择题：本大题共12个小题，每小题5分，共60分。

1.函数的定义域为（）A．B．C。

(—1，1) D．（-1，0）∪（0,1）2。

若错误!d x＝3＋ln 2（a>1），则a的值是( )A．2 B．3 C．4 D．63. 若实数x,y 满足｜x －1｜－ln ＝0，则y 关于x 的函数图象的大致形状是( )4．下列四个结论中正确的个数是( ) ①若q p ∧为假命题，则q p ,均为假命题； ②命题：“1sin ,≤∈∀x R x ”的否定是 “1sin ,00>∈∃x R x ”;③“若,4π=x 则1tan =x ”的逆命题为真命题；④若)(x f 是R 上的奇函数，则0)3(log )2(log 23=+f f A ．1 B ．2 C ．3D ．4 5。

设均为正数,且，，，则（ ）A ．m ＞p ＞qB 。

p ＞m ＞q C. m ＞q ＞p D. p＞q ＞m 6．已知函数(2)11()log 1a a x x f x xx --≤⎧=⎨>⎩,若()f x 在R 上单调递增，则实数a 的取值范围为( )A ．(1,2)B ．(2,3)C ．(2,3]D ．(2,)+∞7.幂函数253(1)m y m m x --=--在()0,x ∈+∞时为减函数，则=m ()A ．—1B ．2C ．2或—1D ．1 8．已知函数()f x 是定义在R 上的奇函数，其最小正周期为3，且3(,0)2x ∈-时,2()log (31)f x x =-+,则(2017)f =（ )A ．2-B ．2C ．4D ．2log 79。

陕西省2017-2018学年高一（普通班）4月月考数学试题一、选择题(本大题共12小题,每小题5分,共60分)1、在ABC ∆中，则=∠B （ ）2、在ABC ∆中，已知5,30,6000===c C A ，则=a （ ）A ．5B ．10C 3、在AB C ∆中，内角C B A ,,的对边分别为c b a ,,，若0120,4,3===C b a ，则AB C ∆的面积是（ ）A ．3B ．33C ．6D ．364、有一长为1公里的斜坡，它的倾斜角为20°，现要将倾斜角改为10°，则坡底要伸长（ ） A. 1公里 B. sin10°公里C. cos10°公里D. cos20°公里5、在ABC ∆中，,4,2,2π=∠==A b a 则=∠B （ ）A.3π B. 6π C. 6π或65π D. 3π或32π 6、在△ABC 中，角A ，B ，C 所对的边分别是a ，b ，c,若cos cos a cA C=，则△ABC 的形状是（ ） A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰或直角三角形7、在△ABC 中，A ，B ，C 的对边分别为a ，b ，c ，且sin B ＝21，sin C ＝23则a ：b ：c 为（ ） A ．2:3:1 B ．3:1:1 C ．3:2:1 D ．3:1:2或3:1:1 8、在⊿ABC 中，A=45°,B=60°,a=10,则b 等于（ ）.A.25B.210C.6310D.65 9.在△ABC 中,A ∶B ∶C=4∶1∶1,则a ∶b ∶c 等于( ) (A)∶1∶1 (B)2∶1∶1 (C)∶1∶2 (D)3∶1∶110.在△ABC 中,a,b,c 分别为角A,B,C 所对的边,c ·cos A=b,则△ABC( ) (A)一定是锐角三角形 (B)一定是钝角三角形 (C)一定是直角三角形 (D)一定是斜三角形11.在△ABC 中,a=6,B=30°,C=120°,则△ABC 的面积为() (A)9(B)8(C)9(D)1812.在三角形ABC 中,若三个内角A 、B 、C 的对边分别是a 、b 、c,a=1,c=4,B=45°,则sin C 的值等于( )(A) (B) (C) (D)二、填空题：（本大题共4小题，每小题5分，共20分）13.在△ABC 中，如果sin :sin :sin 2:3:4A B C =，那么cos C 等于 。

第一师高级中学2017-2018学年第一学期高一年级第一次月考数学试卷第Ⅰ卷（选择题 共60分）一、选择题：（本大题共 12 小题，每小题 5 分，共 60 分.） 1、若{}{}0,1,2,3,|3,A B x x a a A ===∈，则A B ⋂=（A ）{}1,2 （B ）{}0,1 （C ）{}0,3 （D ）{}3 2.下列四组函数，表示同一函数的是（ ）（A ）2)(x x f =,x x g =)( （B ）x x f =)(,xx x g 2)(= （C ）4)(2-=x x f ,22)(-⋅+=x x x g （D ）1)(+=x x f ,⎩⎨⎧-<---≥+=1111)(x x x x x g3.设集合和集合都是实数集，映射B A f →:是把集合中的元素映射到集合中的元素246x x -+，则在映射下，B 中的元素2在A 中所对应的元素组成的集合是（ ）. {2}-. .{2,2}-.4、设全集为R , 函数11)(+⋅-=x x x f 的定义域为M , 则C MR 为………………………… （ ）(A) （－∞，1） (B) ),1[+∞(C) ,1][1,)(∞-⋃+∞-D ,1)(1,)(∞-⋃+∞- 5.设全集{},|-24,{|U R A x x B x y ==≤<=则图中阴影部分表示的集合为（ ）温馨提示：1、本试卷分第Ⅰ卷和第Ⅱ卷两部分，满分150分，考试时间120分钟2、本试卷命题范围：数学必修一第一章集合与函数3、正式开考前，请在规定位置填写班级、姓名、学号，正式开考后才允许答题。

A. {|2}x x ≤-B. {|2}x x >-C. {}|4x x ≥D.{|4}x x ≤6.若不等式组⎩⎨⎧->-≥+2210x x a x 无解，则实数a 的取值范围是（ ）A ．a ≥一1B ．a <－1C ．a ≤1 D.a ≤－17.下列函数中，既是偶函数，又是在区间(0，＋∞)上单调递减的函数为 ( ) A ．y ＝1x 2 B ．y ＝1xC ．y ＝x 2D ．y ＝x 138. f (x )=2211,2,1,xx x x x ⎧-≤⎪⎨+-⎪⎩＞则f 1(2)f ⎛⎫ ⎪⎝⎭的值为A.1516B.1627- C.89D.189．当0≤x ≤2时，a <－x 2＋2x 恒成立，则实数a 的取值范围是 ( ) A ．(－∞，1] B ．(－∞，0] C ．(－∞，0) D ．(0，＋∞)10.已知函数y=f(x)与y=g(x)的图象如图，则y=f(x)·g(x)的大致图象为( )11.知函数()835+++=cx bx ax x f ，且()102=-f ，则函数()2f 的值为（ ）A. -2B.-6C.6D.812、对实数和，定义运算“◎”：◎()()⎩⎨⎧>-≤-11b a b b a a ，设函数()=x f （22-x ）◎（2x x -），R x ∈。

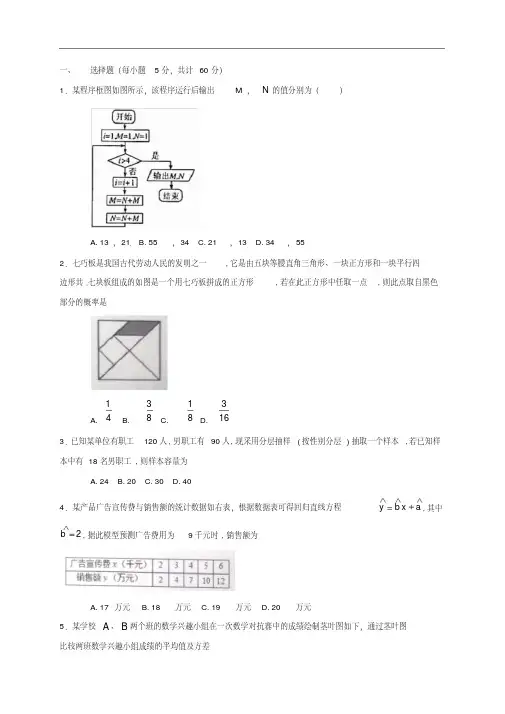
2017-2018学年度第一学期高一月考（1） 数学试题一、选择题（本大题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的.）1.设集合{m Z|3m 2}M =∈-<<，{Z|13}N n n =∈-≤≤,M N = ( )A ．{0,1}B ．{-1,0，1}C ．{0,1,2}D ．{-1,0,1,2}2．二次函数2y x bx c =++的图象的对称轴是2x =，则有( ) A ．(1)(2)(4)f f f << B ．(2)(1)(4)f f f << C ．(2)(4)(1)f f f <<D ．(4)(2)(1)f f f <<3.已知集合{1,2,3,}A a =，2{3,}B a =，则使得()R AB =∅ð成立的a 的值的个数为（ ） A ．2 B ．3 C ．4 D ．54.设函数22 2 1()2 3 1x x x f x x x ⎧--<=⎨-≥⎩，若0()1f x =，则0x = （ ）A ．－1或3 B. 2或3 C.－1或2 D. －1或2或3 5.给定下列函数： ①1()f x x=②()||f x x =- ③()21f x x =-- ④2()(1)f x x =-，满足“对任意12,(0,)x x ∈+∞，当12x x <时，都有 12()()f x f x >”的条件是( )A.①②③B. ②③④C.①②④D.①③④6.设()12g x x =-，()()2210x f g x x x -=≠⎡⎤⎣⎦则12f ⎛⎫= ⎪⎝⎭（ ） A ．4 B ．0 C ．15 D ．167.已知函数2221()2x f x x -=+，则函数()f x 的值域是（ ）A ．1,12⎡⎤-⎢⎥⎣⎦B ．1,22⎡⎤-⎢⎥⎣⎦ C ．1,22⎡⎫-⎪⎢⎣⎭ D ．1,12⎛⎫- ⎪⎝⎭8.若函数()f x =(2)()1f x g x x =-的定义域是（ ）A ．1,12⎡⎤-⎢⎥⎣⎦B ．1,22⎡⎤-⎢⎥⎣⎦ C ．1,22⎛⎤- ⎥⎝⎦ D ．1,12⎛⎫- ⎪⎝⎭9.定义在R 上的函数()f x 满足()()()2f x y f x f y xy +=++（x y ∈R ，），(1)2f =，则(3)f -等于（ ）A ．2B ．3C ．6D ．910.已知函数()()⎪⎩⎪⎨⎧>++≤--=1,11,12x ax ax x x a x f 在(),-∞+∞上单调递增，则实数a 的取值范围为（ ）A ．(]4,1B ．(]4,2C ．()4,2D ．()∞+，2二、填空题(每小题4分，共20分.把答案填在答题卡相应位置.) 11.全集(){},,I x y x R y R =∈∈集合()3,12y A x y x -⎧⎫==⎨⎬-⎩⎭(){},1B x y y x ==+，则()I C A B= 12.已知函数()f x ，()g x 分别由下表给出[(1)]f g 的值为;满足[()][()]f g x g f x >的x 的值是.13.已知函数2()(21)3(0)f x ax a x a =+--≠在区间3[,2]2-上的最大值为1，则a =14.已知函数⎩⎨⎧<-≥+=0,40,4)(22x x x x x x x f 若(32)()f a f a ->,则实数a 的取值范围是 .15.已知函数()f x =在区间[)1,-+∞有意义，则实数a 的取值范围是 .三．解答题（本大题共4小题，共40分。

2017-2018学年高一年级第一次月考试题数 学本题共150分 时间120分钟一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知全集U={0，1，2，3，4}，集合A={1，2，3}，B={2，4}，则（∁U A ）∪B 为（）A ．{1，2，4}B ．{2，3，4}C ．{0，2，4}D ．{0，2，3，4}2．下列哪组中的两个函数是相等函数（） A. ()4444)()(x x g x x f ==， B. 2)(24)(2-=+-=x x g x x x f ， C. ⎩⎨⎧<>==0,10,1)(1)(x x x g x f ， D.33)()(x x g x x f ==， 3．已知集合},1|{2R x x y y M ∈-==，}2|{2x y x N -==，则=N M （） A ．),1[+∞-B ．]2,1[-C ．),2[+∞D ．φ 4．如果函数2()2(1)2f x x a x =+-+在(,4]-?上是减函数，那么实数a 取值范围是（）A ．3a ?B ．3a ?C ．5a £D ．5a ³5．若函数)(x f 满足89)23(+=+x x f ，则)(x f 的解析式是（）A ．89)(+=x x fB ．23)(+=x x fC ．43)(--=x x fD ．23)(+=x x f 或43)(--=x x f6．若)1(-x f 的定义域为［1，2］，则)2(+x f 的定义域为（ ）A ．[0,1] B. [2,3] C. [-2,-1] D. 无法确定7. 下列说法中，正确的有（） ①函数y {1}x x ³ ②函数21y x x =++在0+¥（，）上是增函数； ③函数3()1()f x x x R =+?，若()2f a =，则()2f a -=-；④已知()f x 是R 上的增函数，若0,a b +>则有()()()()f a f b f a f b +>-+-．A ．0个B ．1个C ．2个D ．3个 8．设2)(2++=bx ax x f 是定义在]2,1[a +上的偶函数，则)(x f 的值域为（ ）A. [-10，2]B.[-12，0]C. [-12，2]D. 与b a ,有关，不能确定9．已知函数⎪⎩⎪⎨⎧<-≥-=2,1)21(2,)2()(x x x a x f x 满足对任意的实数21x x ≠都有0)()(2121<--x x x f x f 成立,则实数a 的取值范围为（）A ．)2,(-∞B ．]813,(-∞C ．]2,(-∞D ．)2,813[ 10．已知函数3212++=kx kx y 的定义域为R ，则实数k 的取值范围是（） A. [0，3) B. [0，3] C. (0，3)D. [-3，0] 11.若函数)(x f 为偶函数，且在),0(+∞上是减函数，又0)3(=f ，则0)()(<-+x x f x f 的解集为（）A ．)3,3(-B ．),3()3,(+∞--∞C ．),3()0,3(+∞-D ．)3,0()3,( --∞ 12．对于集合N M ,，定义{}N x M x x N M ∉∈=-且,|，()()M N N M N M -⋃-=⊕，设⎭⎬⎫⎩⎨⎧-≥=49|x x A ，{}0|<=x x B ，则=⊕B A （） ]0,49.(-A )0,49[.-B [)+∞⋃--∞,0)49,(.C ()+∞⋃--∞,0]49,(.D二、填空题(本大题共4小题，每小题5分，共20分.把答案填在题中横线上)13．已知函数)1,0(2)(1≠>+=-a a a x f x 且，则)(x f y =恒过的定点为．14．213125.01041])833(81[])87(3[)8110000(----+⨯⨯-= ． 15．若函数()(0,1)x f x a a a =>?且在[﹣1，2]上的最大值为4，最小值为m，且函数()(14g x m =-[0,)+?上是增函数，则a =．16．设2,,(),.x x a f x x x a <⎧=⎨≥⎩对任意实数b ，关于x 的方程()0f x b -=总有实数根，则a 的取值范围是.三、解答题(本大题共6小题，解答应写出相应的文字说明，证明过程或演算步骤)17.（本小题满分10分）已知集合}73|{≤≤=x x A ，}102|{<<=x x B ，}121|{-≤≤+=m x m x C ．（1）求A B U ；()R C A B I ；（2）若A C C I =，求m 的取值范围．18.（本小题满分12分）某地煤气公司规定，居民每个月使用的煤气费由基本月租费、保险费和超额费组成．每个月的保险费为3元，当每个月使用的煤气量不超过a 3m 时，只缴纳基本月租费c 元；如果超过这个使用量，超出的部分按b 元/3m 计费．（1）请写出每个月的煤气费y (元)关于该月使用的煤气量x (3m )的函数解析式；（2）如果某个居民7—9月份使用煤气与收费情况如下表，请求出．其中，仅7月份煤气使用量未超过a 3m .19.（本小题满分12分）已知函数()f x 是定义域为R 的奇函数，当0x >时，2()21f x x x =-+.(1)求出函数()f x 在R 上的解析式；（2）画出函数()f x 的图象．20．（本小题满分12分）已知函数()f x 的定义域为R ，且满足对于定义域内任意的y x ,都有等式)()()(y f x f y x f +=+成立．（1）求)0(f 的值；（2）判断()f x 的奇偶性并证明；（3）若(4)1f =，且()f x 在),0[+∞上是增函数，解关于x 的不等式3)62()13(≤--+x f x f .21.（本小题满分12分）已知定义域为R 的函数1()21x f x a =++为奇函数． （1）求a 的值；（2）证明函数)(x f 在R 上是减函数；（3）若不等式22(2)(2)f t t f t k -+-0<对任意的实数t 恒成立，求k 的取值范围.22.（本小题满分12分）已知二次函数)(x f 的最小值为1，且3)2()0(==f f .（1）求)(x f 的解析式；（2）若)(x f 在区间]1,2[+a a 上不单调，求实数a 的取值范围；（3）在区间[1,1]-上，)(x f y =的图像恒在122++=m x y 的图像上方，试确定实数m 的取值范围．。

2017-2018第二学期高一数学第一次月考试卷一、选择题（本大题共12小题，共60.0分）1.已知全集U={1，2，3，4，5}，A={1，3}，B={2，4}，则∁U(A∪B)=( )A. 5B. {5}C. ⌀D. {1，2，3，4}【答案】B【解析】解：全集U={1，2，3，4，5}，A={1，3}，B={2，4}，∴A∪B={1，2，3，4}；∴∁U(A∪B)={5}．故选：B．根据并集与补集的定义，写出运算结果即可．本题考查了集合的定义与运算问题，是基础题目．2.函数f(x)=1lg(x+1)+√2−x的定义域为( )A. (−1，0)∪(0，2]B. [−2，0)∪(0，2]C. [−2，2]D. (−1，2]【答案】A【解析】解：由题意得：{x+1>0x+1≠12−x≥0解得：−1<x≤2且x≠0，故选：A．根据对数函数的性质以及二次根式的性质求出函数的定义域即可．本题考查了求函数的定义域问题，考查对数函数以及二次根式的性质，是一道基础题．3.函数f(x)在(−∞，+∞)单调递减，且为奇函数.若f(1)=−1，则满足−1≤f(x−2)≤1的x的取值范围是( )A. [−2，2]B. [−1，1]C. [0，4]D. [1，3]【答案】D【解析】解：∵函数f(x)为奇函数．若f(1)=−1，则f(−1)=1，又∵函数f(x)在(−∞，+∞)单调递减，−1≤f(x−2)≤1，∴f(1)≤f(x−2)≤f(−1)，∴−1≤x−2≤1，解得：x∈[1，3]，故选：D由已知中函数的单调性及奇偶性，可将不等式−1≤f(x−2)≤1化为−1≤x−2≤1，解得答案．本题考查的知识点是抽象函数及其应用，函数的单调性，函数的奇偶性，难度中档．4.已知a=21.3，b=40.7，c=log38，则a，b，c的大小关系为( )A. a<c<bB. b<c<aC. c<a<bD. c<b<a【答案】C【解析】解：∵c=log38<2<a=21.3<b=40.7=21.4，∴c<a<b．故选：C．利用c=log38<2<a=21.3<b=40.7=21.4，即可得出．本题考查了指数函数与对数函数的单调性，考查了推理能力与计算能力，属于基础题．5.幂函数f(x)=(m2−2m+1)x2m−1在(0，+∞)上为增函数，则实数m的值为( )A. 0B. 1C. 2D. 1或2【答案】C【解析】解：∵幂函数f(x)=(m2−2m+1)x2m−1在(0，+∞)上为增函数，∴{m2−2m+1=12m−1>0，解得m=2．故选：C．利用幂函数的定义及性质列出方程组，由此能求出实数m的值．本题考查实数值的求法，是基础题，解题时要认真审题，注意幂函数的定义及性质的合理运用．6.方程log5x+x−2=0的根所在的区间是( )A. (2，3)B. (1，2)C. (3，4)D. (0，1)【答案】B【解析】解：方程log5x+x−2=0的根就是y=log5x+x−2的零点，函数是连续函数，是增函数，可得f(1)=0+1−2=−1<0，f(2)=log52+2−2>0，所以f(1)f(2)<0，方程根在(1，2)．故选：B．方程的根转化为函数的零点，判断函数的连续性以及单调性，然后利用零点判定定理推出结果即可．本题考查函数的零点判定定理的应用，考查计算能力．7.已知α是锐角，a⃗=(34，sinα)，b⃗ =(cosα√3)，且a⃗//b⃗ ，则α为( )A. 15oB. 30oC. 30o或60oD. 15o或75o 【答案】C【解析】解：根据题意，a⃗=(34，sinα)，b⃗ =(cosα√3)，若a⃗//b⃗ ，则有sinαcosα=34×√3=√34，即有sin2α=√32，又由α是锐角，则有0∘<2α<180∘，即2α=60∘或120∘，则α=30o或60o，故选：C．根据题意，由a⃗//b⃗ ，结合向量平行的坐标表示公式可得sinαcosα=34×3=√34，由正弦的二倍角的公式可得sin2α=√32，又由α的范围可得2α=60∘或120∘，即可得答案．本题考查平面向量平行的坐标表示，关键是掌握平面向量平行的坐标表示方法．8.已知sinθ+cosθ=13，则sin2θ=( )A. 89B. −89C. 49D. −49【答案】B【解析】解：将sinθ+cosθ=13左右两边平方得：(sinθ+cosθ)2=19，整理得：sin 2θ+2sinθcosθ+cos 2θ=1+sin2θ=19，则sin2θ=−89．故选B将已知的等式左右两边平方，利用同角三角函数间的基本关系及二倍角的正弦函数公式化简，整理后即可求出sin2θ的值．此题考查了二倍角的正弦函数公式，以及同角三角函数间的基本关系，熟练掌握公式及基本关系是解本题的关键．9. 将函数y =sinx 的图象向左平移π2个单位，得到函数y =f(x)的函数图象，则下列说法正确的是( ) A. y =f(x)是奇函数B. y =f(x)的周期为πC. y =f(x)的图象关于直线x =π2对称D. y =f(x)的图象关于点(−π2，0)对称【答案】D【解析】解：将函数y =sinx 的图象向左平移π2个单位，得y =sin(x +π2)=cosx ．即f(x)=cosx ．∴f(x)是周期为2π的偶函数，选项A ，B 错误；∵cos π2=cos(−π2)=0， ∴y =f(x)的图象关于点(−π2，0)、(π2，0)成中心对称．故选：D ．利用函数图象的平移法则得到函数y =f(x)的图象对应的解析式为f(x)=cosx ，则可排除选项A ，B ，再由 cos π2=cos(−π2)=0即可得到正确选项． 本题考查函数图象的平移，考查了余弦函数的性质，属基础题．10. 已知△ABC 的内角A ，B ，C 的对边分别是a ，b ，c ，若A =π3，则b 2+c 2−a 2bc 的值为( )A. 12B. √32C. 1D. √3 【答案】C【解析】解：∵A =π3，∴cosA =12=b 2+c 2−a 22bc =12⋅b 2+c 2−a 2bc ， ∴b 2+c 2−a 2bc =1．故选：C ．由已知利用余弦定理即可计算得解．本题主要考查了余弦定理在解三角形中的应用，属于基础题．11. 已知△ABC 中，A ：B ：C =1：1：4，则a ：b ：c 等于( )A. 1：1：√3B. 2：2：√3C. 1：1：2D. 1：1：4【答案】A【解析】解：△ABC 中，∵A ：B ：C =1：1：4，故三个内角分别为30∘、30∘、120∘，则a ：b ：c =sin30∘：sin30∘：sin120∘=1：1：√3，故选：A ．利用三角形内角和公式求得三个内角的值，再利用正弦定理求得a ：b ：c 的值．本题主要考查三角形内角和公式、正弦定理的应用，属于基础题．12. 已知函数f(x)={(12)x ,x ≤0log 2(x +2),x >0，若f(x 0)=2，则x 0=( ) A. 2或−1 B. 2 C. −1 D. 2或1【答案】A【解析】解：∵函数f(x)={(12)x ,x ≤0log 2(x +2),x >0，f(x 0)=2， ∴x 0≤0时，f(x 0)=(12)x 0=2，解得x 0=−1；x 0>0时，f(x 0)=log 2(x 0+2)=2，解得x 0=2．∴x 0的值为2或−1．故选：A ．利用分段函数性质求解．本题考查函数值的求法，是基础题，解题时要认真审题，注意分段函数的性质的合理运用．二、填空题（本大题共4小题，共20.0分）13. sin500(1+√3tan100)的值______ ．【答案】1【解析】解：∵sin50∘(1+√3tan10∘)=sin50∘(cos10∘+√3sin10∘cos10∘) =sin50∘⋅2cos50∘cos10∘ =sin100∘cos10∘=cos10∘cos10=1故答案为：1．将所求关系式中的切化弦，利用辅助角公式与诱导公式即可求得答案．本题考查三角函数的恒等变换及化简求值，切化弦，利用辅助角公式是关键，属于中档题．14. 设f(x)为定义在R 上的奇函数，f(1)=1，f(x +2)=f(x)+f(2)，则f(5)= ______ ．【答案】5【解析】解：f(x)为定义在R 上的奇函数，可得f(0)=0；f(1)=1，f(x +2)=f(x)+f(2)，当x =1时，f(3)=f(1)+f(2)=1+f(2)，当x =−1时，f(1)=f(−1)+f(2)，可得f(2)=2．f(5)=f(3)+f(2)=1+2f(2)=1+4=5．故答案为：5．利用奇函数求出f(0)，利用抽象函数求出f(2)，转化求解f(5)即可．本题考查抽象函数的应用，函数值的求法，赋值法的应用，考查计算能力．15. f(x)=Asin(ωx +φ)(A >0，ω>0，−π2<φ<π2)的部分图象如图所示，则函数f(x)的解析式为______ 【答案】f(x)=2sin(2x +π6) 【解析】解：由f(x)=Asin(ωx +φ)(A >0，ω>0，−π2<φ<π2)的部分图象，可得A =2，14⋅2πω=5π12−π6，∴ω=2． 再根据五点法作图可得2⋅π6+φ=π2，∴φ=π6，∴f(x)=2sin(2x +π6).故答案为：f(x)=2sin(2x +π6)．由函数的图象的顶点坐标求出A ，由周期求出ω，由五点法作图求出φ的值，可得函数的解析式．本题主要考查由函数y =Asin(ωx +φ)的部分图象求解析式，由函数的图象的顶点坐标求出A ，由周期求出ω，由五点法作图求出φ的值，属于基础题．16. 计算：(23)0+3×(94)−12+(lg4+lg25)的值是______ ． 【答案】5【解析】解：(23)0+3×(94)−12+(lg4+lg25) =1+3×23+lg100 =1+2+2=5．故答案为：5．利用指数，对数的性质、运算法则求解．本题考查对数式、指数式化简求值，是基础题，解题时要认真审题，注意指数、对数性质及运算法则的合理运用．三、解答题（本大题共6小题，共70.0分）17. 已知向量a ⃗ =(4，3)，b ⃗ =(1，2)．(1)设a ⃗ 与b ⃗ 的夹角为θ，求cosθ的值；(2)若a ⃗ −λb ⃗ 与2a ⃗ +b ⃗ 垂直，求实数λ的值..【答案】解：(1)向量a ⃗ =(4，3)，b ⃗ =(1，2)，则a ⃗ ⋅b ⃗ =4×1+3×2=10，且|a ⃗ |=√42+32=5，|b ⃗ |=√12+22=√5；设a ⃗ 与b ⃗ 的夹角为θ，则cosθ=a⃗ ⋅b ⃗ |a ⃗ |×|b ⃗ |=105×√5=2√55； (2)若a ⃗ −λb ⃗ 与2a ⃗ +b ⃗ 垂直，则(a ⃗ −λb ⃗ )⋅(2a ⃗ +b ⃗ )=0，即2a ⃗ 2+(1−2λ)a ⃗ ⋅b ⃗ −λb ⃗ 2=0，所以2×52+10(1−2λ)−5λ=0，解得λ=125．【解析】(1)根据平面向量的坐标表示与数量积运算，即可求出a⃗、b⃗ 的夹角余弦值；(2)根据两向量垂直，数量积为0，列出方程求出λ的值．本题考查了平面向量的坐标表示与数量积运算问题，是基础题目．18.如图为函数f(x)=Asin(ωx+φ)(A>0，ω>0，|φ|<π2，x∈R)的部分图象．(1)求函数解析式；(2)求函数f(x)的单调递增区间；(3)若方程f(x)=m在[−π2，0]上有两个不相等的实数根，则实数m的取值范围．【答案】解：(1)由题中的图象知，A=2，T4=π3−π12=π4，即T=π，所以ω=2πT=2，根据五点作图法，令2×π12+φ=π2+2kπ，k∈Z，得到φ=π3+2kπ，k∈Z，因为|φ|<π2，所以φ=π3，解析式为f(x)=2sin(2x+π3).…(5分)(2)令2kπ−π2≤2x+π3≤2kπ+π2，k∈Z，解得kπ−5π12≤x≤kπ+π12，k∈Z，所以f(x)的单调递增区间为[kπ−5π12，kπ+π12]，k∈Z.…(9分)(3)由f(x)=2sin(2x+π3)在[−π2，0]上的图象如图知，当m∈(−2，−√3]上有两个不同的实根.…(12分)【解析】(1)由已知图象求出振幅、周期和相位，对的解析式；(2)由(1)的解析式，结合正弦函数的性质求单调增区间；(3)利用数形结合求满足条件的m的范围．本题考查了由三角函数图象求解析式以及利用正弦函数的性质求单调区间以及数形结合求参数范围；熟练掌握三角函数的图象和性质是解答的关键；属于中档题19.已知函数f(x)=a−22x+1是奇函数(a∈R)．(1)求实数a的值；(2)试判断函数f(x)在(−∞，+∞)上的单调性，并证明你的结论；(3)若对任意的t∈R，不等式f(t2−(m+1)t)+f(t2−m−1)>0恒成立，求实数m的取值范围．【答案】解：(1)∵f(x)是奇函数在原点有定义；∴f(0)=a−1=0∴a=1；(2)f(x)=1−22x+1在(−∞，+∞)上单调递增，证明如下：设x1<x2，则：f(x1)−f(x2)=22x2+1−22x1+1=2(2x1−2x2)(2x1+1)(2x2+1)；∵x1<x2；∴2x1<2x2，2x1−2x2<0；∴f(x1)<f(x2)；∴f(x)是(−∞，+∞)上的增函数；(3)由(1)、(2)知，f(x)是(−∞，+∞)上的增函数，且是奇函数；∵f(t2−(m+1)t)+f(t2−m−1)>0；∴f(t2−(m+1)t)>−f(t2−m−1)=f(−t2+m+1)；∴t2−(m+1)t>−t2+m+1；即2t2−(m+1)t−(m+1)>0对任意t∈R恒成立；只需△=(m+1)2+4⋅2(m+1)=m2+10m+9<0；解之得−9<x<−1；∴实数m的取值范围为(−9，−1)．【解析】(1)根据f(x)为奇函数，并且在原点有定义，从而f(0)=0，求出a=1；(2)容易判断f(x)=1−22x+1为增函数，根据增函数定义，设任意的x1<x2，然后作差，通分，根据指数函数的单调性便可证明f(x1)<f(x2)，从而得出f(x)在(−∞，+∞)上单调递增；(3)根据f(x)为奇函数，以及在R上单调递增便可根据不等式f(t2−(m+1)t)+f(t2−m−1)>0恒成立得出不等式2t2−(m+1)t−(m+1)>0对任意t∈R恒成立，从而得出判别式△=m2+10m+9<0，解该不等式便可得出实数m的取值范围．考查奇函数的定义，增函数的定义，指数函数的单调性，以及根据增函数定义证明一个函数为增函数的方法和过程，根据奇函数定义和增函数定义解不等式的方法，一元二次不等式恒大于0时，判别式△的取值情况．20.△ABC的内角A，B，C所对的边分别为a，b，c.向量m⃗⃗⃗ =(a，√3b)与n⃗=(cosA，sinB)平行．(Ⅰ)求A；(Ⅱ)若a=√7，b=2，求△ABC的面积．【答案】解：(Ⅰ)因为向量m⃗⃗⃗ =(a，√3b)与n⃗=(cosA，sinB)平行，所以asinB−√3bcosA=0，由正弦定理可知：sinAsinB−√3sinBcosA=0，因为sinB≠0，所以tanA=√3，可得A=π3；(Ⅱ)a=√7，b=2，由余弦定理可得：a2=b2+c2−2bccosA，可得7=4+c2−2c，解得c=3，△ABC的面积为：12bcsinA=3√32．【解析】(Ⅰ)利用向量的平行，列出方程，通过正弦定理求解A；(Ⅱ)利用A，以及a=√7，b=2，通过余弦定理求出c，然后求解△ABC的面积．本题考查余弦定理以及正弦定理的应用，三角形的面积的求法，考查计算能力．21.已知向量a⃗=(sinx，−1)，b⃗ =(√3cosx，−12).函数f(x)=(a⃗+b⃗ )⋅a⃗−2．(1)求函数f(x)的单调递减区间；(2)已知a，b，c分别为△ABC内角A，B，C的对边，其中A为锐角，a=2√3，c=4，且f(A)=1，求△ABC的面积．【答案】解：(1)向量a⃗=(sinx，−1)，b⃗ =(√3cosx，−12)．函数f(x)=(a⃗+b⃗ )⋅a⃗−2=|a⃗|2+a⃗⋅b⃗ −2=sin2x+1+√3sinxcosx+12−2=12−12cos2x+√32sin2x−12=sin(2x−π6)，令π2+2kπ≤2x−π6≤3π2+2kπ，k∈Z．得：π3+kπ≤x≤5π6+kπ所以函数f(x)的单调递减区间为[π3+kπ，5π6+kπ]，k∈Z．(2)由(1)可知f(x)=sin(2x−π6)那么f(A)═sin(2A−π6)=1∵0<A<π2，∴−π6<2A−π6<5π6．∴2A−π6=π2．则A=π3．由余弦定理：a2=b2+c2−2bc⋅cosA可得：12=b2+16−4b，解得：b=2．∴△ABC的面积S=12cbsinA=4√3．【解析】(1)根据函数f(x)=(a⃗+b⃗ )⋅a⃗−2，利用向量的运算可得f(x)的解析式，即可求出函数f(x)的单调递减区间．(2)根据f(A)=1，求出角A的大小，利用余弦定理求出b，即可求△ABC的面积．本题考查了向量的运算和三角函数的化解能力和性质的运用，以及余弦定理的计算.属于基础题．22.如图，渔船甲位于岛屿A的南偏西60∘方向的B处，且与岛屿A相距12海里，渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行，若渔船甲同时从B出发沿北偏东α的方向追赶渔船乙，刚好用两小时追赶上．(1)求渔船甲的速度；(2)求sinC的值．【答案】解：(1)依题意，∠BAC=120∘，AB=12海里，AC=20海里．在ABC中，由余弦定理得，得BC2=AB2+AC2−2AB×AC×cos∠BAC．=122+202−2×12×20×cos120∘=784．解得BC=28海里，所以渔船甲的速度是=14(海里/小时)(2)在三角形ABC中，因为AB=12海里，∠BAC=120∘，BC=28海里，由正弦定理，得sinC=ABsin120∘BC =3√314．【解析】(1)由题意推出∠BAC=120∘，利用余弦定理求出BC=28，然后推出渔船甲的速度；(2)在△ABC中，直接利用正弦定理求出sinC．本题是中档题，考查三角函数在实际问题中的应用，正弦定理、余弦定理的应用，考查计算能力．。

2018～2018学年度第二学期高一年级第一次月考数学试题（满分150分 考试时间120分钟）一、选择题（每小题5分，共50分）1、 （ ）将-885化为α+k ·360（0≤α＜360，k ∈Z ）的形式是（A ）-165+（-2）·360 (B) 195+（-3）·360（C ）195+（-2）360 （D ）165+（-3）·3602、．（ ）函数f(x)=sin(x-4π)的单调增区间为 （A ）［2k π-4π,2k π+34π］k ∈Z ， （B ）［2k π,2k π+2π］k ∈Z （C ）［2k π-2π,2k π+2π］k ∈Z ， （D ）［k π-2π,k π+2π］k ∈Z 3 、（ ）下列函数，周期为π的奇函数是 （A ）y=sinx (B)y=sin2x (C)y=tanx (D)y=cosx4、 ( )设a=sin(-1),b=cos(-1) ,c=tan(-1),则有（A ）a<b<c (B) b<a<c (C) c<a<b (D) a<c<b5． ( )如果函数y=3cos(2x+φ)的图象关于点（-43π，0）中心对称，那么∣φ∣的最小值为 （A ）6π （B ）4π (C) 3π (D) 2π6、（ ）已知sin1100=a,则cos200等于（A （C ）-a (D) a7．（ ）y=sinx-∣sinx ∣的值域是（A ）［-1，0］ （B ）［0，1］ （C ）［-1，1］ （D ［-2，0］8、 ( )将函数y=sin(x-3π)的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将所得的图象向左平移3π个单位，得到的图象对应的解析式是 （A ）y=sin 12x (B) y=sin(12x-2π) (C)y=sin(12x-6π) (D)y=sin(2x-6π) 9、（ ）已知f(x)=2sin(ωx+φ)的图象如右图所示，则f(x)的表达式为（A ）f(x)=2sin(32x+4π) （B ）f(x)=2sin(32x+54π) （C ）f(x)=2sin(43x+29π) （D ）f(x)= 2sin(43x+2518π) 10、( )若函数f(x)=sin2x+acos2x 的图象关于直线x=-8π对称，则a 的值为（A （B ）（C ）1 （D ）-1二、填空题：（每小题5分，共25分）11、若角α的终边过点P （a ，8），且cos α=-35,则tan α的值为________. 12、已知tan(4π+α)=2,则tan(4π-α)的值为______________。

陕西省商洛市商南县鹿城中学度数学必修一第一次月考数学试题（无答案）班级： 姓名：一．选择题〔每题5分，总分值50分。

把答案填在答题卷上相应的括号中〕1、以下各组对象能组成一个集合的是 〔 〕A 、中国著名的歌唱家；B 、我校一切高一的高个子同窗；C 、不超越20的非正数；D 、∏的近似值的全体。

2、以下四个集合中，空集是 〔 〕、A 、{0}B 、{x|x ﹥8且x ﹤5}C 、{x ∈N|x ﹣1﹦0}D 、{x|x ﹥4}3、假定集合M ﹦{a,b,c},M 中元素是⊿ABC 的三边长，那么⊿ABC 一定不是〔 〕A 、锐角三角形；B 、直角三角形；C 、钝角三角形；D 、等腰三角形。

4、假定{}{}|02,|12A x x B x x =<<=≤<，那么A B ⋃=〔 〕A {}|0x x ≤B {}|2x x ≥C {}02x ≤≤D {}|02x x <<5、方程组⎩⎨⎧=-=+9122y x y x 的解集是 〔 〕A ．()5,4B ．()4,5-C ．(){}4,5-D ．(){}4,5- 6、5．如图，阴影局部所表示的集合为〔 〕A 、A ∩〔B ∩C 〕 B 、〔C S A 〕∩〔B ∩C 〕C 、〔C S A 〕∪〔B ∩C 〕D 、〔C S A 〕∪〔B ∪C 〕7设集合S=｛a,b,c,d,e ｝,那么包括｛a,b ｝的S 的子集共有〔〕 个A 2B 3C 5D 88、设A ﹦{直角三角形},B={等腰三角形}，C={等边三角形}，D={等腰直角三角形}，那么以下结论不正确的选项是〔 〕。

A 、A ∩B=D;B 、A ∩D=D;C 、B ∩C=C;D 、A ∪B=D.9、以下集合中，不是方程〔x+1〕〔x-2〕〔x-3〕=0的解集的集合是〔 〕；A 、{-1,2,3}；B 、{3，-1,2}；C 、{x|〔x+1〕〔x-2〕〔x-3〕=0}；D 、{〔-1,2,3〕}。

第一次月考数学试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，考试时间120分钟，满分150分.考生应首先阅读答题卡上的文字信息，然后在答题卡上作答，在试卷上作答无效，交卷时只交答题卡.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.考生根据要求作答，分别答在答题卡（Ⅰ卷）和答题卡（Ⅱ卷）上．第Ⅰ卷（选择题）一．选择题：本大题共12个小题，每小题5分，共60分.1. 设全集{}1,2,3,4,5U =，集合}2,1{=A ， {}2,4B =，则=)(B A C UY （ ）A. {}1,3,4,5B. {}1,4C. {}3,5 D ．{}1,2,4 2.函数x x y +-=1的定义域为（ ）A ．}{|1x x ≤ B ．}{0|≥x x C ．}{0,1|≤≥x x x 或D ．}{10|≤≤x x．下列图象中表示函数图象的是（ ）A B C D4.已知函数()f x 为奇函数,当0x >时, ()21,f x x x=+,则()1f -= （ ） A.2- B. 0C. 1D. 25．已知则=（ ）A. 3B. 13C. 8D. 18 6.下列四个函数中,与y =x 表示同一函数的是（ ）A.y =(x )2B.y =33xC.y =2xD.y =xx 27.在映射中，，且，则与中的元素对应的中的元素为（ ） A. B. C. D.8.已知集合{}{}1,0,1,0,1A B =-=，设集合{},,C z z x y x A y B ==+∈∈，则集合C 的真子集的个数为（ ）A ． 7B ．8C ．15D ．16 9.若函数满足,则的解析式是( )A. B. C.D.或10．已知函数()]4,[42m x x x x f ∈+-=，的值域是]4,0[,则实数m 的取值范围为（ ） A ．(,0)-∞ B ．[]0,2 C ．(]0,2 D ．[]2,4 11.已知偶函数的定义域为，且在上是增函数，则的大小关系是（ ）A. B. C.D.12.函数()y f x =是R 上的偶函数，且在(]0-∞，上是增函数，若()()2f a f ≤，则实数a 的取值范围是（ ）A ．2a ≤B ．2a ≥-C ．22a -≤≤D ．22a a ≤-≥或 第Ⅱ卷（非选择题）二．填空题：本大题共4小题，每小题5分，共20分.13．若函数x x x f 2)1(2-=+，则)2(f = .14.已知集合A ＝{1，a,5}，B ＝{2，a 2＋1}．若A ∩B 有且只有一个元素，则实数a 的值为________．15．已知函数f (x )的定义域为(－1，0)，则函数f (2x ＋1)的定义域为________． 16.若幂函数f (x )的图像经过点(2,4)，则f (12)=三．解答题：本大题共6小题，共70分.17．(本小题满分10分)设全集为R ，{}|37A x x =≤<，{}|210B x x =<<，求A B ⋃及()R C A B ⋂18. (本小题满分12分)已知集合，，，，求的值．19.(本小题满分12分)已知函数f(x)＝－x2＋2ax＋1－a在x∈[0,1]时有最大值2，求a的值.20. (本小题满分12分)已知集合A＝{x|－2≤x≤7}，B＝{x|m＋1<x<2m－1}．I.(2)若B⊆A，求实数m的取值范围.(1)当m=3时，求A B21.(本小题满分12分) 已知f(x)是定义在(0，+∞)上的增函数，且满足f(xy)＝f(x)＋f(y)，f(2)＝1. （1）求证：f(8)＝3 (2)求不等式f(x)－f(x－2)>3的解集.22. (本小题满分12分) 已知二次函数满足.(1)求的解析式;(2)求在区间()上的最小值.参考答案一、选择题（每小题5分,共60分） 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 CDCACBACBBAD二、填空题（每小题5分,共20分）13． -1 14． 0或－2 15．⎝ ⎛⎭⎪⎫－1，－12 16．14 三.解答题（本大题共6小题，共70分.） 17.解：（1）{}102<<=⋃x x B A |；（2）{}7,3|≥<=x x x A C R 或Θ {}10732|<≤<<=⋂∴x x x B A C R 或）（ 18.∵，∴集合，………6分∴，（另利用⎩⎨⎧=⨯-=+qp 5555也可）……10分 解得 (12)分19.解： f (x )＝－(x －a )2＋a 2－a ＋1，当a ≥1时，f (x )m ax ＝f (1)＝a ； 当0<a <1时，f (x )m ax ＝f (a )＝a 2－a ＋1； 当a ≤0时，f (x )m ax ＝f (0)＝1－a . 根据已知条件得，⎩⎪⎨⎪⎧a ≥1，a ＝2或⎩⎪⎨⎪⎧0<a <1，a 2－a ＋1＝2或⎩⎪⎨⎪⎧a ≤0，1－a ＝2，解得a ＝2或a ＝－1.20.解：(1)当m=3时，B ＝{x |4<x <5}，{|45}A B x x =<<I(2)当B ＝∅时，有m ＋1≥2m －1，则m ≤2；当B ≠∅时，∵B ⊆A ，如图．则⎩⎪⎨⎪⎧m ＋1≥－2，2m －1≤7，m ＋1<2m －1，解得2<m ≤4. 综上，m 的取值范围为m ≤4，21.（1）【证明】 由题意得f (8)＝f (4×2)＝f (4)＋f (2)＝f (2×2)＋f (2)＝ f (2)＋f (2)＋f (2)＝3f (2) 又∵f (2)＝1 ∴f (8)＝3 (2)解： 不等式化为f (x )>f (x －2)+3∵f (8)＝3 ∴f (x )>f (x －2)＋f (8)＝f (8x －16)∵f (x )是（0，+∞）上的增函数∴⎩⎨⎧->>-)2(80)2(8x x x 解得2<x <16722.解：(1)令 则,………2分==…………3分……………4分（另待定系数法可同样类比上述步骤给分）(2),开口向上,对称轴为………………5分当时, 在上为增函数所以时,有最小值为;…………………7分当,即时,在上先减后增,所以时,有最小值为…………………9分当,即时, 在上为减函数所以时,有最小值为;…………………11分综上所述:时,最小值为;时,最小值为;时,最小值为。