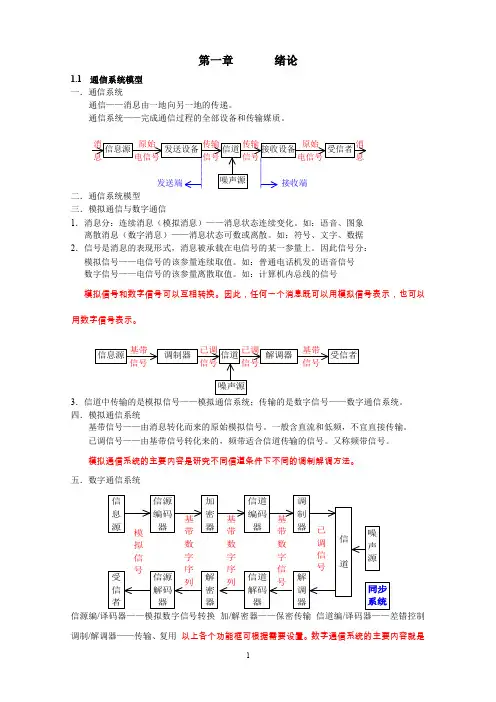
E( X Y ) E( X ) E(Y )
E(XY)称相关函数
物理意义
描述两维随机变量(X,Y)的相互关系
几个概念
独立
f(x,y)=f(x)f(y)
不相关
COV(X,Y)=0
正交
E(XY)=0
3.2 随机过程
一、概念 二、统计特性
一、概念
样本函数:
样本空
S1
间
随机过程
S2
x1(t)
2
P ()d
A2 2
3.4 高斯随机过程与高斯白噪声
信道中的噪声
脉冲噪声 窄带噪声
起伏噪声
热噪声 散弹噪声 宇宙噪声
起伏噪声为高斯随机过程
一、 高斯随机变量
的一个实现 Sn
t
随机过程:
x2(t)
样本函数
的集合
t (t)
任意时刻 的取值为随 机变量
xn(t) t
tk
随机过程没有确定的时间函数,只能从统计角 度,用概率分布和数字特征来描述。
二、统计特性
概率分布 数学期望(均值) 方差 协方差函数 相关函数
1. 概率分布
随机过程ξ(t) 在任一时刻t1的取值是随机变量, 则随机变量ξ(t1)的取值小于等于某一数值x1 的概率为ξ(t)的一维概率分布函数:
的问题大为简化。
例题(例3-1)
设一个随机相位的正弦波为 (t) Acos(ct )
其中,A和c均为常数;是在(0, 2π)内均匀分布的随 机变量。试讨论(t)是否具有各态历经性。
【解】
(1)先求(t)的统计平均值: A2
a(t) 0; R( ) cos c 2
(2) 求(t)的时间平均值
O