北邮通信原理课件 (5)

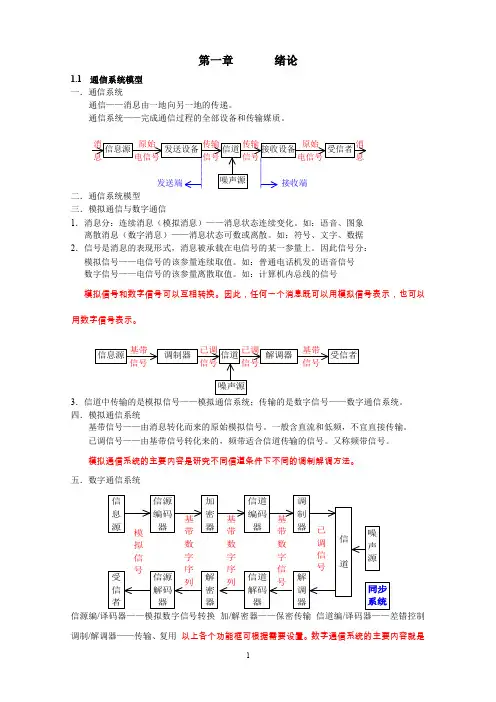
第五章数字基带传输系统主要内容„ „ „ „ „„ „ „ „引言 数字基带信号波形及其功率谱密度 通过AWGN信道传输的数字基带信号的接收 数字PAM信号通过限带基带信道的传输 AWGN干扰下数字PAM信号通过理想限带信道 的最佳基带传输 眼图 信道均衡 部分响应系统 符号同步2数字通信系统模型信 源 信 源 编 码 加 密 器 信 道 编 码 调 制 器信道噪声干扰信 宿信 源 译 码解 密 器信 道 译 码解 调 器3数字信号的基带传输与频带传输„数字信号的基带传输：将数字基带信号通 数字信号的基带传输 将数字基带信号通 过基带信道(传递函数为低通型)传输 —— 信号频谱不搬移 直接传送 信号频谱不搬移，直接传送。

„同轴 缆 双绞线 同轴电缆，双绞线„数字信号的频带传输：将数字带通信号通 过带通信道传输„光纤, 无线4基本概念-信息量„信息量：I ( x ) = − log 2 P ( x ) (比特 )1 = log a P ( x1 , x2 ,= − ∑ log a P ( xi )n i =1I ( x1 , x2 ,, xn ), xn )= ∑ I ( xi )i =1n相互独立事件构成的消息 所含信息量等于各独立事件信息量之和 相互独立事件构成的消息，所含信息量等于各独立事件信息量之和5基本概念-信源熵设离散信息源是一个由 设离散信息源是 个由n个符号组成的符号集，且 个符号组成的符号集 且⎡ x1 ⎢P ( x ) 1 ⎣„x2 P ( x2 )n xn ⎤ ,且 ∑ P P ( xn )⎥ ⎦ i =1( xi )=1每个符号所含信息量的统计平均值(平均信息量)为H ( x) = E ⎡ ⎣ I ( x )⎤ ⎦ = P ( x1 ) ⎡ ⎣ − log 2 P ( x1 ) ⎤ ⎦+ P ( x2 ) ⎡ l 2 P ( x2 )⎤ l 2 P ( xn )⎤ ⎣ − log ⎦ + … P ( xn ) ⎡ ⎣ − log ⎦= ∑ P ( xi ) ⎡ ⎣ − log 2 P ( x i ) ⎤ ⎦ ( bit / 符号 )i =1n信息源的熵M = 2k 且独立等概H ( x ) = log 2 M = k ( bit / 符号 )6基本概念(续)„ „符号传输速率： Rs (Baud) 信息传输速率：Rb (bit/s) Rb ＝ Rs log2 M (bit/s) Rs ＝ Rb /log2 M (baud)„ „误符号率 Ps 误符号率： 误比特率：Pb 频带利用率：单位为bit/s/Hz或Baud/Hz„7主要内容„ „ „ „ „„ „ „ „引言 数字基带信号波形及其功率谱密度 通过AWGN信道传输的数字基带信号的接收 数字PAM信号通过限带基带信道的传输 AWGN干扰下数字PAM信号通过理想限带信道 的最佳基带传输 眼图 信道均衡 部分响应系统 符号同步8数字脉冲幅度调制(PAM)二进制信息序列 M进制幅度序列 MPAM信号∑ b δ ( t − nT )n b nRb =1 Tb码型 编码∑ a δ ( t − nT )n s nM = 2K发送 滤波器s ( t ) = ∑ an gT ( t − nTs )nTs = KTbgT ( t ) ⇔ GT ( f )■s(t) =n = −∞∑a∞ngT ( t − nTs )an ∼ 传输码(线路码 ) 随机序列gT ( t ) ∼ 发送脉冲波形 (矩形、升余弦、高斯、半余弦脉冲)9数字基带系统的构成{bn }码型 编码{a n } d (t)发滤 波器s(t)信道x (t)收滤 波器r (t)抽样 判决{a }' n码型 译码{b }' nGT ( ω )gT ( t )n(t )cp ( t )位同 步器■s(t) =n = −∞∑a∞ngT ( t − nTs )~ 数字脉冲幅度调制(PAM)随机序 an ∼ 传输码(线路码 ) 随机序列∞gT ( t ) ∼ 发送脉冲波形 (矩形、升余弦、高斯、半余弦脉冲)■x (t) =n = −∞∑angT ( t − nTs ) + n ( t )10数字基带系统中各点的波形bn d(t) s(t) TS x(t) 1 τ 0 0 1 1r(t)cp ( t ) d’ ( t )11基本的数字基带信号波形(1)ƒ 二进制单极性不 归零(NRZ)码bn = 0, , 1 ⇔ an = 0, ,1A 0A 011101001Tst⎛ t 1⎞ gT ( t ) = Arect ⎜ − ⎟ ⎝ Ts 2 ⎠ƒ 二进制 双 极 性 不 归零(NRZ)码bn = 0,1 ⇔ an = −1, +1⎛ t 1⎞ gT ( t ) = Arect ⎜ − ⎟ ⎝ Ts 2 ⎠A 0 -A1110100112基本的数字基带信号波形(2)ƒ 二进制单极性归 零(RZ)码bn = 0, , 1 ⇔ an = 0, ,1A 0 τA 011101001Tsτ⎛ t 1⎞ gT ( t ) = Arect ⎜ − ⎟ ⎝τ 2⎠tƒ 二进制 双 极 性 归 零(RZ)码bn = 0,1 ⇔ an = −1, +1⎛ t 1⎞ gT ( t ) = Arect ⎜ − ⎟ ⎝τ 2⎠A 0 -A13基本的数字基带信号波形(2)„差分码：用相邻码元电平是否跳变代表‘0 差分码：用相邻码元电平是否跳变代表 0’或 或‘1 1’bnanbn ∼ 绝对码 an ∼ 相对码 an = bn ⊕ an − 1差分编码 (相对编码)A 0 1 1 0 1 1延迟Tb101001 二进制单极性不归零码1 10 11 00 00 01 1相对码an = bn ⊕ an −1A 001单极性不归零传号差分码 跳变：”1“ 0 0 0 0 1 1 0 1 1相对码an = bnan − 1A 0单极性不归零空号差分码 跳变：”0“14基本的数字基带信号波形(3)„多电平码波形 k个二进制符号bi 例. k =3, M=8b1b2b3 000 001 010 011 100 101 110 111 an +7 +5 +3 +1 -1 1 -3 -5 -7M = 2kbi an75310 -1 1-3 -5 -7 -一个M进制符号an1 1 1 0 1 0 0 1 1-7+3+115数字PAM信号的功率谱密度(1)s(t) =n = −∞∑a∞ngT ( t − nTs )其中 {an } ∼ 广义平稳随机序列， E ( an ) = ma；E an an + k = Ra ( k )gT ( t ) ∼ 发送脉冲波形，t ∈ ⎡ ⎣0, Ts ⎤ ⎦■()∞ ⎡ ∞ ⎤ gT ( t − nTs ) E⎡ ⎣ s ( t )⎤ ⎦ = E ⎢ ∑ an gT ( t − nTs ) ⎥ = ma n∑ = −∞ ⎣ n = −∞ ⎦周期为Ts■Rs ( t , t + τ ) = E ⎡ ⎣ s ( t ) s ( t + τ )⎤ ⎦= =n = −∞ m = −∞ ∞ ∞ n = −∞ m = −∞∑ ∑∞∞E⎡ ⎣ an am ⎤ ⎦ gT ( t − nTs ) gT ( t + τ − mTs ) Ra ( m − n ) gT ( t − nTs ) gT ( t + τ − mTs )∑ ∑Rs ( t + kTs , t + τ + kTs ) = Rs ( t , t + τ )∴ s ( t ) ∼ 循环平稳16数字PAM信号的功率谱密度(2)„循环平稳过程 s(t) 的功率谱密度1 Rs (τ ) = Ts∫∞Ts 2 − Ts 2Rs ( t , t + τ ) dt=m =−∞∑∞Ra ( m )1 ∑T n =−∞ s∞∞∫−TTs 2sg (t 2 T− nTs )gT ( t + τ − nTs − mTs )dt=m =−∞∑Ra ( m )1 ∑T n =−∞ s∞∫nT −TsnTs + Ts 2s2gT ( t ) gT ( t + τ − mTs )dt1 = Ts1 = Tsm =−∞∑∞Ra ( m )∫g ( t ) gT ( t −∞ T+ τ − mTs )dtm = −∞∑∞Ra ( m ) Rg (τ − mTs )Rg (τ )∫∞ −∞gT ( t ) gT ( t + τ ) dt17数字PAM信号的功率谱密度(3)„循环平稳过程 s(t) 的功率谱密度1 Rs (τ ) = Tsm = −∞∑∞Ra ( m ) Rg (τ − mTs )Ps (1 − j 2π f τ = f ) = ∫ Rs (τ )e dτ Ts −∞∞m =−∞∑∞Ra ( m )∫∞ −∞Rg (τ − mTs )e − j 2π f τ dτ1 = Tsm =−∞∑∞Ra ( m )e− j 2π fmTs∫−∞∞Rg (τ − mTs )e − j 2π f (τ − mTs ) dτ=2 1 Pa ( f ) ⋅ GT ( f ) TsgT ( t ) ⇔ GT ( f )∼ 随机序列{an }的功率谱密度Pa ( f )m = −∞∑∞Ra ( m ) e − j 2π fmTsP a ( f ) ⇔ R a (τ)= ∑∞m = −∞Ra( m ) δ (τ− m Ts)18数字PAM信号的功率谱密度(4)„循环平稳过程 s(t) 的功率谱密度Ps ( f ) =2 1 Pa ( f ) ⋅ GT ( f ) Ts其中：Pa ( f ) = 其中m = −∞∑∞Ra ( m ) e − j 2π fmTsgT ( t ) ⇔ GT ( f )数字基带信号 数字 带信号s ( t ) 的功率谱 的功率谱密度与随机序列 度与随机序列{an }的功率谱特性 Pa ( f )以及发送滤波器的频率特性GT ( f ) 有关.19数字PAM信号的功率谱密度(5)„特例：实随机序列{an }的各符号互不相关 特例Cov ( an an + m ) = E ⎡ ⎣ an − E ( an ) ⎤ ⎦⎡ ⎣ an + m − E ( an + m ) ⎤ ⎦ = 0, m ≠ 0{}Ra ( m ) = E ( an an + m ) = Cov ( an an + m ) + E ( an ) E ( an + m )2 2 ⎧ ⎪σ a + ma , m = 0 =⎨ 2 m≠0 ⎪ ⎩ ma ,∴ Pa ( f ) = σ + m2 a∞2 am = −∞∑e∞− j 2π f fmTs2 ma =σ + Ts 2 am = −∞∑∞δ⎜ f −⎝⎛m⎞ ⎟ Ts ⎠m = −∞∑e− j 2π mfTs1 = Tsm = −∞∑∞δ⎜f −⎝⎛m⎞ ⎟ Ts ⎠20数字PAM信号的功率谱密度(6)结论：在实随机序列 {an }的各符号互不相关时，s ( t ) 的PSDPs ( f ) =2σ2 aTsGT ( f ) +2m T2 ∞ a 2 s m = −∞∑⎛m⎞ ⎛ m⎞ GT ⎜ ⎟ δ ⎜ f − ⎟ Ts ⎠ ⎝ Ts ⎠ ⎝„ „连续谱： 形状取决于GT ( f ) 离散谱： 间隔 1 Ts , 可提取位同步信息.若ma = 0,Ps ( f ) =σ a2TsGT ( f )221数字PAM信号的功率谱密度(7)■例1.双极性不归零码，{bn } 各符号互不相关且0、1等概出现an = ±1且等概⎛ t 1⎞ gT ( t ) = Arect ⎜ − ⎟ ⎝ Ts 2 ⎠2 2 2 ma = 0, σ a = E an − ma = 1( )GT ( f ) = ATs Sa ( π fTs ) e − jπ fTs2 = A2Ts ⋅ Sa ( π fTs )Ps ( f ) =σ a2TsGT ( f )2Ps ( f )σ a2 A2Ts−3 Ts−2 Ts−1 Ts1 Ts2 Ts3 Ts22数字PAM信号的功率谱密度(8)■例2.双极性归零码，{bn } 各符号互不相关且0、1等概出现an = ±1且等概⎛ t 1⎞ gT ( t ) = Arect ⎜ − ⎟ ⎝τ 2⎠2 2 2 ma = 0, σ a = E an − ma = 1( )GT ( f ) = Aτ Sa ( π f τ ) e − jπ f τA2τ 2 2 = ⋅ Sa ( π f τ ) TsA2τ 2 TsPs ( f ) =σ a2TsGT ( f )2Ps ( f )−3 τ−2 τ−1 τ1 τ2 τ3 τ23数字PAM信号的功率谱密度(9)■例3.单极性不归零码，{bn } 各符号互不相关且0、1等概出现 2 1 1 ⎛1⎞ 2 2 2 1 = ⋅ − = σ = E a − m ma = 0.5, a an = 0,1且等概 ⎜ 2⎟ n a 2 4 ⎝ ⎠ ⎛ t 1⎞ GT ( f ) = ATs Sa ( π fTs ) e − jπ fT gT ( t ) = Arect ⎜ − ⎟( )sPs (2 ma f ) = σ A Ts ⋅ S ( π fTs ) + 2 Ts 2 a 2 2 a⎝ Ts2⎠m⎞ ⎛ m⎞ 2 2⎛ AT S π T ⋅ δ f − ( s) a ⎜ s T ⎟ ⎜ T ⎟ ∑ m = −∞ s ⎠ ⎝ s ⎠ ⎝∞2 2 2 = σa A Ts ⋅ Sa ( π fTs ) + A2 ma2δ ( f )Ps ( f )σ a2 A2Ts−3 Ts−2 Ts−1 Ts1 Ts2 Ts3 Ts24数字PAM信号的功率谱密度(10)■例4.单极性归零码，{bn } 各符号互不相关且0、1等概出现2 2 2 ma = 0.5, σ a = E an − ma = 1 4( )τ=Ts , 50%占空比 2⎛ t 1⎞ gT ( t ) = Arect ⎜ − ⎟ ⎝τ 2⎠GT ( f ) = Aτ Sa ( π f τ ) e − jπ f τ2 2 ⎛ π fTs ⎞ ma A ⋅S ⎜ ⎟+ 4 2 ⎝ ⎠ 2 aPs ( f ) =σ a2 A2Ts4m⎞ ⎛πm ⎞ ⎛ S ⎜ ∑ ⎟δ ⎜ f − T ⎟ 2 ⎝ ⎠ ⎝ m = −∞ s ⎠∞ 2 aPs ( f )−6 Ts−5 Ts−4 Ts−3 Ts−2 Ts−1 Ts1 Ts2 Ts3 Ts4 Ts5 Ts6 Ts结论：单极性码带有离散谱；归零码、不归零码占用的频带宽度不一样。

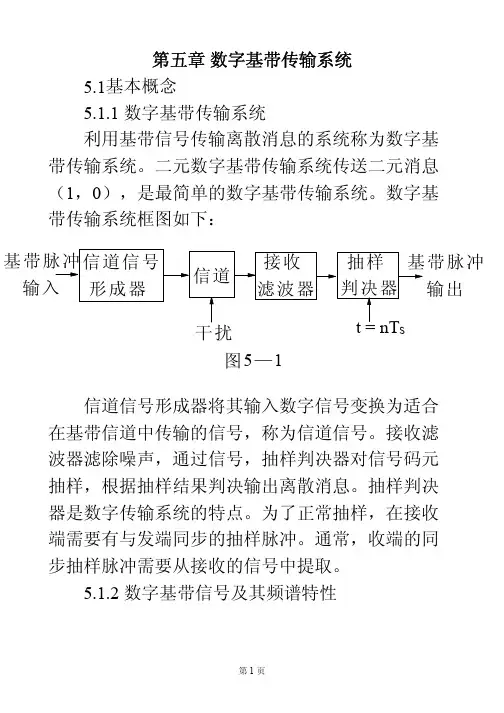
第五章数字基带传输系统基本概念5.1数字基带传输系统5.1.1 利用基带信号传输离散消息的系统称为数字基带传输系统。

二元数字基带传输系统传送二元消息（，），是最简单的数字基带传输系统。

数字基10带传输系统框图如下：S 信道信号形成器将其输入数字信号变换为适合在基带信道中传输的信号，称为信道信号。

接收滤波器滤除噪声，通过信号，抽样判决器对信号码元抽样，根据抽样结果判决输出离散消息。

抽样判决器是数字传输系统的特点。

为了正常抽样，在接收端需要有与发端同步的抽样脉冲。

通常，收端的同步抽样脉冲需要从接收的信号中提取。

数字基带信号及其频谱特性5.1.2 输出干扰图5—1以上是几种基带脉冲信号波形的示意图-E- ca bde f由组成的序列表示信息，即为传送的对象。

我们用基带信号传送此信息，基带信号可表示为： 它是一随机过程，其唯一随机参数是；可求 得其数学期望为：称作的稳态分量，表为，不难证明：是周期为的周期函数；称为 的交变分量，显然它是均值为零的随机过程。

设序列中不同码元统计独立，则 可求得的功率谱密度为：令 a n 表示第n 个二进制信息码元,取值为0,1 ,取0的概率为, P a n = 0P ; 则取1的概率为, P a n = 1P ; 信息码元与对应的基带信号的关系为: 0 g 1t , 1 g 2t ;a n .....a -n a -n -1....a -1a 0a 1......a n -1a n a n +1.....g 1t , g 2t S t ∞∑n = -∞[1-a n g 1t - nT s + a n g 2 t - nT s a n E [S t ] = ∞∑n = -∞[P g 1t - nT s + 1- P g 2 t - nT s S t v t v t u t S t - v t S tS t a k , a j ( k ≠ j )T s随机脉冲序列的功率谱密度包括两部 分：由交变波的连续谱及由稳态波的离散谱组成。