正项级数的敛散性判别法(二)

判别数项级数敛散性的常用方法与技巧判断数项级数的敛散性是数学分析中的一个重要问题。

对于数项级数a₁+a₂+a₃+⋯，判断它的敛散性可以使用多种方法和技巧。

以下是判别数项级数敛散性的常用方法和技巧：1.部分和序列法（也称柯西收敛准则）：数项级数收敛的必要条件是它的部分和序列收敛。

即，如果部分和序列Sₙ=a₁+a₂+⋯+aₙ收敛，则数项级数也收敛。

这个方法常用于证明一些级数的发散。

2.比较判别法：将待判别的级数与已知级数进行比较，从而确定待判别级数的敛散性。

-比较判别法一：如果对于所有n，都有0≤bₙ≤aₙ，且∑aₙ收敛，则∑bₙ也收敛。

如果∑aₙ发散，则∑bₙ也发散。

-比较判别法二：如果对于所有n，都有aₙ≤bₙ≥0，且∑aₙ发散，则∑bₙ也发散。

如果∑aₙ收敛，则∑bₙ也收敛。

比较判别法常见的应用有比较无穷大级数、比较一致收敛级数和比较正项级数等。

3. 极限判别法（拉阿贝尔判别法）：对于正项级数(非负数列构成的级数)，如果存在极限lim(n→∞)(aₙ/aₙ₊₁)，则：-若极限存在且大于1，则级数发散；-若极限存在且小于1，则级数绝对收敛；-若极限等于1，则不能确定级数的敛散性。

极限判别法适用于有常数项的级数以及指数函数和幂函数构成的级数。

4. 积分判别法：对于正项级数∑aₙ，如果存在连续函数f(x)，满足aₙ = f(n)且f(x)在x≥1上单调递减，则∑aₙ和∫f(x)dx同敛散。

即，级数与积分的敛散性相同。

积分判别法适用于正项级数，特别适用于有幂函数构成的级数。

5.序列收敛法：将待判别级数的项化为序列的形式，然后判断这个序列是否收敛。

如果序列收敛，则级数收敛；如果序列发散或趋于正无穷，则级数发散。

序列收敛法适用于特定结构的级数，如差分级数。

以上是常用的判别数项级数敛散性的方法和技巧。

在具体问题中，可以结合使用不同的方法确定级数的敛散性。

需要注意的是，判别数项级数敛散性的方法与技巧是基于数学分析中的定理和推理的，需要熟练掌握并灵活运用。

正项级数敛散性的判别方法正项级数是指级数的所有项都是非负数的级数。

判断正项级数的敛散性的方法主要有以下几种：比较判别法、根式判别法、积分判别法、极限判别法和对数判别法。

一、比较判别法：1. 比较判别法之比较大法：如果对于正项级数∑an和∑bn，当n趋向于无穷大时有an≤bn，那么若∑bn收敛，则∑an也收敛；若∑bn发散，则∑an也发散。

2. 比较判别法之比较小法：如果对于正项级数∑an和∑bn，当n趋向于无穷大时有an≥bn，那么若∑bn发散，则∑an也发散；若∑bn收敛，则∑an也收敛。

二、根式判别法：设an≥0，如果存在正常数p使得lim[(an)^1/n]=a，则1. 若a<1，则级数∑an收敛；2. 若a>1，则级数∑an发散；3.若a=1，根式判别法无法确定级数的敛散性。

三、积分判别法：将正项级数∑an转化为函数f(x)的积分，即∫f(x)dx，如果对于函数f(x)，当x趋向于无穷大时有f(x)递减且连续，则1. 若∫f(x)dx收敛，则级数∑an也收敛；2. 若∫f(x)dx发散，则级数∑an也发散。

四、极限判别法：如果存在常数L>0，使得lim(n→∞)n*an=L，则1. 若L<1，则级数∑an收敛；2. 若L>1，则级数∑an发散；3.若L=1，极限判别法无法确定级数的敛散性。

五、对数判别法：设an≥0，如果存在正常数p使得limln(an)/ln(n)=a，则1. 若a<1，则级数∑an收敛；2. 若a>1，则级数∑an发散；3.若a=1，对数判别法无法确定级数的敛散性。

这些判别方法在实际应用中都有其适用范围和局限性，需要根据具体情况选择合适的方法进行判断。

同时，在判断级数的敛散性时，还可以结合其他定理和方法，如柯西收敛准则、阿贝尔定理、绝对收敛等进行综合分析。

级数敛散性的判别方法级数是数学中一个重要的概念，它在分析、微积分等领域有着广泛的应用。

在研究级数时，一个重要的问题就是判别级数的敛散性。

本文将介绍几种常见的判别方法，帮助读者更好地理解级数的敛散性。

首先，我们来看级数的敛散性定义。

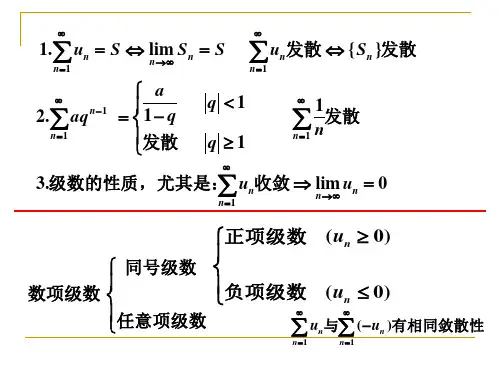
对于一个级数$\sum_{n=1}^{\infty}a_n$，如果它的部分和数列${S_n}$收敛于某个值$S$，即$\lim_{n \to \infty}S_n=S$，那么我们称级数$\sum_{n=1}^{\infty}a_n$是收敛的，$S$称为级数的和。

如果${S_n}$发散，那么级数$\sum_{n=1}^{\infty}a_n$就是发散的。

接下来，我们将介绍几种判别级数敛散性的方法。

一、比较判别法。

比较判别法是判别级数敛散性常用的方法之一。

设$\sum_{n=1}^{\infty}a_n$和$\sum_{n=1}^{\infty}b_n$是两个级数，如果对于所有的$n$，都有$0 \leq a_n \leq b_n$，且$\sum_{n=1}^{\infty}b_n$收敛，那么$\sum_{n=1}^{\infty}a_n$也收敛；如果$\sum_{n=1}^{\infty}b_n$发散，那么$\sum_{n=1}^{\infty}a_n$也发散。

二、比值判别法。

比值判别法是判别正项级数敛散性的一种方法。

对于正项级数$\sum_{n=1}^{\infty}a_n$，计算极限$\lim_{n \to\infty}\frac{a_{n+1}}{a_n}$，如果这个极限存在且小于1，那么级数$\sum_{n=1}^{\infty}a_n$收敛；如果这个极限大于1或者不存在，那么级数$\sum_{n=1}^{\infty}a_n$发散；如果这个极限等于1，比值判别法不起作用，需要使用其他方法进行判别。

三、积分判别法。

积分判别法适用于正项级数。

对于正项级数$\sum_{n=1}^{\infty}a_n$，如果函数$f(x)$在$[1, +\infty)$上连续、单调递减且非负，那么级数$\sum_{n=1}^{\infty}a_n$与积分$\int_{1}^{\infty}f(x)dx$的敛散性是等价的，即$\sum_{n=1}^{\infty}a_n$与$\int_{1}^{\infty}f(x)dx$同时收敛或者同时发散。

淮北师范大学信息学院2012 届学士学位论文级数敛散性的判别方法系别:数学系专业:数学与应用数学学号: 20081884083姓名: 赵高指导教师: 陈冬君指导教师职称: 讲师2012年 5 月10 日级数敛散性的判别方法赵高(淮北师范大学信息学院，淮北，235000)摘要级数有很多重要的性质，其中敛散性是级数的一个非常重要的性质，敛散性的判别方法也一直是人们研究的热点.通过判别级数的敛散性进一步了解级数的性质.本文探论了正项级数、交错级数以及任意项级数敛散性的判别方法，正项级数、交错级数、任意项级数通项的多变性,决定了判别正项级数、交错级数、任意项级数敛散性的方法会有多种，主要有达朗贝尔判别法、柯西判别法、莱布尼茨判别法、狄利克雷判别法.当然由于通项的特殊性也会有特殊的方法判别.本文通过归纳一些判别正项级数与交错级数敛散性的方法,让人们在学习过程中对级数敛散性的判别能够很好的把握，并掌握这些判别法成立的条件.关键词：正项级数、交错级数、敛散性、判别法.The Convergence of the Series of Discriminant MethodZhao GaoCollege of Information Technology Huaibei Normal University, Huaibei,235000AbstractThe series has a lot of important properties, which is the series convergence and divergence of a very important properties, criteria for convergence and divergence has been the focus of study. Through judging the convergence of series to further understand the series nature. This article of the series of positive terms, staggered series as well as any series convergence and divergence sexual discriminant method, a series of positive terms, staggered series, series of any general variability, determines the identification of series of positive terms, staggered series, any of the convergence of the series will have a variety of methods, mainly the d'Alembert discriminant method, Cauchy method, Leibniz method, di Like dilichlet discriminance. Of course due to the particularity of the general will also have the special methods of discriminant. This paper summarized some criteria for positive term series and the convergence of alternate series method, let people in the learning process of convergence of series of discriminant can be a very good grasp of, and grasp the discriminant conditions.Key words: Series of positive terms，Alternating series，Convergence and divergence，Discriminant analysis method目录引言 (1)一、级数及其敛散性的有关概念 (1)二、正项级数敛散性的判别方法 (2)1、比式判别法（达朗贝尔判别法） (2)2、根式判别法（柯西判别法） (3)3、拉贝判别法 (4)4、高斯判别法 (5)5、对数判别法 (5)6、隔项比值判别法 (5)7、运用微分中值定理判别级数敛散性 (6)8、利用数列判别级数的敛散性 (6)9、运用等价无穷小替换判别级数的敛散性 (7)三、交错级数敛散性的判别方法 (8)1、利用级数敛散性定义判定 (8)2、莱布尼茨判别法 (9)3、极限判别法 (10)4、添加括号法 (11)5、通项变形法 (12)6、微分形式判别法 (13)7、比值判别法或根值判别法 (14)四、任意项级数敛散性判别法 (15)总结 (16)参考文献 (16)致谢 (17)引言级数是数学的一个重要组成部分，它是表示函数、研究函数的性质以及数值计算的一种工具.对于一个级数，我们首先要讨论其敛散性，然后才讨论其求和问题.本文就级数的敛散性的判别方法作了一些探讨.正项级数和交错级数是整个级数家族中比较重要和特殊的.对其敛散性的判别方法也有别于一般的级数，除适用于一般级数的敛散性判别法外，还有许多专门针对正项级数和交错级数敛散性的判别方法，常见的如达朗贝尔判别法、柯西判别法、拉贝判别法、莱布尼茨判别法、狄利克雷判别法、微分形式判别法等.其实正项级数敛散性的判别方法远不止这些，下面就介绍几种级数敛散性的判别法.一、级数及其敛散性的有关概念定义1 给定数列{n u }：1u ,2u ,,nu则式子=1n n u ∞∑=12n u u u ++++称为无穷级数，简称为级数.定义2 如果级数=1n n u ∞∑满足n u ≥0（n =1，2，）则称=1n n u ∞∑为正项级数.如果级数是正负项交错出现的，即11234=1=+u n n n u u u u ∞---+∑（-1），或11234=1=+u +u n n n u u u ∞---∑（-1）(n u ≥0，n =1,2) 则称为交错级数.由定义，级数表示无穷多个数的和，但不能理解为无穷多个数逐次求和.事实上，这样也做不到.利用数列极限可以表示级数的和，同时给出级数敛散性的定义.定义3 级数=1n n u ∞∑前n 项之和记为S n =12n u u u +++，称为级数=1n n u ∞∑的第n 次部分和. 当n 分别取1,2, ,n ,时，得到级数=1n n u ∞∑的部分和数列{n S }：12,,,,n S S S 如果当n →∞时，n S 的极限存在，即lim =n n S S →∞时，则称级数=1n n u ∞∑是收敛的，且S 称为级数=1nn u∞∑的和，记为S ==1n n u ∞∑;如果当n →∞时，n S 的极限不存在, 即lim n n S →∞不存在，则称级数=1n n u ∞∑是发散的.由定义，只有收敛的级数才有和的问题，发散的级数没有和，或者说发散级数的和不存在.所以有必要研究级数的敛散性.由于正项级数是各项的符号均为正号的级数，它是数项级数中最简单也是最有代表意义的数项级数. 所以它收敛的最基本的判别方法也是从级数的判敛性质中引出，因此本文先讨论正项级数的敛散性. 有了着一方法来判断某些简单的正项级数的敛散性后，以它作为参照，可以判断另外一些稍微复杂的正项级数的敛散性.下面先来介绍正项级数敛散性的判别方法.二、正项级数敛散性的判别方法1、比式判别法（达朗贝尔判别法）定理[]11 设有正项级数=1n n u ∞∑，如果+1lim=n n nu l u →+∞，则（1） 当0≤l <1时，级数收敛； （2） 当1<l ≤+∞时，级数发散； （3） 当l =1时，此法失效. 例1 判断正项级数=12nn n∞∑的敛散性. 解：1121(1)limlim lim lim ()2(1)(1)1n n n n n n n n n n n n n n n n n n en++→+∞→+∞→+∞→+∞+=<==+++<1所以满足定理1中的（1），故正项级数=12nn n∞∑收敛. 例2 判别正项级数=12!n n ∞∑的敛散性. 解：由2!1(1)!lim lim lim 02(1)!1!n n n n n n n n →+∞→+∞→+∞+===++可知满足定理1中的（1），所以正项级数=12!n n ∞∑收敛. 像正项级数 =1x !nn n ∞∑（x>0）、=1!10n n n ∞∑等都可采用此法判断.2、根式判别法（柯西判别法）定理[]12 设有正项级数=1n n u ∞∑，如果n l ，则（1）当0≤l <1时，级数收敛； （2）当1<l ≤+∞时，级数发散； （3）当l =1时，此法失效.例3 研究级数=12+12nnn ∞-∑（）的敛散性. 解：由于12n n →∞=<所以级数2+12nn-∑（）是收敛的. 注：级数=12n n n ∞∑、=1+1nn na n ∞⎛⎫ ⎪⎝⎭∑ (0)a >、-1=1n n n αβ∞∑（α>0,β>0）等都可采用此法判 断.比式判别法与根式判别法都是建立在正项级数比较判别法基础上的，所用的比较级数是收敛速度相对比较快的等比级数.这两种方法虽然更方便，但是它们也只能用于判别那些比等比级数收敛速度更快的级数，而对于那一类比等比级数收敛速度更缓慢的级数，这两种判别法就无能为力了.这两种判别方法是我们用得比较多，因为它们用起来很方便.但是，对于比值判别法与根值判别法存在两点不足：1) 当=1l 时，判别法失效，既有收敛的，也有发散的级. 2) 判别法可能由于 l 根本不存在而失效.3、拉贝判别法定理[]43 （拉贝判别法） 设n u >0 （n =1,2,3）1。

级数敛散性判别方法的归纳（西北师大）摘要：无穷级数是《数学分析》中的一个重要组成部分，它是研究函数、进行数值运算及数据分析的一种工具，目前，无穷级数已经渗透到科学技术的很多领域，因而级数收敛的判别在级数的研究中亦显得尤为重要，然而判定级数敛散性的方法太多，学者们一时很难把握，本文对级数的敛散性的判别方法作了全面的归纳，以期对学者们有所帮助。

关键词：级数；收敛；判别 ；发散一. 级数收敛的概念和基本性质给定一个数列｛n u ｝，形如n u u u +++21①称为无穷级数(常简称级数),用∑∞=1n n u 表示。

无穷级数①的前n 项之和，记为∑==nn n n u s 1=n u u u +++ 21②称它为无穷级数的第n 个部分和，也简称部分和。

若无穷级数②的部分和数列｛n s ｝收敛于s.则称无穷级数∑∞=1n n u 收敛，若级数的部分和发散则称级数∑n v 发散。

研究无穷级数的收敛问题，首先给出大家熟悉的收敛级数的一些基本定理： 定理1 若级数∑n u 和∑n v 都收敛，则对任意的常数c 和d ，级数)(n n dv cu ∑+亦收敛，且)(n n du cu ∑+=c ∑n u +d ∑n v定理2 去掉、增加或改变级数的有限个项并不改变级数的敛散性定理3 在收敛级数的项中任意加括号，既不改变级数的收敛性，也不改变它的和。

定理4 级数①收敛的充要条件是：任给ε＞0，总存在自然数N ，使得当m ＞N 和任意的自然数p ，都有p m m m u u u ++++++ 21＜ε以上是收敛级数的判别所需的一些最基本定理，但是，在处理实际问题中，仅靠这些是远远不够的，所以在级数的理论中必须建立一系列的判别法，这就是本文的主要任务。

由于级数的复杂性，以下只研究正项级数的收敛判别。

二 正项级数的收敛判别各项都是由正数组成的级数称为正项级数，正项级数收敛的充要条件是：部分和数列{n s }有界，即存在某正整数M ，对一切正整数 n 有n s ＜M 。

关于正项级数敛散性的柯西(cauchy)积分判别法及其证明的几点注记1.柯西(Cauchy)积分判别法认为：如果正项级数以n→∞收敛，则其和sum(sn)=lim(n→∞)得到的结果为它的积分sum(Sn).2.证明柯西(Cauchy)积分判别法：首先，用反证法：假设正项级数Sn不收敛，那么lim(n→∞)Sn != sum(Sn).其次，我们假设正项级数Sn一定会收敛，此时我们可以证明lim(n→∞)Sn=sum(Sn)。

首先，我们用数学归纳法证明：令n=1，令M是该正项级数的极限，如果S1<M，则总和sum(Sn)<M；如果S1=M，则总和sum(Sn)=M。

其次，我们用数学归纳法证明：令N>1，令S1,S2,...,Sn-1<M，则Sn<M，因此sum(Sn)<M；如果S1,S2,...,Sn-1=M，则Sn<M，因此sum(Sn)<M。

最后，综上所述，无论Sn怎么变化，sum(Sn)的最终结果都小于极限M，因而满足总和sum(Sn) = lim(n→∞)Sn。

由此可知，如果正项级数Sn收敛，那么总和sum(Sn) = lim(n→∞)Sn，从而证明了柯西(Cauchy)积分判别法。

综上所述，柯西(Cauchy)积分判别法是完备的，即如果正项级数Sn收敛，则sum(Sn) = lim(n→∞)Sn; 如果正项级数Sn不收敛，则sum(Sn) !=lim(n→∞)Sn。

因此，柯西(Cauchy)积分判别法可以有效地确定积分是否收敛。

如果有多个级数收敛，那么我们可以将多个级数收敛表示成一个函数f(x)，将f(x)在正项级数收敛的区间[a,b]上进行积分，即sum(Sn)=∫f(x)dx；由柯西(Cauchy)积分判别法可知，积分的值sum(Sn)等于极限lim(n→∞)Sn；因此，我们可以用柯西(Cauchy)积分判别法来确定多个级数收敛的总和。

常数项级数内容要点一，概念与性质(一)概念 由数列 ,,,,21n u u u 构成的式子=∑∞=1n nu++++n u u u 21称为无穷级数，简称为级数.n u 称为级数的一般项，∑==ni in us 1称为级数的部分和.如果s s n n =∞→lim ,则称级数∑∞=1n nu收敛，s 称为该级数的和.此时记=∑∞=1n nus .否则称级数发散.（二）性质 1, 若∑∞=1n nu收敛，则.11∑∑∞=∞==n n n nu k ku2, 若∑∞=1n n u ,∑∞=1n nv收敛，则().111∑∑∑∞=∞=∞=±=±n n n n n n nv u v u3, 级数增减或改变有限项，不改变其敛散性.4, 若级数收敛，则任意加括号后所成的级数仍收敛. 5(收敛的必要条件), 若∑∞=1n nu收敛，则.0lim =∞→n n u注意：若.0lim ≠∞→n n u 则∑∞=1n nu必发散.而若∑∞=1n nu发散,则不一定.0lim ≠∞→n n u(三) 两个常用级数 1, 等比级数⎪⎩⎪⎨⎧≥<-=∑∞=1,1,10q q qaaq n n2, -p 级数⎩⎨⎧≤>=∑∞=1,1,11p p n n p 二，正项级数敛散性判别法 (一) 比较判别法设∑∑ℜ=∞=11,n nn n vu 均为正项级数，且),2,1( =≤n v u n n ,则∑∞=1n nv收敛⇒∑∞=1n nu收敛；∑∞=1n nu发散⇒∑∞=1n nv发散(二) 极限判别法如果)0(lim +∞≤<=∞→l l nu n n ,则∑∞=1n nu发散；如果对,1>p )0(lim +∞<≤=∞→l l u n n pn ,则∑∞=1n nu则收敛.(三) 比值判别法 设∑∞=1n nu为正项级数，若⎪⎩⎪⎨⎧⇒>⇒=⇒<==+∞→fb cu u n n n 111lim1ρ 二，交错级数收敛性判别法 莱布尼兹判别法：设())0(111>-∑∞=-n n n n u u 为交错级数，如果满足：1, ),2,1(1 =≥+n u u n n 2, 0lim =∞→n n u则此交错级数收敛.三，任意项级数与绝对收敛 （一） 绝对收敛 如果∑∞=1n nu收敛，则称∑∞=1n nu绝对收敛.（二） 条件收敛 如果∑∞=1n nu收敛，但∑∞=1n nu发散,则称∑∞=1n nu条件收敛.（三） 定理 若级数绝对收敛，则该级数必收敛.函数项级数一、 主要内容 1、基本概念函数列（函数项级数）的点收敛、一致收敛、内闭一致收敛、绝对收敛、和函数幂级数的收敛半径、收敛区间、收敛域 2、一致收敛性 A 、 函数列{()}n f x一致收敛性的判断：（1）定义：用于处理已知极限函数的简单函数列的一致收敛性（2）Cauchy 收敛准则：用于抽象、半抽象的函数列的一致收敛性的判断 （3）确界（最大值方法）：||()()||0n f x f x -→（4）估计方法：|()()|0n n f x f x a -≤→（5）Dini-定理：条件1）闭区间[,]a b ；2）连续性；3）关于n 的单调性注、除Cauchy 收敛准则外，都需要知道极限函数，因此，在判断一致收敛性时，一般应先利用点收敛性计算出极限函数。