机械原理计算自由度习题附答案

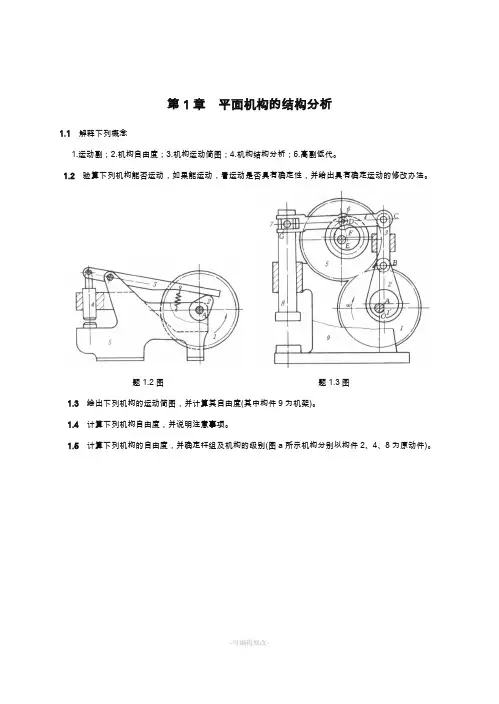
第1章平面机构的结构分析1.1解释下列概念1.运动副；2.机构自由度；3.机构运动简图；4.机构结构分析；5.高副低代。

1.2验算下列机构能否运动，如果能运动，看运动是否具有确定性，并给出具有确定运动的修改办法。

题1.2图题1.3图1.3 绘出下列机构的运动简图，并计算其自由度(其中构件9为机架)。

1.4 计算下列机构自由度，并说明注意事项。

1.5计算下列机构的自由度，并确定杆组及机构的级别(图a所示机构分别以构件2、4、8为原动件)。

题1.4图题1.5图第2章平面机构的运动分析2.1试求图示各机构在图示位置时全部瞬心。

题2.1图2.2在图示机构中，已知各构件尺寸为l AB=180mm , l BC=280mm , l BD=450mm ,l CD=250mm ,l AE =120mm ,φ=30º, 构件AB上点E的速度为v E=150 mm /s ,试求该位置时C、D两点的速度及连杆2的角速度ω2。

2.3 在图示的摆动导杆机构中，已知l AB=30mm , l AC=100mm , l BD=50mm ,l DE=40mm ,φ1=45º,曲柄1以等角速度ω1=10 rad/s沿逆时针方向回转。

求D点和E点的速度和加速度及构件3的角速度和角加速度（用相对运动图解法）。

题2.2图题2.3图2.4 在图示机构中，已知l AB =50mm , l BC =200mm , x D =120mm , 原动件的位置φ1=30º, 角速度ω1=10 rad/s ，角加速度α1=0，试求机构在该位置时构件5的速度和加速度，以及构件2的角速度和角加速度。

题2.4图2.5 图示为机构的运动简图及相应的速度图和加速度图。

（1）在图示的速度、加速度多边形中注明各矢量所表示的相应的速度、加速度矢量。

（2）以给出的速度和加速度矢量为已知条件，用相对运动矢量法写出求构件上D 点的速度和加速度矢量方程。

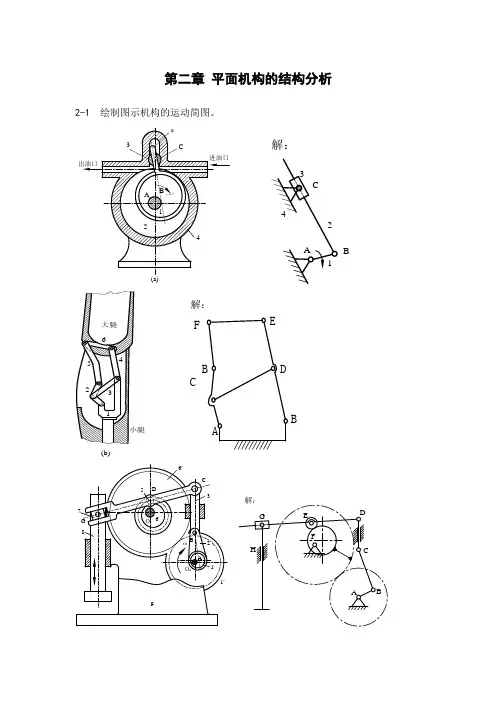
第二章 平面机构的结构分析2-1 绘制图示机构的运动简图。

B解：大腿 小腿213456(b)ACB FEDB解：ABC DE FGH解：2-3 计算图示机构的自由度，并指出复合铰链、局部自由度和虚约束。

ABCDE(a)ABDCE(b)ABCDE(c)(e)(f)(g)解：(a) C 处为复合铰链。

7,n =p h =0，p l =10。

自由度 323721001W l h F n p p =--=⨯-⨯-=。

(b) B 处为局部自由度，应消除。

3n =， p h =2，p l =2自由度 323323121W l h F n p p =--=⨯-⨯-⨯=。

(c) B 、D 处为局部自由度，应消除。

3n =， p h =2，p l =2。

自由度 323323121W l h F n p p =--=⨯-⨯-⨯=。

(d) CH 或DG 、J 处为虚约束，B 处为局部自由度，应消除。

6n =，p h =1，p l =8。

自由度 32362811W l h F n p p =--=⨯-⨯-=。

(e) 由于采用对称结构，其中一边的双联齿轮构成虚约束，在连接的轴颈处，外壳与支架处的连接构成一个虚约束转动副,双联齿轮与外壳一边构成虚约束。

其中的一边为复合铰链。

其中4n =，p h =2，p l =4。

自由度 32342422W l h F n p p =--=⨯-⨯-=。

(f) 其中，8n =，p h =0，p l =11。

自由度 323821102W l h F n p p =--=⨯-⨯-=。

(g) ① 当未刹车时，6n =，p h =0，p l =8，刹车机构自由度为 32362802W l h F n p p =--=⨯-⨯-=② 当闸瓦之一刹紧车轮时，5n =，p h =0，p l =7，刹车机构自由度为 32352701W l h F n p p =--=⨯-⨯-=③ 当两个闸瓦同时刹紧车轮时，4n =，p h =0，p l =6，刹车机构自由度为32342602W l h F n p p =--=⨯-⨯-=知识青年22:53:08当闸瓦之一刹紧车轮时，n=5，ph=0，pl=7，刹车机构自由度为2知识青年22:53:36自由度为1知识青年22:54:22那么左边算虚约束吗左边是机架知识青年22:54:46当两个闸瓦同时刹紧车轮时，n=4，ph=0，pl=6，刹车机构自由度为0知识青年22:55:33四个活动构件是哪些呢？1、2、3、5知识青年22:56:23ＨＤ杆就不算活动构件吗？算知识青年22:59:53四个活动构件是BA\CBD\EC\还有EFGOJHI此时算一个构件吗，而ＨＤ不算活动构件？2-3 判断图示机构是否有确定的运动，若否，提出修改方案。

机械原理习题答案机械原理是工程学科中的一个重要分支，它涉及到机械设计、运动学和动力学等多个方面。

以下是一些机械原理习题的答案示例：习题一：平面机构的自由度计算已知一个平面机构由4个刚体组成，其中包含3个铰链和2个滑动接头。

求该机构的自由度。

答案：根据格伯尔定理，平面机构的自由度计算公式为：\[ F = 3n - 2j - h \]其中，\( n \) 是刚体的数量，\( j \) 是铰链的数量，\( h \) 是滑动接头的数量。

将已知数值代入公式：\[ F = 3 \times 4 - 2 \times 3 - 2 = 12 - 6 - 2 = 4 \]所以，该机构的自由度为4。

习题二：四连杆机构的运动分析考虑一个四连杆机构，其中杆AB和CD固定，杆BC和AD为活动杆。

求当杆AD的长度为L时，杆BC的位移和速度。

答案：设杆AD的长度为\( L \)，杆BC的长度为\( l \)。

根据四连杆机构的几何关系，可以得出杆BC的位移和速度的表达式。

位移表达式：\[ s_{BC} = l \sin(\theta) \]其中，\( \theta \) 是杆AD与杆AB之间的夹角。

速度表达式：\[ v_{BC} = l \cos(\theta) \cdot \omega \]其中，\( \omega \) 是杆AD的角速度。

习题三：齿轮传动的传动比计算已知一对齿轮，主动轮的齿数为20，从动轮的齿数为100。

求传动比。

答案：齿轮传动比的计算公式为：\[ i = \frac{N_2}{N_1} \]其中，\( N_1 \) 是主动轮的齿数，\( N_2 \) 是从动轮的齿数。

代入已知数值：\[ i = \frac{100}{20} = 5 \]所以，传动比为5。

习题四：凸轮机构的从动件运动规律分析考虑一个凸轮机构，凸轮为圆形，半径为R。

从动件在凸轮的上升过程中以匀速运动。

求从动件在凸轮上升过程中的位移和速度。

答案：假设凸轮以角速度\( \omega \) 旋转，凸轮上升的角度为\( \theta \)，则从动件的位移表达式为：\[ s = R \theta \]速度表达式为：\[ v = R \omega \]习题五：机械振动的自由振动分析已知一个单自由度振动系统，其质量为\( m \)，刚度系数为\( k \)，初始位移为\( A \)，初始速度为0。

《机械原理》课后习题答案第2章（P27）2-2 计算下列机构的自由度，如遇有复合铰链、局部自由度、虚约束等加以说明。

（a）n=3，p l=3 F=3*3-2*3=3（b）n=3，p l=3，p h=2 F=3*3-2*3-2=1 （B处有局部自由度）（c）n=7，p l=10 F=3*7-2*10=1（d）n=4，p l=4，p h=2 F=3*4-2*4-2=2 （A处有复合铰链）（e）n=3，p l=4 F=3*3-2*4=1 （A或D处有虚约束）（f）n=3，p l=4 F=3*3-2*4=1 （构件4和转动副E、F引入虚约束）（g）n=3，p l=5 F=(3-1)*3-(2-1)*5=1 （有公共约束）（h）n=9，p l=12，p h=2 F=3*9-2*12-2=1 （M处有复合铰链，C处有局部自由度）2-3 计算下列机构的自由度，拆杆组并确定机构的级别。

（a）n=5，p l=7 F=3*5-2*7=1由于组成该机构的基本杆组的最高级别为Ⅱ级杆组，故此机构为Ⅱ级机构。

（b）n=5，p l=7 F=3*5-2*7=1此机构为Ⅱ级机构。

（c）n=5，p l=7 F=3*5-2*7=1拆分时只须将主动件拆下，其它构件组成一个Ⅲ级杆组，故此机构为Ⅲ级机构。

2-4 验算下列运动链的运动是否确定，并提出具有确定运动的修改方案。

（a）n=3，p l=4，p h=1 F=3*3-2*4-1=0 该运动链不能运动。

修改方案如下图所示：（b）n=4，p l=6 F=3*4-2*6=0 该运动链不能运动。

修改方案如下图所示：或第3章（P42）3-2 下列机构中，已知机构尺寸，求在图示位置时的所有瞬心。

（a）（b）（c）(a) v3=v P13=ω1P14P13μl3-6 在图示齿轮连杆机构中，三个圆互作纯滚，试利用相对瞬心P13来讨论轮1与轮3的传动比i13。

第5章（P80）5-2 一铰接四杆机构（2）机构的两极限位置如下图：（3）传动角最大和最小位置如下图：5-3题略解：若使其成为曲柄摇杆机构，则最短杆必为连架杆，即a 为最短杆。

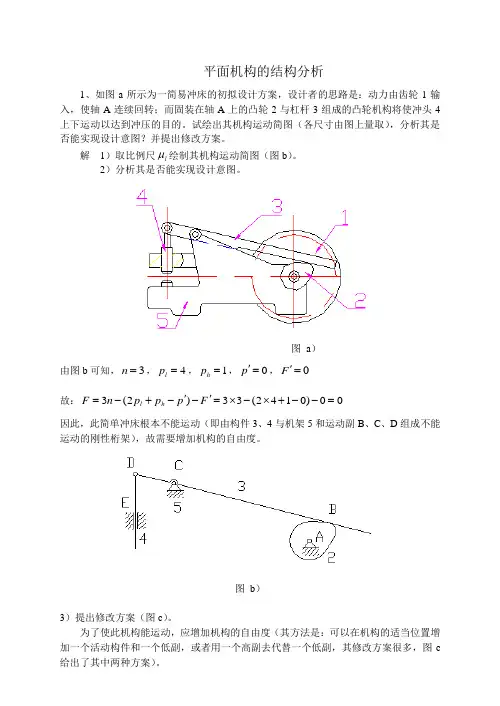
平面机构的结构分析1、如图a 所示为一简易冲床的初拟设计方案，设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。

试绘出其机构运动简图（各尺寸由图上量取），分析其是否能实现设计意图？并提出修改方案。

解 1）取比例尺l μ绘制其机构运动简图（图b ）。

2）分析其是否能实现设计意图。

图 a ） 由图b 可知，3=n ，4=l p ，1=h p ，0='p ，0='F 故：00)0142(33)2(3=--+⨯-⨯='-'-+-=F p p p n F h l因此，此简单冲床根本不能运动（即由构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架），故需要增加机构的自由度。

图 b ）3）提出修改方案（图c ）。

为了使此机构能运动，应增加机构的自由度（其方法是：可以在机构的适当位置增加一个活动构件和一个低副，或者用一个高副去代替一个低副，其修改方案很多，图c 给出了其中两种方案）。

图 c1） 图 c2）2、试画出图示平面机构的运动简图，并计算其自由度。

图a ）解：3=n ，4=l p ，0=h p ，123=--=h l p p n F图 b ）解：4=n ，5=l p ，1=h p ，123=--=h l p p n F3、计算图示平面机构的自由度。

将其中的高副化为低副。

机构中的原动件用圆弧箭头表示。

3－1解3－1：7=n ，10=l p ，0=h p ，123=--=h l p p n F ，C 、E 复合铰链。

3－2解3－2：8=n ，11=l p ，1=h p ，123=--=h l p p n F ，局部自由度3－3 解3－3：9=n ，12=l p ，2=h p ，123=--=h l p p n F4、试计算图示精压机的自由度解：10=n ，15=l p ，0=h p 解：11=n ，17=l p ，0=h p13305232=⨯-+⨯='-'+'='n p p p h l 26310232=⨯-⨯='-'+'='n p p p h l0='F 0='FF p p p n F h l '-'-+-=)2(3 F p p p n F h l '-'-+-=)2(310)10152(103=--+⨯-⨯= 10)20172(113=--+⨯-⨯=（其中E 、D 及H 均为复合铰链） （其中C 、F 、K 均为复合铰链）5、图示为一内燃机的机构简图，试计算其自由度，并分析组成此机构的基本杆组。

第二章 平面机构的结构分析2-1 绘制图示机构的运动简图。

2-3 计算图示机构的自由度，并指出复合铰链、局部自由度和虚约束。

解：(a) C 处为复合铰链。

7,n =p h =0，p l =10。

自由度 323721001W l h F n p p =--=⨯-⨯-=。

(b) B 处为局部自由度，应消除。

3n =， p h =2，p l =2自由度 323323121W l h F n p p =--=⨯-⨯-⨯=。

(c) B 、D 处为局部自由度，应消除。

3n =， p h =2，p l =2。

自由度 323323121W l h F n p p =--=⨯-⨯-⨯=。

(d) CH 或DG 、J 处为虚约束，B 处为局部自由度，应消除。

6n =，p h =1，p l =8。

自由度 32362811W l h F n p p =--=⨯-⨯-=。

(e) 由于采用对称结构，其中一边的双联齿轮构成虚约束，在连接的轴颈处，外壳与支架处的连接构成一个虚约束转动副,双联齿轮与外壳一边构成虚约束。

其中的一边为复合铰链。

其中4n =，p h =2，p l =4。

自由度 32342422W l h F n p p =--=⨯-⨯-=。

(f) 其中，8n =，p h =0，p l =11。

自由度 323821102W l h F n p p =--=⨯-⨯-=。

(g) ① 当未刹车时，6n =，p h =0，p l =8，刹车机构自由度为② 当闸瓦之一刹紧车轮时，5n =，p h =0，p l =7，刹车机构自由度为③ 当两个闸瓦同时刹紧车轮时，4n =，p h =0，p l =6，刹车机构自由度为2-3 判断图示机构是否有确定的运动，若否，提出修改方案。

分析 (a) 要分析其运动是否实现设计意图，就要计算机构自由度，不难求出该机构自由度为零，即机构不能动。

要想使该机构具有确定的运动，就要设法使其再增加一个自由度。

参考答案：2-12： 【解答】: 因n = 8, P L =10, P H =2, 局部自由度F ′=1(滚于5处为局部自由度) 故其自由度为： 11)2102(83)2(3F '=-+⨯-⨯=-+-=F P P n H L2-13： 【解答】: 因n = 3, P L =4, P H =0故其自由度为： 1)042(33)2(3F =+⨯-⨯=+-=H L P P n2-16【解答】(a) 因n = 4, P L =5, P H =1, （点A 处为复合铰链）故其自由度为： 1)152(43)2(3F =+⨯-⨯=+-=H L P P n(b) 因n = 7, P L =8, P H =2, （E 处与F 处的移动副只能各算为一个，局部自由度为2，C 处与E 处滚子为局部自由度)故其自由度为： 12)282(73)2(3F '=-+⨯-⨯=-+-=F P P n H L(c)首先计算虚约束数P ′机构重复部分为CFULKM ，其中F 处为由4个构件组成的复合铰链，有3个转动副；k 处为由3个构件组成的复合铰链，有2个转动副；注意，C 处仍有一个转动副。

则有n ′=7，P L ′=10, P H ′=10, 所以重复部分所带入的虚约束数P ′= 2P L ′+ P H ′-3n ’= 2×10+0-3×6=2然后计算机构的自由度F因n=11，P L =17，P H =0，P ′=2，故自由度为1)20172(113)2(3F '=-+⨯-⨯=-+-=P P P n H L ’‘(d) 因为齿轮3与齿轮5啮合时中心距不变，只能算作一个高副；齿轮5与齿条7啮合时，中心距发生变化，导致在齿的两侧均相互接触，有两个高副。

即齿轮3、5和齿条7与齿轮5的啮合高副所提供的约束数目不相同。

从而n=6，P L =7(A 、B 、C 处均为复合铰链)，P H =3， 故其自由度为1)372(63)2(3F =+⨯-⨯=+-=’‘H L P P n2-21： 【解答】: 因n = 4, P L =5, P H =1故其自由度为： 1)152(43)2(3F =+⨯-⨯=+-=H L P P n2-24： 【解答】: 因n = 5, P L =6（F 处的移动副只能算为一个）, P H =1 ，F ′=1故其自由度为： 11)162(53F )2(3F =-+⨯-⨯=-+-=‘H L P P n高副低代后的运动机构简图如下(1)所示，组成该机构的基本杆组情况如图（2）所示，因此除了原动件外有两个Ⅱ级杆组，故改机构为Ⅱ组机构。

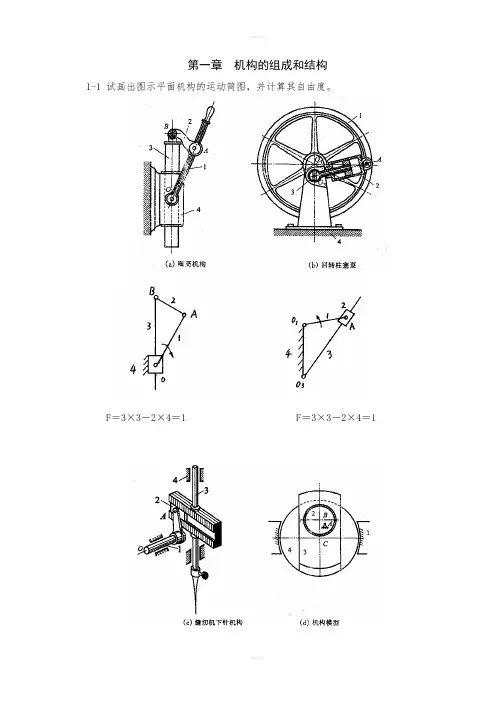
第一章机构的组成和结构1-1 试画出图示平面机构的运动简图，并计算其自由度。

F＝3×3－2×4＝1 F＝3×3－2×4＝1F＝3×3－2×4＝1 F＝3×3－2×4＝11-2 计算图示平面机构的自由度。

将其中高副化为低副。

确定机构所含杆组的数目和级别，以及机构的级别。

（机构中的原动件用圆弧箭头表示。

）F＝3×7－2×10＝1 F＝3×7－2×10＝1含3个Ⅱ级杆组：6-7，4-5，2-3。

含3个Ⅱ级杆组：6-7，4-5，2-3。

该机构为Ⅱ级机构构件2、3、4连接处为复合铰链。

该机构为Ⅱ级机构F＝3×4－2×5－1＝1 F＝3×3－2×3－2＝1F＝3×5－2×7＝1（高副低代后） F＝3×5－2×7＝1（高副低代后）含1个Ⅲ级杆组：2-3-4-5。

含2个Ⅱ级杆组： 4-5，2-3。

该机构为Ⅲ级机构构件2、3、4连接处为复合铰链。

该机构为Ⅱ级机构F＝3×8－2×11－1＝1 F＝3×6－2×8－1＝1F＝3×9－2×13＝1（高副低代后）F＝3×7－2×10＝1（高副低代后）含4个Ⅱ级杆组：8-6，5-7，4-3，2-11。

含1个Ⅱ级杆组6-7。

该机构为Ⅱ级机构含1个Ⅲ级杆组2-3-4-5。

第二章 连 杆 机 构2-1 在左下图所示凸轮机构中，已知r = 50mm ，l OA =22mm ，l AC =80mm,︒=901ϕ，凸轮1的等角速度ω1=10rad/s ，逆时针方向转动。

试用瞬心法求从动件2的角速度ω2。

解：如右图，先观察得出瞬心P 13和P 23为两个铰链中心。

再求瞬心P 12：根据三心定理，P 12应在P 13与P 23的连线上，另外根据瞬心法，P 12应在过B 点垂直于构件2的直线上，过B 点和凸轮中心O 作直线并延长，与P 13、P 23连线的交点即为P 12。