重叠问题2及答案

图中间重叠部分表示两道题都做对的人数，把做第一道题和做对第二道题的人数加起来得21＋18=39人，这39人比全班总人数36多出了39－36=3人，这多出的3人既在做对第一题的人数中算过，也在做对第二道题的人数中算过，即表示两道题都做对的人数。
1
2
例
160厘米
90厘米
？厘米
90+90-160=20（厘米） 答：中间钉在一起的部分长20厘米。
把两块一样长的木板像下图这样钉在一起成了一块木板。如果这块钉在一起的木板长8米，中间重叠部分是2米，这两块木板各长多少米？
【思路导航】把等长的两块木板的一端钉起来，钉在一起的长度就是重叠部分，重叠的部分是2米，所以这两块木板的总长度是8+2＝10米，每块木板的长度是10÷2=5米。
重
叠
问
题
两块木板各长80厘米，如下图，钉在一起。中间钉在一起的地方是15厘米。这两块钉起来的木板长多少厘米？
例
ቤተ መጻሕፍቲ ባይዱ
15厘米
80厘米
80厘米
80+80-15=145（厘米） 答：这两块钉起来的木板长145厘米。
两块各长90厘米的木板钉成一块长160厘米的木板，中间钉在一起的部分长多少厘米？
39+42=81（人） 81-50=31（人） 答：有31人语文、数学都得了100分。
50个同学参加期末考试，每个同学至少有一门是100分。语文得100分的39人，数学得100分的是42人，请问有多少人语文、数学都得了100分？
例
一次数学测试，全班36人中，做对第一道聪明题的有21人，做对第二道聪明题的有18人，每人至少做对一道。问两道聪明题都做对的有几人？ 【思路导航】根据题意，画出下图：

三年级奥数4种重叠问题三年级奥数4种重叠问题随着奥数热潮的兴起，越来越多的家长将孩子送进了奥数班。

而在奥数学习中，涉及到的重叠问题一直是让小学生头疼的难点之一。

下面，我们来分别介绍四种常见的重叠问题及其解法。

问题1：中国古代的皇帝有哪些名字？这是一道典型的排列组合重叠问题，因为存在不同的朝代和不同的皇帝名称，所以我们可以分类讨论。

假设有n个皇帝姓名，m个朝代，则总共可能的情况数为m的n次方。

例如，如果有2个朝代、3个不同的皇帝姓名，则总共可能的组合数为2的3次方，即8种。

问题2：小明手里有红、黄、蓝三个颜色的球各若干个，从中取出2个球，可能出现几种不同的颜色组合？这是一道组合问题，可以通过简单的计算得出答案。

假设红、黄、蓝三种颜色球的数量分别为a、b、c，则不同颜色组合的数量为ab+ac+bc。

问题3：在10个人中随机选取4个人，其中小明和小红不能同时被选中，有多少种可能？这是一道容斥原理的问题。

首先得出在10个人中任意选取4个人的可能组合数，即C(10,4)，然后减去小明和小红都不在其中的可能组合数，即C(8,4)，最后再加上小明和小红都在其中的组合数，即C(8,2)。

计算公式为C(10,4) - C(8,4) + C(8,2)。

问题4：现有红、黄、蓝、白四个颜色的球各m个，从中选取n个球，求使得四种颜色的球都被选中的组合数。

这是一道比较复杂的组合问题，需要采用容斥原理。

首先计算四个颜色都被选中的组合数，即C(m,1)^4，然后减去三个颜色被选中的组合数，即C(4,1)×C(m,1)^3。

但是这样计算仍然会有重复的情况，例如每个颜色都选中了两个球的情况，需要再次修正。

最终的计算公式为C(m,1)^4 - C(4,1)×C(m,1)^3 + C(4,2)×C(m,1)^2 - C(4,3)×C(m,1)。

综上所述，重叠问题在奥数中是十分常见的，但只要我们掌握了相应的解法，便能够轻松解决这些难点问题。

二年级创新思维春季班讲义：第十讲重叠问题（二）姓名：【例4】（1）如果将两块同样长的木条钉在一起共长15厘米，中间钉在一起的长度是3厘米，问：原来每块木条长多少厘米？答：原来每块木条长（）厘米。

（2）两块木条各有8厘米，如果把他们钉在一起时，中间重合部分是3厘米，钉成后这块木条有多少厘米？答：钉成后这块木条有（）厘米。

（3）两块木条各有9厘米，钉成一块长14厘米的木条，中间重合的部分是几厘米？答：中间重合的部分是（）厘米。

练一练（四）1、（1）两块木条各长40厘米，把它们钉在一起，中间钉在一起的地方是10厘米，这块钉起来的木条长多少厘米？答：这块钉起来的木条长（）厘米。

（2）两块木条各长40厘米，钉在一起的木条长70厘米，中间钉在一起的地方长多少厘米？答：中间钉在一起的地方长（）厘米。

2、有两块同样长的木条，钉成了一块长13分米的长木条，中间顶在一起的重叠部分长1分米，这两块木条原来各有多少分米？答：这两块木条原来各有（）分米。

【例5】王老师出了两组数学兴趣题给18名同学做，做对第一组的有10名同学，做队第二组的有12名同学，两题都做对的有多少名同学？答：两题都做对的有（）名同学。

练一练（五）1、有一个班英语、数学期终考试得100分的共有8人，其中英语100分的有5人，数学100分的有6人，两门学科都得100分的有几人？答：两门学科都得100分的有（）人。

2、有100个同学带矿泉水和水果去春游，带矿泉水的有78人，带水果的有71人，两样都带有至少有多少人？答：两样都带有至少有（）人。

3、二（3）班有39人，全班都订了报，订《少年报》的有35人，订《拼音报》有8人，两样报纸都订的有多少人？答：两样报纸都订的有（）人。

4、三年级学生中，音乐爱好者有38名，电脑爱好者有64名，两项都爱好的有27名，这个年级有多少名学生？答：这个年级有（）名学生。

5、在1～30中，既不是3的倍数，又不是5的倍数的数有多少个？答：又不是5的倍数的数有（）个。

第十九讲 重叠问题1. 例题1答案：详解：根据示例标出相应的木板的长度即可．2. 例题2答案：130厘米详解：两块木板总长7080150+=（厘米），重叠的部分是20厘米，用两块木板总长减去一次重叠即可，15020130-=（厘米）．3. 例题3答案：30厘米详解：两块木板总长应为9060150+=（厘米），这150 厘米就比重叠后木板的总长多出15012030-=（厘米），所以这30 厘米就是重叠部分长度，即中间钉在一起的木板长度． 4. 例题4答案：分别是5米详解：方法一：把等长的两根钢筋的一端钉起来，钉在一起的长度就是重叠部分，重叠的部分是2米，所以这两根钢筋的总长度是8210+=（米），每根钢筋的长度是5米．方法二：用现在的总长度减去重叠部分的长度，得到的就是两边的长度，即826-=（米），所以一边的长度就是3米，633=+，一根钢筋的长度就是325+=（米）．5. 例题5答案：53人详解：方法一：根据已知条件，可得做完两科作业的总人数为473380+=（人），但在这80人中，有27人两科作业都做完了．也就是说，这两科作业都做完的27人被算了两次，重复了一次，所以要从总人数80人中去掉重复的27人，802753-=（人），就是全班的总人数． 方法二：根据已知条件，可得只做了语文作业的人数为472720-=（人），只做了数学作业的人数为33276-=（人），所以全班总人数为2027653++=（人）．6. 例题6 语文作业（47）人数学作业 （ 33）人 27人（1）（2）60厘米答案：37个详解：如图，中间重叠部分表示两道智力题都答对的人数，如果把答对第一道题和答对第二道题的人数合起来是5446100+=（个），这100人就比总人数多1006337-=（个），多的37人既在答对第一道题的人中算过，又在答对第二道题的人中算过，所以这多的37人就是两道题都答对的人．7. 练习1答案：简答：根据示例标出相应的木板的长度即可．8. 练习2答案：9米简答：根据已知条件，可得两块木板总长度是5510+=（米），但中间重叠部分长度是1米，所以大木板的长度应该是总长度减去重叠的部分，即1019-=（米）．9. 练习3答案：5米简答：根据已知条件，得两块木板总长度是101020+=（米），这20米就比总长度多出20155-=（米），所以这5米就是重叠部分长度，即中间钉在一起的木板长度．5米（1）（2） 40厘米100厘米第一道题（54）人第二道题 （46）人10. 练习4答案：分别是80厘米简答：把等长的两块木板的一端钉起来，钉在一起的长度就是重叠部分，重叠的部分是40厘米，所以这两块木板的总长度是12040160+=（厘米），1608080=+，所以每块木板的长度是80厘米．（方法不唯一）,11. 作业1答案：简答：根据示例标出相应的木板的长度即可．12. 作业2答案：100厘米简答：根据已知条件，可得两块木板总长度是6060120+=（厘米），但中间重叠部分长度是20厘米，所以大木板的长度应该是总长度减去重叠的部分，即12020100-=（厘米）．13. 作业3答案：10厘米简答：根据已知条件，得两块木板总长度是8080160+=（厘米），这160厘米就比总长度多出（1）（2）50厘米50厘米40厘米15米16015010-=（厘米），所以这10厘米就是重叠部分长度，即中间钉在一起的木板长度．14. 作业4答案：分别是80厘米简答：把等长的两块木板的一端钉起来，钉在一起的长度就是重叠部分，重叠的部分是60厘米，所以这两块木板的总长度是10060160+=（厘米），每块木板的长度是80厘米．（方法不唯一）15. 作业5答案：39人 简答：根据已知条件，可得订报纸的总人数为312859+=（人），但在这59人中，有20人两种报纸都订了．也就是说，这两种报纸都订的20人被算了两次，重复了一次，所以要从总人数59人中去掉重复的20人，592039-=（人），就是全班的总人数．订《数学报》31人订《语文报》28人 20150厘米。

第5讲重叠问题例1:有3根小棒，每根长度都是20厘米，用绳子将它们扎起来连成一根（如图），已知每个接头处长度为3厘米，那么3根连在一起后共长多少厘米？练习：1.有5根小棒，每根长度都是8厘米，用绳子将它们扎起来连成一根，已知每个接头处长度为2厘米，那么5根连在一起后共长多少厘米？2.有8根小棒，每根长度都是10厘米，用绳子将它们扎起来连成一根，已知每个接头处长度为2厘米，那么8根连在一起后共长多少厘米？3.有6根小棒，每根长度都是20厘米，用绳子将它们扎起来连成一根，已知每个接头处长度为2厘米，那么6根连在一起后共长多少厘米？例2：有4根小棒，每根长度都是12厘米，用绳子将它们扎起来连成一根后总共长36厘米，已知每个接头处长度相等，那么每个接头处的长度是多少厘米？练习：1.有3根小棒，每根长度都是12厘米，用绳子将它们扎起来连成一根后总共长30厘米，已知每个接头处长度相等，那么每个接头处的长度是多少厘米？2.有5根小棒，每根长度都是20厘米，用绳子将它们扎起来连成一根后总共长80厘米，已知每个接头处长度相等，那么每个接头处的长度是多少厘米？3.有4根小棒，每根长度都是20厘米，用绳子将它们扎起来连成一根后总共长65厘米，已知每个接头处长度相等，那么每个接头处的长度是多少厘米？例3 ：有若干根小棒，用绳子将它们扎起来后长度共减少6 厘米，已知每个接头处长度为3 厘米，那么一共有多少根小棒？练习：1.有若干根小棒，用绳子将它们扎起来后长度共减少20 厘米，已知每个接头处长度为5 厘米，那么一共有多少根小棒？2.有若干根小棒，用绳子将它们扎起来后长度共减少24 厘米，已知每个接头处长度为4 厘米，那么一共有多少根小棒？例4：一些同学排成一行，从左边数小明是第5 个，从右边数小明是第7 个共有多少个同学？练习：1.一些同学排成一行，无论从左边数还是从右边数小明都是第8 个，一共有多少个同学？2.一些同学排成一列，从前面数小明是第8 个，从右边数小明是第7 个。

作业：数学书110页第2题。
橡皮擦 铅笔
笔芯
只有甲文具盒里的有2种
妈妈文具盒里的文具 爸爸文具盒里的文具
卷笔刀 三角板
橡皮擦 铅笔
笔芯
只有乙文具盒里的有1种
妈妈文具盒里的文具 爸爸文具盒里的文具
卷笔刀 三角板
橡皮擦 铅笔
笔芯
两个文具盒里一共有几种文具？
① ⑤ 三（1）班参加语文小组的有8人，参加数学小 组的有9人，两项都参加的有3人。三（1）班参加 语文和数学课外小组一共有多少人？
两个爸爸和两个儿子一起去看电影，可 他们只买了3张票，便顺利地进了电影院，这 是为什么呢？ 既是爸爸，又
是儿子
妈妈的礼物
爸爸的礼物
甲文具盒里的礼物
乙文具盒里的礼物
卷笔刀 三角板
橡皮擦
铅笔 笔芯
甲文具盒里的文具
乙文具盒里的文具
卷笔刀 三角板
橡皮擦 铅笔
笔芯
甲文具盒里的文具
乙文具盒里的文具
卷笔刀 三角板
橡皮擦 铅笔
笔芯
甲文具盒里有4种文具
甲文具盒里的文具
乙文具盒里的文具
卷笔刀 三角板
橡皮擦 铅笔
笔芯
乙文具盒里有3种文具
甲文具盒里的文具
乙文具盒里的文具
卷笔刀 三角板
橡皮擦 铅笔
笔芯
既是甲文具盒的文具，又是乙文具盒里的文具 有2种
妈妈文具盒里的文具 爸爸文具盒里的文具
卷笔刀 三角板
8+9-3=14（人） 答：三（1）班参加语文和数学课外小 组一共有14人。
妈妈的问题：妈妈想给家里进行一次大扫除，什么都做完 了发现天花板上有蜘蛛网，妈妈犯难了，天花板这么高，既没 有梯子，又没有长的刷子，怎么才能清楚天花板上的蜘蛛网呢？ 你有办法吗？

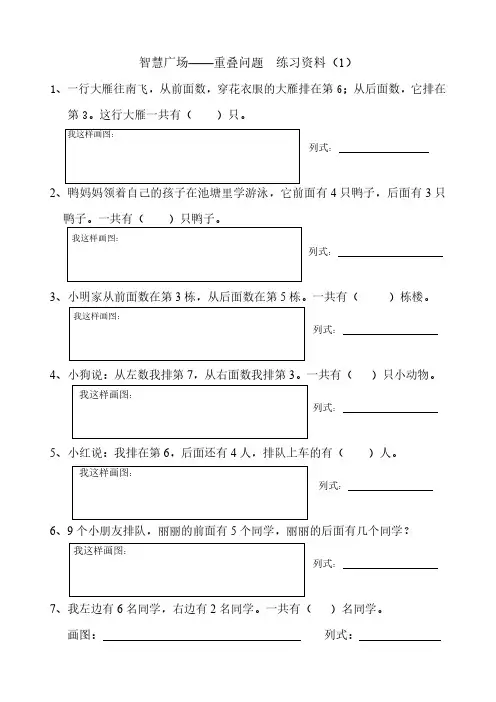
1、一行大雁往南飞，从前面数，穿花衣服的大雁排在第6；从后面数，它排在第3。

这行大雁一共有（）只。

我这样画图：列式：2、鸭妈妈领着自己的孩子在池塘里学游泳，它前面有4只鸭子，后面有3只鸭子。

一共有（）只鸭子。

我这样画图：列式：3、小明家从前面数在第3栋，从后面数在第5栋。

一共有（）栋楼。

我这样画图：列式：4、小狗说：从左数我排第7，从右面数我排第3。

一共有（）只小动物。

我这样画图：列式：5、小红说：我排在第6，后面还有4人，排队上车的有（）人。

我这样画图：列式：6、9个小朋友排队，丽丽的前面有5个同学，丽丽的后面有几个同学？我这样画图：列式：7、我左边有6名同学，右边有2名同学。

一共有（）名同学。

画图：列式：1、从前面数小兔排第4，从后面数它排第5。

一共有（）只。

我这样画图：列式：2、我家前面有4栋楼，后面有5栋楼。

这个小区一共有（）栋楼。

我这样画图：列式：3、小蚂蚁说：从前面数我排第3，后面还有6只。

一共有（）少只。

我这样画图：列式：4、小黄鸡说：我的前面有6只小鸡，后面有3只。

一共有（）只小鸡。

我这样画图：列式：5、小明说：我排第5，我后面还有5个人。

一共有（）个小朋友在排队。

我这样画图：列式：6、有9只小动物正在排队，小猪说：我从后面数排第5，从前面数排第（）。

我这样画图：列式：7、同学们排成一队，小红说：从前面数我排第3。

小兰说：从前面数我排第9。

小红和小兰中间有（）个小朋友。

我这样画图：列式：。

第十单元数学百花园模块一重叠问题（容斥原理）能力提升训练【例题1】四（2）班共有42人，其中会打篮球的有21人，会游泳的有17人，两种运动都不会的有10人，两种运动都会的有多少人？【练习1】四（1）班在一次语文、数学测试中，有32人语文获优，有35人数学获优，其中语文、数学都获优的有28人，语文、数学都没有获优的有6人。

四（1）班共有学生多少人？【例题2】红星小学举办绘画展览。

展示栏展出一至六年级的绘画作品，其中有24幅作品不是一年级的，有22幅作品不是二年级的，一、二年级参展的绘画作品共有8幅，三至六年级参展的绘画作品共有多少幅？【练习2】学校科技室里展出每个年级的科技作品，其中有110件不是一年级的，有100件不是二年级的，一、二年级参展的作品共有32件。

三至六年级参展的作品共有多少件？【例题3】把三根长为10厘米的筷子绑在一起，其中绑在一起的部分长1厘米，那么，绑成后的这根筷子长多少厘米？【练习3】把两根同样长的木条钉在一起，钉成一根长47厘米的木条，中间重叠部分（阴影部分）长11厘米（如下图）。

每根木条长多少厘米？47厘米14厘米【例题4】把四根长为40厘米的尺子，绑成一根长为130厘米的长尺子，那么每两根尺子中间的重叠部分长多少厘米？【练习4】把五根长为40厘米的尺子，绑成一根长为160厘米的长尺子，那么每两根尺子中间的重叠部分长多少厘米？【例题5】四（1）班有48人，其中喜欢看《奥特曼》的有32人，喜欢看《喜羊羊与灰太狼》的有38人，有25人两种动画片都喜欢看。

那么：（1）只喜欢看《奥特曼》而不喜欢看《喜羊羊与灰太狼》的有多少人？（2）只喜欢看《喜羊羊与灰太狼》而不喜欢看《奥特曼》的有多少人？（3）有多少人两种动画片都不喜欢看？【练习5】四（1）班同学中喜欢看《喜羊羊与灰太狼》的有32人，喜欢看《成龙历险记》的有25人，两种动画片都喜欢看的有8人，喜不喜欢看的有2人，五（1）班一共有多少人？【例题6】光明小学组织棋类比赛，分成围棋、中国象棋和国际象棋三个组进行，参加围棋比赛的有42人，参加中国象棋比赛的有55人，参加国际象棋比赛的有33人，同时参加了围棋和中国象棋比赛的有18人，同时参加了围棋和国际象棋比赛的有10人，同时参加了中国象棋和国际象棋比赛的有9人，其中三种棋赛都参加的有5人，问参加棋类比赛的共有多少人？【练习6】三（1）班的学生参加活动班（每人至少参加一个），参加作文班的有18人，参加音乐班的有20人，参加奥数班的有24人。

1. 了解容斥原理二量重叠和三量重叠的内容；2. 掌握容斥原理的在组合计数等各个方面的应用．一、两量重叠问题 在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成：A B A B A B =+-U I (其中符号“U ”读作“并”，相当于中文“和”或者“或”的意思；符号“I ”读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B I ，即阴影面积．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B I ，即阴影面积．包含与排除原理告诉我们，要计算两个集合A B 、的并集A B U 的元素的个数，可分以下两步进行：第一步：分别计算集合A B 、的元素个数，然后加起来，即先求A B +(意思是把A B 、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去C A B =I (意思是“排除”了重复计算的元素个数)．二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数．用符号表示为：A B C A B C A B B C A C A B C =++---+U U I I I I I ．图示如下：教学目标 知识要点7-7-2.容斥原理之重叠问题（二）1．先包含——A B +重叠部分A B I 计算了2次，多加了1次；2．再排除——A B A B +-I把多加了1次的重叠部分A B I 减去．在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考．模块一、三量重叠问题【例 1】 一栋居民楼里的住户每户都订了2份不同的报纸。

重叠问题
1、把两块一样长的木板钉在一起，钉成一块长35厘米的木板。

中间重合部分长11厘米，这两块木板各长多少厘米？
2、两根木棍放在一起，从头到尾共长66厘米，其中一根木棍
长48厘米，中间重叠部分长12厘米。

另一根木棍长多少
厘米？
3、两块木板各长75厘米，钉成一块长130厘米的木板，中间
重合部分是多少厘米？
4、三（5）班有42名同学，会下象棋的有21名同学，会下围
棋的有17名，两种棋都不会的有10名。

两种棋都会下的
有多少名？
5、三（4）班做完语文作业的有37人，做完数学作业的有42
人，两种作业都完成的有31人，每人至少完成一种作业。

三（4）班共有学生多少人？
6、学校乐器队招收了42名新学员，其中会拉小提琴的有25
名，会弹电子琴的有22名，两项都不会的有3名。

两项都会的有多少名？
7、三（4）班有学生56人，做对第一道思考题的有29人，做
对第二道思考题的有27人，两道题都做错的有7人。

两道思考题都做对的有几人？
8、两块木板各长90厘米，像下图这样钉成一块木板，中间重合部分是15厘米，这块钉在一起的木板总长多少厘米？。

重叠问题像这样重叠问题是我们生活中经常遇到的问题，今天我们就来学习有关重叠问题中的“木头重叠”和“人员重叠”。

例1：请按照示例给每个木板标数。

示例：木板长80厘米。

（1）木板长70厘米。

（2）上面的木板长70厘米，下面的木板长60厘米。

练习1：请你按照示例给每块木板标数。

示例：木板重叠部分长30厘米，下面的木板长70厘米。

（1）木板重叠部分长40厘米。

（2）上面的木板长100厘米，下面的木板长100厘米，重叠部分长50厘米。

例2：如图，一块木板长70厘米，另一块木板长80厘米，把它们钉在一起变成一块大木板，中间钉在一起的木板长20厘米。

这块大木板长多少厘米？练习2：如图，两块都是5米长的木板，把它们钉在一起变成一块大木板，中间钉在一起的木板长1米.这块大木板长多少米？对这类题目，我们可以从已知条件入手，认真分析（有时还要作图分析，借助图来思考），找出解题方法。

例3.如图一根木棍长90厘米，另一个木棍长60厘米，两个木棍钉在一起，共长120厘米，那么中间钉在一起的木棍长度是多少厘米？练习3：如图，两块一样长的木板都是10米，:钉在一起时木板共长15米，中间钉在一起的木板长度是多少米？例4：把两根一样长的钢筋焊接成长为8米的钢筋，中间焊接处的重叠部分长2米（如下图），这两根钢筋原来分别长多少米？练习4：把两块一样长的木板:钉成长为120厘米的大木板，中间钉在一起的木板长度是40厘米（如下图），这两块木板原来分别长多少厘米？例5：下午张老师问他们班的学生：“语文作业作文请举手！”有47人举手。

又说：“数学作业做完了请举手！”有33人举手。

“两科作业都做完的请举手！”又有27人举手。

后来张老师发现，每位同学至少做完了一门功课的作业，你能知道张老师班有多少名学生吗？例6：张老师出了两道智力题，让63个学生来回答，其中答对第:一道题的有54个人，答对第二道题的有46个人。

请问：两道题都答对的有几个人？课堂内外：爱上数学主动思考1.请你按照示例给每块木板标数。

小学奥数重叠问题专题日常生活或数学问题中，在把一些数据按照某个标准分类时，常常出现其中的一部分数据同时属于两种或两种以上不同的类别，这样在计算总数时就会出现重复计算的情况，这类问题就叫做重叠问题。

重叠问题中涉及到的容斥原理是奥数的四大原理之一，是奥数重要知识点。

学生学习奥数，一定要掌握容斥原理。

下面小编给大家分享解决重叠的方法。

1. 解答重叠问题要用到数学中一个重要原理——包含与排除原理，即当两个计数部分有重复包含时，为了不重复计数，应从它们的和中排除重复部分。

2. 解答重叠问题的应用题，必须从条件入手进行认真的分析，有时还要画出图示，借助图形进行思考，找出哪些是重复的，重复了几次。

明确需要要求的是哪一部分，从而找出解答方法。

3. 在数学中，我们经常用平面上封闭曲线的内部代表集合和集合之间的关系。

这种图称为韦恩图（也叫文氏图）。

4. 解答重叠问题的常用方法是：先不考虑重叠的情况，把有重复包含的几个计数部分加起来，再从它们的和中排除重复部分元素的个数，使得计算的结果既无遗漏又不重复。

这个原理叫做包含与排斥原理，也叫容斥原理。

5. 容斥原理1：如果被计数的对象，被分为A、B两大类，则：被计数对象的总个数=A 类元素的个数+B类元素的个数-同时属于A类和B类的元素个数。

容斥原理2：如果被计数的对象，被分为A、B、C三大类，则：被计数对象的总个数=A 类元素的个数+B类元素的个数+C类元素的个数-同时属于A类和B类元素的个数-同时属于A类和C类元素个数-同时属于B类和C类元素个数+同时属于A类、B类、C类元素个数。

一、重叠问题之长度：（1）拼接（对接）（2）搭接（3）打结题目1：（搭接正问题：求总长度）把两段同样是20厘米长的纸条粘合在一起，形成一段更长的纸条。

中间重叠的部分是6厘米，粘好的纸条长多少厘米？题目2：（搭接反问题一：等长搭接，求原来长度）把两段一样长的纸条粘合在一起，形成一段更长的纸条。

这段更长的纸条长30厘米，中间重叠的部分是6厘米，原来两条纸条各长多少厘米？题目3：（搭接反问题一：不等长搭接，求原来长度）两根木棍放在一起，从头到尾共长66厘米，其中一根木棍长48厘米，中间重叠部分长12厘米。

重叠问题练习题有答案练习一1、小朋友排队做操，小明从前数起排在第4个，从后数起排在第7个。

这队小朋友共有多少人？○○○●○○○○○○如图：4＋7－1 = 102、学校组织看文艺演出，冬冬的座位从左数起是第12个，从右数起是第21个。

这一行座位有多少个？12＋21－1 =23、同学们排队去参观展览，无论从前数还是从后起起，李华都排在第8个。

这一排共有多少个同学？8＋8－1 = 15练习二1、同学们排队跳舞，每行、每列人数同样多。

小红的位置无论从前数从后数，从左数还是从右数起都是第4个。

跳舞的共有多少人？每排有：4＋4－1 =共有：7×=492、为庆祝“六一”，同学们排成每行人数相同的鲜花队，小华的位置从左数第2个，从右数第4个；从前数第3个，从后数第5个。

鲜花队共多少人？从左到右人数：2＋4－1 =从前到后人数：3＋5－1 =5×=53、三班排成每行人数相同的队伍入场参加校运动会，梅梅的位置从前数是第6个，从后数是第5个；从左数、从右数都是第3个。

三班共有学生多少人？6＋5－1 = 103＋3－1 =10×=0练习三1、把两段一样长的纸条粘合在一起，形成一段更长的纸条。

这段更长的纸条长30厘米，中间重叠部分是6厘米，原来两段纸条各长多少厘米？÷= 182、把两块一样长的木板钉在一起，钉成一块长35厘米的木板。

中间重合部分长11厘米，这两块木板各长多少厘米？÷=33、两根木棍放在一起，从头到尾共长66厘米，其中一根木棍长48厘米，中间重叠部分长12厘米。

另一根木棍长多少厘米？66－48＋1=0练习四1、三班有学生55人，每人至少参加赛跑和跳绳比赛中的一种。

已知参加赛跑的有36人，参加跳绳的有38人。

两项比赛都参加的有几人？36＋38－5= 192、两块木板各长75厘米，像下图这样钉成一块长130厘米的木板，中间重合部分是多少厘米？×=03、三班有42名同学，会下象棋的有21名同学，会下围棋的有17名，两种棋都不会的有10名。

重叠问题练习题答案重叠问题通常指的是在数学或逻辑问题中，两个或多个集合或事件有共同的部分。

下面是一些重叠问题练习题的答案：1. 练习题：一个班级有50名学生，其中30人参加了数学俱乐部，20人参加了科学俱乐部。

如果两个俱乐部共有的学生数为10人，那么没有参加任何俱乐部的学生有多少人？答案：首先，我们计算两个俱乐部的学生总数：30（数学俱乐部）+ 20（科学俱乐部）- 10（两个俱乐部共有的学生）= 40人。

班级总人数为50人，所以没有参加任何俱乐部的学生数为50 - 40 = 10人。

2. 练习题：在一个社区中，有200户家庭，其中100户有宠物，80户有花园。

如果同时拥有宠物和花园的家庭有40户，那么没有宠物也没有花园的家庭有多少户？答案：首先，我们计算有宠物和花园的家庭总数：100（有宠物）+ 80（有花园）- 40（同时拥有宠物和花园）= 140户。

社区总家庭数为200户，所以没有宠物也没有花园的家庭数为200 - 140 = 60户。

3. 练习题：一个图书馆有1000本书，其中300本是科幻小说，200本是历史书籍。

如果同时属于科幻和历史类别的书籍有50本，那么既不是科幻也不是历史的书籍有多少本？答案：首先，我们计算科幻和历史书籍的总数：300（科幻小说）+ 200（历史书籍）- 50（同时属于科幻和历史的书籍）= 450本。

图书馆总书籍数为1000本，所以既不是科幻也不是历史的书籍数为1000 - 450 = 550本。

4. 练习题：一个学校有500名学生，其中200名学生参加了体育队，150名学生参加了合唱团。

如果同时参加体育队和合唱团的学生有50人，那么没有参加任何团队的学生有多少人？答案：首先，我们计算参加体育队和合唱团的学生总数：200（体育队）+ 150（合唱团）- 50（同时参加两个团队的学生）= 300人。

学校总学生数为500人，所以没有参加任何团队的学生数为500 - 300 = 200人。

2.简单的重叠问题（二）一、例题例1：强强要把10张长度是10厘米的纸条连接起来，每两张纸条的粘合处都是2厘米。

连接后的纸条全长是多少厘米？例2：三年级有92名同学，其中订阅了《少年报》的有64人，订阅《小学生周报》的有58人，这两种都没有订的有17人，两种都订的有多少人？二、试一试（1）按下图的方法用小棒搭三角形，搭1个三角形需3根小棒，搭2个三角形需5根小棒，搭3个三角形需7根小棒……那么，搭100个三角形需（）根小棒。

搭200个三角形需（）根小棒。

（2）有100名同学参加联欢晚会，其中18人要表演舞蹈，32人表演合唱，有5人既要参加舞蹈又要参加合唱。

两个项目都不参加的有多少人？（3）同学参加联欢晚会，其中18人要表演舞蹈，32人表演合唱，有5人既要参加舞蹈又要参加合唱。

两个项目都不参加的有55人，参加联欢会的一共有多少人？三、作业1.把10张长度是15厘米的纸条连接起来，每两张纸条的粘合处都是2厘米。

连接后的纸条全长是多少厘米？2.把10张长度是18厘米的纸条连接成全长是153厘米的纸条，且每两张纸条的粘合处长度都相同，问每两张纸条的粘合处长度都是多少厘米？3.三（3）班除了5位同学外，其他的都会打篮球或排球，其中会打篮球的有18人，会打排球的有23人，两种球都会的有9人。

三（3）班一共有多少人？4.三（1）班38位同学排成一路纵队，从前往后数张明排在第23个，从后面往前数李兵排在第28个，在张明与李兵之间还有多少个人？5.三（1）班同学排成一路纵队，从前往后数张明排在第23个，从后面往前数李兵排在第18个，在张明与李兵之间还有5个人。

三（1）班一共有多少人？（提醒：有两种不同的情况：张明可能排在李兵的前面，也可能排在李兵的后面，所以有两种不同的答案。

）。

重叠问题二、练习题1：老师出了两道题，在40人中，做对第一题的有31人，做对第二题的有28人，每人至少做对一题，两道题都做对的有几人？(图)2：教工运动会，参加跳绳比赛的有38人，参加踢毽子比赛的有39人，因病请假的有3人，如果全校教工有55人，那么既参加跳绳比赛又参加踢毽子比赛的老师有多少人？(图)3：校运动会上，四个年级共有118人参加了跑步比赛。

其中一、二年级共有70人参加，一、三年级共有65人参加，二、三年级共有59人参加，问：四年级有多少学生参加跑步比赛？（摘录）4：某校三年级共有三个班级128名学生，一班和二班共有89人，二班和三班共有87人。

三年级各班有多少名学生？（摘录）5、有180个同学参加“六一”游园活动，其中28人要表演舞蹈，有62人要参加合唱，既要表演舞蹈又要参加合唱的有15人，那么既不参加合唱，又不表演舞蹈的有多少人？(图)6、三年级一班有54人上美术课，其中2人没带笔，带油画棒的有28人，带水彩笔的有25人，两种笔都带到有多少人？(图)7、四年级同学参加语文、数学期终测试，有6人语文不及格，有5人数学不及格，若不及格的同学必须补考，四年级同学最少有多少同学补考？最多有多少人？8、四年级一共有210人，一次考试中，语文得优秀的120人，数学得优秀的150人，两科都得优秀的68人，两科都没得优秀的有多少人？(图)9.少先队员排队去参观蝴蝶展览。

从排头数起，小江是第65个；从排尾数起，张颖是第38个。

张颖的后面排着小江。

你知道有多少同学去看蝴蝶展吗？(图)10、180个小朋友平均排成两队去春游。

小刚和小明在一个队里。

从排头往后数，小刚说第49个，从排尾往前数，小明说第58个，你知道小刚和小明中间有几个人？ (图)11、四年级四个班级要分成三大组，甲乙两组有86人，甲丙两组有103人，乙丙两组有97人，四年级共有多少人？甲乙丙三组分别有多少人？（摘录）12、有A、B两种型号的电话机，各买一部共要270元，如果买2部A型与3部B型共要660元。

·题目1：有两张一样长的纸条粘贴起来，成为长30厘米的纸条，粘贴部分长10厘米，求这两张纸条各长几厘米？ A.20 B.15
·题目2：王老师的班上有16人参加竞赛，参加语文竞赛的有9人，参加数学竞赛的有8人，有几个人既参加语文竞赛又参加数学竞赛？ A.1 B.2
·题目3：洗好的18条毛巾晾在绳上，每一块毛巾的两边必须用夹子夹住，同一个夹子可夹住相邻的两块毛巾，这样一共要用多少个夹子？ A.18 B.19
·题目4：10张照片用图钉像下图那样钉在橱窗里一共要用多少个图钉？
图1 A.22 B.24
如图看不清或变形，可以点击图片放大
·题目5：吃饭前，两只手放在桌上的小朋友有5个，只把左手放在桌上的小朋友有6个，只把一只手放在桌上的小朋友有7个，你说吃饭的小朋友有几个？
A.18
B.12。