托勒密定理的向量证明

托勒密定理托勒密(Ptolemy)定理指出，圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。

原文：圆的内接四边形中，两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。

从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式，托勒密定理实质上是关于共圆性的基本性质．证明一、（以下是推论的证明，托勒密定理是其中一种特殊情况）在任意凸四边形ABCD中，作△ABE使∠BAE=∠CAD ∠ABE=∠ACD,连接DE.则△ABE∽△ACD所以BE/CD=AB/AC,即BE·AC=AB·CD (1)由△ABE∽△ACD得AD/AC=AE/AB,又∠BAC=∠EAD,所以△ABC∽△AED.BC/ED=AC/AD,即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又因为BE+ED≥BD（仅在四边形ABCD是某圆的内接四边形时，等号成立，即“托勒密定理”）二．复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数，则AB、CD、AD、BC、AC、BD的长度分别是：(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。

首先注意到复数恒等式：(a− b)(c− d) + (a− d)(b− c) = (a− c)(b− d) ，两边取模，运用三角不等式得。

等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等，这与A、B、C、D四点共圆等价。

四点不限于同一平面。

平面上，托勒密不等式是三角不等式的反演形式。

1.任意凸四边形ABCD，必有AC·BD≤AB·CD+AD·BC，当且仅当ABCD四点共圆时取等号。

2.托勒密定理的逆定理同样成立：一个凸四边形两对对边乘积的和等于两条对角线的乘积，则这个凸四边形内接于一圆、托勒密不等式：凸四边形的两组对边乘积和不小于其对角线的乘积，取等号当且仅当共圆或共线。

证明托勒密(ptolemy)定理
【提纲】
1.介绍托勒密定理
托勒密定理，又称托勒密-费马定理，是一个关于三角形内角和与边长之间关系的数学定理。

该定理的表述为：在同一个三角形中，任意两边之和大于第三边，任意两边之差小于第三边。

2.证明托勒密定理的步骤
证明托勒密定理的方法有多种，这里我们以几何证明法为例：
（1）假设三角形ABC的三边长分别为a、b、c，其中a+b>c、
a+c>b、b+c>a；
（2）作边BC的平行线，交边AC于点D，构造三角形ABD和DBC；
（3）根据平行线性质，可知∠ADB=∠C，∠BDA=∠BC；
（4）在三角形ABD和DBC中，根据三角形内角和为180°，可得
∠ABD+∠ADB+∠BDA=180°；
（5）将∠ADB和∠BDA替换为∠C和∠ABC，得到
∠ABC+∠ABD+∠C=180°；
（6）同理，可得∠ABC+∠ADB+∠BC=180°；
（7）将（4）和（6）两式相减，得到∠AB D-∠C=∠C-∠ABC；
（8）根据步骤1中的条件，可知a+b>c，故∠ABD>∠C，同理
∠C>∠ABC；
（9）结合（7）式，得到∠ABD>∠C>∠ABC，即证明了托勒密定理。

3.托勒密定理的应用
托勒密定理在几何学中具有广泛的应用，如在解决三角形的判定、性质、最值等问题时，都可以利用托勒密定理进行求解。

此外，托勒密定理还可以与其他定理相结合，如与勾股定理、相似三角形等定理相互验证。

4.结论
托勒密定理是一个重要的几何定理，通过几何证明法可以简洁明了地证明其正确性。

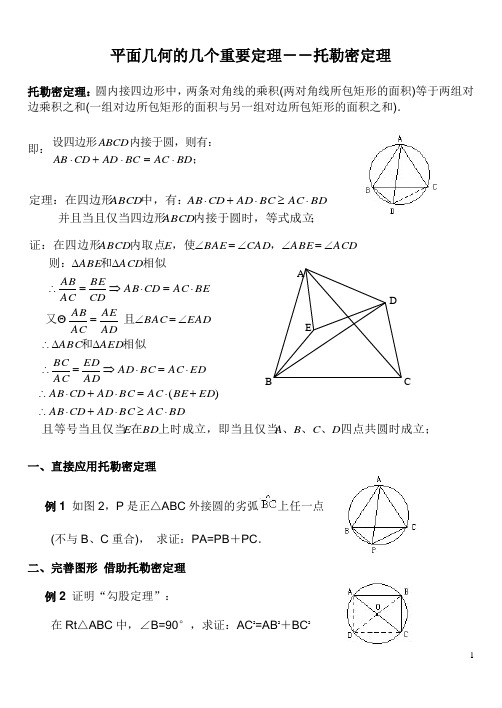
1平面几何的几个重要定理－－托勒密定理托勒密定理：圆内接四边形中，两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和)． 即：；内接于圆，则有：设四边形BD AC BC AD CD AB ABCD ⋅=⋅+⋅；内接于圆时，等式成立并且当且仅当四边形中，有：定理：在四边形ABCD BDAC BC AD CD AB ABCD ⋅≥⋅+⋅一、直接应用托勒密定理例1 如图2，P 是正△ABC 外接圆的劣弧上任一点(不与B 、C 重合)， 求证：PA=PB ＋PC ．二、完善图形 借助托勒密定理例2 证明“勾股定理”：在Rt △ABC 中，∠B=90°，求证：AC 2=AB 2＋BC 2四点共圆时成立；、、、上时成立，即当且仅当在且等号当且仅当相似和且又相似和则：，，使内取点证：在四边形D C B A BD E BDAC BC AD CD AB ED BE AC BC AD CD AB EDAC BC AD AD EDAC BC AED ABC EAD BAC AD AE AC AB BEAC CD AB CD BEAC AB ACD ABE ACDABE CAD BAE E ABCD ⋅≥⋅+⋅∴+⋅=⋅+⋅∴⋅=⋅⇒=∴∆∆∴∠=∠=⋅=⋅⇒=∴∆∆∠=∠∠=∠)(2 例3 如图，在△ABC 中，∠A 的平分 线交外接∠圆于D ，连结BD ，求证：AD ·BC=BD(AB ＋AC)．三、构造图形 借助托勒密定理例4 若a 、b 、x 、y 是实数，且a 2＋b 2=1，x 2＋y 2=1．求证：ax ＋by ≤1．四、巧变原式 妙构图形，借助托勒密定理例5 已知a 、b 、c 是△ABC 的三边，且a 2=b(b ＋c)，求证：∠A=2∠B ．五、巧变形 妙引线 借肋托勒密定理例6 在△ABC 中，已知∠A ∶∠B ∶∠C=1∶2∶4，练习：1.已知△ABC 中，∠B=2∠C 。

托勒密定理及逆定理的证明托勒密定理是著名的数论定理，它是基于17世纪被认为是阿基米德一世完成的一个古老定理，他提出了方阵与它的迹之间的关系。

它说，如果一个正整数n分解成质因子的乘积：n=p1^a1 * p2^a2 * ... * pk^ak其中pi（i=1，2，…k）是独立的质数，而ai（i=1，2，…k）是相应幂，那么Tr(A^n)=(p1^a1+ p2^a2 + ... + pk^ak )其中Tr(A)是一个正整数的迹的定义。

托勒密定理的证明也叫做托勒密·迹证明。

这是一个形式化的正整数乘积的证明。

所述m乘以n是正整数的乘积。

正确证明：先证明m和n的可行前提首先，证明m和n都是正整数。

由于m和n都是正整数，因此它们的值有可行的解决方案。

假设A的m的n次幂的迹Tr (A^{mn})=p1^{a1} + p2^{a2} + ... + pk^{ak}首先，证明：Trace (A^{mn})=Trace (A^m) × Trace (A^n)根据定义，记A的m的n次幂的迹 = Trace (A^{mn})Trace (A^m)的n次幂的迹 = p1^{ma1} + p2^{ma2} + ... + pk^{mak}Trace (A^n)的m次幂的迹 = p1^{na1} + p2^{na2} + ... + pk^{nak}根据上面的推理，以及可行性前提，可得证明托勒密定理：Trace (A^n)=(p1^a1+p2^a2 + ... + pk^ak )给定正整数n和质数p，如果n=p^ai且n和p互素，则a1<a2<…<ak 。

首先证明前提：由于给定n和p是正整数，其他正确性由可行前提提供。

然后证明则a1<a2<…<ak。

根据定义假设n=p^ai则当i>=2时：对于1<i<=k记a1=ai-1,则有a2=a1+1,a3=a2+1,…ak=a(k-1)+1。

证明托勒密(ptolemy)定理
托勒密定理，也称为托勒密定律，是平面几何中的一个重要定理，描述了一个四边形内接于一个圆的性质。

托勒密定理的表述如下：
在一个凸四边形ABCD 中，如果ABCD 的对边（相对的边）的乘积等于对角线AC 和BD 的乘积之和，即AB⋅CD+BC⋅AD=AC⋅BD，那么这个四边形是内接于一个圆的。

以下是托勒密定理的简要证明：
假设四边形ABCD 内接于一个圆，圆心为O。

我们可以使用三角形相似和角平分线定理来证明。

1.证明三角形AOB 与COD 相似：
由于四边形ABCD 是内接于一个圆的，所以角AOC 和BOD 是圆心角，即两者的角度相等。

同理，角AOB 和COD 也相等。

因此，三角形AOB 与COD 相似。

2.利用相似三角形证明托勒密定理：
根据相似三角形AOB 与COD，我们可以得到以下比例：
CDAB=OCOAADBC=ODOB
将这两个比例相加，并整理得到：
CDAB+ADBC=OCOA+ODOB
这样，我们就得到了托勒密定理的表达形式。

通过这个证明，我们可以理解为什么当四边形ABCD 满足托勒密定理时，它是内接于一个圆的。

这个定理在几何学和三角学中有着重要的应用。

证明托勒密(ptolemy)定理摘要：I.引言- 托勒密定理的背景和意义II.托勒密定理的定义- 圆内接四边形的定义- 托勒密定理的表述III.托勒密定理的证明- 证明思路和方法- 证明过程详述IV.结论- 托勒密定理的结论和应用- 总结与展望正文：I.引言托勒密定理是几何学中的一个重要定理，它涉及到圆内接四边形的性质。

该定理的发现者是古希腊数学家托勒密，它在数学、物理等领域有着广泛的应用。

本文将介绍托勒密定理的证明过程，并探讨其在几何学中的重要意义。

II.托勒密定理的定义首先，我们需要了解什么是圆内接四边形。

圆内接四边形是指一个四边形，它的四个顶点都在同一个圆上。

托勒密定理是关于这种四边形的一个性质，它的表述如下：在任意圆内接四边形中，两条对角线的乘积等于两对对边乘积之和。

即，若四边形ABCD 为圆内接四边形，则有AC * BD = AB * CD + AD * BC。

III.托勒密定理的证明托勒密定理的证明方法有很多种，这里我们介绍一种基于相似三角形的证明方法。

证明过程如下：1.在四边形ABCD 中，作AE || BD，CF || AD，E、F 分别为AC、BD 的交点。

2.由于AE || BD，CF || AD，所以四边形AECD 和四边形BFDC 是相似的。

3.同理，四边形ABCF 和四边形ADCB 是相似的。

4.根据相似三角形的性质，我们有AE/BD = CF/AD，即AE * AD = CF * BD。

5.将AE * AD = CF * BD 代入AB * CD + AD * BC = AC * BD，得AB * CD + CF * BD = AC * BD。

6.由于CF || AD，所以∠ACF = ∠DAB，∠BCF = ∠ADC。

7.根据相似三角形的性质，我们有AC/CF = AB/BD，即AC * BD = AB * CF。

8.将AC * BD = AB * CF 代入AB * CD + CF * BD = AC * BD，得AB * CD + AB * CF = AC * BD。

证明托勒密(ptolemy)定理【最新版】目录1.托勒密定理的定义与概述2.托勒密定理的证明方法概述3.纯几何法证明托勒密定理4.托勒密定理的应用5.总结正文托勒密定理是数学中的一个重要定理，该定理描述了圆内接四边形对角线的乘积与两对对边乘积之间的关系。

具体来说，定理指出：圆内接四边形两条对角线的乘积等于两对对边乘积之和。

本文将介绍托勒密定理的证明方法，并简要讨论其应用。

一、托勒密定理的定义与概述托勒密定理最早由古希腊数学家托勒密提出，他在《几何原本》一书中详细阐述了该定理。

托勒密定理在数学中有着广泛的应用，尤其是在几何学、代数学以及数论等领域。

二、托勒密定理的证明方法概述托勒密定理的证明方法有很多，如三角法、复数法、纯几何法等。

下面我们将详细介绍纯几何法的证明过程。

三、纯几何法证明托勒密定理纯几何法是利用几何图形的性质来证明托勒密定理。

具体证明过程如下：1.在圆内接四边形 ABCD 中，作 AE 垂直于 BC，交 BC 于点 E。

2.根据垂直平分线定理，得到 AE 是 BC 的垂直平分线，即 AE=EC。

3.同理，作 AF 垂直于 CD，交 CD 于点 F，得到 AF=FD。

4.由于 AE=EC，AF=FD，所以四边形 AEFC 是矩形。

5.根据矩形的性质，得到 AC=EF，BD=AE。

6.因此，AC×BD=EF×AE，即 AC×BD=AB×CD。

四、托勒密定理的应用托勒密定理在数学中有广泛的应用，下面举一个简单的例子：已知一个圆内接四边形 ABCD，其中 AB=3，BC=4，CD=5，AD=6。

求 AC 的长度。

根据托勒密定理，有 AC×BD=AB×CD，代入已知数值，得到 AC×6=3×5，解得 AC=2.5。

五、总结托勒密定理是数学中的一个基本定理，它描述了圆内接四边形对角线的乘积与两对对边乘积之间的关系。

通过纯几何法的证明，我们可以更好地理解该定理的含义。

模型介绍1.托勒密定理：圆的内接四边形中，两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和．翻译：在四边形ABCD 中，若A 、B 、C 、D 四点共圆，则AC BD AB CD AD BC ⋅=⋅+⋅．证明：在线段BD 上取点E ，使得∠BAE =∠CAD ，易证△AEB ∽△ADC ，∴AB BE AC CD=，即AC BE AB CD ⋅=⋅，当∠BAE =∠CAD 时，可得：∠BAC =∠EAD ，易证△ABC ∽△AED ，∴AD DE AC CB=，即AC DE AD BC ⋅=⋅，∴AC BE AC DE AB CD AD BC ⋅+⋅=⋅+⋅，∴AC BD AB CD AD BC ⋅=⋅+⋅．2.（托勒密不等式）：对于任意凸四边形ABCD ，有AC BD AB CD AD BC⋅≤⋅+⋅证明：如图1，在平面中取点E 使得∠BAE =∠CAD ，∠ABE =∠ACD ，易证△ABE ∽△ACD ，∴AB BE AC CD=，即AC BE AB CD ⋅=⋅①，连接DE ，如图2，∵AB AE AC AD =，∴AB AC AE AD=，又∠BAC =∠BAE +∠CAE =∠DAC +∠CAE =∠DAE ，∴△ABC ∽△AED ，∴AD DE AC BC=，即AC DE AD BC ⋅=⋅②，将①+②得：AC BE AC DE AB CD AD BC ⋅+⋅=⋅+⋅，∴()AC BD AC BE DE AB CD AD BC⋅≤⋅+=⋅+⋅即AC BD AB CD AD BC ⋅≤⋅+⋅，当且仅当A 、B 、C 、D 共圆时取到等号．3.托勒密定理在中考题中的应用（1）当△ABC 是等边三角形时，如图1，当点D 在弧AC 上时，根据托勒密定理有：DB AC AD BC AB CD ⋅=⋅+⋅，又等边△ABC 有AB =AC =BC ，故有结论：DB DA DC =+．证明：在BD 上取点E 使得DE =DA ，易证△AEB ∽△ADC ，△AED ∽△ABC ，利用对应边成比例，可得：DB DA DC =+．如图2，当点D 在弧BC 上时，结论：DA =DB +DC ．【小结】虽然看似不同，但根据等边的旋转对称性，图1和图2并无区别．（2）当△ABC 是等腰直角三角形，如图3，当点D 在弧BC 上时，根据托勒密定理：AD BC AB CD AC BD ⋅=⋅+⋅，又::1:1:2AB AC BC =，代入可得结论：2AD BD CD =+．如图4，当点D 在弧AC 上时，根据托勒密定理：AD BC AB CD AC BD ⋅=⋅+⋅，又::1:1:2AB AC BC =，代入可得结论：2BD AD CD =+．（3）当△ABC 是一般三角形时，若记BC ：AC ：AB =a ：b ：c ，根据托勒密定理可得：a AD b BD c CD⋅=⋅+⋅例题精讲【例1】．如图，正五边形ABCDE 内接于⊙O ，AB ＝2，则对角线BD 的长为1+．解：如图，连接AD、AC．∵五边形ABCDE是正五边形，∴△ABC≌△DCB≌△AED（SAS），∴设BD＝AC＝AD＝x．在圆内接四边形ABCD中，由托勒密定理可得：AB•CD+AD•BC＝AC•BD，即2×2+x•2＝x2，解得：x1＝1+，x2＝1﹣（舍去）．∴对角线BD的长为1+．故答案为：1+．变式训练【变式1-1】．先阅读理解：托勒密（Ptolemy古希腊天文学家）定理指出：圆内接凸四边形两组对边乘积的和等于两条对角线的乘积．即：如果四边形ABCD内接于⊙O，则有AB•CD+AD•BC＝AC•BD．再请完成：（1）如图1，四边形ABCD内接于⊙O，BC是⊙O的直径，如果AB＝AC＝，CD＝1，求AD的长．（2）在（1）的条件下，如图2，设对边BA、CD的延长线的交点为P，求PA、PD的长．解：（1）∵BC是⊙O的直径，∴∠BAC＝∠BDC＝90°，∵AB＝AC＝，∴△ABC是等腰直角三角形，∴BC＝AB＝，∴BD＝＝＝3，∵圆内接凸四边形两组对边乘积的和等于两条对角线的乘积，即：如果四边形ABCD内接于⊙O，则有AB•CD+AD•BC＝AC•BD，即×1+AD×＝×3，解得：AD＝；（2）∵∠PAD＝∠PCB，∠P＝∠P，∴△PAD∽△PCB，∴＝＝，设PA＝x，PD＝y，则＝＝，解得：x＝，y＝，∴PA＝，PD＝．【变式1-2】．如图1，已知⊙O内接四边形ABCD，求证：AC•BD＝AB•CD+AD•BC．证明：如图1，在BD上取一点P，连接CP，使∠PCB＝∠DCA，即使∠1＝∠2．∵在⊙O中，∠3与∠4所对的弧都是，∴∠3＝∠4．∴△ACD∽△BCP．∴＝．∴AC•BP＝AD•BC．①又∵∠2＝∠1，∴∠2+∠7＝∠1+∠7．即∠ACB＝∠DCP．∵在⊙O中，∠5与∠6所对的弧都是，∴∠5＝∠6．∴△ACB∽△DCP．…（1）任务一：请你将“托勒密定理”的证明过程补充完整；（2）任务二：如图2，已知Rt△ABC内接于⊙O，∠ACB＝90°，AC＝6，BC＝8，CD 平分∠ACB交⊙O于点D，求CD的长．解：（1）补全证明：∴，∴AC•DP＝AB•DC②，∴①+②得：AC•BP+AC•DP＝AD•BC+AB•DC，∴AC•（BP+DP）＝AD•BC+AB•DC，即AC•BD＝AD•BC+AB•DC，（2）∵∠ACB＝90°，AC＝6，BC＝8，∴∠ADB＝90°，AB＝＝10，∵CD平分∠ACB交⊙O于点D，∴∠BCD＝∠ACD，∴BD＝AD，∵∠ADB＝90°，∴∠ABD＝45°，∴BD＝AD＝AB•sin45°＝5，∵四边形ABCD内接于⊙O，∴AB•CD＝AC•BD+AD•BC，即10CD＝6×+8×5，∴CD＝7．【例2】．托勒密定理：圆的内接四边形两对对边乘积的和等于两条对角线的乘积．已知：如图1，四边形ABCD内接于⊙O．求证：AB⋅DC+AD⋅BC＝AC⋅BD．证明：如图2，作∠BAE＝∠CAD，交BD于点E，……∴△ABE∽△ACD，∴AB•DC＝AC•BE，……∴△ABC∽△AED，∴AD•BC＝AC•ED，∴AB•DC+AD•BC＝AC•BE+AC•ED＝AC（BE+ED）＝AC•BD．（1）请帮这位同学写出已知和求证，并完成证明过程；（2）如图3，已知正五边形ABCDE内接于⊙O，AB＝1，求对角线BD的长．（1）解：已知：如图1，四边形ABCD内接于⊙O，求证：AB•DC+AD⋅BC＝AC•BD，故答案为：四边形ABCD内接于⊙O，AB•DC+AD•BC＝AC•BD；证明：如图2，作∠BAE＝∠CAD，交BD于点E，∵，∴∠ABE＝∠ACD，∴△ABE∽△ACD，∴＝，∴AB⋅DC＝AC⋅BE．∵，∴∠ACB＝∠ADE．∵∠BAE＝∠CAD，∴∠BAE+∠EAC＝∠CAD+∠EAC，即∠BAC＝∠EAD，∴△ABC∽△AED，∴，∴AD⋅BC＝AC⋅ED，∴AB⋅DC+AD⋅BC＝AC⋅BE+AC⋅ED＝AC（BE+ED）＝AC⋅BD，即AB•DC+AD•BC＝AC•BD；（2）解：在图3中，连接AD、AC．∵五边形ABCDE是正五边形，∴△ABC≌△DCB≌△AED，∴设BD＝AC＝AD＝x．在圆内接四边形ABCD中，由托勒密定理可得：AB•CD+AD•BC＝AC•BD，即1×1+x•1＝x2，解得，（舍去），∴对角线BD的长为．变式训练【变式2-1】．已知：如图1，四边形ABCD内接于⊙O．求证：AB•CD+BC•AD＝AC•BD下面是该结论的证明过程：证明：如图2，作∠BAE＝∠CAD，交BD于点E．∵＝，∠ABE＝∠ACD，∴△ABE∽△ACD，∴，∴AB•CD＝AC•BE；∵＝，∴∠ACB＝∠ADE（依据1），∵∠BAE＝∠CAD，∴∠BAC＝∠EAD，∴△ABC∽△AED（依据2），∴，∴AD•BC＝AC•ED；∴AB•CD+AD•BC＝AC•（BE+ED），即AB•CD+BC•AD＝AC•BD．（1）上述证明过程中的“依据1”是指同弧所对的圆周角相等；“依据2”是指两角分别相等的两个三角形相似．（2）当圆内接四边形ABCD是矩形时，托勒密定理就是我们熟知的勾股定理．（3）如图3，四边形ABCD内接于⊙O，AB＝3，AD＝5，∠BAD＝60°，点C是的中点，求AC的长．解：（1）上述证明过程中的“依据1”是同弧所对的圆周角相等．“依据2”是两角分别相等的两个三角形相似．故答案为：同弧所对的圆周角相等；两角分别相等的两个三角形相似．（2）当圆内接四边形ABCD是矩形时，则AB＝CD，AD＝BC，AC＝BD，∵AB•CD+AD•BC＝AC•BD，∴AB2+AD2＝BD2，托勒密定理就是我们非常熟知的一个定理：勾股定理，故答案为：勾股．（3）连接BD，作CE⊥BD于E．∵四边形ABCD是圆内接四边形，∴∠BAD+∠BCD＝180°，∵∠BAD＝60°，∴∠BCD＝120°，∵，∴CD＝CB，∴∠CDB＝30°，在Rt△CDE中，cos30°＝，∴DE＝CD，∴BD＝2DE＝CD，由托勒密定理：AC•BD＝AD•BC+CD•AB，∴AC•CD＝3CD+5CD，∴AC＝，答：AC的长为．【变式2-2】．圆的内接四边形的两条对角线的乘积等于两组对边乘积的和．即：如图1，若四边形ABCD内接于⊙O，则有________．任务：（1）材料中划横线部分应填写的内容为AC•BD＝AB•CD+BC•AD．（2）已知，如图2，四边形ABCD内接于⊙O，BD平分∠ABC，∠COD＝120°，求证：BD＝AB+BC．解：（1）由托勒密定理可得：AC•BD＝AB•CD+BC•AD 故答案为：AC•BD＝AB•CD+BC•AD（2）如图，连接AC∵∠COD＝120°，∴∠CBD＝∠CAD＝60°∵BD平分∠ABC∴∠ABD＝∠CBD＝60°∴∠ACD＝60°，∴△ACD是等边三角形∴AC＝AD＝CD，∵四边形ABCD是圆内接四边形∴AC•BD＝AB•CD+BC•AD∴BD＝AB+BC1．如图，以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF，对角线交于点O，连接AO，如果AB＝4，AO＝4，那么AC的长等于（）A．12B．16C．4D．8解：在AC上截取CG＝AB＝4，连接OG，∵四边形BCEF是正方形，∠BAC＝90°，∴OB＝OC，∠BAC＝∠BOC＝90°，∴B、A、O、C四点共圆，∴∠ABO＝∠ACO，在△BAO和△CGO中，∴△BAO≌△CGO（SAS），∴OA＝OG＝4，∠AOB＝∠COG，∵∠BOC＝∠COG+∠BOG＝90°，∴∠AOG＝∠AOB+∠BOG＝90°，即△AOG是等腰直角三角形，由勾股定理得：AG＝＝8，即AC＝AG+CG＝8+4＝12．故选：A．2．如图，在⊙O的内接四边形ABCD中，AB＝3，AD＝5，∠BAD＝60°，点C为弧BD的中点，则AC的长是．解：解法一、∵A、B、C、D四点共圆，∠BAD＝60°，∴∠BCD＝180°﹣60°＝120°，∵∠BAD＝60°，AC平分∠BAD，∴∠CAD＝∠CAB＝30°，如图1，将△ACD绕点C逆时针旋转120°得△CBE，则∠E＝∠CAD＝30°，BE＝AD＝5，AC＝CE，∴∠ABC+∠EBC＝（180°﹣∠CAB﹣∠ACB）+（180°﹣∠E﹣∠BCE）＝180°，∴A、B、E三点共线，过C作CM⊥AE于M，∵AC＝CE，∴AM＝EM＝×（5+3）＝4，在Rt△AMC中，AC＝＝＝；解法二、过C作CE⊥AB于E，CF⊥AD于F，则∠E＝∠CFD＝∠CFA＝90°，∵点C为弧BD的中点，∴＝，∴∠BAC＝∠DAC，BC＝CD，∵CE⊥AB，CF⊥AD，∴CE＝CF，∵A、B、C、D四点共圆，∴∠D＝∠CBE，在△CBE和△CDF中∴△CBE≌△CDF，∴BE＝DF，在△AEC和△AFC中∴△AEC≌△AFC，∴AE＝AF，设BE＝DF＝x，∵AB＝3，AD＝5，∴AE＝AF＝x+3，∴5＝x+3+x，解得：x＝1，即AE＝4，∴AC＝＝，故答案为：．3．如图，在等腰△ABC中，AB＝AC＝4，BC＝6，点D在底边BC上，且∠DAC＝∠ACD，将△ACD沿着AD所在直线翻折，使得点C落到点E处，联结BE，那么BE的长为1．解：∵AB＝AC，∴∠ABC＝∠C，∵∠DAC＝∠ACD，∴∠DAC＝∠ABC，∵∠C＝∠C，∴△CAD∽△CBA，∴＝，∴＝，∴CD＝，BD＝BC﹣CD＝，∵∠DAM＝∠DAC＝∠DBA，∠ADM＝∠ADB，∴△ADM∽△BDA，∴＝，即＝，∴DM＝，MB＝BD﹣DM＝，∵∠ABM＝∠C＝∠MED，∴A、B、E、D四点共圆，∴∠ADB＝∠BEM，∠EBM＝∠EAD＝∠ABD，∴△ABD∽△MBE，（不用四点共圆，可以先证明△BMA∽△EMD，推出△BME∽AMD，推出∠ADB＝∠BEM也可以！）∴＝，∴BE＝＝1．故答案为：1．4．如图，P是正方形ABCD内一点，CP＝CD，AP⊥BP，则的值为．解：如图，过点D作AP垂线交AP延长线于E，∵四边形ABCD是正方形，CP＝CD，∴BC＝CP＝CD，∴∠PBC＝∠BPC，∠DPC＝∠PDC，设∠PCD＝x，则∠BPC＝，∠DPC＝，∴∠BPD＝45°+90°＝135°，∵AP⊥BP，∴∠APD＝360°﹣135°﹣90°＝135°，∴∠DPE＝45°，设DE＝PE＝y，∴DP＝＝y，∵∠DAE+∠BAP＝∠BAP+∠ABP＝90°，∴∠DAE＝∠ABP，在△DAE与△ABP中，，∴△APB≌△DEA（AAS），∴AP＝DE＝y，∴＝＝．故答案为：．5．如图，正方形ABCD的边长是6，对角线的交点为O，点E在边CD上且CE＝2，CF⊥BE，连接OF，则：（1）∠OFB45°；（2）OF＝．解：（1）在BE上截取BG＝CF，∵在正方形ABCD，AC⊥BD，∠ABC＝∠BCD＝90°，AC＝BD，BO＝BD，CO＝AC，AC、BD分别平分∠ABC、∠BCD，∴BO＝CO，∠BOC＝90°，∠OBC＝∠OCD＝45°，∵CF⊥BE，∴∠CFE＝90°，∴∠FEC+∠ECF＝90°，∵∠EBC+∠FEC＝90°，∴∠EBC＝∠ECF，∴∠OBC﹣∠EBC＝∠OCD﹣∠ECF，∴∠OBG＝∠FCO，∴△OBG≌△OCF（SAS），∴∠BOG＝∠FOC，OG＝OF，∴∠GOC+∠COF＝90°，∴∠OFG＝∠OGF＝45°，故答案为：45°；（2）在Rt△BCE中，根据勾股定理，得BE＝2，∴CF＝BG＝＝，在Rt△FCE中，根据勾股定理，得EF＝，∴GF＝BE﹣BG﹣EF＝，在Rt△FCE中，根据勾股定理，得OF＝，故答案为：．6．如图，在Rt△ABC中，∠BAC＝90°，D为BC的中点，过点D作DE⊥DF，交BA的延长线于点E，交AC的延长线于点F．若CF＝，AC＝4，AB＝2．则AE＝10．解：延长FD至G，使GD＝FD，连接BG，如图所示：∵D为BC的中点，∴BD＝CD，在△BDG和△CDF中，，∴△BDG≌△CDF（SAS），∴BG＝CF＝，∠G＝∠F，∴BG∥CF，∴△BGH∽△AFH，∴＝＝＝＝，∴＝，AH＝AB＝，∵∠BAC＝90°，AF＝AC+CF＝，∴HF＝＝，∴DH＝FH＝，∵DE⊥DF，∴∠EDH＝90°＝∠BAC，∴∠E+∠EHD＝∠F+∠EHD＝90°，∴∠E＝∠F，∴△DHE∽△AHF，∴＝，即＝，解得：HE＝，∴AE＝HE﹣AH＝﹣＝10；故答案为：10．7．设△ABC是正三角形，点P在△ABC外，且与点A在直线BC异侧，∠BPC＝120°，求证：PA＝PB+PC．解：如图，延长BP至E，使PE＝PC，连接CE，∵∠BAC+∠BPC＝180°，且∠BAC＝60°，∴∠BPC＝120°，∴∠CPE＝60°，又PE＝PC，∴△CPE为等边三角形，∴CP＝PE＝CE，∠PCE＝60°，∵△ABC为等边三角形，∴AC＝BC，∠BCA＝60°，∴∠ACB＝∠PCE，∴∠ACB+∠BCP＝∠PCE+∠BCP，即：∠ACP＝∠BCE，∵在△ACP和△BCE中，，∴△ACP≌△BCE（SAS），∴AP＝BE，∵BE＝BP+PE，∴PA＝PB+PC．8．⊙O半径为2，AB，DE为两条直线．作DC⊥AB于C，且C为AO中点，P为圆上一个动点．求2PC+PE的最小值．解：延长OA到K，使AK＝＝2．∵C是AO的中点，∴OC＝OA＝1，∴＝．又∵∠COP＝∠POK，∴△COP∽△POK，∴，即PK＝2PC．∴2PC+PE＝PE+PK≥EK．作EH⊥BC于点H．∵在直角△COD中，cos∠DOC＝，∴∠DOC＝60°，∴∠EOH＝∠DOC＝60°，∴HE＝OE•sin60°＝2×，∴EK＝．即最小值是2．故答案是：2．9．如图，点P为等边△ABC外接圆，劣弧为BC上的一点．（1）求∠BPC的度数；（2）求证：PA＝PB+PC．（1）解：∵四边形ABPC内接于圆，∴∠BAC+∠BPC＝180．∵等边三角形ABC中，∠BAC＝60°，∴∠BPC＝120°；（2）证明：延长BP到D，使得DP＝PC，连接CD．∵∠BPC＝120，∴∠CPD＝60．又∵PC＝PD，∴△PCD是等边三角形，∴PC＝CD，∠PCD＝60°，∴∠ACM+∠MCP＝PCD+∠MCP，即∠ACP＝∠BCD．∵等边三角形ABC中，∴BC＝AC．∵所对的圆周角是∠DBC与∠PAC，∴∠DBC＝∠PAC．在△DBC和△PAC中，，∴△DBC≌△PAC（ASA），∴AP＝BD．∵BD＝BP+DP，∴AP＝BP+DP，∵DP＝PC，∴PA＝PB+PC．10．如图，⊙O的直径AB的长为10，弦BD的长为6，点C为上的一点，过点B的切线EF，连接AD，CD，CB；（1）求证：∠CDB＝∠CBF；（2）若点D为的中点，求CD的长．（1）证明：连接AC，如图，∵AB为⊙O的直径，∴∠ACB＝90°，∴∠1+∠2＝90°，∵EF为⊙O的切线，∴AB⊥EF，∴∠ABF＝90°，即∠2+∠CBF＝90°，∴∠1＝∠CBF，∵∠1＝∠CDB，∴∠CDB＝∠CBF；（2）解：作CM⊥AD于M，CN⊥DB于N，如图，∵AB为⊙O的直径，∴∠ADB＝90°，∴AD＝＝＝8，∵点C为的中点，∴∠ADC＝∠BDC，∴CA＝CB，CM＝CN，在Rt△ACM和Rt△BCN中，∴Rt△ACM≌Rt△BCN，∴AM＝BN，即AD﹣AM＝DN﹣BD，∴AM+DN＝AD+BD＝8+6＝14，∵四边形CMDN为矩形，CM＝CN，∴四边形CMDN为正方形，∴DM＝DN＝7，∴CD＝DM＝7．11．阅读下列材料，并完成相应的任务．托勒密定理：托勒密（Ptolemy）（公元90年～公元168年），希腊著名的天文学家，他的要著作《天文学大成》被后人称为“伟大的数学书”，托勒密有时把它叫作《数学文集》，托勒密从书中摘出并加以完善，得到了著名的托勒密（Ptolemy）定理．托勒密定理：圆内接四边形中，两条对角线的乘积等于两组对边乘积之和．已知：如图1，四边形ABCD内接于⊙O，求证：AB•CD+BC•AD＝AC•BD下面是该结论的证明过程：证明：如图2，作∠BAE＝∠CAD，交BD于点E．∵∴∠ABE＝∠ACD∴△ABE∽△ACD∴∴AB•CD＝AC•BE∵∴∠ACB＝∠ADE（依据1）∵∠BAE＝∠CAD∴∠BAE+∠EAC＝∠CAD+∠EAC即∠BAC＝∠EAD∴△ABC∽△AED（依据2）∴AD•BC＝AC•ED∴AB•CD+AD•BC＝AC•（BE+ED）∴AB•CD+AD•BC＝AC•BD任务：（1）上述证明过程中的“依据1”、“依据2”分别是指什么？（2）当圆内接四边形ABCD是矩形时，托勒密定理就是我们非常熟知的一个定理：勾股定理．（请写出）（3）如图3，四边形ABCD内接于⊙O，AB＝3，AD＝5，∠BAD＝60°，点C为的中点，求AC的长．解：（1）上述证明过程中的“依据1”是同弧所对的圆周角相等．“依据2”是两角分别相等的两个三角形相似．（2）当圆内接四边形ABCD是矩形时，则AB＝CD，AD＝BC，AC＝BD，∵AB•CD+AD•BC＝AC•BD，∴AB2+AD2＝BD2，托勒密定理就是我们非常熟知的一个定理：勾股定理，故答案为勾股定理．（3）连接BD，作CE⊥BD于E．∵四边形ABCD是圆内接四边形，∴∠BAD+∠BCD＝180°，∵∠BAD＝60°，∴∠BCD＝120°，∵＝，∴CD＝CB，∴∠CDB＝30°，在Rt△CDE中，cos30°＝，∴DE＝CD，∴BD＝2DE＝CD，由托勒密定理：AC•BD＝AD•BC+CD•AB，∴AC•CD＝3CD+5CD，∴AC＝，答：AC的长为．12．在学习了《圆》和《相似》的知识后，小明自学了一个著名定理“托勒密定理：圆内接四边形对角线的乘积等于两组对边乘积之和．”（1）下面是小明对托勒密定理的证明和应用过程，请补充完整．已知：四边形ABCD内接于⊙O．求证：AC•BD＝AB•CD+AD•BC．证明：作∠CDE＝∠BDA，交AC于点E，∵⊙O中，∠1＝∠2，∴△ABD∽△ECD（两角对应相等，两三角形相似）．∴．∴AB•CD＝BD•EC①，．又∵∠BDA+∠3＝∠CDE+∠3，即∠ADE＝∠BDC，∴△DAE∽△DBC（两边对应成比例且夹角相等，两三角形相似）．∴．∴AD•BC＝BD•AE②．∴AB•CD+AD•BC＝BD（EC+AE），∴AB•CD+AD•BC＝AC•BD．（2）利用托勒密定理解决问题：是否存在一个圆内接四边形，它的两条对角线长为5和，一组对边长为1和3，另一组对边的和为4．若存在，求出未知的两边；若不存在，说明理由．（1）证明：作∠CDE＝∠BDA，交AC于点E，∵⊙O中，∠1＝∠2，∴△ABD∽△ECD（两角对应相等，两三角形相似）．∴．∴AB•CD＝BD•EC①，∴．又∵∠BDA+∠3＝∠CDE+∠3，即∠ADE＝∠BDC，∴△DAE∽△DBC（两边对应成比例且夹角相等，两三角形相似）．∴．∴AD•BC＝BD•AE②．∴AB•CD+AD•BC＝BD（EC+AE），∴AB•CD+AD•BC＝AC•BD．故答案为：两角对应相等，两三角形相似，DAE，DBC，两边对应成比例且夹角相等，两三角形相似，AB•CD+AD•BC＝BD（EC+AE）；（2）不存在，理由如下：设未知的两边分别为：a，4﹣a，由托勒密定理可得：5×＝1×3+a（4﹣a），∴（a﹣2）2＝7﹣5＜0，∴方程无解，∴不存在这样的一个圆内接四边形．13．阅读下列相关材料，并完成相应的任务．布拉美古塔定理婆罗摩笈多是古印度著名的数学家、天文学家，他编著了《婆罗摩修正体系》，他曾经提出了“婆罗摩笈多定理”，也称“布拉美古塔定理”．定理的内容是：若圆内接四边形的对角线互相垂直，则垂直于一边且过对角线交点的直线平分对边．某数学兴趣小组的同学写出了这个定理的已知和求证．已知：如图，在圆内接四边形ABCD中，对角线AC⊥BD，垂足为P，过点P作AB的垂线分别交AB，DC于点H，M．求证：M是CD的中点任务：（1）请你完成这个定理的证明过程．（2）该数学兴趣小组的同学在该定理的基础上写出了另外一个命题：若圆内接四边形的对角线互相垂直，则一边中点与对角线交点的连线垂直于对边请判断此命题是真命题．（填“真”或“假”）（3）若PD＝2，HP＝，BP＝3，求MH的长．（1）证明：∵AC⊥BD，∴∠APB＝∠CPD＝90°，∴∠ABP+∠BAP＝90°，∵PH⊥AB，∴∠BAP+∠APH＝90°，∴∠ABP＝∠APH，∴∠MPC＝∠APH，∵＝，∴∠ABP＝∠ACD，∴∠PCM＝∠MPC，∴PM＝MC，同理可得，PM＝DM，∴DM＝CM，∴M是CD的中点；（2）若圆内接四边形的对角线互相垂直，则一边中点与对角线交点的连线垂直于对边，理由如下：已知：如图，在圆内接四边形ABCD中，对角线AC⊥BD，垂足为P，M是CD的中点，连接MP交AB于点H，求证：PH⊥AB；证明：∵M是CD的中点；∴DM＝CM＝PM，∴∠PCM＝∠MPC，∵＝，∴∠ABP＝∠PCM，∵∠MPC＝∠APH，∴∠MPC＝∠APH，∴∠APH+∠HPB＝∠ABP+∠HPB＝90°，∴PH⊥AB；故答案为：真；（3）解：∵BP＝3，HP＝，∴BH＝，∴sin∠HBP＝，∵∠ABP＝∠PCD，∴＝＝，∴CD＝2，∵M是CD的中点，∴PM＝CD＝，∴MH＝2．14．已知△ABC内接于⊙O，∠BAC的平分线交⊙O于点D，连接DB，DC．（1）如图①，当∠BAC＝120°时，请直接写出线段AB，AC，AD之间满足的等量关系式：AB+AC＝AD；（2）如图②，当∠BAC＝90°时，试探究线段AB，AC，AD之间满足的等量关系，并证明你的结论；（3）如图③，若BC＝5，BD＝4，求的值．解：（1）如图①在AD上截取AE＝AB，连接BE，∵∠BAC＝120°，∠BAC的平分线交⊙O于点D，∴∠DBC＝∠DAC＝60°，∠DCB＝∠BAD＝60°，∴△ABE和△BCD都是等边三角形，∴∠DBE＝∠ABC，AB＝BE，BC＝BD，∴△BED≌△BAC（SAS），∴DE＝AC，∴AD＝AE+DE＝AB+AC；故答案为：AB+AC＝AD．（2）AB+AC＝AD．理由如下：如图②，延长AB至点M，使BM＝AC，连接DM，∵四边形ABDC内接于⊙O，∴∠MBD＝∠ACD，∵∠BAD＝∠CAD＝45°，∴BD＝CD，∴△MBD≌△ACD（SAS），∴MD＝AD，∠M＝∠CAD＝45°，∴MD⊥AD．∴AM＝，即AB+BM＝，∴AB+AC＝；（3）如图③，延长AB至点N，使BN＝AC，连接DN，∵四边形ABDC内接于⊙O，∴∠NBD＝∠ACD，∵∠BAD＝∠CAD，∴BD＝CD，∴△NBD≌△ACD（SAS），∴ND＝AD，∠N＝∠CAD，∴∠N＝∠NAD＝∠DBC＝∠DCB，∴△NAD∽△CBD，∴，∴，又AN＝AB+BN＝AB+AC，BC＝5，BD＝4，∴＝．15．问题探究：（1）已知：如图①，△ABC中请你用尺规在BC边上找一点D，使得点A到点BC的距离最短．（2）托勒密（Ptolemy）定理指出，圆的内接四边形两对对边乘积的和等于两条对角线的乘积．如图②，P是正△ABC外接圆的劣弧BC上任一点（不与B、C重合），请你根据托勒密（Ptolemy）定理证明：PA＝PB+PC．问题解决：（3）如图③，某学校有一块两直角边长分别为30m、60m的直角三角形的草坪，现准备在草坪内放置一对石凳及垃圾箱在点P处，使P到A、B、C三点的距离之和最小，那么是否存在符合条件的点P？若存在，请作出点P的位置，并求出这个最短距离（结果保留根号）；若不存在，请说明理由．解：（1）利用尺规作图，过点A作BC的垂线，交BC于D，则点D即为所求；（2）由托勒密定理得，PA•BC＝PB•AC+PC•AB，∵△ABC为正三角形，∴AB＝BC＝AC，∴PA•BC＝PB•BC+PC•BC，∴PA＝PB+PC；（3）以BC为边作正△BCD，使点D与点A在BC两侧，作△BCD的外接圆，连接AD交圆于P，连接PB，作DE⊥AC交AC的延长线于E，则点P即为所求，由（2）得，PD＝PB+PC，∴P到A、B、C三点的距离之和＝DA，且距离之和最小，∵CD＝BC＝30，∠DCE＝∠BCE﹣∠BCD＝30°，∴DE＝CD＝15，由勾股定理得，CE＝＝15，则AD＝＝30，答：P到A、B、C三点的距离之和最小值为30m．16．（1）方法选择如图①，四边形ABCD是⊙O的内接四边形，连接AC，BD，AB＝BC＝AC．求证：BD ＝AD+CD．小颖认为可用截长法证明：在DB上截取DM＝AD，连接AM…小军认为可用补短法证明：延长CD至点N，使得DN＝AD…请你选择一种方法证明．（2）类比探究【探究1】如图②，四边形ABCD是⊙O的内接四边形，连接AC，BD，BC是⊙O的直径，AB＝AC．试用等式表示线段AD，BD，CD之间的数量关系，并证明你的结论．【探究2】如图③，四边形ABCD是⊙O的内接四边形，连接AC，BD．若BC是⊙O的直径，∠ABC＝30°，则线段AD，BD，CD之间的等量关系式是BD＝CD+2AD．（3）拓展猜想如图④，四边形ABCD是⊙O的内接四边形，连接AC，BD．若BC是⊙O的直径，BC：AC：AB＝a：b：c，则线段AD，BD，CD之间的等量关系式是BD＝CD+AD．解：（1）方法选择：∵AB＝BC＝AC，∴∠ACB＝∠ABC＝60°，如图①，在BD上截取DM＝AD，连接AM，∵∠ADB＝∠ACB＝60°，∴△ADM是等边三角形，∴AM＝AD，∵∠ABM＝∠ACD，∵∠AMB＝∠ADC＝120°，∴△ABM≌△ACD（AAS），∴BM＝CD，∴BD＝BM+DM＝CD+AD；（2）类比探究：如图②，∵BC是⊙O的直径，∴∠BAC＝90°，∵AB＝AC，∴∠ABC＝∠ACB＝45°，过A作AM⊥AD交BD于M，∵∠ADB＝∠ACB＝45°，∴△ADM是等腰直角三角形，∴AM＝AD，∠AMD＝45°，∴DM＝AD，∴∠AMB＝∠ADC＝135°，∵∠ABM＝∠ACD，∴△ABM≌△ACD（AAS），∴BM＝CD，∴BD＝BM+DM＝CD+AD；【探究2】如图③，∵若BC是⊙O的直径，∠ABC＝30°，∴∠BAC＝90°，∠ACB＝60°，过A作AM⊥AD交BD于M，∵∠ADB＝∠ACB＝60°，∴∠AMD＝30°，∴MD＝2AD，∵∠ABD＝∠ACD，∠AMB＝∠ADC＝150°，∴△ABM∽△ACD，∴＝，∴BM＝CD，∴BD＝BM+DM＝CD+2AD；故答案为：BD＝CD+2AD；（3）拓展猜想：BD＝BM+DM＝CD+AD；理由：如图④，∵若BC是⊙O的直径，∴∠BAC＝90°，过A作AM⊥AD交BD于M，∴∠MAD＝90°，∴∠BAM＝∠DAC，∴△ABM∽△ACD，∴＝，∴BM＝CD，∵∠ADB＝∠ACB，∠BAC＝∠MAD＝90°，∴△ADM∽△ACB，∴＝＝，∴DM＝AD，∴BD＝BM+DM＝CD+AD．故答案为：BD＝CD+AD17．数学课上，张老师出示了问题：如图1，AC，BD是四边形ABCD的对角线，若∠ACB ＝∠ACD＝∠ABD＝∠ADB＝60°，则线段BC，CD，AC三者之间有何等量关系？经过思考，小明展示了一种正确的思路：如图2，延长CB到E，使BE＝CD，连接AE，证得△ABE≌△ADC，从而容易证明△ACE是等边三角形，故AC＝CE，所以AC＝BC+CD．小亮展示了另一种正确的思路：如图3，将△ABC绕着点A逆时针旋转60°，使AB与AD重合，从而容易证明△ACF是等边三角形，故AC＝CF，所以AC＝BC+CD．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图4，如果把“∠ACB＝∠ACD＝∠ABD＝∠ADB＝60°”改为“∠ACB＝∠ACD＝∠ABD＝∠ADB＝45°”，其它条件不变，那么线段BC，CD，AC三者之间有何等量关系？针对小颖提出的问题，请你写出结论，并给出证明．（2）小华提出：如图5，如果把“∠ACB＝∠ACD＝∠ABD＝∠ADB＝60°”改为“∠ACB＝∠ACD＝∠ABD＝∠ADB＝α”，其它条件不变，那么线段BC，CD，AC三者之间有何等量关系？针对小华提出的问题，请你写出结论，不用证明．解：（1）BC+CD＝AC；理由：如图1，延长CD至E，使DE＝BC，连接AE，∵∠ABD＝∠ADB＝45°，∴AB＝AD，∠BAD＝180°﹣∠ABD﹣∠ADB＝90°，∵∠ACB＝∠ACD＝45°，∴∠ACB+∠ACD＝90°，∴∠BAD+∠BCD＝180°，∴∠ABC+∠ADC＝180°，∵∠ADC+∠ADE＝180°，∴∠ABC＝∠ADE，在△ABC和△ADE中，，∴△ABC≌△ADE（SAS），∴∠ACB＝∠AED＝45°，AC＝AE，∴△ACE是等腰直角三角形，∴CE＝AC，∵CE＝CD+DE＝CD+BC，∴BC+CD＝AC；（2）BC+CD＝2AC•cosα．理由：如图2，延长CD至E，使DE＝BC，∵∠ABD＝∠ADB＝α，∴AB＝AD，∠BAD＝180°﹣∠ABD﹣∠ADB＝180°﹣2α，∵∠ACB＝∠ACD＝α，∴∠ACB+∠ACD＝2α，∴∠BAD+∠BCD＝180°，∴∠ABC+∠ADC＝180°，∵∠ADC+∠ADE＝180°，∴∠ABC＝∠ADE，在△ABC和△ADE中，，∴△ABC≌△ADE（SAS），∴∠ACB＝∠AED＝α，AC＝AE，∴∠AEC＝α，过点A作AF⊥CE于F，∴CE＝2CF，在Rt△ACF中，∠ACD＝α，CF＝AC•cos∠ACD＝AC•cosα，∴CE＝2CF＝2AC•cosα，∵CE＝CD+DE＝CD+BC，∴BC+CD＝2AC•cosα．18．问题背景：如图①，在四边形ADBC中，∠ACB＝∠ADB＝90°，AD＝BD，探究线段AC，BC，CD之间的数量关系．小吴同学探究此问题的思路是：将△BCD绕点D，逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图②），易证点C，A，E在同一条直线上，并且△CDE是等腰直角三角形，所以CE＝CD，从而得出结论：AC+BC＝CD．简单应用：（1）在图①中，若AC＝，BC＝2，则CD＝3．（2）如图③，AB是⊙O的直径，点C、D在⊙上，＝，若AB＝13，BC＝12，求CD的长．拓展规律：（3）如图④，∠ACB＝∠ADB＝90°，AD＝BD，若AC＝m，BC＝n（m＜n），求CD 的长（用含m，n的代数式表示）（4）如图⑤，∠ACB＝90°，AC＝BC，点P为AB的中点，若点E满足AE＝AC，CE＝CA，点Q为AE的中点，则线段PQ与AC的数量关系是PQ＝AC或PQ＝AC．解：（1）由题意知：AC+BC＝CD，∴+2＝CD，∴CD＝3；（2）连接AC、BD、AD，∵AB是⊙O的直径，∴∠ADB＝∠ACB＝90°，∵，∴AD＝BD，将△BCD绕点D顺时针旋转90°到△AED处，如图③，∴∠EAD＝∠DBC，∵∠DBC+∠DAC＝180°，∴∠EAD+∠DAC＝180°，∴E、A、C三点共线，∵AB＝13，BC＝12，∴由勾股定理可求得：AC＝5，∵BC＝AE，∴CE＝AE+AC＝17，∵∠EDA＝∠CDB，∴∠EDA+∠ADC＝∠CDB+∠ADC，即∠EDC＝∠ADB＝90°，∵CD＝ED，∴△EDC是等腰直角三角形，∴CE＝CD，∴CD＝；（3）以AB为直径作⊙O，连接OD并延长交⊙O于点D1，连接D1A，D1B，D1C，如图④由（2）的证明过程可知：AC+＝D1C，∴D1C＝，又∵D1D是⊙O的直径，∴∠DCD1＝90°，∵AC＝m，BC＝n，∴由勾股定理可求得：AB2＝m2+n2，∴D1D2＝AB2＝m2+n2，∵D1C2+CD2＝D1D2，∴CD2＝m2+n2﹣＝，∵m＜n，∴CD＝；（4）当点E在直线AC的左侧时，如图⑤，连接CQ，PC，∵AC＝BC，∠ACB＝90°，点P是AB的中点，∴AP＝CP，∠APC＝90°，又∵CA＝CE，点Q是AE的中点，∴∠CQA＝90°，设AC＝a，∵AE＝AC，∴AE＝a，∴AQ＝AE＝，由勾股定理可求得：CQ＝a，由（2）的证明过程可知：AQ+CQ＝PQ，∴PQ＝a+a，∴PQ＝AC；当点E在直线AC的右侧时，如图⑥，连接CQ、CP，同理可知：∠AQC＝∠APC＝90°，设AC＝a，∴AQ＝AE＝，由勾股定理可求得：CQ＝a，由（3）的结论可知：PQ＝（CQ﹣AQ），∴PQ＝AC．综上所述，线段PQ与AC的数量关系是PQ＝AC或PQ＝AC．。

四点共圆——托勒密定理
在几何学中，“四点共圆”是一个非常重要的定理，它也被称为“托勒密定理”。

这个定理阐述了四个点在同一圆周上的条件，因此被广泛应用于各种圆周相关的问题和证明。

托勒密定理的表述如下：假设有一个圆，该圆的直径为AC。

则另外两个点B和D，如果满足BD与AC垂直且交于点E，则四个点A、B、C、D在同一个圆周上的充分必要条件是AE×CE+BE×DE=AC×BE（其中“×”表示向量的点乘运算）。

这个定理我们可以通过几何图形来理解。

如果四个点在同一圆周上，那么任意两个点之间的弧长和是定值，同时它们组成的四边形ABCD也是圆周上的一段弧，因此关于其对角线的乘积和就有一个特殊的形式。

这个形式就是定理中所表述的AE×CE+BE×DE=AC×BE。

托勒密定理的证明有多种方法，其中一种比较简单的思路是利用向量运算。

我们可以将四个点表示为向量A、B、C、D，根据向量的几何性质，我们可以得到两个向量的点乘运算与它们的夹角和长度的关系。

利用这个基本的向量等式，我们就可以推导出托勒密定理的表述形式。

托勒密定理的应用非常广泛，它可以被用于求解等角线、外心、内心等诸多几何问题。

如果你想深入研究几何学，托勒密定理一定是一个必须掌握的重要工具。