分数的意义和性质 综合练习题(提高篇)

【精品】分数的意义和性质综合练习题(提高篇)一、分数的意义和性质1．的分子加上6，要使分数的大小不变，分母应加上________．【答案】10【解析】【解答】解：3+6=9，9÷3=3；5×3-5=10，分母应加上10。

故答案为：10【分析】先计算现在的分子，然后计算分子扩大的倍数，根据分数的基本性质把分母也扩大相同的倍数后计算分母应加上的数即可。

2．食堂有6吨煤，13天烧完，平均每天烧这堆煤的，每天烧________吨煤.【答案】【解析】【解答】解：6 13= （吨）答：每天烧吨煤3．一排电线杆，原来每两根之间的距离是30米，现在改为45米，如果开始的一根不移动，至少再隔________又会有一根电线杆可以不移动？【答案】 90米【解析】【解答】 30=2×3×5，45=3×3×5，所以30和45的最小公倍数是2×3×3×5=90.故答案为：90米.【分析】根据题意可知，要求至少再隔多少米又会有一根电线杆可以不移动，就是求30和45的最小公倍数，据此解答.4．在，，，四个分数中，________是真分数，________是假分数，________是最简分数。

【答案】，；，；，，【解析】【解答】真分数：、；假分数：、；最简分数：、、故答案为：，；，；，，【分析】真分数是指分子大于分母的分数，假分数是指分子小于分母的分数，最简分数是指分子与分母不可再约分的分数。

根据以上即可判断出正确答案。

5．在横线上填上“＞”“＜”或“＝”。

________ ________ ________【答案】＞；＝；＞【解析】【解答】＞，=，＞故答案为：＞；=；＞【分析】分母不同的分数进行比较，先找其最小公倍数，再进行同分，则分子大的分数值大。

据此进行计算比较大小即可。

6．和这两个分数（）。

A. 意义相同B. 分数单位相同C. 大小相同【答案】 C【解析】【解答】和这两个分数的意义和分数单位都不同，但是它们的大小相同。

分数的意义和性质综合练习题(提高篇)一、分数的意义和性质1．解决实际问题．有一种黄豆，每1千克中大约含有400克蛋白质、290克淀粉和200克脂肪．蛋白质的含量是________，淀粉的含量是________，脂肪的含量是________。

【答案】；；【解析】【解答】解：1千克=1000克，蛋白质的含量：400÷1000=；淀粉的含量：290÷1000=；脂肪的含量：200÷1000=。

故答案为：；；【分析】用三种物质的质量分别除以黄豆的质量即可求出三种物质的含量，用分数表示得数时用被除数作分子，除数作分母。

2．五(1)班的同学借了《儿童文学》，的同学借了《聪明屋》．的同学借了《少年时代》，的同学借了《漫画世界》，还有的人看《笑林》．借阅________刊物的同学一样多？【答案】《儿童文学》《聪明屋》和《少年时代》【解析】【解答】解：，，所以借阅《儿童文学》《聪明屋》和《少年时代》刊物的同学一样多。

故答案为：《儿童文学》《聪明屋》和《少年时代》【分析】根据分数的基本性质把第二个和第三个两个分数约分成最简分数，然后判断哪些图书借阅的人数一样多。

3．一个最简分数，如果把它的分子除以2，分母乘3后，就得到．这个最简分数是【答案】【解析】【解答】解：故答案为：【分析】可以采用倒推的方法，把现在的分数的分子乘2，分母除以3，这样就能计算出原来的分数。

4．里有________个【答案】 325【解析】【解答】解：，所以共有325个。

故答案为：325。

【分析】先把带分数化成假分数，然后把假分数化成分母是140的分数，再根据分子确定分数单位的个数即可。

5．在横线上填上“＞”“＜”或“＝”。

________ ________ ________【答案】＞；＝；＞【解析】【解答】＞，=，＞故答案为：＞；=；＞【分析】分母不同的分数进行比较，先找其最小公倍数，再进行同分，则分子大的分数值大。

人教版五年级数学下册第四单元《分数的意义和性质》能力提升练习题1(含答案)一、填一填。

1.用小数和分数表示各图中的涂色部分。

2.把5kg 大米平均分成6份，这样的2份占这些大米的( )，是( )kg 。

3.在括号里填上最简分数。

870 dm ³＝( )m ³ 15分＝( )时 50千克＝( )吨4.五（1）班女生人数占全班总人数的49，男生人数占全班总人数的( )( )，女生人数是男生人数的( )( )。

5.4( )＝( )15＝2÷5＝8÷( )＝( )(填小数) 6.小明存书的12是12本，小刚存书的23也是12本，小明有（ ）本书，小刚有（ ）本书。

7.两个微信公众号分别每3天、每4天更新一次。

某月1日两个公众号同时更新后，到这个月30日，两个微信号同时更新的日期是该月（ ）日和（ ）日。

8.如果a 6是真分数，a 5是假分数，那么a 等于（ ），则a 6 ○ a5。

（在○里填上“＞”“＜”或“＝”）9.一个分数，它的分数单位是14，如果化成以112作分数单位的分数，那么分子比原来的分子大6，这个分数是（ ）。

二、辨一辨。

（的画“√”，错对的画“×”）1. 3 km 的15和5 km 的13一样长。

（ ）2. 大于1519而小于1719的分数只有1619。

（ ） 三、选一选。

（将正确答案的序号填在括号里）1.将一根绳子连续对折3次，每段是全长的（ ）。

A. 13B. 14C. 18D. 19 2.小红的卧室长4 m ，宽3 m ，用边长为（ ）dm 的正方形地砖能正好铺满。

A. 3B. 4C. 5D. 63.如果a b （b >0）的分子加上2a ，要使分数的大小不变，那么分母应该是（ )。

A. 2a ＋b B. 2ab C. 3b D. 不变4.下面这4个分数都是真分数，其中一定是最简分数的是（ ）。

（a 为非零自然数）A. a 7B. a 8C. a 9D. a 10 5.工程队两周修完一条公路，第一周修了611 km ，第二周修的占全长的611。

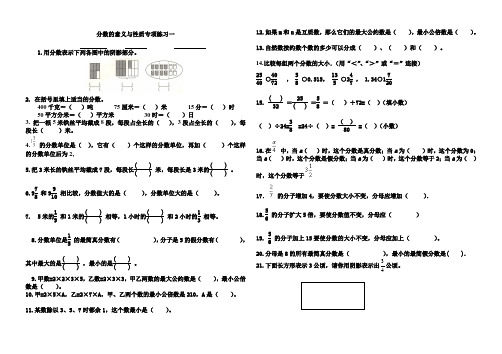
分数的意义与性质专项练习一1.用分数表示下列各图中的阴影部分。

2. 在括号里填上适当的分数。

400千克＝（）吨75厘米＝（）米15分＝（）时50平方分米＝（）平方米30时＝（）日3. 把一根5米铁丝平均截成8段，每段占全长的（），3段占全长的（），每段长（）米。

4.的分数单位是（），它有（）个这样的分数单位，再加（）个这样的分数单位后为2．5.把3米长的铁丝平均截成7段，每段长( )( )米，每段长是3米的( )( )。

6.978和9910相比较，分数值大的是（），分数单位大的是（）。

7. 5米的19和1米的( )( )相等，1小时的( )( )和2小时的13相等。

8.分数单位是15的最简真分数有（），分子是5的假分数有（），其中最大的是( )( )，最小的是( )( )。

9.甲数=2×2×3×5，乙数=2×3×3，甲乙两数的最大公约数是（），最小公倍数是（）。

10.甲=2×5×A，乙=2×7×A，甲、乙两个数的最小公倍数是210，A是（）。

11.某数除以3、5、7时都余1，这个数最小是（）。

12.如果m和n是互质数，那么它们的最大公约数是（），最小公倍数是（）。

13.自然数按约数个数的多少可以分成（）、（）和（）。

14.比较每组两个分数的大小．（用“＜”、“＞”或“＝”连接）2540○4072，58○0.515，135○247， 1.34○172015.( )32＝25( )＝58＝（）÷72=（）（填小数）（）÷24=38=24÷（）=（）80=（）（小数）16.在中，当a（）时，这个分数是真分数；当a为（）时，这个分数为0；当a（）时，这个分数是假分数；当a为（）时，这个分数等于2；当a为（）时，这个分数等于17．的分子增加4，要使分数大小不变，分母应增加（）．18.56的分子扩大5倍，要使分数值不变，分母应（）19.56的分子加上15要使分数的大小不变，分母应加上（）。

【数学】分数的意义和性质综合练习题(提高篇)一、分数的意义和性质1．一个分数用2约分了2次，用3约分了1次，得到的最简分数是．求原来的分数是________．【答案】【解析】【解答】解：故答案为：【分析】根据分数的基本性质，把这个分数的分子和分母同时乘3、2、2即可求出原来的分数。

2．比较下面每组中几个分数的大小，并按从大到小的顺序排列出来．(分数，先填分子，后填分母)、、、和【答案】【解析】【解答】解：所以。

【分析】先比较分子是3的分数的大小，再比较分母是5的两个分数的大小，然后比较这几个分数与的大小关系，这样从大到小排列即可。

3．若a+ =b+ ，则a与b的关系是（）．A. a>bB. a<bC. a=bD. 无法确定【答案】 B【解析】【解答】解：因为，所以a＜b。

故答案为：B。

【分析】先根据分子是1的分数大小的比较方法比较出和的大小，然后确定a与b的大小。

因为和相等，一个加数大，另一个加数一定小。

4．把的分子加10，要使分数的大小不变，分母应变成( )。

A. 54B. 36C. 30D. 28【答案】 A【解析】【解答】解：5+10=15，15÷5=3，分母：18×3=54。

故答案为：A。

【分析】用原来的分子加上10求出现在的分子，然后计算出分子扩大的倍数；把分母也扩大相同的倍数即可求出现在的分母。

5．a是非0自然数，在下面各式中，得数最小的是（）。

A. aB. aC. a【答案】 B【解析】【解答】解：，所以得数最小的是a×。

故答案为：B。

【分析】三个算式都有一个因数a，则另一个因数小，积就小，另一个因数大，积就大。

由此只需要比较另一个因数的大小即可确定积的大小。

6．李师傅为一间长50分米、宽30分米的房间铺设方砖，要想方砖没有剩余，正方形方砖的边长最长是（）分米。

A. 5B. 10C. 15D. 30【答案】 B【解析】【解答】50=5×2×5；30=5×2×3；50和30的最大公因数是：5×2=10，正方形方砖的边长最长是10分米。

【数学】分数的意义和性质综合练习题(提高篇)一、分数的意义和性质1．把一个分数约分，用2约了两次，又用3约了一次，得，原来这个分数是________.(分数,先填分子，后填分母)【答案】【解析】【解答】解：故答案为：【分析】根据分数的基本性质，把这个分数的分子和分母同时依次乘3、2、2即可得到原来的分数。

2．把6米长的绳子平均分成6段，每段长（）米。

A. B. 1 C. 6【答案】 B【解析】【解答】解：把6米长的绳子平均分成6段，每段长1米。

故答案为：B。

【分析】把6米长的绳子当做单位“1”，平均分成6份，每段占总长的，即1米。

3．把一根绳子剪成两段，第一段长米，第二段占全长的，两段相比( )。

A. 第一段长B. 第二段长C. 一样长【答案】 B【解析】【解答】解：两段相比第二段长。

故答案为：B。

【分析】因为第二段占全长的，说明第一段占全长的1-=，>，所以两段相比第二段长。

4．如果一个分数的分子大于分母，这个分数就能化成（）。

A. 整数B. 带分数C. 带分数或整数【答案】 C【解析】【解答】解：如果一个分数的分子大于分母，这个分数就能化成带分数或整数。

故答案为：C。

【分析】分子大于分母，如果分子是分母的倍数就能化成整数，否则能化成带分数。

5．王奶奶有3个孩子，老大3天回家一次，老二5天回家一次，老三6天回家一次，6月1日他们一起回家，那么下一次他们一起回家是几月几日?（）A. 6月31日B. 9月1日C. 7月1日D. 8月24日【答案】 C【解析】【解答】3、5、6的最小公倍数是：3×5×2=30，6月1日他们一起回家，那么下一次他们一起回家是7月1日。

故答案为：C。

【分析】根据题意可知，先求出他们回家时间的最小公倍数，然后用开始的时间+最小公倍数=下一次一起回家的时间，据此解答。

6．下面四种说法：①最小的质数和最小的合数的最大公因数是1；②互质的两个数的最大公因数是1；③两个数的公因数的个数是有限的；④两个合数的最大公因数不可能是1。

分数的意义和性质综合练习题(提高篇)一、分数的意义和性质1．填上适当的分数.361平方分米=________平方米2130毫升=________升【答案】；【解析】【解答】361平方分米=361÷100=平方米，2160毫升=2130÷1000=升【分析】解答此题首先要明确1平方米=100平方分米，1升=1000毫升，低级单位化成高级单位要除以进率，然后根据分数与除法的关系，用分数表示各个数字即可。

2．（1）已知：A=2×3×5B=3×5×7则：[A，B]=________（2）已知：A=2×2×5[A，B]=2×2×5×7则：B=________×5×________【答案】（1）210（2）2；7【解析】【解答】（1）已知：A=2×3×5B=3×5×7则：[A，B]=2×3×5×7=210.（2）已知：A=2×2×5[A，B]=2×2×5×7则：B=2×5×7.故答案为：（1）210；（2）2；7.【分析】用分解质因数的方法求两个数的最小公倍数，把这两个数公有的质因数和各自独有的质因数相乘，它们的乘积就是这两个数的最小公倍数，据此解答.3．和这两个分数（）。

A. 意义相同B. 分数单位相同C. 大小相同【答案】 C【解析】【解答】和这两个分数的意义和分数单位都不同，但是它们的大小相同。

故答案为：C。

【分析】根据题意可知，这两个分数的分母不同，所以分数的意义和分数单位都不同，将约分可得，据此解答。

4．的分子减少3，要使分数的大小不变，分母应该（）。

A. 减少3B. 减少6C. 减少4D. 增加4【答案】 C【解析】【解答】解：6-3=3，6÷3=2；8÷2-4=4，分母应该减少4。

【数学】分数的意义和性质能力提升题一、分数的意义和性质1．如果，，，那么a，b，c中最大的是________，最小的是________．【答案】c；a【解析】【解答】a==1-，b==1-，c==1-，因为＜＜，所以a＜b＜c，即最大的是c，最小的是a.故答案为：c；a.【分析】首先将a、b、c拆分，再根据拆分后所得分数分子相同，分母大的反而小，再用1分别减去这几个分数得出1减去大的数差小，减去小的数差大，进而得出最大的数和最小的数.2．（1）已知：A=2×3×5B=3×5×7则：[A，B]=________（2）已知：A=2×2×5[A，B]=2×2×5×7则：B=________×5×________【答案】（1）210（2）2；7【解析】【解答】（1）已知：A=2×3×5B=3×5×7则：[A，B]=2×3×5×7=210.（2）已知：A=2×2×5[A，B]=2×2×5×7则：B=2×5×7.故答案为：（1）210；（2）2；7.【分析】用分解质因数的方法求两个数的最小公倍数，把这两个数公有的质因数和各自独有的质因数相乘，它们的乘积就是这两个数的最小公倍数，据此解答.3．把、、、按从小到大的顺序排列________【答案】【解析】【解答】解：，，，所以。

故答案为：。

【分析】把化成分子是2和3的分数，然后根据同分母、同分子分数大小的比较方法从小到大排列即可。

4．填上“>”“<”或“=”。

________ 1 ________ ________【答案】<；>；=【解析】【解答】解：、，所以。

，，所以。

故答案为：<；>；=。

第四单元 分数的意义和性质模块一 分数的意义【例题1】填空：有一块布长5米，正好可以做6条童裤。

每条童裤用这块布的（ ），每条童裤用布（ ）米。

【练习1】填空：把18个桃子平均分给2只小猴，每只猴子分得桃子总数的（ ），每只猴子分得（ ）个桃子。

【例题2】填空：7米的91和1米的（ ）相等，1千克的（ ）和3千克的41相等。

【练习2】（1）填空：85kg 表示把（ ）kg 平均分成（ ）份，取这样的（ ）份；也表示把（ ）kg 平均分成（ ）份，取其中的( )份。

（2）判断：8kg 的91和1kg 的98一样重。

（ ）【例题3】填空：五年级人数的61与六年级人数的71相等。

（ ）年级人数多一些。

【练习3】选择：下面两根彩带露出的部分同样长，两根相比（ ）。

A.甲长B.乙长C.同样长D.无法比较长短37【例题4】选择：一班和二班各有21的人参加合唱比赛。

那么，比较参加合唱比赛的人数， （ ）。

A.一班人多B.二班人多C.两班一样多D.无法确定【练习4】选择：(1)小红与小兰放学回家后，小红喝了一杯水的21，小兰也喝了一杯水的21。

那么，比较她们 的喝水量，（ ）。

A.小红多B.小兰多C.两人一样多D.无法确定 (2)妈妈买了一个西瓜，爸爸吃了它的21，明明吃了剩下的21。

（ ）吃得多。

A.爸爸B.明明C.两人一样多D.无法确定 （3）在为希望工程捐款的活动中，小明捐了零花钱的41捐的多。

A.小明B.小芳C.两人一样多D.无法确定 【例题5】有两根同样长的电线，第一根剪去12米，第二根剪去它的12，哪根电线剩下的长？【练习5】两堆同样重的沙子，第一堆运走31吨，第二堆运走31。

哪堆沙子运走的质量多？【例题6】选择：将一根绳子剪成两段，第一段长74米，第二段占全长的74，两段绳子相比较，（ ）。

A. 一样长B. 第一段长C. 第二段长D.无法确定【练习6】选择：将一根铁丝剪成两段，第一段长52米，第二段占全长的52，两段铁丝相比较，（ ）。