大学物理 振动与波练习题

(3) 波速 c ？ (4) t 3 秒时 x 3.5 厘米处的质点的振动速度 v ？
【解】：(1) y 5cos(20 4x) 厘米
(2) y 5cos(3t 11) 厘米
(3) y 5cos3(t 4 x 5) ， c 3 (cm/ s)
33
4
(4) y 5cos(3t 9) ， yI 15 sin(3t 9) 0
23、一平面简谐波沿 x 轴正方向传播，波速 c=8 m/s， 若 t=0 时的波形曲线如图 2-23 所示 （1）写出波动方程 （2）画出 t=1.25 s 时的波形曲线 【解】：
t=0 时，y=0, v>0 cm T=5s
所以 2 。 波长= 40
y 4.0 cos[0.4t ] (cm) 2
B 点的振动方程
yA
(t)
5 c os [10
(t
20) 300
2
]
5 c os (10t
7 6
)cm
（2）
A,B 相位相同
（3） 或 O 点的振动方程
yo
(t)
5
cos(10t
2
)
(cm)
O 点相位
o
2
OB,OA 间的相位差
oA
oB
2 3
O 比 A 超前
oA
o
A
2 3
A
7 6
同时 B 点
13、已知一个谐振动的振幅 A 0.02 米，园频率 4 弧度／秒，初相 / 2 。 (1)
写出谐振动方程； (2) 以位移为纵坐标，时间为横坐标，画出谐振动曲线。
【解】： x 0.02cos(4 t 2) (m) ，
T
2
1 2

）
（A） 2 ；
答案：（D）
（B）
m1 m2
2
；
（C）
m2 m1
2
；
（D） 2
m2 . m1
一物体作简谐振动，振动方程为
x
A cos(t
1 4
) 。在
t = T/4（T
为周期）时刻，物体的
加速度为 ( )
(A)
2 2
A 2
；
(B)
2 2
A 2 ；
(C)
3 2
A 2
；
(D)
3 2
A 2
。
一弹簧振子，当把它水平放置时，它作简谐振动。若把它竖直放置或放在光滑斜面上，试判
一弹簧振子作简谐振动，当其偏离平衡位置的位移的大小为振幅的 1/4 时，其动能为振 动总能量的
(A) 7/16 ； (B) 9/16 ； (C) 11/16 ； (D) 15/16 。 []
答案：（D）
第十章 波动
10-1 机械波的几个概念
10-2 平面简谐波的波函数
如图所示，有一平面简谐波沿 x 轴负方向传播，
断下列情况正确的是
（A）竖直放置作简谐振动，在光滑斜面上不作简谐振动；
（B）竖直放置不作简谐振动，在光滑斜面上作简谐振动；
（C）两种情况都作简谐振动；
（D）两种情况都不作简谐振动。
[]
竖直放置 放在光滑斜面上
答案：（C）
同一弹簧振子悬挂相同的质量，分别按如图（a）、（b）、（c）所示的三种方式放置，摩擦力都
(A) 曲线 3，1，2 分别表示 x，v，a 曲线； (B) 曲线 2，1，3 分别表示 x，v，a 曲线； (C) 曲线 1，2，3 分别表示 x，v，a 曲线； (D) 曲线 2，3，1 分别表示 x，v，a 曲线.

答案：[（A）]
8*、一平面简谐波，其振辐为A,频率为,沿X轴正向传播.设
t=t0时刻波形如所示.则X=0处质点振动方程为：
（A) y =Acos[2 (t +t0) + /2]; （B) y =Acos[2 (t -t0) + /2]; （C） y =Acos[2 (t -t0) - /2]; （D） y =Acos[2 (t -t0) + ]。
答案：[（C）]
4、图a为某质点振动图线,其初相记为1，图b为某列行波在
t=0时的波形曲线，0点处质点振动的初相记为2；图C为另一
行波在t=T/4时刻的波形曲线，0点处质点振动的初相为3，
则：
（A） 1 =2 =3 = / 2；
Y
（B） 1 =3 /2，2 =3 = / 2 ；
（C） 1 =2 =3 = 3 /2 ； （D） 1 =3 /2，2 = /2 ，3 =0 。
8m
6m
X
C
B
A
答案.：y =510 -2 cos（ 4 t+0.2 x);
y =510 -2 cos（ 4 t+0.2 x -1.2 ); y =510 -2 cos（ 4 t-2.8 )。
11*、一平面简谐波在空中传播。己知波线上P点的振动规律为: y =Acos (t + );根据图中所示两种情况,分别列出以O点为 原点时的波动方程。对于图a是： 对于图b是：
3
Байду номын сангаас
（D）0 =- /2，2 = /2 ，3 = 。 0 1 2 4
u X(m)
答案：[（C）]
7*、一质点沿Y方向振动,振辐为A,周期为T,平衡位置在坐标原 点,己知t=0时刻质点向y轴负方向运动,由该点发出的波波长为， 则沿X轴正向传播的简谐波波动方程为：

06振动与波、波动光学练习题 一、选择题 1 一物体作简谐振动，振动方程为)4cos(πω+=t A y在4T t =（T 为周期）时刻，物体的加速度为 [ ]2222321)(,321)(,221)(,221)(ωωωωA D A C A B A A -- 2 两个质点各自作简谐振动，它们的振幅相同、周期相同，第一个质点的振动方程为)cos(1αω+=t A y 。

当第一个质点从相对平衡位置的正位移处回到平衡位置时，第二个质点正在最大位移处，则第二个质点的振动方程为 [ ])cos()(),23cos()()2cos()(),2cos()(2222παωπαωπαωπαω++=-+=-+=++=t A y D t A y C t A y B t A y A 3一质点沿y 轴作简谐振动，振动方程为)SI (),32cos(1042παπ++⨯=-t y ，从t = 0时刻起，到质点位置在x = －2 cm 处，且向x 轴正方向运动的最短时间间隔为[ ]s 61)(s,31)(s,21)(s,41)(s,81)(E D C B A 4 已知两个简谐振动曲线如图所示，1x 相位比2x 的相位 [ ]ππππ超前，落后，超前，落后)()(2)(2)(D C B A5题图 7题图5 一质点作简谐振动，周期为T 。

质点由平衡位置向X 轴正方向运动时，由平衡位置到二分之一最大位移这段路程所需要的时间为 [ ],8)(6)(12)(4)(T D T C T B T A ，，， 6 在下面几种说法中，正确的说法是： [ ]（A ）波源不动时，波源的振动周期与波动的周期在数值上是不同的，（B ）波源振动的速度与波速相同，(C) 在波传播方向上的任一质点的振动相位总是比波源的相位滞后，(D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前。

7一平面简谐波，沿X 轴负方向传播，角频率为ω，波速为u 。

设4T t =时刻的波形如图所示，则该波的表达式为： [ ]])(cos[)(),(cos )(]21)(cos[)(),(cos )(πωωπωω++=+=+-=-=ux t A y D u x t A y G u x t A y B ux t A y A 8 当机械波在媒质中传播时，一媒质质元的最大变形量发生在 [ ](A)媒质质元离开其平衡位置最大位移处，（B ）媒质质元离开其平衡位置)2/2(A 处，（C ）媒质质元在其平衡位置处，（D ）媒质质元离开其平衡位置A/2处(A 是振动振幅)。

振动波动一、例题（一）振动1。

证明单摆是简谐振动，给出振动周期及圆频率.2. 一质点沿x 轴作简谐运动，振幅为12cm,周期为2s 。

当t = 0时， 位移为6cm ，且向x 轴正方向运动。

求： （1） 振动表达式；(2) t = 0.5s 时，质点的位置、速度和加速度；(3)如果在某时刻质点位于x =—0.6cm ，且向x 轴负方向运动，求从该位置回到平衡位置所需要的时间。

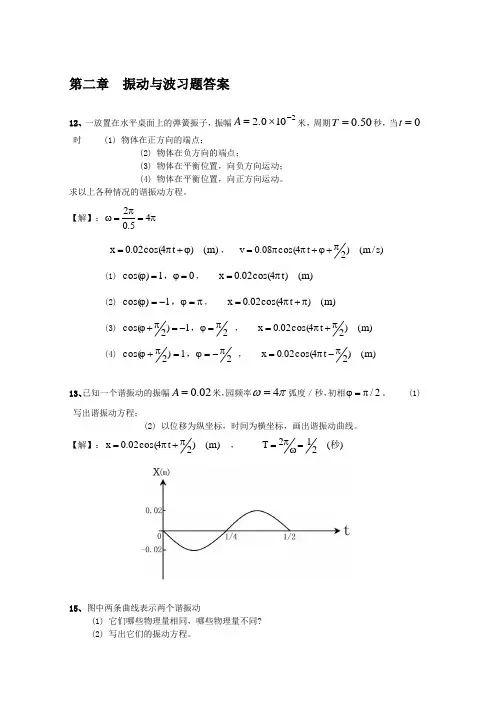
3。

已知两同方向，同频率的简谐振动的方程分别为：x 1= 0.05cos （10 t + 0.75π) 20.06cos(100.25)(SI)x t π=+求：(1)合振动的初相及振幅.(2)若有另一同方向、同频率的简谐振动x 3 = 0。

07cos (10 t +ϕ 3 ）, 则当ϕ 3为多少时 x 1 + x 3 的振幅最大？又ϕ 3为多少时 x 2 + x 3的振幅最小？（二）波动1. 平面简谐波沿x 轴正方向传播，振幅为2 cm ，频率为 50 Hz ，波速为 200 m/s.在t = 0时，x = 0处的质点正在平衡位置向y 轴正方向运动，求:(1）波动方程(2)x = 4 m 处媒质质点振动的表达式及该点在t = 2 s 时的振动速度。

2. 一平面简谐波以速度m/s 8.0=u 沿x 轴负方向传播.已知原点的振动曲线如图所示.求:（1）原点的振动表达式；(2）波动表达式；（3）同一时刻相距m 1的两点之间的位相差.3. 两相干波源S 1和S 2的振动方程分别是1cos y A t ω=和2cos(/2)y A t ωπ=+.S 1距P 点3个波长，S 2距P 点21/4个波长。

求:两波在P 点引起的合振动振幅。

4。

沿X 轴传播的平面简谐波方程为：310cos[200(t )]200x y π-=- ，隔开两种媒质的反射界面A 与坐标原点O 相距2。

25m ，反射波振幅无变化，反射处为固定端，求反射波的方程.二、习题课（一)振动1. 一质点在x 轴上作简谐振动，振辐A = 4 cm,周期T = 2 s ，其平衡位置取作坐标原点.若t = 0时刻质点第一次通过x = -2 cm 处，且向x 轴负方向运动，则O 2.25m Ax t O A/2 -A x 1 x 2 质点第二次通过x = -2 cm 处的时刻为［ ］（A) 1 s (B) (2/3) s (C ） (4/3) s （D ） 2 s2.已知某简谐振动的振动曲线如图所示，则此简谐振动的振动方程为(A ） ⎪⎭⎫ ⎝⎛+=3232cos 2ππt x ;（B ） ⎪⎭⎫ ⎝⎛-=332cos 2ππt x ;（C) ⎪⎭⎫ ⎝⎛+=3234cos 2ππt x ；（D ） ⎪⎭⎫ ⎝⎛-=334cos 2ππt x 。

振动与波练习题2005一、填空题1.一物体作简谐振动，振动方程为x = A cos (ωt +π/ 4 )。

在t =T / 4 (T 为周期)时刻，物体的加速度为 .2.一质点沿x 轴作简谐振动，振动方程为x = 4×10－2 cos (2πt + π31) (SI) 。

从t = 0 时刻起，到质点位置在x = －2 cm 处，且向x 轴正方向运动的最短时间间隔为 0t =时，03πφ=；t 时刻，20x cm υ=->且43πφ所以＝。

433t ππωπ∆=-=由可得0.5()2t s ππωπ∆===3.已知两个简谐振动曲线如图1所示。

x 1的位相比x 2的位相为 B 。

(A) 落后π/2 （B ）超前π/2 (C) 落后π (D) 超前π4.一质点作简谐振动，周期为T 。

质点由平衡位置向X 轴正方向运动时，由平衡位置到二分之一最大位移这段路程所需要的时间为2222sin(/4)sin(/4)2cos(/4)cos(/4)/4112,222dx A t A t dt T d a A t A t dt T t T A a A πυωωπωπυπωωπωπυωω=-+=-+=-+=-+==＝＝代入得＝－解：由旋转矢量图可知6πϕ＝∆，所以1226TTt==∆=∆ππωϕ5.一平面简谐波，沿x轴负方向传播。

圆频率为ω，波速为u 。

设t＝T/4时刻的波形如图2所示，则该波的表达式为。

由t = 0的旋转矢量图可知：y0=－A，φπ=O点振动方程cos()y A tωπ=+波动方程：cos()xy A tuωπ⎡⎤=++⎢⎥⎣⎦6.当机械波在媒质中传播时，一媒质质元的最大变形量发生在位置处。

平衡位置处7.如图3所示两相干波源S1和S2相距λ/4，（λ为波长）S1的位相比S2的位相超前π/2,在S1，S2的连线上，S1外侧各点（例如P点）两波引起的两谐振动的位相差是.解：P点情况()21211222()2242r r S P S Pπππϕϕλλλπππλ---+=+=+=8.一质点作简谐振动。

大学物理学——振动和波振 动班级 学号 姓名 成绩内容提要1、简谐振动的三个判据（1）；（2）；（3）2、描述简谐振动的特征量： A 、T 、γ；T1=γ，πγπω22==T3、简谐振动的描述：（1）公式法 ；（2）图像法；（3）旋转矢量法4、简谐振动的速度和加速度：)2cos()sin(v00πϕωϕωω++=+-==t v t A dt dx m ； a=）（）（πϕωϕωω±+=+=0m 0222t a t cos -dtxd A 5、振动的相位随时间变化的关系：6、简谐振动实例弹簧振子：，单摆小角度振动：，复摆：0mgh dt d 22=+θθJ ,T=2mghJπ 7、简谐振动的能量：222m 21k 21A A Eω==系统的动能为：）（ϕωω+==t sin m 21mv 212222A E K ；系统的势能为：）ϕω+==t (cos k 21kx 21222A E P8、两个简谐振动的合成（1）两个同方向同频率的简谐振动的合成合振动方程为：）（ϕω+=t cos x A其中，其中；。

＊(2) 两个同方向不同频率简谐振动的合成拍：当频率较大而频率之差很小的两个同方向简谐运动合成时，其合振动的振幅表现为时而加强时而减弱的现象，拍频：12-γγγ=＊（3）两个相互垂直简谐振动的合成合振动方程：）（1221221222212-sin )(cos xy 2y x ϕϕϕϕ=--+A A A A ，为椭圆方程。

练习一一、 填空题1．一劲度系数为k 的轻弹簧，下端挂一质量为m 的物体，系统的振动周期为T 1。

若将此弹簧截去一半的长度，下端挂一质量为m/2的物体，则系统的周期T 2等于 。

2．一简谐振动用余弦函数表示，其振动曲线如图所示，则此简谐振动的三个特征量为：A ＝ ；=ω ;=ϕ 。

3．如图，一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上，做成一复摆。

已知细棒绕过其一端的轴的转动惯量J ＝3/2ml ，此摆作微小振动的周期为 。

(A) x 0 .12 cos （ t 4、机械波的表达式为 y 0.05cos 6πt 0. 06πx m ，则 （ （Ａ） 波长为100 ｍ （Ｂ） 波速为10 ｍ·ｓ-1 ） ）
（Ｃ） 周期为1/3 ｓ （Ｄ） 波沿x 轴正方向传播 5、 两分振动方程分别为 x1=3cos (50πt+π/4) ㎝ 和 x2=4cos (50πt+3π/4)㎝， 则它们的合振动的振幅为 （ (A) 1 ㎝ （B）3 ㎝ （C）5 ㎝ （D）7 ㎝ 6、一平面简谐波，波速为 =5 cm/s，设t= 3 s时刻的波形 如图所示，则x=0处的质点的振动方程为 （ － (A) y=2×10 2cos (πt/2－π/2) (m) － (B) y=2×10 2cos (πt + π) (m) －2 (C) y=2×10 cos(πt/2+π/2) (m) －2 (D) y=2×10 cos (πt－3π/2) (m) ）
y
u
A X －A
17．一平面简谐波，沿 X 轴负方向传播，波长λ=8 m。已知 x=2 m 处质点的振动方程为 y 4 cos(10t
5 x ) ; 8 12 2 （C） y 4 cos(10 t x ); 4 3
（A）
) ， 则该波的波动方程为（ 6
（B）
20．在驻波中，两个相邻波节间各质点的振动（
1、一个弹簧振子和一个单摆，在地面上的固有振动周期分别为 T1 和 T2，将它们拿到月球上去，相应 的周期分别为 1 和 2 ，则它们之间的关系为 1 T1 且 2 T2 。 。
2、一弹簧振子的周期为T，现将弹簧截去一半，下面仍挂原来的物体，则其振动的周期变为 3、一平面简谐波的波动方程为 y 0.08cos 4 πt 2 πx

⼤学物理振动与波题库及答案⼀、选择题：（每题3分）1、把单摆摆球从平衡位置向位移正⽅向拉开，使摆线与竖直⽅向成⼀微⼩⾓度θ，然后由静⽌放⼿任其振动，从放⼿时开始计时．若⽤余弦函数表⽰其运动⽅程，则该单摆振动的初相为(A) π． (B) π/2．(C) 0 ． (D) θ．［2、两个质点各⾃作简谐振动，它们的振幅相同、周期相同．第⼀个质点的振动⽅程为x 1 = A cos(ωt + α)．当第⼀个质点从相对于其平衡位置的正位移处回到平衡位置时，第⼆个质点正在最⼤正位移处．则第⼆个质点的振动⽅程为(A) )π21cos(2++=αωt A x ． (B) )π21cos(2-+=αωt A x ． (C) )π23cos(2-+=αωt A x ． (D) )cos(2π++=αωt A x ．［］3、⼀个弹簧振⼦和⼀个单摆（只考虑⼩幅度摆动），在地⾯上的固有振动周期分别为T 1和T 2．将它们拿到⽉球上去，相应的周期分别为1T '和2T '．则有(A) 11T T >'且22T T >'． (B) 11T T <'且22T T <'．(C) 11T T ='且22T T ='． (D) 11T T ='且22T T >'．［］4、⼀弹簧振⼦，重物的质量为m ，弹簧的劲度系数为k ，该振⼦作振幅为A 的简谐振动．当重物通过平衡位置且向规定的正⽅向运动时，开始计时．则其振动⽅程为：(A) )21/(cos π+=t m k A x (B) )21/cos(π-=t m k A x (C) )π21/(cos +=t k m A x (D) )21/cos(π-=t k m A x (E) t m /k A x cos = ［］5、⼀物体作简谐振动，振动⽅程为)41cos(π+=t A x ω．在 t = T /4（T 为周期）时刻，物体的加速度为(A) 2221ωA -． (B) 2221ωA ． (C) 2321ωA -． (D) 2321ωA ．［］6、⼀质点作简谐振动，振动⽅程为)cos(φω+=t A x ，当时间t = T /2（T 为周期）时，质点的速度为(A) φωsin A -． (B) φωsin A ．(C) φωcos A -． (D) φωcos A ．［］7、⼀质点作简谐振动，周期为T ．当它由平衡位置向x 轴正⽅向运动时，从⼆分之⼀最⼤位移处到最⼤位移处这段路程所需要的时间为(A) T /12． (B) T /8．(C) T /6． (D) T /4．［］8、两个同周期简谐振动曲线如图所⽰．x 1的相位⽐x 2的相位 (A) 落后π/2． (B) 超前π/2． (C) 落后π． (D) 超前π．［］9、⼀质点作简谐振动，已知振动频率为f ，则振动动能的变化频率是(A) 4f . (B) 2 f . (C) f .(D) 2/f . (E) f /4 ［］10、⼀弹簧振⼦作简谐振动，当位移为振幅的⼀半时，其动能为总能量的(A) 1/4. (B) 1/2. (C) 2/1. (D) 3/4. (E) 2/3. ［］11、⼀弹簧振⼦作简谐振动，当其偏离平衡位置的位移的⼤⼩为振幅的1/4时，其动能为振动总能量的(A) 7/16. (B) 9/16. (C) 11/16.(D) 13/16. (E) 15/16. ［］12 ⼀质点作简谐振动，已知振动周期为T ，则其振动动能变化的周期是(A) T /4． (B) 2/T ． (C) T ．(D) 2 T ． (E) 4T ．［］13、当质点以频率ν作简谐振动时，它的动能的变化频率为(A) 4 ν． (B) 2 ν． (C) ν． (D) ν21．［］14、图中所画的是两个简谐振动的振动曲线．若这两个简谐振动可叠加，则合成的余弦振动的初相为(A) π23． (B) π． (C) π21． (D) 0．［］15、若⼀平⾯简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C 为正值常量，则(A) 波速为C ． (B) 周期为1/B ．(C) 波长为 2π /C ． (D) ⾓频率为2π /B ．［］16、下列函数f (x , t )可表⽰弹性介质中的⼀维波动，式中A 、a 和b 是正的常量．其中哪个函数表⽰沿x 轴负向传播的⾏波？(A) )cos(),(bt ax A t x f +=． (B) )cos(),(bt ax A t x f -=．(C) bt ax A t x f cos cos ),(?=． (D) bt ax A t x f sin sin ),(?=．［］17、频率为 100 Hz ，传播速度为300 m/s 的平⾯简谐波，波线上距离⼩于波长的两点振动的相位差为π31，则此两点相距(A) 2.86 m ． (B) 2.19 m ．A/ -(C) 0.5 m ． (D) 0.25 m ．［］18、已知⼀平⾯简谐波的表达式为 )cos(bx at A y -=（a 、b 为正值常量），则(A) 波的频率为a ． (B) 波的传播速度为 b/a ．(C) 波长为π / b ． (D) 波的周期为2π / a ．［］19、⼀平⾯简谐波的表达式为 )3cos(1.0π+π-π=x t y (SI) ，t = 0时的波形曲线如图所⽰，则(A) O 点的振幅为-0.1 m ．(B) 波长为3 m ． (C) a 、b 两点间相位差为π21 ． (D) 波速为9 m/s ．［］20、机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ，则 (A) 其振幅为3 m ． (B) 其周期为s 31．(C) 其波速为10 m/s ． (D) 波沿x 轴正向传播．［］21、图为沿x 轴负⽅向传播的平⾯简谐波在t = 0时刻的波形．若波的表达式以余弦函数表⽰，则O 点处质点振动的初相为(A) 0．(B) π21． (C) π． (D) π23．［］22、⼀横波沿x 轴负⽅向传播，若t 时刻波形曲线如图所⽰，则在t + T /4时刻x 轴上的1、2、3三点的振动位移分别是 (A) A ，0，-A. (B) -A ，0，A. (C) 0，A ，0. (D) 0，-A ，0. ［］23⼀平⾯简谐波表达式为 )2(sin 05.0x t y -π-= (SI)，则该波的频率ν (Hz)，波速u (m/s)及波线上各点振动的振幅 A (m)依次为(A) 21，21，－0.05． (B) 21，1，－0.05． (C) 21，21，0.05． (D) 2，2，0.05．［］24、在下⾯⼏种说法中，正确的说法是：(A) 波源不动时，波源的振动周期与波动的周期在数值上是不同的．(B) 波源振动的速度与波速相同．(C) 在波传播⽅向上的任⼀质点振动相位总是⽐波源的相位滞后(按差值不⼤于π计)．(D) 在波传播⽅向上的任⼀质点的振动相位总是⽐波源的相位超前．(按差值不⼤于π计) ［］25、在简谐波传播过程中，沿传播⽅向相距为λ21（λ为波长）的两点的振动速度必定x y O u(A) ⼤⼩相同，⽽⽅向相反． (B) ⼤⼩和⽅向均相同．(C) ⼤⼩不同，⽅向相同． (D) ⼤⼩不同，⽽⽅向相反．［］26、⼀平⾯简谐波沿x 轴负⽅向传播．已知 x = x 0处质点的振动⽅程为)c o s (0φω+=t A y ．若波速为u ，则此波的表达式为(A) }]/)([cos{00φω+--=u x x t A y ． (B) }]/)([cos{00φω+--=u x x t A y ． (C) }]/)[(cos{00φω+--=u x x t A y ． (D) }]/)[(cos{00φω+-+=u x x t A y ．［］27、⼀平⾯简谐波，其振幅为A ，频率为ν．波沿x 轴正⽅向传播．设t = t 0时刻波形如图所⽰．则x = 0处质点的振动⽅程为(A) ]21)(2cos[0π++π=t t A y ν． (B) ]21)(2cos[0π+-π=t t A y ν． (C) ]21)(2cos[0π--π=t t A y ν． (D) ])(2cos[0π+-π=t t A y ν．［］28、⼀平⾯简谐波的表达式为 )/(2c o s λνx t A y -π=．在t = 1 /ν时刻，x 1 = 3λ /4与x 2 = λ /4⼆点处质元速度之⽐是(A) -1． (B) 31． (C) 1． (D) 3 ［］29、在同⼀媒质中两列相⼲的平⾯简谐波的强度之⽐是I 1 / I 2 = 4，则两列波的振幅之⽐是(A) A 1 / A 2 = 16． (B) A 1 / A 2 = 4．(C) A 1 / A 2 = 2． (D) A 1 / A 2 = 1 /4．［］30、如图所⽰，两列波长为λ的相⼲波在P 点相遇．波在S 1点振动的初相是φ 1，S 1到P 点的距离是r 1；波在S 2点的初相是φ 2，S 2到P 点的距离是r 2，以k 代表零或正、负整数，则P 点是⼲涉极⼤的条件为：(A) λk r r =-12． (B) π=-k 212φφ． (C) π=-π+-k r r 2/)(21212λφφ． (D) π=-π+-k r r 2/)(22112λφφ．［］31、沿着相反⽅向传播的两列相⼲波，其表达式为)/(2c o s1λνx t A y -π= 和 )/(2c o s 2λνx t A y +π=．叠加后形成的驻波中，波节的位置坐标为 (A) λk x ±=． (B) λk x 21±=． (C) λ)12(21+±=k x ． (D) 4/)12(λ+±=k x ． x y t =t 0u O其中的k = 0，1，2，3, …．［］32、有两列沿相反⽅向传播的相⼲波，其表达式为)/(2c o s1λνx t A y -π= 和 )/(2c o s 2λνx t A y +π=．叠加后形成驻波，其波腹位置的坐标为：(A) x =±k λ． (B) λ)12(21+±=k x ． (C) λk x 21±=． (D) 4/)12(λ+±=k x ．其中的k = 0，1，2，3, …． [ ]33某时刻驻波波形曲线如图所⽰，则a 、b 两点振动的相位差是(A) 0 (B) π21(C) π． (D) 5π/4．［］34、沿着相反⽅向传播的两列相⼲波，其表达式为)/(2c o s1λνx t A y -π= 和 )/(2c o s 2λνx t A y +π=．在叠加后形成的驻波中，各处简谐振动的振幅是(A) A ． (B) 2A ．(C) )/2cos(2λx A π． (D) |)/2cos(2|λx A π．［］35、在波长为λ的驻波中，两个相邻波腹之间的距离为(A) λ /4． (B) λ /2．(C) 3λ /4． (D) λ．［］36、在波长为λ的驻波中两个相邻波节之间的距离为(A) λ． (B) 3λ /4．(C) λ /2． (D) λ /4．［］37在真空中沿着x 轴正⽅向传播的平⾯电磁波，其电场强度波的表达式是)/(2c o s 0λνx t E E z -π=，则磁场强度波的表达式是：(A) )/(2cos /000λνµεx t E H y -π=． (B) )/(2cos /000λνµεx t E H z -π=．(C) )/(2cos /000λνµεx t E H y -π-=． (D) )/(2cos /000λνµεx t E H y +π-=．［］38、在真空中沿着z 轴负⽅向传播的平⾯电磁波，其磁场强度波的表达式为)/(co s 0c z t H H x +-=ω，则电场强度波的表达式为：(A) )/(cos /000c z t H E y +=ωεµ． (B) )/(cos /000c z t H E x +=ωεµ． (C) )/(cos /000c z t H E y +-=ωεµ．(D) )/(cos /000c z t H E y --=ωεµ．［］39、电磁波的电场强度E 、磁场强度 H 和传播速度 u 的关系是：(A) 三者互相垂直，⽽E 和H 位相相差π21． (B) 三者互相垂直，⽽且E 、H 、 u 构成右旋直⾓坐标系． (C) 三者中E 和H 是同⽅向的，但都与 u 垂直． (D) 三者中E 和H 可以是任意⽅向的，但都必须与 u 垂直．［］40、电磁波在⾃由空间传播时，电场强度E 和磁场强度H(A) 在垂直于传播⽅向的同⼀条直线上．(B) 朝互相垂直的两个⽅向传播．(C) 互相垂直，且都垂直于传播⽅向．(D) 有相位差π21．［］⼆、填空题：（每题4分）41、⼀弹簧振⼦作简谐振动，振幅为A ，周期为T ，其运动⽅程⽤余弦函数表⽰．若t = 0时，(1) 振⼦在负的最⼤位移处，则初相为______________________；(2) 振⼦在平衡位置向正⽅向运动，则初相为________________；(3) 振⼦在位移为A /2处，且向负⽅向运动，则初相为______．42、三个简谐振动⽅程分别为 )21c o s (1π+=t A x ω，)67cos(2π+=t A x ω和)611cos(3π+=t A x ω画出它们的旋转⽮量图，并在同⼀坐标上画出它们的振动曲线．43、⼀物体作余弦振动，振幅为15×10-2 m ，⾓频率为6π s -1，初相为0.5 π，则振动⽅程为x = ________________________(SI)．44、⼀质点沿x 轴作简谐振动，振动范围的中⼼点为x 轴的原点．已知周期为T ，振幅为A ．(1) 若t = 0时质点过x = 0处且朝x 轴正⽅向运动，则振动⽅程为x =_____________________________．(2) 若t = 0时质点处于A x 21=处且向x 轴负⽅向运动，则振动⽅程为 x =_____________________________．45、⼀弹簧振⼦，弹簧的劲度系数为k ，重物的质量为m ，则此系统的固有振动周期为______________________．46、在两个相同的弹簧下各悬⼀物体，两物体的质量⽐为4∶1，则⼆者作简谐振动的周期之⽐为_______________________．47、⼀简谐振动的表达式为)3cos(φ+=t A x ，已知 t = 0时的初位移为0.04 m ，初速度为0.09 m/s ，则振幅A=_____________ ，初相φ =________________．48、⼀质点作简谐振动，速度最⼤值v m = 5 cm/s ，振幅A = 2 cm ．若令速度具有正最⼤值的那⼀时刻为t = 0，则振动表达式为_________________________．49、两个简谐振动曲线如图所⽰，则两个简谐振动的频率之⽐ν1∶ν2=__________________，加速度最⼤值之⽐a 1m ∶a 2m =__________________________，初始速率之⽐v 10∶v 20=____________________．50、有简谐振动⽅程为x = 1×10-2cos(π t +φ)(SI)，初相分别为φ1 = π/2，φ2 = π，φ3 = -π/2的三个振动．试在同⼀个坐标上画出上述三个振动曲线．51、⼀简谐振动曲线如图所⽰，则由图可确定在t = 2s时刻质点的位移为 ____________________，速度为 __________________．52、已知两个简谐振动的振动曲线如图所⽰．两简谐振动的最⼤速率之⽐为_________________．53、⼀⽔平弹簧简谐振⼦的振动曲线如图所⽰．当振⼦处在位移为零、速度为-ωA 、加速度为零和弹性⼒为零的状态时，应对应于曲线上的________点．当振⼦处在位移的绝对值为A 、速度为零、加速度为-ω2A 和弹性⼒为-kA 的状态时，应对应于曲线上的____________点．x (cm)t (s)O- x (cm)54、⼀简谐振动⽤余弦函数表⽰，其振动曲线如图所⽰，则此简谐振动的三个特征量为A =_____________；ω =________________；φ =_______________．55、已知两个简谐振动曲线如图所⽰．x 1的相位⽐x 2 的相位超前_______．56、两个简谐振动⽅程分别为 t A x ωcos 1=，)31cos(2π+=t A x ω在同⼀坐标上画出两者的x —t 曲线．xtO57、已知⼀简谐振动曲线如图所⽰，由图确定振⼦：(1) 在_____________s 时速度为零．(2)在____________ s 时动能最⼤．(3) 在____________ s 时加速度取正的最⼤值．58、已知三个简谐振动曲线如图所⽰，则振动⽅程分别为： x 1 =______________________， x 2 =_____________________，x 3 =_______________________．59、图中⽤旋转⽮量法表⽰了⼀个简谐振动．旋转⽮量的长度为0.04 m ，旋转⾓速度ω = 4π rad/s ．此简谐振动以余弦函数表 x (cm)t (s)O 12⽰的振动⽅程为x =__________________________(SI)．60、⼀质点作简谐振动的⾓频率为ω、振幅为A ．当t = 0时质点位于A x 21=处，且向x 正⽅向运动．试画出此振动的旋转⽮量图．61、两个同⽅向的简谐振动曲线如图所⽰．合振动的振幅为_______________________________，合振动的振动⽅程为________________________________． 62、⼀平⾯简谐波．波速为6.0 m/s ，振动周期为0.1 s ，则波长为___________．在波的传播⽅向上，有两质点（其间距离⼩于波长）的振动相位差为5π /6，则此两质点相距___________．63、⼀个余弦横波以速度u 沿x 轴正向传播，t 时刻波形曲线如图所⽰．试分别指出图中A ，B ，C 各质点在该时刻的运动⽅向．A _____________；B _____________ ；C ______________ ． 64、⼀横波的表达式是 )30/01.0/(2sin 2x t y -π=其中x 和y 的单位是厘⽶、t 的单位是秒，此波的波长是_________cm ，波速是_____________m/s ．65、已知平⾯简谐波的表达式为 )cos(Cx Bt A y -=式中A 、B 、C 为正值常量，此波的波长是_________，波速是_____________．在波传播⽅向上相距为d 的两点的振动相位差是____________________．66、⼀声波在空⽓中的波长是0.25 m ，传播速度是340 m/s ，当它进⼊另⼀介质时，波长变成了0.37 m ，它在该介质中传播速度为______________．67、已知波源的振动周期为4.00×10-2 s ，波的传播速度为300 m/s ，波沿x 轴正⽅向传播，则位于x 1 = 10.0 m 和x 2 = 16.0 m 的两质点振动相位差为__________．68、⼀平⾯简谐波沿x 轴正⽅向传播，波速 u = 100 m/s ，t = 0时刻的波形曲线如图所⽰．可知波长λ = ____________；振幅A = __________；频率ν = ____________．69、频率为500 Hz 的波，其波速为350 m/s ，相位差为2π/3 的两点间距离为________________________．70、⼀平⾯简谐波沿x 轴正⽅向传播．已知x = 0处的振动⽅程为 )cos(0φω+=t y ，波速为u ．坐标为x 1和x 2的两点的振动初相位分别记为φ 1和φ 2，则相位差φ 1－φ 2 =_________________．·---71、已知⼀平⾯简谐波的波长λ = 1 m ，振幅A = 0.1 m ，周期T = 0.5 s ．选波的传播⽅向为x 轴正⽅向，并以振动初相为零的点为x 轴原点，则波动表达式为y = _____________________________________(SI)．72、⼀横波的表达式是)4.0100(2sin 02.0π-π=t y (SI)，则振幅是________，波长是_________，频率是__________，波的传播速度是______________．77、已知⼀平⾯简谐波的表达式为 )cos(bx at A -，（a 、b 均为正值常量），则波沿x 轴传播的速度为___________________．74、⼀简谐波的频率为 5×104 Hz ，波速为 1.5×103 m/s ．在传播路径上相距5×10-3 m 的两点之间的振动相位差为_______________．75、⼀简谐波沿BP ⽅向传播，它在B 点引起的振动⽅程为 t A y π=2cos 11．另⼀简谐波沿CP ⽅向传播，它在C 点引起的振动⽅程为)2cos(22π+π=t A y ．P 点与B 点相距0.40 m ，与C 点相距0.5 m （如图）．波速均为u = 0.20 m/s ．则两波在P 点的相位差为______________________．76、已知⼀平⾯简谐波的表达式为 )cos(Ex Dt A y -=，式中A 、D 、E 为正值常量，则在传播⽅向上相距为a 的两点的相位差为______________．77、在简谐波的⼀条射线上，相距0.2 m 两点的振动相位差为π /6．⼜知振动周期为0.4 s ，则波长为_________________，波速为________________．78、⼀声纳装置向海⽔中发出超声波，其波的表达式为)2201014.3cos(102.153x t y -??=- (SI)则此波的频率ν = _________________ ，波长λ = __________________，海⽔中声速u = __________________．79、已知14℃时的空⽓中声速为340 m/s ．⼈可以听到频率为20 Hz ⾄20000 Hz 范围内的声波．可以引起听觉的声波在空⽓中波长的范围约为______________________________．80、⼀平⾯简谐波（机械波）沿x 轴正⽅向传播，波动表达式为)21cos(2.0x t y π-π= (SI)，则x = -3 m 处媒质质点的振动加速度a 的表达式为________________________________________．。

物体的振动和波动练习题一、选择题1. 下列哪个不属于机械振动的基本特征？A. 振幅B. 周期C. 频率D. 波长2. 以下哪种波不需要介质传播？A. 机械波B. 横波C. 纵波D. 都需要介质传播3. 以下哪个现象不属于机械波传播中的失能?A. 反射B. 折射C. 干涉D. 散射4. 把频率为30Hz的振动用电路方式表示，需要设备的最小档位是A. 10sB. 1sC. 1msD. 1us5. 振幅越大，波的能量传播速度越快，这一说法A. 对B. 错6. 当一个横波传播时，传播介质上的每一个质点的振动方向A. 垂直于波的传播方向B. 与波的传播方向相同C. 与波的传播方向相反D. 与波的振动方向相同7. 下列不属于机械波的是A. 音波B. 光波C. 水波D. 地震波8. 声音能传播的介质是A. 真空B. 水C. 铁D. 木头9. 长度为0.1m的弦上传播的频率为500Hz的波，其波长为A. 10cmB. 20cmC. 40cmD. 50cm10. 一个在弹簧中传播的波，它所具有的振动特点可以用频率 f 表示。

当频率 f 增大时，振动速度将A. 不变B. 增大C. 减小D. 变为零二、填空题1. 机械波在介质中的传播速度与_________、_________有关。

2. 波长和_________成反比。

3. 波的频率和振动的_________有关。

4. 当光束从水中垂直射入空气时，光的_________发生折射。

5. 在两根相互平行的弹簧上各拧一节，右手拇指指向电流的方向，右手四指的弯曲方向表示_________。

三、简答题1. 请简要说明机械波和电磁波的区别。

2. 请解释频率和周期的概念，并写出它们的单位。

3. 什么是衰减? 请说明衰减对波传播的影响。

4. 什么是驻波? 它是如何形成的？5. 请举例说明机械波的反射和折射现象。

四、计算题1. 一支弦上传播的横波的振动频率为100Hz，波长为0.5m。

一 选择题 (共60分)1. (本题 3分)(0327) 一轻弹簧，上端固定，下端挂有质量为m 的重物，其自由振动的周期为T ．今已知振子离开平衡位置为x 时，其振动速度为v ，加速度为a ．则下列计算该振子劲度系数的公式中，错误的是：(A) 2max 2max/x m k v =． (B) x mg k /=． (C) 22/4T m k π=． (D) x ma k /=． ［ ］2. (本题 3分)(3255) 如图所示，在一竖直悬挂的弹簧下系一质量为m 的物体，再用此弹簧改系一质量为4m 的物体，最后将此弹簧截断为两个等长的弹簧并联后悬挂质量为m 的物体，则这三个系统的周期值之比为(A) 1∶2∶2/1． (B) 1∶21∶2 ． (C) 1∶2∶21． (D) 1∶2∶1/4 ． ［ ］3. (本题 3分)(3256) 图(a)、(b)、(c)为三个不同的简谐振动系统．组成各系统的各弹簧的原长、各弹簧的劲度系数及重物质量均相同．(a)、(b)、(c)三个振动系统的ω2（ω为固有角频率）值之比为(A) 2∶1∶21． (B) 1∶2∶4 ．(C) 2∶2∶1 ． (D) 1∶1∶2 ．［ ］(a)(b)4. (本题 3分)(5507) 图中三条曲线分别表示简谐振动中的位移x ，速度v ，和加速度a ．下列说法中哪一个是正确的？(A) 曲线3，1，2分别表示x ，v ，a 曲线；(B) 曲线2，1，3分别表示x ，v ，a 曲线； (C) 曲线1，3，2分别表示x ，v ，a 曲线； (D) 曲线2，3，1分别表示x ，v ，a 曲线；(E) 曲线1，2，3分别表示x ，v ，a 曲线． ［ ］x, v , at O123已知某简谐振动的振动曲线如图所示，位移的单位为厘米，时间单位为秒．则此简谐振动的振动方程为：(A) )3232cos(2π+π=t x ．(B) )3232cos(2π−π=t x ．(C) )3234cos(2π+π=t x ．(D) )3234cos(2π−π=t x ．(E) )4134cos(2π−π=t x ． ［ ］6. (本题 3分)(3028) 一弹簧振子作简谐振动，总能量为E 1，如果简谐振动振幅增加为原来的两倍，重物的质量增为原来的四倍，则它的总能量E 2变为 (A) E 1/4． (B) E 1/2．(C) 2E 1． (D) 4 E 1 ． ［ ］7. (本题 3分)(3023) 一弹簧振子，当把它水平放置时，它可以作简谐振动．若把它竖直放置或放在固定的光滑斜面上，试判断下面哪种情况是正确的：(A) 竖直放置可作简谐振动，放在光滑斜面上不能作简谐振动． (B) 竖直放置不能作简谐振动，放在光滑斜面上可作简谐振动．(C) 两种情况都可作简谐振动．(D) 两种情况都不能作简谐振动． ［ ］放在光滑斜面上8. (本题 3分)(5181) 一质点作简谐振动，已知振动频率为f ，则振动动能的变化频率是 (A) 4f . (B) 2 f . (C) f .(D) 2/f . (E) f /4 ［ ］9. (本题 3分)(3560) 弹簧振子在光滑水平面上作简谐振动时，弹性力在半个周期内所作的功为(A) kA 2． (B) 221kA ．(C) (1/4)kA 2． (D) 0． ［ ］10. (本题 3分)(3066) 机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ，则(A) 其振幅为3 m ． (B) 其周期为s 31．(C) 其波速为10 m/s ． (D) 波沿x 轴正向传播． ［ ］一平面余弦波在t = 0时刻的波形曲线如图所示，则O 点的振动初相φ 为：(A) 0. (B) π21(C) π (D) π23（或π−21） ［ ］xyOu12. (本题 3分)(3151) 图中画出一向右传播的简谐波在t 时刻的波形图，BC 为波密介质的反射面，波由P 点反射，则反射波在t 时刻的波形图为 ［ ］13. (本题 3分)(3072) 如图所示，一平面简谐波沿x 轴正向传播，已知P 点的振动方程为)cos(0φω+=t A y ，则波的表达式为 (A) }]/)([cos{0φω+−−=u l x t A y ． (B) })]/([cos{0φω+−=u x t A y ．(C) )/(cos u x t A y −=ω．(D) }]/)([cos{0φω+−+=u l x t A y ． ［ ］14. (本题 3分)(3071) 一平面简谐波以速度u 沿x 轴正方向传播，在t = t ＇时波形曲线如图所示．则坐标原点O 的振动方程为 (A) 2)(cos[π+′−=t t b u a y ． (B) ]2)(2cos[π−′−π=t t b u a y ． (C) ]2)(cos[π+′+π=t tb u a y ．(D) 2)(cos[π−′−π=t t b u a y ． ［ ］15. (本题 3分)(3286) 在同一媒质中两列相干的平面简谐波的强度之比是I 1 / I 2 = 4，则两列波的振幅之比是(A) A 1 / A 2 = 16． (B) A 1 / A 2 = 4．(C) A 1 / A 2 = 2． (D) A 1 / A 2 = 1 /4． ［ ］一列机械横波在t 时刻的波形曲线如图所示，则该时刻能量为最大值的媒质质元的位置是：(A) o ＇，b ，d ，f ． (B) a ，c ，e ，g ．(C) o ＇，d ． (D) b ，f ．［ ］17. (本题 3分)(3289) 图示一平面简谐机械波在t 时刻的波形曲线．若此时A 点处媒质质元的振动动能在增大，则(A) A 点处质元的弹性势能在减小． (B) 波沿x 轴负方向传播．(C) B 点处质元的振动动能在减小．(D)各点的波的能量密度都不随时间变化． ［ ］18. (本题 3分)(3090) 一平面简谐波在弹性媒质中传播，在媒质质元从平衡位置运动到最大位移处的过程中：(A) 它的动能转换成势能． (B) 它的势能转换成动能．(C) 它从相邻的一段质元获得能量其能量逐渐增大．(D) 它把自己的能量传给相邻的一段质元，其能量逐渐减小． ［ ］19. (本题 3分)(5321) S 1和S 2是波长均为λ 的两个相干波的波源，相距3λ /4，S 1的相位比S 2超前π21．若两波单独传播时，在过S 1和S 2的直线上各点的强度相同，不随距离变化，且两波的强度都是I 0，则在S 1、S 2连线上S 1外侧和S 2外侧各点，合成波的强度分别是(A) 4I 0，4I 0． (B) 0，0．(C) 0，4I 0 ． (D) 4I 0，0． ［ ］20. (本题 3分)(3101) 在驻波中，两个相邻波节间各质点的振动(A) 振幅相同，相位相同． (B) 振幅不同，相位相同．(C) 振幅相同，相位不同． (D) 振幅不同，相位不同． ［ ］二 填空题 (共81分)21. (本题 4分)(3010) 有两相同的弹簧，其劲度系数均为k ．(1) 把它们串联起来，下面挂一个质量为m 的重物，此系统作简谐振动的周期为___________________；(2) 把它们并联起来，下面挂一个质量为m 的重物，此系统作简谐振动的周期为___________________________________．22. (本题 3分)(3041) 一简谐振动曲线如图所示，则由图可确定在t = 2s时刻质点的位移为 ____________________，速度为__________________．23. (本题 5分)(3398) 一质点作简谐振动．其振动曲线如图所示．根据此图，它的周期T =___________，用余弦函数描述时初相φ =_________________．24. (本题 5分)(3400) 试在下图中画出简谐振子的动能，振动势能和机械能随时间t 而变的三条曲线（设t = 0时物体经过平衡位置）．EtTT/2T 为简谐振动的周期25. (本题 3分)(3569) 如图所示的是两个简谐振动的振动曲线，它们合成的余弦振动的初相为__________________．21−一质点同时参与了三个简谐振动，它们的振动方程分别为)31cos(1π+=t A x ω, )35cos(2π+=t A x ω, )cos(3π+=t A x ω其合成运动的运动方程为x = ______________．27. (本题 4分)(5315) 两个同方向同频率的简谐振动，其合振动的振幅为20 cm ，与第一个简谐振动的相位差为φ –φ1 = π/6．若第一个简谐振动的振幅为310 cm = 17.3 cm ，则第二个简谐振动的振幅为___________________ cm ，第一、二两个简谐振动的相位差φ1 − φ2为____________．28. (本题 5分)(3075) 一平面简谐波的表达式为 )37.0125cos(025.0x t y −= (SI)，其角频率ω =__________________________，波速u =______________________，波长λ = _________________．29. (本题 4分)(3862) 一横波的表达式是 )30/01.0/(2sin 2x t y −π=其中x 和y 的单位是厘米、t 的单位是秒，此波的波长是_________cm ，波速是_____________m/s ．30. (本题 5分)(3074) 一平面简谐波的表达式为 )/(cos u x t A y −=ω)/cos(u x t A ωω−= 其中x / u 表示_____________________________；ωx / u 表示________________________；y 表示______________________________．31. (本题 5分)(3863) 已知平面简谐波的表达式为 )cos(Cx Bt A y −=式中A 、B 、C 为正值常量，此波的波长是_________，波速是_____________．在波传播方向上相距为d 的两点的振动相位差是____________________．一简谐波沿BP 方向传播，它在B 点引起的振动方程为t A y π=2cos 11．另一简谐波沿CP 方向传播，它在C 点引起的振动方程为)2cos(22π+π=t A y ．P 点与B 点相距0.40 m ，与C 点相距0.5 m （如图）．波速均为u = 0.20 m/s ．则两波在P 点的相位差为______________________．33. (本题 5分)(3063) 一平面简谐波沿x 轴正方向传播，波速 u = 100 m/s ，t = 0时刻的波形曲线如图所示．可知波长λ = ____________； 振幅A = __________；频率ν = ____________．34. (本题 5分)(3133) 一平面简谐波沿Ox 轴正方向传播，波长为λ．若如图P 1点处质点的振动方程为)2cos(1φν+π=t A y ，则P 2点处质点的振动方程为_________________________________；与P 1点处质点振动状态相同的那些点的位置是___________________________．OP 1P 235. (本题 3分)(3301) 如图所示，S 1和S 2为同相位的两相干波源，相距为L ，P 点距S 1为r ；波源S 1在P 点引起的振动振幅为A 1，波源S 2在P 点引起的振动振幅为A 2，两波波长都是λ，则P 点的振幅A = _________________________________________________________．1236. (本题 4分)(5517) S 1，S 2为振动频率、振动方向均相同的两个点波源，振动方向垂直纸面，两者相距λ23（λ为波长）如图．已知S 1的初相为π21．(1) 若使射线S 2C 上各点由两列波引起的振动均干涉相消，则S 2的初相应为________________________．(2) 若使S 1 S 2连线的中垂线MN 上各点由两列波引起的振动均干涉相消，则S 2的初位相应为_______________________．37. (本题 3分)(3595) 一驻波的表达式为 )2cos()/2cos(2t x A y νλππ=．两个相邻波腹之间的距离是___________________．一驻波表达式为t x A y ωλcos )/2cos(2π=，则λ21−=x 处质点的振动方程是___________________________________________；该质点的振动速度表达式是______________________________________．39. (本题 5分)(3107) 如果入射波的表达式是)(2cos 1λxT t A y +π=，在x = 0处发生反射后形成驻波，反射点为波腹．设反射后波的强度不变，则反射波的表达式y 2 =___________________________________________； 在x = 2λ /3处质点合振动的振幅等于______________________．40. (本题 3分)(3462) 在真空中一平面电磁波的电场强度波的表达式为：103(102cos[100.6882×−×π×=−xt E y (SI)则该平面电磁波的波长是____________________．三 计算题 (共74分)41. (本题10分)(3022) 一质点在x 轴上作简谐振动，选取该质点向右运动通过A 点时作为计时起点( t = 0 )，经过2秒后质点第一次经过B 点，再经过2秒后质点第二次经过B 点，若已知该质点在A 、B 两点具有相同的速率，且AB = 10 cm 求：(1) 质点的振动方程；(2) 质点在A 点处的速率．42. (本题 5分)(3045) 一质点作简谐振动，其振动方程为x = 0.24)3121cos(π+πt (SI)，试用旋转矢量法求出质点由初始状态（t = 0的状态）运动到x = -0.12 m ，v < 0的状态所需最短时间∆t ．43. (本题 5分)(3085) 在弹性媒质中有一沿x 轴正向传播的平面波，其表达式为)214cos(01.0π−π−=x t y (SI)．若在x = 5.00 m 处有一媒质分界面，且在分界面处反射波相位突变π，设反射波的强度不变，试写出反射波的表达式．如图，一平面简谐波沿Ox 轴传播，波动表达式为])/(2cos[φλν+−π=x t A y (SI)，求(1) P 处质点的振动方程；(2) 该质点的速度表达式与加速度表达式．OP45. (本题 5分)(3332) 如图所示，一简谐波向x 轴正向传播，波速u = 500 m/s ，x 0 = 1 m, P 点的振动方程为 )21500cos(03.0π−π=t y (SI).(1) 按图所示坐标系，写出相应的波的表达式；(2) 在图上画出t = 0时刻的波形曲线．46. (本题 8分)(5516) 平面简谐波沿x 轴正方向传播，振幅为2 cm ，频率为 50 Hz ，波速为 200m/s ．在t = 0时，x = 0处的质点正在平衡位置向y 轴正方向运动，求x = 4 m 处媒质质点振动的表达式及该点在t = 2 s 时的振动速度．47. (本题 8分)(3078) 一平面简谐波沿x 轴正向传播，其振幅为A ，频率为ν ，波速为u ．设t = t ＇时刻的波形曲线如图所示．求 (1) x = 0处质点振动方程；(2) 该波的表达式．xu O t =t ′y48. (本题 8分)(3138) 某质点作简谐振动，周期为2 s ，振幅为0.06 m ，t = 0 时刻，质点恰好处在负向最大位移处，求(1) 该质点的振动方程；(2) 此振动以波速u = 2 m/s 沿x 轴正方向传播时，形成的一维简谐波的波动表达式，（以该质点的平衡位置为坐标原点）；(3) 该波的波长．49. (本题10分)(3146) 如图为一平面简谐波在t = 0 时刻的波形图，已知波速u = 20 m/s ．试画出P 处质点与Q 处质点的振动曲线，然后写出相应的振动方程．如图所示，两列相干波在P 点相遇．一列波在B 点引起的振动是 t y π×=−2cos 103310 (SI)；另一列波在C 点引起的振动是)212cos(103320π+π×=−t y (SI)； 令=BP 0.45 m ，=CP 0.30m ，两波的传播速度u = 0.20 m/s ，不考虑传播途中振幅的减小，求P 点的合振动的振动方程．51. (本题 5分)(3336) 如图所示，两列波长均为λ 的相干简谐波分别通过图中的O 1和O 2点，通过O 1点的简谐波在M 1 M 2平面反射后，与通过O 2点的简谐波在P 点相遇．假定波在M 1 M 2平面反射时有相位突变π．O 1和O 2两点的振动方程为 y 10 =A cos(πt ) 和y 20 = A cos(πt )，且 λ81=+mP m O ， λ32=P O （λ 为波长），求：(1) 两列波分别在P 点引起的振动的方程；(2) P 点的合振动方程．（假定两列波在传播或反射过程中均不衰减）2。

大学物理-习题-简谐振动和波-学生版一．选择题《机械振动和机械波》模块习题 1. 对一个作简谐振动的物体，下面哪种说法是正确的？---------------------------------- 【C 】 (A) 物体处在运动正方向的端点时，速度和加速度都达到最大值； (B) 物体位于平衡位置且向负方向运动时，速度和加速度都为零； (C) 物体位于平衡位置且向正方向运动时，速度最大，加速度为零； (D) 物体处在负方向的端点时，速度最大，加速度为零。

2. 一个质点作简谐运动，振幅为 A，在起始时刻质点的位移为- A ，且向 x 轴正方向运动， 2 代表此简谐运动的旋转矢量为---------------------------------------------------------------------【B 】3. 一质点沿 x 轴作简谐振动，振动方程为x = 0.04 cos(2p t +1 p ) （SI），从 t = 0 时刻起， 3 到质点位置在 x = -0.02 m 处，且向 x 轴正方向运动的最短时间间隔为--------- 【D 】 1 1 1 1 (A) s ； (B) s ； (C) s ； (D) s 8 64 2 4 一弹簧振子，振动方程为x=0.1cos(πt-π/3)·m，若振子从 t=0 时刻的位置到达 x=-0.05m处，且向 X 轴负向运动，则所需的最短时间为------------------------【D 】（A）s/3；（B） 5s/3；（C） s/2；（D） 1s。

1 5. 频率为 100 Hz，传播速度为 300 m/s 的平面简谐波，波线上距离小于波长的两点振动的相位差为 p ，则此两点相距 --------------------------------------------------------------【C 】 3 (A) 2.86 m (B) 2.19 m (C) 0.5m (D) 0.25 m T 6. 一平面简谐波，沿 x 轴负方向传播，角频率为ω，波速为 u．设t = 时刻的波形如图（a） 4 所示，则该波的表达式为---------------------------------------------------------------------【】é æ x ö ùé æ x ö p ù （A）y = A cos êw ç t - u ÷ + p ú （B） y= A cos êw ç t - u ÷ + 2 ú ë è ø û ë è ø û é æx ö p ù é æ x ö ù （C）y = A cos êw ç t + u ÷ - 2ú （D）y = A cos êw ç t + u ÷ + p ú ë è ø û ë èø û 7. 在简谐波传播过程中，沿传播方向相距为l/2 ，（l为波长）的两点的振动速度必定：【A 】 (A) 大小相同，而方向相反； (B) 大小和方向均相同； (C) 大小不同，方向相同； (D) 大小不同，而方向相反。

振动和波检测题一、选择题1.轻弹簧上端固定，下系一质量为m1的物体，稳定后在m1下边又系一质量为m2的物体，于是弹簧又伸长了△X，若将m2移去，并令其振动，则振动周期为( )A.T=2B.T=2C.T=2D.2. 一简谐振动曲线如右图所示，则震动周期为（）A.2.26sB.2.40sC.2.20sD.2.00s3. 一质点作简谐振动，其振动方程为X=Acos( t+ )，在求质点的振动动能时，得出下面5个表达式：（1）（2）（3）（4）（5）其中m是质点的质量，k是弹簧的劲度系数，T是振动的周期，这些表达式中（）A.（1），（4）是对的B.（2），（4）是对的C.（1），（5）是对的D.（3），（5）是对的E.（2），（5）是对的4. 右图为沿X轴负方向传播的平面简谐波在t=0时刻的波形，若波的表达式以余弦函数表示，则O点处质点振动的初相为（）A.0B.C. D.5. 若一平面简谐波的表达式为y=Acos(Bt-Cx)，式中A,B,C为正值常量，则（）A.波速为CB.周期为1/BC.波长为2 /CD.角频率为2 /B6. 一平面简谐波以速度u沿x轴正方向传播，在t=t‘时波形曲线如右图所示,则坐标原点O的振动方程为（）A. B.C. D.7. 一简谐波沿Ox轴正方向传播，t=0时刻波形曲线如右图所示，已知周期为2s，则P点处质点的振动速度v与时间t的关系曲线为（）A. B.C. D.8. 一平面简谐波在弹性媒质中传播，在媒质质元从平衡位置运动到最大位移处的过程中（）A.它的动能转换成势能B.它的势能转换成动能C.它从相邻的一段质元获得能量，其能量逐渐增大D.它把自己的能量传给相邻的一段质元，其能量逐渐减小9. 如右图所示，S1和S2为两相干波源，它们的振动方向均垂直于图面，发出波长为的简谐波，P点是两列波相遇区域中的一点，已知=2 ，=2.2 ，两列波在P点发生相消干涉，若S1的振动方程为y1= ，则S2的振动方程为（）A. B.C. D.10. 着相反方向传播的两列相干波，其表达式为和，叠加后形成的驻波中，波节的位置坐标为（）A. B.C. D.11 质点作简谐振动，速度最大值=5cm/s，振幅A=2cm，若令速度具有正最大值的那一刻作t=0，则振动表达式为12. 谐振子的振动曲线如右图所示，则以余弦函数表示的振动方程为13. 点同时参与了三个简谐振动，它们的振动方程分别为，，，其合成运动的运动方程为14. 弦线传播的一入射波的表达式为，波在x=L处(B点)发生反射，反射点为固定端，如右图所示，设波在传播和反射过程中振幅不变，则反射波的表达式为y2=15. 图所示，一平面简谐波在t=2s时刻的波形图，波的振幅为0.2m，周期为4s，则图中P点处质点的振动方程为16. 谐波沿Ox轴负方向传播，x轴上P1点处的振动方程为yp1=（SI）,x轴上P2点的坐标减去P1点的坐标等于（为波长），则P2点的振动方程为17. （1）一列波长为的平面简谐波沿x轴正方向传播，已知在x=处振动的方程为y=Acos ，则该平面简谐波的表达式为（2）如果在上述波的波线上x=L(L> )处放一如右图所示的反射面，且假设反射波的振幅为A‘，则反射波得表达式为（x<=L）18. 如右图所示，两相干波源S1与S2相距，为波长，设两波在S1S2连线上传播时，它们的振幅都是A，并且不随距离变化，已知在该直线上在S1左侧各点的合成波强度为其中一个波强度的4倍，则两波源应满足的相位条件是19. 如右图所示，波源S1和S2发出的波在P点相遇，P点距离波源S1和S2的距离分别为和，为两列波在介质中的波长，若P点的合振幅总是极大值，则两波在P点的振动频率，波源S1的相位比S2的相位领先20. 如右图所示，S1和S2为同相位的两相干波源，相距为L，P点距S1为r；波源S1在P点引起的振动振幅为A1，波源S2在P点引起的振动振幅为A2，两波波长都是，则P点的振幅A=21. 一轻弹簧在60N的拉力下伸长30cm，现把质量为4kg的物体悬挂在该弹簧的下端并使之静止，再把物体向下拉10cm，然后由静止释放并开始计时，求：（1）物体的振动方程；（2）物体在平衡位置上方5cm时弹簧对物体的拉力；（3）物体从第一次越过平衡位置时刻起到它运动到上方5cm处所需要的最短时间。

B 2 ；波的周期为 B C lC ；此质元的初相位为
；波长为
2 C
；离波源距离为 l
lC 。
6.1.5 一平面简谐波沿 ox 轴正向传播，波动方程为 y A cos[ (t 振动方程为 为 2 1 二、选择题
x ) ] ，则 x L1 处质点的 u 4
y A cos[ (t
由 t=0 和 t=0.25 时的波形图，得
O
t
x
2 x x 2 10 (t ) ] 0.2 cos[2t x ] （2）波动表式为 y A cos[ ( t ) 0 ] 0.2 cos[ 1 0.6 2 3 2 u
O 点的振动表式为
y 0 | t 0 A cos 0 0 ， v 0 | t 0 A sin 0 0 ， 0
3 , 4
x1 x3振幅最大 。
2
0 20 , 0 20
5 3 (或 )时, x2 x3振幅最小 4 4
0 , 0 20 84 o 48时, x1 x 2 x3振幅最大 0 0
6.4.2
2
o

4

2
3

4

2
6.2.6 两相干平面简谐波沿不同方向传播，如图所示，波速均为 u 0.40m / s ，其中一列波在 A 点 引 起 的 振 动 方 程 为 y 1 A1 cos( 2 t

2
) ，另一列波在 B 点引起的振动方程为
y 2 A2 cos( 2 t
［ A ］ （A）0； （B） /2； （C） ； （D）3 /2。 三、简答题

机械振动机械波一、选择题1．对一个作简谐振动的物体，下面哪种说法是正确的（A ）物体处在运动正方向的端点时，速度和加速度都达到最大值； （B ）物体位于平衡位置且向负方向运动时，速度和加速度都为零； （C ）物体位于平衡位置且向正方向运动时，速度最大，加速度为零； （D ）物体处在负方向的端点时，速度最大，加速度为零。

2．质点作简谐振动，振动方程为)cos(φω+=t A x ，当时间2/T t =（T 为周期）时，质点的速度为（A ）φωsin A v -=； （B ）φωsin A v =； （C ）φωcos A v-=； （D ）φωcos A v =。

…3．一物体作简谐振动，振动方程为⎪⎭⎫ ⎝⎛+=4cos πωt A x 。

在4T t =（T 为周期）时刻，物体的加速度为 （A ）2221ωA -； （B ）2221ωA ； （C ）2321ωA -； （D ）2321ωA 。

4．已知两个简谐振动曲线如图所示，1x 的位相比2x 的位相（A ）落后2π； （B ）超前2π；（C ）落后π； （D ）超前π。

5．一质点沿x 轴作简谐振动，振动方程为⎪⎭⎫⎝⎛+⨯=-ππ312cos 1042t x （SI ）。

从0=t 时刻起，到质点位置在cm x 2-=处，且向x 轴正方向运动的最短时间间隔为 （A ）s 8/1； （B ）s 4/1；【第题图（C ）s 2/1； （D ）s 3/1。

6．一个质点作简谐振动，振幅为A ，在起始时刻质点的位移为2/A ，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为；7．一个简谐振动的振动曲线如图所示。

此振动的周期为（A ）s 12； （B ）s 10；（C ）s 14； （D ）s 11。

8．一简谐振动在某一瞬时处于平衡位置，此时它的能量是（A ）动能为零，势能最大； （B ）动能为零，机械能为零； （C ）动能最大，势能最大； （D ）动能最大，势能为零。

机械振动机械波一、选择题1．对一个作简谐振动的物体，下面哪种说法是正确的（A ）物体处在运动正方向的端点时，速度和加速度都达到最大值； （B ）物体位于平衡位置且向负方向运动时，速度和加速度都为零； （C ）物体位于平衡位置且向正方向运动时，速度最大，加速度为零； （D ）物体处在负方向的端点时，速度最大，加速度为零。

2．质点作简谐振动，振动方程为)cos(φω+=t A x ，当时间2/T t =（T 为周期）时，质点的速度为（A ）φωsin A v -=； （B ）φωsin A v =； （C ）φωcos A v-=； （D ）φωcos A v =。

3．一物体作简谐振动，振动方程为⎪⎭⎫⎝⎛+=4cos πωt A x 。

在4T t =（T 为周期）时刻，物体的加速度为 （A ）2221ωA -； （B ）2221ωA ； （C ）2321ωA -； （D ）2321ωA 。

4．已知两个简谐振动曲线如图所示，1x 的位相比2x 的位相（A ）落后2π； （B ）超前2π；（C ）落后π； （D ）超前π。

5．一质点沿x 轴作简谐振动，振动方程为⎪⎭⎫ ⎝⎛+⨯=-ππ312cos 1042t x （SI ）。

从0=t 时刻起，到质点位置在cm x 2-=处，且向x 轴正方向运动的最短时间间隔为 （A ）s 8/1； （B ）s 4/1； （C ）s 2/1； （D ）s 3/1。

6．一个质点作简谐振动，振幅为A ，在起始时刻质点的位移为2/A ，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为7．一个简谐振动的振动曲线如图所示。

此振动的周期为（A ）s 12； （B ）s 10；（C ）s 14； （D ）s 11。

8．一简谐振动在某一瞬时处于平衡位置，此时它的能量是（A ）动能为零，势能最大； （B ）动能为零，机械能为零； （C ）动能最大，势能最大； （D ）动能最大，势能为零。

1． 有一弹簧，当其下端挂一质量为m 的物体时，伸长量为9.8 ⨯ 10－2 m 。

若使物体上下振动，且规定向下为正方向。

（1）t =0时，物体在平衡位置上方8.0 ⨯ 10－2 m处，由静止开始向下运动，求运动方程。

（2）t = 0时，物体在平衡位置并以0.60 m/s 的速度向上运动，求运动方程。

题1分析：求运动方程，也就是要确定振动的三个特征物理量A 、ω，和ϕ。

其中振动的角频率是由弹簧振子系统的固有性质（振子质量m 及弹簧劲度系数k ）决定的，即m k /=ω，k 可根据物体受力平衡时弹簧的伸长来计算；振幅A 和初相ϕ需要根据初始条件确定。

解：物体受力平衡时，弹性力F 与重力P 的大小相等，即F = mg 。

而此时弹簧的伸长量m l 2108.9-⨯=∆。

则弹簧的劲度系数l mg l F k ∆=∆=//。

系统作简谐运动的角频率为1s 10//-=∆==l g m k ω（1）设系统平衡时，物体所在处为坐标原点，向下为x 轴正向。

由初始条件t = 0时，m x 210100.8-⨯=，010=v 可得振幅m 100.8)/(2210102-⨯=+=ωv x A ；应用旋转矢量法可确定初相πϕ=1。

则运动方程为])s 10cos[()m 100.8(121π+⨯=--t x（2）t = 0时，020=x ，120s m 6.0-⋅=v ，同理可得m 100.6)/(22202022-⨯=+=ωv x A ，2/2πϕ=；则运动方程为]5.0)s 10cos[()m 100.6(122π+⨯=--t x2．某振动质点的x －t 曲线如图所示，试求：（1）运动方程；（2）点P 对应的相位；（3）到达点P 相应位置所需要的时间。

题2分析：由已知运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题。

本题就是要通过x －t 图线确定振动的三个特征量量A 、ω，和0ϕ，从而写出运动方程。