大学物理 振动和波

⼤学物理实验讲义~弦振动和驻波研究⽅案弦振动与驻波研究【实验⽬的】1．观察在弦上形成的驻波；2．确定弦线振动时驻波波长与张⼒的关系； 3．学习对数作图和最⼩⼆乘法进⾏数据处理。

【实验原理】在⼀根拉紧的弦线上，其中张⼒为T ，线密度为µ，则沿弦线传播的横波应满⾜下述运动⽅程：2222xyT t y ??=??µ (1) 式中x 为波在传播⽅向（与弦线平⾏）的位置坐标，y 为振动位移。

将(1)式与典型的波动⽅程 22222x y V t y ??=?? 相⽐较，即可得到波的传播速度: µTV =若波源的振动频率为f ，横波波长为λ，由于波速λf V =，故波长与张⼒及线密度之间的关系为：µλTf1=(2)为了⽤实验证明公式(2)成⽴，将该式两边取对数，得：11lg lg lg lg 22T f λµ=-- (3)固定频率f 及线密度µ，⽽改变张⼒T ，并测出各相应波长λ，作lg λ-lg T 图，若得⼀直线，计算其斜率值（如为21），则证明了λ∝21T的关系成⽴。

弦线上的波长可利⽤驻波原理测量。

当两个振幅和频率相同的相⼲波在同⼀直线上相向传播时，其所叠加⽽成的波称为驻波，⼀维驻波是波⼲涉中的⼀种特殊情形。

在弦线上出现许多静⽌点，称为驻波的波节。

相邻两波节间的距离为半个波长。

【实验仪器】1、可调频率数显机械振动源；2、振动簧⽚；3、弦线（铜丝）；4、可动⼑⽚⽀架；5、可动⼑⼝⽀架；6、标尺；7、固定滑轮；8、砝码与砝码盘；9、变压器;10、实验平台；11、实验桌图1 实验装置⽰意图图2 可调频率数显机械振动源⾯板图（1、电源开关 2、频率调节 3、复位键 4、幅度调节 5、频率指⽰）实验装置如图1所⽰，⾦属弦线的⼀端系在能作⽔平⽅向振动的可调频率数显机械振动源的振簧⽚上，频率变化范围从0-200Hz 连续可调，频率最⼩变化量为0.01Hz ，弦线⼀端通过定滑轮⑦悬挂⼀砝码盘⑧；在振动装置(振动簧⽚)的附近有可动⼑⽚⽀架④，在实验装置上还有⼀个可沿弦线⽅向左右移动并撑住弦线的可动⼑⼝⑤。

第七章 电磁感应本章提要1. 法拉第电磁感应定律· 当穿过闭合导体回路所包围面积的磁通量发生变化时，导体回路中就将产生电流，这种现象称为电磁感应现象，此时产生的电流称为感应电流。

· 法拉第电磁感应定律表述为：通过导体回路所包围面积的磁通量发生变化石，回路中产生地感应电动势i e 与磁通量m Φ变化率的关系为d d t＝－F e其中Φ为磁链，负号表示感应电动势的方向。

对螺线管有N 匝线圈，可以有m N Φ=Φ。

2. 楞次定律· 楞次定律可直接判断感应电流方向，其表述为：闭合回路中感应电流的方向总是要用自己激发的磁场来阻碍引起感应电流的磁通量的变化。

3. 动生电动势· 磁感应强度不变，回路或回路的一部分相对于磁场运动，这样产生的电动势称为动生电动势。

动生电动势可以看成是洛仑兹力引起的。

· 由动生电动势的定义可得：()d bab ae 醋ò＝v B l· 洛伦兹力不做功，但起能量转换的作用。

4. 感生电动势·当导体回路静止，而通过导体回路磁通量的变化仅由磁场的变化引起时，导体中产生的电动势称为感生电动势。

d dd d d d L S t te F =??蝌Ñ－＝－i E r B S 其中E i 为感生电场强度。

5. 自感· 当回路中的电流发生变化，它所激发的磁场产生的通过自身回路的磁通量也会发生变化，此变化将在自身回路中产生感应电动势，这种现象称为自感现象，产生的电动势为自感电动势，其表达式为：d d L iL te =-（L 一定时）负号表明自感电动势阻碍回路中电流的变化，比例系数L 称为电感或自感系数。

· 自感系数表达式为：L iY =· 自感磁能212m W LI =6. 互感· 对于两个临近的载流回路，当其中一回路中的电流变化时，电流所激发的变化磁场在另一回路中产生感应电动势。

⼤学物理振动与波题库及答案⼀、选择题：（每题3分）1、把单摆摆球从平衡位置向位移正⽅向拉开，使摆线与竖直⽅向成⼀微⼩⾓度θ，然后由静⽌放⼿任其振动，从放⼿时开始计时．若⽤余弦函数表⽰其运动⽅程，则该单摆振动的初相为(A) π． (B) π/2．(C) 0 ． (D) θ．［2、两个质点各⾃作简谐振动，它们的振幅相同、周期相同．第⼀个质点的振动⽅程为x 1 = A cos(ωt + α)．当第⼀个质点从相对于其平衡位置的正位移处回到平衡位置时，第⼆个质点正在最⼤正位移处．则第⼆个质点的振动⽅程为(A) )π21cos(2++=αωt A x ． (B) )π21cos(2-+=αωt A x ． (C) )π23cos(2-+=αωt A x ． (D) )cos(2π++=αωt A x ．［］3、⼀个弹簧振⼦和⼀个单摆（只考虑⼩幅度摆动），在地⾯上的固有振动周期分别为T 1和T 2．将它们拿到⽉球上去，相应的周期分别为1T '和2T '．则有(A) 11T T >'且22T T >'． (B) 11T T <'且22T T <'．(C) 11T T ='且22T T ='． (D) 11T T ='且22T T >'．［］4、⼀弹簧振⼦，重物的质量为m ，弹簧的劲度系数为k ，该振⼦作振幅为A 的简谐振动．当重物通过平衡位置且向规定的正⽅向运动时，开始计时．则其振动⽅程为：(A) )21/(cos π+=t m k A x (B) )21/cos(π-=t m k A x (C) )π21/(cos +=t k m A x (D) )21/cos(π-=t k m A x (E) t m /k A x cos = ［］5、⼀物体作简谐振动，振动⽅程为)41cos(π+=t A x ω．在 t = T /4（T 为周期）时刻，物体的加速度为(A) 2221ωA -． (B) 2221ωA ． (C) 2321ωA -． (D) 2321ωA ．［］6、⼀质点作简谐振动，振动⽅程为)cos(φω+=t A x ，当时间t = T /2（T 为周期）时，质点的速度为(A) φωsin A -． (B) φωsin A ．(C) φωcos A -． (D) φωcos A ．［］7、⼀质点作简谐振动，周期为T ．当它由平衡位置向x 轴正⽅向运动时，从⼆分之⼀最⼤位移处到最⼤位移处这段路程所需要的时间为(A) T /12． (B) T /8．(C) T /6． (D) T /4．［］8、两个同周期简谐振动曲线如图所⽰．x 1的相位⽐x 2的相位 (A) 落后π/2． (B) 超前π/2． (C) 落后π． (D) 超前π．［］9、⼀质点作简谐振动，已知振动频率为f ，则振动动能的变化频率是(A) 4f . (B) 2 f . (C) f .(D) 2/f . (E) f /4 ［］10、⼀弹簧振⼦作简谐振动，当位移为振幅的⼀半时，其动能为总能量的(A) 1/4. (B) 1/2. (C) 2/1. (D) 3/4. (E) 2/3. ［］11、⼀弹簧振⼦作简谐振动，当其偏离平衡位置的位移的⼤⼩为振幅的1/4时，其动能为振动总能量的(A) 7/16. (B) 9/16. (C) 11/16.(D) 13/16. (E) 15/16. ［］12 ⼀质点作简谐振动，已知振动周期为T ，则其振动动能变化的周期是(A) T /4． (B) 2/T ． (C) T ．(D) 2 T ． (E) 4T ．［］13、当质点以频率ν作简谐振动时，它的动能的变化频率为(A) 4 ν． (B) 2 ν． (C) ν． (D) ν21．［］14、图中所画的是两个简谐振动的振动曲线．若这两个简谐振动可叠加，则合成的余弦振动的初相为(A) π23． (B) π． (C) π21． (D) 0．［］15、若⼀平⾯简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C 为正值常量，则(A) 波速为C ． (B) 周期为1/B ．(C) 波长为 2π /C ． (D) ⾓频率为2π /B ．［］16、下列函数f (x , t )可表⽰弹性介质中的⼀维波动，式中A 、a 和b 是正的常量．其中哪个函数表⽰沿x 轴负向传播的⾏波？(A) )cos(),(bt ax A t x f +=． (B) )cos(),(bt ax A t x f -=．(C) bt ax A t x f cos cos ),(?=． (D) bt ax A t x f sin sin ),(?=．［］17、频率为 100 Hz ，传播速度为300 m/s 的平⾯简谐波，波线上距离⼩于波长的两点振动的相位差为π31，则此两点相距(A) 2.86 m ． (B) 2.19 m ．A/ -(C) 0.5 m ． (D) 0.25 m ．［］18、已知⼀平⾯简谐波的表达式为 )cos(bx at A y -=（a 、b 为正值常量），则(A) 波的频率为a ． (B) 波的传播速度为 b/a ．(C) 波长为π / b ． (D) 波的周期为2π / a ．［］19、⼀平⾯简谐波的表达式为 )3cos(1.0π+π-π=x t y (SI) ，t = 0时的波形曲线如图所⽰，则(A) O 点的振幅为-0.1 m ．(B) 波长为3 m ． (C) a 、b 两点间相位差为π21 ． (D) 波速为9 m/s ．［］20、机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ，则 (A) 其振幅为3 m ． (B) 其周期为s 31．(C) 其波速为10 m/s ． (D) 波沿x 轴正向传播．［］21、图为沿x 轴负⽅向传播的平⾯简谐波在t = 0时刻的波形．若波的表达式以余弦函数表⽰，则O 点处质点振动的初相为(A) 0．(B) π21． (C) π． (D) π23．［］22、⼀横波沿x 轴负⽅向传播，若t 时刻波形曲线如图所⽰，则在t + T /4时刻x 轴上的1、2、3三点的振动位移分别是 (A) A ，0，-A. (B) -A ，0，A. (C) 0，A ，0. (D) 0，-A ，0. ［］23⼀平⾯简谐波表达式为 )2(sin 05.0x t y -π-= (SI)，则该波的频率ν (Hz)，波速u (m/s)及波线上各点振动的振幅 A (m)依次为(A) 21，21，－0.05． (B) 21，1，－0.05． (C) 21，21，0.05． (D) 2，2，0.05．［］24、在下⾯⼏种说法中，正确的说法是：(A) 波源不动时，波源的振动周期与波动的周期在数值上是不同的．(B) 波源振动的速度与波速相同．(C) 在波传播⽅向上的任⼀质点振动相位总是⽐波源的相位滞后(按差值不⼤于π计)．(D) 在波传播⽅向上的任⼀质点的振动相位总是⽐波源的相位超前．(按差值不⼤于π计) ［］25、在简谐波传播过程中，沿传播⽅向相距为λ21（λ为波长）的两点的振动速度必定x y O u(A) ⼤⼩相同，⽽⽅向相反． (B) ⼤⼩和⽅向均相同．(C) ⼤⼩不同，⽅向相同． (D) ⼤⼩不同，⽽⽅向相反．［］26、⼀平⾯简谐波沿x 轴负⽅向传播．已知 x = x 0处质点的振动⽅程为)c o s (0φω+=t A y ．若波速为u ，则此波的表达式为(A) }]/)([cos{00φω+--=u x x t A y ． (B) }]/)([cos{00φω+--=u x x t A y ． (C) }]/)[(cos{00φω+--=u x x t A y ． (D) }]/)[(cos{00φω+-+=u x x t A y ．［］27、⼀平⾯简谐波，其振幅为A ，频率为ν．波沿x 轴正⽅向传播．设t = t 0时刻波形如图所⽰．则x = 0处质点的振动⽅程为(A) ]21)(2cos[0π++π=t t A y ν． (B) ]21)(2cos[0π+-π=t t A y ν． (C) ]21)(2cos[0π--π=t t A y ν． (D) ])(2cos[0π+-π=t t A y ν．［］28、⼀平⾯简谐波的表达式为 )/(2c o s λνx t A y -π=．在t = 1 /ν时刻，x 1 = 3λ /4与x 2 = λ /4⼆点处质元速度之⽐是(A) -1． (B) 31． (C) 1． (D) 3 ［］29、在同⼀媒质中两列相⼲的平⾯简谐波的强度之⽐是I 1 / I 2 = 4，则两列波的振幅之⽐是(A) A 1 / A 2 = 16． (B) A 1 / A 2 = 4．(C) A 1 / A 2 = 2． (D) A 1 / A 2 = 1 /4．［］30、如图所⽰，两列波长为λ的相⼲波在P 点相遇．波在S 1点振动的初相是φ 1，S 1到P 点的距离是r 1；波在S 2点的初相是φ 2，S 2到P 点的距离是r 2，以k 代表零或正、负整数，则P 点是⼲涉极⼤的条件为：(A) λk r r =-12． (B) π=-k 212φφ． (C) π=-π+-k r r 2/)(21212λφφ． (D) π=-π+-k r r 2/)(22112λφφ．［］31、沿着相反⽅向传播的两列相⼲波，其表达式为)/(2c o s1λνx t A y -π= 和 )/(2c o s 2λνx t A y +π=．叠加后形成的驻波中，波节的位置坐标为 (A) λk x ±=． (B) λk x 21±=． (C) λ)12(21+±=k x ． (D) 4/)12(λ+±=k x ． x y t =t 0u O其中的k = 0，1，2，3, …．［］32、有两列沿相反⽅向传播的相⼲波，其表达式为)/(2c o s1λνx t A y -π= 和 )/(2c o s 2λνx t A y +π=．叠加后形成驻波，其波腹位置的坐标为：(A) x =±k λ． (B) λ)12(21+±=k x ． (C) λk x 21±=． (D) 4/)12(λ+±=k x ．其中的k = 0，1，2，3, …． [ ]33某时刻驻波波形曲线如图所⽰，则a 、b 两点振动的相位差是(A) 0 (B) π21(C) π． (D) 5π/4．［］34、沿着相反⽅向传播的两列相⼲波，其表达式为)/(2c o s1λνx t A y -π= 和 )/(2c o s 2λνx t A y +π=．在叠加后形成的驻波中，各处简谐振动的振幅是(A) A ． (B) 2A ．(C) )/2cos(2λx A π． (D) |)/2cos(2|λx A π．［］35、在波长为λ的驻波中，两个相邻波腹之间的距离为(A) λ /4． (B) λ /2．(C) 3λ /4． (D) λ．［］36、在波长为λ的驻波中两个相邻波节之间的距离为(A) λ． (B) 3λ /4．(C) λ /2． (D) λ /4．［］37在真空中沿着x 轴正⽅向传播的平⾯电磁波，其电场强度波的表达式是)/(2c o s 0λνx t E E z -π=，则磁场强度波的表达式是：(A) )/(2cos /000λνµεx t E H y -π=． (B) )/(2cos /000λνµεx t E H z -π=．(C) )/(2cos /000λνµεx t E H y -π-=． (D) )/(2cos /000λνµεx t E H y +π-=．［］38、在真空中沿着z 轴负⽅向传播的平⾯电磁波，其磁场强度波的表达式为)/(co s 0c z t H H x +-=ω，则电场强度波的表达式为：(A) )/(cos /000c z t H E y +=ωεµ． (B) )/(cos /000c z t H E x +=ωεµ． (C) )/(cos /000c z t H E y +-=ωεµ．(D) )/(cos /000c z t H E y --=ωεµ．［］39、电磁波的电场强度E 、磁场强度 H 和传播速度 u 的关系是：(A) 三者互相垂直，⽽E 和H 位相相差π21． (B) 三者互相垂直，⽽且E 、H 、 u 构成右旋直⾓坐标系． (C) 三者中E 和H 是同⽅向的，但都与 u 垂直． (D) 三者中E 和H 可以是任意⽅向的，但都必须与 u 垂直．［］40、电磁波在⾃由空间传播时，电场强度E 和磁场强度H(A) 在垂直于传播⽅向的同⼀条直线上．(B) 朝互相垂直的两个⽅向传播．(C) 互相垂直，且都垂直于传播⽅向．(D) 有相位差π21．［］⼆、填空题：（每题4分）41、⼀弹簧振⼦作简谐振动，振幅为A ，周期为T ，其运动⽅程⽤余弦函数表⽰．若t = 0时，(1) 振⼦在负的最⼤位移处，则初相为______________________；(2) 振⼦在平衡位置向正⽅向运动，则初相为________________；(3) 振⼦在位移为A /2处，且向负⽅向运动，则初相为______．42、三个简谐振动⽅程分别为 )21c o s (1π+=t A x ω，)67cos(2π+=t A x ω和)611cos(3π+=t A x ω画出它们的旋转⽮量图，并在同⼀坐标上画出它们的振动曲线．43、⼀物体作余弦振动，振幅为15×10-2 m ，⾓频率为6π s -1，初相为0.5 π，则振动⽅程为x = ________________________(SI)．44、⼀质点沿x 轴作简谐振动，振动范围的中⼼点为x 轴的原点．已知周期为T ，振幅为A ．(1) 若t = 0时质点过x = 0处且朝x 轴正⽅向运动，则振动⽅程为x =_____________________________．(2) 若t = 0时质点处于A x 21=处且向x 轴负⽅向运动，则振动⽅程为 x =_____________________________．45、⼀弹簧振⼦，弹簧的劲度系数为k ，重物的质量为m ，则此系统的固有振动周期为______________________．46、在两个相同的弹簧下各悬⼀物体，两物体的质量⽐为4∶1，则⼆者作简谐振动的周期之⽐为_______________________．47、⼀简谐振动的表达式为)3cos(φ+=t A x ，已知 t = 0时的初位移为0.04 m ，初速度为0.09 m/s ，则振幅A=_____________ ，初相φ =________________．48、⼀质点作简谐振动，速度最⼤值v m = 5 cm/s ，振幅A = 2 cm ．若令速度具有正最⼤值的那⼀时刻为t = 0，则振动表达式为_________________________．49、两个简谐振动曲线如图所⽰，则两个简谐振动的频率之⽐ν1∶ν2=__________________，加速度最⼤值之⽐a 1m ∶a 2m =__________________________，初始速率之⽐v 10∶v 20=____________________．50、有简谐振动⽅程为x = 1×10-2cos(π t +φ)(SI)，初相分别为φ1 = π/2，φ2 = π，φ3 = -π/2的三个振动．试在同⼀个坐标上画出上述三个振动曲线．51、⼀简谐振动曲线如图所⽰，则由图可确定在t = 2s时刻质点的位移为 ____________________，速度为 __________________．52、已知两个简谐振动的振动曲线如图所⽰．两简谐振动的最⼤速率之⽐为_________________．53、⼀⽔平弹簧简谐振⼦的振动曲线如图所⽰．当振⼦处在位移为零、速度为-ωA 、加速度为零和弹性⼒为零的状态时，应对应于曲线上的________点．当振⼦处在位移的绝对值为A 、速度为零、加速度为-ω2A 和弹性⼒为-kA 的状态时，应对应于曲线上的____________点．x (cm)t (s)O- x (cm)54、⼀简谐振动⽤余弦函数表⽰，其振动曲线如图所⽰，则此简谐振动的三个特征量为A =_____________；ω =________________；φ =_______________．55、已知两个简谐振动曲线如图所⽰．x 1的相位⽐x 2 的相位超前_______．56、两个简谐振动⽅程分别为 t A x ωcos 1=，)31cos(2π+=t A x ω在同⼀坐标上画出两者的x —t 曲线．xtO57、已知⼀简谐振动曲线如图所⽰，由图确定振⼦：(1) 在_____________s 时速度为零．(2)在____________ s 时动能最⼤．(3) 在____________ s 时加速度取正的最⼤值．58、已知三个简谐振动曲线如图所⽰，则振动⽅程分别为： x 1 =______________________， x 2 =_____________________，x 3 =_______________________．59、图中⽤旋转⽮量法表⽰了⼀个简谐振动．旋转⽮量的长度为0.04 m ，旋转⾓速度ω = 4π rad/s ．此简谐振动以余弦函数表 x (cm)t (s)O 12⽰的振动⽅程为x =__________________________(SI)．60、⼀质点作简谐振动的⾓频率为ω、振幅为A ．当t = 0时质点位于A x 21=处，且向x 正⽅向运动．试画出此振动的旋转⽮量图．61、两个同⽅向的简谐振动曲线如图所⽰．合振动的振幅为_______________________________，合振动的振动⽅程为________________________________． 62、⼀平⾯简谐波．波速为6.0 m/s ，振动周期为0.1 s ，则波长为___________．在波的传播⽅向上，有两质点（其间距离⼩于波长）的振动相位差为5π /6，则此两质点相距___________．63、⼀个余弦横波以速度u 沿x 轴正向传播，t 时刻波形曲线如图所⽰．试分别指出图中A ，B ，C 各质点在该时刻的运动⽅向．A _____________；B _____________ ；C ______________ ． 64、⼀横波的表达式是 )30/01.0/(2sin 2x t y -π=其中x 和y 的单位是厘⽶、t 的单位是秒，此波的波长是_________cm ，波速是_____________m/s ．65、已知平⾯简谐波的表达式为 )cos(Cx Bt A y -=式中A 、B 、C 为正值常量，此波的波长是_________，波速是_____________．在波传播⽅向上相距为d 的两点的振动相位差是____________________．66、⼀声波在空⽓中的波长是0.25 m ，传播速度是340 m/s ，当它进⼊另⼀介质时，波长变成了0.37 m ，它在该介质中传播速度为______________．67、已知波源的振动周期为4.00×10-2 s ，波的传播速度为300 m/s ，波沿x 轴正⽅向传播，则位于x 1 = 10.0 m 和x 2 = 16.0 m 的两质点振动相位差为__________．68、⼀平⾯简谐波沿x 轴正⽅向传播，波速 u = 100 m/s ，t = 0时刻的波形曲线如图所⽰．可知波长λ = ____________；振幅A = __________；频率ν = ____________．69、频率为500 Hz 的波，其波速为350 m/s ，相位差为2π/3 的两点间距离为________________________．70、⼀平⾯简谐波沿x 轴正⽅向传播．已知x = 0处的振动⽅程为 )cos(0φω+=t y ，波速为u ．坐标为x 1和x 2的两点的振动初相位分别记为φ 1和φ 2，则相位差φ 1－φ 2 =_________________．·---71、已知⼀平⾯简谐波的波长λ = 1 m ，振幅A = 0.1 m ，周期T = 0.5 s ．选波的传播⽅向为x 轴正⽅向，并以振动初相为零的点为x 轴原点，则波动表达式为y = _____________________________________(SI)．72、⼀横波的表达式是)4.0100(2sin 02.0π-π=t y (SI)，则振幅是________，波长是_________，频率是__________，波的传播速度是______________．77、已知⼀平⾯简谐波的表达式为 )cos(bx at A -，（a 、b 均为正值常量），则波沿x 轴传播的速度为___________________．74、⼀简谐波的频率为 5×104 Hz ，波速为 1.5×103 m/s ．在传播路径上相距5×10-3 m 的两点之间的振动相位差为_______________．75、⼀简谐波沿BP ⽅向传播，它在B 点引起的振动⽅程为 t A y π=2cos 11．另⼀简谐波沿CP ⽅向传播，它在C 点引起的振动⽅程为)2cos(22π+π=t A y ．P 点与B 点相距0.40 m ，与C 点相距0.5 m （如图）．波速均为u = 0.20 m/s ．则两波在P 点的相位差为______________________．76、已知⼀平⾯简谐波的表达式为 )cos(Ex Dt A y -=，式中A 、D 、E 为正值常量，则在传播⽅向上相距为a 的两点的相位差为______________．77、在简谐波的⼀条射线上，相距0.2 m 两点的振动相位差为π /6．⼜知振动周期为0.4 s ，则波长为_________________，波速为________________．78、⼀声纳装置向海⽔中发出超声波，其波的表达式为)2201014.3cos(102.153x t y -??=- (SI)则此波的频率ν = _________________ ，波长λ = __________________，海⽔中声速u = __________________．79、已知14℃时的空⽓中声速为340 m/s ．⼈可以听到频率为20 Hz ⾄20000 Hz 范围内的声波．可以引起听觉的声波在空⽓中波长的范围约为______________________________．80、⼀平⾯简谐波（机械波）沿x 轴正⽅向传播，波动表达式为)21cos(2.0x t y π-π= (SI)，则x = -3 m 处媒质质点的振动加速度a 的表达式为________________________________________．。

大学物理振动和波动 知识点总结1．简谐振动的基本特征（1）简谐振动的运动学方程: cos()x A t ϖϕ=+（2）简谐振动的动力学特征:F kx =-r r 或 2220d x x d t ϖ+= （3）能量特征： 222111222k p E E E mv kx KA =+=+=， k p E E = （4）旋转矢量表示: 做逆时针匀速转动的旋转矢量A r 在x 轴上的投影点的运动可用来表示简谐振动。

旋转矢量的长度A r 等于振动的振幅,旋转矢量的角速度等于谐振动的角频率,旋转矢量在0t =时刻与坐标轴x 的夹角为谐振动的初相。

2．描述简谐振动的三个基本量（1）简谐振动的相位：t ωϕ+，它决定了t 时刻简谐振动的状态；其中：00arctan(/)v x ϕω=-（2）简谐振动的振幅：A ，它取决于振动的能量。

其中：A =（3）简谐振动的角频率：ω，它取决于振动系统本身的性质。

3．简谐振动的合成(1)两个同方向同频率简谐振动的合成:合振动的振幅：A =合振幅最大： 212,0,1,2....k k ϕϕπ-==；合振幅最小：21(21),0,1,2....k k ϕϕπ-=+=（2）不同频率同方向简谐振动的合成：当两个分振动的频率都很大，而两个频率差很小时，产生拍现象，拍频为21ννν∆=-；合振动不再是谐振动，其振动方程为21210(2cos 2)cos 222x A t t ννννππ-+=（3）相互垂直的两个简谐振动的合成：若两个分振动的频率相同，则合成运动的轨迹一般为椭圆；若两个分振动的频率为简单的整数比，则合成运动的轨迹为李萨如图形。

（4）与振动的合成相对应，有振动的分解。

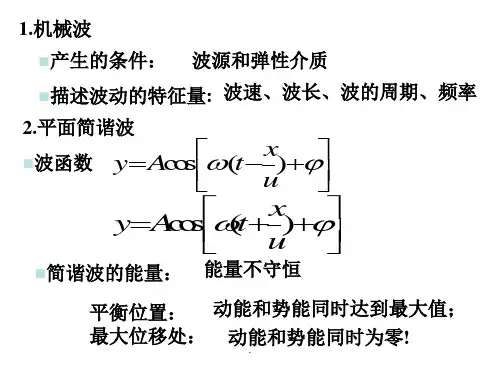
4．阻尼振动与受迫振动、共振：阻尼振动： 220220d x dx x dt dt βϖ++=；受迫振动 220022cos d x dx x f t dt dtβϖϖ++= 共振: 当驱动力的频率为某一特定值时,受迫振动的振幅将达到极大值.5．波的描述（1）机械波产生条件:波源和弹性介质（2）描述机械波的物理量:波长λ、周期T （或频率ν）和波速u ，三者之间关系为：uT λ= u λν=（3）平面简谐波的数学描述：(,)cos[()]xy x t A t uωϕ=±+； 2(,)cos()x y x t A t πωϕλ=±+；(,)cos 2()t x y x t A T πϕλ=±+ 其中，x 前面的±号由波的传播方向决定，波沿x 轴的正(负)向传播，取负(正)号。

大学物理实验中的波动与振动分析波动与振动是大学物理课程中的重要内容之一。

通过物理实验的手段，可以更好地理解和研究波动与振动的特性和规律，从而提升对物理学的理解和应用能力。

本文将对大学物理实验中的波动与振动进行分析。

一、实验背景和目的波动与振动是物理学的基本概念，广泛应用于多个领域。

通过进行波动与振动的实验，可以更好地理解其特性和规律，为理论的学习打下坚实的基础。

本实验旨在通过实验手段，探索波动与振动的相关原理，深入了解其性质和特征。

二、实验器材和步骤1. 实验器材：- 弹簧：用于研究弹性振动的特性，可以选择不同大小和材质的弹簧。

- 振动装置：用于产生振动，例如弹簧振子、简谐振子等。

- 高频发生器：产生高频信号，用于产生波动。

- 波动绳：用于研究波动传播的特性。

- 频率计：用于测量振动或波动的频率。

- 振动传感器：用于测量或检测振动的特征参数。

- 示波器：用于显示振动或波动的图像。

- 实验台和支架：用于固定实验器材。

2. 实验步骤：a. 振动实验：1) 根据实验要求选择合适的振动装置。

2) 将振动装置固定在实验台上。

3) 通过高频发生器产生振动信号，并调节频率。

4) 使用振动传感器测量振动的频率和振幅。

5) 使用示波器观察振动的图像，并记录关键数据和观察现象。

b. 波动实验：1) 将波动绳固定在实验台上，并保持一定的张力。

2) 通过高频发生器产生波动信号，并调节频率。

3) 使用示波器观察波动的传播和幅度变化。

4) 使用频率计测量波动的频率。

5) 记录关键数据和观察现象。

三、实验结果与分析1. 振动实验：- 通过调节高频发生器的频率，可以观察到振动信号的频率变化，并通过示波器显示出振动的图像。

- 随着频率的增加，振动的幅度可能发生变化。

- 使用振动传感器进行测量，可以得到振动的频率和振幅。

2. 波动实验：- 通过高频发生器产生波动信号，并使用波动绳进行传播实验。

- 使用示波器观察波动的传播和幅度变化。

振 动 学 基 础内容提要一、振动的基本概念1、振动 某物理量随时间变化，如果其数值总在一有限范围内变动，就说该物理量在振动；2、周期振动 如果物理量在振动时，每隔一定的时间间隔其数值就重复一次，称为周期振动；3、机械振动 物体在一定的位置附近作往复运动称为机械振动；4、简谐振动 如果物体振动的位移随时间按余(正)弦函数规律变化，即：()0cos ϕω+=t A x这样振动称为简谐振动；5、周期T 物体进行一次完全振动所需的时间称为周期，单位：秒。

一次完全振动指物体由某一位置出发连续两次经过平衡位置又回到原来的状态。

6、振动频率ν 单位时间内振动的次数，单位：次/秒，称为赫兹〔Ｈz 〕；7、振动圆频率ω 振动频率的π2倍，单位是弧度/秒〔rad /s 〕，即Tππνω22== 8、振幅A 物体离开平衡位置〔0=x 〕的最大位移的绝对值； 9、相位ϕ0ϕωϕ+=t 称为相位或相，单位：弧()rad 。

它是时间的单值增函数，每经历一个周期T ，相位增加π2，完成一次振动； 10、初相位0ϕ 开始计时时刻的相位；11、振动速度v 表示振动物体位移快慢的物理量，即：()⎪⎭⎫ ⎝⎛++=+-==2cos sin 00πϕωωϕωωt A t A dt dx v 说明速度的相位比位移的相位超前2π； 12、振动加速度a 表示振动物体速度变化快慢的物理量，即：()()πϕωωϕωω++=+-===020222cos cos t A t A dtx d dt dv a加速度的相位比速度的相位超前2π，比位移的相位超前π； 13、初始条件 在0=t 时刻的运动状态〔位移和速度〕称为初始条件，它决定振动的振幅和初位相，即：⎪⎩⎪⎨⎧-======000000sin cos ϕωϕA v v A x x t t 则可求得： ⎪⎪⎩⎪⎪⎨⎧-=+=00022020x v tg v x A ωϕω二、旋转矢量法简谐振动可以用一旋转矢量在x 轴上的投影来表示。

大学物理 ——波（一）引言概述：波是一种常见的物理现象，在自然界和人类日常生活中都能观察到。

本文旨在介绍大学物理学习中的第一部分——波的基本概念和性质。

通过本文的学习，读者将了解波的定义、波的分类以及波动方程等重要概念，并深入探讨机械波和电磁波的性质以及波的传播规律。

正文：1. 波的概念- 定义：波是一种能量传播的方式，以振动或震动形式传递能量而不传递物质的现象。

- 特点：波具有传播、反射、折射和干涉等特点，能够对物体进行作用。

- 分类：根据振动方向和能量传播方式的不同，波可分为机械波和电磁波两大类。

2. 机械波- 定义：机械波是通过介质（如水、空气等）传播的波动现象。

- 特点：机械波必须依赖介质进行传播，传播速度取决于介质的性质。

- 分类：根据粒子振动方向的不同，机械波可分为横波和纵波两种。

- 性质：机械波具有反射、折射、干涉和衍射等特性。

3. 电磁波- 定义：电磁波是通过电场和磁场相互作用而传播的波动现象。

- 特点：电磁波可以在真空中传播，其传播速度为光速。

- 分类：根据波长和频率的不同，电磁波可分为射线、微波、红外线、可见光、紫外线、X射线和γ射线等。

- 性质：电磁波可以反射、折射、干涉和衍射，并具有波粒二象性。

4. 波动方程- 定义：波动方程是描述波动现象的数学表达式。

- 机械波方程：对于一维机械波，波动方程一般表示为∂²u/∂x ² = (1/v²) * ∂²u/∂t²，其中v为波速。

- 电磁波方程：对于电磁波，波动方程一般表示为∇²E - (1/c²) * ∂²E/∂t² = 0，其中c为光速。

5. 波的传播规律- 原理：波的传播遵循赫兹和惠更斯原理。

- 赫兹原理：根据赫兹原理，波会沿着直线传播，且传播方向垂直于波前。

- 惠更斯原理：根据惠更斯原理，波会在达到障碍物或波前边缘时发生衍射，形成新的波前。

根底物理〔II 〕第9、10章测验试题一、单项选择题：〔每题4分，共40分〕1、 一个质点作简谐运动，振幅为A ，在起始时刻质点的位移为2A -，且向x 轴正方向运动，代表此简谐运动的旋转矢量为〔 〕题5-１ 图分析与解：〔b 〕图中旋转矢量的矢端在x 轴上投影点的位移为－A /2，且投影点的运动方向指向O x 轴正向，即其速度的x 分量大于零，故满足题意．因而正确答案为〔B 〕．2、 一简谐运动曲线如下图，那么运动周期是〔 〕〔A 〕 〔B 〕2.40s 〔C 〕 〔D 〕分析与解： 由振动曲线可知，初始时刻质点的位移为2A，且向x 轴正方向运动，其相应的旋转矢量图〔b 〕，由旋转矢量法可知初始相位为3π-。

b振动曲线上给出质点从2A处运动到0=x 处所需时间为1s ，由对应旋转矢量图可知相应的相位差6523πππϕ∆=+=，那么角频率为165-⋅=∆∆=s rad t πϕω，周期s T 40.22==ωπ，应选〔B 〕.3、 两个同周期简谐运动曲线如图〔a 〕所示，x 1的相位比x 2 的相位〔 〕 〔A 〕 落后2π 〔B 〕超前2π 〔C 〕落后π 〔D 〕超前π 分析与解： 由振动曲线图作出相应的旋转矢量图〔b 〕，t=0时x1在x 轴上位移为零；x2的位移为负的最大， 即可得到答案为〔b 〕．4、 两个同振动方向，同频率，振幅均为A 的简谐运动合成后，振幅仍位A ，那么这两个简谐运动的相位差为〔 〕〔A 〕o 60 〔B 〕o 90 〔C 〕o 120 〔D 〕o 180分析与解： 由旋转矢量图可知，只有当两个简谐运动1和2的相位差为o 120时，合成后的简谐运动3的振幅仍为A 。

正确答案是〔C 〕.5、 图〔a 〕表示t ＝0 时的简谐波的波形图，波沿x 轴正方向传播，b图〔b 〕为一质点的振动曲线．那么图〔a 〕中所表示的x ＝0 处振动的初相位与图〔b 〕所表示的振动的初相位分别为〔 〕〔Ａ〕均为零; 〔Ｂ〕 均为2π; 〔Ｃ〕均为2π-; 〔D 〕2π 与2π-; 〔Ｅ〕2π-与2π分析与解： 此题给了两个很相似的曲线图，但本质却完全不同．求解此题要弄清振动图和波形图不同的物理意义．图〔a 〕描述的是连续介质中沿波线上许许多多质点振动在t 时刻的位移状态．其中原点x=0处质点位移为零，其运动方向由图中波形状态和波的传播方向可以知道是沿y 轴负向(它将继承前一个质点的状态)，利用旋转矢量法可以求出该质点振动的初相位为π/2．而图〔b 〕是一个质点的振动曲线图，该质点在t ＝0 时位移为0，t ＞0 时，质点向y 轴正向运动，故由旋转矢量法可判知初相位为－π/2，答案为〔D 〕．6、一横波以速度u 沿x 轴负方向传播，t 时刻波形图如图〔a 〕所示，那么该时刻〔 〕。