2014-2015年七年级下第1周数学题训(1)

2015 年七年级下学期《平面直角坐标系中几何综合题》2015-07一．解答题（共17 小题）1．（ 2015 春?玉环县期中）如图在平面直角坐标系中，A（ a，0），B（b，0），（﹣ 1，2）．且 |2a+b+1|+=0．（1）求 a、b 的值；（2）①在 y 轴的正半轴上存在一点 M ，使 S△COM= S△ABC，求点 M 的坐标．（注明：三角形 ABC 的面积表示为S△ABC）②在坐标轴的其他地址可否存在点M ，使 S△COM= S△ABC仍成立？若存在，请直接写出吻合条件的点M 的坐标．2．（ 2015 春?汕头校级期中）如图，在下面直角坐标系中，已知 A （ 0，a），B（b，0），C（ 3，c）三点，其中a、b、2c 满足关系式：|a﹣ 2|+（ b﹣ 3） +=0．（ 1）求 a、b、 c 的值；（ 2）若是在第二象限内有一点P（ m，），请用含m 的式子表示四边形ABOP 的面积；（3）在（ 2）的条件下，可否存在负整数 m，使四边形 ABOP 的面积不小于△AOP 面积的两倍？若存在，求出所有满足条件的点 P 的坐标，若不存在，请说明原由．3．（ 2015 春 ?鄂城区期中）如图，在平面直角坐标系中，点 A ，B 的坐标分别为 A （ a，0）， B（ b， 0），且 a、 b 满足 a=+﹣1，现同时将点 A ， B 分别向上平移 2 个单位，再向右平移 1 个单位，分别获取点 A ，B 的对应点 C， D，连接 AC ，BD ， CD ．（ 1）求点 C， D 的坐标及四边形ABDC 的面积 S 四边形ABDC．P 的坐标；若不（ 2）在 y 轴上可否存在一点P，连接 PA， PB，使 S△PAB=S 四边形ABDC？若存在这样一点，求出点存在，试说明原由．（ 3）点P 是线段BD 上的一个动点，连接PC， PO，当点P 在BD 上搬动时（不与 B ，D 重合）的值可否发生变化，并说明原由．4．（2014 春?富顺县校级期末）在平面直角坐标系中， A（ a，0），B（ b，0），C（﹣ 1，2）（见图 1），且 |2a+b+1|+ =0 （ 1）求 a、b 的值；（ 2）①在 x 轴的正半轴上存在一点M ，使△COM 的面积 =△ABC的面积，求出点M 的坐标；② 在坐标轴的其他地址可否存在点M ，使△ COM 的面积 = △ ABC 的面积依旧成立？若存在，请直接写出吻合条件的点 M 的坐标；（ 3）如图2，过点 C 作CD⊥y 轴交y 轴于点 D ，点P 为线段CD 延长线上的一动点，连接OP， OE 均分∠ AOP ，OF⊥ OE ．当点P 运动时，的值可否会改变？若不变，求其值；若改变，说明原由．5．（ 2014 春 ?泰兴市校级期末）已知：如图①，直线 MN ⊥直线 PQ，垂足为 O，点 A 在射线 OP 上，点 B 在射线 OQ 上（ A、 B 不与 O 点重合），点 C 在射线 ON 上且 OC=2，过点 C 作直线 l∥ PQ，点 D 在点 C 的左边且 CD=3 ．（1）直接写出△ BCD 的面积．（2）如图②，若 AC ⊥BC ，作∠ CBA 的均分线交 OC 于 E，交 AC 于 F，求证：∠ CEF= ∠ CFE．（3）如图③，若∠ ADC= ∠ DAC ，点 B 在射线 OQ 上运动，∠ ACB 的均分线交 DA 的延长线于点 H ，在点 B 运动过程中的值可否变化？若不变，求出其值；若变化，求出变化范围．26．（ 2014 春 ?江岸区期末）如图 1，在平面直角坐标系中， A （ a ，0）， B （ b ， 3），C （ 4， 0），且满足（ a+b ） +|a﹣ b+6|=0 ，线段 AB 交 y 轴于 F点．（ 1）求点 A 、 B 的坐标．（ 2）点 D 为 y 轴正半轴上一点，若 ED ∥ AB ，且 AM ，DM 分别均分∠ CAB ，∠ ODE ，如图 2，求∠ AMD 的度数．（ 3）如图 3，（也可以利用图 1）① 求点 F 的坐标； ② 点 P 为坐标轴上一点，若△ABP的三角形和 △ABC 的面积相等？若存在，求出 P 点坐标．7．（ 2014 春?黄陂区期末） 在直角坐标系中，已知点 A 、B 的坐标是（ a ，0）（ b ，0），a ，b 满足方程组，c 为 y 轴正半轴上一点，且S △ ABC =6 ．（ 1）求 A 、 B 、 C 三点的坐标；（ 2）可否存在点 P （ t ， t ），使 S △PAB =S △ABC ？若存在，央求出P 点坐标；若不存在，请说明原由；（ 3）若 M 是 AC 的中点，N 是 BC 上一点，CN=2BN ，连 AN 、BM 订交于点 D ，求四边形 CMDN 的面积是．8．（ 2014 春 ?海珠区期末）在平面直角坐标系中，点 A （ a ， b ）是第四象限内一点， AB ⊥ y 轴于 B ，且 B （0， b ）是 y 轴负半轴上一点， b 2=16 ， S △AOB =12．（ 1）求点 A 和点 B 的坐标；（ 2）如图 1，点 D 为线段 OA （端点除外）上某一点，过点∠ AFD 的均分线订交于N ，求∠ 的度数．D 作AO垂线交x 轴于E，交直线AB 于F，∠EOD、（ 3）如图E，交直线2，点AB 于D 为线段 OA（端点除外）上某一点，当点F，∠ EOD，∠ AFD 的均分线订交于点D 在线段上运动时，过点 D 作直线 EF 交 xN．若记∠ ODF= α，请用α的式子表示∠ONF轴正半轴于的大小，并说明原由．9．（ 2014 春 ?黄梅县校级期中）如图，在下面的直角坐标系中，已知 A （ 0， a），B（ b， 0）， C（ b， 4）三点，其中a，b 满足关系式．（ 1）求a，b 的值；（ 2）若是在第二象限内有一点P（ m，），请用含m 的式子表示四边形ABOP 的面积；（ 3）在（ 2）的条件下，可否存在点若不存在，请说明原由．P，使四边形ABOP 的面积与△ ABC 的面积相等？若存在，求出点P 的坐标；10．（ 2014 春 ?通州区校级期中）在如图直角坐标系中，已知 A （ 0， a）， B（ b，0）， C（ b， c）三点，其中a、 b、 c满足关系式2 2+（ b﹣ 3） =0 ，（ c﹣ 4）≤0．（1）求 a、b、 c 的值；（2）若是点 P（ m， n）在第二象限，四边形 CBOP 的面积为 y，请你用含 m， n 的式子表示 y；（ 3）若是点P 在第二象限坐标轴的夹角均分线上，并且y=2S 四边形CBOA，求 P 点的坐标．11．（2014 春 ?鄂州校级期中）如图，A 、B 两点坐标分别为2=0，A（a，4），B（ b，0），且 a，b 满足（ a﹣2b+8） +E 是 y 轴正半轴上一点．（1）求 A 、 B 两点坐标；（2）若 C 为 y 轴上一点且 S△AOC= S△AOB，求 C 点的坐标；（ 3）过 B 作 BD ∥ y 轴，∠ DBF=∠DBA，∠ EOF=∠ EOA，求∠ F与∠ A间的数量关系．12．（ 2014 春 ?东湖区期中）如图，平面直角坐标系中 A （﹣ 1，0）， B（ 3， 0），现同时将 A 、B 分别向上平移 2 个单位，再向右平移 1 个单位，分别获取 A 、 B 的对应点C、D ，连接 AC 、BD（ 1）直接写出C、D 的坐标： C D及四边形ABCD 的面积：（ 2）在 y 轴负半轴上可否存在点 M ，连接 MA 、 MB 使得 S△MAB＞ S 四边形ABCD？若存在，求出 M 点纵坐标的取值范围；若不存在说明原由（ 3）点 P 为线段 BD 上一动点，连PC、PO，当点 P 在 BD 上搬动（不含端点）现给出①的值不变，②的值不变，其中有且只有一个正确，请你找出这个结论并求其值．13．（ 2014 春 ?台州月考）如图，在平面直角坐标系中，点 A ， B 的坐标分别为 A （ 0，α）， B（ b，α），且α、 b 满22 个单位，再向左平移 1 个单位，分别获取点 A ，B 的对应足（ a﹣ 2） +|b﹣ 4|=0，现同时将点 A ，B 分别向下平移点 C，D ，连接 AC ， BD ，AB ．（ 1）求点 C， D 的坐标及四边形ABDC 的面积 S 四边形ABCD（2）在 y 轴上可否存在一点 M ，连接 MC ， MD ，使 S△MCD =S 不存在，试说明原由．（3）点 P 是线段 BD 上的一个动点，连接 PA， PO，当点 P 在四边形ABDC？若存在这样一点，求出点M 的坐标，若BD 上搬动时（不与B， D 重合）的值可否发生变化，并说明原由．14．（ 2014 春 ?海安县月考）如图，在平面直角坐标系中，点 A ，B ，C 的坐标分别为（﹣1， 0），（ 3， 0），（ 0， 2），图中的线段 BD 是由线段 AC 平移获取．（ 1）线段 AC 经过怎样的平移可获取线段BD ，所得四边形是什么图形，并求出所得的四边形ABDC 的面积 S 四边形ABDC；（ 2）在 y 轴上可否存在点 P，连接 PA， PB，使 S =S 四边形ABDC？若存在，求出点P 的坐标；若不存在，试说△ PAB明原由；（ 3）点 P 是线段 BD 上的一个动点，连接PC、 PO，当点 P 在 BD 上搬动时（不与 B ，D 重合）给出以下结论：①的值不变；②的值不变，其中有且只有一个是正确的，请你找出这个结论并求其值．15．（ 2014 春 ?武汉月考）已知，在平面直角坐标系中，2；点 A（0，m），点 B（ n，0），m、n 满足（ m﹣ 3） =﹣（ 1）求 A 、 B 的坐标；（ 2）如图1， E 为第二象限内直线 AB 上一点，且满足S△AOE= S△AOB，求 E 的坐标．（ 3）如图 2，平移线段 BA 至 OC，B 与 O 是对应点， A 与 C 对应，连 AC ．E 为 BA 的延长线上一动点，连 EO．OF均分∠ COE，AF 均分∠ EAC ，OF 交 AF 于 F 点．若∠ ABO+ ∠ OEB= α，请在图 2 中将图形补充完满，并求∠F（用含α的式子表示）．16．（ 2013 秋 ?江岸区校级月考）如图，已知点 A （﹣ m， n）， B（ 0， m），且 m、 n 满足2+（ n﹣5） =0，点 C在 y 轴上，将△ ABC 沿 y 轴折叠，使点 A 落在点 D 处．（1）写出 D 点坐标并求 A 、 D 两点间的距离；（2）若 EF 均分∠ AED ，若∠ ACF ﹣∠ AEF=20 °，求∠ EFB 的度数；（3）过点 C 作 QH 平行于 AB 交 x 轴于点 H，点 Q 在 HC 的延长线上， AB 交 x 轴于点 R，CP、RP 分别均分∠ BCQ和∠ ARX ，当点 C 在 y 轴上运动时，∠CPR 的度数可否发生变化？若不变，求其度数；若变化，求其变化范围．17．（ 2013 春 ?武汉校级月考）如图，在平面直角坐标系中，点 A ， B 的坐标分别为 A （﹣ 1， 0）、 B（ 3， 0）．现同时将点 A ， B 分别向上平移 2 个单位，再向右平移 1 个单位，分别获取点 A ， B 的对应点C、 D，连接 AC ， BD ．（ 1）直接写出点C、 D 的坐标，求四边形ABDC 的面积S 四边形ABDC；（ 2）在坐标轴上可否存在一点P，使S△PAC=S 四边形ABDC？若存在这样一点，求出点P 的坐标；若不存在，试说明原由．（ 3）如图 3，在线段 CO 上取一点 G，使 OG=3CG ，在线段 OB 上取一点 F，使 OF=2BF ， CF 与 BG 交于点 H，求四边形OGHF 的面积 S 四边形OGHF．。

一、选择题1．已知{}min ,,a b c 表示取三个数中最小的那个数．例如：当2x =-时，()(){}23min 2,2,28---=-，当{}21min ,,16x x x =时，则x 的值为（ ） A ．116 B ．18C ．14D ．122．如示意图，小宇利用两个面积为1 dm 2的正方形拼成了一个面积为2 dm 2的大正方形，并通过测量大正方形的边长感受了2dm 的大小． 为了感知更多无理数的大小，小宇利用类似拼正方形的方法进行了很多尝试，下列做法不能实现的是（ ）A ．利用两个边长为2dm 8的大小B ．利用四个直角边为3dm 18的大小C 2的正方形以及一个直角边为2dm 6dm 的大小D ．利用四个直角边分别为1 dm 和3 dm 的直角三角形以及一个边长为2 dm 的正方形感知10的大小3．已知T 122119311242++，T 22211497123366++，T 32211134++21313()1212，⋯，T 22111(1)n n +++n 为正整数．设S n =T 1+T 2+T 3+⋯+T n ，则S 2021值是（ ） A ．202120212022B ．202120222022C ．120212021D ．1202220214．以下11个命题：①负数没有平方根；②内错角相等；③同旁内角互补，两直线平行；④一个正数有两个立方根，它们互为相反数；⑤无限不循环小数是无理数；⑥数轴上的点与实数有一一对应关系；⑦过一点有且只有一条直线和已知直线垂直；⑧不相交的两条直线叫做平行线；⑨从直线外一点到这条直线的垂线段，叫做这点到直线的距离．⑩开方开不尽的数是无理数；⑪相等的两个角是对顶角；其中真命题的个数为（ ） A ．5B ．6C ．7D ．85．若225a =，3b =，则a b +所有可能的值为（ ） A ．8B ．8或2C ．8或2-D ．8±或2±6．下列说法：①所有无理数都能用数轴上的点表示；②若一个数的平方根等于它本身，则这个数是0或1；③任何实数都有立方根；164±，其中正确的个数有（ ） A ．0个B ．1个C ．2个D ．3个7．a ，小数部分为b ，则a-b 的值为（） A．6B6C．8D88．下列说法中：①0是最小的整数；②有理数不是正数就是负数；③﹣2π不仅是有理数，而且是分数；④237是无限不循环小数，所以不是有理数；⑤无限小数不一定都是有理数；⑥正数中没有最小的数，负数中没有最大的数；⑦非负数就是正数；⑧正整数、负整数、正分数、负分数统称为有理数；其中错误的说法的个数为（ ） A ．7个 B ．6个 C ．5个 D ．4个 9．设n 为正整数，且nn+1，则n 的值为（ ） A ．5B ．6C ．7D ．810．有一个数阵排列如下：1 2 4 7 11 16 22 3 5 8 12 17 23 6 9 13 18 24 10 14 19 2515 20 2621 2728则第20行从左至右第10个数为（ ） A ．425B ．426C ．427D ．428二、填空题11．在数轴上，点M ，N 分别表示数m ，n ，则点M ，N 之间的距离为|m ﹣n |． （1）若数轴上的点M ，N 分别对应的数为2M ，N 间的距离为 ___，MN 中点表示的数是 ___．（2）已知点A ，B ，C ，D 在数轴上分别表示数a ，b ，c ，d ，且|a ﹣c |＝|b ﹣c |＝23|d ﹣a |＝1（a ≠b ），则线段BD 的长度为 ___．12．对于任意有理数a ，b ，规定一种新的运算a ⊙b ＝a （a +b ）﹣1，例如，2⊙5＝2×（2+5）﹣1＝13．则（﹣2）⊙6的值为_____ 13．若|x |＝3，y 2＝4，且x ＞y ，则x ﹣y ＝_____．14．某校数学课外小组利用数轴为学校门口的一条马路设计植树方案如下：第k 棵树种植在点k x 处，其中11x =，当2k ≥时，112()()55k k k k x x T T ---=+-，()T a 表示非负实数a 的整数部分，例如(26)2T .=，(02)0T .=. 按此方案，第6棵树种植点6x 为________；第2011棵树种植点2011x ________.15．对于正整数n ，定义2,10()(),10n n F n f n n ⎧<=⎨≥⎩其中()f n 表示n 的首位数字､末位数字的平方和．例如：2(6)636F ==，2(123)(123)1F f ==2310+=．规定1()()F n F n =，()1()()k k F n F F n +=．例如：1(123)(123)10F F ==，()21(123)(123)F F F =(10)1F ==．按此定义2021(4)F =_____．16．我们可以用符号f (a )表示代数式．当a 是正整数时，我们规定如果a 为偶数，f (a )＝0.5a ；如果a 为奇数，f (a )＝5a +1．例如：f (20)＝10，f (5)＝26．设a 1＝6，a 2＝f (a 1)，a 3＝f (a 2)…；依此规律进行下去，得到一列数：a 1，a 2，a 3，a 4…(n 为正整数)，则2a 1﹣a 2+a 3﹣a 4+a 5﹣a 6+…+a 2013﹣a 2014+a 2015＝_____．17．定义一种新运算a b ※，其规则是：当a b >时，2a b a b =-※，当a b =时，a b a b =+※，当a b <时，2a b b a =-※，若()21x -=※，则x =____________． 18．定义：如果将一个正整数a 写在每一个正整数的右边，所得到的新的正整数能被a 整除，则这个正整数a 称为“魔术数”．例如：将2写在1的右边得到12，写在2的右边得到22，……，所得到的新的正整数的个位数字均为2，即为偶数，由于偶数能被2整除，所以2是“魔术数”．根据定义，在正整数3，4，5中，“魔术数”为____________；若“魔术数”是一个两位数，我们可设这个两位数的“魔术数”为x ，将这个数写在正整数n 的右边，得到的新的正整数可表示为()100n x +，请你找出所有的两位数中的“魔术数”是_____________． 19．材料：一般地，n 个相同因数a 相乘：n a a a a a⋅⋅⋅⋅⋅个记为n a ．如328=，此时3叫做以2为底的8的对数，记为2log 8（即2log 83=）．那么3log 9=_____，()2231log 16log 813+=_____． 20．若[)x 表示大于x 的最小整数，如[)56=，[)1.81-=-，则下列结论中正确的有______（填写所有正确结论的序号）．①[)01=；②33055⎡⎫-=⎪⎢⎣⎭；③[)0x x -<；④[)1x x x <≤+；⑤存在有理数x 使[)0.2x x -=成立．三、解答题21．阅读下列解题过程：为了求23501222...2+++++的值，可设23501222...2S =+++++，则2345122222...2S =+++++，所以得51221S S -=-，所以5123505121:1222...221S =-+++++=-，即； 仿照以上方法计算：（1）2320191222...2+++++= . （2）计算：2320191333...3+++++ （3）计算：101102103200555...5++++22．如果有一列数，从这列数的第2个数开始，每一个数与它的前一个数的比等于同一个非零的常数，这样的一列数就叫做等比数列（Geometric Sequences ）．这个常数叫做等比数列的公比，通常用字母q 表示（q ≠0）．（1）观察一个等比列数1，1111,,,24816，…，它的公比q ＝ ；如果a n （n 为正整数）表示这个等比数列的第n 项，那么a 18＝ ，a n ＝ ； （2）如果欲求1+2+4+8+16+…+230的值，可以按照如下步骤进行：令S＝1+2+4+8+16+…+230…①等式两边同时乘以2，得2S＝2+4+8+16++32+…+231…②由② ﹣①式，得2S﹣S＝231﹣1即（2﹣1）S＝231﹣1所以3131212121S-==--请根据以上的解答过程，求3+32+33+…+323的值；（3）用由特殊到一般的方法探索：若数列a1，a2，a3，…，a n，从第二项开始每一项与前一项之比的常数为q，请用含a1，q，n的代数式表示a n；如果这个常数q≠1，请用含a1，q，n的代数式表示a1+a2+a3+…+a n．23．据说，我国著名数学家华罗庚在一次访问途中，看到飞机邻座的乘客阅读的杂志上有一道智力题：一个数32768，它是一个正数的立方，希望求它的立方根，华罗庚不假思索给出了答案，邻座乘客非常惊奇，很想得知其中的奥秘，你知道华罗庚是怎样准确计算出的吗？请按照下面的问题试一试：（1）由33101000,1001000000==，因为1000327681000000<<______位数；（2）由32768的个位上的数是8________，划去32768后面的三位数768得到32，因为333=27,4=64_____________(3)已知13824和110592-分别是两个数的立方，仿照上面的计算过程，请计算：________=24．（概念学习）规定：求若干个相同的有理数（均不等于0）的除法运算叫做除方，如2÷2÷2，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）等．类比有理数的乘方，我们把2÷2÷2记作2③，读作“2的圈3次方”，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）记作（﹣3）④，读作“﹣3的圈4次方”，一般地，把n个a（a≠0）记作aⓝ，读作“a的圈n次方”．（初步探究）（1）直接写出计算结果：2③＝，（﹣12）⑤＝；（深入思考）我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘方运算呢？（1）试一试：仿照上面的算式，将下列运算结果直接写成乘方的形式．（﹣3）④＝；5⑥＝；（﹣12）⑩＝．（2）想一想：将一个非零有理数a的圈n次方写成乘方的形式等于；25．阅读材料：求1+2+22+23+24+…+22017的值．解：设S=1+2+22+23+24+ (22017)将等式两边同时乘以2得：2S=2+22+23+24+…+22017+22018将下式减去上式得2S-S=22018-1即S=22018-1 即1+2+22+23+24+…+22017=22018-1 请你仿照此法计算： (1)1+2+22+23+…+29=_____；(2)1+5+52+53+54+…+5n (其中n 为正整数)； (3)1+2×2+3×22+4×23+…+9×28+10×29． 26．a 是不为1的有理数，我们把11a-称为a 的差倒数．如:2的差倒数是1112=--，现已知a 1=12，a 2是a 1的差倒数，a 3是a 2的差倒数，a 4是a 3的差倒数，… (1)求a 2，a 3，a 4的值；(2)根据(1)的计算结果，请猜想并写出a 2016•a 2017•a 2018的值； (3)计算：a 33+a 66+a 99+…+a 9999的值．27．我们知道，任意一个正整数x 都可以进行这样的分解：x m n =⨯（m ，n 是正整数，且m n ≤），在x 的所有这种分解中，如果m ，n 两因数之差的绝对值最小，我们就称m n ⨯是x 的最佳分解，并规定：()=nf x m．例如：18可分解成118⨯，29⨯或36⨯，因为1819263->->-，所以36⨯是18的最佳分解，所以()311862f == （1）填空：()6f = ；()16=f ；（2）一个两位正整数t （10t a b =+，19a b ≤≤≤，a ，b 为正整数），交换其个位上的数字与十位上的数字得到的新数减去原数所得的差为54，求出所有的两位正整数；并求()f t 的最大值； （3）填空：①()22357f ⨯⨯⨯= ；②()42357f ⨯⨯⨯= ；28．对于有理数a 、b ，定义了一种新运算“※”为：()()223a b a b a b a b a b ⎧-≥⎪=⎨-<⎪⎩※如：532537=⨯-=※，2131313=-⨯=-※． （1）计算：①()21-=※______；②()()43--=※______；（2）若313m x =-+※是关于x 的一元一次方程，且方程的解为2x =，求m 的值； （3）若3241A x x x =-+-+，3262B x x x =-+-+，且3A B =-※，求322x x +的值． 29．先阅读下面的材料，再解答后面的各题：现代社会会保密要求越来越高，密码正在成为人们生活的一部分，有一种密码的明文（真实文）按计算机键盘字母排列分解，其中,,,,,Q W E N M 这26个字母依次对应1,2,3,,25,26这26个自然数（见下表）．给出一个变换公式：(126,3)3217(126,31)318(126,32)3J J J xx x x x x x x x x x x x x x ⎧=≤≤⎪⎪+⎪=+≤≤⎨⎪+⎪=+≤≤⎪⎩是自然数，被整除是自然数，被除余是自然数，被除余 将明文转成密文，如4+24+17=193⇒，即R 变为L ：11+111+8=123⇒，即A 变为S ．将密文转成成明文，如213(2117)210⇒⨯--=，即X 变为P ：133(138)114⇒⨯--=，即D 变为F ．（1）按上述方法将明文NET 译为密文．（2）若按上方法将明文译成的密文为DWN ，请找出它的明文．30．如果有一列数，从这列数的第2个数开始，每一个数与它的前一个数的比等于同一个非零的常数，这样的一列数就叫做等比数列（Geometric Sequences ）．这个常数叫做等比数列的公比，通常用字母q 表示（q ≠0）．（1）观察一个等比列数1，1111,,,24816，…，它的公比q ＝ ；如果a n （n 为正整数）表示这个等比数列的第n 项，那么a 18＝ ，a n ＝ ； （2）如果欲求1+2+4+8+16+…+230的值，可以按照如下步骤进行： 令S ＝1+2+4+8+16+…+230…①等式两边同时乘以2，得2S ＝2+4+8+16++32+…+231…② 由② ﹣ ①式，得2S ﹣S ＝231﹣1 即（2﹣1）S ＝231﹣1 所以 3131212121S -==-- 请根据以上的解答过程，求3+32+33+…+323的值；（3）用由特殊到一般的方法探索：若数列a 1，a 2，a 3，…，a n ，从第二项开始每一项与前一项之比的常数为q ，请用含a 1，q ，n 的代数式表示a n ；如果这个常数q ≠1，请用含a 1，q ，n 的代数式表示a 1+a 2+a 3+…+a n ．【参考答案】***试卷处理标记，请不要删除一、选择题1．C 解析：C 【分析】2111161616x x ===，，的x 值，找到满足条件的x 值即可． 【详解】116=时，1256x =，x <当2116x =时，14x =±，当14x =-时，2x x <，不合题意；当14x =12=，2x x << 当116x =时，21256x =，2x x <，不合题意， 故选：C ． 【点睛】本题主要考查了实数大小比较，算术平方根及其最值问题，解决此题时，注意分类思想的运用．2．C解析：C 【分析】在拼图的过程中，拼前，拼后的面积相等，所以我们只需要分别计算拼前，拼后的面积，看是否相等，就可以逐一排除． 【详解】A ：222=8⨯，2=8，不符合题意；B ：4×(3×3÷2)=18，2=18，不符合题意；C ：22224+⨯÷=，26=，符合题意；D ：24(132)210⨯⨯÷+=，210=，不符合题意． 故选：C ． 【点睛】本题考查了利用二次根式计算面积，解题的关键是在拼图的过程中，拼前，拼后的面积相等．3．A解析：A 【分析】根据数字间的规律探索列式计算 【详解】解：由题意可得：T 1312+1=212⨯⨯，T 2723+1=623⨯⨯，T 31334+1=1234⨯⨯∴T ()()1+11n n n n ++ ∴T 2021=20212022+120212022⨯⨯∴S 2021=T 1+T 2+T 3+⋯+T 2021=371320212022+1+++...261220212022⨯+⨯ =11111++1++1++...1+261220212022+⨯=11112021++++ (261220212022)=11112021++++...+12233420212022⨯⨯⨯⨯ =11111112021+1++...+2233420212022⎛⎫-+--- ⎪⎝⎭ =12021+12022⎛⎫- ⎪⎝⎭=202120212022故选：A ． 【点睛】本题考查实数数字类的规律探索，探索规律，准确计算是解题关键．4．A解析：A 【分析】根据相关知识逐项判断即可求解． 【详解】解：①“负数没有平方根”，是真命题②“内错角相等”，缺少两直线平行这一条件，是假命题；③“同旁内角互补，两直线平行”，是真命题；④“一个正数有两个立方根，它们互为相反数”，一个正数有一个立方根，是假命题；⑤“无限不循环小数是无理数”，是真命题；⑥“数轴上的点与实数有一一对应关系”，是真命题；⑦“过一点有且只有一条直线和已知直线垂直”，缺少在同一平面内条件，是假命题；⑧“不相交的两条直线叫做平行线”，缺少在同一平面内条件，是假命题；⑨“从直线外一点到这条直线的垂线段，叫做这点到直线的距离”，应为“从直线外一点到这条直线的垂线段的长度，叫做这点到直线的距离”，是假命题．⑩“开方开不尽的数是无理数”，是真命题；⑪“相等的两个角是对顶角”，相等的角有可能是对顶角，但不一定是对顶角，是假命题． 所以真命题有5个．故选：A 【点睛】本题考查判断真假命题、平方根、立方根、平行线的判定、无理数、实数与数轴关系、直线外一点到直线的距离、对顶角等知识，综合性较强，熟知相关知识点是解题关键．5．D解析：D 【分析】先求出a 、b 的值，再计算即可． 【详解】 解：∵225a =， ∴a =±5， ∵3b =， ∴b =±3，当a =5，b =3时，8a b +=； 当a =5，b =-3时，2a b +=； 当a =-5，b =3时，2a b +=-； 当a =-5，b =-3时，8a b +=-； 故选：D ． 【点睛】本题考查了绝对值、平方根和有理数加法运算，解题关键是分类讨论，准确计算．6．C解析：C 【分析】分别根据相关的知识点对四个选项进行判断即可． 【详解】解：①所有无理数都能用数轴上的点表示，故①正确； ②若一个数的平方根等于它本身，则这个数是0，故②错误； ③任何实数都有立方根，③说法正确；2±，故④说法错误； 故其中正确的个数有：2个． 故选：C ． 【点睛】本题考查的是实数，需要注意掌握实数的概念、平方根以及立方根的相关知识点．7．A解析：A 【分析】先根据无理数的估算求出a 、b 的值，由此即可得． 【详解】91516<<，<34<<，3,3a b ∴==，)336a b ∴-=-=故选：A ． 【点睛】本题考查了无理数的估算，熟练掌握估算方法是解题关键．8．B解析：B 【分析】根据有理数的分类依此作出判断，即可得出答案． 【详解】解：①没有最小的整数，所以原说法错误； ②有理数包括正数、0和负数，所以原说法错误； ③﹣2π是无理数，所以原说法错误； ④237是无限循环小数，是分数，所以是有理数，所以原说法错误； ⑤无限小数不都是有理数，所以原说法正确；⑥正数中没有最小的数，负数中没有最大的数，所以原说法正确； ⑦非负数就是正数和0，所以原说法错误；⑧正整数、负整数、正分数、负分数和0统称为有理数，所以原说法错误； 故其中错误的说法的个数为6个． 故选：B ． 【点睛】本题考查了有理数的分类，认真掌握正数、负数、整数、分数、正有理数、负有理数、非负数的定义与特点是解题的关键．注意整数和正数的区别，注意0是整数，但不是正数．9．D解析：D 【分析】n 的值． 【详解】解：∵∴89，∵n n+1，∴n=8， 故选；D ． 【点睛】10．B解析：B【解析】试题解析：寻找每行数之间的关系，抓住每行之间的公差成等差数列，便知第20行第一个数为210，而每行的公差为等差数列，则第20行第10个数为426，故选B.二、填空题11．2【分析】（1）直接根据定义，代入数字求解即可得到两点间的距离；根据两点之间的距离得出其一半的长度，然后结合其中一个端点表示的数求解即可得中点表示的数；（2）先根据|a ﹣c|＝|b ﹣c|与a≠解析：2【分析】（1）直接根据定义，代入数字求解即可得到两点间的距离；根据两点之间的距离得出其一半的长度，然后结合其中一个端点表示的数求解即可得中点表示的数；（2）先根据|a ﹣c |＝|b ﹣c |与a ≠b 推出C 为AB 的中点，然后根据题意分类讨论求解即可．【详解】解：（1）由题意，M ，N 间的距离为(222==；∵2MN =， ∴112MN =， 由题意知，在数轴上，M 点在N 点右侧，∴MN 的中点表示的数为1；（2）∵1a c b c -=-=且a b ，∴数轴上点A 、B 与点C 不重合，且到点C 的距离相等，都为1，∴点C 为AB 的中点，2AB =， ∵213d a -=， ∴32d a -=， 即：数轴上点A 和点D 的距离为32，讨论如下：1>若点A位于点B左边：①若点D在点A左边，如图所示：此时，37222 BD AD AB=+=+=；②若点D在点A右边，如图所示：此时，31222 BD AB AD=-=-=；2>若点A位于点B右边：①若点D在点A左边，如图所示：此时，31222 BD AB AD=-=-=；②若点D在点A右边，如图所示：此时，37222 BD AD AB=+=+=；综上，线段BD的长度为12或72，故答案为：2；21；12或72．【点睛】本题考查数轴上两点间的距离，以及与线段中点相关的计算问题，理解数轴上点的特征以及两点间的距离表示方法，灵活根据题意分类讨论是解题关键．12．-9【分析】直接利用已知运算法则计算得出答案．【详解】（﹣2）⊙6＝﹣2×（﹣2+6）﹣1＝﹣2×4﹣1＝﹣8﹣1＝﹣9．故答案为﹣9．【点睛】此题考察新定义形式的有理数计算，解析：-9【分析】直接利用已知运算法则计算得出答案．【详解】（﹣2）⊙6＝﹣2×（﹣2+6）﹣1＝﹣2×4﹣1＝﹣8﹣1＝﹣9．故答案为﹣9．【点睛】此题考察新定义形式的有理数计算，正确理解题意是解题的关键，依据题意正确列代数式计算即可.13．1或5．【分析】根据题意，利用绝对值的代数意义及平方根定义求出x与y的值，代入原式计算即可得到结果．【详解】解：根据题意得：x＝3，y＝2或x＝3，y＝﹣2，则x﹣y＝1或5．故答案为1解析：1或5．【分析】根据题意，利用绝对值的代数意义及平方根定义求出x与y的值，代入原式计算即可得到结果．【详解】解：根据题意得：x＝3，y＝2或x＝3，y＝﹣2，则x﹣y＝1或5．故答案为1或5．【点睛】此题考查了代数式求值，熟练掌握运算法则是解本题的关键．14．403【解析】当k=6时，x6=T（1）+1=1+1=2，当k=2011时,=T()+1=403.故答案是:2,403.【点睛】本题考查了坐标确定位置，读懂题目信息，理解xk 的表达 解析：403【解析】当k=6时，x 6=T （1）+1=1+1=2，当k=2011时,2011 x =T(20105)+1=403. 故答案是:2,403.【点睛】本题考查了坐标确定位置，读懂题目信息，理解xk 的表达式并写出用T 表示出的表达式是解题的关键．15．145【分析】根据题意分别求出F1（4）到F8（4），通过计算发现，F1（4）=F8（4），然后根据所得的规律即可求解．【详解】解：F1（4）=16，F2（4）=F （16）=37，F3（4解析：145【分析】根据题意分别求出F 1（4）到F 8（4），通过计算发现，F 1（4）=F 8（4），然后根据所得的规律即可求解．【详解】解：F 1（4）=16，F 2（4）=F （16）=37，F 3（4）=F （37）=58，F 4（4）=F （58）=89，F 5（4）=F （89）=145，F 6（4）=F （145）=26，F 7（4）=F （26）=40，F 8（4）=F （40）=16，……通过计算发现，F 1（4）=F 8（4），∴202172885÷=， ∴20215(4)(4)145F F ==；故答案为：145．【点睛】本题考查了有理数的乘方，新定义运算，能准确理解定义，多计算一些数字，进而确定循环规律是解题关键． 16．7【分析】本题可以根据代数式f （a ）的运算求出a1，a2，a3，a4，a5，a6 ，a7的值，根据规律找出部分an 的值，进而发现数列每7个数一循环，根据数的变化找出变化规律，依照规律即可得出结论解析：7【分析】本题可以根据代数式f （a ）的运算求出a 1，a 2，a 3，a 4，a 5，a 6 ，a 7的值，根据规律找出部分a n 的值，进而发现数列每7个数一循环，根据数的变化找出变化规律，依照规律即可得出结论．【详解】解：观察，发现规律：a 1=6，a 2=f （a 1）=3，a 3=f （a 2）=16，a 4=f （a 3）=8，a 5=f （a 4）=4，a 6=f （a 5）=2，a 7=f （a 6）=1，a 8=f （a 7）=6，…，∴数列a 1，a 2，a 3，a 4…（n 为正整数）每7个数一循环，∴a 1-a 2+a 3-a 4+…+a 13-a 14=0，∵2015=2016-1=144×14-1，∴2a 1-a 2+a 3-a 4+a 5-a 6+…+a 2013-a 2014+a 2015=a 1+a 2016+（a 1-a 2+a 3-a 4+a 5-a 6+…+a 2015-a 2016）=a 1+a 7=6+1=7．故答案为7．【点睛】本题考查了规律型中的数字的变化类以及代数式求值，解题的关键是根据数的变化找出变换规律，并且巧妙的借助了a 1-a 2+a 3-a 4+…+a 13-a 14=0来解决问题．17．或﹣5【分析】根据新定义运算法则，分情况讨论求解即可．【详解】解：当x ＞﹣2时，则有，解得：，成立；当x=﹣2时，则有，解得：x=3，矛盾，舍去；当x ＜﹣2时，则有，解得：x=﹣5，成立 解析：12-或﹣5 【分析】根据新定义运算法则，分情况讨论求解即可．【详解】解：当x ＞﹣2时，则有()22(2)1x x -=--=※，解得：12x =-，成立；当x =﹣2时，则有()2(2)1x x -=+-=※，解得：x =3，矛盾，舍去；当x ＜﹣2时，则有()22(2)1x x -=⨯--=※，解得：x =﹣5，成立，综上，x =12-或﹣5， 故答案为：12-或﹣5． 【点睛】本题考查新定义下的实数运算、解一元一次方程，理解新定义运算法则，运用分类讨论思想正确列出方程是解答的关键．18．10、20、25、50．【分析】①由“魔术数”的定义，分别对3、4、5三个数进行判断，即可得到5为“魔术数”；②由题意，根据“魔术数”的定义通过分析，即可得到答案．【详解】解：根据解析：10、20、25、50．【分析】①由“魔术数”的定义，分别对3、4、5三个数进行判断，即可得到5为“魔术数”； ②由题意，根据“魔术数”的定义通过分析，即可得到答案．【详解】解：根据题意，①把3写在1的右边，得13，由于13不能被3整除，故3不是魔术数；把4写在1的右边，得14，由于14不能被4整除，故4不是魔术数；把5写在1的右边，得15，写在2的右边得25，……由于个位上是5的数都能被5整除，故5是魔术数；故答案为：5；②根据题意，这个两位数的“魔术数”为x ，则1001001n x n x x+=+， ∴100n x为整数， ∵n 为整数， ∴100x为整数， ∴x 的可能值为：10、20、25、50； 故答案为：10、20、25、50．【点睛】本题考查了新定义的应用和整数的特点，解题的关键是熟练掌握新定义进行解题． 19．3； ．【分析】由可求出，由，可分别求出，，继而可计算出结果．【详解】解：（1）由题意可知：，则，（2）由题意可知：，，则，，∴，故答案为：3；．【点睛】本题主解析：3； 1173． 【分析】由239=可求出2log 93=，由4216=，43=81可分别求出2log 164=，3log 814=，继而可计算出结果．【详解】解：（1）由题意可知：239=，则2log 93=，（2）由题意可知：4216=，43=81，则2log 164=，3log 814=， ∴223141(log 16)log 811617333+=+=， 故答案为：3；1173． 【点睛】本题主要考查定义新运算，读懂题意，掌握运算方法是解题关键．20．①④⑤【分析】根据题意表示大于x 的最小整数，结合各项进行判断即可得出答案．【详解】解：①，根据表示大于x 的最小整数，故正确；②，应该等于，故错误；③，当x=0.5时，，故错误；④，根据解析：①④⑤【分析】根据题意[)x 表示大于x 的最小整数，结合各项进行判断即可得出答案．【详解】解：①[)01=，根据[)x 表示大于x 的最小整数，故正确；②33055⎡⎫-=⎪⎢⎣⎭，应该等于333215555⎡⎫-=-=⎪⎢⎣⎭，故错误； ③[)0x x -<，当x=0.5时，[)10.5=0.50x x -=-＞，故错误；④[)1x x x <≤+，根据定义可知[)x x <，但[)x 不会超过x+1，所以[)1x x x <≤+成立，故正确；⑤当x=0.8时，[)1-0.8=0.2x x -=，故正确．故答案为：①④⑤．【点睛】本题主要考查了对题意的理解，准确的理解题意是解决本题的关键．三、解答题21．（1）202021-；（2）2020312-；（3）201101554-. 【分析】仿照阅读材料中的方法求出所求即可．【详解】解：（1）根据2350511222...221+++++=-得：2320191222...2+++++=202021-（2）设2320191333...3S =+++++，则234202033333...3S =+++++，∴2020331S S -=-， ∴2020312S -= 即：2020232019311333 (32)-+++++= （3）设232001555...5S =+++++，则23420155555...5S =+++++，∴201551S S -=-， ∴201514S -= 即：20123200511555 (5)4-+++++= 同理可求⸫10123100511555 (54)-+++++= ∵1011021032002320023100555...51555...5)(1555...5)++++=+++++-+++++（ 201101201101101102103200515155555 (5444)---∴++++=-= 【点睛】此题考查了规律型：数字的变化类，弄清题中的规律是解本题的关键．22．（1）12，1712，n-112；（2）24332-；（3）()11111na aa--【分析】（1）12÷1即可求出q，根据已知数的特点求出a18和a n即可；（2）根据已知先求出3S，再相减，即可得出答案；（3）根据（1）（2）的结果得出规律即可．【详解】解：（1）12÷1＝12，a18＝1×（12）17＝1712，a n＝1×（12）n﹣1＝112n-，故答案为：12，1712，112n-；（2）设S＝3+32+33+ (323)则3S＝32+33+…+323+324，∴2S＝324﹣3，∴S＝24332-（3）a n＝a1•q n﹣1，a1+a2+a3+…+a n＝() 11111na aa--．【点睛】本题考查了整式的混合运算的应用，主要考查学生的理解能力和阅读能力，题目是一道比较好的题目，有一定的难度．23．（1）两；（2）2，3；（3）24，-48．【分析】（1）根据题中所给的分析方法先求出这32768的立方根都是两位数；（2）继续分析求出个位数和十位数即可；（3）利用（1）（2）中材料中的过程进行分析可得结论．【详解】解：（1）由103=1000，1003=1000000，∵1000＜32768＜100000，∴10100，∴故答案为：两；（2）∵只有个位数是2的立方数是个位数是8，∴2划去32768后面的三位数768得到32，因为33=27，43=64，∵27＜32＜64，∴3040．∴3．故答案为：2，3；（3）由103=1000，1003=1000000，1000＜13824＜1000000，∴10100，∴∵只有个位数是4的立方数是个位数是4，∴4划去13824后面的三位数824得到13，因为23=8，33=27，∵8＜13＜27，∴2030．∴；由103=1000，1003=1000000，1000＜110592＜1000000，∴10100，∴∵只有个位数是8的立方数是个位数是2，∴8，划去110592后面的三位数592得到110，因为43=64，53=125，∵64＜110＜125，∴4050．∴；故答案为：24，-48．【点睛】此题考查立方根，解题关键在于理解一个数的立方的个位数就是这个数的个位数的立方的个位数．24．初步探究：（1）12，-8；深入思考：（1）(−13)2，(15)4，82；（2）21na-⎛⎫⎪⎝⎭【分析】初步探究：（1）分别按公式进行计算即可；深入思考：（1）把除法化为乘法，第一个数不变，从第二个数开始依次变为倒数，由此分别得出结果；（2）结果前两个数相除为1，第三个数及后面的数变为1a ，则11na aa-⎛⎫=⨯ ⎪⎝⎭ⓝ；【详解】解：初步探究：（1）2③=2÷2÷2=12， 111111-=-----222222⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫÷÷÷÷ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⑤111=1---222⎛⎫⎛⎫⎛⎫÷÷÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ()11-2--22⎛⎫⎛⎫÷÷ ⎪ ⎪⎝⎭⎝⎭=-8； 深入思考：（1）（-3）④=（-3）÷（-3）÷（-3）÷（-3）=1×(−13)2=(−13)2； 5⑥=5÷5÷5÷5÷5÷5=(15)4； 同理可得：（﹣12）⑩＝82； （2）21n a a -⎛⎫= ⎪⎝⎭ⓝ【点睛】本题是有理数的混合运算，也是一个新定义的理解与运用；一方面考查了有理数的乘除法及乘方运算，另一方面也考查了学生的阅读理解能力；注意：负数的奇数次方为负数，负数的偶数次方为正数，同时也要注意分数的乘方要加括号，对新定义，其实就是多个数的除法运算，要注意运算顺序．25．(1)210-1；(2)n 1514+-；(3)9×210+1． 【分析】（1）根据题目中材料可以得到用类比的方法得到1+2+22+23+…+29的值；（2）根据题目中材料可以得到用类比的方法得到1+5+52+53+54+…+5n 的值．（3）根据题目中的信息，运用类比的数学思想可以解答本题．【详解】解：（1）设S=1+2+22+23+ (29)将等式两边同时乘以2得：2S=2+22+23+24+…+29+210，将下式减去上式得2S-S=210-1，即S=210-1，即1+2+22+23+…+29=210-1．故答案为210-1；（2）设S=1+5+52+53+54+…+5n ，将等式两边同时乘以5得：5S=5+52+53+54+55+…+5n +5n+1，将下式减去上式得5S-S=5n+1-1，即S=n1514+-，即1+5+52+53+54+…+5n=n1514+-；（3）设S=1+2×2+3×22+4×23+…+9×28+10×29，将等式两边同时乘以2得：2S=2+2×22+3×23+4×24+…+9×29+10×210，将上式减去下式得-S=1+2+22+23+…+29+10×210，-S=210-1-10×210，S=9×210+1，即1+2×2+3×22+4×23+…+9×28+10×29=9×210+1．【点睛】本题考查有理数的混合运算、数字的变化类，解题的关键是明确题意，发现数字的变化规律．26．（1）a2=2，a3=-1，a4=1 2（2）a2016•a2017•a2018= -1（3）a33+a66+a99+…+a9999=-1【分析】(1)将a1=12代入11a-中即可求出a2，再将a2代入求出a3，同样求出a4即可.(2)从（1）的计算结果可以看出，从a1开始，每三个数一循环，而2016÷3=672，则a2016=-1,a2017=12,a2018=2然后计算a2016•a2017•a2018的值；(3)观察可得a3、a6、a9、…a99，都等于-1，将-1代入，即可求出结果.【详解】（1）将a1=12，代入11a-，得21=211-2a=；将a2=2，代入11a-，得31=-11-2a=；将a3=-1，代入11a-，得411=1--12a=（）.（2）根据(1)的计算结果，从a1开始，每三个数一循环，而2016÷3=672，则a2016=-1,a2017=12,a2018=2所以，a2016•a2017•a2018=（-1）×12×2= -1（3）观察可得a3、a6、a9、…a99，都等于-1，将-1代入，a33+a66+a99+…+a9999=（-1）3+（-1）6+（-1）9+…+（-1）99=（-1）+1+（-1）+…(-1)=-1【点睛】此类问题考查了数字类的变化规律，解题的关键是要严格根据定义进行解答，同时注意分析循环的规律．27．（1）23，1；（2）两位正整数为39，28，17，()f t 的最大值为47；（3）①2021；②2021【分析】（1）仿照样例进行计算即可；（2）由题设可以看出交换前原数的十位上数字为a ，个位上数字为b ，则原数可以表示为10a+b ，交换后十位上数字为b ，个位上数字为a ，则交换后数字可以表示为10b+a ，根据“交换其个位上的数字与十位上的数字得到的新数减去原数所得的差为54”确定出a 与b 的关系式，进而求出所有的两位数，然后求解确定出()f t 的最大值即可；（3）根据样例分解计算即可．【详解】解：（1）61623=⨯=⨯，∵6132->-，∴()263f =； 161162844=⨯=⨯=⨯∵1618244->->-，∴()161f =， 故答案为：23；1； （2）由题意可得：交换后的数减去交换前的数的差为：10109()54b a a b b a +--=-=，∴6b a -=，∵19a b ≤≤≤，∴93b a ==，或82b a ==，或71b a ==，，∴t 为39，28，17；∵39＝1×39＝3×13，∴()33913f =； 28＝1×28＝2×14＝4×7，∴()28f ＝47； 17＝1×17，∴()11717f =；∴()f t 的最大值47． （3）①∵223572021⨯⨯⨯=⨯∴()220235721f ⨯⨯⨯=； ②423574042⨯⨯⨯=⨯∴()4402023574221f ⨯⨯⨯==； 故答案为：2021；2021【点睛】本题主要考查了有理数的运算，理解最佳分解的定义，并将其转化为有理数的运算是解题的关键．28．（1）①5；②2-；（2）1；（3）16．【分析】(1)根据题中定义代入即可得出；(2)根据2x =，讨论3和 m 的两种大小关系，进行计算；(3)先判定A 、B 的大小关系，再进行求解．【详解】（1）根据题意：∵21>-，∴()()212215-=⨯--=※，∵43-<-，∴()()()243434223--=--⨯-=-+=-※． （2）∵2x =，∴31325m =-+⨯=※，① 若3m >，则235m ⨯-=，解得1m =，②若3m <， 则2353m -⨯=，解得3m =-(不符合题意)， ∴1m =．（3）∵()()323224162210A B x x x x x x x -=-+-+--+-+=--<，∴A B <， ∴()3232224162333A B A B x x x x x x =-=-+-+--+-+=-※， 得380x x +-=，∴3222816x x +=⨯=．【点睛】本题考查了一种新运算，读懂题意掌握新运算并能正确化简是解题的关键．29．（1）N,E,T 密文为M,Q,P;（2）密文D,W,N 的明文为F,Y ,C ．【分析】(1) 由图表找出N,E,T 对应的自然数,再根据变换公式变成密文.(2)由图表找出N=M,Q,P 对应的自然数，再根据变换.公式变成明文.【详解】解：（1）将明文NET 转换成密文：2522517263N M +→→+=→ 3313E Q →→=→ 5158103T P +→→+=→ 即N,E,T 密文为M,Q,P;（2）将密文D,W,N 转换成明文：()133138114D F →→⨯--=→2326W Y →→⨯=→253(2517)222N C →→⨯--=→即密文D,W,N 的明文为F,Y ,C ．【点睛】本题考查有理数的混合运算，此题较复杂，解答本题的关键是由图表中找到对应的数或字母，正确运用转换公式进行转换．30．（1）12 ，1712 ，n-112 ；（2）24332-；（3）()11111n a a a -- 【分析】（1）12÷1即可求出q ，根据已知数的特点求出a 18和a n 即可； （2）根据已知先求出3S ，再相减，即可得出答案；（3）根据（1）（2）的结果得出规律即可．【详解】解：（1）12÷1＝12， a 18＝1×（12）17＝1712，a n ＝1×（12）n ﹣1＝112n -， 故答案为：12，1712，112n -； （2）设S ＝3+32+33+ (323)则3S ＝32+33+…+323+324，∴2S ＝324﹣3，∴S ＝24332-（3）a n＝a1•q n﹣1，a1+a2+a3+…+a n＝() 11111na aa--．【点睛】本题考查了整式的混合运算的应用，主要考查学生的理解能力和阅读能力，题目是一道比较好的题目，有一定的难度．。

海门市东洲国际·中南国际2014-2015学年度第一学期期中考试七年级数学调研卷一、选择题：（本大题共有8小题，每小题3分，共24分.在每小题所给出的四个选项，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置．．．．．．．上） 1.如果运进72吨记作+72，那么-56吨表示【▲】A 、运进56吨B 、运出56吨C 、运出-56吨D 、运进-56吨 答案：B运进72吨记作+72，那么-56吨表示运出56吨，故选B 2.已知下列方程：①x x 22=-;②13.0=x ;③152-=x x;④;342=-x x ⑤x=6;⑥x+2y=0.其中一元一次方程的个数是【▲】A 、2B 、3C 、4D 、5 一元一次方程的概念是只含有一个未知数，未知数的最高次为2次的整式方程，则②⑤正确，选A3.方程2x+a-4=0的解是x=-2,则a 等于【▲】A 、-8B 、0C 、2D 、8 解方程得24a x -=,则224-=-a，解得a=8,选D4.下列各组数中，相等的一组是【▲】A 、-1和（-4）+（-3）B 、3- 和-（-3）C 、23和32 D 、23-和()23-A 选项（-4）+（-3）=-71-≠，A 不正确，B 选项33-=，-（-3）=3，B 正确，C 选项23=6，32=8，故C 不正确，D 选项23-=-9，()23-=9，故D 不正确，故选B5.在①-a 表示负数；②近似数2.5万精确到十分位；③如果a<0,b>0，那么ab<0;④多项式122+-a a 是二次多项式中，正确的个数有【▲】A 、1个B 、2个C 、3个D 、4个 ①-a 不一定表示负数；②近似数2.5万中最后一位5在千位，所以2.5万精确到千位，③a<0,b>0，则a,b 异号，那么ab<0，正确，④多项式122+-a a 是二次多项式正确，故共2个正确，选B6.下列等式的变形，正确的是【▲】A 、如果ay ax =,那么x=yB 、如果x=y,那么x-5=5-yC 、如果0=+b ax ,那么a b x -= D 、如果x=y,那么1122+=+a ya xA,若a=0，不成立，B 不正确，C 若a=0,不成立，D 等式两边同时除以不为零的数等式成立，故答案选D7.已知关于x 的方程3x-2=kx+7有整数解，则满足条件的所有整数k 有【▲】个 A 、4 B 、5 C 、6 D 、8 由题意，可得x=k-39,∵关于x 的方程3x-2=kx+7有整数解，那么3-k=9或3或1或-1或-3或-9，那么符合题意的k 值共6个8.将一列有理数-1，2，-3，4，-5，6，……，如图所示有序排列.根据图中的排列规律可知，“峰1”中峰顶的位置（C位置）是有理数4，那么，”峰6“中C的位置是有理数，2008应排在A、B、C、D、E中的位置.其中两个填空依次为【▲】A、-28，CB、-29，BC、-30，DD、-31，E由图可知每5个数为一个循环组依次循环，所以，“峰n”中峰顶C的位置的数的绝对值为5n﹣1，当n=6时，5×6﹣1=30﹣1=29，∵29是奇数，∴“峰6”中C的位置的有理数是﹣29；∵“峰402”峰顶C上的数的绝对值为，且2009为奇数，∴“峰402”峰顶C的位置的有理数是-2009，∴2008应排在“峰402”中B的位置故答案选B二、填空题（本大题共有10小题，每小题2分，共20分.不需要写出解答过程，请把答案上）直接填写在答题卡相应位置．．．．．．．9.2008年北京奥运会火炬接力传递距离约为137000千米，将137000用科学记数法表示为 .537.1⨯10137000=5.1⨯371010.某股票星期一收盘时每股18元，星期二收盘每股跌了1.8元，星期三收盘每股涨了1.1元，则星期三的收盘价为每股元.由题意：18-1.8+1.1=17.311.若单项式ny x 232与32y x m -是同类项，则m-n 的值为 . 由题意：单项式ny x 232与32y x m -是同类项，则有m=2,n=3,m-n=-112.已知a 、b 互为相反数，m 、n 互为倒数,x 的绝对值为2，则22x nm ba mn --++-= .a 、b 互为相反数,a+b=0, m 、n 互为倒数,则mn=1, x 的绝对值为2,则x=2或-2,即x 2=4 原式=-64-012-=+⨯13.已知点A 在数轴上表示的数是-2，B 在数轴上，AB=3,则B 点所表示的数是 . ∵AB=3，点A 在数轴上表示的数是-2，则B 和A 的距离为3，则B 点所表示的数为1或-514.把一些图书分给某班学生阅读，若每人分3本，则剩余20本;若每人分4本，则还缺25本，这个班有多少学生？设这个班有x 名学生，则由题意可列方程 .15.已知多项式832-+my x 与多项式722++-y nx 的和中，不含有x 、y 项，则m(m+n)= .()()()12372-83222-++-=+++-+y m x n y nx my x ，不含有x 、y 项；所以，3-n=0且m+2=0,得n=3,m=-2, m(m+n)=-216.已知：x-2y+3=0，则代数式()14222-+--y x x y 的值为 .∵x-2y+3=0，∴x-2y=-3原式=()()()1413231)2(2222=--⨯--=----y x y x17.一列方程如下排列：1214=-+x x 的解是x=2，1226=-+x x 的解是x=3，1238=-+x x 的解是x=4，根据观察得到的规律写出其中解是x=6的方程： . 由题意可知解是x=6的方程为：12512=-+x x18.轮船从甲地到乙地顺流行驶需4小时，从乙地到甲地逆流行驶需6小时，有一木筏由甲地漂流至乙地需 小时.三、解答题（本大题共有8小题，共56分.请在答题卡指定区域内作答，解答时就写出文字说明、证明过程或是演算步骤） 19、计算（每小题4分，共8分）(1)214-314211-321+⎪⎭⎫ ⎝⎛+; (2)()2314123--1-24⎪⎭⎫ ⎝⎛⨯÷ （1）原式=06-629-23-3133529-31323-35==⎪⎭⎫ ⎝⎛++=+⎪⎭⎫ ⎝⎛+ 原式=941-94-1-91499-1-==⨯÷20、解方程（每小题4分，共8分）(1)()()318173+-=-+x x x ; (2)511312x --=+x 解析：（1）318773--=-+x x x731873+-=++x x x2211=x 2=x（2）()()1315125--=+x x3315510+-=+x x5315310-+=+x x 1313=x1=x21、(5分)先化简，在求值：⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛--y x y x x 312331221,其中x=-1,y=2. 原式=y x y x x 312332221+-+- y y x x x 323123221++--= y x +-=3把x=-1,y=2代入上式可得原式=()6213=+-⨯-22、(6分)某同学做数学题：已知两个多项式A 、B ，其中7342+-=x x B ，他在求A+B时，把A+B 错看成A-B ，求得的结果为182++x x ，请你帮助这位同学求出A+B 的正确结果.根据题意可得：182++=-x x B A ，7342+-=x x B ，可求的821218734222+-=++++-=x x x x x x A ）（15516)8212(734222+-=+-++-=+x x x x x x B A23、(6分)某自行车厂计划一周生产自行车1400辆，平均每天生产200辆，但由于种种原因，实际每天生产量与计划量相比有出入，下表是某周的生产情况（超产记为正、减产记为负）：（1）根据记录的数据可知该厂星期六生产自行车 216 _辆； （2）根据记录的数据可知该厂本周实际生产自行车 1408 辆； （3）产量最多的一天比产量最少的一天多生产自行车 26 辆；（4）该厂实行每周计件工资制，每生产一辆车可得50元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣20元，那么该厂工人这一周的工资总额是多少元？ 解：（1）200+（+16）=216；（2）∵（+5）+（﹣2）+（﹣4）+（+12）+（﹣10）+（+16）+（﹣9）， =5﹣2﹣4+12﹣10+16﹣9， =33﹣25， =8，∴1400+8=1408；（3）（+16）﹣（﹣10）， =16+10， =26；（4）50×1408+8×15， =70400+120， =70520．故答案为：（1）216，（2）1408，（3）26，（4）70520． 24、(6分)有理数a 、b 、c 在数轴上的位置如图，(1)判断正负，用“>”或“<”填空：c-b 0,a-b 0,a+c 0. (2)化简：c a b a b c +--+-> < > ⑵－2a观察数轴可知c 在b 的右边所以c-b>0;a<0,b>0, a-b<0;0,>+>c a a c 所以 ∵c-b>0,a-b<0,a+c>0,则()ac a a b b c c a b a b c 2-=+--+-=+--+-25、(9分)将连续自然数1至366按如图所示的方式排成一个长方形阵列，用一个小正方形任意圈出其中的9个数，设圈出的9个数的中心数为a ． （1）用含a 的式子表示的这9个数的和；（2）这9个数的和可能是135吗？可能是2014吗？为什么？（3）用一个小正方形任意圈出其中的25个数，设圈出的25个数的中心数为b ，这25个数的和可能是2100吗？答案：（1）9a （2）9个数的和可能是135，不可能是2016（3）这25个数的和可能是2100 解：（1）规律是横排中相邻数据相差1，竖排中上下相邻数据相差6， 所以当中心的数为a ，用含有a 的代数式表示这9个数的和为a+a+1+a ﹣1+a ﹣6+a+6+a ﹣7+a+7+a ﹣5+a+5=9a ； （2）设中间数为x ，当和为135时，由题意得，9x=135， 解得：x=15，当和为2014时，由题意得，9x=2014， 解得：x=22397（不是整数不符合题意）． 故这9个数的和可能是135，不可能是2016； （3）由题意得，25b=2100， 解得：b=234．答：这25个数的和可能是2100．26、（8分）动点A 从原点出发向数轴负方向运动，同时，动点B 也从原点出发向数轴正方向运动，3秒后，两点相距15个单位长度.已知动点A 、B 的速度比是1：4(速度单位：单位长度/秒)（1）求出两个动点运动的速度，并在数轴上标出A、B两点从原点出发运动3秒时的位置；（2）若A、B两点从（1）中的位置同时向数轴负方向运动，几秒后原点恰好处在两个动点正中间；（3）在（2）中A、B两点继续同时向数轴负方向运动时，另一动点C同时从B点位置出发向A运动，当遇到A后，立即返回向B点运动，遇到B点后立即返回向A点运动，如此往返，直到B追上A时，C立即停止运动．若点C一直以20单位长度/秒的速度匀速运动，那么点C从开始到停止运动，运动的路程是多少单位长度．答案：（1）A点的运动速度是1单位长度/秒，B点的速度是4单位长度/秒；（2）（3）64解：（1）设A点运动速度为x单位长度/秒，则B点运动速度为4x单位长度/秒．由题意得：3x+3×4x=15解得：x=1∴A点的运动速度是1单位长度/秒，B点的速度是4单位长度/秒；（2）设y秒后，原点恰好处在A、B的正中间．由题意得：y+3=12﹣4y解得：答：经过秒后，原点恰处在A、B的正中间；（3）设B追上A需时间z秒，则：4×z﹣1×z=2×（+3）解得：，=64．答：C点行驶的路程是64长度单位．。

七年级数学有理数规律题难点专题训练学校: _____________ 姓名： ______________班级： ______________ 考号： _____________一.填空题1.按照规律填空 1, -2,3, -4,5, -6,7, -8, _______________ ,... 2・观察下而一列数：一 1, -9丄，…，按照这个规律,第2016个数是 ______________12343. 按所列数的规律填上适当的数:3, 5, 7, 9. ____________ , _______ .4. 按规律填数:16, -8, 4, ______________ , _____________, 一丄・2 5. 如图，下面每个图形中的四个数都是按相同的规律填写的，根据此规律确左X 的值为 _______ ■6. 观察下列各式，探索发现规律：23-l = l×3: 32-l=2×4: 42-l=3×5; 52-I =4X6：….按此规律,第n 个等式为_7. (4分)观察下列算式，你发现了什么规律？F =竺;F +，=竺;F+ 2』+F =坯;F+ 2彳+F +军=!^；……4 4 44(1) 根据你发现的规律，计算下面算式的值：/+23+33+……+ F= ____________________ : (2) _____________________________________________________________ 请用一个含”的算式表示这个规律:l 3 +23 +33 +……+ √ = ______________________________二、解答题8. 请你参考黑板中老师的讲解，用运算规律简便计算: 利用运算规律有时能进行简便计算例 1： 999×12 = (1000-l)×12 = 12∞0-12 = 11988 例厶—16x233+17x233 = (—16+17)x233 = 233(1) 999×(-15);I -Il 3^4"3"4H Hθ □(2) 999×118∣ + 999×f-l-999x18-5 9.观察探索:1 _ 1 12^3"2~3（I ）按规律请写出：（4分）1 4x512014x2015 一（2）用上述规律计算：（2分）+(-一 X —1-)=2015 201611・观察下列各式:亠―=丄亠—U+J 丄2222 32363 43 412（1）根据上述规律写出第5个等式是 1 1_ X2018 2019拓展应用:计算：Ix-■+ —X —+ —X —+ —,×-+•••+/ / 丿参考答案1 1 1----------1 ----------- 1 ---------- F1×2 2×3 3x410・观察下列各式:(2)(3) H -----------------2014x2015I l _ I l —1 × — = —1 + — 92 21 --- × -----= 1∞ 101 ----------------你发现的规律是：-丄X 丄H H +1用规律计算：(—lx —) + (—×—) + (—x —)+・•・ + ( ---------------- × -------- ) 22 33 42014 2015猜想::5为正整数）（2）规律应用: 1 1----- × ------2017 2019计算:(Il)_ _ X — + …+3 4丿1.9【解析】【分析】根据题中信息，奇数是正数，偶数是负数，且按第几个数绝对值就是几，进行排列，故应填的数是9.【详解】下一个数是第q个数，为正且绝对值为q,故填9.【点睛】本题考査有理数的认识和探索规律，探索规律的题目，通常按照一泄的顺序给岀一系列呈：, 要求我们根据这些已知的量找出一般规律.揭示的规律，常常包含着事物的序列号.所以，把变量和序列号放在一起加以比较，就比较容易发现其中的奥秘.2.丄2016【解析】试题分析：根据题意可得：第n个数为(-1)"丄，则第2016个数是一1—.n2016考点：规律题3.11； 13【解析】试题分析：观察所给的数列可知：数列是连续的奇数，所以结果为：11； 13.考点：数字规律.4.-2 1【解析】【分析】由16, -8.4可知后一个数是前一个数的(-l),'+,^倍，根据这个规律可直接得出答案.【详解】答案第5页，总6贞+ 83 =因为由16, -8.4可知后一个数是前一个数的(-l)n+,∣倍(n 为正整数)， 所以可得16,4-2,1-1・ 2故答案为：-2： 1. 【点睛】本题主要考查有理数的规律题，关键是根据题意得出数字之间的规律，进而求解即可.5. 370.【解析】试题分析：观察可得左下角数字为偶数，右上角数字为奇数，所以2n=20, m=2n- 1,解得 n=10, m=19,又因右下角数字：第一个：1=1x2-1,第二个：10=3x4-2,第三个：27=5x6 -3,由此可得第 n 个:2n (2n- 1) - n,即可得 x= 19x20 - 10=370. 考点：数字规律探究题.6. (n+l)2-l=n(n+2)【解析】根据已知可以得出，左边的规律是：第n 个式子为(n+l) :-1,右边是即n (n+2). 解：V2s -l=l×3> 3-1=2×4, 4-1=3×5, 5-1=4×6, •••规律为(n+l) S -I=n (n+2). 故答案为(n+l) ^~l=n (n+2)・“点睛”此题主要考查了数字变化规律，要求学生通过观察，分析、归纳发现其中的规律， 并应用发现的规律解决问题・对于等式，要注意分别发现：等式的左边和右边的规律.【解析】试题分析:⑴由卜罟=(罟)"+芜芽几(2)由(1)即可得到结论・试题解析：(I) I 3 = —= (—)2> l 3 +23 =(-)2 ,..., 15 +23 +33 +4 2 28×9 , 64x817. (1)64x81 4(2)n 2(n + 1)24得到 l 3+23+33++ 83z 8×9x . 64x81( ---- 广二------- :2 4+ 83 =⑵ H+ 3，+……+沪『心+ 1)]—厂(〃 +厅.24考点：规律型：数字的变化类.8. (1) -14^85-(2) 99900【解析】 【分析】(1) 根拯乘法分配律即可简便运算； (2) 很据乘法分配律即可简便运算.【详解】(1) 999×(-15)=-(1000-l)×15=-1000×15+I5 =-15000+15 =-14985(2) 999×118- + 999×∣-1]-999×18-= 999×1(X)=99900.【点睛】此题考査的目的是使学生理解掌握乘法分配律、乘法结合律的意义，并且能够灵活运用乘法 的运算立律进行简便计算.【解析】 试题分析：从题意得等式的左右两边乘号或减号前的整数等于乘号或减号后的分数的分子, 而分母加1,从而得到规律・1______ 12014^2015(2)2014 2015试题解析：(I)4x5 4 5= 999 ×木卷由系统自动生成•请仔細校对后使用，答案仅供参考。

2014——2015学年第二学期期末考试参考答案七年级数学一、(每小题3分，共24分)1-----5 DABDD 6-----8 DBA二、(每小题3分，共21分)9.、2、3 12. 113. 89° 14. -5，-5 15. 26三、(本大题共8个小题，满分75分)16.（8分）（1）-122（2）-6-17.（7分） a=-3, b=-218. （8分） -1<x ≤314，画图略. 19. （10分）(1)S △ABC =12×≈6-1.5×1.414≈3.9(2)画图略.A’ （-5，2）、B’（2）、C’(0,5).20. （10分）解：设甲每天完成的零件数为x 个，乙每天完成的零件数为y 个，列方程组为：⎩⎨⎧=++-=++43032362430222y y x y x x 解得：⎩⎨⎧==4470y x 答：甲每天完成的零件数为70个，乙每天完成的零件数为44个.21. （10分）（1）∵∠1=∠4=1:2 ∠1=36° ∴∠4=72°又∵A B ∥CD ∴∠1+∠2+∠4=180°∴∠2=180°-36°-72°=72°又∵∠2+∠3=180° ∴∠3=180°-72°=108°(2) ∵AB ∥CD ∴∠ABE=∠4=72°∵∠2=72° ∴AB 平分∠EBG22. （10分）(1)500 (2)按先后顺序依次为A 80 C 160 D60 (3)4400023. （12分）（1）设购进A 型号的电脑x 台，那么购进B 型号的电脑(25-x )台，根据题意得：4000x+2500(25-x)≤80000 解得：x≤1123∵A型号的电脑购进不能低于8台，∴8≤x≤112 3∴电脑城有4种购进电脑的方案:①A型号购进8台时B型号购进17台②A型号购进9台时B型号购进16台③A型号购进10台时B型号购进15台④A型号购进11台时B型号购进14台.（2）∵A型号电脑的利润低，∴A型号电脑进的越少，B型号电脑进的越多时利润就越大，∴按方案①进货利润最大.最大利润为：8×800+17×1000=23400（元）。

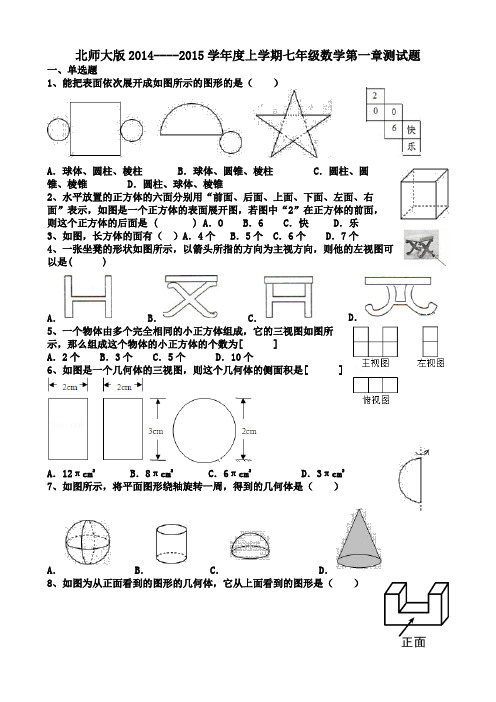
北师大版2014----2015学年度上学期七年级数学第一章测试题一、单选题1、能把表面依次展开成如图所示的图形的是（ ）A ．球体、圆柱、棱柱B ．球体、圆锥、棱柱C ．圆柱、圆锥、棱锥 D ．圆柱、球体、棱锥2、水平放置的正方体的六面分别用“前面、后面、上面、下面、左面、右面”表示，如图是一个正方体的表面展开图，若图中“2”在正方体的前面，则这个正方体的后面是 ( ) A ．O B ．6 C ．快 D ．乐3、如图，长方体的面有（ ）A ．4个 B ．5个 C ．6个 D ．7个4、一张坐凳的形状如图所示，以箭头所指的方向为主视方向，则他的左视图可以是( )5、一个物体由多个完全相同的小正方体组成，它的三视图如图所示，那么组成这个物体的小正方体的个数为[ ]A ．2个B ．3个C ．5个D ．10个6、如图是一个几何体的三视图，则这个几何体的侧面积是[ ]A ．12πcm 2B ．8πcm 2C ．6πcm 2D ．3πcm 27、如图所示，将平面图形绕轴旋转一周，得到的几何体是（ ）A ．B ．C ．D ．8、如图为从正面看到的图形的几何体，它从上面看到的图形是（ ）A ．B ．C ．D ．A． B． C． D．9、如图是由几个相同的小立方块组成的三视图，小立方块的个数是[ ] A．3个 B．4个 C．5个 D．6个10、骰子是一种特别的数字立方体（如图），它符合规则：相对两面的点数之和总是7．下面四幅图中可以折成符合规则的骰子的是（）A． B．C． D．11、用平面去截下图中的正方体，截面形状不可能是（）A． B． C． D．12、如图，模块①﹣⑤均由4个棱长为1的小正方体构成，模块⑥由15个棱长为1的小正方体构成．现从模块①﹣⑤中选出三个放到模块⑥上，使得模块⑥成为一个棱长为3的大正方体．则下列选择方案中，能够完成任务的为（）A．模块①，②，⑤B．模块①，③，⑤C．模块②，④，⑤D．模块③，④，⑤下的几何体面的个数和棱的条数分别为（）A．6，14 B．7，14 C．7，15 D．6，1514、如图是一个立体图形的二视图，根据图示的数据求出这个立体图形的体积是（）A．24cm3 B．48cm3 C．72cm3 D．192cm315、如图所示的平面图形中，不可能围成圆锥的是（）A． B．C． D．二、填空题(注释)16. 如图，长方体中，与棱AA′平行的面是________________．17、一个五棱柱有____个面，用一个平面去截五棱柱，则得到的截面的形状不可能是____（填“七边形“或“八边形“）18、展开图：几何体名称：_______，_______，_______，_______．19、如图是正方体的一种平面展开图，它的每个面上都有一个汉字，那么在原正方体的表面上，与汉字“香”相对的面上的汉字是____．20、如图，正方体每个侧面的面积为2平方米，用经过A，B，C三点的平面截这个正方体，则所得的切面的周长是____米．21、一个矩形绕着它的一边旋转一周，所得到的立体图形是________________．22、三棱柱的三视图如图所示，△EFG中，EF=8cm，EG=12cm，∠EGF=30°，则AB的长为 cm．23、一个物体的外形是长方体，其内部构造不详．用一组水平的平面截这个物体时，得到了一组（自下而上）截面，截面形状如图所示，这个长方体的内部构造可能是________．三、解答题24、如图1，大正方体上截去一个小正方体后，可得到图2的几何体．（1）设原大正方体的表面积为S，图2中几何体的表面积为S′，那么S′与S的大小关系是（）A、S′＞SB、S′=SC、S′＜SD、不确定（2）小明说：“设图1中大正方体各棱的长度之和为c，图2中几何体各棱的长度之和为c′，那么c′比c正好多出大正方体3条棱的长度．”若设大正方体的棱长为1，小正方体的棱长为x，请问x为何值时，小明的说法才正确？（3）如果截去的小正方体的棱长为大正方体棱长的一半，那么图3是图2中几何体的表面展开图吗？如有错误，请在图3中修正．25、一个正方体，截掉一个角，剩余部分还有几个角？26、将一个正方体的表面涂上颜色．如图把正方体的棱2等分，然后沿等分线把正方体切开，能够得到8个小正方体，通过观察我们可以发现8个小正方体全是3个面涂有颜色的．如果把正方体的棱三等分，然后沿等分线把正方体切开，能够得到27个小正方体，通过观察我们可以发现这些小正方体中有8个是3个面涂有颜色的，有12个是2个面涂有颜色的，有6个是1个面涂有颜色的，还有1个各个面都没有涂色．（1）如果把正方体的棱4等分，所得小正方体表面涂色情况如何呢？把正方体的棱n等分27.如图，这6个图形虽然形状各异，但是可以将它们各剪一刀，各自能拼成一个正方形，你会做到吗？28、把图中的几何体分类，并简要说明理由．29、如图所示，用1、2、3、4标出的四块正方形，以及由字母标出的八块正方形中任意一块，一共要用5块连在一起的正方形折成一个无盖方盒，共有几种不同的方法？请选择合适的方法．30、指出下列平面图形是什么几何体的展开图：。

北京市东城区普通中学2014-2015学年度第二学期七年级数学第八章 二元一次方程组 单元测试一、选择题（每题3分，共15分）1、若x a - b －2y a + b - 2＝11是二元一次方程，那么的a 、b 值分别是（ ） A 、1，0 B 、0，－1 C 、2，1 D 、2，－32、在二元一次方程x+3y=1的解中，当x=2时，对应的y 的值是（ ）。

A 、31B 、31- C 、1D 、43、下列二元一次方程组中，以为12x y =⎧⎨=⎩解的是（ ） A 、135x y x y -=⎧⎨+=⎩ B 、135x y x y -=-⎧⎨+=-⎩ C 、331x y x y -=⎧⎨-=⎩ D 、2335x y x y -=-⎧⎨+=⎩4、若2(341)3250x y y x +-+--=则x =（ ） A 、-1 B 、1 C 、2 D 、-25、我校运动员分组训练，若每组7人，余3人；若每组8人，则缺5人；设运动员人数为x 人，组数为y 组，则列方程组为（ ）A 、 ⎩⎨⎧=++=x y x y 5837B 、⎩⎨⎧=-+=x y x y 5837C 、⎩⎨⎧+=-=5837x y x yD 、⎩⎨⎧+=+=5837x y x y二、填空题（每题3分，共21分）6、将方程3x-y=1变形成用y 的代数式表示x ，则x =___________。

7、写出一个以23x y =⎧⎨=⎩为解的二元一次方程组__________________ 。

8、在y kx b =+中，当1x =时，4y =，当2x =时，10y =，则k = ，b = 。

9、已知43x y =⎧⎨=⎩是方程组512ax by bx ay +=⎧⎨+=-⎩的解，则a b += 。

10、关于x 、y 的方程组⎩⎨⎧-=+=-225453by ax y x 与⎩⎨⎧=--=+8432by ax y x 有相同的解，则()b a -= 。

新人教版2014-2015年七年级下学期期中考试数学试题及答案启用前*绝密新人教版2014-2015年七年级下学期期中考试数学试题时间：120分钟满分：120分日期：2015.5.3第Ⅰ卷（选择题，共30分）一、选择题（每题3分，共30分）1.9的算术平方根是A。

±3 B。

±9 C。

3 D。

-32.在平面直角坐标系中，点P（-3，5）所在的象限是A。

第一象限 B。

第二象限 C。

第三象限 D。

第四象限3.在同一个平面内，两条直线的位置关系是A。

平行或垂直 B。

相交或垂直 C。

平行或相交 D。

不能确定4.如图所示，四幅汽车标志设计中，能通过平移得到的是奥迪。

本田。

大众。

铃木5.如图，梯子的各条横档互相平行，若∠1=80，则∠2的度数是BD)3A。

80 B。

100 C。

120 D。

1506.如图，点E在AC的延长线上，下列条件能判断AB∥CD的是A。

∠3=∠4 B。

∠1=∠2 C。

∠D=∠DCED D。

∠D+∠ACD=180°7.已知直角坐标系中点P到y轴的距离为5，且点P到x 轴的距离为3，则这样的点P的个数是A。

1 B。

2 C。

3 D。

48.在实数-2，0.7，34，π，16中，无理数的个数是A。

1 B。

2 C。

3 D。

49.如图，将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上，如果∠1=27°，那么∠2的度数为A。

53° B。

55° C。

57° D。

60°10.如图，直线l1 ∥ l2，∠A=125°，∠B=85°，则∠1+∠2=A。

30° B。

35° C。

36° D。

40°第Ⅱ卷（非选择题共90分）二、填空题：(每题3分，共18分)11.在直角坐标系中，写出一个在纵轴的负半轴上点的坐标。

12.若一个数的平方根等于它本身，则这个数是________。

2014-2015学年上海市浦东新区第四教育署七年级（下）期中数学试卷一、单项选择题（共6题，每题2分，满分12分）1．下列各数中：0、﹣、、、π、0.3737737773…（它的位数无限且相邻两个“3”之间“7”的个数依次加1个），无理数有（）A．1个B．2个C．3个D．4个2．下列四个式子中，正确的是（）A．=±9 B．﹣=6 C．（+）2=5 D．16=43．如图，要使AD∥BC，那么可以选择下列条件中的（）A．∠1=∠4 B．∠2=∠3 C．∠1+∠B=180°D．∠B=∠D4．点P为互相垂直的直线a、b外一点，过点P分别画直线c、d，使c∥a、d⊥a，那么下列判断中正确的是（）A．c∥b B．c∥d C．b⊥c D．b⊥d5．下列说法中，正确的是（）A．两条直线被第三条直线所截，同位角相等B．联结直线外一点到直线上各点的所有线段中，垂线最短C．经过一点，有且只有一条直线与已知直线平行D．经过一点，有且只有一条直线与已知直线垂直6．如图，在数轴上表示1、的对应点分别为A、B，B关于点A的对称点为点C，则点C所表示的数是（）A．﹣2 B．2﹣C．﹣1 D．1﹣二、填空题（共14题，每题2分，满分28分）7．16的平方根是．8．如果a4=81，那么a=．9．比较大小：﹣2﹣3（填“＜”或“=”或“＞”）10．计算：8=．11．计算：（+2）2013•（﹣2）2013=．12．根据浦东新区2010年第六次全国人口普查公报，浦东新区常住人口为5 044 430人，数字5 044 430可用科学记数法表示为（保留3个有效数字）．13．在数轴上，如果点A、点B所对应的数分别为﹣、2，那么A、B两点的距离AB=．14．写出图中∠B的一个同位角．15．如图，直线c与a、b都相交，a∥b，如果∠2=110°，那么∠1=．16．如图，若∠BOC=44°，BO⊥DE，垂足为O，则∠AOD=度．17．如图，△ABC中，CD⊥AC，CE⊥AB，垂足分别是C、E，那么点C到线段AB的距离是线段的长度．18．如图，直线a∥b，点A、B位于直线a上，点C、D位于直线b上，且AB：CD=2：3，如果△ABC 的面积为6，那么△BCD的面积为．19．如图，将两个大小一致的小正方形沿对角线剪开，拼成一个大正方形ABCD，若小正方形的边长是1厘米，则大正方形ABCD的边长是厘米．20．一个角的两边与另一个角的两边分别平行，其中一个角为40°，则另一角为．三、计算题（共5题，21、22每题5分，23、24、25每题6分，满分28分）21．计算：﹣++．22．计算：×（）﹣1÷．23．计算：×（﹣）2×÷．24．计算：3﹣27+（）﹣2﹣（+2）0．25．利用幂的运算性质计算：2×÷．四、解答题（共4题，26、27、28每题6分，29题8分，满分26分）2）在图中画出表示点P到直线a距离的线段PM；（2）过点P画出直线b的平行线c，与直线a交于点N；（3）如果直线a与b的夹角为40°，那么∠MPN=°．27．如图，已知AB∥CD，∠1=（4x﹣25）°，∠2=（85﹣x）°，求∠1的度数．28．已知：如图，∠A=∠D，∠B=∠C，那么∠1与∠2互补吗？为什么？2）如图（a），如果∠B+∠E+∠D=360°，那么AB、CD有怎样的关系？为什么？解：过点E作EF∥AB，如图（b），则∠ABE+∠BEF=180°（）因为∠ABD+∠BED+∠EDC=360°（已知）所以∠FED+∠EDC=°（）所以（）所以AB∥CD时，∠1，∠2，∠3，∠4满足．五、综合题（满分6分）30．皓皓同学在学习了“平方根”这节课后知道了“负数在实数范围内没有平方根”，她对这句话产生了兴趣，她想知道负数在其他范围内是否有平方根，所以她上网查找了以下一些资料．数的概念是从实践中产生和发展起来的，在学习了实数以后，像x2=﹣1这样的方程还是没有实数解的，因为没有一个实数的平方等于﹣1，即负数在实数范围内没有平方根，所以为了了解形如x2=﹣1这类方程的解，就要引入一个新的数i．定义：如果一个数的平方等于﹣1，记为i2=﹣1，这个数i叫做虚数单位．在这种情况下，i可以与实数b相乘再同实数a相加从而得到形如“a+bi”（a、b为实数）的数，人们把这种数叫作复数，a叫这个复数的实部，b叫做这个复数的虚部．它的加、减、乘法运算与整式的加、减、乘法运算类似．比如：（1）（2+i）+（4﹣3i）=6﹣2i（2）（i）2=﹣3（3）（5+i）（5﹣i）=52﹣i2=25﹣（﹣1）=26这样数的范围就由实数扩充到了复数，在这种规定下，负数在复数范围内就有平方根．比如：±i就是﹣1的平方根．根据上面的材料解答以下问题：（1）计算：①（2+i）﹣（3﹣2i）=②i3=③（3+i）2=（2）在负数范围内﹣9的平方根是（3）在复数范围内分解因式x4﹣4=．2014-2015学年上海市浦东新区第四教育署七年级（下）期中数学试卷参考答案与试题解析一、单项选择题（共6题，每题2分，满分12分）1．下列各数中：0、﹣、、、π、0.3737737773…（它的位数无限且相邻两个“3”之间“7”的个数依次加1个），无理数有（）A．1个B．2个C．3个D．4个考点：无理数．分析：无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．解答：解：无理数有：﹣，π，0.3737737773…（它的位数无限且相邻两个“3”之间“7”的个数依次加1个），共3个．故选C．点评：此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．2．下列四个式子中，正确的是（）A．=±9 B．﹣=6 C．（+）2=5 D．16=4考点：实数的运算；分数指数幂．分析：A、表示81的算术平方根；B、先算﹣6的平方，然后再求的值；C、利用完全平方公式计算即可；D、=．解答：解：A、，故A错误；B、﹣==﹣6，故B错误；C、=2+2+3=5+2，故C错误；D、==4，故D正确．故选：D．点评：本题主要考查的是实数的运算，掌握算术平方根、平方根和二次根式的性质以及完全平方公式是解题的关键．3．如图，要使AD∥BC，那么可以选择下列条件中的（）A．∠1=∠4 B．∠2=∠3 C．∠1+∠B=180°D．∠B=∠D考点：平行线的判定．分析：根据内错角相等两直线平行即可做出选择．解答：解：A、欲证AD∥BC，那可以选择：同位角相等，内错角相等，同旁内角互补，∵∠1和∠4是内错角，且∠1=∠4，∵要使AD∥BC，那么可以选择∠1=∠4．故本选项正确；B、∵∠2=∠3，可以证明AB∥CD，而不能证明AD∥BC，故本选项错误；C、∵∠1和∠B不是同旁内角，故本选项错误；D、∵∠B和∠D不是同位角，也不是内错角，所以不能证明AB∥CD；故选A．点评：此题主要考查学生对平行线的判定这一知识点的理解和掌握，比较简单，属于基础题．4．点P为互相垂直的直线a、b外一点，过点P分别画直线c、d，使c∥a、d⊥a，那么下列判断中正确的是（）A．c∥b B．c∥d C．b⊥c D．b⊥d考点：平行线的判定与性质；垂线．分析：根据题意作出图形后即可得到正确结论．解答：解：根据题意作出如下图形：根据图形知：b⊥c．故选C．点评：本题考查了平行线的性质与判定及垂线的定义，解题的关键是根据题意作出图形，也可以一步步的推导．5．下列说法中，正确的是（）A．两条直线被第三条直线所截，同位角相等B．联结直线外一点到直线上各点的所有线段中，垂线最短C．经过一点，有且只有一条直线与已知直线平行D．经过一点，有且只有一条直线与已知直线垂直考点：命题与定理．分析：分别利用平行线的性质、垂线段最短、平行线的判定以及垂直的判定分析得出即可．解答：解：A、两条平行线被第三条直线所截，同位角相等，错误；B、联结直线外一点到直线上各点的所有线段中，垂线段最短，错误；C、经过直线外一点，有且只有一条直线与已知直线平行，错误；D、经过一点，有且只有一条直线与已知直线垂直，正确；故选D．点评：此题主要考查了命题与定理，正确把握相关定义是解题关键．6．如图，在数轴上表示1、的对应点分别为A、B，B关于点A的对称点为点C，则点C所表示的数是（）A．﹣2 B．2﹣C．﹣1 D．1﹣考点：实数与数轴．分析：首先根据表示1、的对应点分别为点A、点B可以求出线段AB的长度，然后根据点B和点C关于点A对称，求出AC的长度，最后可以计算出点C的坐标．解答：解：∵表示1、的对应点分别为点A、点B，∴AB=﹣1，∵点B关于点A的对称点为点C，∴CA=AB，∴点C的坐标为：1﹣（﹣1）=2﹣．故选B．点评：本题考查的知识点为实数与数轴，解决本题的关键是求数轴上两点间的距离就让右边的数减去左边的数．知道两点间的距离，求较小的数，就用较大的数减去两点间的距离．二、填空题（共14题，每题2分，满分28分）7．16的平方根是±4．考点：平方根．专题：计算题．分析：根据平方根的定义，求数a的平方根，也就是求一个数x，使得x2=a，则x就是a的平方根，由此即可解决问题．解答：解：∵（±4）2=16，∴16的平方根是±4．故答案为：±4．点评：本题考查了平方根的定义．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．8．如果a4=81，那么a=3或﹣3．考点：有理数的乘方．分析：根据有理数的开方运算计算即可．解答：解：∵a4=81，∴（a2）2=81，∴a2=9，∴a=3或﹣3．故答案为：3或﹣3．点评：本题考查了有理数的乘方运算的逆运算，解题时注意不用漏解．9．比较大小：﹣2＞﹣3（填“＜”或“=”或“＞”）考点：实数大小比较．分析：根据负数比较大小的法则进行解答即可．解答：解：因为|﹣2|=2≈2.828＜|﹣3|=3，所以：﹣2＞﹣3，故答案为：＞．点评：本题考查的是实数的大小比较，熟知负数比较大小的法则是解答此题的关键．10．计算：8=．考点：分数指数幂．分析：首先把8化成23，然后根据幂的乘方的计算方法，求出算式8的值是多少即可．解答：解：8=（23）==．故答案为：．点评：（1）此题主要考查了分数指数幂问题，要熟练掌握，解答此题的关键是把8化成23．（2）此题还考查了幂的乘方，要熟练掌握，解答此题的关键是要明确：（a m）n=a mn（m，n是正整数）．11．计算：（+2）2013•（﹣2）2013=﹣1．考点：二次根式的混合运算．分析：首先逆用积的乘方公式将原式变形为[（）（）]2013，然后利用平方差公式计算出（）（\sqrt{3}．﹣2）的值，最后再计算乘方即可解答：解：原式=[（）（）]2013=（﹣1）2013=﹣1．点评：本题主要考查的是二次根式的计算，逆用积的乘方公式和平方差公式是解题的关键．12．根据浦东新区2010年第六次全国人口普查公报，浦东新区常住人口为5 044 430人，数字5 044 430可用科学记数法表示为 5.04×106（保留3个有效数字）．考点：科学记数法与有效数字．分析：较大的数保留有效数字需要用科学记数法来表示．用科学记数法保留有效数字，要在标准形式a×10n中a的部分保留，从左边第一个不为0的数字数起，需要保留几位就数几位，然后根据四舍五入的原理进行取舍．解答：解：数据5 044 430用科学记数法（结果保留三个有效数字）表示为：5.04×106，故答案为：5.04×106．点评：此题考查了科学记数法的表示方法，以及用科学记数法表示的数的有效数字的确定方法．13．在数轴上，如果点A、点B所对应的数分别为﹣、2，那么A、B两点的距离AB=3．考点：两点间的距离；实数的运算．分析：求数轴上两点之间的距离：数轴上表示两个点所对应的两个数的差的绝对值，即用较大的数减去较小的数即可．解答：解：∵点A、点B所对应的数分别为﹣、2，∴A、B两点的距离AB=2﹣（﹣），=3．故答案为：3．点评：本题主要考查了两点间的距离，能根据求数轴上两点间的距离的方法，列出式子是本题的关键．14．写出图中∠B的一个同位角∠ECD或∠ACD．考点：同位角、内错角、同旁内角．专题：开放型．分析：根据同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，进行分析可得答案．解答：解：∠B的同位角是∠ECD，∠ACD，故答案为：∠ECD或∠ACD．点评：此题主要考查了三线八角，关键是掌握同位角的边构成“F“形．15．如图，直线c与a、b都相交，a∥b，如果∠2=110°，那么∠1=70°．考点：平行线的性质．分析：先根据平行线的性质求出∠3的度数，再由补角的定义即可得出结论．解答：解：∵a∥b，∠2=110°，∴∠3=∠2=110°，∴∠1=1820°﹣∠3=180°﹣110°=70°．故答案为：70°．点评：本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．16．如图，若∠BOC=44°，BO⊥DE，垂足为O，则∠AOD=46度．考点：垂线．分析：本题需先根据已知条件和所给的图形，列出所要求的式子，即可求出答案．解答：解：∵∠BOC=44°，BO⊥DE，∴∠AOD=180°﹣44°﹣90°=46°．故答案为：46°．点评：本题主要考查了垂线，在解题时要根据已知有条件，再结合图形列出式子是本题的关键．17．如图，△ABC中，CD⊥AC，CE⊥AB，垂足分别是C、E，那么点C到线段AB的距离是线段CE的长度．考点：点到直线的距离．专题：常规题型．分析：根据点到直线的距离的定义，找出点C到AB的垂线段即可．解答：解：如图，∵CE⊥AB，垂足是E，∴点C到线段AB的距离是线段CE的长度．故答案为：CE．点评：本题考查了点到直线的距离的定义，点到直线的距离就是这个点到这条直线的垂线段的长度．18．如图，直线a∥b，点A、B位于直线a上，点C、D位于直线b上，且AB：CD=2：3，如果△ABC 的面积为6，那么△BCD的面积为9．考点：平行线之间的距离；三角形的面积．分析：根据两平行线间的距离处处相等，结合三角形的面积公式，知△BCD和△ABC的面积比等于CD：AB，从而进行计算．解答：解：∵a∥b，∴△BCD的面积：△ABC的面积=CD：AB=3：2，∴△BCD的面积=6×=9．故答案为：9．点评：此题考查了平行线间的距离以及三角形的面积比的一种方法，即等高的两个三角形的面积比等于它们的底的比．19．如图，将两个大小一致的小正方形沿对角线剪开，拼成一个大正方形ABCD，若小正方形的边长是1厘米，则大正方形ABCD的边长是厘米．考点：正方形的性质．专题：数形结合．分析：易得大正方形的面积，求得大正方形面积的算术平方根即为所求的边长．解答：解：∵小正方形的边长是1厘米，∴小正方形的面积为1平方厘米，∴大正方形的面积为2平方厘米，∴大正方形的边长为厘米，故答案为．点评：考查有关正方形的计算；根据正方形的面积求边长是解决此类问题的基本思路．20．一个角的两边与另一个角的两边分别平行，其中一个角为40°，则另一角为40°或140°．考点：平行线的性质．分析：由一个角的两边与另一个角的两边分别平行，可得这两个角相等或互补，又由其中一个角为40°，则可求得另一角的度数．解答：解：∵一个角的两边与另一个角的两边分别平行，∴这两个角相等或互补，∵一个角为40°，∴另一角为：40°或140°．故答案为：40°或140°．点评：此题考查了平行线的性质．此题比较简单，解题的关键是掌握若一个角的两边与另一个角的两边分别平行，则这两个角相等或互补．三、计算题（共5题，21、22每题5分，23、24、25每题6分，满分28分）21．计算：﹣++．考点：二次根式的加减法．分析：直接合并同类项即可．解答：解：原式=（﹣++）=（4﹣1）=3．点评：本题考查的是二次根式的加减法，熟知二次根式相加减，先把各个二次根式化成最简二次根式，再把被开方数相同的二次根式进行合并，合并方法为系数相加减，根式不变是解答此题的关键．22．计算：×（）﹣1÷．考点：二次根式的乘除法．分析：先算负指数幂，再从左向右的顺序运算即可．解答：解：×（）﹣1÷=×÷，=3÷，=3．点评：本题主要考查了二次根式的乘除法，解题的关键是熟记二次根式的乘除法的法则．23．计算：×（﹣）2×÷．考点：二次根式的乘除法．分析：先开方及乘方，再从左向右运算即可．解答：解：×（﹣）2×÷=（﹣1）×3×÷，=（9﹣3），=9﹣3．点评：本题主要考查了二次根式的乘除法，解题的关键是熟记二次根式的乘除法的法则．24．计算：3﹣27+（）﹣2﹣（+2）0．考点：二次根式的混合运算；分数指数幂；零指数幂；负整数指数幂．分析：利用分数指数幂，零指数幂及负整数指数幂的法则结合二次根式的混合运算顺序求解即可．解答：解：3﹣27+（）﹣2﹣（+2）0=﹣3+3﹣1，=﹣1．点评：本题主要考查了二次根式的混合运算，解题的关键是熟记分数指数幂，零指数幂及负整数指数幂的法则．25．利用幂的运算性质计算：2×÷．考点：分数指数幂．分析：首先分别求出2、、的值各是多少，然后根据同底数幂的乘法、同底数幂的除法的运算方法，求出算式2×÷的值是多少即可．解答：解：2×÷=2×=23=8点评：（1）此题主要考查了分数指数幂问题，要熟练掌握，解答此题的关键是求出2的值是多少．（2）此题还考查了同底数幂的乘法、同底数幂的除法的运算方法，要熟练掌握．四、解答题（共4题，26、27、28每题6分，29题8分，满分26分）2）在图中画出表示点P到直线a距离的线段PM；（2）过点P画出直线b的平行线c，与直线a交于点N；（3）如果直线a与b的夹角为40°，那么∠MPN=50°．考点：作图—基本作图．分析：（1）以点P为圆心，以大于点P到a的距离的长度为半径画弧，与直线a相交于两点，再分别以这两点为圆心，以大于它们之间距离的一半为半径画弧，两弧相交于一点，过这一点与点P 作直线，与a相交于点M，PM就是所要求作的垂线段；（2）以点P为顶点，画一条直线为一边，作∠P等于这条直线与直线b所成的夹角，则∠P的另一边所在的直线就是所要求作的直线c；（3）根据两直线平行，内错角相等求出∠MNP=∠40°，再根据直角三角形的两锐角互余即可求出∠MPN的度数．解答：解：（1）如图1所示，PM就是所要求作的点P到直线a距离的垂线段；（2）如图2所示，直线c就是所要求作的直线b的平行线；（3）如图3，∵直线a与b的夹角为40°，∴∠PNM=40°，∴∠MPN=90°﹣40°=50°．故答案为：50°．点评：本题考查了过直线外一点作已知直线的垂线，过直线外一点作已知直线的平行线，以及平行线的性质，直角三角形两锐角互余的性质，是小综合题，难度不大，只要细心便不难求解27．如图，已知AB∥CD，∠1=（4x﹣25）°，∠2=（85﹣x）°，求∠1的度数．考点：平行线的性质．专题：探究型．分析：先根据平行线的性质得出∠3的度数，再根据∠1=∠3可知∠1+∠2=180°，把，∠1=（4x﹣25）°，∠2=（85﹣x）°代入求出x的值，进而可得出结论．解答：解：∵AB∥CD，∴∠2+∠3=180°（两直线平行，同旁内角互补）．∵∠1=∠3（对顶角相等）∴∠1+∠2=180°，即（4x﹣25）+（85﹣x）=180，解得x=40．∴∠1=4x﹣25°=135°．点评：本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．28．已知：如图，∠A=∠D，∠B=∠C，那么∠1与∠2互补吗？为什么？考点：平行线的判定与性质．分析：首先根据内错角相等得两条直线平行，再根据平行线的性质得内错角相等，运用等量代换的方法得∠AFC=∠D，再根据平行线的判定得两条直线平行，从而根据平行线的性质证明结论．解答：解：∠1与∠2互补．理由如下：∵∠C=∠B，∴AB∥DC，∴∠A=∠AFC，∵∠A=∠D，∴∠AFC=∠D；∴AF∥ED，∴∠1+∠2=180°．点评：此题考查平行线的判定和性质，注意综合运用平行线的性质与判定．2）如图（a），如果∠B+∠E+∠D=360°，那么AB、CD有怎样的关系？为什么？解：过点E作EF∥AB，如图（b），则∠ABE+∠BEF=180°（两直线平行，同旁内角互补）因为∠ABD+∠BED+∠EDC=360°（已知）所以∠FED+∠EDC=180°（等式的性质）所以EF∥CD（同旁内角互补，两直线平行）所以AB∥CD时，∠1，∠2，∠3，∠4满足∠1+∠3=∠2+∠4．考点：平行线的性质．分析：过点E作EF∥AB，由平行线的性质可得出∠ABE+∠BEF=180°，∠ABD+∠BED+∠EDC=360°可得出∠FED+∠EDC=180°，故可得出FE∥CD，由此可得出结论．解答：解：过点E作EF∥AB，如图（b），则∠ABE+∠BEF=180°（两直线平行，同旁内角互补）．因为∠ABD+∠BED+∠EDC=360°（已知），所以∠FED+∠EDC=180°（等式的性质），所以EF∥CD（同旁内角互补，两直线平行），所以AB∥CD时，∠1，∠2，∠3，∠4满足∠1+∠3=∠2+∠4．故答案为：两直线平行，同旁内角互补，180，等式的性质，同旁内角互补，两直线平行，∠1+∠3=∠2+∠4．点评：本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．五、综合题（满分6分）30．皓皓同学在学习了“平方根”这节课后知道了“负数在实数范围内没有平方根”，她对这句话产生了兴趣，她想知道负数在其他范围内是否有平方根，所以她上网查找了以下一些资料．数的概念是从实践中产生和发展起来的，在学习了实数以后，像x2=﹣1这样的方程还是没有实数解的，因为没有一个实数的平方等于﹣1，即负数在实数范围内没有平方根，所以为了了解形如x2=﹣1这类方程的解，就要引入一个新的数i．定义：如果一个数的平方等于﹣1，记为i2=﹣1，这个数i叫做虚数单位．在这种情况下，i可以与实数b相乘再同实数a相加从而得到形如“a+bi”（a、b为实数）的数，人们把这种数叫作复数，a叫这个复数的实部，b叫做这个复数的虚部．它的加、减、乘法运算与整式的加、减、乘法运算类似．比如：（1）（2+i）+（4﹣3i）=6﹣2i（2）（i）2=﹣3（3）（5+i）（5﹣i）=52﹣i2=25﹣（﹣1）=26这样数的范围就由实数扩充到了复数，在这种规定下，负数在复数范围内就有平方根．比如：±i就是﹣1的平方根．根据上面的材料解答以下问题：（1）计算：①（2+i）﹣（3﹣2i）=﹣1+3i②i3=﹣i③（3+i）2=8+6i（2）在负数范围内﹣9的平方根是±3i（3）在复数范围内分解因式x4﹣4=（x+）（x﹣）（x+i）（x﹣i）．考点：实数的运算；因式分解的应用．专题：阅读型．分析：（1）①根据合并同类项法则计算即可；②根据积的乘方进行运算，③根据完全平方公式计算；（2）根据平方根的概念计算；（3）根据因式分解的方法进行计算即可．解答：解：（1）①（2+i）﹣（3﹣2i）=2+i﹣3+2i=﹣1+3i，②i3=i2•i=﹣i，③（3+i）2=9+6i+i2=8+6i；（2）±=±3i；（3）x4﹣4=（x2+2）（x2﹣2）=（x+i）（x﹣i）（x﹣）（x+）．故答案为：（1）①﹣1+3i②﹣i③8+6i；（2）±3i；（3）（x+i）（x﹣i）（x﹣）（x+）．点评：本题考查的是实数的运算和因式分解的应用，理解新定义、正确运用因式分解的方法是解题的关键．。

七下数学周末练习1一、选择题：1．在下列四个汽车标志图案中，能用平移变换来分析其形成过程的图案是【 】2．∠1与∠2是两条直线被第三条直线所截的同位角，若∠1＝50°，则∠2为【 】A 、50°B 、130°C 、50°或130°D 、不能确定3．下列五幅图案中，⑵、⑶、⑷、⑸中的哪个图案可以由(1)图案平移得到？【 】 A ．⑵ B ．⑶ C ．⑷ D ．⑸4.下列图形中，由AB CD ∥，能得到12∠=∠的是【 】5.以下列各组线段长为边，能组成三角形的是【 】A ．1cm ，2cm ，4cmB ．7cm ，6cm ，5cm ；C ．12cm ，6cm ，6cmD ．2cm ，3cm ，6cm 6.如图11，OP∥QR∥ST，则下列各式中正确的是【 】 A ．∠1＋∠2＋∠3＝180° B ．∠1＋∠2－∠3＝90° C ．∠1－∠2＋∠3＝90° D ．∠2＋∠3－∠1＝180°7.如图是一块电脑主板的示意图，每一转角处都是直角，数据如图所示，则该主板的周长是 【 】 A ．88mm B ．96mm C ．80mm D ．84mm8.在同一平面内，有12条互不重合的直线 ，若 ，2l ∥3l ，43l l ⊥，4l ∥5l ……以此类推，则1l 和12l 的位置关系是【 】A 、平行B 、垂直C 、平行或垂直D 、无法确定9.如图，一个人从A 点出发向北偏东30°方向走到B 点，再从B 点出发向南偏东15°方向走到C 点，那么∠ABC 等于【 】 A 、45° B 、75° C 、90° D 、105°10．如图，Rt△ABC 中，∠ACB=90°，∠A=55°，将其折叠，使点A 落在边CB 上A′处，折痕为CD ，则∠A′DB=【 】 A ． 40° B ．30° C ．20° D ．10°二、填空题：1.等腰三角形两边长分别为3、7，则其周长为 ；2.如图，直线b a ,被直线l 所截，∠3=50°，当∠1=_______°时，a ∥b ；3.一个三角形的两边长是3cm 和4cm ，周长是整数，则这样的三角形有_______个．4.如图，AD ∥BC ，BD 平分∠ABC ，且∠A ＝100°，则∠D ＝______度；5.如图大矩形的长10cm ，宽8cm ，阴影部分的宽2cm ，则空白部分的面积是 _cm2。