材料力学课后答案第12章 习题解答PPT课件

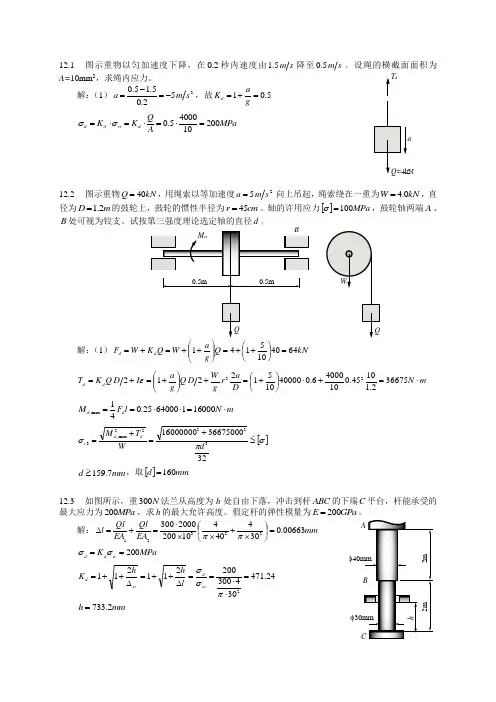
12.1 图示重物以匀加速度下降，在2.0秒内速度由s m 5.1降至s m 5.0。

设绳的横截面面积为A=10mm 2，求绳内应力。

解：（1）252.05.15.0s m a -=-=，故5.01=+=g a K dMPa A Q K K d st d d 2001040005.0=⋅=⋅=⋅=σσ12.2 图示重物kN Q 40=，用绳索以等加速度25s m a =向上吊起，绳索绕在一重为kN W 0.4=，直径为m D 2.1=的鼓轮上，鼓轮的惯性半径为cm r 45=。

轴的许用应力[]MPa 100=σ，鼓轮轴两端A 、B解：（1）kN Q g a W Q K W F d d 6440105141=⎪⎭⎫ ⎝⎛++=⎪⎪⎭⎫ ⎝⎛++=+= m N D a r g W D Q g a I D Q K T d d ⋅=+⋅⎪⎭⎫ ⎝⎛+=+⎪⎪⎭⎫ ⎝⎛+=+=366752.11045.01040006.0400001051221222ε m N l F M d d ⋅=⋅⋅==1600016400025.041max , []σπσ≤+=+=32366750001600000032222max ,3d WT M d d rmm d 7.159≥，取[]mm d 160=12.3 如图所示，重N 300法兰从高度为h 处自由下落，冲击到杆ABC 的下端C 平台，杆能承受的最大应力为MPa 200，求h 的最大允许高度。

假定杆的弹性模量为E 200=解：mm EA Ql EA Ql l 00663.030440410200200030022321=⎪⎭⎫ ⎝⎛⨯+⨯⨯⋅=+=∆ππ MPa K st d d 200==σσ24.4713043002002112112=⋅⋅==∆++=∆++=πσσst d st d l h h K mm h 2.733=12.4 如图所示，重N 100物体从mm h 500=位置自由下落到铝制梁AB 上的C 点，求截面C 的位移和梁上的最大应力。

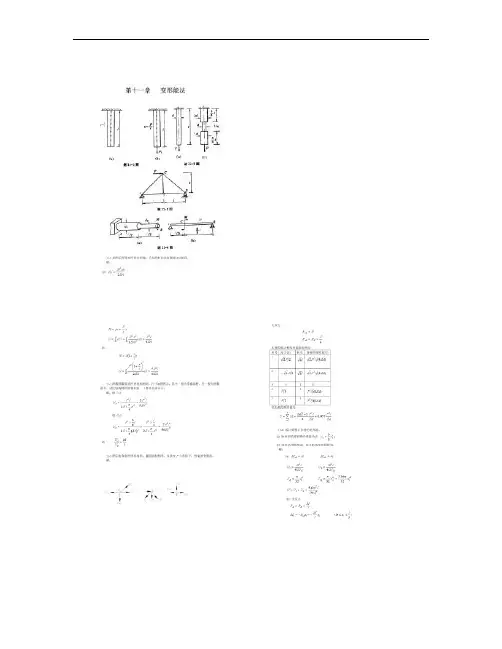
− LP ⋅ sin α ⋅ L ⋅ δ CH = EJ L 2L L PL cos α ⋅⋅ 3 2 3 = Pl ( 2 cos α − 3sin α 2+ EJ 6 EJ δ cv δ CH 3 ⎛⎞ 2 ⎜ 4sin α − cos α ⎟ 2 ⎠ = tgα = ⎝ ( 2 cos α − 3sin α 8 − 3ctgα = 2 − 3tgα ctgα − tgα = 2 ，2tgα 1 − tg 2α 2tgα =1 1 − tg 2α ∵ tg 2α =α l T2 T1 B b h ∴ tg 2α = 1 ，α = 22.5� 11-29 图示矩形截面梁 AB，设其底面和顶面的温度分别升高 T1oC 和 T2oC，沿横截面高度按线性规律变化，试用单位载荷法计算 A 端横截面的铅垂位移和水平位移。

解：dθ = a ( T1 − T2 dx h d 2v dx 2 = ∴ d 2 v a (T1 − T2 = dx 2 h M = EJa ( T1 − T2 h ∵ M = EJ l yA = ∫ ' xA =∫ 0 MM y dx 0 EJ al 2 (T1 − T2 2h 0 MM x dx l = a (T1 − T2 0 EJ 2 l求的单位力求水平位移的单位力由于梁轴线因 T1 ， T2 影响将发生平位移xA '' xA = a (T1 + T2 '' l 2 ∴ ' '' xA = xA + xA = a ⋅ L ⋅ T1 11-30 图示三角支架，两杆横截面面积均为 A ，材料相同，材料的应力 - 应变关系是σ = B ε ，其中 B 为常数，这一关系对于拉伸和压缩是相同的。

试用虚功原理求 A 节点的水平位移与铅直位移。

解：L2 = L cos α ， L1 = LN2 = P sin α 2 ，N1 = Pctgα 2 ⎛ σ ⎞⎛ Pctgα ⎞ ε1 = ⎜ 1 ⎟ = ⎜⎟⎝ B ⎠⎝ A⋅B ⎠ P ⎛⎞ ε2 = ⎜⎟⎝ A ⋅ B sin α ⎠ 2 ⎛ Pctgα ⎞ ∆1 = L ⋅ ε1 = l ⋅⎜⎟⎝ A⋅ B ⎠∆2 = 2 l l ⎛ P ⎞⋅ε2 = ⋅⎜⎟ cos α cos α ⎝ A ⋅ B sin α⎠∆1 cos α + ∆ 2 sin α 2 0 δ AV = N10 ⋅ ∆1 + N 2 ⋅ ∆2 = 0 δ AH = N10 ⋅ ∆1 + N 2 ⋅ ∆ 2 = ∆1。

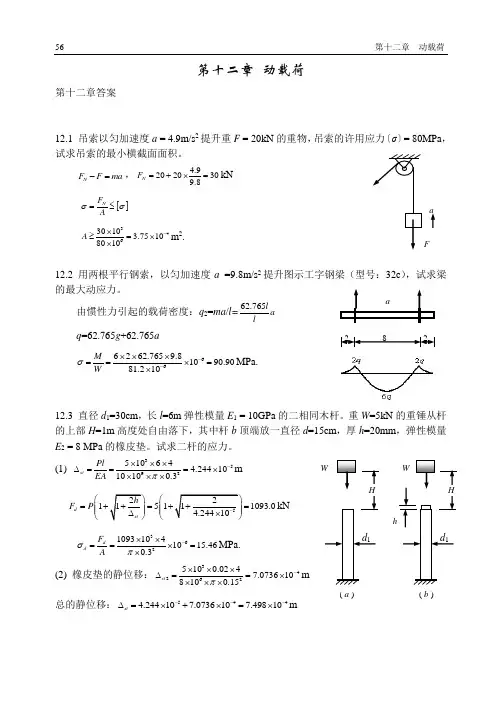
56 第十二章 动载荷第十二章 动载荷第十二章答案12.1 吊索以匀加速度a = 4.9m/s 2提升重F = 20kN 的重物，吊索的许用应力〔σ〕= 80MPa ，试求吊索的最小横截面面积。

N F F ma -=， 4.92020309.8N F =+⨯=kN []NF Aσσ=≤ 3463010 3.75108010A -⨯≥=⨯⨯m 2.12.2 用两根平行钢索，以匀加速度a =9.8m/s 2提升图示工字钢梁（型号：32c ），试求梁的最大动应力。

由惯性力引起的载荷密度：q 2=ma /l=62.765la lq =62.765g +62.765a 666262.7659.81090.9081.210M W σ--⨯⨯⨯==⨯=⨯MPa.12.3 直径d 1=30cm ，长l =6m 弹性模量E 1 = 10GPa 的二相同木杆。

重W =5kN 的重锤从杆的上部H =1m 高度处自由落下，其中杆b 顶端放一直径d =15cm ，厚h =20mm ，弹性模量E 2 = 8 MPa 的橡皮垫。

试求二杆的应力。

(1) 3592510644.2441010100.3st Pl EA π-⨯⨯⨯∆===⨯⨯⨯⨯m 1511093.0d F P ⎛⎛=== ⎝⎝kN 36210931041015.460.3d d F A σπ-⨯⨯==⨯=⨯MPa. (2) 橡皮垫的静位移：342625100.0247.0736108100.15st π-⨯⨯⨯∆==⨯⨯⨯⨯m 总的静位移：5444.244107.0736107.49810st ---∆=⨯+⨯=⨯maF( a )( b )第十二章 动载荷 5751260d F ⎛== ⎝kN 362260.710410 3.690.3d σπ-⨯⨯=⨯=⨯MPa. 12.4 图示装置,直径d = 4cm ,长l = 4m 的钢杆,上端固定,下端有一托盘,钢杆的弹性模量 E = 200GPa,许用应力〔σ〕=120MPa,弹簧刚度k =160kN/cm,自由落体重P = 20kN,试求容许高度h 为多少。

材料力学习题第12章12-1 一桅杆起重机，起重杆AB 的横截面积如图所示。

钢丝绳的横截面面积为10mm 2。

起重杆与钢丝的许用力均为MPa 120][=σ，试校核二者的强度。

12-2 重物F =130kN 悬挂在由两根圆杆组成的吊架上。

AC 是钢杆，直径d 1=30mm ，许用应力[σ]st =160MPa 。

BC 是铝杆，直径d 2= 40mm, 许用应力[σ]al = 60MPa 。

已知ABC 为正三角形，试校核吊架的强度。

12-3 图示结构中，钢索BC 由一组直径d =2mm 的钢丝组成。

若钢丝的许用应力[σ]=160MPa,横梁AC 单位长度上受均匀分布载荷q =30kN/m 作用，试求所需钢丝的根数n 。

若将AC 改用由两根等边角钢形成的组合杆，角钢的许用应力为[σ] =160MPa ，试选定所需角钢的型号。

12-4 图示结构中AC 为钢杆，横截面面积A 1=2cm 2；BC 杆为铜杆，横截面面积A 2=3cm 2。

[σ]st = 160MPa ，[σ]cop = 100MPa ，试求许用载荷][F 。

12-5 图示结构，杆AB 为5号槽钢，许用应力[σ] = 160MPa ，杆BC 为b h = 2的矩形截面木杆，其截面尺寸为b = 5cm, h = 10cm,许用应力[σ] = 8MPa ，承受载荷F = 128kN ，试求：（1）校核结构强度；（2）若要求两杆的应力同时达到各自的许用应力，两杆的截面应取多大？ 12-6 图示螺栓，拧紧时产生∆l 的轴向变形，试求预紧力F ，并校核螺栓强度。

已知d 1=8mm, d 2=6.8mm, d 3=7mm, l 1=6mm, l 2=29mm, l 3=8mm; E =210GPa, [σ]=500MPa 。

12-7 图示传动轴的转速为n=500r/min ，主动轮1输入功率P 1=368kW ，从动轮2和3分别输出功率P 2=147kW 和P 3=221kW 。