谐波分析实验-精74-潘杰-2007010586

简谐振动中的谐波实验探究在物理学中，简谐振动是一种重要的现象，它具有周期性和谐波性质。

在本文中，我们将探究简谐振动中的谐波实验，以了解谐波的产生和性质。

本实验使用简单的装置和仪器，通过实际观察和数据分析，揭示了谐波的奇妙之处。

实验所需材料和装置：1. 弹簧振子：用来实现简谐振动的主要装置，由弹簧和挂在其上的质量块组成。

2. 直尺：用于测量振子的位移。

3. 计时器：用于测量振子的振动周期。

4. 铅笔和纸：用于记录实验数据。

实验步骤：1. 将弹簧振子固定在水平位置，并保持其自由悬挂。

2. 将振子拉至一定位移，然后松开，观察振子的振动情况，并用直尺测量振子的位移。

3. 启动计时器，并记录振子完成一个完整的往复振动所需的时间，即振动周期。

4. 重复步骤2和3，至少进行5次实验，以获得准确的数据。

数据分析：1. 绘制振子的位移-时间图像，通过该图像可以观察到振子的周期性振动。

2. 根据记录的振动周期数据，计算出平均振动周期。

讨论和结论：通过上述实验，我们可以得出以下结论：1. 弹簧振子在受到外力作用下产生了简谐振动，并具有周期性。

2. 振子的位移随时间的变化呈现谐波形态，这是谐波性质的体现。

3. 根据实验数据和计算结果，我们可以验证振子的平均振动周期与弹簧的劲度系数和挂在弹簧上的质量无关。

实验的局限性：1. 实验中未考虑其他因素对振子的影响，如空气阻力、振子本身的摩擦等。

2. 实验中所使用的弹簧振子可能存在一定的误差，对结果的准确性可能有一定影响。

推广和应用：谐波在许多领域中都有广泛的应用，例如声学、电磁学和光学等。

掌握谐波的产生和性质对于我们理解自然界中的现象以及应用于工程和技术领域具有重要意义。

通过这个实验，我们可以进一步学习和深入研究谐波的其他方面，如共振、阻尼等。

总结：简谐振动中的谐波实验探究了谐波的产生和性质。

通过实际观察和数据分析，我们发现弹簧振子在受到外力作用下能够产生周期性的谐波振动，并且振子的位移随时间的变化呈现谐波形态。

1.测正弦波的电压和频率
（1）从信号发生器输出一个正弦信号到CH1，设好信号的输出幅度及频率，调节示波器Time/div按钮，使波形显示幅度合适、显示一两个稳定的正弦波，记下频率f和峰值电压Vp-p.
（2）利用网格线测出正弦波的波峰到波谷的垂直距离dy，并记录Vol/div的值
（3）计算Vp-p=a*dy
五、数据处理:
次数
dy
V/div
Vpp
1
5.2cm
0.2V/cm
1.04V
2
2.1cm
0.5V/cm
1.05V
次数
dx
T/div
T
1
1.9cm
5ms/cm
9.5ms
2
3.8cm
2.5ms/cm
9.5ms
fx(Hz)
fy(Hz)
图形
nx
ny
fx:fy
nx:ny
1
100
100
1
1
1:1
1:1
2
100
200
2、双踪示波器的原理：电子开关使两个待测电压信号YCH1和YCH2周期性地轮流作用在Y偏转板，这样在荧光屏上忽而显示YCH1信号波形，忽而显示YCH2信号波形。由于荧光屏荧光物质的余辉及人眼视觉滞留效应，荧光屏上看到的是两个波形。当扫描信号的周期与被测信号的周期一致或是整数倍，屏上一般会显示出完整周期的正弦波形。
3.将两信号分别接入CH1和CH2，对应做好记录。将示波器的屏幕显示波形，选择列表里，选中CH1，CH2下的X-Y。
4.不能；同步旋钮是使每次扫描都扫描同一个起始相位，使一个示波器内只有一个稳定的图形,但从李萨如图形的形成原理来看,调同步旋钮式不能使它稳定下来的。应该是调频率。

3. 同步附加转矩
• 同步附加转矩产生条件： 产生转矩的定子、转子磁场彼此独立； 定子、转子磁场极对数相等； 定子、转子磁场相对静止（即在某一转子 转速下该定子、转子磁场空间转速相同） • 以上条件见 p.36 式（2-16），（2-17）
• 当µa=νb ，堵转时产生同步附加转矩 • 当µa=－νb，产生同步附加转矩时转子转速 nst=－120 f / k Z2 见p.36 式（2-18） • 产生同步附加转矩的槽配合见p.47表2-15， 应注意避免或采取措施削弱
• 式（2-21）最后一项∑bν×∑ bµ可能包含低 阶次径向力 由 νb次定子磁场与 µa次转子磁场作用产生的 一对径向力波阶次见式（2-22） 力波 频率见式（2-23） 槽配合36/28的力波次数/力波频率示例见 表2-10 • mi =νb ±µa 为小的整数时，成为产生磁噪 声的强大力波
• 径向力 fr =b2 /2µ0 波 bp见p.32 式（2-11）； 定子谐波 bν见p.32 式（2-12）； 转子谐波 bµ见p.35 式（2-14）
基
• 径向力可表示为各种不同阶次和角频率的 旋转力波的合成 见 p.38 式（2-20），图示见 图2-14 重点注意mi≤4 低阶次径向力波
• Fp×λ0---基波磁场 ∑Fν×λ0---定子磁动势谐波磁场 ∑Fµ×λ0---转子磁动势谐波磁场 Fp×∑λ1---定子磁导谐波磁场 Fp×∑λ2--转子磁导谐波磁场 • 基波磁场 极对数p 转速n1=60 f/p ( r/min)
f---电源频率
• 磁动势谐波分 解 1—实际磁动势 2—相带电流均布 时磁动势 3—齿谐波磁动势 （1，2之差） 4—基波磁动势 5—相带谐波磁动 势（2，4之差）
a) mi=0

文库资料 ©2016 Guangzhou ZHIYUAN Electronics Stock Co., Ltd.文章源自ZLG 致远电子，转载或引用请注明出处1 谐波分析实验及习题思考一、实验目的1、检测电机在不同负载运行状态下的50次谐波畸变率及各次谐波幅值2、分析电机控制器输出电力的品质。

二、实验步骤1、检查系统。

检查系统接线，电源电压是否正常，插座是否已经插好，如无异常，开启控制柜电源，打开电机测试软件，查看控制柜绿灯是否点亮，完成后系统准备就绪。

2、进入测试界面。

查看配置信息，是否和实际的信息一致，如果一致即可进入测试阶段。

打开，进入开放测试界面，点击按钮启动开放测试。

这时，如果有勾选更新数据选项，数据显示栏将会有部分数据显示跳动；如无，只需要将更新数据选项勾选上，即可在数据显示栏里显示数据。

图19.1 勾选使能与更新数据3、点击使能负载和使能被测，在负载转速和油门比例输入栏里边输入数据，在“负载转速（rpm ）”输入栏里边输入“600”，然后“回车”，速度稳定后后在“油门比例（%）”的输入栏里边输入“20”然后“回车”。

4、通过功率分析仪，查看并记录驱动器输出的谐波畸变率，谐波幅值等相应的数据（具体操作请查看功率分析仪的使用手册）。

5、改变运行状态，测试不同运行状态下的谐波畸变率和相关参数。

注意：调节油门时，避免调节跨度太大，以免PID 过程中损坏设备。

如果发生电机运行状态异常，请立即结束测试，有必要时请按下红色急停开关。

6、根据已有的数据分析电机控制器的输出电力品质。

三、实验总结和思考1、驱动器输出的谐波畸变率，谐波幅值等相应数据和电机的运行状态有什么关系？2、驱动器输出为什么会存在谐波，跟驱动器驱动的算法有什么关系？查找资料是否有办法降低谐波畸变率？。

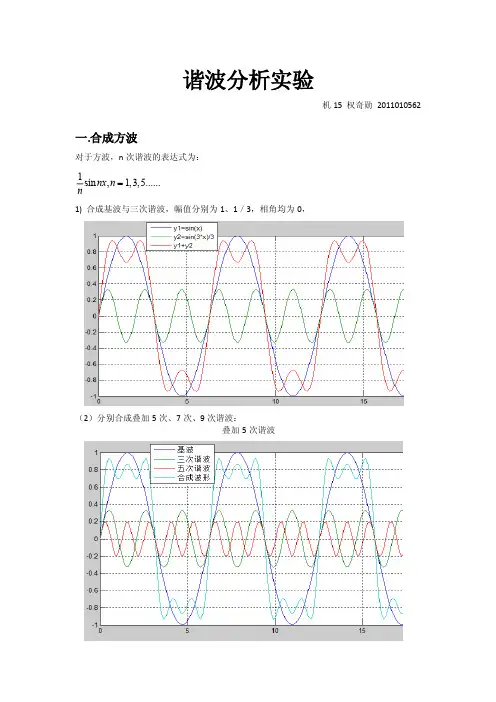
谐波分析实验机15 权奇勋2011010562一.合成方波对于方波，n次谐波的表达式为：1sin nx,n=1,3,5......n1) 合成基波与三次谐波，幅值分别为1、1／3，相角均为0，（2）分别合成叠加5次、7次、9次谐波：叠加5次谐波叠加7次谐波叠加9次谐波通过观察波形，发现：叠加谐波次数越高，合成波形越趋近于方波。

（3）分别改变3、5次谐波与基波间的相角，研究谐波间相角改变对合成波形的影响将3次谐波的初相角改为-π/2将5次谐波的初相角改为-π/2分析结论：改变谐波与基波间的相角，会使合成波形与方波相比有较大的失真。

且改变相角的谐波次数越低，失真越大。

（4）分别改变3、5次谐波与基波间的幅值比例关系，研究谐波间幅值比例改变对合成波形的影响3次谐波幅值改为(1/3)×2=2/35次谐波幅值改为(1/5)×2=2/5分析结论：改变谐波的幅值，会使合成波形与方波相比产生失真；且幅值改变的倍率相同的情况下，改变谐波的次数越低，失真越大。

二.合成锯齿波（最高谐波次数选为9）对于锯齿波，n次谐波的表达式为：π1nx+p),n=1,2,3......1)合成波的形状与谐波次数的关系叠加2次谐波叠加4次谐波叠加9次谐波通过观察波形，发现：叠加谐波次数越高，合成波形越趋近于锯齿波。

（2）分别改变2、4次谐波与基波间的幅值比例关系2次谐波的幅值改为(1/2)×2=14次谐波的幅值改为(1/4×2)=1/2分析结论：改变谐波的幅值，会使合成波形与锯齿波相比产生失真；且幅值改变的倍率相同的情况下，改变谐波的次数越低，失真越大。

（3）分别改变2、4次谐波与基波间的相角2次谐波的初相角改为pi+pi/2=3pi/24次谐波的初相角改为pi+pi/2=3pi/2分析结论：改变谐波与基波间的相角，会使合成波形与锯齿波相比有较大的失真。

且改变相角的谐波次数越低，失真越大。

三.合成三角波（最高谐波次数选为9）对于三角波，n次谐波的表达式为：π×π1nx,n=1,3,5......1)合成波的形状与谐波次数的关系叠加3次谐波叠加5次谐波叠加9次谐波通过观察波形，发现：叠加谐波次数越高，合成波形越趋近于三角波。

ipiq谐波检测实验报告1．引言随着现代工业和科学技术的发展，电力电子装置被广泛应用，在为人类创造物质文明的同时也导致人量谐波注入电网，使电网电压和电流波形发生畸变，电能质量日益下降"。

使用无源滤波装置来解决无功和谐波问题是一种传统的解决方案，但存在许多缺点，为此有源电力滤波器(Active Power Filter，APF)应运而生2。

这种装置通过向电网注入与原有谐波和无功电流大小相等方向相反的补偿电流，使电网的总谐波和无功电流为零，从而达到净化电网的目的，因而受到广泛的应用。

对于有源电力滤波器而言，实时准确地检测出谐波电流是非常关键的，它直接决定了装置的整体滤波性能。

目前应用最为广泛的检测万法是基于瞬北2功率理论的ip-iq法。

该方法采用内部的参考正余弦信号,没有直接使用系统电压信息参与运算，不受电网电压畸变或不对称的影响，因此检测的结果更准确"。

本文在阐述ip-iq。

谐波检测法的原理基础上建立了该算法的仿真模型，并构建了相应的实验系统，设计了电流信号调理电路和锁相环及倍频电路等硬件电路。

从仿真和实验研究两方面验证该算法的合理性与准确性。

2. ip-iq谐波检测法的原理三相瞬时无功功率理论自1983年由赤木论泰文提出以来，首先在谐波和无功电流实时检测方面得到了成功应用l5。

以该理论为基础，计算ip、iq ,为出发点可以得出三相电路谐波电流检测方法，称之为ip-iq检测法。

根据瞬时无功功率理论可推导出瞬时有功电流i,和瞬时无功电流i,的表达式为该方法中,需用到与A相电网电压e,同相位的正弦信号sinot和对应的余弦-cosot，它们由一个锁相环和一个正、余弦信号发生电路得到。

根据定义可以计算出i,、iq，经低通滤波器滤波得出i,、iq的直流分量ip、iq。

这里，ip、 iq是由i f、iof、ie产生的，因此由ip、iq即可计算出iar、ir、ie为将i、i、ic与iaf、ior、iex相减，进而计算出i、ib、ic的谐波分量ia、 ioh 、 ich3．仿真及实验系统设计3.1仿真模型的建立为了验证ip-i,检测法的可行性和准确性，我们首先从仿真的角度出发，建立了如图2所示的仿真模型，实现了ip-i,算法的功能,并在Matlab/Simulink环境下对其进行仿真，主要包括C32、C 计算模块、低通滤波器模块以及反变换C1、Cz;模块。

a、将3次谐波的相角改为-π/2：
b、将3次谐波的相角改为+π/2：
c、将5次谐波的相角改为-π/2：
d、将5次谐波的相角改为+π/2：
分析结论：改变谐波与基波的相角会使合成波形与理想状态相比有较大变形失真。
（4）改变3、5次谐波与基波幅值比例关系：
a、3次谐波幅值为1／18：
b、3次谐波幅值为2／9：
（3）锯齿波仅保留偶次谐波后输出波形图：
由波形图可见，此时输出的波的频率变为关闭奇次谐波之前的2倍，在本次实验中为4π。
分析结论：改变谐波与基波的相角会使合成波形与理想状态相比有较大变形失真。
（4）改变3、5次谐波与基波幅值比例关系：
a、3次谐波幅值为1／6：
b、3次谐波幅值为2／3：
c、5次谐波幅值为1／10：
d、5次谐波幅值为2／5：
分析结论：改变谐波的幅值会使合成波形产生失真。
可见与前述方波相比，锯齿波谐波幅值不变为1/n（反比例逐次减小），但包含有偶次谐波，且相角都为π。
方波：
锯齿波：
三角波：
三种波形的相频图（最高9次谐波）：
方波：
锯齿波：
三角波：
二、问题讨论
（1）由“一、1、（3）（4）”的分析结论可见，相角对波形影响大。对于“一、1、”中的方波，改变相角会使整个波形产生较大变形失真，但改变幅值只会对波峰波谷处的波形有较大影响。
（2）用正弦波表合成“一、3、”中三角波时，由三角变换关系可知此种情况下相角相对“一、1、”中方波为π/2（见下图），即三种波都用正弦波叠加而成时，若方波相角为0，则锯齿波相角为π，三角波为π/2。
c、5次谐波幅值为1／50：
d、5次谐波幅值为2／25：
分析结论：改变谐波的幅值会使合成波形产生较小失真。

实验一 谐波分析实验一、实验目的1）了解分解、合成非正弦周期信号的物理过程2）观察合成某一确定的周期信号时，所必须保持的合理的频率结构，正确的幅值比例和初始相位关系。

二、实验原理本实验主要运用傅立叶分解的方式对方波、锯齿波以及三角波进行分解与合成。

下面就对这三种波形的傅立叶分解原理进行介绍。

傅立叶分解原理对某一个非正弦周期信号X(t)（在有限区间上满足狄里赫利条件的函数），若其周期为T 、频率为f ，则可以分解为无穷项谐波之和。

即010100122()(cos sin )22sin()2sin(2)2n n n n n n n n n a n n x t a t b t T T a n A t T a A f t πππφπφ∞=∞=∞==++ =++ =++∑∑∑ 上式表明，各次谐波的频率分别是基波频率0f 的整数倍。

只要选择符合要求的不同频率成分和相应幅值比例及相位关系的谐波，便可近似地合成相应的方波、三角波等非正弦周期波形，以及任何在有限区间上满足狄里赫利条件的函数。

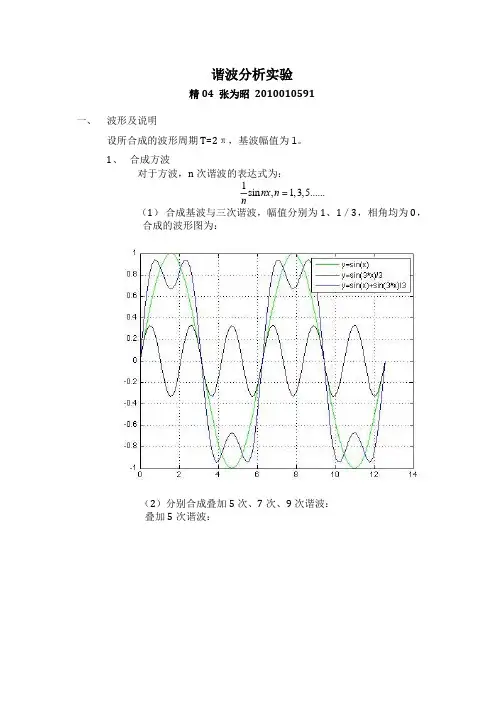
三、实验内容（一）方波1）方波的谐波分析，右图的一个方波(),022()0,2()()E T x t t T x t t T x t nT x t ⎧=≤≤⎪⎪⎪= ≤≤ ⎨⎪+=⎪⎪⎩进行谐波分析可知：00n a a ==/20/22()sin (1cos )2,1,3,5...0,2,4,6...T n T b x t n tdt T En n En n n ωπππ-= =-⎧ =⎪ =⎨⎪ =⎩⎰ 所以 000211()(sin sin 3sin 5...)35Ex t t t t ωωωπ=+++ 根据实验要求取基波的幅值为1，即212E E ππ=⇒=为了方便，可以取01ω=即方波可以展开成傅立叶级数为：11()(sin sin 3sin 5...)35x t t t t =+++2）合成方波根据讲义的讲解，编写以下程序实现功能要求 a 、一次谐波、三次谐波合成 x=0:4*pi/100:4*pi; y1=sin(x); y2=sin(3*x)/3;plot(x,y1,x,y2,x,y1+y2); grid onb 、一次谐波、三次谐波、五次谐波合成 x=0:4*pi/100:4*pi;y1=sin(x);y2=sin(3*x)/3;y3=sin(5*x)/5;plot(x,y1,x,y2,x,y3,x,y1+y2+y3);grid on之后的谐波合成类似，省略程序，得到的合成方波分别如图所示一次谐波、三次谐波、五次谐波、七次谐波合成方波一次谐波、三次谐波、五次谐波、七次谐波、九次谐波合成方波总结：方波可以通过谐波的叠加得到，叠加的谐波级次越高，方波的失真越小。

本章实训 谐波分析法的验证实训任务引入和介绍在电路分析的应用过程中，遇到非正弦周期电流电路的情况并不少见。

有时候，电流波形非常简单（如矩形波、三角波等），可以通过简单的计算得出其有效值、平均值及平均功率；但有时候非正弦周期电流的波形非常复杂，那么通过谐波分析法来进行电路分析就显得尤为重要。

本次实训我们就以一个简单的电路为基础，通过简单的理论计算和实际测量的结合来验证谐波分析法。

实训目的1.掌握非正弦周期电流电路的测量方法；2.理解谐波分析法的基本原理；3.学会用谐波分析法进行简单的电路分析。

实训条件 100V 直流电源、150V/50Hz 交流电源、100V/100Hz 交流电源、功率计、R=10Ω、L=1H 、C=1.11*103uF 、电压表、电流表。

操作步骤（1）连接电路。

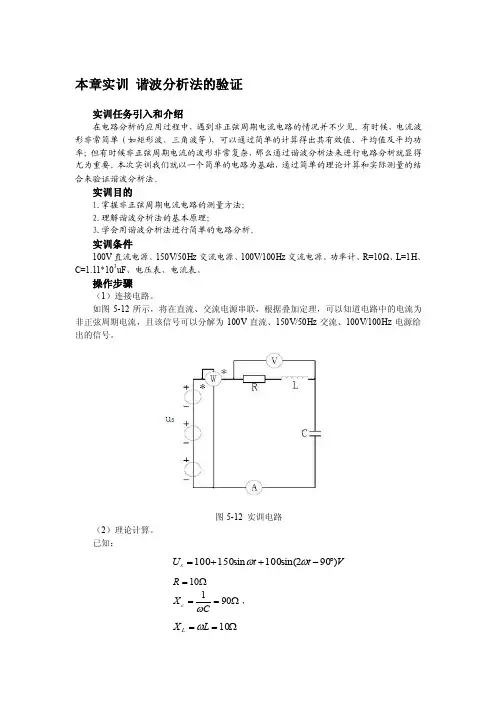
如图5-12所示，将在直流、交流电源串联，根据叠加定理，可以知道电路中的电流为非正弦周期电流，且该信号可以分解为100V 直流、150V/50Hz 交流、100V/100Hz 电源给出的信号。

图5-12 实训电路（2）理论计算。

已知：V t t U s )902sin(100sin 150100︒-++=ωωΩ=10RΩ==901CX c ω， Ω==10L X L ω① 直流分量作用于电路时，电感相当于短路，电容相当于开路。

故有：0,0,0000===P U I② 一次谐波作用于电路时，有：V U s ︒∠=021501A j X X j R U I C L s ︒∠=-+︒∠=-+=9.8232.1)9010(1002150)(1111 V j U ︒∠=+︒∠=9.1275.18)1010(9.8231.11③ 二次谐波作用于电路时，有：A j X X j R U I C L s ︒-∠=-+︒-∠=-+=8.2163.2)4520(10902100)(2222 V j U ︒∠=+︒-∠=6.418.58)2010(8.2163.22综合以上，根据谐波分析公式（5-11）、（5-12）及功率的计算公式，可计算得出电流、电压的有效值及有功功率：W P V U A I 6.861063.21032.17.618.585.18094.263.232.1022222222=⨯+⨯==++===++=（3）测量比较。

实验一谐波分析实验 2011010541 机14 林志杭一、实验目的1. 了解分解、合成非正弦周期信号的物理过程。

2. 观察合成某一确定的周期信号时，所必须保持的合理的频率结构，正确的幅值比例和初始相位关系。

二、实验原理对某一个非正弦周期信号x(t)，若其周期为T 、频率为f ，则可以分解为无穷项谐波之和。

即010012()sin()sin(2)n n n n n n nx t a A t Ta A nf t πϕπϕ∞=∞==++=++∑∑ 上式表明，各次谐波的频率分别是基波频率f 0的整数倍。

如果f(t)是一个锯齿波，其波形如图1所示，其数学表达式为：(), 02()()E Ex t t t TT x t nT x t =-≤≤+=-E/2E/2-T Ttx(t)图1对f(t)进行谐波分析可知00, , 2n n Ea A nφππ=== 所以101002()sin()2 sin(2)21 {sin(2)sin[2(2)]...}22n n E nx t t n TEnf t n E f t f t πππππππππππ∞=∞==+=+=++++∑∑即锯齿波可以分解成为基波的一次、二次•••n 次•••无数项谐波之和，其幅值分别为基波幅值的1n ，且各次谐波之间初始相角差为零（基波幅值为2Eπ）。

反过来，用上述这些谐波可以合成为一个锯齿波。

同理，只要选择符合要求的不同频率成份和相应的幅值比例及相位关系的谐波，便可近似地合成相应的方波、三角波等非正弦周期波形。

三、实验内容及操作步骤 1 合成方波周期方波信号x(t)在一个周期中的表达式为：1, 02() 1, 02T t x t T t ⎧--<<⎪⎪=⎨⎪<<⎪⎩波形如图2所示图2 方波波形傅立叶级数为：4, 1,3,5...0, b , 0(1,3,5...)0, 2,4,6...n n n n a n n n φπ⎧=⎪====⎨⎪=⎩展开成傅里叶级数表达式为：411()(sin sin 3sin 5...)35x t t t t π=+++ ①观察基波与三次谐波幅值分别为1、1/3，相位差为零时的合成波波形，如图3所示。

6 有效自由度
υeff = uc4 u +u υA υB
4 A 4 B
=1.67×107
[5] 刘智敏 ,刘风 .现代不确定度方法与应用 [M]. 北京 :中国计量 出版社,1997.
Veff →∞ 按此有效自由度， 当置信概率 P 取 95％时， 覆盖因子 k＝ 1.96
上接 11 页
参考文献：
模增益 Kd 无关。反馈网络通常是无源网络， 无源元件可选用 高稳定性的元件， 因而电路增益可获得很高的稳定性， 也就抑 制了运放参数变化引起的运算误差。 但是，在模拟运算电路中引入负反馈带来的潜在问题之 一， 是可能引起电路不稳定 （振荡 ） 。 由式 （8 ） 可知， 当环路增益 KdF=- 1 时， Kf →∞， 结果是电路阻塞 （lockup ） 或振荡。因 Kd 和 F 都是频率的函数， 故如何在可能的工作频率变化范围内， 都 不满足 KdF=- 1 的条件， 负反馈是需要仔细设计的[5,6]。 [1] 张国雄.测控电路[M].北京:机械工业出版社,2007:121- 138. [2] Bruce Carter, Thomas R. Brown. Handbook of Operational Amplifier Applications[EB/OL]. /lit/an/sboa09 2a/sboa092a.pdf, 2008- 05- 01. [3] Paul R Gray, Paul J Hurst, Stephen H Lewis, et al. Analysis and Design of Analog Integrated Circuits[M]. 4th ed. New York (NY, USA): John Wiley & Sons, 2001: 748- 803. [4] Bruce Carter. Noise Analysis in Operational Amplifier Circuits [EB/OL]./lit/an/slva043b/slva043b.pdf,2008- 0 4- 12. [5] Ron Mancini (Editor in Chief). Op Amps for Everyone[EB/OL]. /lit/an/slod006b/slod006b.pdf, 2008- 05- 10. [6] Benjamin C. Kuo, Farid Golnaraghi. Automatic Control Systems [M]. 8th ed. New York (NY, USA): John Wiley & Sons, 2003: 8- 11, 211- 232. [7] 周胜海,郭淑红.测控电路设计中运算放大器的若干误用 [J]. 电子质量,2008,(2):42- 44. [8] 周胜海,郭淑红 .基于低噪声运放的传感器前置放大器设计 [J].仪表技术与传感器,2006,(9):38- 40. 基金项目：河南省教育厅自然科学研究计划项目 （2009A510010 ）

谐波测试报告报告编号：XXXXX
测试日期：XXXX/XX/XX
测试对象：
型号：XXXXX
生产商：XXXXX
测试标准：
IEC61000-3-2，限值符合Class A标准
测试仪器：
万用表、电流夹、功率分析仪
测试环境：
温度：XX℃
湿度：XX%
电压：XXXV AC
测试结果：
1. 谐波电流测试结果：
序号频率 / Hz 电流 / A
1 50 0.1
2 100 0.3
3 150 0.2
4 200 0.1
5 250 0.1
6 300 0.2
7 350 0.1
8 400 0
9 450 0
10 500 0
2. 谐波总畸变率测试结果：
序号谐波次序合成畸变率 / %
1 3 5.5
2 5 2.9
3 7 1.8
4 9 1.5
5 11 1.2
6 13 1.1
7 15 1.0
8 17 0.9
9 19 0.8
10 21 0.7
11 23 0.6
12 25 0.5
13 27 0.5
14 29 0.4
结论：
本次测试结果显示，XXXXX型号的谐波电流符合IEC61000-3-
2 Class A标准要求。

同时，谐波总畸变率处于合理范围内，电气
产品对协议网的干扰较小。

注意事项：
本测试仅基于现场测试条件，测试结果受现场环境影响。

同时，测试结果不能代表本对象在所有情况下的谐波情况。

建议客户在
后期使用过程中定期进行谐波测试，以保证谐波干扰控制在合理
范围内。

第16卷　第6期2006年11月 黑　龙　江　科　技　学　院　学　报Journal of Heil ongjiang I nstitute of Science &Technol ogy　Vol .16No .6 Nov .2006文章编号:1671-0118(2006)06-0338-04谐波分析及谐波抑制方法王雪丹1,2,　刘芳霞1(1.黑龙江科技学院电气与信息工程学院,哈尔滨150027;2.中国矿业大学电气与信息工程学院,江苏徐州221008)摘　要:为解决电网谐波污染的问题,对带直流电动机负载的可控变流器交流侧电流进行谐波分析,叙述了并联型有源电力滤波器(APF )的基本工作原理,着重分析了有源电力滤波器谐波抑制的实现,并给出了采用LC 滤波器及有源电力滤波器(APF )滤波的仿真实验结果。

结果表明,两者组合使用,可以降低成本,提高效率,扩大容量,可获得更好的补偿特性。

关键词:谐波抑制;可控变流器;有源电力滤波器;LC 滤波器 中图分类号:T M714.1文献标识码:AHa r moni c contr o l so l uti o n and its rea li za ti o nWAN G X uedan1,2,　L I U Fangxia1(1.College of Electric and I nf or mati on Engineering,Heil ongjiang I nstitute of Science and Technol ogy,Harbin 150027,China;2.College of I nf or mati on and Electrical Engineering,C UMT,Xuzhou 221008,China )Abstract:To s olve seri ous polluti on of har monics,this paper analyses the har monics in current of the AC side of contr olled converter with DC mot or .The basic operati on p rinci p le of the shunt active pow 2er filter (APF )is given in this paper .Realizati on of har monics contr olled is analyzed e mphatically by using active power filter and si m ulati on result was given .The results sho w it can cost cutting,enhance efficien 2cy,expand capacity and get better compensati on if active power filter and LC filter are used t ogether .Key words:har monic contr ol;contr olled converter;active po wer filter;LC filter 收稿日期:2006-06-27 基金项目:黑龙江省教育厅骨干教师项目(1052G039)0　引　言20世纪70年代以来,随着电力电子技术的飞速发展,特别是功率半导体器件和变流技术的发展,大容量电力整流、换流设备等电力电子装置和非线性负载的广泛使用,电网的谐波污染问题变得日益严重,由谐波引起的各种故障和事故也不断产生,谐波危害的严重性引起人们的高度关注。

作， 给电 动执 行机构 加载 不同 的力 矩。当 电动 执行
机构 运行 转速 稳定后 ，电 能质 量分 仪测试 电动 执行
机构 输入 侧的 电压、 电流 数据 等， 示波器 采集 输入
侧的 畸变电 流波形 。
水 泥电 阻 电网 电源
断路器 pf98 30 电能质量分析仪 强 电隔 离装 置
R S232转USB 210通信线 TDS2 10 示波器
防护等级：IP 67；
出厂编 号：0 7512 0168；
出厂日 期：2 007- 09；
内置变频器：T0.75，（数据 0.75 表示功率，单
位：k W）。 2.3 测试仪器与仪表
图 2 PF 9830/3 电压 3 电流系统（3V3A）接线图
示波器采用美国 TEK 公司 TDS210 数字存储示
PE 电力电子
变频器谐波电流测试与分析
秦旭东 王金全 陈晓宁 张 琦
（解放军理工大学工程兵工程学院，南京 210007）
摘要 本文测试了变频器输入侧谐波电流，对比分析了测试数据和测试波形，得到示波器可 进行 谐波电 流测 试的 结论 。
关键词 ：变频 器； 谐波 电流 ；测试 ；示 波器
Testing and Analyzing of Har monic Cur r ent to Fr equency Changer
2 变频器输入侧谐波电流测试
2.1 测试电路设计 由于风 机、 水泵 类负 载功率 较大 ，控 制困 难，
无法 模拟精 确的 风机 、水 泵的 实际加 载情 况； 而由 解放 军理工 大学 工程 兵工 程学 院和扬 州电 力修 造厂 合作 研发的 电动 执行 机构 调试 台，可 以对 电动 执行 机构 进行精 确加 载调 试。 通过 调试台 加减 负载 ，即 改变 电机拖 动负 载的 大小 ，从 而改变 变频 器的 负载 大小 。因此 ，本 文选 用变 频式 电动执 行机 构为 测试 对象，设计的谐波电流的测试电路如图 1 所示。测 试原 理：调 节磁 粉加 载仪 ，使 调试台 磁粉 95.3

谐波分析⼀、谐波：1、谐波频率与基波频率的⽐值（n=fn/f1）称为谐波次数。

电⽹中有时也存在⾮整数倍谐波，称为⾮谐波（Non-harmonics ）或分数谐波。

谐波实际上是⼀种⼲扰量，使电⽹受到“污染”。

电⼯技术领域主要研究谐波的发⽣、传输、测量、危害及抑制，其谐波范围⼀般为2≤n ≤40。

根据公式（1）计算谐波电流补偿率KK = ×100%电流总谐波畸变率：THD I =IH I1；IH=（Ih ）2∞=2×100%；Ih---第h 次谐波电流（⽅均根值）I1---基波电流（⽅均根值）第h 次谐波电流含有率：HRI h =Ih I1×100%2、现有有源滤波器的补偿效果注：试验所⽤负载为三相整流⾮线性负载，（2～25）次谐波单机100补偿率:50%负载以上补偿率⼤于90%；50%负载以下补偿率在70%～90%单机100A 动态响应时间在1ms ～20ms单机100A 功率消耗：8%左右单机100A 噪声：70dB单机100A ⽆功补偿：补偿前0.2～0.8（容性或感性），补偿后能达到0.98⼆、谐波负载现状分析：电⽹谐波产⽣主要有以下⼏种情况：⼀是发电源质量不⾼产⽣谐波；⼆是输配电系统产⽣谐波；三是⽤电设备产⽣的谐波。

如下：1、变频器（风机、⽔泵、电梯）、吸塑机负载主要谐波次数：5次、7次2、电焊机、列车负载主要谐波次数：3次谐波3、中频炉负载主要谐波次数：5、7、11、13次谐波4、电弧炉、电⽯炉主要谐波次数：27次5、节能灯负载主要谐波次数：3次谐波6、整流设备（电⼒机车、铝电解槽、充电装置、开关电源等）产⽣的谐波主要看3次最严重，6脉整流会带来 6n+1 6N-1谐波主要就是5次和7次谐波； 12脉整流就会有 12n+1 12n-1谐波主要11次和13次谐波 18脉则是 18n+1 补偿前谐波电流畸变率THDi —补偿后谐波电流畸变率THDi补偿前谐波电流畸变率THDi18n-1 17次和19次谐波，⼀般情况下主要产⽣5、7次谐波！晶闸管整流设备。

电力谐波综合治理技术实验报告学院：信息科学与工程学院指导教师：危韧勇实验二谐波产生和抑制一．实验目的1.加深对电磁干扰抑制技术的了解。

2.了解谐波的产生3.了解谐波治理的各种方法4．理解无源滤波和有源滤波的原理二．实验设备1.电力谐波及FACTS综合实验台2.MALAB仿真平台三．实验原理目前在电力系统中抑制或减小谐波主要从两个方面进行。

第一方面是从产生谐波的谐波源装置本身入手，在这些装置设计时就考虑减小谐波的方法，增加谐波抑制环节以减少电网的谐波注入量，此方法被称为主动治理措施。

主动治理措施主要有增加变流装置的相数或脉冲数，采用多重化技术，采用脉宽调制(PWM:Pulse Width Modulation)技术，设计或采用高功率因数变流器等。

第二个谐波治理的重要方面是研究对系统中的谐波进行有效滤除和补偿的方法和措施，此方法被称为被动治理措施。

一般有三种：一是无源滤波包括低通滤波器和高通滤波器，二是有源电力滤波。

三是混合有源滤波。

混合有源滤波结合了无源滤波和有源滤波进行谐波治理，该方法将有效的克服单一使用无源滤波器和单一使用有源滤波器的缺点，而是综合了两者的优点，从而实现谐波电流的实时动态补偿。

即实现无源滤波器进行大容量的谐波补偿，有源滤波器进行微调补偿，从而有效降低有源滤波器的容量，不但能够实现谐波的动态补偿而且可以大大降低成本。

注入式混合有源滤波器是比较成熟的混合有源滤波技术，它的注入支路利用单调谐滤波器在基波频率处谐振时阻抗很小的特点，使得有源滤波器既不承受基波电压也不承受基波电流，从而大大减小有源滤波器的容量，使其更适于高压系统。

有源电力滤波器基本原理如图2.1所示。

设负载电流为l i ，谐波检测器从负载电流中检测出谐波电流h i ，令指令电流*c h i i =-，补偿电流控制算法控制逆变器产生补偿电流*c c i i =，注入母线，抵消负载电流中的谐波，达到抑制谐波电流流向电源的目的。

实验一谐波分析实验（波形分解、合成不失真条件研究）2015-3-30精25班李新基2012010630实验一、谐波分析实验（波形分解、合成不失真条件研究）目录一、实验目的 (1)二、实验原理 (1)三、实验内容及操作步骤 (3)1 合成方波 (3)2 合成锯齿波 (5)3.合成三角波 (7)四、讨论以下问题 (9)五、回答下列思考题 (11)六、实验小结 (12)一、实验目的1.了解分解、合成非正弦周期信号的物理过程。

2.观察合成某一确定的周期信号时，所必须保持的合理的频率结构，正确的幅值比例和初始相位关系。

二、实验原理对某一个非正弦周期信号x(t)，若其周期为T、频率为f，则可以分解为无穷项谐波之和。

即x(t)=a0+∑A n sin(2πnTt+∅n)∞n=1=a0+∑A n sin(2πnf0+∅0)∞n=1(1−1)上式表明，各次谐波的频率分别是基波频率f0的整数倍。

如果f(t)是一个锯齿波，其波形如图1.1所示，则其数学表达式为：x(t)=ET t−E2, 0≤t≤Tx(t+nT)=x(t)(1−2)对f(t)进行谐波分析可知a0=0,A n=Eπn,∅n=π所以图1.1x(t)=∑Eπnsin (2πnT∞n=1t+π)=∑Eπnsin(2πnf0+π)∞n=1=Eπ{sin(2πf0t+π)+12sin[2π(2f0)t+π+⋯} (1−3)即，锯齿波可以分解成为基波的一次、二次……n次……无数项谐波之和，其幅值分别为分别为基波幅值的，且各次谐波之间初始相角差为零（基波幅值为）。

反过来，用上述这些谐波可以合成为一个锯齿波。

同理，只要选择符合要求的不同频率成份和相应的幅值比例及相位关系的谐波，便可近似地合成相应的方波、三角波等非正弦周期波形。

三、实验内容及操作步骤1 合成方波周期方波信号x(t)在一个周期中的表达式为：波形如图1.2所示图1.2傅立叶级数为：展开成傅里叶级数表达式为：(1)观察基波与三次谐波幅值分别为1、1/3，相位差为零时的合成波波形，如图1.3所示。