workbench12.0悬臂梁的谐响应分析(具体步骤)(完整资料).doc

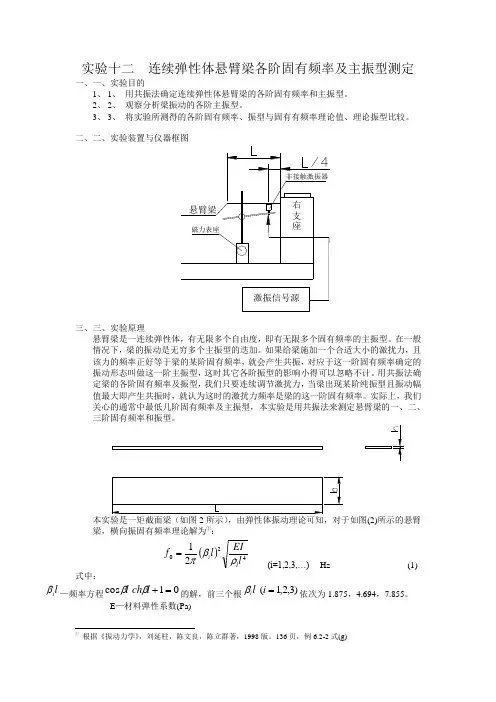
实验十二 连续弹性体悬臂梁各阶固有频率及主振型测定一、一、实验目的1、 1、 用共振法确定连续弹性体悬臂梁的各阶固有频率和主振型。

2、 2、 观察分析梁振动的各阶主振型。

情况下，梁的振动是无穷多个主振型的迭加。

如果给梁施加一个合适大小的激扰力，且该力的频率正好等于梁的某阶固有频率，就会产生共振，对应于这一阶固有频率确定的振动形态叫做这一阶主振型，这时其它各阶振型的影响小得可以忽略不计。

用共振法确定梁的各阶固有频率及振型，我们只要连续调节激扰力，当梁出现某阶纯振型且振动幅值最大即产生共振时，就认为这时的激扰力频率是梁的这一阶固有频率。

实际上，我们关心的通常中最低几阶固有频率及主振型，本实验是用共振法来测定悬臂梁的一、二、l i β①根据《振动力学》，刘延柱，陈文良，陈立群著，1998版。

136页，例6.2-2式(g)A — A — 梁横截面积(m 2)l ρ—材料线密度(kg/m) l ρ=ρAρ—材料密度（kg/m 3） I —梁截面弯曲惯性矩(m 4)对矩形截面，弯曲惯性矩：123bhI = (m 4) (2)式中： b —梁横截面宽度(m) h —梁横截面高度(m) 本实验取l =( ) m b=( ) m h=( ) mE=20×1011Pa ρ=7800kg/m 3 各阶固有频率之比：f 1:f 2:f 3:f 4……=1:6.27:17.55 (3)理论计算可得悬臂梁的一、二、三阶固有频率的振型如图(3)所示：0.10.20.30.40.50.60.70.80.91-10120 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1-2020 0.10.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 10.511.5beam transvers vibration with one end clasped四、四、实验方法1、 1、 选距固定端L/4之处为激振点，将激振器端面对准悬臂梁上的激振点，保持初始间隙δ=6~8mm 。

基于W orkb e n c h 的箱形伸缩臂模态及谐响应分析The model and harmonic response analysis of trunk telescopic boom by Wor kbenc h刘 涛，王卫辉，鹿 飞，袁仁武LIU Tao, WANG Wei-hui, LU Fei, YUAN Ren-wu(第二炮兵工程大学，西安 710025)摘 要：采用大型C a D 软件Proe 建立箱型伸缩臂的三维模型，并基于W o rk be nch 对伸缩臂进行了模态 分析和谐响应分析。

通过模态分析，得出了伸缩臂的前15阶固有频率及振型，为了解伸缩臂 的动态性能，对伸缩臂进行优化设计起到了指导作用，并为谐响应分析提供了频率范围。

通 过谐响应分析，得出三种工况下的位移频率响应曲线，分析出伸缩臂模型最易产生共振的频 率，为后续的分析奠定了基础。

中图分类号：TH213.6 文献标识码：a 文章编号：1009-0134(2015)02(下)-0080-04 Doi ：10.3969/j.issn.1009-0134.2015.02(下).240 引言现今，汽车起重机因其良好的移动性和高度的灵活 性而备受青睐，使得作为主要受力构件的伸缩臂的设计 就显得尤为重要[1]。

伸缩臂传统设计多考虑的是结构的 静强度和刚度，依靠安全系数的选取保证其强度及可靠 性，这样未能充分考虑伸缩臂工作过程中所受动态载荷 带来的冲击和振动问题。

因此，对伸缩臂进行动态分析 是十分必要的。

模态分析用于确定设计结构的振动特性，即结构的 固有频率和振型。

对伸缩臂进行模态分析，可以为结构 系统的振动分析、振动故障诊断和预报以及结构动力特 性的优化设计提供依据。

谐响应分析是机械结构在承受随时间按正弦规律变 化的动载荷时在特定频率下的响应[2]，帮助设计人员检 验结构在受迫振动下能否克服共振、疲劳及其他影响。

1 模型建立基本臂下方与变幅油缸铰接，根部与转台铰接，主 臂采用700MPa 高强度结构钢板制造，各节臂之间通过 滑块支撑吊臂并传递载荷。

悬臂梁模态分析实验报告一、实验目的通过对悬臂梁进行模态分析实验，了解悬臂梁在不同振动模态下的固有频率和振型，并验证计算模态分析结果的准确性。

二、实验原理悬臂梁是一种常见的结构形式，其在振动过程中会出现不同的振动模态，每个振动模态对应一个固有频率和振型。

模态分析是通过实验或计算的方法，确定一个结构在振动中的固有频率和振型的过程。

在本实验中，我们选择一根长度为L的悬臂梁，将其固定在一个支撑架上。

在悬臂梁上施加一个外力，使梁发生振动。

利用振动传感器测量悬臂梁不同位置处的振动加速度，并通过信号处理来得到悬臂梁的模态信息。

三、实验器材和仪器1.悬臂梁：长度为L、直径为d的悬臂梁2.支撑架：用来支撑悬臂梁的架子3.外力施加装置：用来在悬臂梁上施加外力的装置4.振动传感器：用来测量悬臂梁不同位置的振动加速度5.信号处理器：用来对振动信号进行处理和分析的设备四、实验步骤1.将悬臂梁固定在支撑架上，并调整支撑架的角度和高度，使悬臂梁处于水平状态。

2.在悬臂梁上选择一个合适的位置，安装振动传感器，并将传感器连接到信号处理器上。

3.利用外力施加装置，在悬臂梁上施加一个单一方向的外力。

4.启动信号处理器，并进行振动信号的采集和处理。

5.分析处理后的振动信号数据，得到悬臂梁的固有频率和振型。

五、实验结果及讨论根据实验数据，我们得到了悬臂梁的固有频率和振型，并与理论计算值进行比较。

整个实验过程中，我们进行了多次实验，分别在不同的外力大小下进行了振动测试。

通过对比实验数据和计算结果，验证了模态分析方法的准确性。

六、实验结论通过模态分析实验，我们成功地确定了悬臂梁在不同振动模态下的固有频率和振型，并验证了计算模态分析结果的准确性。

这对于进一步研究和应用悬臂梁的振动特性具有重要的意义。

七、实验心得通过本次实验，我深刻了解了悬臂梁的振动特性和模态分析的原理和方法。

实验过程中，我学会了如何正确选择和安装振动传感器，以及如何对振动信号进行分析处理。

实验报告悬臂梁的模态实验姓名： xxx学号： xxx专业： xxx系别： xxx一、试验装置二、实验原理本实验采用锤击法测定悬臂梁的频响函数，将第S 点沿坐标X S 方向作用的锤击力和第r 点沿X r 方向的响应分别由相应的传感器转换为电信号，在由动态分析仪，按照随机振动理论，运算得出r,s 两点间的频响函数rs H ~，∑=+-==ni i i i k i s i r s r rs i k F X H 12)()()(0)21(~~λζλϕϕ （1） 又由于响应信号是加速度，同时圆频率为ω，位移函数,sin t X x ω=其加速度为,sin 22x t X a ωωω-=-=用复数表示后，参照（1）可得到加速度频响函数为：∑=+--=-=ni i i i k i s i r s r a rs i kF X H 12)()()(202)21(~~λζλϕϕωω （2） 由公式（2）可知，当k ωω=时，1=k λ，此时式（2）可近似写为：,22)(~)()()()()()(2kk k s k r k k k sk r k k a rs m i k i H ζϕϕζϕϕωωω-=-== （3） 它对应频响函数a rs H ~的幅频曲线的第k 个峰值，其中在上面（3），k m kk k 2()(ω）式中=为各阶主质量．．．n k ,3,2,1=。

改变s 点的位置，在不同点激振，可以得到不同点与点r之间的频响函数，当s=r 时，就可得到点r 处的原点频响函数，表示为：∑=+--=ni i i i i i r i r a rr i k H 12)()()(2)21(~λζλϕϕω （4） 它的第k 个峰值为：,2)(~)()()(2kk k r k r k k a rr k i H ζϕϕωωω-== （5）由（3）/（5）得到：（6）若另1)(=k rϕ，就可得到：（7）由（7）式，另s=1,2,3，．．．．．．ｎ，就可得到第k 阶主振型的各个元素。

ANSYSWorkbench正弦响应分析之详细版这是 ANSYS 工程实战第 42 篇文章问题描述：正弦分析选用的项目模块为谐响应分析（Harmonic Response），这里对谐响应分析的关键知识点和正弦分析具体分析步骤和方法进行了详细介绍。

1. 谐响应分析理论介绍1.1 谐响应分析的定义谐响应分析是用于确定线性结构在承受一个或多个随时间按正弦（简谐）规律变化的载荷时稳态响应的一种技术。

1.2 谐响应分析的目的谐响应分析的目的是计算出结构在几种频率下的响应并得到一些响应值对频率的曲线（如位移对频率曲线），从这些曲线上可以找到“峰值”响应，并进一步考察频率对应的应力。

1.3 谐响应分析的输入条件谐响应分析的输入条件：相同频率的多种载荷。

1.4 谐响应分析的运算求解方法谐响应分析的运算求解方法包括完全法（Full）和模态叠加法(Mode Superposition)。

完全法是一种最简单的方法，不需要先进行模态分析，但求解更耗时，对于复杂结构，8核并行运算，一般计算时间在3h以上。

模态叠加法是 Workbench 谐响应计算的默认求解方法，从模态分析中叠加模态振型。

采用模态叠加法进行谐响应分析时，首先需要自动进行一次模态分析，虽然首先进行的是模态分析，但谐响应部分的求解仍然比完全法快的多。

一般对于复杂结构，8核并行运算，谐响应部分的计算时间小于0.5h。

2. 用完全法进行正弦分析的分析步骤及设置2.1 插入响应模块完全法进行正弦分析时直接将 Analysis Systems 下的 Harmonic Response 谐响应模块拉到项目管理区中或者直接引用项目管理区中模态分析的模型（Model），如图 1 所示。

图 1 插入响应模块2.2 三维模型导入及处理在 Inventor 软件中对行波管进行建模，经过模型干涉检查合格后，将建立好的模型生成stp 格式，导入到有限元软件ANSYS Workbench 中，行波管模型如图 2 所示，包括底板、包装件、电子枪、收集极和高频等组件。

使用Ansys Workbench进行谐响应分析的基本流程坐倚北风谐响应分析（Harmonic Response Analysis）是用于确定线性结构在承受一个或多个随时间按正弦（简谐）规律变化的载荷时稳态响应的一种技术。

分析的目的是计算出结构在几种频率下的响应并得到一些响应值（通常是位移）对应频率的曲线。

从这些曲线上可以找到“峰值”响应，并进一步考察频率对应的应力。

如下图所示则为本文示例中最终求解出的轴承支撑座座的von-Mises米歇尔应力图。

图1 轴承支撑座von-Mises米歇尔应力图谐响应分析技术只计算结构的稳态受迫振动。

发生在激励开始时的瞬态振动不在谐响应分析中考虑。

谐响应分析是一种线性分析，任何非线性特性，如塑性和接触（间隙）单元，即使被定义了也将被忽略，但在分析中可以包含非对称系统矩阵，如分析流体―结构相互作用问题，谐响应分析同样也可以分析有预应力的结构，如小提琴的弦（假定简谱应力比预加的拉伸应力小得多）。

谐响应分析通常用于如下结构的设计与分析：（1）旋转设备（如压缩机．发动机、泵、涡轮机械等）的支座固定装置和部件等；（2）受涡流影响的结构，包括涡轮叶片、飞机机翼、桥和塔等。

进行谐响应分析的目的是确保一个给定的结构能经受住不同频率的各种正弦载荷（例如以不同速度运行的发动机）；探测共振响应，必要时可避免其发生（例如借助于阻尼器来避免共振等）。

下面以一个轴承支座的谐响应分析为例，介绍在Ansys Workbench中进行谐响应分析的基本步骤。

（在Ansys Mechanical APDL中进行谐响应分析的方法可参考本站文章《Ansys谐响应分析的步骤及单自由度系统求解实例》）进入Workbench后，首先新建一个Harmonic Response谐响应分析工程，如下图所示。

图2 Harmonic Response 谐响应分析工程1、前处理前处理和其它有限元分析一样，进行模型处理、材料设置、网格划分，这里不再赘述。

（完整word版）悬臂梁固有频率的计算悬臂梁固有频率的计算试求在0x =处固定、x l =处⾃由的等截⾯悬臂梁振动的固有频率（求解前五阶）。

解：法⼀：欧拉-伯努利梁理论悬臂梁的运动微分⽅程为：4242(,)(,)+0w x t w x t EI A x t ρ??=??；悬臂梁的边界条件为：2222(0)0(1),(0)0(2)0(3),(EI )0(4)x l x ldw w ww x x dx x x x ========，；该偏微分⽅程的⾃由振动解为(x,t)W(x)T(t)w =，将此解带⼊悬臂梁的运动微分⽅程可得到1234(x)C cos sin cosh sinh W x C x C x C x ββββ=+++，(t)Acos t Bsin t T w w =+；其中24A EIρωβ=将边界条件（1）、（2）带⼊上式可得13C 0C +=，24C 0C +=；进⼀步整理可得12(x)C (cos cosh )(sin sinh )W x x C x x ββββ=-+-；再将边界条件（3）、（4）带⼊可得12(cos cosh )C (sin sinh )0C l l l l ββββ-+-+=；12(sin sinh )C (cos cosh )0C l l l l ββββ--+-+=要求12C C 和有⾮零解，则它们的系数⾏列式必为零，即(cos cosh )(sin sinh )=0(sin sinh )(cos cosh )l l l l l l l l ββββββββ-+-+--+-+所以得到频率⽅程为：cos()cosh()1n n l l ββ=-；该⽅程的根n l β表⽰振动系统的固有频率：1224()(),1,2,...n n EI w l n Al βρ==满⾜上式中的各n l β（1,2,...n =）的值在书P443表8.4中给出，现罗列如下：123451.875104 4.6940917.85475710.99554114.1372l l l l l βββββ=====，，，，；若相对于n β的2C 值表⽰为2n C ，根据式中的1n C ，2n C 可以表⽰为21cos cosh ()sin sinh n n n nn n l l C C l lββββ+=-+；因此1cos cosh (x)C (cos x cosh x)(sin x sinh x),1,2,...sin sinh n n n n n n n n n n l lW n l l ββββββββ??+=---=??+??由此可得到悬臂梁的前五阶固有频率，分别将n=1,2,3,4,5带⼊可得：1112222221234441.875104() 4.694091()7.854757()EI EI EI Al Al Alωωωρρρ===，，， 112222454410.995541()14.1372()EI EI Al Alωωρρ==，；法⼆、铁摩⾟柯梁梁理论1.悬臂梁的⾃由振动微分⽅程：4242442224(,)(,)(1)0w x t w x t E w I w EI A I kG kG x t x t t ρρρ+-++=?；边界条件：(0)(0)0w x x φ====（1），0x lx lw x x φφ==??-==??（2）；设⽅程的通解为：(,)Csincos n n xw x t w t lπ=；易知边界条件（1）满⾜此通解，将通解带⼊上⾯的微分⽅程可得到频率⽅程为：422222224442224r ()(1)0nnn r n r E n w w kG l l kG l ρππαπ-+++=；其中22I EI r A Aαρ==，；若转动惯量与剪切变形的影响均忽略，上式的频率⽅程简化为222n n w l απ=；当n=1,2,3,4,5时可分别求得固有频率为：12345w w w w w =====多⾃由度系统频率的计算⽅法等效质量：连续系统悬臂梁简化为5个相等的集中质量12345m5m m m m m =====。