薄透镜成像公式和放大率共38页

h1′ = h 2
′ h2 = h3
垂轴放大率为 β = h ′ / h 1
′ ′ ′ ′ hk h1′h 2 h3 hk β = = L = β 1β 2 β 3 L βk h 1 h 1h 2 h 3 hk
系统总的垂轴放大率为各单球面的垂 轴放大率之乘积。 轴放大率之乘积。
′ h′h2h3 ′ ′ ′ hk hk 1 β= = L = β1β 2β 3Lβk h1 h1h2h3 hk
P2′ =
P2 f ′ f1′
f2′P 2 P′ = 2 P − f2 2
f ′ = f1′ ( P′ = 2
P f′ P′ = 2 2 f1′
′ ′ f2 f1′f2 )= P − f2 −∆ 2
′ P f1′f2 P (∆ − f2 ) 2 2 ′= ′ × =− f2 f2 f1′ − ∆ ∆ ∆
S
− P /(− f ) = (h − h′) /(−h′)
f′ f + =1 P′ P
P′ / f ′ = (h − h′) / h
xx′ = ff ′
共轴系统的高斯公式和牛顿公式与薄透 镜和单球面中的公式在形式上完全相同。 镜和单球面中的公式在形式上完全相同。 共轴系统的一对焦点， 共轴系统的一对焦点，一对主点和一对 节点，统称为系统的基点（ 节点，统称为系统的基点（cardinal points） ） 对于给定的光学系统， 对于给定的光学系统，其基点之位置可 通过光线追迹逐步成像，作图或计算求得。 通过光线追迹逐步成像，作图或计算求得。 2、计算法求组合共轴球面系统的基点 、
3a −3a + =1 得 P′ − a 1
−3 P′ = a = −1.5a 1 2
同理对于第二个透镜， 同理对于第二个透镜，有

40
2.公式： m

h（i 像長） h（o 物長）

q p
證
如上圖所示，物長和像長分別為ho和h，i 並令正立時 為正值，倒立時為負值。
41
∵ ABO ~
hi q 橫向放大率 m hi q。
ho p
ho
p
42
m h（i 像長） q h（o 物長） p
且像越大。
19
※物體在兩倍焦距上( p ＝2f )
在鏡後兩倍焦距處形成一等大的倒立實像。
20
※焦點與兩倍焦距間( f ＜ p ＜2f )
(1)在鏡後兩倍焦距外形成一放大的倒立實像。 (2)若物體越接近透鏡（未到達 f 處），則像的位置越
遠離透鏡，且像越大。
21
※物體在焦點上( p＝f )
所有的折射光線皆互相平行，成像於無窮遠處。
放大實像1113020q???60cmq??60230????21020cmih??????像長246範例22共軛成像物體與紙屏相距100公分在其間置一凸透鏡可生一清晰的實像于紙屏上今將凸透鏡向紙屏移近20公分再一次生清晰實像于紙屏上但兩次成像的大小不同如下圖所示此現像稱為共軛成像
一、球面透鏡 二、凸透鏡的成像作圖 三、凹透鏡的成像作圖 四、薄透鏡的成像公式 五、橫向放大率
(1)當 m 1時，代表成 放大 的像； 當 m 1時，代表成 縮小 的像。
(2)當m 0 時，代表成 正立 的像； 當m 0 時，代表成 倒立 的像。
43
範例1
1 透鏡成像
一物體高度10公分，置於焦距為20公分的凸透鏡前 主軸上，距透鏡30公分，試回答下列問題。
(1)用作圖法完成右 圖，求得像的位 置和性質 。

实物实像 实物实像 像放大 像缩小
第二象限
S′
f′
f
虚物实像 虚物实像
第一象限
β = 1
o
β = +1
虚物虚像 虚物虚像
第四象限
S
实物虚像 实物虚像
第三象限
球面 折射 系统
n′ n n′ n = s′ s r
f′ f + =1 s′ s
反射 系统
y′ ns′ β= = y n′s
空气中 薄透镜
物体经过薄凸透镜成像 物体上每个点都有自己 的像，这些点的像合起 来，就是物体的像。作 图时，通常只要作出物 体上两个端点A和B的像 就行了。
A A
B
F
O
F B
A
物体置于透像二倍焦距之外（ 物体置于透像二倍焦距之外（u>2f)
A
B
F
O
F
B B A
A
F
B
O
F
物体置于透像二倍焦距之内， 物体置于透像二倍焦距之内，一 倍焦距之外（ 倍焦距之外（2f>u>f)
1 1 1 = . s′ s f ′
（ 7）
若薄透镜为两个相等球面组成： 若薄透镜为两个相等球面组成： 物方焦距
f = nr /(n′ n)
像方焦距
f ′ = n′r /(n′ n)
f' f + =1, s' s xx′ = ff ′
（ 8）
称为薄透镜物像公式的高斯形式和牛顿形式。 称为薄透镜物像公式的高斯形式和牛顿形式。
x f γ= = f ' x'
D. α，β，γ的关系 的关系 P
1
n
n’
y

8
f f1f2 (6) 4 3cm
8
xH
f1d
(4) 4 2cm 8
第31页/共37页
xH
f2d
4 4 2cm 8
由此可见，H 和 H´重合，均在球心 O处。
H H´
.
F1
（2）
. . H1 H1´
F2 F
O H2 H2´. .
.
F´ F1´ F2´
P 8cm
横向放大率：
f f 1 P Pf 4.8cm
由于 F´是在透镜右表面的左方，故此透镜是发散的。
第29页/共37页
例题：半径为2厘米，折射率为1.5的玻璃球放在空气中，求： （1）球的焦距和主面、焦点的位置。 （2）若一物置于距球面6厘米处,求从球心到像的距离,并确定垂轴放大率。
解：（1）
f1
n n
n
r1
1 1.5 1
2
4cm
f1
n n
n
的曲率半径为 r1 、r2，则可得
n1 n1 nL n 1
r1
r1
n2 n2
n n L
2
r2
r2
(nL 1)(1/ r1 1/ r2)
透镜制造者公式（lens-maker，s formula）
ff
1
(nL 1)(1/ r1 1/ r2)
1
1
1 (nL 1)[
1
(nL 1)d ]
复合光学系统光焦度公式：
2
1 1 cm
f 2
20
1 2 d12
1 1 0.06 1 ( 1 ) 1.5m1
0.2 0.2
0.2 0.2
f 1 2m f 1 2m

本节前言第四节透镜成像公式公元前3世纪，我国晋代《博物志》记有：“削冰令圆，举以向日，以艾于后成其影，则得火。

”那时还未发明玻璃，我们的祖先就知道用冰做成凸透镜来会聚太阳光再用艾草取火了。

从古到今，透镜一直有着广泛的应用，就连现在高科技的光纤通信设备中也离不开透镜。

为了把一路光信号输进极细的光导纤维中，必须用凸透镜使光线会聚才行。

象显微镜、望远镜及照相机中的重要部件就是透镜。

本节中运用动画演示蜡烛经透镜的成像过程，总结透镜成像规律，重在透镜成像公式理解和应用，透镜成像放大率。

大家在学习过程中要循序渐进，逐步掌握。

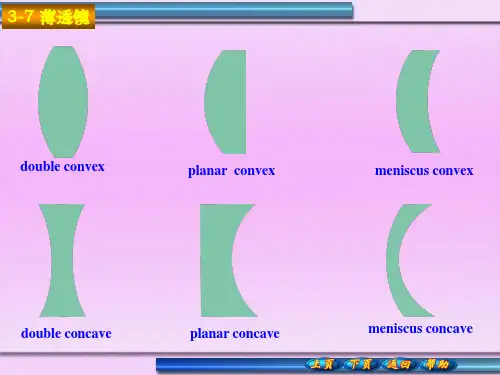
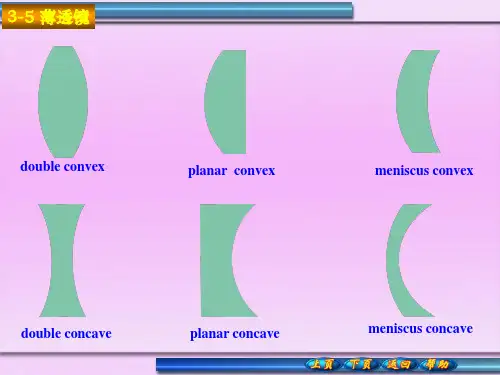
§1.4 透镜成像公式透镜是利用光的折射定律控制光路和成像的光学器件，透镜分为凸透镜和凹透镜两种，透镜的两个面为球面，中间厚边缘薄的透镜为凸透镜，中间薄边缘厚的透镜为凹透镜，两个面所在球面的球心的连线称为透镜的主轴，凸透镜对光线有汇聚作用，凹透镜对光线有发散作用。

所以我们通常称凸透镜为会聚透镜，称凹透镜为发散透镜。

薄透镜薄透镜是物理上建立的一个理想化的实体模型，在研究问题时，将透镜的厚度忽略不计。

透镜的光轴、光心、焦点、焦距通过透镜两球面球心的直线叫透镜的主光轴。

主光轴与透镜两球面的交点，对薄透镜而言，可看成是重合在一起的，该点称为光心。

通过光心的光线叫光轴，除主光轴而外，其它光轴叫副光轴。

平行于主光轴的光线，经凸透镜后会聚于一点，这个点叫焦点，用F表示，它是由实光线会聚而成的，又叫实焦点。

平行于主光轴的光线经凹透镜后被发散，发散光线的反向延长线也交于主光轴的一点，这个点也叫焦点，因为不是光线的实际会聚点，所以又叫虚焦点。

透镜的焦点与光心的距离叫焦距，用f表示。

透镜成像现在我们通过实验来研究透镜成像的规律。

如图：把蜡烛、透镜、光屏安装在光具座上，蜡烛和光屏距透镜的距离都可以从光具座导轨刻度尺上读出。

大家可通过做透镜的成像实验来掌握其成像规律。

下面的动画是模拟透镜成像的情况。

（1）先做凸透镜成像，拖动左边的蜡烛，仔细观察成像情况。

11-4 薄透镜成像 11-
•球面反射成像的物像公式 球面反射成像的物像公式: 球面反射成像的物像公式
1 1 2 + = p p′ R
或
B
1 1 1 + = p p′ f
R i′
i
α
P
C
ϕ
β
h
O
P′
y′ p′ •横向放大率： 横向放大率： 横向放大率 m= = − y p 符号法则： 符号法则：
p
p′
1.物点 P 在镜前时，物距为正；物点 P 在镜后时， 1.物点 在镜前时，物距为正； 在镜后时， 物距为负。 物距为负。 2.像点在镜前时，像距为正；像点在镜后时，像距为 2.像点在镜前时 像距为正；像点在镜后时， 像点在镜前时， 负。 3.凹面镜的曲率半径 R 取正，凸面镜的曲率半径 R 3.凹面镜的曲率半径 取正， 取负。 取负。
n1
P
O 1
C2
n2
n1
O 2 C1 ′ p2
P′
P′ 1
p1
t
′ p1
p2
P′为入射于右侧球面光线的一个虚物点 1 为入射于右侧球面光线的一个虚
′ ∴−p2 = p1 − t ≈ p′ 1
n1 n2 n2 n1 n2 − n1 n1 − n2 + + + = + p1 p′ p2 p′ R1 R2 1 2
′ p1
p2
n1 n2 n2 − n1 + = 光线在透镜的左侧面折射： 光线在透镜的左侧面折射： p1 p′ R1 1 n2 n1 n1 − n2 光线在透镜内右侧面入射： 光线在透镜内右侧面入射： + = p2 p′ R2 2 n1 n2 n2 n1 n2 − n1 n1 − n2 两式相加： 两式相加： + + + = + p1 p′ p2 p′ R1 R2 1 2

透镜成像公式引言透镜成像是光学中一个重要的概念，它描述了透过透镜后光线的传播和成像规律。

透镜成像公式是描述透镜成像的数学表达式，可以帮助我们理解和计算光线经过透镜后的成像位置和大小。

本文将介绍透镜成像公式的推导和应用。

透镜成像公式的推导透镜成像公式可以从透镜的焦距和物距得到。

这里我们假设光线从左侧垂直射入透镜，成像位置为右侧。

透镜的焦点位置标记为F，物体距离透镜的位置标记为O，成像位置标记为I。

根据透镜成像的性质，我们可以得到以下几个关键概念：1.物距（对象距离）：从物体到透镜的距离，标记为p。

2.像距（像位置距离）：从像到透镜的距离，标记为q。

3.焦距：透镜的特性，标记为f。

根据透镜成像的规律，我们可以得到以下关系：1.物距和像距的关系：1/p + 1/q = 1/f2.放大率的关系：M = -q/p透镜成像公式的应用透镜成像公式可以用于计算透镜成像的位置和大小。

通过测量物体和透镜的距离，我们可以得到物距p；通过测量成像位置和透镜的距离，我们可以得到像距q。

利用透镜成像公式，我们可以计算出物距和像距的关系，并进而计算出放大率M。

例子1：凸透镜成像考虑一个凸透镜，其焦距为f，物体距离透镜的距离为p。

假设p>0，即物体在透镜左侧。

根据透镜成像公式，我们可以得到： 1/p + 1/q = 1/f通过简单的代数运算，我们可以得到： q = (p * f) / (p - f)根据透镜成像的性质，当p无限大时，像位置q趋近于焦点位置，即q趋近于f。

当p等于焦距时，像位置q也等于焦点位置。

当p小于焦距时，像位置q会变成虚像，即透镜右侧。

例子2：凹透镜成像考虑一个凹透镜，其焦距为f，物体距离透镜的距离为p。

假设p>0，即物体在透镜左侧。

根据透镜成像公式，我们可以得到： 1/p + 1/q = 1/f通过简单的代数运算，我们可以得到： q = (p * f) / (f - p)与凸透镜相比，凹透镜的成像规律有所不同。

薄透镜成像公式及作图法薄透镜成像公式及作图法薄透镜成像公式及作图法 2011年04月01日本节向您讲述透镜成像的各种有效的作图法，以及薄透镜成像公式应用，您一定会在这里找到许多有用的方法。

[内容综述]如果一个透明物体的两个界面都是球面，或者一个界面是球面，另一个界面是平面，这就是透镜，中央部分比边缘厚的，叫凸透镜，它具有会聚光线的性能，所以也叫做会聚透镜。

透镜中央部分比边缘薄的，叫凹透镜，它具有发散光线的性能，也以也叫做发散透镜。

如果透镜的厚度比两球面的曲率半径小得多，叫做薄透镜。

本讲主要的重点、难点是薄透镜成像公式的应用及透镜成像的作图法。

[要点讲解]1、单球面折射成像公式如图15-28所示，设单球面左、右方的折射率分别为1和n，S’是S的像，因为是近轴光线，所以i与r均很小，所以有(R为球面曲率半径)，代入?及，?式即为单球面成像公式，当时的v就是焦距f，所以2、薄透镜成像公式透镜实质上是两个单折射球面组成，它的成像过程就是连续两次的单球面成像过程。

下面讨论薄透镜成像。

如图15-29所示，设左球面的半径为，右球面半径为，透镜材料的折射率为n。

点光源S发出的近轴光经左球面折射后设成像于S’’，由于透镜很薄，两球面顶点可视为一点，设为O，设SO=u，OS’’=V’，由单球面折射成像公式可得原应成像于S"的光束在尚未会聚前又被第二个球面折射，第二次成像。

S’’成为物，是虚物，折射后成像于S’。

现在的物距是-v’，像距为v，则 ?+?可得，这就是薄透镜成像公式。

这里，u,v, , 均有正、负，规则同前面所规定的。

对图15-29，u,v, 均为正，为负，当时，当时，当透镜两边处于同一介质中时f=f ’。

当f和f’>0的透镜称为会聚透镜(凸透镜)。

当f 和f’<0的透镜称为发散透镜(凹透镜)。

用焦距表示，可将?式透镜的成像公式写成 (当f=f ’时)上式称为高斯公式。

3(透镜成像作图法(1)基本光线作图法如图15-30所示，从物方焦点发出的任意光线径透镜折射后必成为平行于主轴的光;平行于主轴射向透镜的任意光线径透镜折射后必经过像方焦点;过光心的光线径透镜后方向不变。

解：（逐次求象法） 1）由球面折射成像公式可得物体发出的光束经第一个球面 （凸球面）透射所成象的位置
n n n n s s r 1.5 1 1.5 1 s 6 4 s 36cm
此象的横向放大率：
ny ny 0 s s y ns y ns y ns 1 (36) 1 4 y ns 1.5 (6)
O
F
物体置于透像二倍焦距之内，一 倍焦距之外（2f>u>f)
物体置于透像一倍焦距之内（u<f)
凹透镜成像作图法 当发光点不在主轴上时，经过凹透镜的三 条特殊光线的方向为：
跟主轴平行的光线经过透 镜后，其反向沿长线过焦点； 通过光心的光线经透镜 后，方向不变； 沿长线过焦点的光线， 经过透镜后，跟主轴平行。
n1
S
n2
O1 O2
S
S1
s
s1
s
将（1）式与（2）式两边相加，得
n2 n1 n n1 n2 n ' S S r1 r2
称为薄透镜物像公式。
上式右边为薄透镜的光焦度，即
（ 3）
1 2
式中
(4)
n n1 1 , r1
n2 n 2 r2
f' f 1 s' s
称为薄透镜物像公式的高斯形式。
由薄透镜的焦距公式
f n2 f n1
(5)
即薄透镜 焦距之比等于两边的折射率之比 的负值.
空气中的薄透镜焦距为
ff 1 1 1 (n0 1.0)( ) r1 r2 .
(6)
f = f 0 时为正透镜, 又称为凸透镜;
' 1
f' f 1 s' s 2

透镜成像规律有哪些重要定律透镜成像规律的重要定律1、凸透镜成像定律11 物距大于二倍焦距时，成倒立、缩小的实像。

此时像距在一倍焦距与二倍焦距之间。

这是照相机的成像原理。

111 物距等于二倍焦距时，成倒立、等大的实像。

此时像距也等于二倍焦距。

112 物距在一倍焦距与二倍焦距之间时，成倒立、放大的实像。

此时像距大于二倍焦距。

这是投影仪的成像原理。

113 物距等于一倍焦距时，不成像。

114 物距小于一倍焦距时，成正立、放大的虚像。

放大镜就是利用这一原理工作的。

2、凹透镜成像定律21 凹透镜始终成正立、缩小的虚像。

3、成像公式31 1/u ＋ 1/v ＝ 1/f ，其中 u 表示物距，v 表示像距，f 表示焦距。

4、光路可逆原理41 光路可逆是指在光的传播过程中，光线沿着某一路径传播，如果让光线沿着原来的出射光线的相反方向入射，那么它将沿着原来的入射光线的相反方向出射。

411 在透镜成像中，这意味着如果将物体和像的位置互换，仍然能够成像，只是成像的性质（大小、虚实、倒立或正立）会发生相应的变化。

5、放大率51 横向放大率 m ＝ v/u ，表示像的长度与物的长度之比。

511 纵向放大率通常等于横向放大率。

6、像的性质与物和像的位置关系61 当像距大于物距时，像放大；当像距小于物距时，像缩小。

7、薄透镜近似71 在很多情况下，当透镜的厚度远小于其焦距时，可以将透镜视为薄透镜，从而简化成像的分析和计算。

8、像的清晰度和像差81 实际的透镜成像可能会存在像差，如球差、彗差、像散、场曲和畸变等，影响像的清晰度和质量。

9、多透镜系统91 在复杂的光学系统中，多个透镜组合使用时，成像规律需要综合考虑各个透镜的特性和它们之间的相对位置。

10、应用领域101 透镜成像规律在许多领域有广泛的应用，如显微镜、望远镜、眼镜、摄像机等光学仪器的设计和制造。

1011 医学领域中的眼科检查和治疗设备也依赖于透镜成像规律。

1012 工业生产中的检测和测量设备同样利用了这些规律。

反向延长线通过虚焦点通过透镜射向虚焦点方向不变注意凹透镜透镜成像的位置除了用作图法可以得到外能不能用更简捷的办法得到呢
第七章 光的反射和折射
十、透镜成像公式
复习提问



透镜成像作图法的基本方法是什么？ 选取三条特殊光线中的任意两条： ⑴跟主轴平行的光线，折射 注意 后 （反向延长线）通过（虚）焦点 ； 凹透 ⑵ 通过（透镜射向虚）焦点 的光线， 镜 折射后跟主轴平行； ⑶通过光心的光线，经过透镜 后 方向不变 。
小魔方站作品 盗版必究
谢谢您下载使用！
更多精彩内容，微信扫描二维码获取
扫描二维码获取更多资源
附赠 中高考状元学习方法
前
言
高考状元是一个特殊的群体，在许 多人的眼中，他们就如浩瀚宇宙里璀璨夺 目的星星那样遥不可及。但实际上他们和 我们每一个同学都一样平凡而普通，但他 们有是不平凡不普通的，他们的不平凡之 处就是在学习方面有一些独到的个性，又 有着一些共性，而这些对在校的同学尤其 是将参加高考的同学都有一定的借鉴意义。
坚持做好每个学习步骤
武亦文的高考高分来自于她日常严谨的学习 态度，坚持认真做好每天的预习、复习。 “高中三年，从来没有熬夜，上课跟着老师 走，保证课堂效率。”武亦文介绍，“班主 任王老师对我的成长起了很大引导作用，王 老师办事很认真，凡事都会投入自己所有精 力，看重做事的过程而不重结果。每当学生 没有取得好结果，王老师也会淡然一笑，鼓 励学生注重学习的过程。”
孙老师说，杨蕙心学习效率很高，认真执行老师 的复习要求，往往一个小时能完成别人两三个小 时的作业量，而且计划性强，善于自我调节。此 外，学校还有一群与她实力相当的同学，他们经 常在一起切磋、交流，形成一种良性的竞争氛围。 谈起自己的高考心得，杨蕙心说出了“听话” 两个字。她认为在高三冲刺阶段一定要跟随老师 的脚步。“老师介绍的都是多年积累的学习方法， 肯定是最有益的。”高三紧张的学习中，她常做 的事情就是告诫自己要坚持，不能因为一次考试 成绩就否定自己。高三的几次模拟考试中，她的 成绩一直稳定在年级前5名左右。

N
S´
O
S F´
M
S
§1-5 共轴球面系统
一、共轴球面系统的逐次成像
由 k 个折射球面组成一共轴球面系统， 物体 SQ 经过这个光学系统所成的像为 SKQK
对应 k 个球面，可得 k 个物像距公式
n1 n1 n1 n1
P1 P1
r1
两相邻球面顶点的距离为
nk nk nk nk
hk h1h2h3 hk 1 2 3 k
h1 h1h2h3 hk
拉格朗日—亥姆霍兹恒等式
n1h11 n1h11 n2h22 nk hk k
例：惠更斯目镜 由两个凸透镜 L1 L2组成，用逐次成像
法求像位置。
已知：f1 3a, f2 a, d 2a 物点 Q 位于L1前a处 解：
薄透镜的成像公式和放大率
各种薄透镜
对第一折射面
对第二折射面
n1 n1 n1 n1 1
P1 P1
r1
P1 P2
n2 n2 n2 n2 2
P2 P2
r2
n1 n2
薄透镜成像公式
n2 P2

n1 P1

1

2


n n P P
ff
1
(nL 1)(1/ r1 1/ r2)
1
1
1 (nL 1)[

1
(nL 1)d ]
f f
r1 r 2 nr1r 2
薄透镜的高斯公式： f f 1
P P
1 1 1 P P f
二、薄透镜成像作图法
根据焦点和光心的特征，对于一个发光物 点可找到三条典型光线。

成像放大率公式成像放大率公式，这可是光学领域里一个相当重要的概念！咱先来说说啥是成像放大率。

简单来讲，成像放大率就是像的大小和物的大小的比值。

比如说，你通过一个放大镜看一只小蚂蚁，原本小小的蚂蚁看起来变大了好多，这个变大的程度就是成像放大率在起作用。

在光学成像的世界里，成像放大率公式通常有横向放大率和纵向放大率两种。

横向放大率用β表示，它等于像的长度与物的长度之比。

纵向放大率用α表示，等于像的纵向长度与物的纵向长度之比。

给大家讲个我自己的经历吧。

有一次，我带着一群小朋友去科技馆玩。

在光学展示区，有一个巨大的显微镜装置，小朋友们都好奇地围了上去。

我就趁机给他们讲解成像放大率的知识。

其中一个小朋友特别可爱，瞪着大眼睛问我：“老师，那这个放大率能让小虫子变得像大象那么大吗？”我笑着回答：“宝贝，如果放大率足够大，理论上是可以的，但在实际中可没那么容易做到哦。

”然后我指着显微镜下的一片树叶切片，跟他们说：“你们看，这原本小小的细胞，通过显微镜的作用，是不是看起来大多啦？这就是成像放大率在帮忙呢。

”横向放大率的公式是β = -v/u ，这里的 v 是像距，u 是物距。

可别被这些字母吓到，其实理解起来不难。

像距就是像到透镜的距离，物距就是物到透镜的距离。

当像距大于物距时，成像放大，像就变大；当像距小于物距时，成像缩小，像就变小。

纵向放大率的公式是α = β² 。

这两个公式结合起来，就能很好地描述成像的放大或缩小情况啦。

在实际应用中，成像放大率公式可有用了。

比如说在照相机里，通过调整镜头和感光元件之间的距离，就能改变成像放大率，从而拍出不同大小、不同效果的照片。

还有啊，医生在使用显微镜观察细胞和组织的时候，也得依靠成像放大率来准确判断病情。

想象一下，如果医生看不清楚细胞的细微结构，那诊断病情可就困难重重了。

在天文学中，望远镜也是利用成像放大率让我们能看到遥远的星球和星系。

那些璀璨的星空，原本遥不可及，但通过成像放大率，仿佛一下子拉近了和我们的距离。

§1.3 薄透镜成像
一．薄透镜
两个折射球面组成，主光轴重合，顶点间距。

即可以认
为,两球面顶点,
重合为，称为光心。

二.薄透镜成像公式
1.逐次成像法
透镜折射率为,左右两侧的折射率为和。

物点Q先经第一球面成
像,作为物点，
再经第二折射面成像,即为Q经透镜后成的像。

这种让光线依次通过球面成像方法为逐次成像法。

（1） Q经成像
，
（2） 再经成像
，
两式相加，有 = =
2．焦点与焦平面
，得到物方焦距
， 得到像方焦距
与单球面类似，可以定义焦点和焦平面。

如果取，有，称为磨镜者公式。

有Gauss公式。

如果用到焦点的距离表示物像的位置，即
，，Gauss公式化为，
即有，Newton物像公式。

焦距的正负取决于两球面的曲率半径，
，像点在透镜右侧，为汇聚透镜，称为正透镜，实焦点；
，像点在透镜左侧，为发散透镜，称为负透镜，虚焦点。

3．经过光心的光线
由于透镜很薄，，光心处相当于平行折射面，故通过光心的光线不改变方向。

三．薄透镜成像的作图法
四．像的横向放大率
总放大率为两次成像的放大率的乘积。

五．Lagrange-Helmhotz恒等式
Lagrange-Helmhotz恒等式依然成立，为。