第四讲极限与配合的选择原则
- 格式:ppt
- 大小:741.51 KB
- 文档页数:14

一.极限与配合配合制同一极限制的孔和轴组成配合的一种制度,称为配合制。
轴通常,指工件的圆柱形外表面,包括非圆柱形外表面(由二平行平面与切面形成的被包容面)基准轴在基轴制配合中选作基准的轴,即上偏差为零的轴。
孔通常,指工件的圆柱形内表面,也包括非圆柱形内表面(由二平行平面或切面形成的包容面)基准孔在基孔制配合中选作基准的孔,即下偏差为零的孔尺寸以特定单位表示线性尺寸值的数值基本尺寸通常它应用上,下偏差可算出极限尺寸的尺寸实际尺寸通过测量获得的某一孔,轴的尺寸局部实际尺寸一个孔或轴的任意截面中的任一距离,即任何两相对电之间测得的尺寸极限尺寸一个孔或轴允许的尺寸的两个极端,实际尺寸也应位于其中,也可达到极限尺寸最大极限尺寸孔或轴允许的最大尺寸最小极限尺寸孔或轴允许的最小尺寸极限制经标准化的公差与偏差制度零线在极限与配合图解中,表示基本尺寸的一条直线,以其为基准确定偏差和公差。
通常,零线沿水平绘制,正偏差位于其上,负偏差位于其下偏差某一尺寸(实际尺寸,极限尺寸等等)减其基本尺寸所得的代数差极限偏差上偏差和下偏差上偏差(ES,es)最大极限尺寸减其基本尺寸所得的代数差下偏差(EI,ei)最小极限尺寸减其基本尺寸所得的代数差基本偏差确定公差带相对零线位置的那个极限偏差(可以是上偏差或下偏差,一般是靠近零线的那个偏差)尺寸公差(简称公差)最大极限尺寸减最小极限尺寸之差,或上偏差减下偏差之差。
它是允许尺寸的变动量。
(尺寸公差是一个没有符号的绝对值)标准公差(IT)本标准极限与配合制中,所规定的任一公差(字母IT为“国际公差”的符号)标准公差等级在本标准极限与配合制中,同一公差等级对所有基本尺寸的一组公差被认为具有同等精度公差带在公差带图解中,由代表上偏差和下偏差或最大极限尺寸和最小极限尺寸的两条直线所限定的一个区域。
它是用公差大小和其相对零线的位置来确定基准公差带因子(I,i)在本标准极限与配合制中,用以确定标准公差的基本单位,该因子是基本尺寸的函数标准公差因子i用于基本尺寸至500mm标准公差因子I用于基本尺寸大于500mm间隙孔的尺寸减去相配合的轴的尺寸之差为正最小间隙在间隙配合中,孔的最小极限尺寸减轴的最大尺寸之差最大间隙在间隙配合或过渡配合中,孔的最大极限尺寸减轴的最大极限尺寸之差过盈孔的尺寸减去相配合的轴的尺寸之差为负最小过盈在过盈配合中,孔的最大极限尺寸减轴的最小极限尺寸之差最大过盈在过盈配合或过渡配合中,孔的最小极限尺寸减轴的最大极限尺寸之差配合基本尺寸相同的,相互结合的孔和轴公差带之间的关系间隙配合具有间隙(包括最小间隙等于零)的配合。



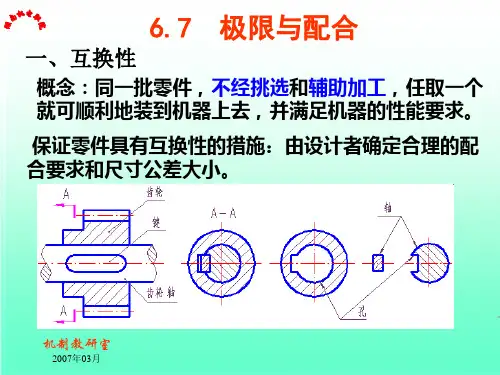
极限与配合极限与配合的基本概念标准公差与基本偏差配合公差与配合在图样上的标注极限与配合的基本概念为什么要制定极限与配合的标准?1. 零件的互换性在相同规格的一批零件或部件中,不需选择,不经修配就能装在机器上,达到规定的性能要求,零件的这种性质就称为互换性。
零件的互换性是现代化机械工业的重要基础,既有利于装配或维修机器又便于组织生产协作,进行高效率的专业化生产。
极限与配合制度,是实现互换性的一个基本条件。
零件的互换性2. 尺寸公差为保证零件的互换性,必须将零件的尺寸控制在允许的变动范围内,这个允许的尺寸变动量称为尺寸公差。
1)基本尺寸D(d)30基本尺寸设计给定的尺寸。
2)实际尺寸零件制成后,通过测量所得的尺寸。
3)极限尺寸允许零件实际尺寸变化的两个极限值,其中较大的一个尺寸称为最大极限尺寸,较小的一个称为最小极限尺寸。
φ30.020φ30本尺寸φ29.980小极限尺寸大极限尺寸零件合格的条件:最小极限尺寸≤实际尺寸≤最大极限尺寸4)尺寸偏差某一尺寸减去基本尺寸所得的代数差。
上偏差= 最大极限尺寸—基本尺寸。
上偏差代号:孔为ES,轴为es下偏差= 最小极限尺寸—基本尺寸。
下偏差代号:孔为EI,轴为ei实际偏差= 实际尺寸—基本尺寸。
上偏差与下偏差统称为极限偏差。
4)尺寸偏差最小极限尺寸最大极限尺寸φ30.020φ30基本尺寸φ29.980+0.020上偏差–0.020下偏差5)尺寸公差允许的尺寸变动量。
公差= 最大极限尺寸—最小极限尺寸= 上偏差—下偏差5)尺寸公差最小极限尺寸最大极限尺寸φ30.020φ30基本尺寸φ29.980+0.020上偏差–0.020上偏差0.016公差6)尺寸公差带公差带表示公差范围和相对零线位置的一个区域。
6)尺寸公差带为简化起见,一般只画出孔和轴的上、下偏差围成的方框简图,称为公差带图。
其中零线是表示基本尺寸的一条直线。
6)尺寸公差带下偏差公差带+0.008-0.008+0.008+0.024-0.006-0.022公差带图可以直观地表示出公差的大小及公差带相对于零线的位置。



极限与配合知识点总结一、极限的定义和性质1. 极限的定义当自变量x无限接近于某一特定值a时,函数f(x)的取值也无限接近于某一特定值L,我们称L为当x趋于a时函数f(x)的极限,记作lim(x->a)f(x)=L。
其中,x->a表示x无限接近于a,L表示函数f(x)的极限值。
2. 极限的性质(1)唯一性:如果极限存在,则极限值唯一。
(2)有界性:如果函数f(x)在x趋于a时有极限L,则f(x)在x趋于a的邻域内有界。
(3)保号性:如果函数f(x)在x趋于a的邻域内有界且趋近于某一值L,则L的左右邻域内函数f(x)的取值要么都大于L,要么都小于L。
二、极限存在的条件及运算法则1. 极限存在的条件(1)左极限和右极限相等。
(2)夹逼定理成立。
(3)函数在某一点的邻域内有界且趋近于某一值。
2. 极限的运算法则(1)和差法则:lim(x->a)[f(x)±g(x)]=lim(x->a)f(x)±lim(x->a)g(x)。
(2)积法则:lim(x->a)[f(x)×g(x)]=lim(x->a)f(x)×lim(x->a)g(x)。
(3)商法则:lim(x->a)[f(x)/g(x)]=lim(x->a)f(x)/lim(x->a)g(x)(前提是lim(x->a)g(x)≠0)。
三、导数的定义和性质1. 导数的定义函数y=f(x)在点x处的导数定义为:f'(x)=lim(h->0)[f(x+h)-f(x)]/h。
其中,h表示自变量x 的增量,f(x+h)-f(x)表示函数值的增量,f'(x)表示函数在点x处的导数。
2. 导数的性质(1)可导性与连续性:函数在某一点可导,则该点连续;函数在某一点连续,则该点可导。
(2)导数的代数运算性质:导数具有加法、减法、乘法和除法的代数运算法则。