二次函数与图形面积

二次函数与图形面积问题1、阅读材料：如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部的线段的长度叫△ABC的“铅垂高”（h）.我们可行出生种计算三角形面积的新方示：y=a(x-1)2+4 ，即三角形面积等于水平宽与铅垂高乘积的一半.解答下列问题:如图2，抛物线顶点C（1，4），交x轴于点A（3，0），交y轴于点B.（1）求抛物线和直线AB的解析式；（2）求△ABC的铅垂高CD及S △ ABC（3）设点P是抛物线（在第一象限内）上的一个动点，是否存在一点P，使a=-1 ，且S△PAB=9/8 S△CAB若存在，求出P点的坐标；若不存在，请说明理由.2、如图,已知抛物线y=ax2+bx+c经过点A（2,3）,B（6,1）,C（0,-2）．（1）求此抛物线的解析式,并用配方法把解析式化为顶点式；（2）点P是抛物线对称轴上的动点,当AP⊥CP时,求点P的坐标；（3）设直线BC与x轴交于点D,点H是抛物线与x轴的一个交点,点E（t,n）是抛物线上的动点,四边形OEDC的面积为S．当S取何值时,满足条件的点E只有一个?当S取何值时,满足条件的点E有两个?3、如图，已知平面直角坐标系xOy中，点A（m，6），B（n，1）为两动点，其中0＜m＜3，连接OA，OB，OA⊥OB。

（1）求证：mn=-6；（2）当S△AOB=10时，抛物线经过A，B两点且以y轴为对称轴，求抛物线对应的二次函数的关系式；（3）在（2）的条件下，设直线AB交y轴于点F，过点F作直线l交抛物线于P，Q两点，问是否存在直线l，使S△POF：S△QOF=1：3？若存在，求出直线l对应的函数关系式；若不存在，请说明理由。

4、如图1，在平面直角坐标系中，点A的坐标为（1，2），点B的坐标为（3，1），二次函数y=x2的图象记为抛物线l1。

（1）平移抛物线l1，使平移后的抛物线过点A，但不过点B，写出平移后的一个抛物线的函数表达式：______ （任写一个即可）；（2）平移抛物线l1，使平移后的抛物线过A，B两点，记为抛物线l2，如图2，求抛物线l2的函数表达式；（3）设抛物线l2的顶点为C，K为y轴上一点，若S△ABK=S△ABC，求点K的坐标；（4）请在图3上用尺规作图的方式探究抛物线l2上是否存在点P，使△ABP为等腰三角形，若存在，请判断点P共有几个可能的位置（保留作图痕迹）；若不存在，请说明理由。

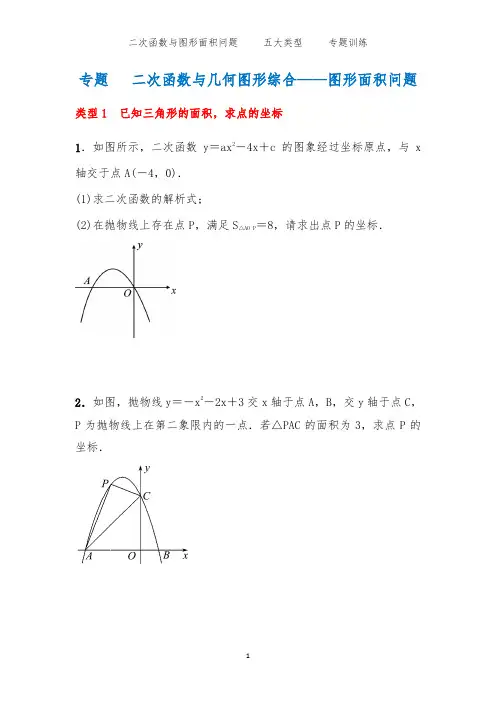
专题二次函数与几何图形综合——图形面积问题类型1 已知三角形的面积，求点的坐标
1．如图所示，二次函数y＝ax2－4x＋c的图象经过坐标原点，与x 轴交于点A(－4，0)．
(1)求二次函数的解析式；
(2)在抛物线上存在点P，满足S△AO P＝8，请求出点P的坐标．
2．如图，抛物线y＝－x2－2x＋3交x轴于点A，B，交y轴于点C，P为抛物线上在第二象限内的一点．若△PAC的面积为3，求点P的坐标．
类型2 已知三角形面积之间的数量关系，求点的坐标
3．如图是二次函数y＝(x＋m)2＋k的图象，其顶点坐标为M(1，－4)．(1)求出图象与x轴的交点A，B的坐标；
(2)在二次函数的图象上是否存在点P，使S△PAB＝5
4
S△MAB？若存在，求出点P的坐标；若不存在，请说明理由．
类型3 求三角形面积的最值
4．如图，直线l：y＝－3x＋3与x轴、y轴分别相交于A，B两点，抛物线y＝ax2－2ax＋a＋4(a＜0)经过点B.
(1)求该抛物线的函数解析式；
(2)已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM，BM.设点M的横坐标为m，△ABM的面积为S，求S关于m的函数解析式，并求出S的最大值．。

22.3 实际问题与二次函数第1课时 二次函数与图形面积问题置疑导入 归纳导入 复习导入 类比导入如图22－3－1，用12米长的木料，做一个有一条横档的矩形窗框，为了使窗户透进的光线最多，窗框的长、宽应各是多少？图22－3－1[说明与建议] 说明：通过对周长一定的矩形面积最大值的实际问题的导入，激发学生的学习兴趣和探究新知的欲望，从而引导学生研究二次函数与图形面积问题的一般方法.建议：可以对以上问题挖空让学生填写：设宽为x 米，面积为S 米2.根据题意并结合图形可得S ＝x （6－32x ） ＝ －32x 2＋6x .∵－32 ＜ 0，∴S 有最 大 值，当x ＝ －62×（－32）＝2 时，S 最 大 ，此时6－32x ＝ 3 ，即当窗框的长为 3米 ，宽为 2米 时，窗户透进的光线最多.（1）（做一做）请你画一个周长为12厘米的矩形，算一算它的面积是多少.再和周围同学所画的矩形比一比，你发现了什么？谁画的矩形的面积最大？（2）（练一练）已知一个矩形的周长为12米，它的一边长为x 米，那么矩形面积S （平方米）与x （米）之间有怎样的关系？自变量的取值范围是什么？（3）（试一试）若想设计一个周长为12米的矩形广告牌，假如你是设计师，你知道怎么设计才能使广告牌的面积最大吗？[说明与建议] 说明：（1）题比较简单，但对学生有很大的吸引力和挑战性，可有效地激发学生的学习兴趣.（2）题在（1）题的基础上提出问题，引导学生对实际问题与二次函数展开联想.（3）题在（2）题的基础上加入实际背景求最值，这样低起点，快反馈，能有效地提高学生的数学建模能力.建议：教师要重点关注学生能否正确求解，考虑问题是否全面以及学生能否将实际问题转化为数学问题.——第49页探究1用总长为60 m的篱笆围成矩形场地，矩形面积S随矩形一边长l的变化而变化.当l是多少米时，场地的面积S最大？【模型建立】利用二次函数解决几何图形的最大（小）面积问题，先利用几何图形的面积公式得到关于面积的二次函数解析式，再由二次函数的图象和性质确定二次函数的最大（小）值，从而确定几何图形面积的最大（小）值.【变式变形】1.用一段长为30 m的篱笆围成一个一边靠墙的矩形菜园，墙长为18 m，这个矩形菜园的长，宽各为多少时，它的面积最大？最大面积是多少？[答案：长为15 m，宽为7.5 m时，它的面积最大，最大面积为112.5 m2]2.如图22－3－2，用长为24米的篱笆，围成中间隔有一道篱笆的矩形花圃，且花圃的长可借用一段墙体（墙体的最大可用长度a＝10米）：（1）如果所围成的花圃的面积为45平方米，试求花圃的宽AB；（2）按题目的设计要求，能围成面积比45平方米更大的花圃吗？图22－3－2[答案：（1）AB＝5米（2）能]3.如图22－3－3，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有两道篱笆的矩形花圃.设花圃的边AB长为x米，面积为S平方米.（1）求S与x之间的函数解析式及自变量的取值范围；（2）当x取何值时，所围成的花圃面积最大，最大值是多少？（3）若墙的最大可用长度为8米，求围成的花圃的最大面积.图22－3－3[答案：（1）S＝－4x2＋24x（0<x<6）（2）当x＝3时，所围成的花圃面积最大，最大值为36平方米（3）最大面积是32平方米]4.[教材第52页习题22.3第9题]分别用定长为L的线段围成矩形和圆，哪种图形的面积大？为什么？[答案：圆理由略]——第52页习题22.3第7题如图22－3－4，点E，F，G，H分别位于正方形ABCD的四条边上.四边形EFGH也是正方形.当点E位于何处时，正方形EFGH的面积最小？图22－3－4【模型建立】通过设未知数建立函数关系，把几何问题转化为函数问题，把动点问题转化为函数问题，通过对函数的变化规律的研究来解决几何问题.【变式变形】如图22－3－5，在边长为4的正方形ABCD中，点E在AB边上（不与点A，B重合），点F在BC边上（不与点B，C重合）.第一次操作：将线段EF绕点F顺时针旋转，当点E落在正方形的边上时，记为点G；第二次操作：将线段FG绕点G顺时针旋转，当点F落在正方形的边上时，记为点H；…依此操作下去.（提示：旋转前、后的图形全等.）图22－3－5（1）图②中的△EFD是经过两次操作后得到的，其形状为等边三角形，求此时线段EF的长.（2）若经过三次操作可得到四边形EFGH.①四边形EFGH的形状为正方形，此时AE与BF的数量关系是AE＝BF；②以①中的结论为前提，设AE的长为x，四边形EFGH的面积为y，求y与x之间的函数解析式及面积y的取值范围.[答案：（1）EF＝－4 2＋4 6（2）y＝2x2－8x＋16（0<x<4）8≤y<16][命题角度1] 利用二次函数的性质解决图形面积的最值问题此类问题常见题型：（1）利用二次函数解决图形的最大（小）面积问题，如教材P49探究1，P52习题22.3T4，T9.（2）几何图形上点的运动问题，何时面积最大（小），如教材P52习题22.3T6，T7，解决此类问题，关键是求二次函数的最值（二次函数图象的顶点的纵坐标或在使实际问题有意义的自变量取值范围内，根据二次函数的增减性找最值）.例福建中考如图22－3－6，在足够大的空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，其中AD≤MN，已知矩形菜园的一边靠墙，另外三边一共用了100米木栏.（1）若a＝20，所围成的矩形菜园的面积为450平方米，求所利用旧墙AD的长；（2）求矩形菜园ABCD面积的最大值.图22－3－6[答案：（1）AD的长为10米（2）当a≥50时，S的最大值为1250；当0＜a＜50时，S 的最大值为50a －12a 2] [命题角度2] 在几何图形运动过程中，判断函数图象此类问题一般作为中考选择题的最后一道题，难度较大.注意把几何图形的性质转化为求函数解析式的条件，然后再判断图象.例 孝感中考如图22－3－7，在△ABC 中，∠B ＝90°，AB ＝3 cm ，BC ＝6 cm ，动点P 从点A 开始沿AB 边向点B 以1 cm /s 的速度移动，动点Q 从点B 开始沿BC 边向点C 以2 cm /s 的速度移动，若P ，Q 两点分别从点A ，B 同时出发，点P 到达点B 时两点同时停止运动，则△PBQ 的面积S 与出发时间t 之间的函数关系图象大致是（ C ）图22－3－7图22－3－8[命题角度3] 二次函数与周长、面积、线段等最值存在性问题此类问题一般作为中考的压轴题，常与三角形或四边形知识紧密结合，体现了初中数学知识的灵活性和综合性.例 如图22－3－9，在平面直角坐标系中，抛物线y ＝ax 2＋bx ＋1交y 轴于点A ，交x轴正半轴于点B （4，0），与过点A 的直线相交于另一点D （3，52），过点D 作DC ⊥x 轴，垂足为C.（1）求抛物线的函数解析式；（2）点P 在线段OC 上（不与点O ，C 重合），过点P 作PN ⊥x 轴，交直线AD 于点M ，交抛物线于点N ，连接CM ，求△PCM 面积的最大值.图22－3－9[答案：（1）y＝－34x2＋114x＋1（2）△PCM面积的最大值为2516]1. 如图，已知：正方形ABCD的边长为1，E、F、G、H分别为各边上的点，且AE=BF=CG=DH，设小正方形EFGH的面积为S，AE为x，则S关于x的函数图象大致是（）2. 用长度为2l的材料围成一个矩形场地，中间有2个隔墙，要使矩形的面积最大，则隔墙的长度为（）A．14l B．13l C．12l D．l3. 已知一个直角三角形两直角边之和为20 cm，则这个直角三角形的最大面积为.4. 给你长8 m的铝合金条，请问：（1）你能用它制成一矩形窗框吗？（2）怎样设计，窗框的透光面积最大？（3）如何验证？参考答案1．B2．A3．50 cm24．解：（1）能.（2）设计成边长为2 m的正方形时，窗框的透光面积最大.（3）设矩形的一边长为x m，则另一边长为(4－x)m，设矩形窗框的面积为y m2，则y=x(4－x)=－x2+4x=－(x－2)2+4.所以当x=2时，y有最大值，y最大=4.所以当设计成边长为2 m的正方形时，窗框的透光面积最大，最大面积为4 m2.一位仁道主义的数学家——阿涅泽意大利科学家阿涅泽(Maria Gaetana Agnesi,1718~1799)在自然科学与哲学的著作对整个学术世界开启了一扇窗．而她最著名的数学作品，《分析讲义》，被公认是第一部完整的微积分教科书之一。

2020年中考数学必考经典专题2二次函数与图形面积的最值及定值压轴问题【方法指导】面积是平面几何中一个重要的概念，关联着平面图形中的重要元素边与角，由动点而生成的面积问题，是抛物线与直线形结合的觉形式，常见的面积问题有规则的图形的面积（如直角三角形、平行四边形、菱形、矩形的面积计算问题）以及不规则的图形的面积计算，解决不规则的图形的面积问题是中考压轴题常考的题型，此类问题计算量较大。

有时也要根据题目的动点问题产生解的不确定性或多样性。

解决动点产生的面积问题，常用到的知识和方法有：（1）如果三角形的某一条边与坐标轴平行，计算这样“规则”的三角形的面积，直接用面积公式．（2）三角形的三条边没有与坐标轴平行的，计算这样“不规则”的三角形的面积，用“割”或“补”的方法．（3）同底等高三角形的面积相等．平行线间的距离处处相等．（4）同底三角形的面积比等于高的比．（5）同高三角形的面积比等于底的比．【题型剖析】【类型1】二次函数与面积最值问题【例1】如图，抛物线2(1)y x k =-+与x 轴相交于A ，B 两点（点A 在点B 的左侧），与y 轴相交于点(0,3)C -．P 为抛物线上一点，横坐标为m ，且0m >．（1）求此抛物线的解析式；（2）当点P 位于x 轴下方时，求ABP ∆面积的最大值；（3）设此抛物线在点C 与点P 之间部分（含点C 和点)P 最高点与最低点的纵坐标之差为h ．①求h 关于m 的函数解析式，并写出自变量m 的取值范围；②当9h =时，直接写出BCP ∆的面积．【变式训练】如图，抛物线22(0)y ax ax c a =-+≠与y 轴交于点(0,4)C ，与x 轴交于点A 、B ，点A 坐标为(4,0)．（1）求该抛物线的解析式；（2）抛物线的顶点为N ，在x 轴上找一点K ，使CK KN +最小，并求出点K 的坐标；（3）点Q 是线段AB 上的动点，过点Q 作//QE AC ，交BC 于点E ，连接CQ ．当CQE ∆的面积最大时，求点Q 的坐标；【类型2】二次函数与面积定值问题【例2】抛物线229y x bx c =-++与x 轴交于(1,0)A -，(5,0)B 两点，顶点为C ，对称轴交x 轴于点D ，点P 为抛物线对称轴CD 上的一动点（点P 不与C ，D 重合）．过点C 作直线PB 的垂线交PB 于点E ，交x 轴于点F ．（1）求抛物线的解析式；（2）当PCF ∆的面积为5时，求点P 的坐标；（3）当PCF ∆为等腰三角形时，请直接写出点P 的坐标．【变式训练】已知抛物线23y ax bx =++经过点(1,0)A 和点(3,0)B -，与y 轴交于点C ，点P 为第二象限内抛物线上的动点．（1）抛物线的解析式为____，抛物线的顶点坐标为____；（2）如图1，连接OP 交BC 于点D ，当:1:2CPD BPD S S ∆∆=时，请求出点D 的坐标；（3）如图2，点E 的坐标为(0,1)-，点G 为x 轴负半轴上的一点，15OGE ∠=︒，连接PE ，若2PEG OGE ∠=∠，请求出点P 的坐标；（4）如图3，是否存在点P ，使四边形BOCP 的面积为8？若存在，请求出点P 的坐标；若不存在，请说明理由．【类型3】二次函数与等面积问题【例3】如图，二次函数23y x bx =-++的图象与x 轴交于点A 、B ，与y 轴交于点C ，点A 的坐标为(1,0)-，点D 为OC 的中点，点P 在抛物线上．（1）b =______；（2）若点P 在第一象限，过点P 作PH x ⊥轴，垂足为H ，PH 与BC 、BD 分别交于点M 、N ．是否存在这样的点P ，使得PM MN NH ==？若存在，求出点P 的坐标；若不存在，请说明理由；（3）若点P 的横坐标小于3，过点P 作PQ BD ⊥，垂足为Q ，直线PQ 与x 轴交于点R ，且2PQB QRB S S ∆∆=，求点P 的坐标．【变式训练】如图，抛物线2y ax bx c =++的图象过点(1,0)A -、(3,0)B 、(0,3)C ．（1）求抛物线的解析式；（2）在抛物线的对称轴上是否存在一点P ，使得PAC ∆的周长最小，若存在，请求出点P 的坐标及PAC ∆的周长；若不存在，请说明理由；（3）在（2）的条件下，在x 轴上方的抛物线上是否存在点M （不与C 点重合），使得PAM PAC S S ∆∆=？若存在，请求出点M 的坐标；若不存在，请说明理由．【类型4】二次函数与面积数量关系【例4】如图，已知二次函数的图象与x 轴交于A 、B 两点，D 为顶点，其中点B 的坐标为(5,0)，点D 的坐标为(1,3)．（1）求该二次函数的表达式；（2）点E 是线段BD 上的一点，过点E 作x 轴的垂线，垂足为F ，且ED EF =，求点E 的坐标．（3）试问在该二次函数图象上是否存在点G ，使得ADG ∆的面积是BDG ∆的面积的35？若存在，求出点G 的坐标；若不存在，请说明理由．【变式训练】如图抛物线2y ax bx c =++经过点(1,0)A -，点(0,3)C ，且OB OC =．（1）求抛物线的解析式及其对称轴；（2）点D 、E 在直线1x =上的两个动点，且1DE =，点D 在点E 的上方，求四边形ACDE 的周长的最小值．（3）点P 为抛物线上一点，连接CP ，直线CP 把四边形CBPA 的面积分为3:5两部分，求点P 的坐标．【达标检测】1．如图，已知抛物线23y ax bx =+-与x 轴交于点(3,0)A -和点(1,0)B ，交y 轴于点C ，过点C 作//CD x 轴，交抛物线于点D ．（1）求抛物线的解析式；（2）若直线(30)y m m =-<<与线段AD 、BD 分别交于G 、H 两点，过G 点作EG x ⊥轴于点E ，过点H 作HF x ⊥轴于点F ，求矩形GEFH 的最大面积；（3）若直线1y kx =+将四边形ABCD 分成左、右两个部分，面积分别为1S ，2S ，且12:4:5S S =，求k 的值．2．如图，抛物线2(0)y ax bx a =+<过点(10,0)E ，矩形ABCD 的边AB 在线段OE 上（点A 在点B 的左边），点C ，D 在抛物线上．设(,0)A t ，当2t =时，4AD =．（1）求抛物线的函数表达式．（2）当t 为何值时，矩形ABCD 的周长有最大值？最大值是多少？（3）保持2t =时的矩形ABCD 不动，向右平移抛物线．当平移后的抛物线与矩形的边有两个交点G ，H ，且直线GH 平分矩形的面积时，求抛物线平移的距离．3．已知：如图，抛物线223y x x =--与x 轴交于A 、B 两点，与y 轴交于点C ，该抛物线的顶点为M ．（1）求点A 、B 、C 的坐标．（2）求直线BM 的函数解析式．（3）试说明：90CBM CMB ∠+∠=︒．（4）在抛物线上是否存在点P ，使直线CP 把BCM ∆分成面积相等的两部分？若存在，请求出点P 的坐标；若不存在，请说明理由．4．如图1，抛物线21:C y x ax =+与22:C y x bx =-+相交于点O 、C ，1C 与2C 分别交x 轴于点B 、A ，且B 为线段AO 的中点．（1）求a b的值；（2）若OC AC ⊥，求OAC ∆的面积；（3）抛物线2C 的对称轴为l ，顶点为M ，在（2）的条件下：①点P 为抛物线2C 对称轴l 上一动点，当PAC ∆的周长最小时，求点P 的坐标；②如图2，点E 在抛物线2C 上点O 与点M 之间运动，四边形OBCE 的面积是否存在最大值？若存在，求出面积的最大值和点E 的坐标；若不存在，请说明理由．5．如图，在平面直角坐标系中，已知抛物线232y x bx c =++与x 轴交于(1,0)A -，(2,0)B 两点，与y 轴交于点C ．（1）求该抛物线的解析式；（2）直线y x n =-+与该抛物线在第四象限内交于点D ，与线段BC 交于点E ，与x 轴交于点F ，且4BE EC =．①求n 的值；②连接AC ，CD ，线段AC 与线段DF 交于点G ，AGF ∆与CGD ∆是否全等？请说明理由；（3）直线(0)y m m =>与该抛物线的交点为M ，N （点M 在点N 的左侧），点M 关于y 轴的对称点为点M '，点H 的坐标为(1,0)．若四边形OM NH '的面积为53．求点H 到OM '的距离d 的值．6．如图，已知二次函数23(2)34y ax a x =--+的图象经过点(4,0)A ，与y 轴交于点B ．在x 轴上有一动点(C m ，0)(04)m <<，过点C 作x 轴的垂线交直线AB 于点E ，交该二次函数图象于点D ．（1）求a 的值和直线AB 的解析式；（2）过点D 作DF AB ⊥于点F ，设ACE ∆，DEF ∆的面积分别为1S ，2S ，若124S S =，求m 的值；（3）点H 是该二次函数图象上位于第一象限的动点，点G 是线段AB 上的动点，当四边形DEGH 是平行四边形，且DEGH 周长取最大值时，求点G 的坐标．7．如图①，在平面直角坐标系xOy 中，抛物线23y ax bx =++经过点(1,0)A -、(3,0)B 两点，且与y 轴交于点C ．（1）求抛物线的表达式；（2）如图②，用宽为4个单位长度的直尺垂直于x 轴，并沿x 轴左右平移，直尺的左右两边所在的直线与抛物线相交于P 、Q 两点（点P 在点Q 的左侧），连接PQ ，在线段PQ 上方抛物线上有一动点D ，连接DP 、DQ ．（Ⅰ）若点P 的横坐标为12-，求DPQ ∆面积的最大值，并求此时点D 的坐标；（Ⅱ）直尺在平移过程中，DPQ ∆面积是否有最大值？若有，求出面积的最大值；若没有，请说明理由．8．已知抛物线2(1)y a x =-过点(3,1)，D 为抛物线的顶点．（1）求抛物线的解析式；（2）若点B 、C 均在抛物线上，其中点1(0,)4B ，且90BDC ∠=︒，求点C 的坐标；（3）如图，直线4y kx k =+-与抛物线交于P 、Q 两点．①求证：90PDQ ∠=︒；②求PDQ ∆面积的最小值．9．如图，在平面直角坐标系中，抛物线222433y x x =--与x 轴交于A ，B 两点（点A 在点B 左侧），与y 轴交于点C ．（1）求点A ，B ，C 的坐标；（2）点P 从A 点出发，在线段AB 上以每秒2个单位长度的速度向B 点运动，同时，点Q 从B 点出发，在线段BC 上以每秒1个单位长度的速度向C 点运动，当其中一个点到达终点时，另一个点也停止运动．设运动时间为t 秒，求运动时间t 为多少秒时，PBQ ∆的面积S 最大，并求出其最大面积；（3）在（2）的条件下，当PBQ ∆面积最大时，在BC 下方的抛物线上是否存在点M ，使BMC ∆的面积是PBQ ∆面积的1.6倍？若存在，求点M 的坐标；若不存在，请说明理由．10．如图，已知抛物线2342y ax x =++的对称轴是直线3x =，且与x 轴相交于A ，B 两点(B 点在A 点右侧）与y 轴交于C 点．（1）求抛物线的解析式和A 、B 两点的坐标；（2）若点P 是抛物线上B 、C 两点之间的一个动点（不与B 、C 重合），则是否存在一点P ，使PBC ∆的面积最大．若存在，请求出PBC ∆的最大面积；若不存在，试说明理由；（3）若M 是抛物线上任意一点，过点M 作y 轴的平行线，交直线BC 于点N ，当3MN =时，求M 点的坐标．。

二次函数的积分与面积计算解析二次函数是高中数学的一个重要知识点，它在数学及其他学科中有着广泛的应用。

在本文中，我将详细解析二次函数的积分与面积计算方法，并通过具体的例子进行说明。

一、二次函数的一般形式二次函数的一般形式为：f(x) = ax^2 + bx + c，其中a、b、c为常数，a ≠ 0。

这里a决定了抛物线的开口方向和大小，b决定了抛物线在x轴方向的位置，c决定了抛物线的位置在y轴方向上的位置。

对于给定的二次函数，我们可以通过积分的方式计算其面积。

二、二次函数的积分要求二次函数f(x) = ax^2 + bx + c的积分，我们可以采用不同的方法来计算。

下面将介绍两种常见的积分计算方法。

1. 定积分法定积分法是通过定义积分的概念，将二次函数拆分成多个小梯形或小矩形的面积求和来计算。

例如，对于二次函数f(x) = 2x^2 + 3x + 1，我们要计算其在区间[a, b]上的积分。

首先，将[a, b]区间等分成n个小区间，每个小区间的宽度为△x = (b-a)/n。

然后，计算每个小区间上的函数值，将其乘以△x，最后将所有小区间上的面积求和，即可得到定积分的近似值。

2. 不定积分法不定积分法是通过反求导的方式来计算二次函数的积分。

对于二次函数f(x) = ax^2 + bx + c，不定积分的结果为F(x) =(a/3)x^3 + (b/2)x^2 + cx + C，其中C为常数。

这里的F(x)称为原函数。

通过不定积分法，我们可以求得任意二次函数的积分。

需要注意的是，求解不定积分时，我们需要考虑函数的定义域，并在积分结果中加上常数C。

三、二次函数的面积计算对于给定的二次函数f(x) = ax^2 + bx + c，我们可以通过计算其与x轴和两条垂直于x轴的直线所围成的图形的面积来求解。

1. 面积计算方法一当函数f(x)在区间[a, b]上为正值时，可以通过定积分法计算其面积。

面积的计算公式为：S = ∫[a, b]f(x)dx。