相交线与平行线单元复习

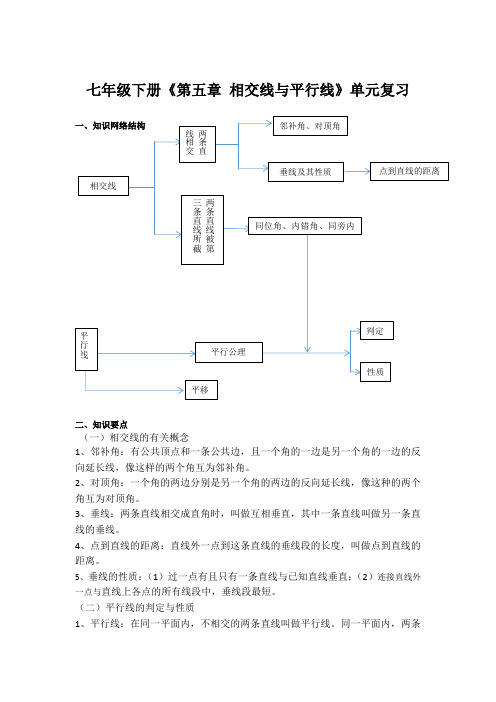
七年级下册《第五章相交线与平行线》单元复习二、知识要点（一）相交线的有关概念1、邻补角：有公共顶点和一条公共边，且一个角的一边是另一个角的一边的反向延长线，像这样的两个角互为邻补角。

2、对顶角：一个角的两边分别是另一个角的两边的反向延长线，像这种的两个角互为对顶角。

3、垂线：两条直线相交成直角时，叫做互相垂直，其中一条直线叫做另一条直线的垂线。

4、点到直线的距离：直线外一点到这条直线的垂线段的长度，叫做点到直线的距离。

5、垂线的性质：（1）过一点有且只有一条直线与已知直线垂直；（2）连接直线外一点与直线上各点的所有线段中，垂线段最短。

（二）平行线的判定与性质1、平行线：在同一平面内，不相交的两条直线叫做平行线。

同一平面内，两条不重合直线的位置关系有平行和相交。

2、平行公理：经过直线外一点有且只有一条直线与已知直线平行。

3、平行公理的推论：如果两条直线都与第三条直线平行，那么这两条直线也相互平行。

4、平行线的判定：判定1：同位角相等，两直线平行。

判定2：同位角相等，两直线平行。

判定3：同旁内角互补，两直线平行。

5、平行线的性质：性质1：两直线平行，同位角相等。

性质2：两直线平行，同位角相等。

性质3：两直线平行，同旁内角互补。

（三）命题1、命题：判断一件事情的语句叫做命题。

每个命题由题设和结论两部分组成；命题分为真命题和假命题。

2、一个经过推理证实得到的真命题，叫做定理；一个命题的正确性需要经过推理，才能做出判断，这个推理过程叫做证明。

（四）平移1、平移：在同一平面内，将一个图形沿某个方向移动一定的距离，图形的这种移动叫做平移。

2、平移的特征：（1）经过平移之后的图形与原来的图形的对应线段平行（或在同一直线上）且相等，对应角相等，图形的形状与大小都没有发生变化。

（2）经过平移后，对应点所连的线段平行（或在同一直线上）且相等。

七年级下学期数学复习第五章相交线与平行线一、知识结构图相交线相交线垂线同位角、内错角、同旁内角平行线平行线及其判定平行线的判定平行线的性质平行线的性质命题、定理平移二、知识定义邻补角：两条直线相交所构成的四个角中，有且有的两个角是邻补角。

邻补角的性质：邻补角。

对顶角：一个角的两边分别是另一个叫的两边的，像这样的两个角互为对顶角。

对顶角的性质：对顶角。

例1如图，直线AB,CD,EF相交于点O，∠AOE=54°，∠EOD=90°，求∠EOB，∠COB的度数。

O CBA 1ODC BA212.平面内三条直线交点的个数有个。

3.如下图，O为直线AB上一点，∠COB=26°30′，则∠1=4.如上图，直线AB,CD相交于O，∠1-∠2=85°，∠AOC=垂线：垂线：两条直线相交成两条直线相交成时，叫做互相垂直，其中一条叫做另一条的。

形成的角称为直角，直角。

垂线的性质：性质1：。

性质2：最短。

例1.如果直线b⊥a，c⊥a，那么b c。

2.与一条已知直线垂直的直线有条。

E ODCBA3.A 村正南有一条公路MN ，由A 村到公路最近的路线是经过点A 作AD ⊥MN ，垂足为点D ，这种设计的理由是 ；B 村与A 村相邻，两村村民来往的最短路线是线段AB 的长，理由是 。

4.已知∠AOB 与∠BOC 互为邻补角，OD 是∠AOB 的平分线，OE 在∠BOC内，∠BOE=21∠EOC ，∠DOE=72°，求∠EOC 的度数。

平行线：平行线：在在 内， 的两条直线叫做平行线。

平行公理： 。

平行的传递性： 。

例1.在同一平面内，过直线l 外的两点A ，B 所作直线与直线l 的位置关系30°北北BA是 同位角、内错角、同旁内角：结合右边图形，哪些是同位角，内错角和同旁内角 同位角： 内错角： 同旁内角：例．1.一个人从A 点出发向北偏东60°方向走到B 点，再从B 点出发向南偏西15°方向走到C 点，则∠ABC 等于( )A.135°B.105°C.75°D.45° 2.由点A 测得点B 的方向是平行线的判定：判定1： 。

相交线平行线单元复习知识网络目标认知学习目标：1．经历对本章所学知识回顾与思考的过程,将本章内容条理化、系统化, 梳理本章的知识结构。

2．通过对知识的疏理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形。

3．认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行线的性质,理解平移的性质,能利用平移设计图案。

重点：平面内两条直线的相交和平行的位置关系,以及相交平行的综合应用。

难点：垂直、平行的性质和判定的综合应用。

知识要点梳理知识点一：对顶角、邻补角⑴对顶角是成对出现的，对顶角是具有特殊位置关系的两个角。

对顶角的特征:有公共顶点，角的两边互为反向延长线；⑵如果∠α与∠β是对顶角，那么一定有∠α=∠β；反之如果∠α=∠β，那么∠α与∠β不一定是对顶角⑶如果∠α与∠β互为邻补角，则一定有∠α+∠β=180°；反之如果∠α+∠β=180°，则∠α与∠β不一定是邻补角。

邻补角的特征:有公共顶点，有一条公共边，另一边互为反向延长线． ⑷两直线相交形成的四个角中，每一个角的邻补角有两个，而对顶角只有一个。

知识点二：垂线及其性质、距离1、垂线的定义：当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足。

如图1所示，符号语言记作：AB ⊥CD ，垂足为O注：要判断两条直线是否垂直，只需看它们相交所成的四个角中，是否有一个角是直角，两条线段垂直，是指这两条线段所在的直线垂直。

2、垂线的画法：过直线上一点画已知直线的垂线；过直线外一点画已知直线的垂线。

要点诠释：⑴画一条线段或射线的垂线，就是画它们所在直线的垂线；⑵过一点作线段的垂线，垂足可在线段上，也可以在线段的延长线上。

⑶具体画法：①一靠：用三角尺一条直角边靠在已知直线上;②二移：移动三角尺使一点落在另一条直角边上;③三画：沿着这条直角边画直线。

精编版平行线与相交线知识点整理总复习平行线与相交线是几何学中重要的概念，它们在平面几何、解析几何以及立体几何中都有广泛的应用。

下面对平行线与相交线的相关知识点进行整理总复习。

一、平行线的定义与性质：1.定义：在平面上的两条直线，如果它们没有交点，就称为平行线。

2.平行线的判定方法：（1）同一条直线上的两条直线，如果与另一条直线平行，则它们互相平行。

（2）用直角板判定法：如果两直线上各取一点P和Q，再通过P、Q各画一条与给定直线垂直的直线，则这两条垂直线相交的点连同P、Q四点是否共线，如果共线，则给定直线与这两条垂直线平行；否则，不平行。

（3）用平行线定理判定：如果两直线上各取一点P和Q，并通过Q画一条与给定直线平行的线段，则通过P和平行线段的直线相交的点与P、Q、两直线上平行线段的两个端点是否共线，如果共线，则给定直线与平行线段平行；否则，不平行。

3.平行线性质：（1）平行线具有等斜率。

（2）平行线的判定是对称的，即如果直线l与直线m平行，那么直线m与直线l也平行。

（3）平行线的传递性。

（4）平行线的交线和倾斜度。

（5）两个平行线与同一直线的交线上的对应角相等。

（6）两个平行线分别与同一直线的两条截线上的对应角相等。

二、相交线与交角的定义与性质：1.定义：在平面上的两条直线如果有一个交点，就称为相交线。

2.存在且唯一：平面上任意两条不平行的直线都有一个且仅有一个交点。

如果两条直线有两个或多个交点，则它们必定重合。

3.交角的定义：两条相交线之间的夹角。

三、平行线与相交线的相关知识点：1.平行线的判定与构造：可以通过几何推理来判定两条直线是否平行，也可以通过构造垂直线段或平行线段等方法来构造平行线。

2.平行线于直线的夹角：直线与平行线的夹角为0度。

3.平行线与截线的夹角：一条直线与平行线的截线上的各个角的和等于180度。

4.形成平行线的条件：如果两个直线分别与一条第三条直线相交，在交点两侧所夹的内角或外角相等，则这两个直线平行。

第五章 相交线与平行线一．知识框架 二．知识梳理 1.邻补角互补注意：（1）邻补角指明了位置关系，又指明了数量关系，“邻”指位置上的相邻；“补”指两个角的和为180°； （2）邻补角的条件：①有公共顶点；②其中一边公共；③另一组边互为反向延长线； （3）邻补角是成对的 2.对顶角相等注意： （1）定义：有一个公共顶点，且有一个角的两边分别是另一角两边的反向延长线（2）性质：对顶角相等3.垂线⑴定义，当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足。

⑵垂线性质1：过一点有且只有一条直线与已知直线垂直 (与平行公理相比较记)⑶垂线性质2：连接直线外一点与直线上各点的所有线段中，垂线段最短。

简称：垂线段最短。

4.点到直线的距离直线外一点到这条直线的垂线段的长度，叫做点到直线的距离. 5.三线八角概念两条直线被第三条直线所截形成八个角，它们构成了同位角.内错角与同旁内角. 如图，直线b a ,被直线l 所截①∠1与∠5在截线l 的同侧，同在被截直线b a ,的上方 叫做同位角（位置相同）；（一边共线）②∠5与∠3在截线l 的两旁（交错），在被截直线b a ,之间（内），叫做内错角（位置在内且交错）； ③∠5与∠4在截线l 的同侧，在被截直线b a ,之间（内），叫做同旁内角. 6.如何判别三线八角判别同位角.内错角或同旁内角的关键是找到构成这两个角的“三线”，有时需要将有关的部分“抽出”或把无关的线略去不看，有时又需要把图形补全.模型：同位角是“F ”型；内错角是“Z ”型；同旁内角是“U ”型.ABC DO abl1 2 3 45 6 7 87.平行线的概念及公理一般地，在同一平面内，不相交的两条直线叫做平行线.记作“a∥b”平行公理：经过直线外一点，有且只有一条直线与这条直线平行.如果两条直线都与第三条直线平行，那么这两条直线也互相平行8.平行线的判定两条直线被第三条直线所截，如果同位角相等，那么两直线平行。