浙江省杭州外国语学校2014届高三3月月考数学(文科)试卷

石油铁矿城镇井泉时令河绿洲例020406080100196019701980199020002010（年）城市化水平(%)乙图浙江省杭州外国语学校2014届高三3月月考文科综合能力测试试卷一、选择题（每小题4分，共35题140分。

请将正确答案填入答题卷相应位置）图中①②③④为内蒙古自治区的四个特色旅游规划区，读图回答第1题。

1. 图中数码与旅游规划区匹配最合理的是A. ①—草原、民俗和辽文化旅游区B. ②—沙漠和历史文化遗址旅游区C. ③—都市圈旅游区D. ④—森林、草原、冰雪旅游区甲图为世界某区域略图，乙图为该区域城市化进程图，读图回答2～3题。

100°110°120°100°°110°°40°120°2．下列城镇服务等级由高到低排序正确的是A ．①②③④ B. ①③②④ C. ②③①④ D. ②①③④ 3．关于该区域城市化的叙述正确的是A. 20世纪60年代第三产业快速发展是推进该区域城市化的主要动力B. 20世纪80年代以来该区域城市化速度较缓是逆城市化造成的影响C. 近40年以来该区域城市化发展带动本区域大牧场放牧业的发展D. 近40年以来该区域城市化受资源开发及自然条件影响较大图甲为1999～2007年我国耕地减少的重心转移示意图，图乙为1999～2007年我国耕地面积与粮食产量变化曲线图。

读图完成4～5题。

4．1999～2003年，我国耕．地减少．．．的重心转移的主要原因是 A ．东南沿海地区城市化速度快 B ．东南沿海地区种植业结构调整 C ．西部大开发 D ．西北地区合理开发耕地后备资源 5．2003～2007年，我国粮食产量变化的主要原因是A ．资金、科技投入加大B ．交通条件不断改善C ．农业劳动力增加D ．经济作物种植面积扩大2012年12月7日，日本东北(33.0°N ，144.6°E)发生了里氏7.3级地震。

杭高2013学年第二学期第六次月考高三数学试卷（文科）注意事项：1、本次考试时间120分钟，满分150分．2、在考试过程中不得使用计算器．3、答案一律做在答卷页上．一、选择题：本大题共10小题，每小题5分, 共50分，在每个小题给出的四个选项中，有且只有一项是符合题目要求的．1．集合{}{}22|log (2),|540==-=-+<A x y x B x x x ，则A B =I （ ） A ．∅B.()2,4C.()2,1-D.()4,+∞2. i 是虚数单位。

已知复数413(1)3iZ i i+=++-，则复数Z 对应点落在（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 3.已知R a ∈，则"21"≥+aa 是"0">a 的（ ） A ．充分非必要条件 B ．必要非充分条件C ．充要条件D ．既不充分也不必要条件 4．设α表示平面，b a ,表示直线，给定下列四个命题：(1)αα⊥⇒⊥b b a a ,//； (2)αα⊥⇒⊥b a b a ,//;(3)αα//,b b a a ⇒⊥⊥; (4)b a b a //,⇒⊥⊥αα.其中正确命题的个数有 （ ） A.1个 B.2个 C.3个 D.4个5. 如右图，此程序框图的输出结果为（ ） A ． 94 B.98 C.115 D.11106. 定义式子运算为12142334a a a a a a a a =-将函数sin 3()cos 1xf x x =的图像向左平移(0)n n >个单位，所得图像对应的函数为奇函数，则n 的最小值为 （ ）A ．6πB ．3πC ．56πD ．23π7.已知0,0a b>>且1ab=,则函数x axf=)(与xxgblog)(-=的图象可能是（）A B C D8.已知,0,0>>ba函数abxbaabxxf+--+=)4()(2是偶函数，则)(xf的图象与y 轴交点纵坐标的最小值为（）A. 16B. 8C.4D.229．曲线x eyC21:1=关于直线xy=对称得曲线2C，动点P在1C上，动点Q在2C上，则||PQ最小值为（）A. 2ln1- B.)2ln1(2- C. 2ln1+ D. )2ln1(2+10.如图，)0,0(,1:222221>>=-babyaxCFF是双曲线、的左右焦点，过1F的直线与的左、右两支分别交于AB,两点。

浙江省杭州二中2014届高三第五次（3月）月考文科综合试卷本试卷分选择题和非选择题两部分，满分300分，考试用时150分钟。

注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的校名、姓名、考号填写在答题卡的密封线内。

2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其它答案；不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在另发的答题卷各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效。

4．考生必须保持答题卡的整洁，考试结束后，将答题卷和答题卡一并收回。

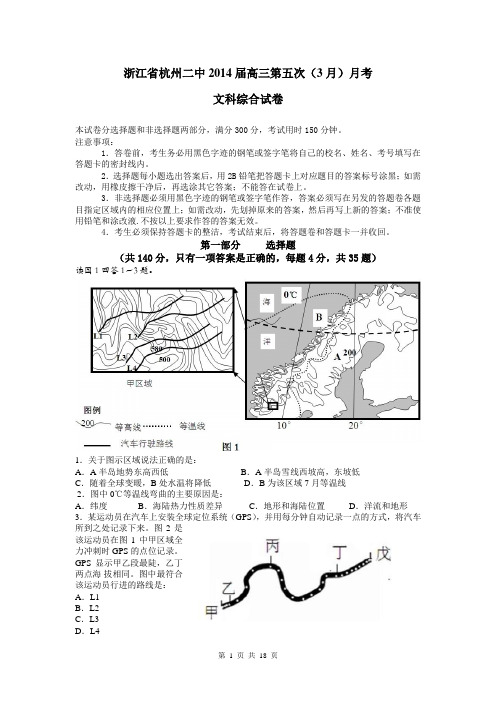
第一部分选择题（共140分，只有一项答案是正确的，每题4分，共35题）读图1回答1～3题。

1．关于图示区域说法正确的是：A．A半岛地势东高西低B．A半岛雪线西坡高，东坡低C．随着全球变暖，B处水温将降低D．B为该区域7月等温线2．图中0℃等温线弯曲的主要原因是：A．纬度B．海陆热力性质差异C．地形和海陆位置D．洋流和地形3．某运动员在汽车上安装全球定位系统（GPS），并用每分钟自动记录一点的方式，将汽车所到之处记录下来。

图2是该运动员在图1中甲区域全力冲刺时 GPS的点位记录。

GPS显示甲乙段最陡，乙丁两点海拔相同。

图中最符合该运动员行进的路线是：A．L1B．L2C．L3D．L4下图是雪线（终年积雪下限），高山寒漠土、林线（山地森林分布的最高界线）和对流层高度随纬度的变化曲线，读图2回答4~5题。

4．图中与林线高度对应的曲线是： A ．① B ．② C ．③ D ．④5．与图中高山寒漠土随纬度分布规律基本相似的是：A ．气温随纬度的分布规律B ．雪线随纬度的分布规律C ．海水蒸发量随纬度的分布规律D ．昼夜长短年变化幅度随纬度的分规律下图示意我国部分地区日均气温稳定通过≥10.0℃初期和终期等值线的分布。

2014年春红安三中高二年级3月月考数 学 试 题 （文科）（时间 分钟，满分150分）一、选择题（每小题5分，共50分） 1.下列命题中特称命题的个数是（ ）（1）有些三角形是等腰三角形 （2）2,230x Z x x ∃∈--= （3）存在一个三角形，它的内角和是0170 （4）矩形都是平行四边形 A ．0B ．1C ．2D ．32.若ABC ∆的两个顶点坐标(4,0),(4,0)A B -,ABC ∆的周长为18，则顶点C 的轨迹方程为（ ）A ．221259x y +=B ．221(0)259y x y +=≠C ．221(0)169x y y +=≠ D ．221(0)259x y y +=≠ 3."lg lg "x y >>的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件 4.下列命题中逆命题为真命题的是（ ） （1）若2320x x -+=，则12x x ==或； （2）若23x -≤<，则(2)(3)0x x +-≤； （3）若220,0x y x y ==+=则（4）已知,x y N *∈，若,x y 是偶数，则x y +是偶数A ．（1）B ．（2）C ．（3）D ．（4）5.抛物线24y x =的焦点弦被焦点分成长是m 和n 的两部分，则m 与n 的关系是（ ） A ．m n m n += B ．4m n += C ．4mn = D ．无法确定6.下列命题中的真命题是（ ）A ．,sin cos 2x R x x ∃∈+=使得B ．(0,),sin cos 2x x x π∀∈>使得C ．2,1x R x x ∃∈+=-使得D ．2,12x R x x ∀∈+≥使得7.由下列各组命题构成的复合命题中，""p q 或为真命题，""p q 且为假命题，""p 非为真命题的一组为（ ）A ．p ：3为偶数，q ：4为奇数B ．:3,:53p q π<>C ．:{,},:{}{,}p a a b q a a b ∈⊂D ．:,:p Q R q N Z ⊂=8.双曲线22163x y -=的渐近线与圆222(3)(0)x y r r -+=>相切，则r = （ ） AB ．2C ．3D ．69.已知,a b R ∈，下列四个命题中为真命题的是（ ） ①若||a b >，则22a b > ② 若22a b >，则||a b >③若||a b >，则22a b > ④ 若22a b >，则||a b > A ．①③B ．①④C ．②③D ．②④10.过双曲线22221(0,0)x y a b a b-=>>的一个焦点F 引它的一条渐近线的垂线，垂足为M ，延长FM 交y 轴于E ，若M 为EF 的中点，则该双曲线的离心率为（ ） A ．2 BC ．3 D二、填空题（每小题5分，共35分）11.命题“所有的奇数的立方是奇数”的否定是_______________.12.椭圆22135x y k +=+的离心率为2，则k 的值为____________. 13.已知(,0),(1,),(3)(3)a x b y a b a b ==+⊥-且，则点P (,)x y 的轨迹方程为__________.14.若2():sin cos ,():10r x x x m s x x mx +>++>，如果对于,()x R r x ∀∈为假命题且()s x 为真命题，则实数m 的取值范围是____________.15. ABC ∆的两个顶点A ，B 的坐标分别是(5,0),(5,0)-，边AC ，BC 所在直线的斜率之积为12-，则顶点C 的轨迹方程是_________________.16.已知点A ，F 分别是椭圆22221(0)x y a b a b+=>>的右顶点和左焦点，点B 为椭圆短轴的一个端点，若0BF BA =，则椭圆的离心率e 为____________.17.给出下列四个命题：（1）有理数是实数； （2）有些平行四边形不是菱形； （3）2,20x R x x ∀∈->； （4）,21x R x ∃∈+为奇数； 以上命题为真命题的序号是___________.三、解答题（共5题，65分）18.（12分）求适合下列条件的圆锥曲线标准方程：（1）过点（－3，2）且与22194x y +=有相同焦点的椭圆的标准方程； （2）以原点为顶点，坐标轴为对称轴，并且经过点(4,P --的抛物线的标准方程19.（12分）若条件22:2310,:(21)(1)0P x x q x a x a a -+≤-+++≤条件。

2014年高考模拟试卷 数学（文科）本试卷分为选择题和非选择题两部分。

考试时间120分种。

请考生按规定用笔将所有试题的答案标号涂、写在答题纸上。

参考公式：球的表面积公式 柱体的体积公式24πS R = V=Sh球的体积公式 其中S 表示锥体的底面积，h 表示锥体的高34π3V R =台体的体积公式： 其中R 表示球的半径 V=31h （2211S S S S ++）棱锥的体积公式 其中21,s s 分别表示台体的上、下底面积，V=31Sh h 表示台体的高 其中S 表示锥体的底面积， 如果事件A B ，互斥，那么h 表示锥体的高 ()()()P A B P A P B +=+选择题部分一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.设集合M={1,2,4,8},N={x|x 是2的倍数}，则M ∩N=（ ）A.{2,4}B.{1,2,4}C.{2,4,8} D{1,2,8} 【命题意图】：主要考察集合间的基本运算。

【答案】C-------【原创】 2.“1a =”是“对任意的正数x ，21ax x+≥”的（ ） A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 【命题意图】：主要考察与基本不等式（打钩函数）结合，判断必要条件、充分条件与充要条件。

【答案】A------------【原创】3. 已知三条不同直线l ，m ，n ，三个不同平面γβα，，，有下列命题： ①若m ∥α，n ∥α，则m ∥n ； ②若α∥β，α⊂l ，则l ∥β； ③若γβγα⊥⊥，，则α∥β；④若m ，n 为异面直线，α⊂m ，β⊂n ，m ∥β，n ∥α，则α∥β.其中正确的命题个数是( )A ．0B ．1C ．2D ．3 【命题意图】：本题主要考察了立体几何中线面之间的位置关系及其中的公理和判定定理，也蕴含了对定理公理综合运用能力的考察。

杭州外国语学校2018-2019学年高三上学期第三次月考试卷数学含答案 班级__________ 座号_____ 姓名__________ 分数__________一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1． 已知定义在R 上的奇函数f （x ）满足f （x ）=2x ﹣4（x ＞0），则{x|f （x ﹣1）＞0}等于（ ） A ．{x|x ＞3} B ．{x|﹣1＜x ＜1} C ．{x|﹣1＜x ＜1或x ＞3} D ．{x|x ＜﹣1}2． 若()()()()2,106,10x x f x f f x x -≥⎧⎪=⎨+<⎡⎤⎪⎣⎦⎩,则()5f 的值为（ ）A ．10B ．11 C.12 D ．133． 若变量x y ，满足约束条件22024010x y x y x +-≥⎧⎪-+≥⎨⎪-≤⎩，则目标函数32z x y =-的最小值为（ ）A ．-5B ．-4 C.-2 D ．3 4． 某工厂产生的废气经过过虑后排放，过虑过程中废气的污染物数量P （单位：毫克/升）与时间t （单位：小时）间的关系为0e ktP P -=（0P，k 均为正常数）．如果前5个小时消除了10%的污染物，为了消除27.1% 的污染物，则需要（ ）小时. A.8B.10C. 15D. 18【命题意图】本题考指数函数的简单应用，考查函数思想，方程思想的灵活运用，体现“数学是有用的”的新课标的这一重要思想.5． 487被7除的余数为a （0≤a ＜7），则展开式中x ﹣3的系数为（ ）A ．4320B ．﹣4320C ．20D ．﹣206． 设集合{}|||2A x R x =∈≤，{}|10B x Z x =∈-≥，则A B =（ ）A.{}|12x x <≤B.{}|21x x -≤≤C. {}2,1,1,2--D. {}1,2【命题意图】本题考查集合的概念，集合的运算等基础知识，属送分题．7． 定义：数列{a n }前n 项的乘积T n =a 1•a 2•…•a n ，数列a n =29﹣n ，则下面的等式中正确的是（ ） A ．T 1=T 19B ．T 3=T 17C ．T 5=T 12D ．T 8=T 118． 椭圆22:143x y C +=的左右顶点分别为12,A A ，点P 是C 上异于12,A A 的任意一点，且直线1PA 斜率的取值范围是[]1,2，那么直线2PA 斜率的取值范围是（ ）A ．31,42⎡⎤--⎢⎥⎣⎦ B ．33,48⎡⎤--⎢⎥⎣⎦ C ．1,12⎡⎤⎢⎥⎣⎦ D ．3,14⎡⎤⎢⎥⎣⎦【命题意图】本题考查椭圆的标准方程和简单几何性质、直线的斜率等基础知识，意在考查函数与方程思想和基本运算能力． 9． 已知1()21x f x =+，则331(log 2)(log )2f f +=（ ） A ．12B ．1C ．2D ．4 10．若复数12,z z 在复平面内对应的点关于y 轴对称，且12i z =-，则复数12z z 在复平面内对应的点在（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限【命题意图】本题考查复数的几何意义、代数运算等基础知识，意在考查转化思想与计算能力．11．圆222(2)x y r -+=（0r >）与双曲线2213y x -=的渐近线相切，则r 的值为（ ） AB ．2 CD．【命题意图】本题考查圆的一般方程、直线和圆的位置关系、双曲线的标准方程和简单几何性质等基础知识，意在考查基本运算能力．12．在正方体1111ABCD A B C D -中，M 是线段11AC 的中点，若四面体M ABD -的外接球体积为36p ， 则正方体棱长为（ ）A ．2B ．3C ．4D ．5【命题意图】本题考查以正方体为载体考查四面体的外接球半径问题，意在考查空间想象能力和基本运算能力．二、填空题（本大题共4小题，每小题5分，共20分.把答案填写在横线上）13．已知[2,2]a ∈-，不等式2(4)420x a x a +-+->恒成立，则的取值范围为__________.14．当0,1x ∈（）时，函数()e 1xf x =-的图象不在函数2()g x x ax =-的下方，则实数a 的取值范围是___________．【命题意图】本题考查函数图象间的关系、利用导数研究函数的单调性，意在考查等价转化能力、逻辑思维能力、运算求解能力．15．若直线：012=--ay x 与直线2l ：02=+y x 垂直，则=a . 16．将曲线1:C 2sin(),04y x πωω=+>向右平移6π个单位后得到曲线2C ，若1C 与2C 关于x 轴对称，则ω的最小值为_________.三、解答题（本大共6小题，共70分。

2012届杭州市第十四中学高三3月月考数学（文科）试题(2012.3)本试题卷分选择题和非选择题两部分．全卷共4页，选择题部分1至2页，非选择题部分2至4页．满分150分，考试时间120分钟．请考生按规定用笔将所有试题的答案涂、写在答题纸上．选择题部分（共50分）注意事项：1．答题前，考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上．2．每小题选出答案后，用2B 铅笔把答题纸上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号，不能答在试题卷上．参考公式：如果事件A ，B 互斥，那么 柱体的体积公式 ()()()P A B P A P B +=+ V Sh =如果事件A ，B 相互独立，那么 其中S 表示柱体的底面积，h 表示柱体的高()()()P A B P A P B ⋅=⋅ 锥体的体积公式如果事件A 在一次试验中发生的概率是p ，那么 13V Sh =n 次独立重复试验中事件A 恰好发生k 次的概率 其中S 表示锥体的底面积，h 表示锥体的高()()()1,0,1,2,,n kk kn n P k C p p k n -=-= 球的表面积公式台体的体积公式 24πS R =()1213V h S S = 球的体积公式其中12,S S 分别表示台体的上底、下底面积， 34π3V R =h 表示台体的高 其中R 表示球的半径一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．(1) 设{}2|,R A y y x x ==∈，{}(,)|2B x y y x ==+，则A B =(A) ∅(B) {}1,4(C) {}(1,1),(2,4)-(D) {}(1,4)(2) 若x ∈R ．则“(x －1)(x ＋3)<0”是“(x ＋1)(x －3)＜0”的 (A) 充分非必要条件 (B) 必要非充分条件 (C) 充要条件 (D) 既非充分也非必要条件(3) 设复数 z 1＝1＋i ，z 2＝1－i （i 是虚数单位），则 1221z zz z +＝(A) －i (B) i (C) 0 (D) 1(4) 设α，β，γ是三个互不重合的平面，m ，n 是两条不重合的直线，则下列命题中正确的是 (A) 若α⊥β，β⊥γ，则α⊥γ (B) 若α//β，m ⊄β，m //α，则m //β (C) 若α⊥β，m ⊥α，则m //β (D) 若m //α，n //β，α⊥β，则m ⊥n（第11题）(5) 要得到函y ＝sin2x ＋cos2x 的图象，只需将曲线y＝sin2x 上所有的点 (A) 向左平移π8个单位 (B) 向右平移π8个单位(C) 向左平移π4个单位 (D) 向右平移π4个单位(6) 已知点O 是边长为1的正△ABC 的中心（如图所示），则()()OA OB OA OC +⋅+＝(A) 19(B) 19-(C) 16(D) 16-(7) 设某程序框图如图所示，则该程序运行后输出的s 值为 (A) 102 (B) 410 (C) 614 (D) 1638 (8) 设数列{a n }，{b n }都是公差为1的等差数列，其首项分别为a 1，b 1．若a 1＋b 1＝5，a 1>b 1，a 1，b 1∈N*，n ∈N*，则数列{}n b a 的前10项的和等于 (A) 55 (B) 70 (C) 85 (D) 100(9) 若圆C ：x 2＋y 2＋2x －4y ＋3＝0关于直线2ax ＋by ＋6＝0对称，则由点(a ,b )向圆所作的切线长的最小值是 (A) 2 (B) 3 (C) 4 (D) 6 (10) 设 P (x ,y )，Q (x ′,y ′) 是椭圆 22221x y a b+=（a >0，b >0）上的两点，则下列四个结论：① a 2＋b 2≥(x ＋y )2；② 2221111a b x y ⎛⎫+≥+ ⎪⎝⎭；③ 22224a b x y +≥；④ 221xx yy a b''+≤．其中正确的个数为(A) 1个 (B) 2个 (C) 3个 (D) 4个非选择题部分 (共100分)二、 填空题: 本大题共7小题, 每小题4分, 共28分。

2014-2015学年某某省某某外国语学校高三（上）周练数学试卷（文科）（十）一.选择题1．在复平面内，复数对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限2．下列说法正确的是（）A．若a∈R，则“＜1”是“a＞1”的必要不充分条件B．“p∧q为真命题”是“p∨q为真命题”的必要不充分条件C．若命题p：“∀x∈R，sinx+cosx≤”，则￢p是真命题D．命题“∃x0∈R，使得x02+2x0+3＜0”的否定是“∀x∈R，x2+2x+3＞0”3．设S n是等差数列a n的前n项和，若，则=（）A．B．C．D．4．若△ABC为锐角三角形，则下列不等式中一定能成立的是（）A．log cosC＞0 B．log cosC＞0C．log sinC＞0 D．log sinC＞05．把函数图象上各点的横坐标缩短到原来的倍（纵坐标不变），再将图象向右平移个单位，那么所得图象的一条对称轴方程为（）A．B．C．D．6．某几何体的三视图如图所示，则其侧面积为（）A．B．C．D．7．对任意非零实数a，b，若a⊗b的运算规则如图的程序框图所示，则（3⊗2）⊗4的值是（）A．0 B．C．D．98．设实数x，y满足约束条件，则u=的取值X围是（）A．[，] B．[，] C．[，] D．[，]9．若函数f（x）=ax3+bx2+cx+d（a，b，c＞0）在R上是单调函数，则的取值X围为（）A．（4，+∞）B．（2+2，+∞）C．[4，+∞）D．[2+2，+∞）10．（5分）在区间[1，5]和[2，4]分别取一个数，记为a，b，则方程表示焦点在y轴上且离心率小于的椭圆的概率为（）A．B．C．D．11．已知函数f（x）=|x+a|（a∈R）在[﹣1，1]上的最大值为M（a），则函数g（x）=M（x）﹣|x2﹣1|的零点的个数为（）A．1个B．2个C．3个D．4个12．过双曲线﹣=1（a＞0，b＞0）的一个焦点F引它到渐近线的垂线，垂足为M，延长FM交y轴于E，若=2，则该双曲线离心率为（）A．B．C．D．313．已知P、M、N是单位圆上互不相同的三个点，且满足||=||，则的最小值是（）A．﹣B．﹣C．﹣D．﹣114．设函数y=f（x）的定义域为D，若函数y=f（x）满足下列两个条件，则称y=f（x）在定义域D上是闭函数．①y=f（x）在D上是单调函数；②存在区间[a，b]⊆D，使f（x）在[a，b]上值域为[a，b]．如果函数f（x）=为闭函数，则k的取值X围是（）A．（﹣1，﹣] B．[，1﹚C．（﹣1，+∞）D．（﹣∞，1）二.填空题15．（5分）（2014某某二模）已知||=2，||=2，||=2，且++=，则++=．16．设，若当且仅当x=3，y=1时，z取得最大值，则k的取值X围为．17．（5分）（2014某某一模）已知点P是椭圆=1（x≠0，y≠0）上的动点，F1，F2为椭圆的两个焦点，O是坐标原点，若M是∠F1PF2的角平分线上一点，且=0，则|的取值X围是．18．对于定义在区间D上的函数f（X），若存在闭区间[a，b]⊊D和常数c，使得对任意x1∈[a，b]，都有f（x1）=c，且对任意x2∈D，当x2∉[a，b]时，f（x2）＜c恒成立，则称函数f（x）为区间D上的“平顶型”函数．给出下列说法：①“平顶型”函数在定义域内有最大值；②函数f（x）=x﹣|x﹣2|为R上的“平顶型”函数；③函数f（x）=sinx﹣|sinx|为R上的“平顶型”函数；④当t≤时，函数，是区间[0，+∞）上的“平顶型”函数．其中正确的是．（填上你认为正确结论的序号）三.解答题19．（12分）（2014正定县校级三模）已知△ABC是半径为R的圆内接三角形，且2R（sin2A ﹣sin2C）=（a﹣b）sinB．（1）求角C；（2）试求△ABC面积的最大值．20．（12分）（2014某某二模）某公司研制出一种新型药品，为测试该药品的有效性，公司选定2000个药品样本分成三组，测试结果如表：分组A组B组C组药品有效670 a b药品无效80 50 c已知在全体样本中随机抽取1个，抽到B组药品有效的概率是0.35．（1）现用分层抽样的方法在全体样本中抽取360个测试结果，问应在C组抽取样本多少个？（2）已知b≥425，c≥68，求该药品通过测试的概率（说明：若药品有效的概率不小于90%，则认为测试通过）．21．（12分）（2015某某模拟）已知几何体A﹣BCED的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形．（1）求此几何体的体积V的大小；（2）求异面直线DE与AB所成角的余弦值；（3）试探究在DE上是否存在点Q，使得AQ⊥BQ并说明理由．22．（12分）（2014春雁峰区校级月考）在平面直角坐标系xOy中，已知中心在坐标原点且关于坐标轴对称的椭圆C1的焦点在抛物线C2：y2=﹣4x的准线上，且椭圆C1的离心率为．（1）求椭圆C1的方程，（2）若直线l与椭圆C1相切于第一象限内，且直线l与两坐标轴分别相交与A，B两点，试探究当三角形AOB的面积最小值时，抛物线C2上是否存在点到直线l的距离为．23．（12分）（2014某某校级模拟）已知函数f（x）=lnx+x2﹣ax（a为常数）．（1）若x=1是函数f（x）的一个极值点，求a的值；（2）当0＜a≤2时，试判断f（x）的单调性；（3）若对任意的a∈（1，2），x0∈[1，2]，使不等式f（x0）＞mlna恒成立，某某数m的取值X围．2014-2015学年某某省某某外国语学校高三（上）周练数学试卷（文科）（十）参考答案与试题解析一.选择题1．在复平面内，复数对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限【分析】利用复数的运算法则、几何意义即可得出．【解答】解：复数==﹣i﹣1对应的点（﹣1，﹣1）位于第三象限，故选：C．【点评】本题考查了复数的运算法则、几何意义，考查了推理能力与计算能力，属于基础题．2．下列说法正确的是（）A．若a∈R，则“＜1”是“a＞1”的必要不充分条件B．“p∧q为真命题”是“p∨q为真命题”的必要不充分条件C．若命题p：“∀x∈R，sinx+cosx≤”，则￢p是真命题D．命题“∃x0∈R，使得x02+2x0+3＜0”的否定是“∀x∈R，x2+2x+3＞0”【分析】利用充要条件的定义，可判断A，B，判断原命题的真假，进而根据命题的否定与原命题真假性相反，可判断C，根据存在性（特称）命题的否定方法，可判断D．【解答】解：若“＜1”成立，则“a＞1”或“a＜0”，故“＜1”是“a＞1”的不充分条件，若“a＞1”成立，则“＜1”成立，故“＜1”是“a＞1”的必要条件，综上所述，“＜1”是“a＞1”的必要不充分条件，故A正确；若“p∧q为真命题”，则“p，q均为真命题”，则“p∨q为真命题”成立，若“p∨q为真命题”则“p，q存在至少一个真命题”，则“p∧q为真命题”不一定成立，综上所述，“p∧q为真命题”是“p∨q为真命题”的充分不必要条件，故B错误；命题p：“∀x∈R，sinx+cosx=sin（x+）≤”为真命题，则￢p是假命题，故C 错误；命题“∃x0∈R，使得x02+2x0+3＜0”的否定是“∀x∈R，x2+2x+3≥0”，故D错误；故选：A．【点评】本题以命题的真假判断为载体，考查了充要条件，命题的否定等知识点，是简单逻辑的简单综合应用，难度中档．3．设S n是等差数列a n的前n项和，若，则=（）A．B．C．D．【分析】由题意可得 S3、S6﹣S3、S9﹣S6、S12﹣S9也成等差数列，由此可得 S6=S9+S3①，S12=3S9﹣3S6+S3②，再由可得 S12=S6③，利用①、②、③化简可得的值．【解答】解：∵S n是等差数列a n的前n项和，∴S3、S6﹣S3、S9﹣S6、S12﹣S9也成等差数列，∴S6﹣2S3=S9﹣2S6+S3，∴S6=S9+S3①．同理可得，S12﹣2S9+S6=S9﹣2S6+S3，即 S12=3S9﹣3S6+S3②．而由可得 S12=S6③．由①、②、③化简可得S3=S9，∴=，故选：C．【点评】本题主要考查等差数列的性质的应用，属于中档题．4．若△ABC为锐角三角形，则下列不等式中一定能成立的是（）A．log cosC＞0 B．log cosC＞0C．log sinC＞0 D．log sinC＞0【分析】由锐角三角形ABC，可得1＞cosC＞0，0＜A＜，0＜B＜，，利用正弦函数的单调性可得sinB＞sin（﹣A）=cosA＞0，再利用对数函数的单调性即可得出．【解答】解：由锐角三角形ABC，可得1＞cosC＞0，0＜A＜，0＜B＜，，∴0＜＜B＜，∴sinB＞sin（﹣A）=cosA＞0，∴1＞＞0，∴＞0．故选：B．【点评】本题考查了锐角三角形的性质、锐角三角函数函数的单调性、对数函数的单调性等基础知识与基本技能方法，属于中档题．5．把函数图象上各点的横坐标缩短到原来的倍（纵坐标不变），再将图象向右平移个单位，那么所得图象的一条对称轴方程为（）A．B．C．D．【分析】先对函数进行图象变换，再根据正弦函数对称轴的求法，即令ωx+φ=即可得到答案．【解答】解：图象上各点的横坐标缩短到原来的倍（纵坐标不变），得到函数；再将图象向右平移个单位，得函数，根据对称轴处一定取得最大值或最小值可知是其图象的一条对称轴方程．故选A．【点评】本小题综合考查三角函数的图象变换和性质．图象变换是考生很容易搞错的问题，值得重视．一般地，y=Asin（ωx+φ）的图象有无数条对称轴，它在这些对称轴上一定取得最大值或最小值．6．某几何体的三视图如图所示，则其侧面积为（）A．B．C．D．【分析】从三视图可以推知，几何体是四棱锥，底面是一个直角梯形，一条侧棱垂直底面，易求侧面积．【解答】解：几何体是四棱锥，底面是一个直角梯形，一条侧棱垂直底面．且底面直角梯形的上底为1，下底为2，高为1，四棱锥的高为1．四个侧面都是直角三角形，其中△PBC的高PB===故其侧面积是S=S△PAB+S△PBC+S△PCD+S△PAD==故选A【点评】本题考查三视图求面积、体积，考查空间想象能力，是中档题．7．对任意非零实数a，b，若a⊗b的运算规则如图的程序框图所示，则（3⊗2）⊗4的值是（）A．0 B．C．D．9【分析】由框图知，a⊗b的运算规则是若a≤b成立，则输出，否则输出，由此运算规则即可求出（3⊗2）⊗4的值【解答】解：由图a⊗b的运算规则是若a≤b成立，则输出，否则输出，故3⊗2==2，（3⊗2）⊗4=2⊗4==故选C．【点评】本题考查选择结构，解题的关键是由框图得出运算规则，由此运算规则求值，此类题型是框图这一部分的主要题型，也是这几年对框图这一部分考查的主要方式．8．设实数x，y满足约束条件，则u=的取值X围是（）A．[，] B．[，] C．[，] D．[，]【分析】作出不等式组对应的平面区域，利用数形结合将目标函数进行转化，利用直线的斜率结合分式函数的单调性即可得到结论．【解答】解：作出不等式组对应的平面区域如图：则对应的x＞0，y＞0，则u==，设k=，则u==，由图象可知当直线y=kx，经过点A（1，2）时，斜率k最大为k=2，经过点B（3，1）时，斜率k最小为k=，即．∴，，∴，即，即≤z≤，故选：C【点评】本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合是解决本题的关键，综合性较强，运算量较大．9．若函数f（x）=ax3+bx2+cx+d（a，b，c＞0）在R上是单调函数，则的取值X围为（）A．（4，+∞）B．（2+2，+∞）C．[4，+∞）D．[2+2，+∞）【分析】利用导数求解，由函数f（x）=ax3+bx2+cx+d（a，b，c＞0）在R上是单调函数，可得f′（x）＞0恒成立，找出a，b，c的关系，再利用基本不等式求最值．【解答】解：∵函数f（x）=ax3+bx2+cx+d（a，b，c＞0）在R上是单调函数，∴f′（x）≥0在R上恒成立，即3ax2+2bx+c≥0恒成立，即△=4b2﹣12ac≤0 即b2≤3ac，∴==++2≥2+2≥4．故选C．【点评】考查利用导数即基本不等式的解决问题的能力，把问题转化为恒成立问题解决是本题的关键，应好好体会这种问题的转化思路．10．（5分）在区间[1，5]和[2，4]分别取一个数，记为a，b，则方程表示焦点在y轴上且离心率小于的椭圆的概率为（）A．B．C．D．【分析】根据椭圆的性质结合椭圆离心率，求出a，b满足的条件，求出对应的面积，结合几何概型的概率公式进行求解即可．【解答】解：∵在区间[1，5]和[2，4]分别取一个数，记为a，b，∴，若方程表示焦点在y轴上且离心率小于，则，由e=＜得c＜a，平方得c2＜a2，即a2﹣b2＜a2，即b2＞a2，则b＞a或b a（舍），即，作出不等式组对应的平面区域如图：则F（2，2），E（4，4），则梯形ADEF的面积S==4，矩形的面积S=4×2=8，则方程表示焦点在y轴上且离心率小于的椭圆的概率P=，故选：C．【点评】本题主要考查几何概型的概率的计算，根据椭圆的性质求出a，b的条件，求出对应的面积，利用数形结合是解决本题的关键．11．已知函数f（x）=|x+a|（a∈R）在[﹣1，1]上的最大值为M（a），则函数g（x）=M（x）﹣|x2﹣1|的零点的个数为（）A．1个B．2个C．3个D．4个【分析】求出M（a）的解析式，根据函数g（x）=M（x）﹣|x2﹣1|的零点，即函数M（x）=与函数y=|x2﹣1|交点的横坐标，利用图象法解答．【解答】解：∵函数f（x）=|x+a|（a∈R）在[﹣1，1]上的最大值为M（a），∴M（a）=，函数g（x）=M（x）﹣|x2﹣1|的零点，即函数M（x）=与函数y=|x2﹣1|交点的横坐标，由图可得：函数M（x）=与函数y=|x2﹣1|有三个交点，故函数g（x）=M（x）﹣|x2﹣1|有3个零点，故选：C【点评】本题考查函数图象的作法，熟练作出函数的图象是解决问题的关键，属中档题．12．过双曲线﹣=1（a＞0，b＞0）的一个焦点F引它到渐近线的垂线，垂足为M，延长FM交y轴于E，若=2，则该双曲线离心率为（）A．B．C．D．3【分析】先利用FM与渐近线垂直，写出直线FM的方程，从而求得点E的坐标，利用已知向量式，求得点M的坐标，最后由点M在渐近线上，代入得a、b、c间的等式，进而变换求出离心率【解答】解：设F（c，0），则c2=a2+b2∵双曲线﹣=1（a＞0，b＞0）的渐近线方程为y=±x∴垂线FM的斜率为﹣∴直线FM的方程为y=﹣（x﹣c）令x=0，得点E的坐标（0，）设M（x，y），∵=2，∴（x﹣c，y）=2（﹣x，﹣y）∴x﹣c=﹣2x且y=﹣2y即x=，y=代入y=x得=，即2a2=b2，∴2a2=c2﹣a2，∴=3，∴该双曲线离心率为故选C【点评】本题考查了双曲线的几何性质，求双曲线离心率的方法，向量在解析几何中的应用13．已知P、M、N是单位圆上互不相同的三个点，且满足||=||，则的最小值是（）A．﹣B．﹣C．﹣D．﹣1【分析】由题意可得，点P在MN的垂直平分线上，不妨设单位圆的圆心为O（0，0），点P （0，1），点M（x1，y1），则点N（﹣x1，y1），由得=，求出最小值．【解答】解：由题意可得，点P在MN的垂直平分线上，不妨设单位圆的圆心为O（0，0），点P（0，1），点M（x1，y1），则点N（﹣x1，y1），﹣1≤y1＜1∴=（x1，y1﹣1），=（﹣x1，y1﹣1），．∴===2﹣，∴当y1=时的最小值是故选：B．【点评】本题主要考查两个向量的数量积公式，二次函数的性质，属于中档题．14．设函数y=f（x）的定义域为D，若函数y=f（x）满足下列两个条件，则称y=f（x）在定义域D上是闭函数．①y=f（x）在D上是单调函数；②存在区间[a，b]⊆D，使f（x）在[a，b]上值域为[a，b]．如果函数f（x）=为闭函数，则k的取值X围是（）A．（﹣1，﹣] B．[，1﹚C．（﹣1，+∞）D．（﹣∞，1）【分析】若函数f（x）=为闭函数，则存在区间[a，b]，在区间[a，b]上，函数f（x）的值域为[a，b]，即，故a，b是方程x2﹣（2k+2）x+k2﹣1=0（x，x≥k）的两个不相等的实数根，由此能求出k的取值X围．【解答】解：若函数f（x）=为闭函数，则存在区间[a，b]，在区间[a，b]上，函数f（x）的值域为[a，b]，即，∴a，b是方程x=的两个实数根，即a，b是方程x2﹣（2k+2）x+k2﹣1=0（x，x≥k）的两个不相等的实数根，当k时，，解得﹣1＜k≤﹣．当k＞﹣时，，无解．故k的取值X围是（﹣1，﹣]．故选A．【点评】本题考查函数的单调性及新定义型函数的理解，解题时要认真审题，仔细解答，注意挖掘题设中的隐含条件，合理地进行等价转化．二.填空题15．（5分）（2014某某二模）已知||=2，||=2，||=2，且++=，则++= ﹣12 ．【分析】把++=两边平方，变形可得++=（），代入数据计算可得．【解答】解：∵++=，∴平方可得（++）2=2，∴+2（++）=0，∴++=（）=（4+8+12）=﹣12故答案为：﹣12【点评】本题考查平面向量数量积的运算，由++=两边平方是解决问题的关键，属中档题．16．设，若当且仅当x=3，y=1时，z取得最大值，则k的取值X围为（﹣，1）．【分析】作出不等式对应的平面区域，利用线性规划的知识，确定目标取最优解的条件，即可求出a的取值X围．【解答】解：作出不等式对应的平面区域如图：由z=kx﹣y得y=kx﹣z，要使目标函数z=kx﹣y仅在x=3，y=1时取得最大值，即此时直线y=kx﹣z的截距最小，则阴影部分区域在直线y=kx﹣z的上方，目标函数处在直线x+2y﹣5=0和x﹣y﹣2=0之间，而直线x+2y﹣5=0和x﹣y﹣2=0的斜率分别为﹣，和1，即目标函数的斜率k，满足﹣＜k＜1，故答案为：（﹣，1）．【点评】本题主要考查线性规划的应用，利用数形结合是解决线性规划题目的常用方法．根据条件目标函数z=kx﹣y仅在点A（3，1）处取得最大值，确定直线的位置是解决本题的关键．17．（5分）（2014某某一模）已知点P是椭圆=1（x≠0，y≠0）上的动点，F1，F2为椭圆的两个焦点，O是坐标原点，若M是∠F1PF2的角平分线上一点，且=0，则|的取值X围是．【分析】延长PF2、F1M，交与N点，连接OM，利用等腰三角形的性质、三角形中位线定理和椭圆的定义，证出|OM|=||PF1|﹣|PF2||．再利用圆锥曲线的统一定义，化简得||PF1|﹣|PF2||=|x0|，利用椭圆上点横坐标的X围结合已知数据即可算出|的取值X围．【解答】解：如图，延长PF2、F1M，交与N点，连接OM，∵PM是∠F1PF2平分线，且=0可得F1M⊥MP，∴|PN|=|PF1|，M为F1F2中点，∵O为F1F2中点，M为F1N中点∴|OM|=|F2N|=||PN|﹣|PF2||=||PF1|﹣|PF2||设P点坐标为（x0，y0）∵在椭圆=1中，离心率e==由圆锥曲线的统一定义，得|PF1|=a+ex0，|PF2|=a﹣ex0，∴||PF1|﹣|PF2||=|a+ex0﹣a+ex0|=|2ex0|=|x0|∵P点在椭圆=1上，∴|x0|∈[0，4]，又∵x≠0，y≠0，可得|x0|∈（0，4），∴|OM|∈故答案为：【点评】本题求两点间的距离的取值X围，着重考查了椭圆的定义、等腰三角形的性质、三角形中位线定理和椭圆的简单几何性质等知识，属于中档题．18．对于定义在区间D上的函数f（X），若存在闭区间[a，b]⊊D和常数c，使得对任意x1∈[a，b]，都有f（x1）=c，且对任意x2∈D，当x2∉[a，b]时，f（x2）＜c恒成立，则称函数f（x）为区间D上的“平顶型”函数．给出下列说法：①“平顶型”函数在定义域内有最大值；②函数f（x）=x﹣|x﹣2|为R上的“平顶型”函数；③函数f（x）=sinx﹣|sinx|为R上的“平顶型”函数；④当t≤时，函数，是区间[0，+∞）上的“平顶型”函数．其中正确的是①④．（填上你认为正确结论的序号）【分析】根据题意，“平顶型”函数在定义域内某个子集区间内函数值为常数c，且这个常数是函数的最大值，但是定义并没有指出函数最小值的情况．由此定义再结合绝对值的性质和正弦函数的图象与性质，对于四个选项逐个加以判断，即得正确答案．【解答】解：对于①，根据题意，“平顶型”函数在定义域内某个子集区间内函数值为常数c，且这个常数是函数的最大值，故①正确．对于②，函数f（x）=x﹣|x﹣2|=的最大值为2，但不存在闭区间[a，b]⊊D和常数c，使得对任意x1∈[a，b]，都有f（x1）=2，且对任意x2∈D，当x2∉[a，b]时，f（x2）＜2恒成立，故②不符合“平顶型”函数的定义．对于③，函数f（x）=sinx﹣|sinx|=，但是不存在区间[a，b]，对任意x1∈[a，b]，都有f（x1）=2，所以f（x）不是“平顶型”函数，故③不正确．对于④当t≤时，函数，，当且仅当x∈[0，1]时，函数取得最大值为2，当x∉[0，1]且x∈[0，+∞）时，f（x）=＜2，符合“平顶型”函数的定义，故④正确．故答案为：①④．【点评】本题以命题真假的判断为载体，着重考查了函数的最值及其几何意义、带绝对值的函数和正弦函数的定义域值域等知识点，属于中档题．三.解答题19．（12分）（2014正定县校级三模）已知△ABC是半径为R的圆内接三角形，且2R（sin2A ﹣sin2C）=（a﹣b）sinB．（1）求角C；（2）试求△ABC面积的最大值．【分析】（1）根据正弦定理，已知等式中的角转换成边，可得a、b、c的平方关系，再利用余弦定理求得cosC的值，可得角C的大小；（2）根据正弦定理算出c=R，再由余弦定理c2=a2+b2﹣2abcosC的式子，结合基本不等式找到边ab的X围，利用正弦定理的面积公式加以计算，即可求出△ABC面积的最大值．【解答】解：（1）∵2R（sin2A﹣sin2C）=（a﹣b）sinB，∴根据正弦定理，得a2﹣c2=（a﹣b）b=ab﹣b2，可得a2+b2﹣c2=ab∴cosC===，∵角C为三角形的内角，∴角C的大小为（2）由（1）得c=2Rsin=R由余弦定理c2=a2+b2﹣2abcosC，可得2R2=a2+b2﹣ab≥2ab﹣ab=（2﹣）ab，当且仅当a=b时等号成立∴ab≤=（）R2∴S△ABC=absinC≤（）R2=R2即△ABC面积的最大值为R2【点评】本题给出三角形的外接圆半径为R，在已知角的关系式情况下，求三角形面积最大值．着重考查了三角形的外接圆、正余弦定理和基本不等式求最值等知识，属于中档题．20．（12分）（2014某某二模）某公司研制出一种新型药品，为测试该药品的有效性，公司选定2000个药品样本分成三组，测试结果如表：分组A组B组C组药品有效670 a b药品无效80 50 c已知在全体样本中随机抽取1个，抽到B组药品有效的概率是0.35．（1）现用分层抽样的方法在全体样本中抽取360个测试结果，问应在C组抽取样本多少个？（2）已知b≥425，c≥68，求该药品通过测试的概率（说明：若药品有效的概率不小于90%，则认为测试通过）．【分析】（1）利用抽样的性质先求出a，再根据样本总个数得出b+c=500，从而根据分层抽样的特点确定应在C组抽取样本多少个；（2）列举（b，c）的所有可能性，找出满足b≥425，c≥68，情况，利用古典概型概率公式计算即可．【解答】解：（1）∵，∴a=700∵b+c=2000﹣670﹣80﹣700﹣50=500∴应在C组抽取样本个数是个．（2）∵b+c=500，b≥425，c≥68，∴（b，c）的可能性是（425，75），（426，74），（427，73），（428，72），（429，71），（430，70），（431，69），（432，68）若测试通过，则670+700+b≥2000×90%=1800∴b≥430∴（b，c）的可能有（430，70），（431，69），（432，68）∴通过测试的概率为．【点评】本题考查分层抽样的性质，古典概型概率公式的应用，属于中档题．21．（12分）（2015某某模拟）已知几何体A﹣BCED的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形．（1）求此几何体的体积V的大小；（2）求异面直线DE与AB所成角的余弦值；（3）试探究在DE上是否存在点Q，使得AQ⊥BQ并说明理由．【分析】（1）由该几何体的三视图知AC⊥面BCED，且EC=BC=AC=4，BD=1，则体积可以求得．（2）求异面直线所成的角，一般有两种方法，一种是几何法，其基本解题思路是“异面化共面，认定再计算”，即利用平移法和补形法将两条异面直线转化到同一个三角形中，结合余弦定理来求．还有一种方法是向量法，即建立空间直角坐标系，利用向量的代数法和几何法求解．（3）假设存在这样的点Q，使得AQ⊥BQ．解法一：通过假设的推断、计算可知以O为圆心、以BC为直径的圆与DE相切．解法二：在含有直线与平面垂直垂直的条件的棱柱、棱锥、棱台中，也可以建立空间直角坐标系，设定参量求解．这种解法的好处就是：1、解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理，因为这些可以用向量方法来解决．2、即使立体感稍差一些的学生也可以顺利解出，因为只需画个草图以建立坐标系和观察有关点的位置即可．以C为原点，以CA，CB，CE所在直线为x，y，z轴建立空间直角坐标系．设满足题设的点Q存在，其坐标为（0，m，n），点Q在ED上，∴存在λ∈R（λ＞0），使得=λ，解得λ=4，∴满足题设的点Q存在，其坐标为（0，，）．【解答】解：（1）由该几何体的三视图知AC⊥面BCED，且EC=BC=AC=4，BD=1，∴S梯形BCED=×（4+1）×4=10∴V=S梯形BCED AC=×10×4=．即该几何体的体积V为．（3分）（2）解法1：过点B作BF∥ED交EC于F，连接AF，则∠FBA或其补角即为异面直线DE与AB所成的角．（5分）在△BAF中，∵AB=4，BF=AF==5．∴cos∠ABF==．即异面直线DE与AB所成的角的余弦值为．（7分）解法2：以C为原点，以CA，CB，CE所在直线为x，y，z轴建立空间直角坐标系．则A（4，0，0），B（0，4，0），D（0，4，1），E（0，0，4）∴=（0，﹣4，3），=（﹣4，4，0），∴cos＜，＞=﹣∴异面直线DE与AB所成的角的余弦值为．（3）解法1：在DE上存在点Q，使得AQ⊥BQ．（8分）取BC中点O，过点O作OQ⊥DE于点Q，则点Q满足题设．（10分）连接EO、OD，在Rt△ECO和Rt△OBD中∵∴Rt△ECO∽Rt△OBD∴∠EOC=∠OBD∵∠EOC+∠CEO=90°∴∠EOC+∠DOB=90°∴∠EOB=90°．（11分）∵OE==2，OD==∴OQ===2∴以O为圆心、以BC为直径的圆与DE相切．切点为Q∴BQ⊥CQ∵AC⊥面BCED，BQ⊂面CEDB∴BQ⊥AC∴BQ⊥面ACQ（13分）∵AQ⊂面ACQ∴BQ⊥AQ．（14分）解法2：以C为原点，以CA，CB，CE所在直线为x，y，z轴建立空间直角坐标系．设满足题设的点Q存在，其坐标为（0，m，n），则=（﹣4，m，n），=（0，m﹣4，n）=（0，m，n﹣4），=（0，4﹣m，1﹣n）∵AQ⊥BQ∴m（m﹣4）+n2=0①∵点Q在ED上，∴存在λ∈R（λ＞0）使得=λ∴（0，m，n﹣4）=λ（0，4，m，1﹣n）⇒m=，n=②②代入①得（﹣4）（）2=0⇒λ2﹣8λ+16=0，解得λ=4∴满足题设的点Q存在，其坐标为（0，，）．【点评】本小题主要考查空间线面关系、面面关系、二面角的度量、几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．22．（12分）（2014春雁峰区校级月考）在平面直角坐标系xOy中，已知中心在坐标原点且关于坐标轴对称的椭圆C1的焦点在抛物线C2：y2=﹣4x的准线上，且椭圆C1的离心率为．（1）求椭圆C1的方程，（2）若直线l与椭圆C1相切于第一象限内，且直线l与两坐标轴分别相交与A，B两点，试探究当三角形AOB的面积最小值时，抛物线C2上是否存在点到直线l的距离为．【分析】（1）由题意设椭圆C1的方程，（a＞b＞0），且，由此能求出椭圆C1的方程．（2）设直线l的方程为y=kx+m（k＜0，m＞0）由，得（3+4k2）x2+8kmx+4m2﹣12=0，由此利用根的判别式、韦达定理、点到直线距离公式、弦长公式能推导出抛物线C2上不存在点到直线l的距离为．【解答】解：（1）∵椭圆C1的焦点在抛物线C2：y2=﹣4x的准线上，且椭圆C1的离心率为．∴椭圆焦点在x轴上，设椭圆C1的方程：，（a＞b＞0），且，解得a=2，b=，∴椭圆C1的方程为．（2）∵直线l与椭圆C1相切于第一象限内，∴直线l的斜率存在且小于零，设直线l的方程为y=kx+m（k＜0，m＞0）由，得（3+4k2）x2+8kmx+4m2﹣12=0，由题可知，△=0，∴m2=4k2+3，当即时上式等号成立，此时，直线l为设点D为抛物线C2上任意一点，则点D到直线l的距离为，利用二次函数的性质知，∴抛物线C2上不存在点到直线l的距离为．【点评】本题考查椭圆方程的求法，考查当三角形面积最小时满足条件的点是否存在的判断与求法，解题时要认真审题，注意根的判别式、韦达定理、点到直线距离公式、弦长公式的合理运用．23．（12分）（2014某某校级模拟）已知函数f（x）=lnx+x2﹣ax（a为常数）．（1）若x=1是函数f（x）的一个极值点，求a的值；（2）当0＜a≤2时，试判断f（x）的单调性；（3）若对任意的a∈（1，2），x0∈[1，2]，使不等式f（x0）＞mlna恒成立，某某数m的取值X围．【分析】（1）求导数，利用极值的定义，即可求a的值；（2）当0＜a≤2时，判断导数的符号，即可判断f（x）的单调性；（3）问题等价于：对任意的a∈（1，2），不等式1﹣a＞mlna恒成立．即恒成立．【解答】解：．（1）由已知得：f'（1）=0，∴1+2﹣a=0，∴a=3．…（3分）（2）当0＜a≤2时，f′（x）=因为0＜a≤2，所以，而x＞0，即，故f（x）在（0，+∞）上是增函数．…（8分）（3）当a∈（1，2）时，由（2）知，f（x）在[1，2]上的最小值为f（1）=1﹣a，故问题等价于：对任意的a∈（1，2），不等式1﹣a＞mlna恒成立．即恒成立记，（1＜a＜2），则，…（10分）令M（a）=﹣alna﹣1+a，则M'（a）=﹣lna＜0所以M（a），所以M（a）＜M（1）=0…（12分）故g'（a）＜0，所以在a∈（1，2）上单调递减，所以即实数m的取值X围为（﹣∞，﹣log2e]．…（14分）【点评】本题考查导数知识的综合运用，考查函数的极值，考查函数的单调性，考查恒成立问题，正确分离参数是关键．。

浙江省杭州外国语学校2014届高三3月月考英语试卷考试须知：1. 英语试卷总分值120分，总答题时间120分钟。

2. 本试卷分“试题卷”、“答题卷”和“答题卡”，其中“试题卷”11页，“答题卷”2页，“答题卡”1张。

3. 请将选择题答案写在“答题卡”上，其他题答案写在“答题卷”上，否则无效。

请务必注意试题序号和答题序号相对应。

（注意：61-65题需填涂在答题卡81-85题处。

）4. 所有选择题请用2B铅笔在“答题卡”相应的位置上涂黑，其他题答题一律用蓝色、黑色的钢笔、水笔或圆珠笔，否则无效。

选择题部分（共80分）第一部分：英语知识运用（共两节，满分30分）第一节：单项填空（共20题，每小题0.5分，满分10分）从A、B、C和D四个选项中，选出可以填入空白处的最佳选项，并在答题纸将该选项标号涂黑。

1. ---I am so glad to find you at home. Can you do me a favor?---Sure. ______________?A. Why notB. What’s upC. How comeD. How is it going2.Nothing can be more fascinating than a smile, which can produce hope in even __________ situations.A. embarrassingB. confidentC. desperateD. secure3.How silly I was to have thrown the lottery ticket away! I _______________ the jackpot.A. had better have hitB. might have hitC. should have hitD. must have hit4.Tommy lost his ____________ and began to vomit shortly after he ate the street food.A. enthusiasmB. delightC. pressureD. appetite5.Florence in Italy, __________ beauty is beyond description, is the city that I have been dreaming ofvisiting.A. whichB. thatC. whoseD. who6.We shouldn’t put labels on other people ___________ based on one thing or a few words we’ve heard.A. reallyB. merelyC. rarelyD. approximately7._____________ others when they are talking to us is usually considered rude and inappropriate.A. InterruptingB. InterruptC. Having interruptedD. To be interrupted8. It is required by law that a driving test ______________ taken before a man gets a license.A. wasB. beC. wereD. is9. A daily stretching and yoga practice are the best two ways to _________ back pain.A. relieveB. refreshC. liberateD. comfort10. I came cross Mr. Read on the square the other day. We didn’t talk much because he __________________ to catch the bus.A. had rushedB. had been rushingC. was rushingD. would rush11. --- Believe it or not, my brother once won the first prize in a speech contest.---Really? When was _______?---_______ was in 2005 when he was still in college.A.it; ThisB. this; ItC. that; ThisD. that; It12. Good students involve themselves in class activities, ______________ questions and sharing ideas tolearn from peers.A. risingB. misunderstandingC. copyingD. raising13. Our club has reached the point _______________ all the members should work together to seekcommon ground while reserving differences.A. whereB. whichC. thatD. why14. _________________ her performance in study, no one can match her in the grade. However, learningtakes up all her time and she hasn’t developed other abilities, which is a great pity.A. On behalf ofB. In terms ofC. As a result ofD. In charge of15. Yang Gang, _____ national political advisor, is under _____ investigation for “suspected serious law anddiscipline violations”.A. a; theB. 不填; 不填C. 不填; anD. a; 不填16. Scientists have now reached the conclusion _____ humans have been the dominant cause of globalwarming trends since the 1950s.A. howB. thatC. whichD. whether17. The important thing is not just to _____ more products but to improve the quality and reduce the cost.A. make outB. take outC. turn outD. give out18. In this book, the word is used in its original sense unless _____ stated.A. otherwiseB. thusC. thereforeD. anyway19. _____ with depression, eating disorders and alcohol abuse for years, he now understands how importantbeing healthy is.A. StrugglingB. Having struggledC. StruggledD. To struggle20. ---You must find such long hours very tiring.---_____ - I enjoy it.A. Not yetB. Don’t mention itC. Not in the leastD. I co uldn’t agree more第二节：完形填空（共20小题；每小题1分，满分20分）阅读下列短文，掌握其大意，然后从21-40各题所给的四个选项（A、B、C和D）中，选出最佳选项，并在答题纸上将该选项标号涂黑。