宁夏大学附属中学2013-2014学年高一下学期期中考试数学试题 Word版无答案

考试时间：120分钟 试卷满分：150分一、选择题：（本大题共12小题，每小题5分，共60分．在每小题的4个选项中，只有一项是符合题目要求的）．1．设全集R ，{}{}0,1A x x B x x =>=>，则RAB =（ ）A ．{}01x x ≤<B ．{}01x x <≤C ．{}0x x <D ．{}1x x > 2．下列四个图形中，不是．．以x 为自变量的函数的图象是 （ ）3．下列四组中的函数()f x 与()g x ，是同一函数的是 （ ） A ．2()ln(1)ln(1),()ln(1)f x x x g x x =-++=- B ．2()lg ,()2lg f x x g x x ==C ． 2()11,()1f x x x g x x +-=- D ．21(),()11x f x g x x x -==+-4. 函数log ,log ,log ,log a b c d y x y x y x y x====如图所示，则,,,a b c d 的大小挨次（ ） A ．1c d b a <<<< B ．1d c a b <<<< C. 1d c a b <<<< D ．1c d a b <<<<5．下列函数中既是偶函数又在(0,)+∞上是增函数的是 （ ）A ．3y x =B ． 1y x =+C ． 21y x =-+ D ． 2x y -=6．已知函数122()(1)a f x a a x-=--为幂函数，则a = （ ） A ．1- 或 2B ．2- 或 1C ．1-D ．17．若21log 0,()12b a <> ，则 （ ）A ．1,0a b >>B ．1,0a b ><C ．01,0a b <<>D ．01,0a b <<<8．函数164xy =- （ ）A ．[0,4) B. (0,4] C ．[0,4] D ．(0,4)9．函数2x y -=的反函数的图像为 （ ）10．已知函数()f x 在[0,)+∞上是增函数，()()g x f x =-，若(lg )(1)g x g > ，则x 的取值范围是（ ）A . 1(,10)10B . ()0,10C . ()10,+∞D .()1(,10)10,10+∞11．已知函数2log ,0()(3), 0x x f x f x x ⎧=⎨≤⎩＞＋，则(10)f -的值是（ ） A ．－2B ．－1C ．0D ．112. 已知0x 是函数1()21xf x x =+－的一个零点．若1020(1,),(,)x x x x ∈∈+∞ ，则（ ） A ．12()0,()0f x f x << B ．12()0,()0f x f x <> C ．12()0,()0f x f x ><D ．12()0,()0f x f x >>二、填空题：（本大题共4小题，每小题5分，共20分，将答案填在题中横线上） 13．{}{}25,,A x x B x x a A B=-≤≤=>⊆，则a 取值范围是 ．14．函数22log y x=-的定义域是 ．15．满足28244x x ->－的x 的取值集合是 ． 16．设函数1()()lg 1f x f x x =⋅+，则(10)f = .三、解答题：（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤）Oyx 1AyOx 1BOyx1CO yx1Dlog d y x=log c y x= log b y x=log a y x=(第4题)yxO117．(10分)设集合{}2220,M x ax x x R=-+=∈至多有个一元素，求实数a 的取值范围.18．(12分) 已知函数2()ln2xf x x -=+ ．(1)求函数()f x 的定义域；(2)推断函数()f x 的奇偶性，并说明理由．20. (12分)已知221,02()68,2x x f x x x x ⎧-≤<⎪=⎨-+≥⎪⎩ . （1）画出()f x 的图像； （2）若()1f m =，求实数m 的值。

1、如果0,0a b <>，那么下列不等中正确的是（ ）A ．11a b< B< C ．22a b < D ．a b > 2、若0,0,0x y a ay +><>，则x y -的值（ ）A ．大于0B ．等于0C ．小于0D ．符号不能确定 3、若01,01x y <<<<，则在22,,2x y x y xy ++ ）A ．2xyB ．x y + C． D ．22x y + 4、在ABC ∆中，32a b c +=，233a b c +=，则sin :sin :sin A B C 等于（ ）A ．2:3:4B ．3:4:5C ．4:5:6D ．3:5:7 5、若集合{}{}*(21)(3)0,5A x x x B x N x =+-<=∈≤，则A B 是（ ）A ．{}1,2,3B ．{}1,2C ．{}4,5D ．{}1,2,3,4,5 6、在ABC ∆中，已知3sin b B =，且cos cos B C =，则ABC ∆的形状是（ ）A ．直角三角形B ．等腰三角形C ．等边三角形D ．等腰直角三角形 7、若2()31f x x x =-+，2()21g x x x =+-，则()f x 与()g x 的大小关系是（ ） A ．()()f x g x < B ．()()f x g x = C ．()()f x g x > D ．随x 的变化而变化8、由不等式组10100x y x y x ++≥⎧⎪-+≥⎨⎪≤⎩，所表示的平面区域的面积是（ ）A ．2B ．1C ．12D ． 4 9、在数列2，9，23，44，72，… 中，紧接着72后面的那一项应该是（ ） A ．82 B ．107 C ．100 D ．83 10、设等比数列{}n a 的公比2q =，前n 项和为n S ，则42S a =（ ）A ．2B ．4C ．152 D ．17211、在等差数列{}n a 中，其前n 项和为n S ，若15160,0S S ><，则在15121215,S S S a a a 中最大的是（ ） A ．11S a B ．88S a C ．99S a D ．1515S a 12、已知实数12,,,x a a y 等成等差列，12,,,x b b y 成等比数列，则21212()a a b b +的取值范围是（ ）A ．[)4,+∞B ．(][),44,-∞-+∞ C ．(][),04,-∞+∞ D ．不能确定二、填空题（每小题5分，共20分）13、ABC ∆中，三边长分别为7,5,6AB BC CA ===，则cos()A C += 。

宁夏大学附属中学2013-2014学年高一下学期期中考试英语试题第Ⅰ卷(选择题）第一部分听力(共两节，满分20分)第一节：(共5小题；每小题1分，满分5分)1. Which sport does the man like?A. Basketball.B. Golf.C. Ping-pong.2. How many people are sharing the room now?A. 3.B. 4.C. 5.3. What are the speakers talking about?A. A new building.B. A bad fire five years ago.C. Ruins caused by a big fire.4. Where is the woman most probably now?A. At home.B. In hospital.C. In the office.5. What place does the man dream of?A. Paris.B. Rome.C. London.第二节：（共15小题，每小题1分，满分15分）听第6段材料，回答第6至8题。

6. When did the woman begin to prepare for the performance?A. On May 4.B. In April.C. Three months ago.7. Where is the performance going to be put on?A. In the woman’s school.B. At the People’s Theatre.C. At the Youth Square.8. Why would the woman want to put on the performance?A. To collect money to repair the Youth Square.B. To help the government celebrate May 4 for free.C. To collect money for the Hope Project.听第7段材料，回答第9至11题。

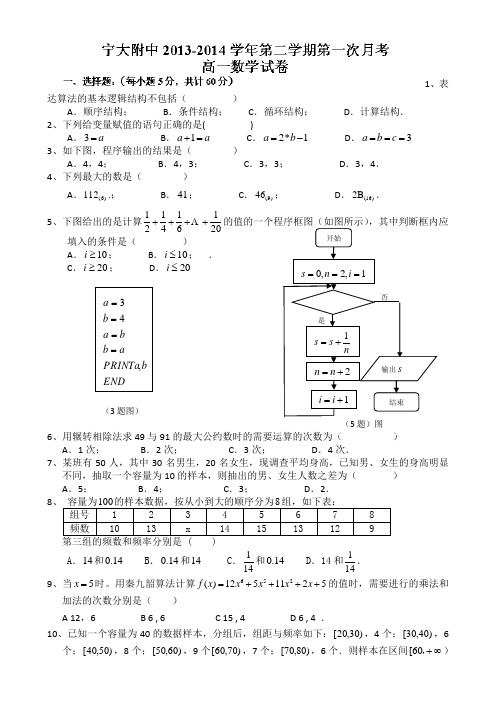
1、表达算法的基本逻辑结构不包括（ ）A ．顺序结构；B ．条件结构；C ．循环结构；D ．计算结构． 2、下列给变量赋值的语句正确的是( )A ．3a =B ．1a a +=C ．2*1a b =-D ．3a b c === 3、如下图，程序输出的结果是（ ）A ．4，4；B ．4，3；C ．3，3；D ．3，4． 4、下列最大的数是（ ）A ．(6)112.；B ．41；C ．(9)46；D ．(16)2B ． 5、下图给出的是计算201614121++++填入的条件是（ ）A ．10≥i ；B ．10≤i ； ．C ．20≥i ；D ．20≤i6、用辗转相除法求49与91A ．1次； B ．2次； C ．3次； D ．4次．7、某班有50人，其中30名男生，20名女生，现调查平均身高，已知男、女生的身高明显不同，抽取一个容量为10的样本，则抽出的男、女生人数之差为（ ） A ．5； B ．4； C ．3； D ．2． 8A ．14和0.14 B ．0.14和14 C ．141和0.14 D ．14和141．9、当5x =时。

用秦九韶算法计算652()1251125f x x x x x =++++的值时，需要进行的乘法和加法的次数分别是（ ）A 12，6B 6 , 6C 15 , 4D 6 , 4 ．10、已知一个容量为40的数据样本，分组后，组距与频率如下：)30,20[，4个；)40,30[，6个；)50,40[，8个；)60,50[，9个)70,60[，7个；)80,70[，6个．则样本在区间∞+，60[）（3题图）上的频率是（ ）A ．10%；B ．20%；C ．32.5%；D ．40%． 11、下列程序执行后，输出的结果是（ ）11S 1DOS S* 1LOOP UNTIL 9PRINT S ENDi ii i i ====-<A 110B 990C 8D 7920 12、如右图所示，给出一个程序框图，其作用是输入x 的值，输出相应的y 的值．若要使输入的x 的值与输出的y 的值相等，则输入的这样的x 的值有( )．A ．1个B ．2个C ．3个D ．4个 二、填空题：（每小题5分，共计20分）13、二进制数110101转换成八进制数的结果是 14、用更相减损术求459与357的最大公约数是_____15、为了了解参加运动会的2000名运动员的年龄情况，从中抽取100名运动员；就这个问题，下列说法中正确的有 ；①2000名运动员是总体；②每个运动员是个体；③所抽取的100名运动员是一个样本；④样本容量为100；⑤这个抽样方法可采用按年龄进行分层抽样；⑥每个运动员被抽到的概率相等16、若总体中含有1650个个体，现在要采用系统抽样法，从中抽取一个容量为35的样本，分段时应从总体中随机剔除 个个体，编号后应均分为 _段，每段有 个个体高一年级数学答题卷13______________________________14_______________________________ 15______________________________16 三、解答题：（ 本题共6个小题，17题10分，其余小题个12分，满分80分）17、某校有学生2000人，其中高一年纪的学生与高三年级的学生之比为3:4，从中抽取一个容量为40的样本，高二年级恰好抽取了12人.求各年级的人数及高一年级、高三年级各抽取的人数.18、对任意正整数是n，求111123sn=⨯⨯⨯⋅⋅⋅⨯的值，请完善下列程序，并画出相对应的程序框图INPUT nS=___i=1DO_____i=i+1LOOP NUTIL _____PRINT SEND19、甲乙两台机床同时生产一种零件，10中，两台机床每天出的次品数分别是：甲 4 1 0 2 2 1 3 1 2 4乙 2 3 1 1 3 2 2 1 2 3计算上述两组数据的平均数和方差，从统计结果看，那台机床的性能较好？20、某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：［50,60），［60,70），［70,80），［80,90），［90,100］.（1）求图中a的值并计算[70,100]的人数；（2）根据频率分布直方图，估计这100名学生语文成绩的平均分.21、22题在反面21.给出一个算法的程序框图（如图所示）.（1）说明该程序的功能；（2）请用WHILE型循环语句写出程序.22．某工厂对某产品的产量与成本的资料分析后有如下数据：(1)(2)求成本y与产量x之间的线性回归方程．(3)当成本为15万元时，试估计产量为多少件？（保留两位小数）(b^＝∑i＝1nxiyi－n x－y－∑i＝1nx2i－n x－2,a^＝y－－b^x－)。

宁大附中2013-2014学年第二学期第一次模拟考试高三数学（文）试卷一、选择题（每小题5分，共60分）1、已知集合{}2log ,1A y y x x ==≥，{B x y ==，则AB =（ ）A ．[]0,1B ．(0,1)C ．[)0,1D ．(]0,1 2、复数11i-的共轭复数为（ ） A ．1122i - B ．1122i + C ．1122i -- D ．1122i -+ 3、下列说法正确的是（ ）A ．若命题,p q ⌝都是真命题，则命题“p q ∧”为真命题B ．命题“若0xy =，则0x =或0y =”的否命题为“若0xy ≠则0x ≠或0y ≠”C ．命题“R,20x x ∀∈>”的否定是“00R,20x x ∃∈≤”D ．“1x =-”是“2560x x --=”的必要不充分条件 4、如图所示，程序框图的输出结果是（ ）A ．16B ．2524 C ．34 D ．11125、如图，若一个空间几何体的三视图，正视图和侧视图都是直角三角形，其直角边均为1，则该几何体的表面积为（ ）A ．1+B ．2+C ．13D ．26、关于函数()sin(2)3f x x π=+的四个命题：①()f x 的图象关于直线12x π=对称；②()f x 的图象关于点(,0)4π对称； ③()f x 的最小正周期为π；④()f x 在0,2π⎡⎤⎢⎥⎣⎦上为增函数，其中正确的是命题是 。

A ．②③ B ．①② C ．②④ D ．①③7、已知函数12,1()22,1x x f x x x --⎧≤-=⎨+>-⎩，则()2f a >的实数a 的取值范围是（ ）A ．(,2)(0,)-∞-+∞B ．(2,1)--C ．(2,0)-D ．(,2)(1,)∞--+∞8、已知双曲线22221(0,0)x y a b a b-=>>，且其一条渐近线经过点(2,4)，则双曲线的离心率为（ ）A B C D 9、已知直线0(0)x y k k +-=>与圆224x y +=交于不同的两点A 、B ，O 是坐标原点，且有OA OB AB +=，那么k 的值为（ ）A ．2B ．CD ．410、已知ABC ∆的内角为,,A B C ，且2sin 12A BC +=，则角C 的大小为（ ）A ．23π B ．2π C ．3π D ．6π第Ⅱ卷本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22题～第24题为选考题，考生根据要求做答． 二、填空题（每小题5分，共20分）13、设变量,x y 满足约束条件3602030x y x y y +-≥⎧⎪--≤⎨⎪-≤⎩，则目标函数2z y x =-的最小值是 。

1、已知Z 为整数集，集合{}260U x Z x x =∈-≥，集合M 满足Z M U ⊆ð，且{}{}1,2,31,2M=，则M 的个数是A ．1B ．2C ．3D ．4 2、已知复数11Z i=+，则Z i ⋅在复平面内对应的点位于 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 3、若直线2320tx y ++=与直线620x ty +-=平行，则实数t 等于 A ．12或12- B ．12 C ．12- D ．144、在正项等比数列{}n a 中，3578a a a =，则10a = A ．1128 B ．1256 C ．1512 D ．110245、一个几何体的三视图如图所示，已知这个几何体的体积为h 的值为A BC ．D ．6、设0x 是方程ln 4x x +=的解，则0x 在下列哪个区间内A ．(0,1)B ．(1,2)C ．(2,3)D ．(3,4) 7、执行如图所示的程序框图，若输入n 的值为6，则输出s 的值为 A ．17 B ．16 C ．10 D ．98、如图，平行四边形ABCD 中，2,1,60AB AD A ==∠=︒，点M 在AB 边上，且13AM AB =，则DM DB ⋅等于A ．2-B ．2C ．1-D ．1 9、已知α、β、γ是三个不重合平面，,a b 是两条不重合直线，有下列三个条件：①//,b αγβ⊂，②//,//b αγβ，③//,b a βγ⊂。

如果命题“,a b αβγ=⊂，且 ，则//a b ”为真命题，则可以在横线处填入的条件是A ．②或③B ．①或②C ．①或③D ．①或②或③10、将某选手的9个得分去掉1个最高分，去掉1个最低分，7个剩余分数的平均分为91，现场做的9个分数的茎叶图后来有一个数据模糊，无法辨认，在图中以x 表示： 则7个剩余的方差为8 7 7 941x 91A ．1169 B ．367 C ．36 D 11、同时满足以下4个条件的集合记作k A ：（1）所有元素都是正整数；（2）最小元素为1；（3）最大元素为2014；（4）各个元素可以从小到大排成一个公差为*(N )k k ∈的等差数列。

1、下列命题中的假命题是（ ）A.以矩形的一边所在直线为旋转轴，其余三边旋转形成的曲面所围成的旋转体叫圆柱；B.以直角三角形的一条边所在的直线为旋转轴，其余两边旋转形成的曲面的旋转体叫圆锥；C.以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的曲面围成的旋转体叫圆锥；D.以等腰三角形的底边上的高所在直线为旋转轴，其余各边旋转形成的曲面围成的旋转体叫圆锥． 2、有一个几何体的三视图依次如右图所示， 这个几何体应是一个( )A.棱台；B.棱锥；C.棱柱； D.都不对．3、如图，正方体1111D C B A ABCD -的面对角线1AD 和面对角线C B 1所成的角为（ ）A. 30B. 45C. 60D. 904、若某空间几何体的三视图如右图所示，则该 几何体的体积是 （ ）A 、31B 、23 C 、1 D 、25、一个水平放置的平面图形的斜二测直观图是一个底角为45，腰和上底边均为1的等腰梯形，则这个平面图形的面积是 （ ） A.2221+B. 22+C. 21+D. 221+ 6、函数()ln 2f x x x =-+的零点个数为（ ）A 、1个B 、2个C 、3个D 、0个7、c b a ,,为三条不重合的直线，γβα,,为三个不重合的平面，现给出六个命题：①b a c b c a //////⇒⎭⎬⎫；②b a b a //////⇒⎭⎬⎫γγ；③βαβα//////⇒⎭⎬⎫c c ；④βαγβγα//////⇒⎭⎬⎫； ⑤a c a c //////αα⇒⎭⎬⎫；⑥a a //////αγαγ⇒⎭⎬⎫其中正确的命题是（ ）D 1C 1B 1A 1DCBA 左视图A .①②③； B.①④⑤； C.①④； D.①④⑤⑥8、若球的表面积扩大到原来的2倍，则球的体积扩大到原来的（ ） A.2倍； B.2倍； C.22倍； D.23倍 9、、已知n m ,是不重合的直线，βα,是不重合的平面，有下列命题： ①若αα//,n m ⊂,则n m //；②若βα//,//m m ，则βα//；③若,//,n m n =βα 则 βα//,//m m ；则βα//其中正确的命题的个数是（ ）A.0个；B.1个；C.2个；D.3个 10、若一个圆锥的轴截面是等边三角形，其面积为3，则这个圆锥的全面积为（ ）A 、π3；B 、π33； C 、π6； D 、π911、圆锥的中截面（过圆锥高的中点且平行于底面的截面）把圆锥侧面分成两部分，这两部分面积的比为（ ） A.1:1； B.2:1； C.3:1； D.4:1 12、如图，在长方体1111D C B A ABCD -中，3,4,61===AA AD AB ， 分别过BC 、11D A 的两个平行截面将长方体分成三部分， 其体积分别记为111DFD AEA V V -=，C F C B E B V V 11113==。

1、已知H (aq)OH (aq)+-+ 2H O(1) 57.3kJ /mol H ∆=- ，其中aq 代表稀溶液，以下四个反应方程中，反应热为57.3kJ /mol - 的是（ ） A ．24H SO (aq)2NaOH(aq)+ 242N a S O (a q )2HO (1)+ B ．24211H SO (aq)BaOH (aq)22+ 421BaSO (s)H O(1)2+C ．HCl(aq)NaOH(aq)+ 2N a C l (a q )H O (1)+ D ．32HCl(aq)NH H O(aq)+⋅ 42NH Cl(aq)H O(1)+ 2、下列叙述正确的是（ ）A ．已知2232SO O 2SO +的正反应为放热反应，则2SO 的能量一定高于3SO 的能量B ．热化学方程式前面的化学计量数代表分子个数C ．2S(s)+O (g) 2S O (g ) 1H ∆；2S(g)O (g)+ 2S O (g ) 2H ∆，则12H H ∆<∆D ．已知22C(s)+2O (g) 22C O (g ) 1H ∆；22C(s)O (g)+ 2C O (g ) 2H ∆，则12H H ∆<∆3、下列热化学方程式书写正确的是（ ）A ．23S(s)+O (g)23S O (g ) 315k J /m o H ∆=-（燃烧热） B ．NaOH(aq)+HCl(aq) 2a C l (a q )+H O (1) 57.3k J /m H ∆=-（中和热） C ．252C H OH+3O 222CO +3H O 1368.8k J /m H ∆=-（燃烧热） D ．22H O(g) 222H (g)+O (g) 483.6k J /m H ∆=-（反应热）4、甲、乙两容器内都在进行A B →的反应，甲容器内每分钟减少了4mol A ，乙容器内每分钟减小了2mol A ，则甲容器内的反应速率比乙容器内的反应速率（ ） A ．快 B ．慢 C ．相等 D ．无法判断5、在恒温恒容的容器里进行下列反应：223N +3H 2NH ，其他条件不变，向容器中充入氩气，则此反应速率会（ ）A ．变大B ．变小C ．不变D ．无法判断6、在气体反应中，改变条件：①增大反应物的浓度；②升高温度；③增大压强；④移去生成物；⑤加入催化剂。

宁夏大学附属中学2014-2015学年高一上学期期中考试数学试卷（解析版）一、选择题1．设全集R ，{}{}0,1A x x B x x =>=>，则R AB =ð（ ）A ．{}01x x ≤<B ．{}01x x <≤C ．{}0x x <D ．{}1x x > 【答案】B 【解析】试题分析：由补集定义得{}1|≤=x x B C R ，所以{}10|≤<=⋂x x B C A R 考点：集合的运算.2．下列四个图形中，不是．．以x 为自变量的函数的图象是（ ）【答案】C【解析】试题分析：根据函数定义，对自变量x 的任意一个值，有且只有唯一一个实数（函数值）与它对应。

显然A,B,D 满足，C 不满足. 考点：函数的概念．3．下列四组中的函数()f x 与()g x ，是同一函数的是（ ） A ．2()ln(1)ln(1),()ln(1)f x x x g x x =-++=- B ．2()lg ,()2lg f x x g x x == C ．()()f x g x ==D ．21(),()11x f x g x x x -==+- 【答案】A 【解析】试题分析：定义域相同，对应法则相同的函数是同一函数.A 满足，定义域均为{}11|<<-x x ，B 中)(x f 的定义域为{}0|≠x x ，)(x g 的定义域为{}0|>x x ，C 中)(x f 的定义域为{}1|≥x x ，)(x g 的定义域为{}11|≥-≤x x x 或，D 中)(x f 的定义域为{}1|≠x x ，)(x g 的定义域为R .考点：同一函数的概念.4．函数log ,log ,log ,log a b c d y x y x y x y x ====的图像如图所示，则,,,a b c d 的大小顺序（ ）A ．1c d b a <<<<B ．1d c a b <<<<C ．1d c a b <<<<D ．1c d a b <<<< 【答案】D 【解析】试题分析：作直线1=y 分别与log ,log ,log ,log a b c d y x y x y x y x ====的交点为)1,(a ，)1,(b ， )1,(c ，)1,(d .结合图像知1c d a b <<<<.考点：对数函数的图象与性质.5．下列函数中既是偶函数又在(0,)+∞上是增函数的是（ ）A ．3y x =B ．1y x =+C ．21y x =-+ D ．2xy -=【答案】B 【解析】试题分析：A 是奇函数，C ，D 是偶函数且在(0,)+∞上单调递减. 考点：函数的奇偶性与单调性.6．已知函数122()(1)a f x a a x-=--为幂函数，则a =（ ）A ．1- 或 2B ．2- 或 1C ．1-D ．1 【答案】C 【解析】试题分析：因122()(1)a f x a a x-=--为幂函数，所以112=--a a ，所以12-=或a ，又02≠-a ， 所以1-=a .考点：幂函数的定义.7．若21log 0,()12b a <> ，则（ ） A ．1,0a b >> B ．1,0a b >< C ．01,0a b <<> D ．01,0a b <<< 【答案】D 【解析】试题分析：因1log 0log 22=<a ，所以10<<a ，又0)21(1)21(=>b ，所以0<b .考点：不等式性质及对数、指数函数的单调性.8．函数y =的值域是（ ）A ．[0,4)B ．(0,4]C ．[0,4]D ．(0,4) 【答案】A 【解析】试题分析：因为1640≤<x，所以0416<-≤-x，164160<-≤x，所以44160<-≤x考点：函数的值域.9．函数2x y -=的反函数的图像为（ ）【答案】D 【解析】试题分析：因为x xy )21(2==-与x y 21log =互为反函数，所以选D.考点：反函数的定义及图象.10．已知函数()f x 在[0,)+∞上是增函数，()()g x f x =-，若(lg )(1)g x g > ，则x 的取值范围是（ ） A ．1(,10)10 B ．()0,10 C ．()10,+∞ D.()1(,10)10,10+∞【答案】A 【解析】试题分析：因为(lg )(1)g x g >，所以)1()lg (f x f <，又()f x 在[0,)+∞单调递增，所以1lg 0<≤x ，解得10101<<x . 考点：函数的单调性及不等式. 11．已知函数2log ,0()(3), 0x x f x f x x ⎧=⎨≤⎩＞＋，则(10)f -的值是（ ）A ．－2B ．－1C ．0D ．1 【答案】D 【解析】试题分析：因为12log )2()1()4()7()10(2===-=-=-=-f f f f f . 考点：分段函数.12．已知0x 是函数1()21xf x x=+－的一个零点．若1020(1,),(,)x x x x ∈∈+∞ ，则（ ） A ．12()0,()0f x f x << B ．12()0,()0f x f x <> C ．12()0,()0f x f x >< D ．12()0,()0f x f x >> 【答案】B 【解析】试题分析：据增函数+增函数=增函数，所以)(x f 为增函数，又2011x x x <<<，0x 为)(x f 的一个零点，所以)(0)()(201x f x f x f <=<. 考点：函数的零点，单调性.二、填空题13．{}{}25,,A x x B x x a A B =-≤≤=>⊆，则a 取值范围是 ．【答案】(,2)-∞- 【解析】试题分析：画出数轴图，可以得到2-<a . 考点：集合的运算. 14．函数y =的定义域是 ．【答案】]4,0( 【解析】40≤<x .试题分析由得考点：函数的定义域.15．满足28244x x ->－的x 的取值集合是 ． 【答案】{}24|>-<x x x 或 【解析】试题分析：由x x 282->-得42-<>x x 或考点：指数函数的性质及不等式解法.16．设函数1()()lg 1f x f x x=⋅+，则(10)f = ． 【答案】1 【解析】试题分析：令10=x 得1)101()10(+=f f ①，令101=x 得1)1()10()101(+-⋅=f f ②，由①②得1)10(=f . 考点：抽象函数，特值法.三、解答题17．（10分）设集合{}2220,M x ax x x R =-+=∈至多有个一元素，求实数a 的取值范围.【答案】0a =或12a ≥. 【解析】试题分析：集合M 至多一个元素，则M 只有一个元素或为空集，当M 为空集时，方程没⎩⎨⎧≥->0log 202x x有实数根，注意字母a 的讨论；当M 只有一个元素时，方程的根有且只有一个，此题容易漏掉0a =的情况. 试题解析：若集合{}2220,M x ax x x R =-+=∈至多有个一元素 则M 只有一个元素或为空集那么0a =或2(2)42480a a ∆=--⨯=-≤ 所以0a =或12a ≥． 考点： 集合、元素的概念. 18．（12分） 已知函数2()ln2xf x x-=+ ． （1）求函数()f x 的定义域；（2）判断函数()f x 的奇偶性，并说明理由． 【答案】（1）(2,2)-；（2）f （x ）为奇函数.【解析】 试题分析：（1）函数的定义域是使得自变量有意义的取值范围，由对数函数真数大于0即可求得定义域为(2,2)-，此时注意分式不等式的解法；（2）只需按照奇函数与偶函数定义证明即可.即根据定义第一步，任取值；第二步，作差；第三步，判断符号；第四步，下结论；注意步骤.试题解析：解：（1）由202xx-＞+，得22x -<<，故函数f （x ）的定义域为(2,2)-； （2）函数f （x ）是偶函数，理由如下：由（1）知，函数f （x ）的定义域关于原点对称， 且22()ln ln ()22x xf x f x x x+--==-=--+ 故函数f （x ）为奇函数．考点： 函数的定义域与单调性. 19．（12分） 化简或求值（1）110232418(2)2(2)()5427--+⨯- ；（2）2lg5+【答案】（1）21；（2）1 【解析】试题分析：（1）（2）用指数、对数式运算性质即可.指数幂运算的一般思路（1）有括号的先算括号里的，无括号的先进行指数运算．（2）先乘除后加减，负指数幂化成正指数幂的倒数．（3）若底数是负数，则先确定符号；若底数是小数，则先化成分数；若底数为带分数，则先化成假分数．对数的运算一般有两种解题方法：一是把对数先转化成底数相同的形式，再把对数运算转化成对数真数的运算；二是把对数式化成最简单的对数的和、差、积、商、幂，合并同类项以后再运算． 试题解析：（1）1111022333224181321221(2)2(2)()=1[()][()]=1+54274234332---+⨯-+⨯-⨯-= ； （2）2lg5++2l 12(g2)lg2(1lg2)22=+⋅-+221111(lg 2)lg 2(lg 2)1lg 22222=+-+- 1=考点：对数、指数式的运算.20．（12分）已知221,02()68,2x x f x x x x ⎧-≤<⎪=⎨-+≥⎪⎩ ．（1）画出()f x 的图像；（2）若()1f m =，求实数m 的值。