高中物理电路简化
- 格式:docx
- 大小:50.68 KB
- 文档页数:3

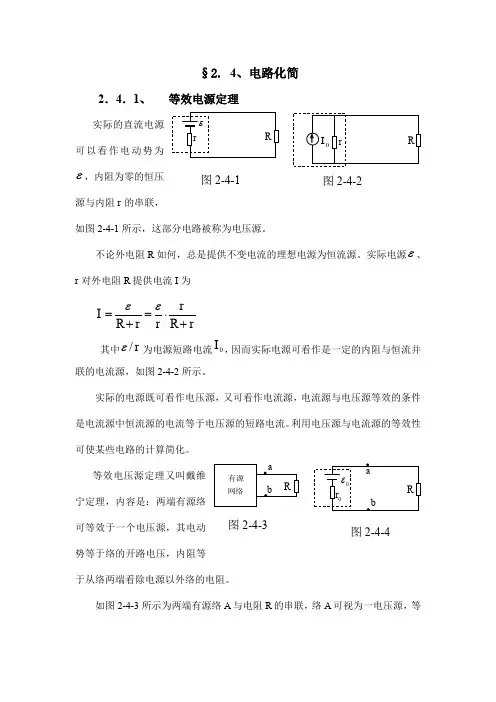
§2. 4、电路化简2.4.1、 等效电源定理实际的直流电源可以看作电动势为ε,内阻为零的恒压源与内阻r 的串联,如图2-4-1所示,这部分电路被称为电压源。
不论外电阻R 如何,总是提供不变电流的理想电源为恒流源。
实际电源ε、r 对外电阻R 提供电流I 为r R rr r R I +⋅=+=εε其中r /ε为电源短路电流0I ,因而实际电源可看作是一定的内阻与恒流并联的电流源,如图2-4-2所示。
实际的电源既可看作电压源,又可看作电流源,电流源与电压源等效的条件是电流源中恒流源的电流等于电压源的短路电流。
利用电压源与电流源的等效性可使某些电路的计算简化。
等效电压源定理又叫戴维宁定理,内容是:两端有源络可等效于一个电压源,其电动势等于络的开路电压,内阻等于从络两端看除电源以外络的电阻。
如图2-4-3所示为两端有源络A 与电阻R 的串联,络A 可视为一电压源,等图2-4-1图2-4-2图2-4-3图2-4-4效电源电动势0ε等于a 、b 两点开路时端电压,等效内阻0r 等于络中除去电动势的内阻,如图2-4-4所示。
等效电流源定理 又叫诺尔顿定理,内容是:两端有源络可等效于一个电流源,电流源的0I 等于络两端短路时流经两端点的电流,内阻等于从络两端看除电源外络的电阻。
例4、如图2-4-5所示的电路中,Ω=Ω=Ω=Ω=Ω===0.194,5.43,0.101,0.12,5.01,0.12,0.31R R R R r r V V εε (1)试用等效电压源定理计算从电源()22r 、ε正极流出的电流2I ;(2)试用等效电流源定理计算从结点B 流向节点A 的电流1I 。
分析: 根据题意,在求通过2ε电源的电流时,可将ABCDE 部分电路等效为一个电压源,求解通过1R 的电流时,可将上下两个有源支路等效为一个电流源。
解: (1)设ABCDE 等效电压源电动势0ε,内阻0r ,如图2-4-6所示,由等效电压源定理,应有VR R R r R 5.1132111=+++=εε()Ω=+++++=5321132110R R R r R R r R r电源00r 、ε与电源22r 、ε串联,故Ar R r I 02.0240022-=+++=εε2图2-4-5图2-4-62I <0,表明电流从2ε负极流出。

高中物理等势点法简化电路等势点法是物理学中用于简化电路分析的一种常用方法,它基于电势的概念,通过将电路中的各个点分为等势电位,简化电路的计算过程。
本文将介绍等势点法的基本原理和应用,并通过几个例子展示其在简化电路分析中的重要性和实用性。
一、等势点法的基本原理设想一个电路由多个元件(如电阻、电容等)连接而成,每个元件的两端存在一定的电势差。
而等势点法的核心思想是,将电路中的各个点划分为不同的电势区域,在同一电势区域内的点具有相同的电势。
这样一来,原本复杂的电路可以被简化为几个电势区域,从而大大降低了计算电路参数的难度。
为了理解等势点法更加直观,下面以一个简单的电路示例进行说明。
考虑一个由电压源和两个电阻组成的串联电路,我们需要计算通过电路的电流。
首先,我们假设电源的一个端点为零电位点,即该点的电势为零。
然后,我们寻找电路中的其他等势点。
根据电阻的特性,电阻两端的电势差与电流成正比,因此,我们可以在两个电阻的中间分别选取一个等势点,并分别标记电势为V1和V2。
接下来,我们通过连接这些等势点的虚拟导线,我们得到了一个等势图,图中每一条虚拟导线表示一个等势面。
在该等势图中,我们可以清晰地看到电源两端的0V等势面和电阻两端的V1、V2等势面。
我们可以用箭头表示电流的流动方向,箭头的方向始终指向电势较高的一侧。
在本例中,电流从电源的正极流向负极,通过两个电阻。
通过等势点法,我们可以更有效地理解电路的电势分布情况,避免了大量复杂的计算。
二、等势点法在实际电路中的应用等势点法在实际电路分析中有着广泛的应用,下面将通过几个具体例子来展示它的实用性。
例一:并联电阻考虑一个并联电阻的电路,我们需要计算总电阻。
通过等势点法,我们只需将各个电阻连接的两个等势点划分为不同的等势区域,然后直接计算并联电阻即可,无需对每个电阻的分支电流进行复杂的计算。
例二:三角电路的简化考虑一个由三个电阻组成的三角电路,我们需要计算其中一条边上的电流。



高中物理七大电路图
1.串联电路图:将多个电器依次连接起来,电流经过每个电器时电压逐渐降低,电阻总和等于各电器电阻之和。
2. 并联电路图:将多个电器并排连接起来,电流在各电器中分流,每个电器电压相等,电阻总和为各电器电阻倒数之和的倒数。
3. 电容充放电电路图:通过充电电路将电容器充满电,然后通过放电电路释放电容器中的电荷,电容器电荷随时间变化的曲线为指数函数。
4. 交流电路图:表示交流电源、电感、电容在交流电路中的连接方式,电流随时间变化呈正弦函数,在电阻、电感、电容中的响应不同。
5. 三极管放大电路图:利用三极管的放大作用,将输入信号放大,输出信号为输入信号的倍数,常用于电子放大器、收音机等。
6. 逻辑门电路图:由逻辑门(与门、或门、非门等)和开关组成,用于数字电路中的逻辑运算。
7. 数字时钟电路图:由计数器、分频器、显示器等组成,可以实现时间的定时、计数等功能。
- 1 -。

高中物理等势点法简化电路在解决复杂电路问题时,等势点法是一种常用的简化电路的方法。
利用等势点法,我们可以将一个复杂的电路简化为一个等效电路,从而更加方便地进行分析和计算。
在采用等势点法简化电路时,我们首先需要找到电路中的所有等势点,即电势相同的点。
等势点一般位于电路中的分支交汇处以及导线连接点。
通过找到这些等势点,我们可以将电路分解为若干个小段,每个小段的等效电阻相同,电流也相同。
接下来,我们需要在电路中选择一个参考点,一般选择电源的负极或地线作为参考点。
以参考点为基准,我们可以得到所有等势点的电势差,即各个小段的电压。
根据欧姆定律,我们可以通过电势差和等效电阻求解出各个小段的电流。
在求解完各个小段的电流后,我们可以再次应用等势点法,将电路中的等效电路进一步简化。
通过将电路分解为更小的段落,我们可以使用串联电阻和并联电阻的计算公式,得到整个电路的等效电阻和电流。
除了简化电路的结构,等势点法还可以帮助我们分析电路的特性。
通过等势点法,我们可以直观地理解电路中不同元件之间的关系,例如电流的分配和电压的分压。
这为我们进一步分析电路性能提供了基础。
在实际应用中,等势点法可以用于解决各种电路问题,例如计算电路中的电流、电压以及功率消耗等。
通过简化电路结构,我们可以更加方便地进行计算,从而更好地理解和应用物理学原理。
综上所述,高中物理中的等势点法可以帮助我们简化复杂电路,提高问题解决的效率。
通过找到等势点并计算等效电路,我们可以准确地求解电路中的电流和电压,并进一步分析电路的特性。
通过学习和应用等势点法,我们可以更好地掌握物理学知识,提高解决实际问题的能力。


物理高中电路知识点总结电路是指电流在导体内流动的路径,是电流在电子器件中的组织形式。
它是电子器件、电源、电源开关等元件或电路组成的一个整体。
电路在实际应用中是为了完成电能转换、控制、传输的目的而进行组织的,因此也可以看成是完成特定功能的一种需要电流来完成的工作装置。
电路在现代电子技术中起着非常重要的作用,电路知识是物理高中学习的一个重要内容。
下面就来总结一下高中电路知识点。
一、电路的基本概念电路是由电源(电池或发电机)、导线、开关、电阻、电容、电感等元件构成的。
电路可以分为串联电路、并联电路和混联电路。
1. 串联电路串联电路是指电路中的各个元件依次连接在一起,电流只有一条通路可以流过所有的元件。
串联电路的特点是电流大小相同,但电压不同。
例如,在串联电路中,电压和电阻都是直接相加,即串联电路的总电阻等于各个电阻的和。
2. 并联电路并联电路是指电路中的各个元件同时与电源相连,从而形成多条通路,使电流可以分流。
并联电路的特点是电压相同,但电流不同。
在并联电路中,电流和电压之间的关系是相反的,即并联电路的总电流等于所有分支电流之和。
3. 混联电路混联电路是指电路中既有串联元件又有并联元件。
在混联电路中,要根据各个分支电路的性质做具体的分析,以确定电流和电压的关系。
二、电阻的基本概念电阻是材料对电流流动的阻碍作用,它可以转换电能。
电阻的单位是欧姆(Ω)。
电阻可以分为固定电阻和可变电阻。
1. 固定电阻固定电阻的电阻值是不变的,不可调节。
固定电阻的种类有炭膜电阻、金属膜电阻、金属氧化物膜电阻等。
2. 可变电阻可变电阻的电阻值可以通过调节器件的物理结构改变。
可变电阻的种类有电位器和热敏电阻等。
三、电压、电流和电功电压是电荷在电场中移动时所具有的能量。
电压的单位是伏特(V)。
电流是电荷在导体中流动的数量。
电流的单位是安培(A)。
电功是电压与电流的乘积,表示电能的大小。
1. 电压的表示和测量电压可以用示波器、万用表或电压表来测量。

高中物理电路的简化的方法?[标签:高中物理,电路]解决时间:2009-09-26 00:33满意答案好评率:66%1、节点法就是标出所有的连接点(电路元件左右两端),用导线直接连在一起的算一个连接点,用同一个字符来标示,然后画出串、并联关系非常明确的等效电路图,再进行简化。
2、局部化简法从局部入手,找出其中的串联、并联部分。
例,某段电路有R1、R2两个电阻串联,又与R3并联。
则把R1、R2这两个电阻去掉,换成一个电阻,记为R12,连入原图中。
然后把R12和R3都去掉,换成一个电阻,记为R(12)/3连入原图中。
你会发现这样下去,电路图越来越简单,并且看你自己标记的电阻符号,你就知道其关系了。
如果1、2两电阻串联,3、4两电阻串联,然后再并上。
记为R(12)/(34)如2、3并联,前串1、后串4,记为R1(2/3)4求高中物理电路图简化方法2009-1-23 13:52浏览次数:1426次2009-1-23 13:55最佳答案:1、元件的等效处理,理想电压表--开路、理想电流表--短路;2、电流流向分析法:从电源一极出法,依次画出电流的分合情况。
注意:○1有分的情况,要画完一路再开始第二路,不要遗漏。
○2一般先画干路,再画支路。
3、等势点分析法:先分析电路中各点电势的高低关系,再依各点电势高低关系依次排列,等电势的点画在一起,再将各元件依次接入相应各点,就能看出电路结构了。
4、弄清结构后,再分析各电表测量的是什么元件的电流或电压。
说明:2、3两点往往是结合起来用的。
这是我复制来的,多做些题目仔细体会一下高中物理串联、并联电路的简化来源:4221学习网整理| 作者:未知| 本文已影响683 人在我们平常所遇到的串联、并联电路问题中,最头痛的莫过于碰到一个复杂的电路而不知如何下手。
其实,对于物理中的复杂电路计算,可采取简化电路的方法,化为几个简单的问题进行解决。
简化电路的原则是根据题目提出的要求,取消被短路与开路的器件,保留通路的器件,从而简化出其等效电路。

高中物理解析解决电路题的方法总结在高中物理学习中,电路题是一个较为重要的部分。
解析解决电路题需要掌握一些基本方法和技巧,本文将对解决电路题的方法进行总结。
一、电路分析基本原理在解决电路问题时,我们要掌握以下基本原理:1.欧姆定律:电流在电路中的分布满足欧姆定律,即I=U/R,其中I 为电流大小,U为电压大小,R为电阻大小。
2.基尔霍夫电流定律:电流在交叉节点处的代数和为零,即∑I=0。
这一原理可以用来分析复杂电路中的电流分布。
3.基尔霍夫电压定律:沿闭合回路的电压代数值之和等于零,即∑U=0。
这一原理可以用来计算电路中各元件之间的电压关系。
二、串联电阻和并联电阻的计算方法当电路中有多个电阻相连时,我们可以根据串联电阻和并联电阻的计算方法进行简化。
1.串联电阻计算方法:串联电阻的总阻值等于各电阻之和,即Rt=R1+R2+…+Rn。
2.并联电阻计算方法:并联电阻的总阻值等于各电阻的倒数之和再取倒数,即1/Rt=1/R1+1/R2+…+1/Rn。
三、电路中功率的计算方法在解决电路题时,我们经常需要计算电路中的功率。
常见的功率计算公式为P=UI,其中P表示功率,U表示电压,I表示电流。
四、简单电路的解析解决方法对于一些简单的电路问题,我们可以运用基本原理和计算方法进行解析解决。
以下是一些常见情况的解决方法:1.串联电路的解析解决方法:按照串联电阻计算方法,可以计算出总阻值。
再根据欧姆定律,可以计算出总电流。
最后,利用总电流和各电阻的阻值可以计算出各个分支电流和电压。
2.并联电路的解析解决方法:根据并联电阻计算方法,可以计算出总阻值。
再根据欧姆定律,可以计算出总电流。
最后,利用总电流和各个分支的电阻关系可以计算出各个分支电流和电压。
3.交流电路的解析解决方法:对于交流电路,我们需要使用交流电压的有效值,即计算出交流电压的幅值。
与直流电路类似,根据欧姆定律和基尔霍夫电压定律,可以计算出电流和电压的分布情况。
高中物理解析电路电路在物理学中是一个研究电流和电压以及它们在各个部件中传递的系统。
解析电路是指使用数学和物理的原理来分析和理解电路的性质以及其中的各个元件之间的关联与作用。
解析电路的过程能够帮助我们深入了解电路的工作原理以及解决电路中出现的问题。
一、串联电路串联电路是指电路中元件依次连接在一起,电流只能沿着一条路径流动的电路。
通过解析串联电路,我们可以计算出电路中的总电压和总电阻。
假设我们有一个由三个电阻R₁、R₂和R₃串联而成的电路,在电源的两端加上电压V,如图所示。
根据欧姆定律,我们可以知道电路中的电流I等于总电压V与总电阻R之间的比值,即I=V/R,而总电阻R等于三个电阻的电阻之和,即R=R₁+R₂+R₃。
这样,我们就可以通过求解这个简单的方程组,得到电路中的电流和各个电阻的电压。
二、并联电路并联电路是指电路中的元件同时连接在同一电势差之间的电路。
通过解析并联电路,我们可以计算出电路中的总电流和总电阻。
假设我们有一个由三个电阻R₁、R₂和R₃并联而成的电路,在电源的两端加上电压V,如图所示。
根据欧姆定律,我们可以知道电路中的电流I等于总电压V与总电阻R之间的比值,即I=V/R,而总电阻R的倒数等于三个电阻的倒数之和的倒数,即1/R=1/R₁+1/R₂+1/R₃。
这样,我们就可以通过求解这个简单的方程,得到电路中的电流和各个电阻的电压。
三、电路中的电功率解析电路不仅可以帮助我们计算电流和电压,还可以帮助我们研究电路中的电功率。
电功率表示单位时间内传输的电能量,通常使用单位瓦特(W)表示。
根据欧姆定律和功率公式P=IV,我们可以计算出电路中的功率。
例如,在一个串联电路中,如果我们已知电流I和总电阻R,我们可以通过计算P=I²R得到电路中的功率。
类似地,在一个并联电路中,如果我们已知电流I和总电阻R,我们可以通过计算P=IV得到电路中的功率。
四、电路中的电阻和电容除了电阻和电流以外,电路中还常常涉及到电容的概念。
理解高中物理中的电路分析与计算电路分析与计算是高中物理学习中的一个重要部分,它涉及了电路的构成、特性以及电流、电阻、电压等相关概念的计算和分析。
通过深入理解电路分析与计算的原理和方法,能够帮助我们更好地理解和应用电路知识,从而提升我们在物理学习中的水平和能力。
一、电路的基本概念在进行电路分析与计算之前,我们首先需要了解电路的基本概念。
电路由电源、导线和电器元件组成,是电流在闭合导路中的流动。
在电路中,电流是由正极流向负极,而电子则相反。
电流的大小用安培表示,电压则表示电流推动电子流动的力量,单位为伏特。
电阻是电流在电路中受到的阻碍,单位为欧姆。
二、串联电路的分析与计算串联电路是指电流从一个电器元件依次通过多个电器元件的电路。
在串联电路中,总电流相等,而电压则在各个电器元件之间按比例分配。
使用欧姆定律可以很好地分析和计算串联电路。
欧姆定律表达了电流与电压、电阻之间的关系,即I = U/R,其中I表示电流,U表示电压,R表示电阻。
三、并联电路的分析与计算并联电路是指电流从一个节点分为多个支路通过多个电器元件的电路。
在并联电路中,总电压相等,而电流则在各个支路之间按比例分配。
根据欧姆定律,我们可以很方便地分析和计算并联电路。
在计算并联电阻时,可以使用倒数相加法,即1/Rt = 1/R1 + 1/R2 + ... + 1/Rn,其中Rt表示总电阻,R1、R2、...、Rn表示各个支路的电阻。
四、混合电路的分析与计算混合电路是指由串联和并联电路组成的复杂电路。
在分析和计算混合电路时,我们需要将其拆分为串联和并联电路进行分别计算,最后再将结果综合考虑。
通过对混合电路进行合理的拆分和计算,我们能够更好地理解和应用电路分析与计算的原理和方法。
五、电路中的功率与能量在电路分析与计算中,功率和能量是我们需要注意的重要概念。
功率是指单位时间内消耗或提供的能量,用瓦表示。
功率的计算公式为P = UI,其中P表示功率,U表示电压,I表示电流。
以下您看到的分析方法由溜溜为您整理,坚持免费,大家共享简单的电路化简方法之节点法电路化简的步骤如下:1. 首先寻找节点。
何谓节点,简单的说就是线的交点,如图,我们可以找到6个节2。
节点编号。
编号是要注意,电源的正极(或负极)编1号,负极(或正极)编最后一个号。
如果发现两个节点间有导线或者电流表连接,那么这两个节点编为同一号。
如果是电流表在同一号节点间的,需要记住表两端接的电阻号。
3. 重新连线。
重新连线应在草稿纸上完成,首先在纸上同一线上画上4个点并编上号,点间距离最好大一点,,然后依次从电路中找到节点之间的电阻或者电表画在四个点间。
为了避免漏画,可以画一个从图上标出一个,直到原电路图上的仪器全都画到了图上为止。
如图。
4.转化为规范化电路图。
相信做完上一步后,您已经可以看出电路的组成了,如果发现点与点之间有断开的情况,只要将点适当的移位就可。
关于这道题的规范化电路图,在此就省略吧。
在使用过程中觉得此方法非常的简单,而且解题过程非常机械。
当然有时因为节点编号的问题出现画完以后还是看不出来的问题,不过只要将点进行简单的移位,便可以一目了然。
下面是化简的万能十条法则。
电路简化的基本原则初中物理电学中的复杂电路可以適过如下原则进行简化:•第一不计导线电阻,认定R线P On有电流琉过的导线两端电压为零*斷开时开关歪端可以测得电压t电路中没有苴他断点)。
•第二匕开关闭合时等效于一根导銭:开其断幵时等效于断路,可从电路两书点间去掉.开关闭合有电流谎过时■开关两端电压宵零」斷开时开关两端可以测得电压(电路中设有苴他断点)・・第三:电流表內阴很小」在分析电路的连接方式时,有电流表的地方可看作一根导线.-第戒乂电压表内阴很大> 在分折电路的连接方式时*有电压表的地方可视作断路> 从电路两节点间去撞.・第孤用电器(电阻)短路:用电器(电阻)和导銭(开关、电流表)并联时,用电器中无电流通过(如下图示)> 可以把用电器从电路的两节点间拆除(去掉).•第七:根据瓠并联电路电流和电压规律坤联分压、并联分流冷析总电流、总电J3 和分电流、分电压肉关系, •第八:电流表和哪个用电器串联就测哪个用电器的电流’电压表和哪个用电器并联 就测哪个用电器的电压。
高中物理复杂电路的简化嘿,同学们!咱今天来聊聊高中物理复杂电路的简化呀!这可真是个有趣又有点头疼的事儿呢!你想想看,那些电路就像一团乱麻,各种电阻、电容、电感啥的交织在一起,简直让人眼花缭乱!但别怕,咱有办法把这团乱麻给理清楚。
就好比你要去一个陌生的地方,一开始看着地图觉得乱七八糟的,不知道该咋走。
但只要你静下心来,一点点分析,找出关键的路线,那就能轻松找到目的地啦!电路简化也是一样的道理。
咱先从最简单的开始,把那些明显的串联、并联关系找出来。
串联就像是串珠子,一个接一个,电流只有一条路可走;并联呢,就像岔路口,电流可以分成好几条路走。
这不难理解吧?然后呢,咱再看看有没有可以等效替换的部分。
比如说,几个电阻组合起来的效果和一个特定电阻一样,那咱就把它们换成那个特定电阻,这不就简单多啦?这就好像你有一堆零钱,换成一张整钱,多方便呀!有时候遇到一些复杂的电路图,别急着发愁。
你就把它当成一个谜题,一点点去解开。
你可以从电源出发,顺着电流的方向走,看看都经过了哪些元件,它们之间是啥关系。
还有啊,别小看了那些小小的符号和线条,它们可都有大用处呢!就像密码一样,你得破解它们才能读懂电路的秘密。
再给大家举个例子吧,想象一下电路是一个大迷宫,你就是那个要找到出口的人。
你得仔细观察迷宫的结构,找到最快捷的路。
有时候可能会走一些弯路,但别灰心,多尝试几次,总会找到正确的路。
简化复杂电路就像是一场冒险,虽然过程中可能会遇到一些困难,但当你成功简化后,那种成就感简直无与伦比!你会发现,原来那些看似复杂的电路也不过如此嘛!所以啊,同学们,别害怕复杂电路。
只要我们有耐心,有方法,就一定能把它们搞定!让我们一起在电路的海洋里畅游,探索其中的奥秘吧!相信自己,我们一定行!。
例谈综合法简化电路
一、简化电路的具体方法
1.支路电流法:电流是分析电路的核心。
从电源正极出发顺着电流的走向,经各电阻外电路巡行一周至电源的负
极,凡是电流无分叉地依次流过的电阻均为串联,凡是电流有分叉地依次流过的电阻均为并联。
例 1:试判断图 1 中三灯的连接方式。
【解析】由图 1 可以看出,从电源正极流出的电流在 A 点分成三部分。
一部分流过灯L1,一部分流过灯L2,一部分流过灯L3,然后在 B 点汇合流入电源的负极,从并联电路的特点可知此三灯并联。
【题后小结】支路电流法,关键是看电路中哪些点有电流分叉。
此法在解决复杂电路时显得有些力不从心。
2.等电势法:将已知电路中各节点(电路中三条或三条以上支路的交叉点,称为节点)编号,按电势由高到低的顺
序依次用 1、 2、 3⋯⋯数码标出来(接于电源正极的节点电势最高,接于电源负极的节点电势最低,等电势的节点
用同一数码)。
然后按电势的高低将各节点重新排布,再将各元件跨接到相对应的两节点之间,即可画出等效电路。
例 2:判断图 2 各电阻的连接方式。
【解析】( 1)将节点标号,四个节点分别标上1、 2。
(2)将各个节点沿电流的流向依次排在一条直线上。
(3)将各个电路元件对号入座,画出规范的等效电路图,如图3 所示。
(4)从等效电路图可判断,四个电阻是并联关系。
【题后小结】等电势法,关键是找各等势点。
在解复杂电路问题时,需综合以上两法的优点。
二、综合法:支路电流法与等电势法的综合。
注意点:( 1)给相同的节点编号。
(2)电流的流向:由高电势点流向低电势点(等势点间无电流),每个节点流入电流之和等于流出电流之和。
例 3:由 5 个 1Ω电阻连成的如图 4 所示的电路,导线的电阻不计,则A、 B 间的等效电阻为_______Ω。
【策略】采用综合法,设 A 点接电源正极, B 点接电源负极,将图示电路中的节点找出,凡是用导线相连的节点可
认为是同一节点,然后按电流从 A 端流入,从 B 端流出的原则来分析电流经过电路时的各电阻连接形式就表现出来了。
【解析】由于节点A、D 间是用导线相连,这两点是等势点(均标1),节点C、 F 间是用导线相连,这两点是
等势点(均标2),节点E、 B 间是用导线相连,这两点是等势点(均标3),则 A 点电势最高, C(F)次之, B 点电势最低,根据电流由高电势流向低电势,易得出各电阻的电流方向。
由于电阻 R1,R2 均有一端接点 1,另一端接点 2;电阻 R4, R5 均有一端接点 2,另一端接点 3;电阻 R3 一端接点 1,另一端接点 3,易得其等效电路如图 5 所示。
或者用图 4 中所标电流方向,也可得其等效电路如图5,相比第一种方法更简单。
故AB 间总电阻力0. 5Ω 。
【题后小结】在分析电路时,首先应找出各个节点,凡是用导线相连的两节点是等势点,可以等效为一个节点
(如图 4 中的 A 与 D、 C 与 F、 E 与 B),连在两个相邻的节点间的电阻是并联的(如图 4 中的电阻 1 和电阻 2,电阻 4 和电阻 5),当把最基本的电路等效后,再对高一级电路进一步分析,即电阻1、2 并联后与电阻4、 5 并联后串联,之后再与电阻 3 并联。
这种逐级分析的方法在分析等效电路中是很有效的。
(此方法侧重于等电势法)
但是,若将图 4 改为图 6,即使画出等效电路图5,(按习惯总将电流表看作导线),也无济于事,而且将电
流表置于图 5 中的合适位置更是难上加难。
若根据图中的电流方向则易得:电流表A1 测的是电阻R2 和 R3 的电流之和;电流表A2 测的是电阻R1 和 R2 的电流之和;电流表A3 测的是电阻R3 和 R4 的电流之和。
注:有些初学者凭感觉认为:电流可以沿
点,不可能由点1( A)经点 2( C)又流回点
A→C→ D⋯方向流动,这是错误的。
因为电流由高电势点流向低电势
1( D)。
其它点同理可得电流流向。
三、含电容器、电流表、电压表的复杂电路:画等效电路时,①电流表视为导线,电容器、电压表视为断路(若考虑内阻,则将其视为一个大电阻),与电容器、电压表串联的用电器视为短路即可。
②画等效电路图的同时,根
据图中电流方向将电流表接入电路;根据图中所标节点数字,将电压表和电容器接入电路。
③无电流的支路删去即
可。