阀控马达控制系统仿真(DOC)
- 格式:doc
- 大小:915.50 KB
- 文档页数:10

MATLABSIMULINK永磁同步电机矢量控制系统仿真一、本文概述随着电机控制技术的快速发展,永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)在工业、交通和能源等领域的应用越来越广泛。
矢量控制作为PMSM的一种高效控制策略,能够实现对电机转矩和磁链的精确控制,从而提高电机的动态性能和稳态性能。
然而,在实际应用中,矢量控制系统的设计和调试过程往往复杂且耗时。
因此,利用MATLAB/Simulink进行永磁同步电机矢量控制系统的仿真研究,对于深入理解矢量控制原理、优化控制策略以及提高系统性能具有重要意义。
本文旨在通过MATLAB/Simulink平台,建立永磁同步电机矢量控制系统的仿真模型,并对其进行仿真分析。
本文将对永磁同步电机的基本结构和数学模型进行介绍,为后续仿真模型的建立提供理论基础。
本文将详细阐述矢量控制策略的基本原理和实现方法,包括坐标变换、空间矢量脉宽调制(SVPWM)等关键技术。
在此基础上,本文将利用MATLAB/Simulink中的电机控制库和自定义模块,搭建永磁同步电机矢量控制系统的仿真模型,并对其进行仿真实验。
本文将根据仿真结果,对矢量控制系统的性能进行分析和评价,并提出优化建议。
通过本文的研究,读者可以全面了解永磁同步电机矢量控制系统的基本原理和仿真实现方法,为后续的实际应用提供有益的参考和指导。
本文的研究结果也为永磁同步电机控制技术的发展和应用提供了有益的探索和启示。
二、永磁同步电机数学模型永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)是一种高性能的电机,广泛应用于各种工业领域。
为了有效地对其进行控制,我们需要建立其精确的数学模型。
PMSM的数学模型主要包括电气方程、机械方程和磁链方程。
PMSM的电气方程描述了电机的电压、电流和磁链之间的关系。
在dq旋转坐标系下,电气方程可以表示为:V_d &= R_i I_d + \frac{d\Phi_d}{dt} - \omega_e \Phi_q \ V_q &= R_i I_q + \frac{d\Phi_q}{dt} + \omega_e \Phi_d其中,(V_d) 和 (V_q) 分别是d轴和q轴的电压;(I_d) 和 (I_q) 分别是d轴和q轴的电流;(\Phi_d) 和 (\Phi_q) 分别是d轴和q轴的磁链;(R_i) 是定子电阻;(\omega_e) 是电角速度。

异步电动机矢量控制系统的设计与仿真.异步电动机矢量控制系统的设计与仿真在矢量控制技术出现之前,现代交流调速系统采用了恒压频比控制策略。
这种控制策略的缺点是,当电机低速旋转或在加减速、负载加减等动态条件下,系统性能显著降低,导致交流调速系统在低速、启动时转矩的动态响应和整个系统的稳定性方面不如DC调速系统,无法满足人们对高精度的要求。
后来,交流异步电动机控制开始从标量控制向矢量控制迈进。
以下是矢量控制理论的简要介绍。
矢量控制发展的基础和核心理论支撑是电机的一些概念,如坐标转换原理、机电能量转换理论等。
这种控制的基本思想和方法是将异步电机模拟成DC电机来控制。
只要建立等效于三相交流绕组组的两相绕组,就可以建立等效于异步电机的DC电机模型,并增加相应的比例积分调节环节,从而可以按照DC 电机的控制策略来控制异步电机。
因此,矢量控制可以实现对电机电磁转矩的动态实时控制,从而优化和提高调速性能。
根据这一思想,我在本项目中成功地进行了MATLAB仿真。
关键词:交流电机;矢量控制调速系统;矢量控制系统的设计与仿真交流调速系统的仿真采用常V/f比控制方法,通常称为标量控制。
采用这种方法的系统在电机低速运行时或在加速、减速、增加负载、减少负载等情况下会出现重大缺陷。
采用矢量控制的交流电机可以达到与恒流电机相同的控制性能,从此交流异步电机控制从标量控制向矢量控制迈进了一大步。
以下是矢量控制理论的简要介绍。
矢量控制发展的基础和核心理论支撑是电机的一些概念,如坐标转换原理、机电能量转换理论等。
这种控制的基本思想和方法是将异步电机模拟成DC电机来控制。
只要建立等效于三相交流绕组组的两相绕组,就可以建立等效于异步电机的DC电机模型,并增加相应的比例积分调节环节,从而可以按照DC电机的控制策略来控制异步电机。
因此,矢量控制可以实现对电机电磁转矩的动态实时控制,从而优化和提高调速性能。
根据这一思想,我在本项目中成功地进行了MATLAB仿真。


基于MatlabSimulink的异步电机矢量控制系统仿真一、本文概述随着电力电子技术和控制理论的不断发展,异步电机矢量控制系统已成为现代电机控制领域的重要分支。
该系统通过精确控制异步电机的磁通和转矩,实现了对电机的高效、稳定和动态性能的优化。
Matlab/Simulink作为一种强大的仿真工具,为异步电机矢量控制系统的研究和设计提供了便捷的平台。
本文旨在探讨基于Matlab/Simulink的异步电机矢量控制系统仿真方法。
文章将简要介绍异步电机矢量控制的基本原理和关键技术,包括空间矢量脉宽调制(SVPWM)技术、转子磁链观测技术以及矢量控制策略等。
详细阐述如何利用Matlab/Simulink搭建异步电机矢量控制系统的仿真模型,包括电机模型、控制器模型以及系统仿真模型的构建过程。
文章还将探讨仿真模型的参数设置、仿真过程以及仿真结果的分析方法。
通过本文的研究,读者可以深入了解异步电机矢量控制系统的基本原理和仿真方法,掌握基于Matlab/Simulink的仿真技术,为异步电机矢量控制系统的实际设计和应用提供有益的参考和借鉴。
本文的研究也有助于推动异步电机矢量控制技术的发展和应用领域的拓展。
二、异步电机基本原理异步电机,又称感应电机,是一种广泛应用于工业领域的电动机。
其基本原理基于电磁感应和电磁力作用。
异步电机主要包括定子(静止部分)和转子(旋转部分)。
定子通常由铁芯和三相绕组构成,而转子则可能由实心铁芯、鼠笼型或绕线型结构组成。
当异步电机通电时,定子绕组中的三相电流会产生旋转磁场。
这个旋转磁场与转子中的导体相互作用,根据法拉第电磁感应定律,会在转子导体中产生感应电动势和感应电流。
这些感应电流在旋转磁场的作用下,受到电磁力的作用,从而使转子产生旋转力矩,驱动转子旋转。
异步电机的旋转速度与定子旋转磁场的旋转速度并不完全同步,这也是其被称为“异步”电机的原因。
异步电机的旋转速度通常略低于旋转磁场的同步速度,这是由于转子导体的电感和电阻导致的电磁延迟效应。

目录0绪论 01 控制系统介绍 (1)1.1控制系统的分类 (1)1.2 控制系统的组成 (2)2系统的设计及校正方法 (2)2.1系统设计的问题 (2)2.2性能指标 (3)2.3校正结构 (3)2.4校正装置的设计方法 (4)2.5串联校正 (5)2.6反馈校正 (9)3设计应用仿真 (10)3.1仿真软件简介 (10)3.2利用串联校正和反馈校正来实现系统校正 (12)3.3利用串联超前—滞后校正实现系统校正 (16)4结论 (21)参考文献 (22)控制系统校正装置仿真绪论在科学技术飞速发展的今天,自动控制所起的作用越来越重要,无论是在宇宙飞船,导弹制导的尖端技术领域,还是在机器制造业及工业过程控制中,它所取得的成就是惊人的。
自动控制理论与实践的不断发展,为人们提供了最佳的设计系统的方法,大大提高了生产效率,同时促进了技术的进步。
然而在进行系统的设计时,常常遇到初步设计出来的系统往往不能满足已经给出的所有性能指标的要求。
而直接去改变未校正系统的其他参数是比较困难的,这样就得在原系统的基础上采取另外的一些措施,即对系统加以“校正”。
所谓校正其实就是在所设计的未能满足预期设计要求的系统中加入一些参数,可以根据需要而改变原有系统的机构或装置,从而使系统的整个特性发生变化,满足给定的各项性能指标。
这附加的装置使未校正的系统的缺陷得到补偿,这就是校正的作用。
所以一个系统的校正装置的校正效果直接影响该系统的性能指标以及工作状况。
随着自动控制理论的不断发展,目前在控制系统的校正方式中,比较常用的校正方式主要有:串联校正,反馈校正,前馈校正和复合校正。
在实际系统中不同的系统所侧重的性能指标也是不一样的,不同的校正方式校正的效果也是不一样的,这就需要设计人员有选择性地选用适合系统实际状况的校正方式进行设计。
紧接着,如何去设计校正装置的方法问题被提出来了。
随着计算机技术的高速发展,计算机仿真技术随着计算机语言的不断更新,也在不断发展。


基于Matlab永磁同步电机矢量控制的仿真分析《工业控制计算机》2021年第24卷第9期本文应用Matlab 强大的建模和仿真能力,在Matlab /Simulink 中搭建PMSM 矢量控制系统的仿真模型,这为PMSM伺服控制系统的分析与设计提供了有效的手段和工具。
1PMSM 的数学模型以及矢量控制原理1.1PMSM 的数学模型为了便于分析,电机的数学模型推导前作如下假设:①忽略铁心饱和、涡流和磁滞损耗;②永磁转子没有阻尼作用;③三相定子绕组在空间呈星形对称分布,定子各绕组的电枢电阻和电感相等;④感应电动势及气隙磁场均按正弦分布,且不计磁场的各项谐波。
则电机三相绕组的电压回路方程如下:u au b u c=r 000r 000M M r i ai b i c+p L M M M L M M M M MLi ai b i c+p φf sin (θr φf sin (θr -2π3φf sin (θr +2π3(1其中:u a 、u b 、u c 分别为三相定子绕组电压;i a 、i b 、i c 分别为三相定子绕组电流;r 每相定子绕组电阻;φf 转子永磁体磁链;L 每相绕组的自感;M 每相绕组的互感;θr 转子位置角,即转子q 轴与a 相轴线的夹角;p 微分算子,p=d /dt 。
因为三相绕组为星形连接,有i a +i b +i c =0(2将(2代入(1中,则可得到PMSM 在abc 静止坐标系的电压方程:u a u b u c MM =r+p (L-M000r+p (L-M00r+p (L-M MMi a i b i cMM+pφfsin (θrφfsin (θr-2πφfsin (θr +2π3(3利用clark 和park 变换,先将三相abc 静止坐标系变换到两相αβ静止坐标系,再变换到两相dq 旋转坐标系,得到相应的动态磁链以及电压方程:φd =L d i d +φf φq =L q i qM (4u d =ri d +L d pi d -ωr φq u q =ri q +L q pi q +ωr φdM(5其中:ωr 为转子电角速度,有θr =ωr t ;电机是表面式PMSM ,所以L d =L q =L-M ,分别为直、交轴同步电感;u d ,u q ,i d ,i q ,φd ,φq 分别为直、交轴上的电压、电流和磁链分量。
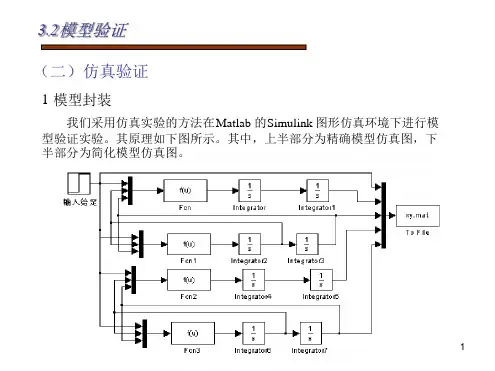


引言液压伺服系统是以液体压力能为动力的机械量(位移、速度和力)自动控制系统按系统。
控机械量的不同,它又可以分为电液位置伺服系统、电液速度伺服控制系统和电液力控制系统三种。
电液控制系统的基本元件包括电磁阀、电液开关控制阀、光电耦合器、功率放大器、电—机械转换器、普通电液伺服阀(频宽数十赫)、高频电液伺服阀(国内产品 400 赫)、电液比例流量阀、电液比例压力阀、电液比例方向阀、电液复合阀、电液比例泵、电液通断控制阀、电液数字阀、电液数字缸、电液数字泵等。
它们广泛用于机床工业、冶金工业、船舶工业、煤炭工业和工程机械等的控制系统中。
本文要研究的是电液速度控制系统及其仿真分析,是对电液速度控制系统的各个环节进行了数学模型的建立,并应用Matlab/Simulink对电液速度控制系统进行了仿真分析,通过幅频特性和相频特性的变化得到数学模型中各个部分对整个控制系统的影响。
1 绪论液压控制是液压技术领域的重要分支。
近20年来,许多工业部门和技术领域对高响应、高精度、高功率—重量比和大功率液压控制系统的需要不断扩大,促使液压控制技术迅速发展。
特别是控制理论在液压系统中的应用、计算及电子技术与液压技术的结合,使这门技术不论在元件和系统方面、理论与应用方面都日趋完善和成熟,并形成一门学科。
目前液压技术已经在许多部门得到广泛应用,诸如冶金、机械等工业部门及飞机、船舶部门等。
我国于50年代开始液压伺服元件和系统的研究工作,现已生产几种系列电液伺服产品,液压控制系统的研究工作也取得很大进展。
1.1电液控制技术的发展及趋势液压技术的发展与流体力学理论研究相互关联。
自1650年帕斯卡提出静态液体中的压力传播规律--帕斯卡原理以来,1686年牛顿揭示了粘性液体的内摩擦定律,18世纪建立了流体力学的连续性方程。
这些理论的建立为液压技术的发展奠定了理论基础。
从1795年,英国人首先制造出世界上第一台水压机起,液压传动开始进入工程领域。
1.应用背景
在海上风机吊装工程中,经常需要进行速度控制,如原动机调速、吊臂垂直及回转装置的速度控制等。
在该项目的工程设计及应用当中的电液位置伺服系统也经常采用速度局部反馈回路来提高系统的刚度和减小伺服阀等参数变化的影响,提高系统的精度。
电液速度控制系统按控制方式可分为:阀控液压马达速度控制系统和泵空液压马达速度控制系统。
阀控液压马达系统一般用于小功率系统,而泵控马达系统一般用于大功率系统。
在本次的实验中,主要针对阀控马达速动控制系统的校正前后变化,通过MATLAB的simulink对其进行仿真比较分析。
2.电液速度控制系统原理
首先给出阀控液压马达速度控制系统的实际物理模型:
如图1所示,该系统由伺服放大器、电液伺服阀、液压马达、测速电动机等组成。
测速电机轴与负载机轴相联,用于检测负载轴的速度,检测到的速度信号与指令信号差(误差信号)经伺服放大器进行功率放大,产生的电流用来控制电液伺服阀的阀芯位置,电液伺服阀输出压力油驱动液压马达及负载旋转。
根据所建立的物理模型,可以建立相对应的闭环控制系统原理的方框图:
图2 阀控马达速度控制系统方框图
3.系统各环节数学模型
3.1伺服放大器
伺服放大器输出电流ΔI与输入电压Ue近似成正比,其传递函数可用伺服放大器增益Ka表示:
(1)
但通常的速度控制系统采用积分放大器,对原系统加以校正才能稳定工作。
校正后的积分放大器增益Ka表示为:
(2)
式中:Ue为积分放大器额定电压,V;
Ka为积分放大器增益,A/V。
3.2伺服阀
伺服阀的流量增益为:
(3) 式中:为伺服阀流量增益,m
3/(s*A);
为伺服阀空载流量,m3/s;
为伺服阀额定电流,A。
伺服阀传递函数为:
(4)
式中:Q 0为伺服阀流量,m3/s;
ΔI为电流增量,A;
为伺服阀固有频率,rad/s;
为伺服阀的阻尼比。
3.3液压马达
负载总惯量为:
(5)
式中:为负载总惯量,kg*m2;
为液压马达惯量,kg*m2;
为负载的惯量,kg*m2。
因而求得液压的固有频率:
(6)
式中:为液压固有频率,rad/s;
为液压马达排量,m3/rad;
为液压油的有效体积弹性模量,Pa;
为总压缩体积,m3。
及阻尼比:
(7)
式中:为液压马达的阻尼比;
为阀的流量压力系数,m3/ (s·Pa)。
最终可以求得液压马达的传递函数:
(8)
式中:是液压马达负载的传递函数;
为液压马达的的增益,m3/ S·A。
3.4测速机
速度传感器(测速机)的数学模型为:
(9)
式中:为传感器电压,V;
为速度传感器增益,(Vs/rad)。
4.仿真系统动态方块图
根据所给出的系统原理方框图以及所求得的各环节数学模型,可以得出仿真系统经过积分环节校正后的系统动态方块图如下:
图3 积分环节校正后的速度控制系统方块图
5.问题描述
现有一阀控液压伺服速度控制系统,其原理图如图1,考虑伺服阀的动态,伺服参数为:=3060e-6,=600,=0.5,液压缸的参数为=1.25e6,=388,=0.94,放大器增益=0.05,试用simulink对该系统进行动态分析,并比较校正前后系统稳定性,分析校正前后的变化。
6.解题步骤
(1)根据给定的参数,利用simulink对该系统进行未加积分环节校正的系统建模,如下图所示:
图4 未校正系统的simulink模型
给上述模型中的变量赋值,编写matlab程序,之后对上述闭环模型进行仿真,结果出错,得不出闭环仿真结果,说明闭环系统不稳定。
(2)绘制未校正系统的伯德图。
Matlab程序如下:
clear all;clc;
Wsv=600;zuni1=0.5;Ksv=3060e-6;Ka=0.05;i=3;Kf=0.175;
Wh=388;zuni2=0.94;Kh=1.25e6;
sys=tf(Ka*Ksv*i*Kf*Kh,conv([1/Wsv^2 2*zuni1/Wsv 1],[1/Wh^2
2*zuni2/Wh 1]));
figure(1);margin(sys);
grid;
figure(2);subplot(121);
pzmap(sys);
grid on;
subplot(122);
nyquist(sys);
figure(3);subplot(121);
impulse(feedback(sys,Kf*i));
grid;
subplot(122);
step(feedback(sys,Kf*i));
运行上述程序后,得到未校正开环系统的奈氏图:
图5 未校正系统开环的奈氏图
由上图看出开环传递函数右极点个数为0,而奈氏曲线绕(-1,0)点圈数为2,两者不等,所以系统闭环不稳定;
同样的,从下图的伯德图亦可看出:
图6 未校正系统的伯德图
从图6可看出系统的稳定裕量(Gm=-32.6dB,Pm=-128°)为负,可以断定其闭环系统是不稳定的。
及时K0值调很低,对数幅频特性曲线也是以-80dB/dec 或-40dB/dec的斜率穿过零分贝线,系统的相位裕量和幅值裕量都趋于负值,使系统不稳定。
为了使系统有一定的稳定裕度量,必须加校正环节。
在速度控制系统中,可以用运算放大器组成积分放大器代替原来的放大器。
积分放大器如
下图所示:
图7 积分放大器
其传递函数为:
其中,Ka=0.05。
加了校正之后的系统仿真方框图如下:
图8 校正后速度控制系统的仿真框图
运行该模型后得到系统的阶跃响应曲线如图9所示。
从图上可以看出该闭环系统趋于稳定,峰值2.17,峰值上升时间0.0258s,稳态值1.9,调整时间ts约为0.0628s,超调量为14%。
图9 校正后系统的阶跃响应曲线
(3)由上图可以看出校正后的速度控制系统是稳定的,那么在分析其伯德图和奈氏图判断系统是否稳定。
运行matlab程序如下:
clear all;clc;
Wsv=600;zuni1=0.5;Ksv=3060e-6;Ka=0.05;i=3;Kf=0.175;
Wh=388;zuni2=0.94;Kh=1.25e6;
sys=tf(Ka*Ksv*Kh,conv([1/Wsv^2 2*zuni1/Wsv 1 0],[1/Wh^2 2*zuni2/Wh 1]));
figure(1);margin(sys);
grid;
figure(2);subplot(121);
pzmap(sys);
grid on;
subplot(122);
nyquist(sys);
figure(3);subplot(121);
impulse(feedback(sys,Kf*i));
grid;
subplot(122);
step(feedback(sys,Kf*i));
运行后,首先分析伯德图:
图10 校正后系统伯德图
从伯德图看出校正后的系统穿越频率下降到247 rad/s,Gm=4.09dB,Pm=26.7deg,可看出系统有正的相角裕度,因而该系统闭环是稳定的。
其次再看奈氏图:
图11 校正后系统的奈氏图
从校正后的奈氏图可以看出,开环函数的右极点数为0,正好奈氏曲线包围(-1,0)点圈数也是0,因而同样可以确定校正后的闭环系统是稳定的。
同时可以看出,当输入Ur=1V时,系统所对应的的希望输出为:
1.9rad/s
7.结论
建立的数学模型较好的反映了系统的实际情况,可以根据仿真模型来分析电液速度控制系统的运行情况以及稳定性。
经过积分放大器校正后的液压伺服控制系统的穿越频率比未校正回路的穿越频率低得多。
但是为了保证系统
的稳定性,不得不牺牲相应速度和精度。